Geum.ru

Одномерные деформации нелинейно упругих микрополярных тел

Вид материалаДокументы

Содержание


1. Уравнения равновесия в ортогональных криволинейных координатах.
2. Частные решения, приводящие к одномерным краевым задачам.
Подобный материал:
ОДНОМЕРНЫЕ ДЕФОРМАЦИИ НЕЛИНЕЙНО УПРУГИХ МИКРОПОЛЯРНЫХ ТЕЛ

Л. М. Зубов

Южный федеральный университет, Ростов-на-Дону, Россия

Определен класс конечных деформаций упругой микрополярной среды, при которых система уравнений равновесия сводится к обыкновенным дифференциальным уравнениям. Найденные семейства деформаций описывают, в частности, изгиб и кручение микрополярных тел различной геометрической формы. Для физически линейного континуума Коссера получен ряд точных решений о больших деформациях трехмерных тел.

1. Уравнения равновесия в ортогональных криволинейных координатах. Микрополярная среда (или континуум Коссера) – это материальное тело, каждая частица которого имеет шесть степеней свободы абсолютно твердого тела, то есть характеризуется положением в пространстве и ориентацией. Взаимодействие частей микрополярного тела осуществляется не только обычными (силовыми), но и моментными напряжениями. Удельная потенциальная энергия деформации континуума Коссера задается как функция двух тензорных аргументов [1, 2]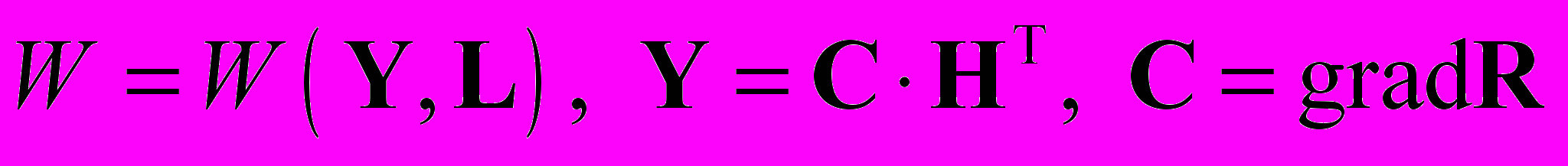

, (1.1)

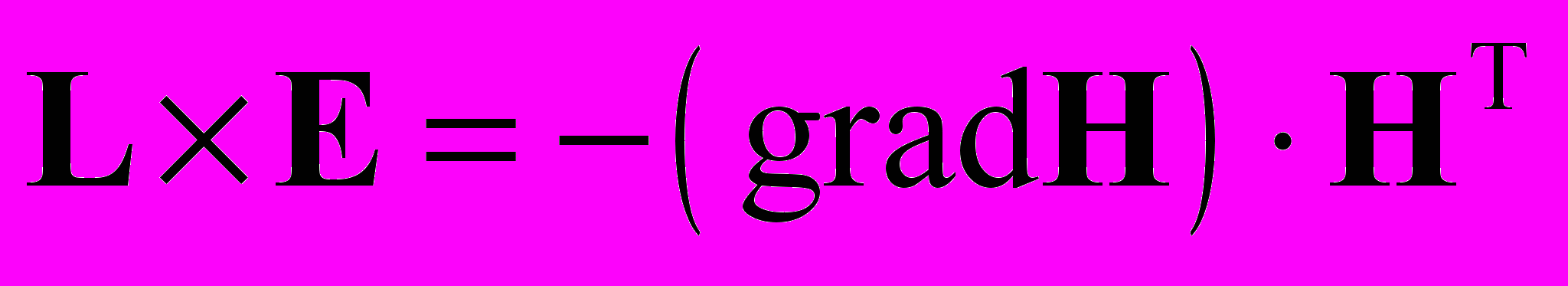. (1.2)

Здесь – мера деформации, – тензор изгибной деформации, – градиент деформации, – собственно ортогональный тензор микроповорота, – единичный тензор, – вектор положения частиц деформированного тела, 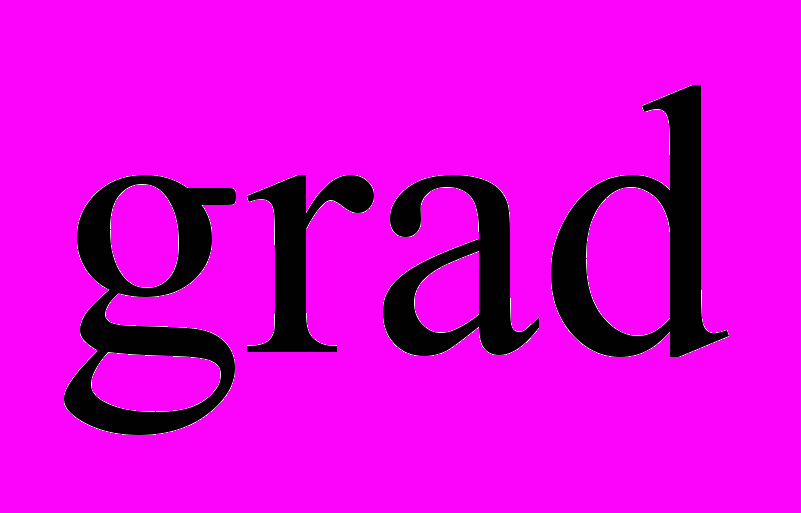– оператор градиента в лагранжевых координатах.

Рассматривая задачу статики микрополярного тела, уравнения равновесия запишем в виде [2]

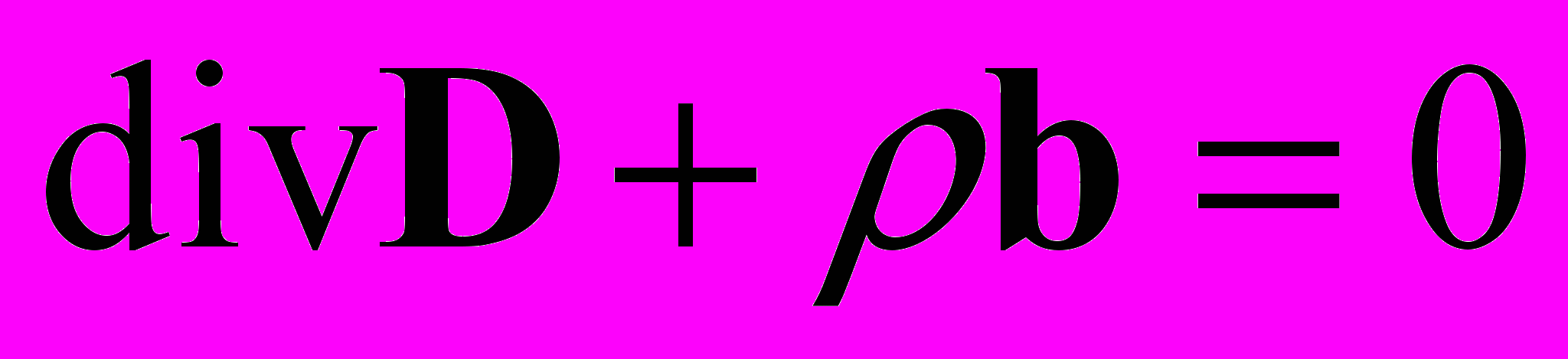, (1.3)

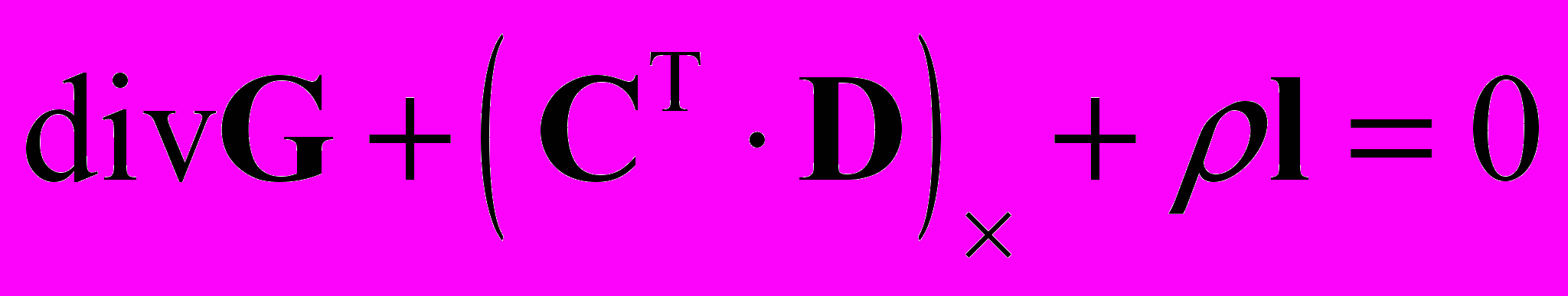, (1.4)

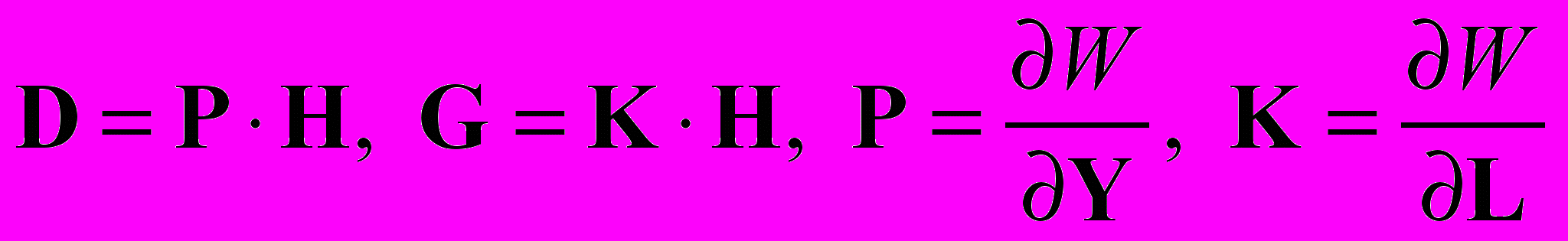, (1.5)

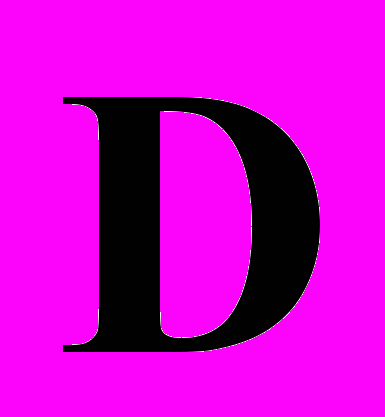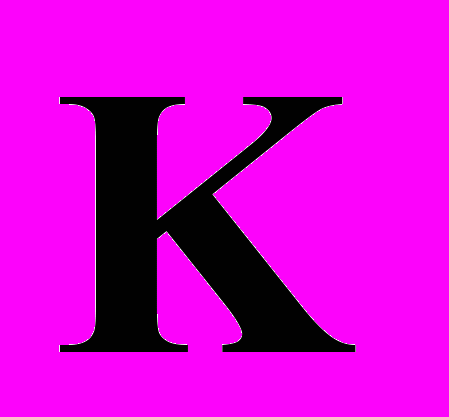В (1.3)–(1.5) и – тензоры напряжений и моментных напряжений типа Пиолы, и – тензоры напряжений и моментных напряжений типа Кирхгофа, 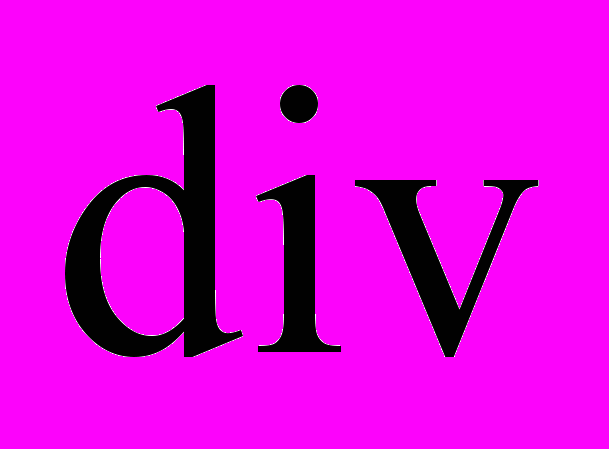– оператор дивергенции в лагранжевых координатах, 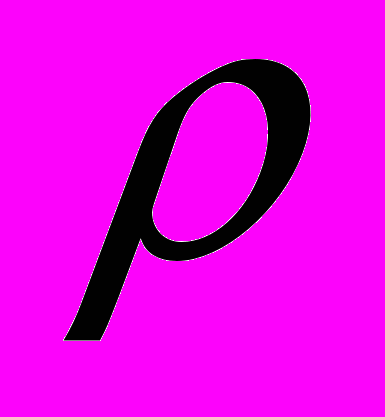– плотность материала в отсчетной конфигурации, – массовая сила, – интенсивность массовой моментной нагрузки, индекс «» в (1.4) означает векторный инвариант тензора второго ранга [3].

Пусть 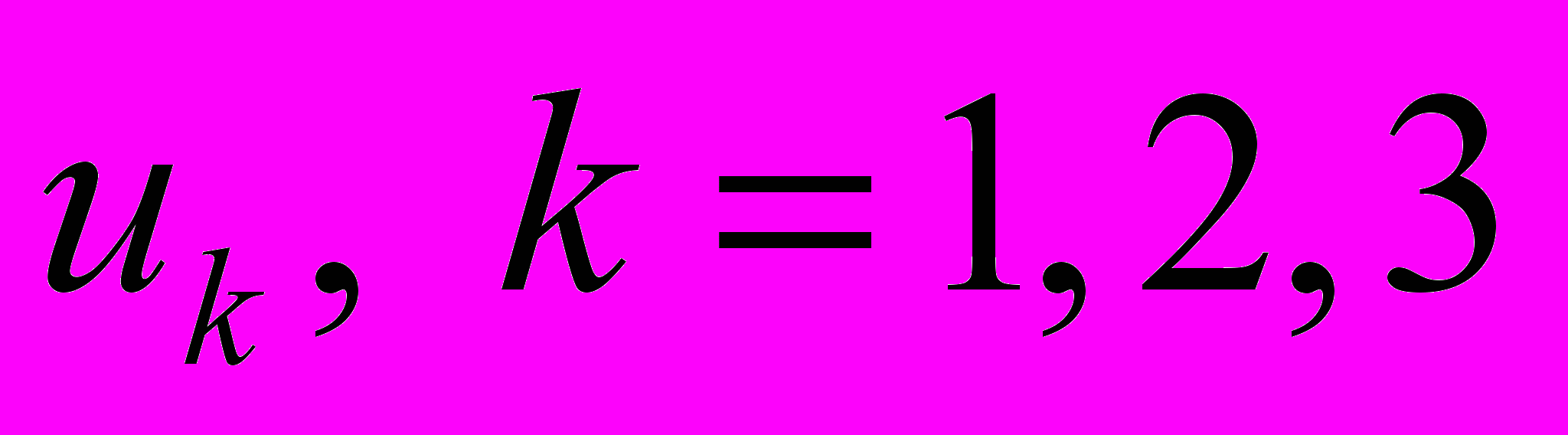– некоторые ортогональные криволинейные координаты в отсчетной конфигурации материального тела (лагранжевы координаты), – какие-либо ортогональные криволинейные координаты в пространстве (эйлеровы координаты). Коэффициенты Ляме этих координат обозначим соответственно 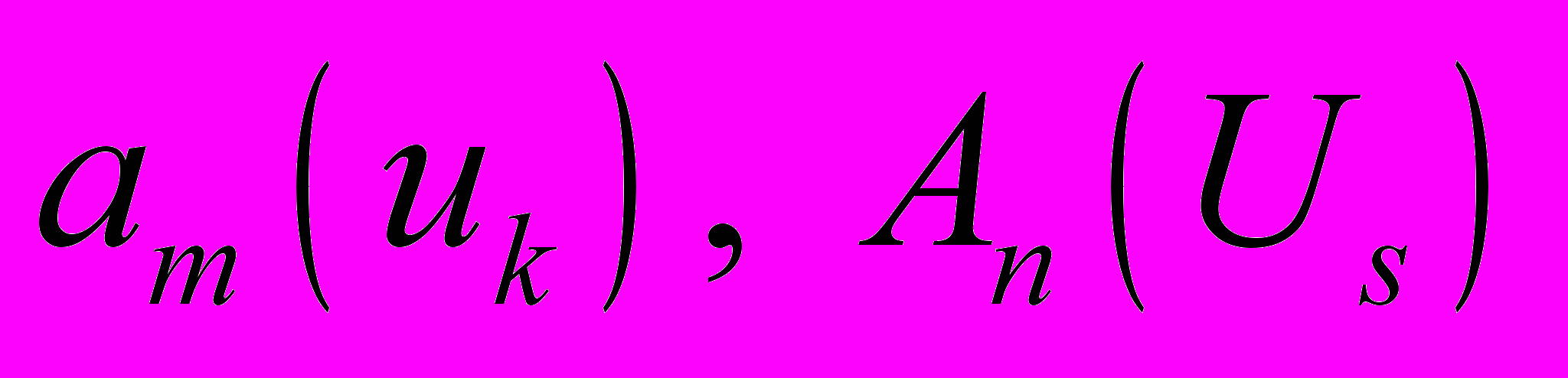, а ортонормированные векторные базисы, ассоциированные с указанными координатами, обозначим 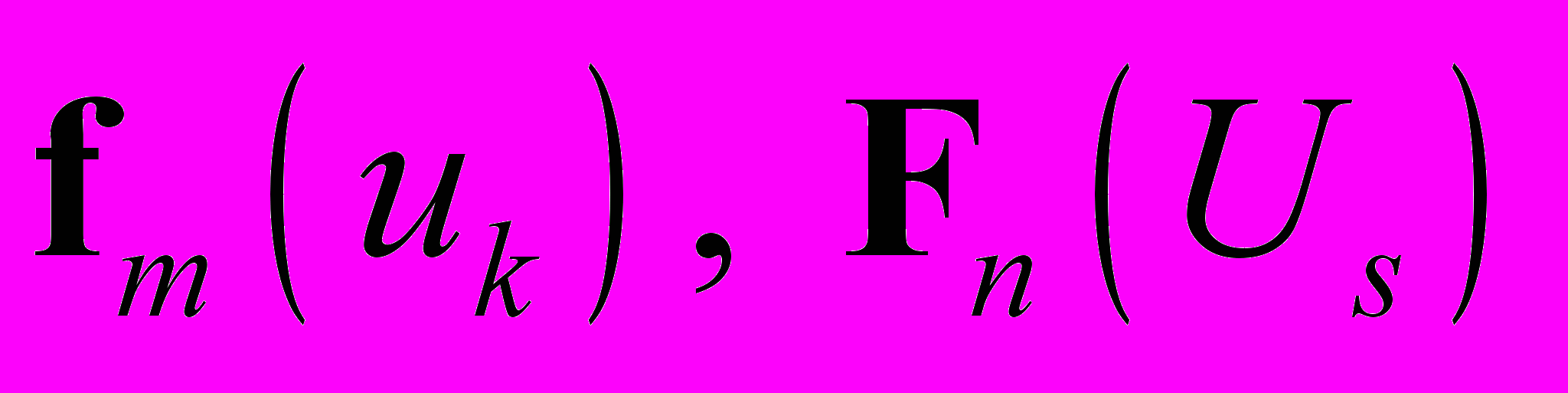. Предполагается, что векторные базисы 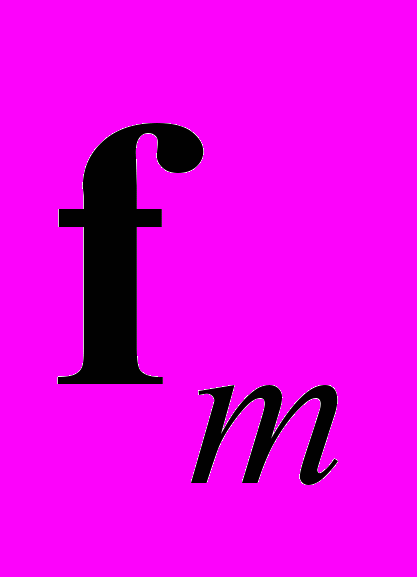и 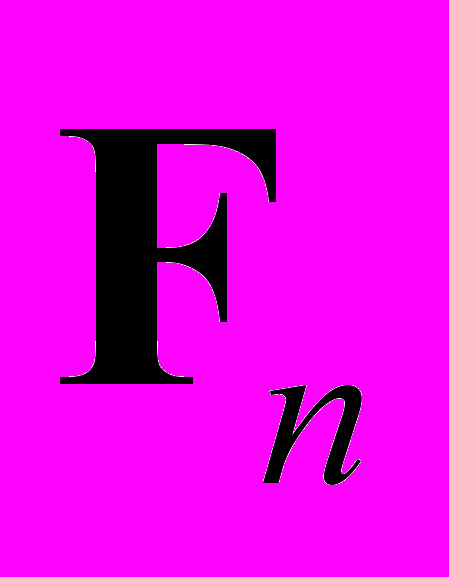имеют одноименную ориентацию. Будем использовать следующие разложения введенных выше векторов и тензоров

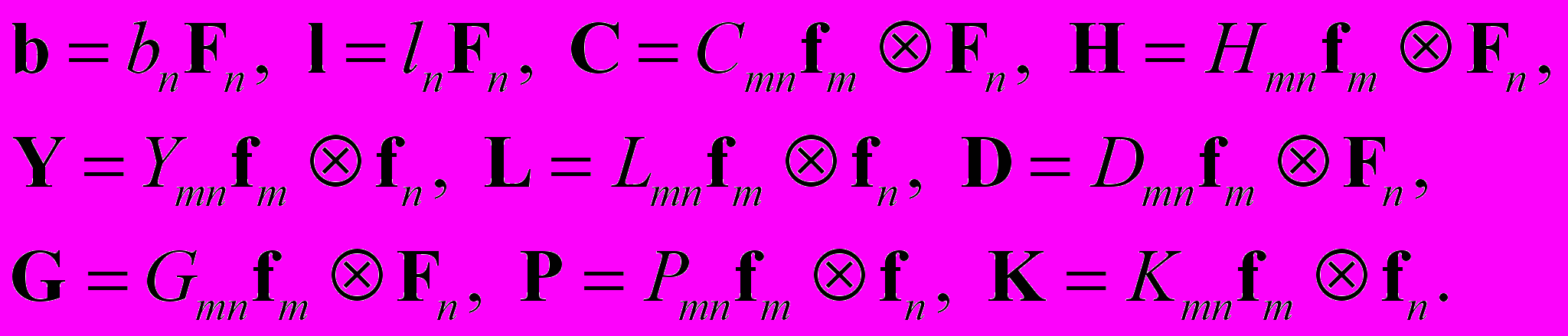(1.6)

Из (1.1), (1.5), (1.6) следуют формулы

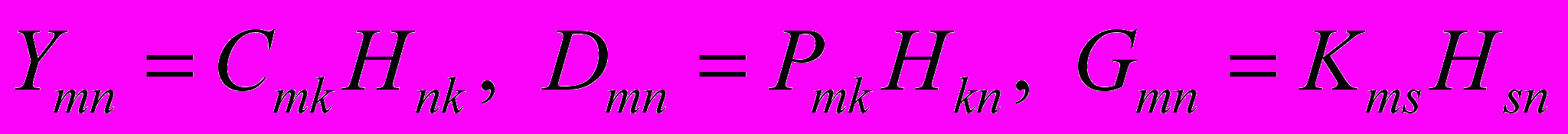. (1.7)

Пусть деформация среды Коссера задана при помощи функций

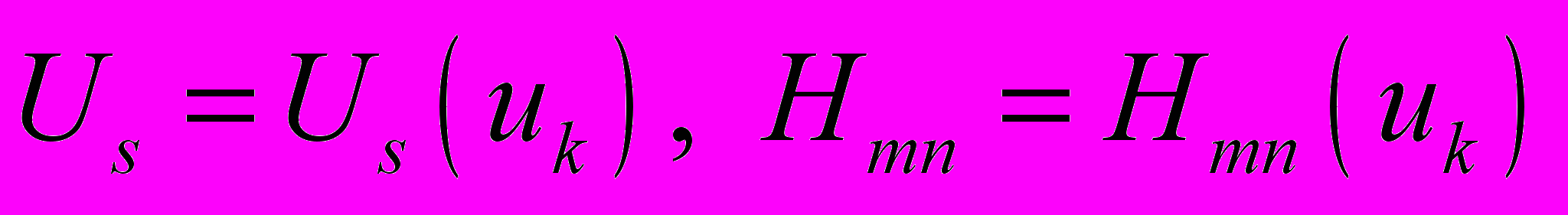. (1.8)

Справедливо представление

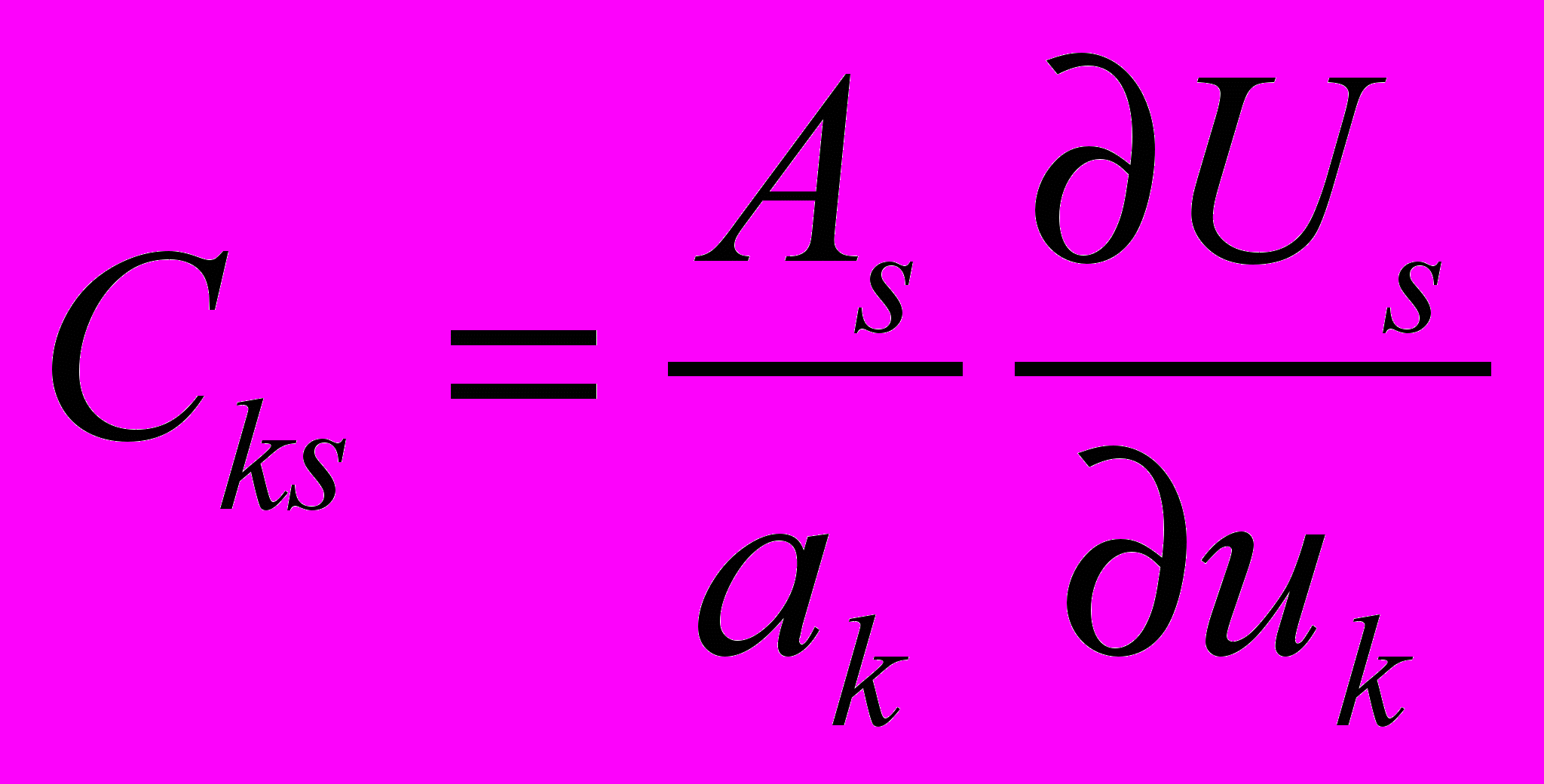(не суммировать по 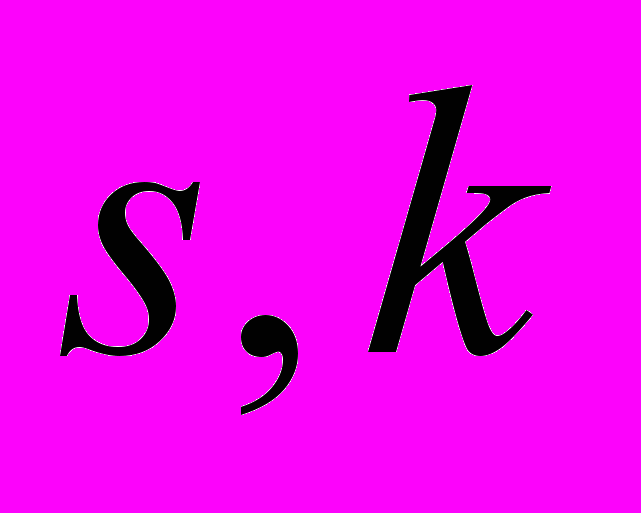). (1.9)

Уравнения равновесия (1.3), (1.4) примут вид

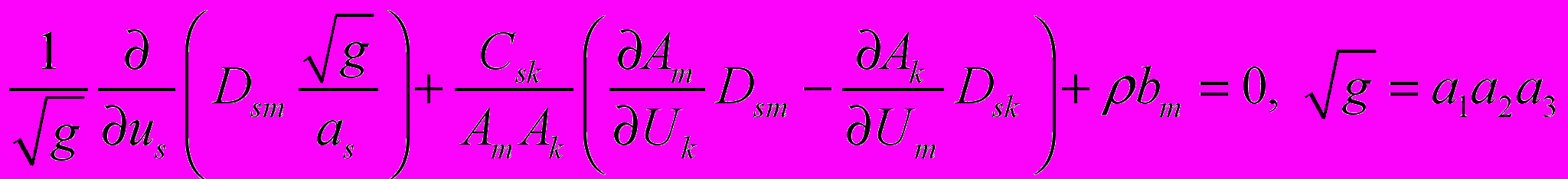, (1.10)

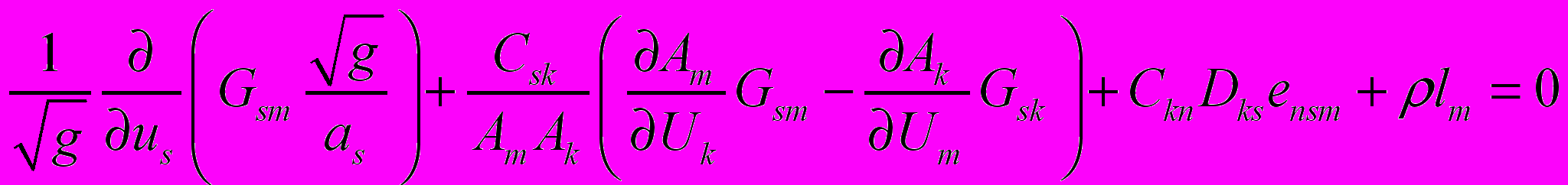. (1.11)

В (1.10), (1.11) – символ Леви-Чивиты и подразумевается суммирование по 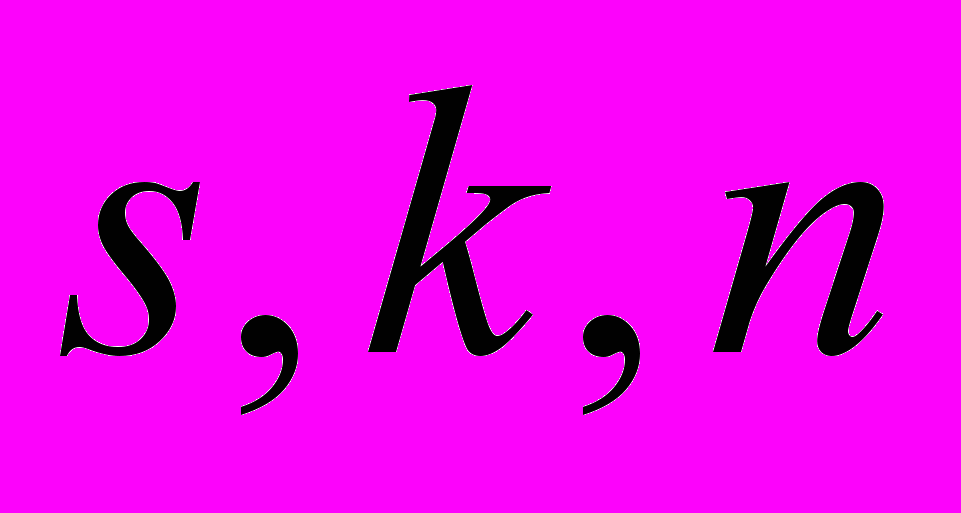от 1 до 3. По индексу 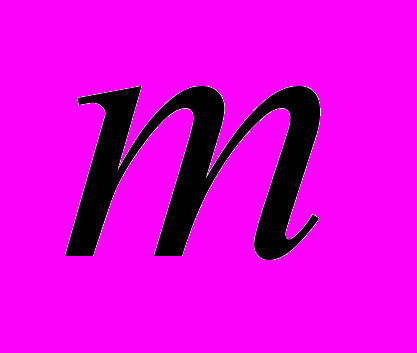суммирования нет.

2. Частные решения, приводящие к одномерным краевым задачам. В дальнейшем предполагается, что массовыми силами и массовыми моментами можно пренебречь: 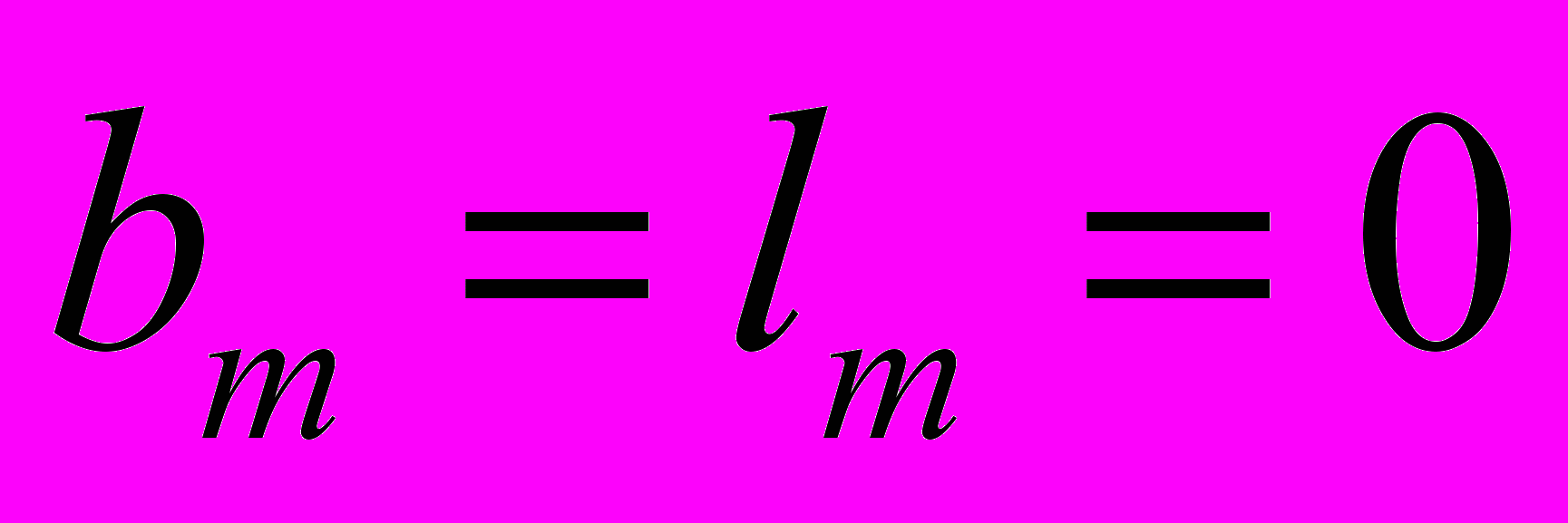. Будем использовать такие координатные системы 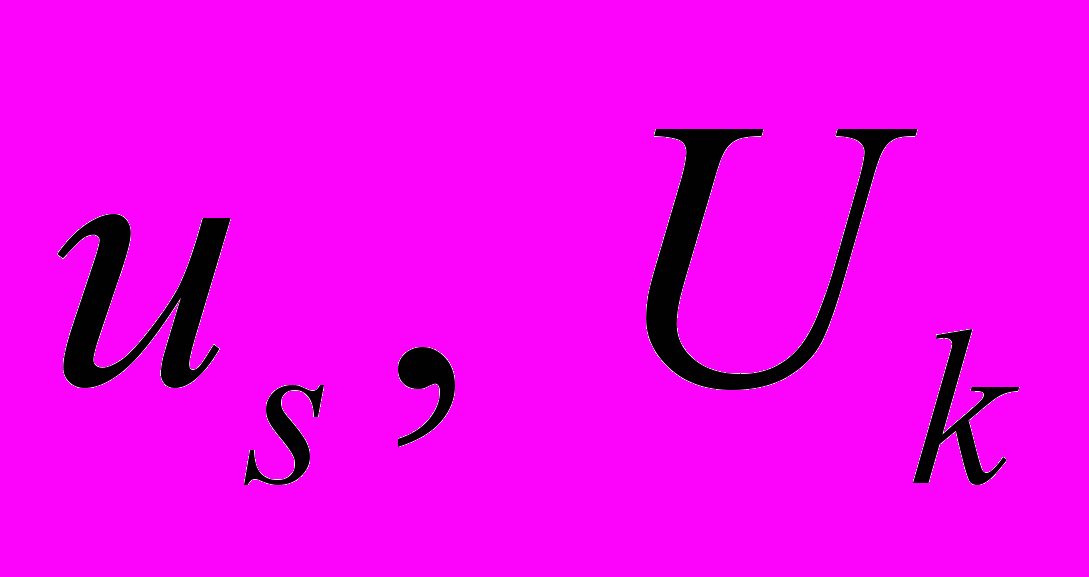, коэффициенты Ляме которых зависят лишь от одной координаты: 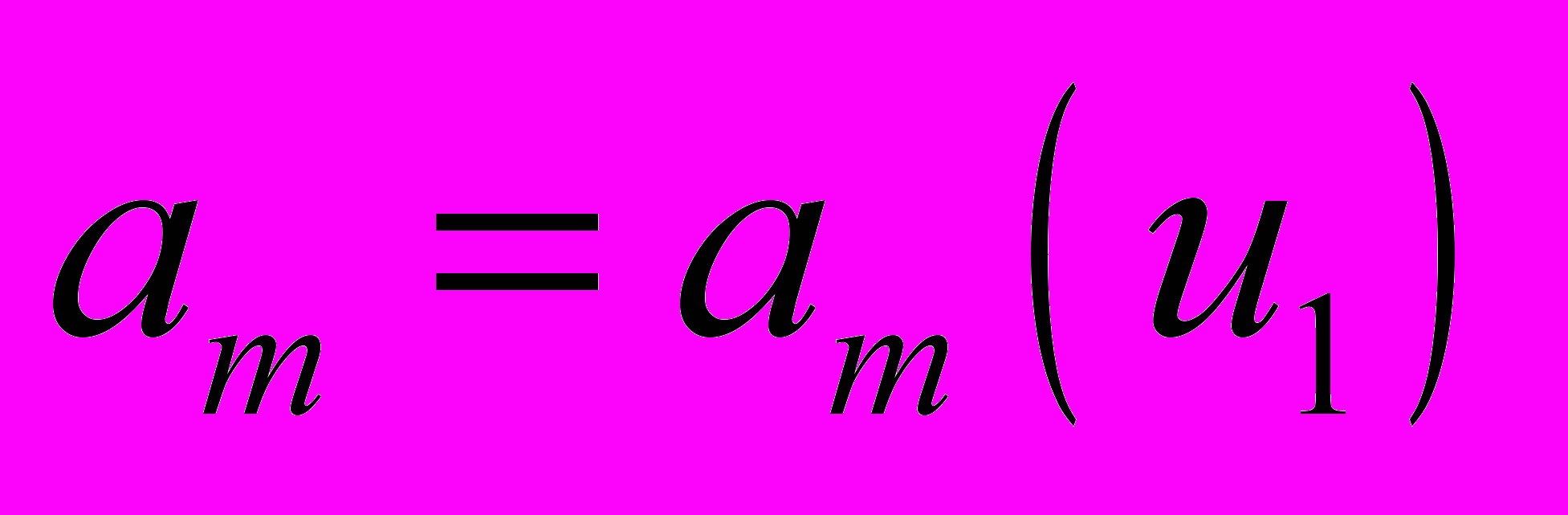, 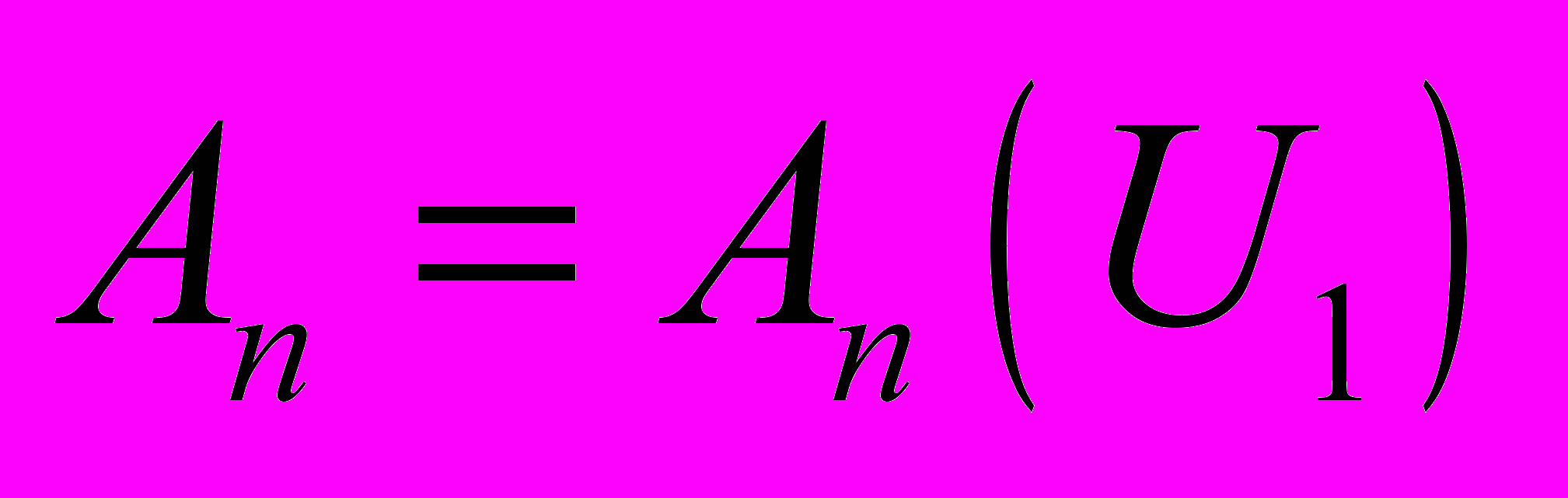. Этому условию удовлетворяют декартовы и круговые цилиндрические координаты. Рассмотрим следующие семейства конечных деформаций континуума Коссера

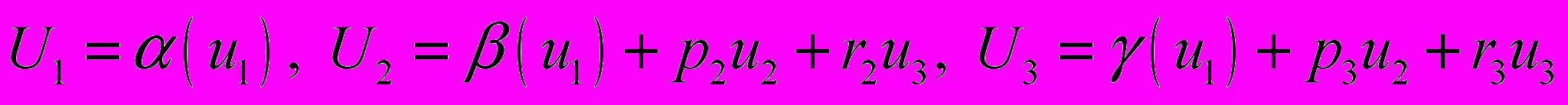, (2.1)

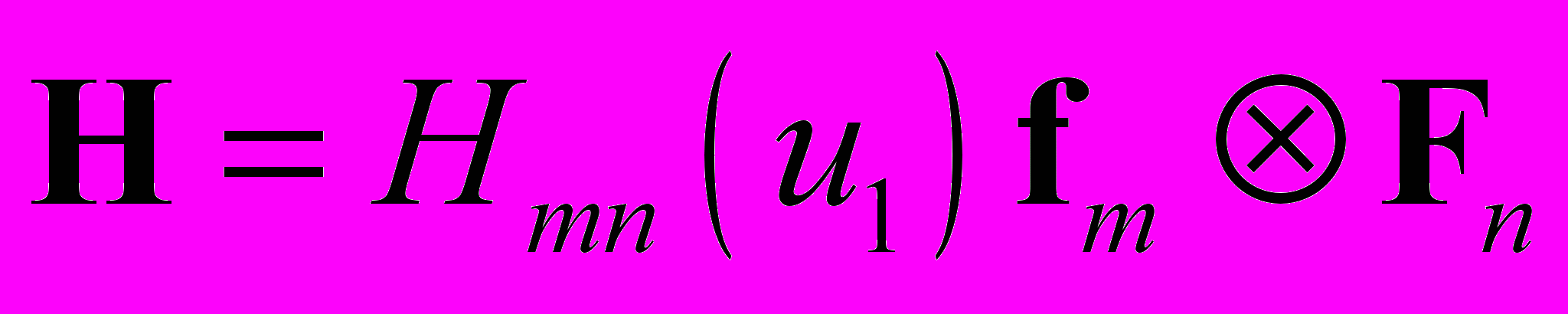. (2.2)

Здесь 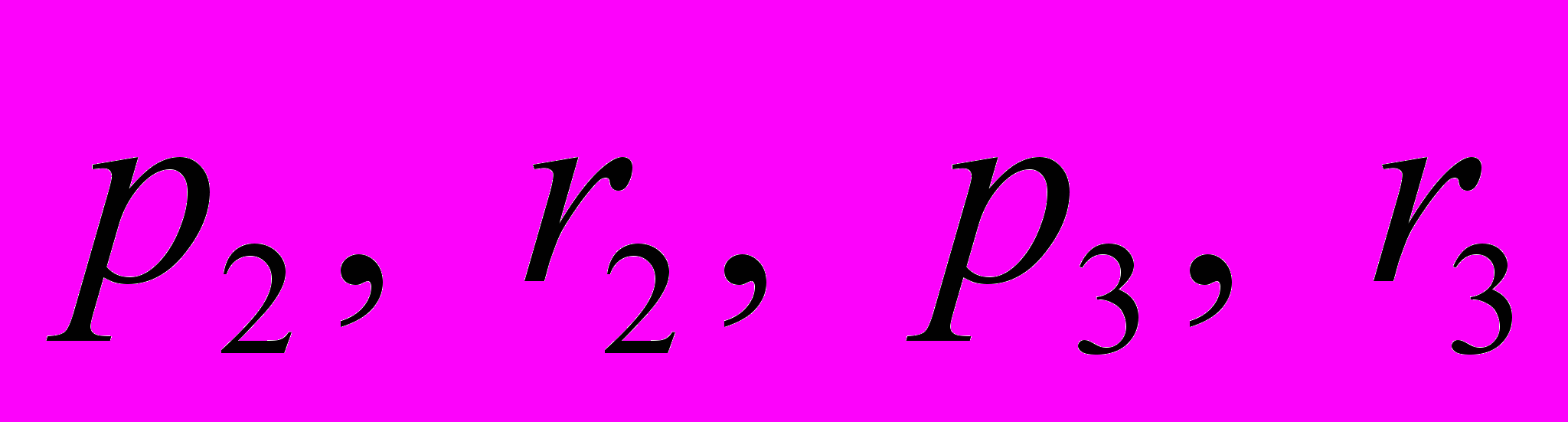– постоянные, 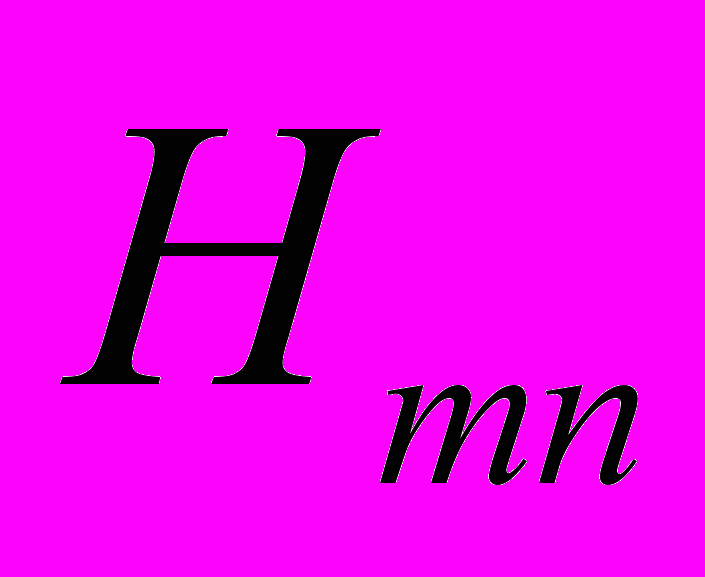– элементы собственно ортогональной матрицы, общее представление которой можно взять в виде ( 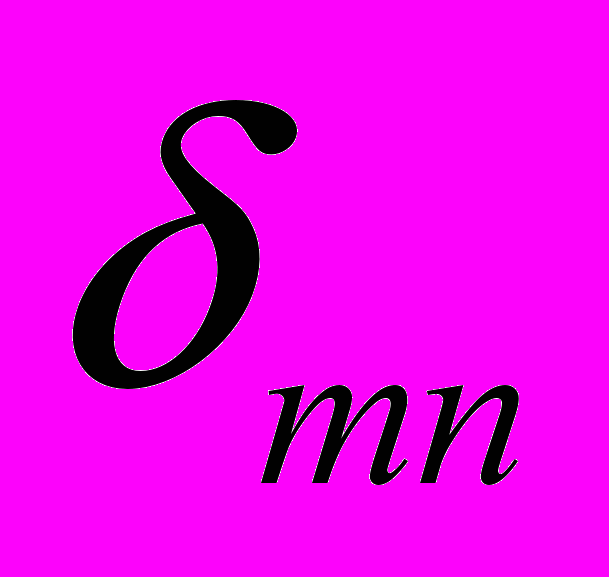– символ Кронекера)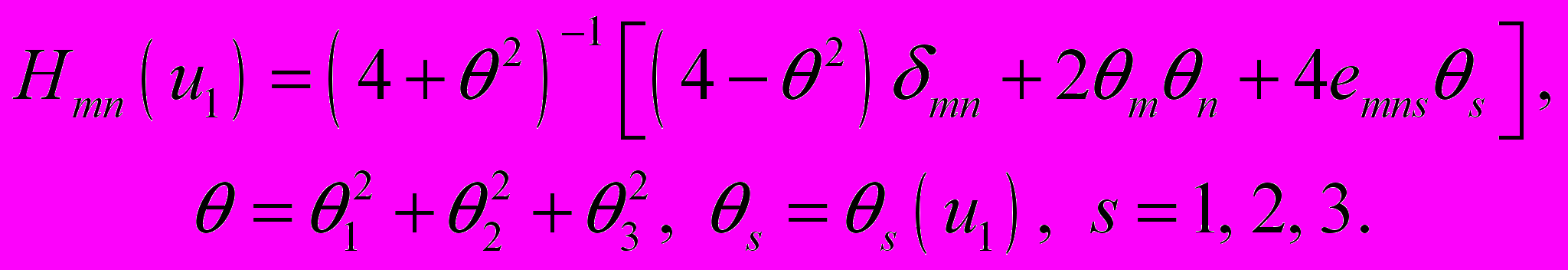



Из соотношений (1.1), (1.6), (1.7) видно, что при деформациях вида (2.1), (2.2) величины 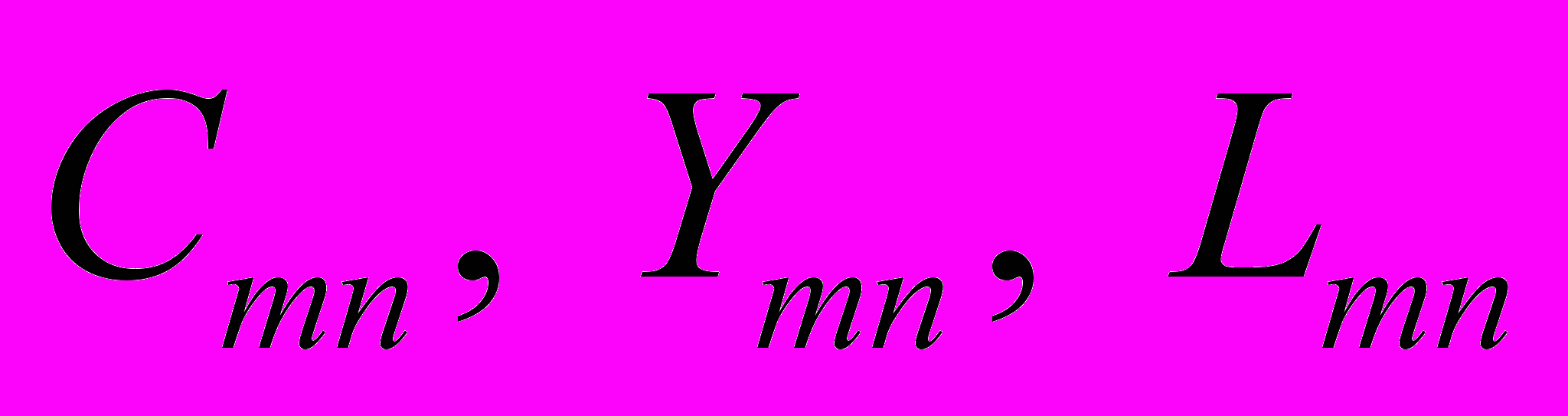зависят только от координаты 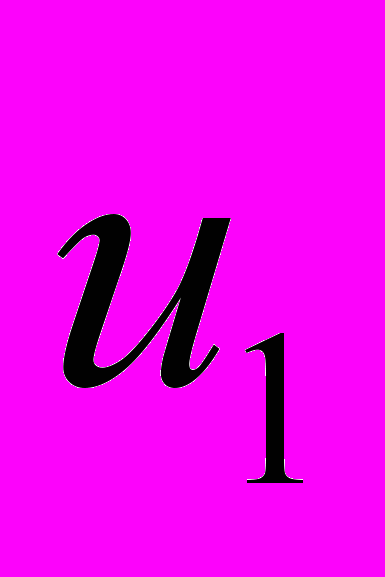. Если микрополярная среда однородна и изотропна, то доказывается, что компоненты напряжений 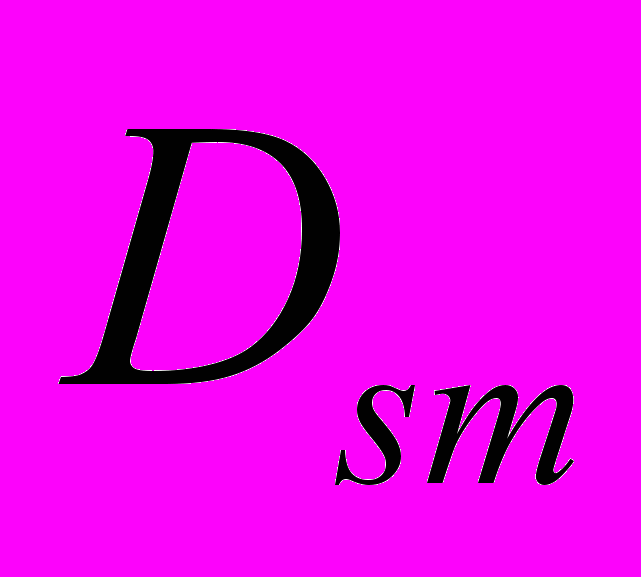и моментных напряжений 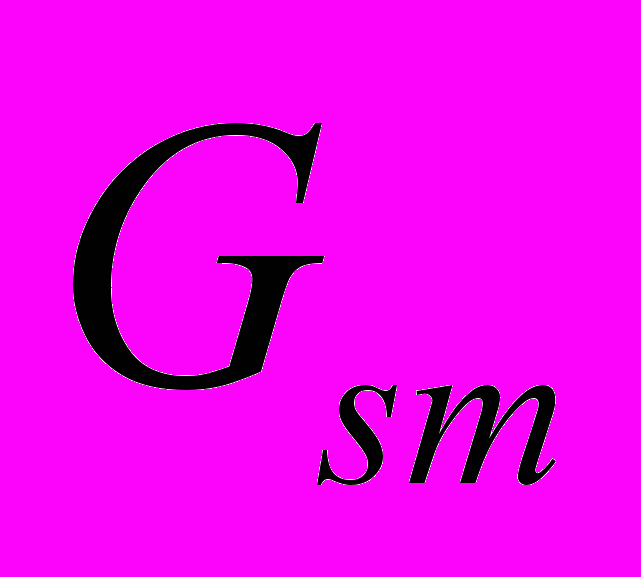также не зависят от координат 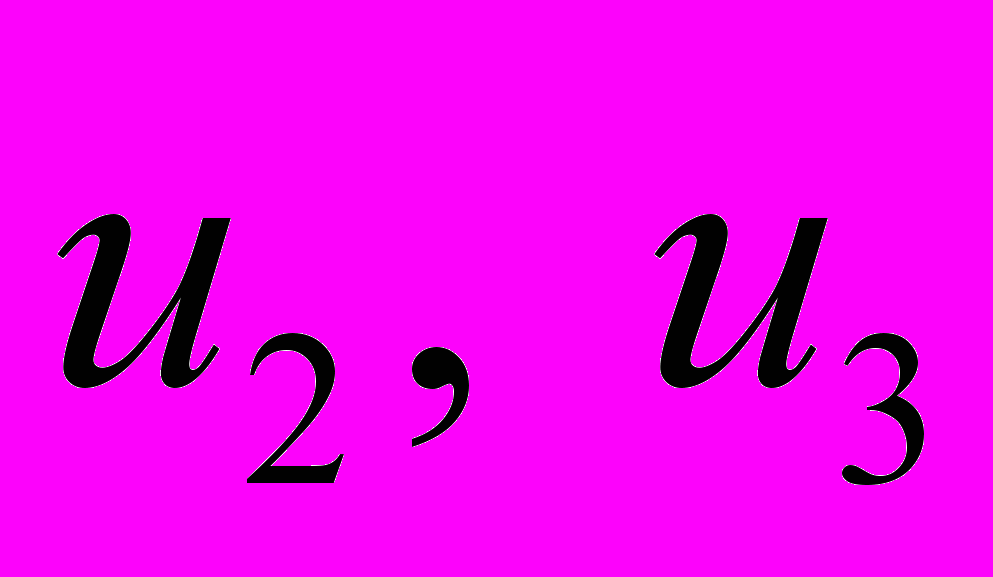. Отсюда вытекает, что на семействах деформаций (2.1), (2.2) система уравнений равновесия (1.10), (1.11) сводится к системе шести обыкновенных дифференциальных уравнений для шести функций одной переменной: 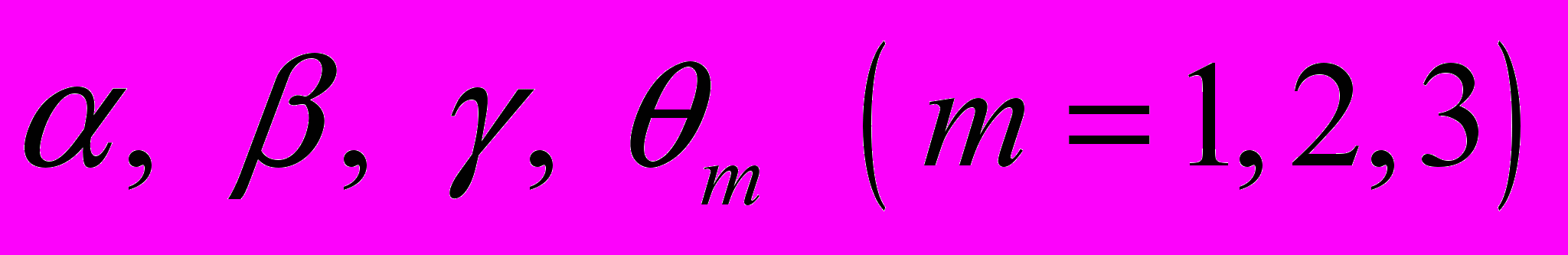. В силу указанного свойства данные деформации называются одномерными. В качестве граничных условий при одномерных деформациях на двух поверхностях 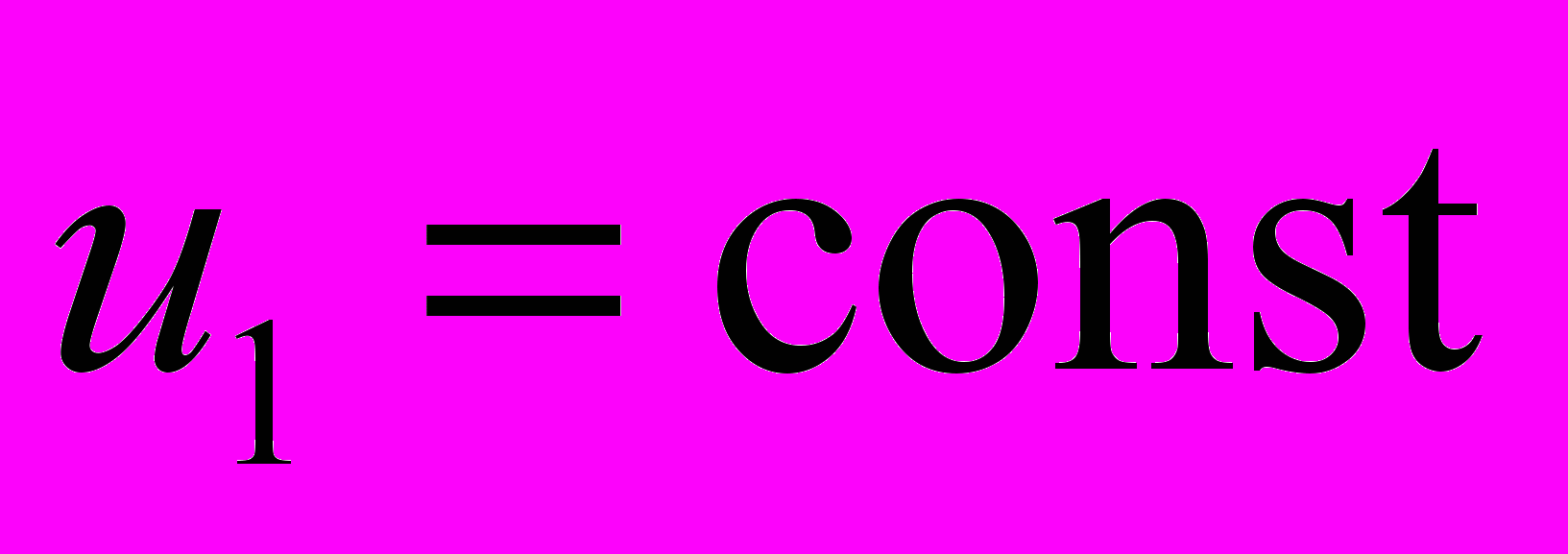могут быть заданы постоянные составляющие напряжений и моментных напряжений 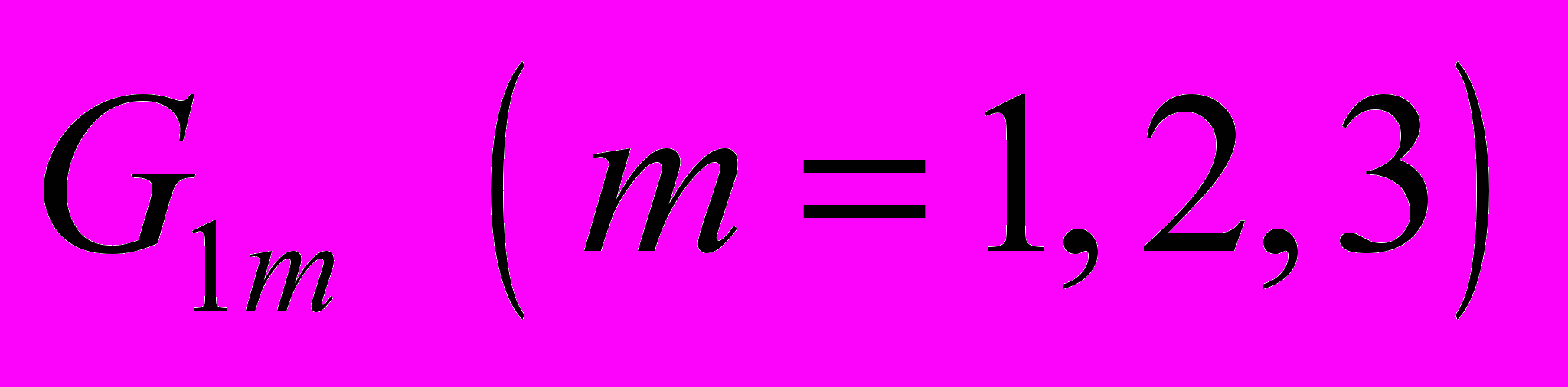. Краевые условия на остальной части поверхности тела могут быть выполнены лишь в некотором интегральном (осредненном) смысле за счет подбора постоянных .

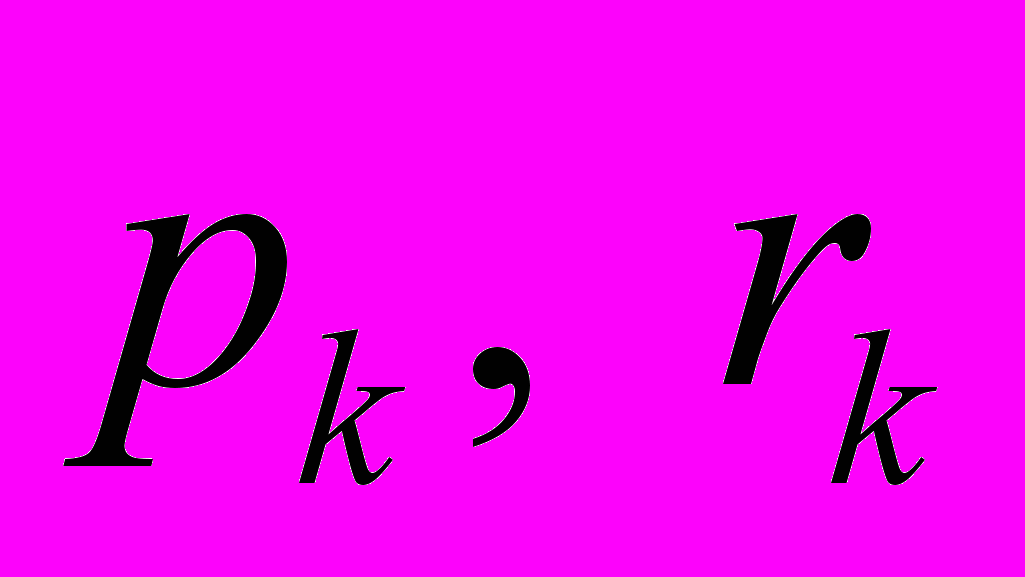В частном случае, когда координаты 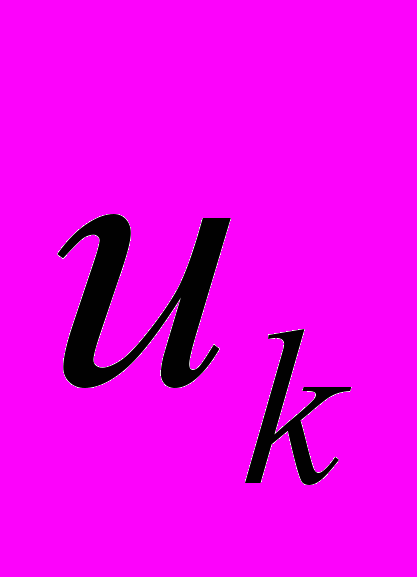– декартовы, а координаты 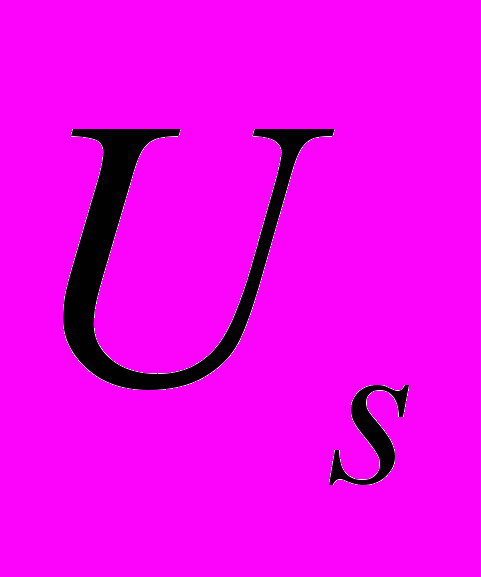– цилиндрические, формулы (2.1), (2.2) описывают изгиб прямоугольной плиты, при котором она превращается в сектор полого кругового цилиндра или замкнутый цилиндр (трубу). Указанный цилиндрический сектор подвергается затем кручению, растяжению и осевому сдвигу.

В классе одномерных деформаций (2.1), (2.2) существуют такие, для которых часть из уравнений равновесия (1.10), (1.11) удовлетворяется тождественно. Например, если в (2.1) положить 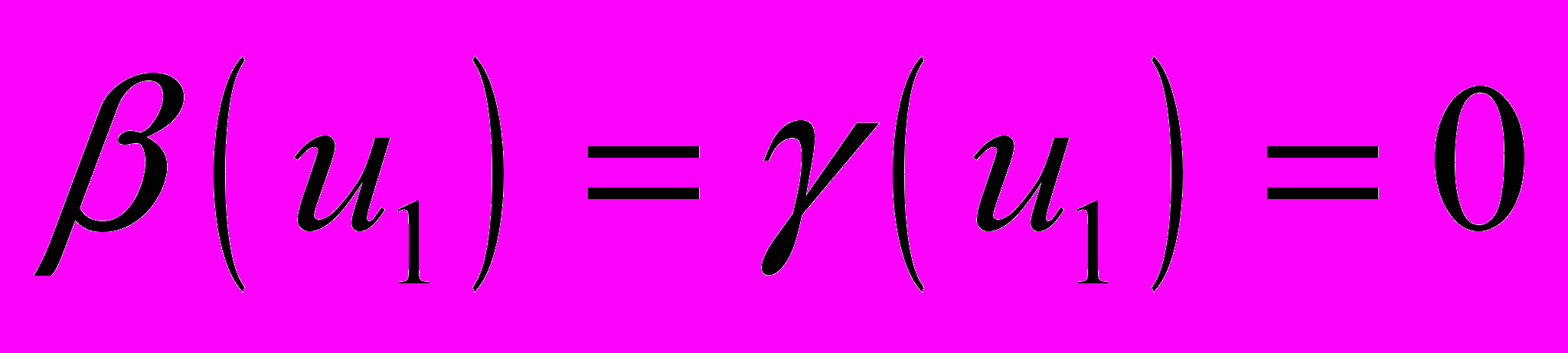, а тензор микроповорота взять в виде

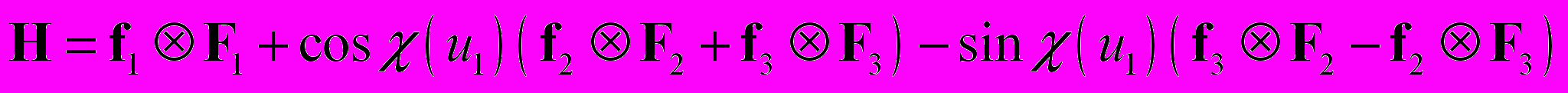, (2.3)

то в случае изотропного материала тождественно удовлетворяются уравнения (1.10) и (1.11) пр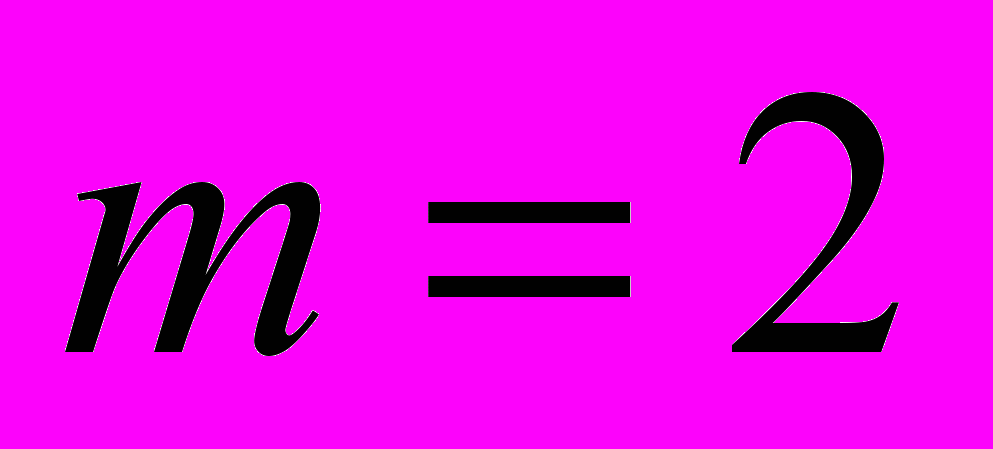и и 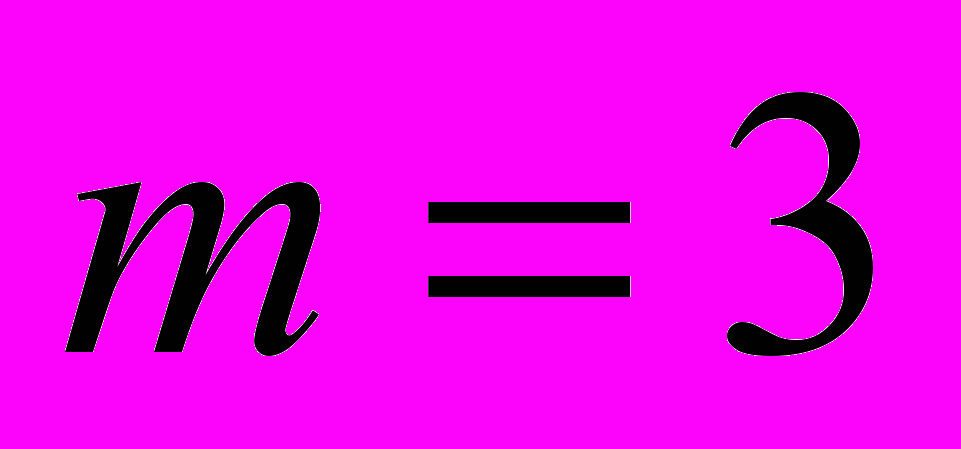, и задача сводится к двум обыкновенным уравнениям относительно функци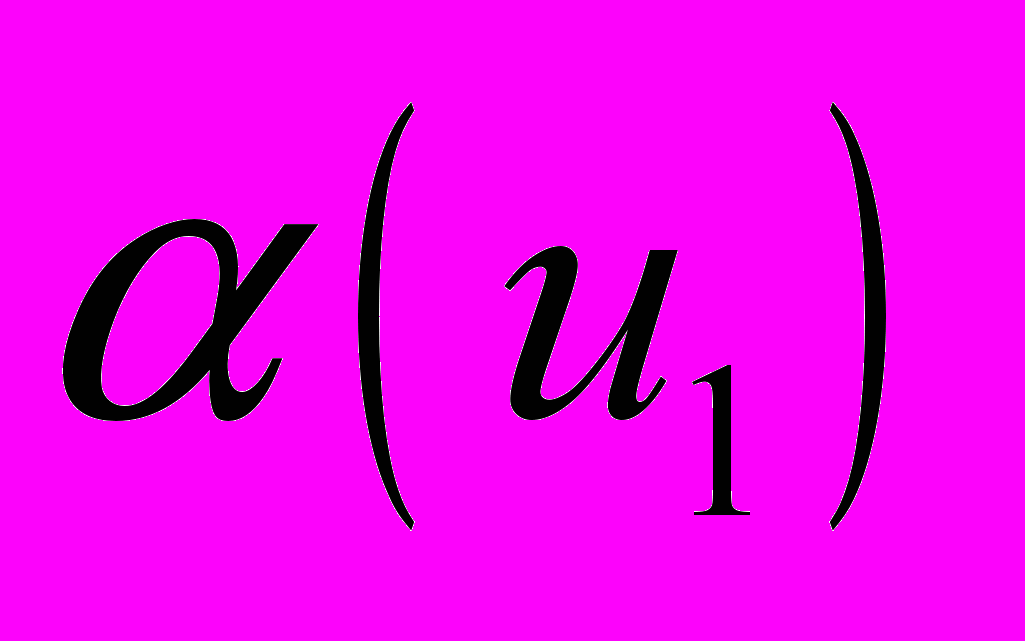й и 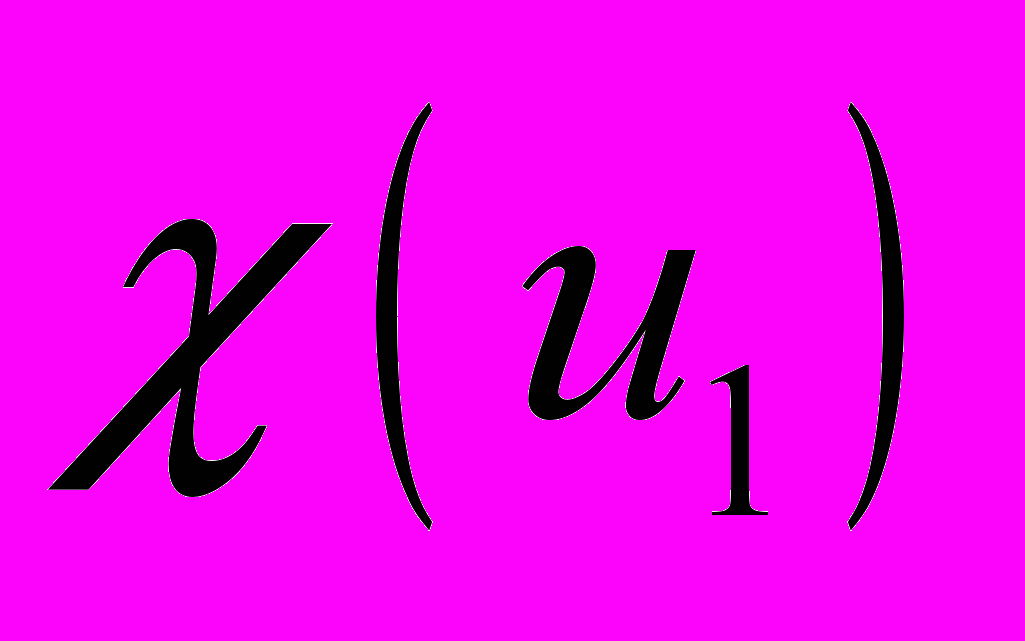. Отметим наиболее важные случаи деформации, которые можно описать соотношениями (2.1) при 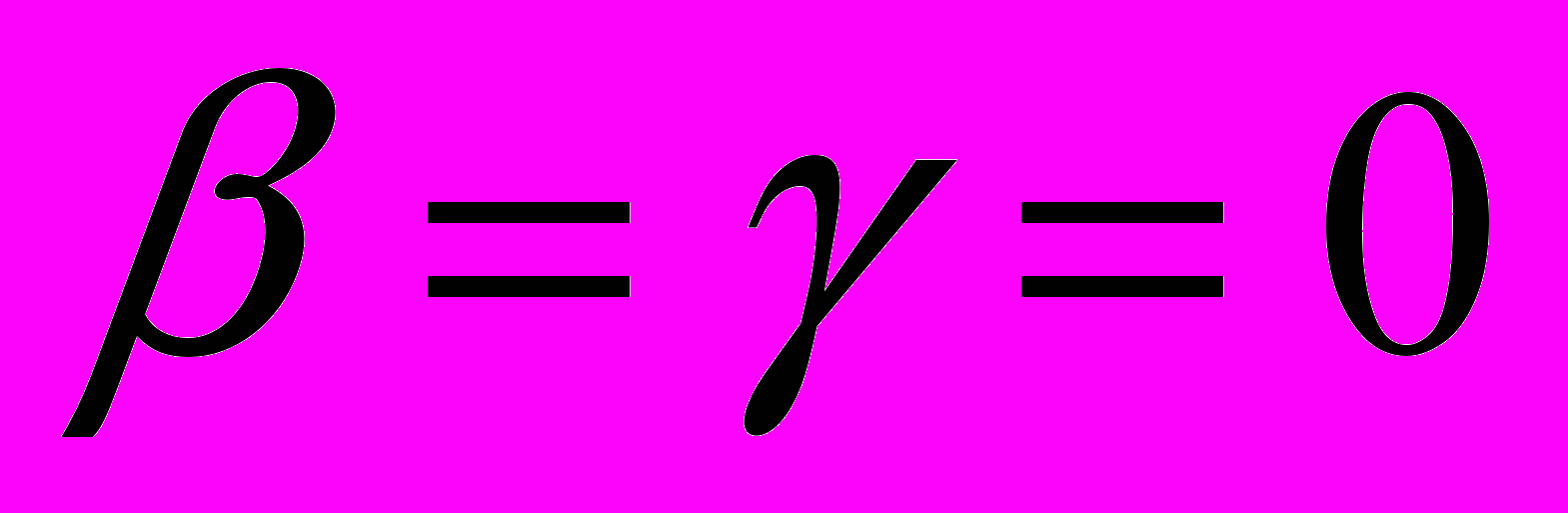и (2.3): изгиб прямоугольного параллелепипеда, цилиндрический изгиб или выпрямление сектора полого кругового цилиндра, раздувание, растяжение вдоль оси и кручение полого кругового цилиндра, образование винтовой дислокации в полом цилиндре, выворачивание круглой трубы. В задачах о круговом цилиндре указанное семейство деформаций содержит достаточный произвол для удовлетворения условий на торцах в смысле Сен-Венана.

Простейшей моделью изотропного сжимаемого микрополярного тела является физически линейный материал [2], для которого упругий потенциал 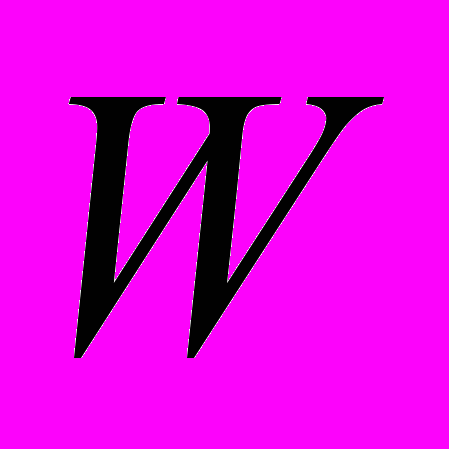– квадратичная форма тензоров 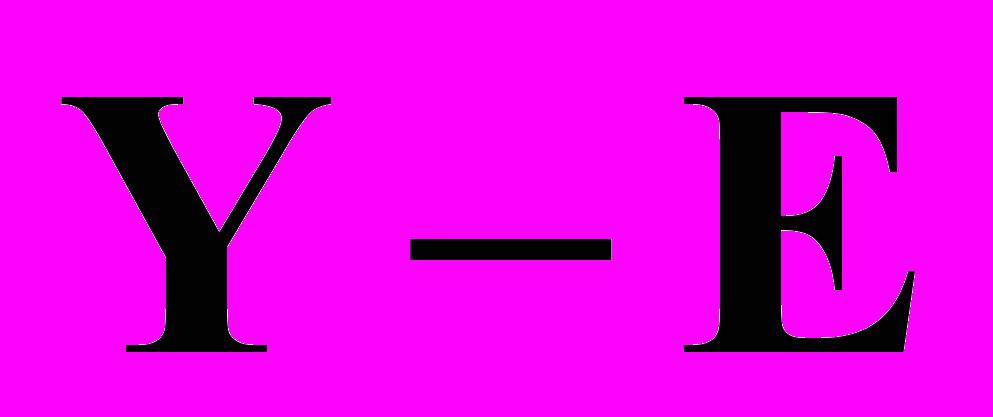и

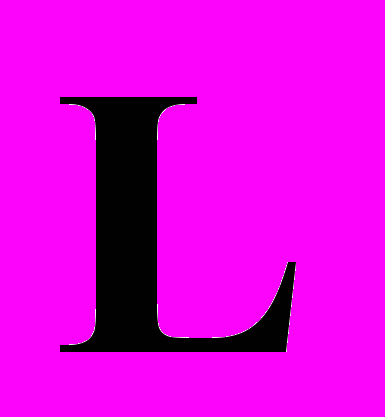
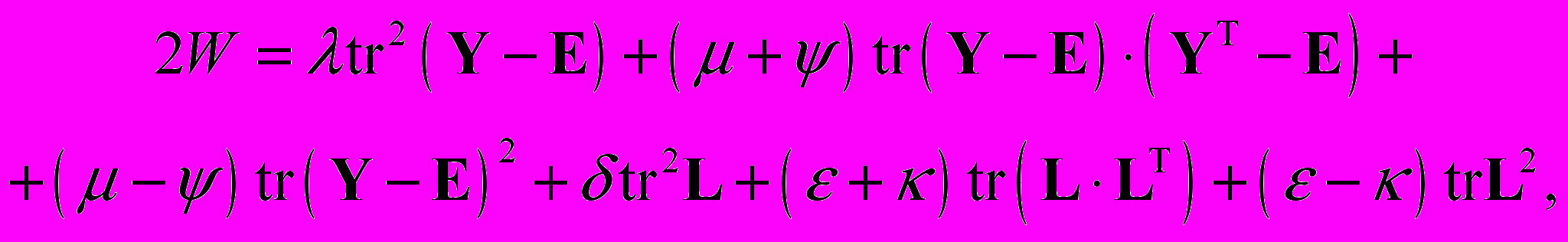(2.4)

где 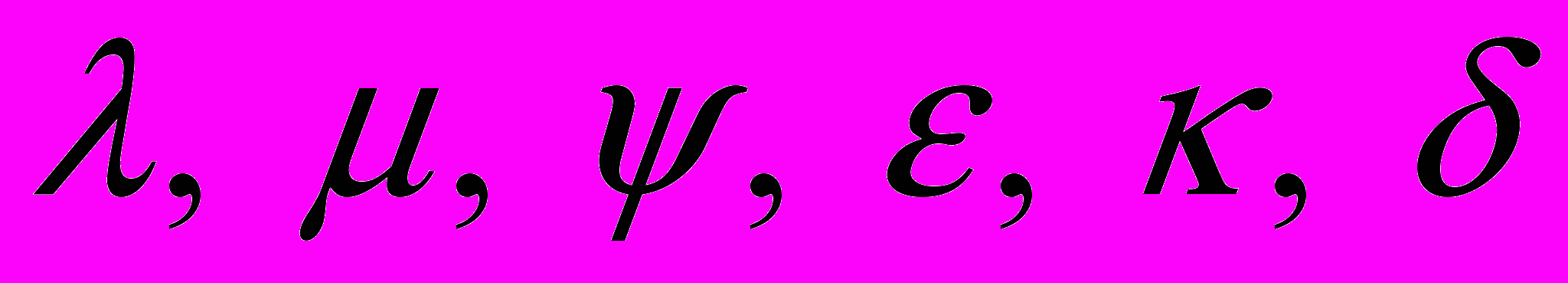– материальные постоянные. В рамках модели (2.4) ряд практически важных случаев из перечисленных выше семейств деформаций приводит к дифференциальным уравнениям, допускающим точное явное решение. Это позволило построить несколько решений в замкнутой форме, характеризующих поведение микрополярных тел при больших деформациях.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 09-01-00459).

Литература

1. Toupin R.A. Theories of elasticity with couple-stress // Arch. Ration. and Mech. Anal. – 1964. – V. 17. – №. 5. – P. 85–112.

2. Zubov L.M. Nonlinear Theory of Dislocations and Disclinations in Elastic Bodies. – Berlin: Springer, 1997.

3. Зубов Л.М., Карякин М.И. Тензорное исчисление: Основы теории. – М.: Вуз. кн., 2006.