К. Э. Циолковского Кафедра «Высшей математики» Курсовая
| Вид материала | Курсовая |
- К. Э. Циолковского Кафедра английского языка Курсовая, 475.55kb.
- Научные идеи К. Э. Циолковского и современность, 1028.06kb.
- М. В. Ломоносова Факультет вычислительной математики и кибернетики Кафедра математической, 6.81kb.
- Черты из моей жизни, 822.33kb.
- Калуга Циолковского – взгляд из космоса, 162.5kb.
- Общая программа высшая математика для экономических специальностей высших учебных заведений, 153.3kb.
- Вдистанционный курс высшей математики входит: информация о проведении занятий; лекции, 102.11kb.
- Нижний Новгород Кафедра математики, информатики и естественных наук курсовая, 275.29kb.
- Ю. П. Драница Судоводительский факультет мгту, кафедра высшей математики и программного, 443.51kb.
- И. И. Мечникова Институт математики, экономики и механики Кафедра менеджмента и математического, 246.65kb.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО НАУКЕ И ОБРАЗОВАНИЮ РФ
«МАТИ» - Российский государственный технологический университет
им. К.Э. Циолковского
Кафедра «Высшей математики»
Курсовая работа
по дисциплине «Вычислительная математика»
Вариант №12
Выполнил
студент группы: .
2АСУ-2ДБ-074
Проверил
Старший преподаватель: Душкин Ю.И.
Москва 2006
СОДЕРЖАНИЕ
1. Задание I: Метод дихотомии 3
1.1. Постановка задачи 3
1.2. Разработка алгоритма 3
1.3. Структурограмма 4
1.4. Программа решения задания 5
1.5. Результат счета 6
2. Задание II: Метод простой итерации 8
2.1. Постановка задачи 8
2.2. Разработка алгоритма 8
2.3. Структурограмма 9
2.4. Программа решения задания 10
2.5. Результат счета 11
3. Задание III: Метод Ньютона 12
3.1. Постановка задачи 12
3.2. Разработка алгоритма 12
3.3. Структурограмма 13
3.4. Программа решения задания 14
3.5. Результат счета 14
4. Задание IV: Метод секущих 15
4.1. Постановка задачи 15
4.2. Разработка алгоритма 15
4.3. Структурограмма 16
4.4. Программа решения задания 17
4.5. Результат счета 17
5. Задание V: Гибридный метод 18
5.1. Постановка задачи 18
5.2. Разработка алгоритма 18
5.3. Структурограмма 19
5.4. Программа решения задания 20
5.5. Результат счета 20
6. Задание VI: Решение системы линейных алгебраических уравнений 21
6.1. Постановка задачи 21
6.2. Разработка алгоритма 21
6.3. Структурограмма 22
6.4. Программа решения задания 23
6.5. Результат счета 25
7. Задание VII: Решение системы нелинейных уравнений 26
7.1. Постановка задачи 26
7.2. Разработка алгоритма 26
7.3. Структурограмма 27
7.4. Программа решения задания 28
7.5. Результат счета 29
Список литературы 30
Задание I: Метод дихотомии
1.1. Постановка задачи
Задано нелинейное уравнение
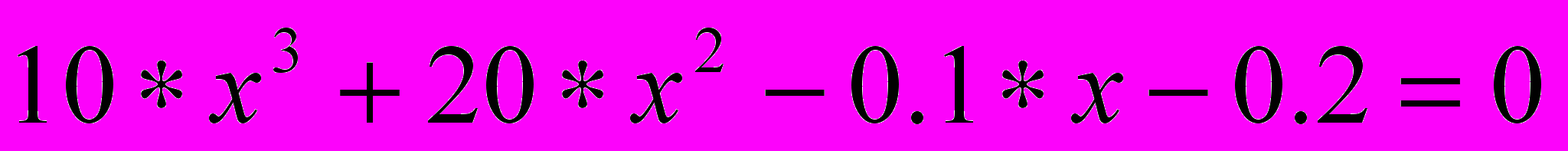
Требуется найти корни этого уравнения, т.е. те значения
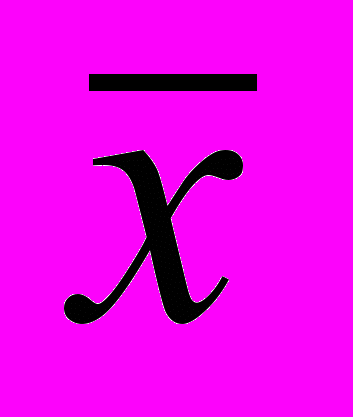 , при подстановке которых уравнение обращается в тождество
, при подстановке которых уравнение обращается в тождество 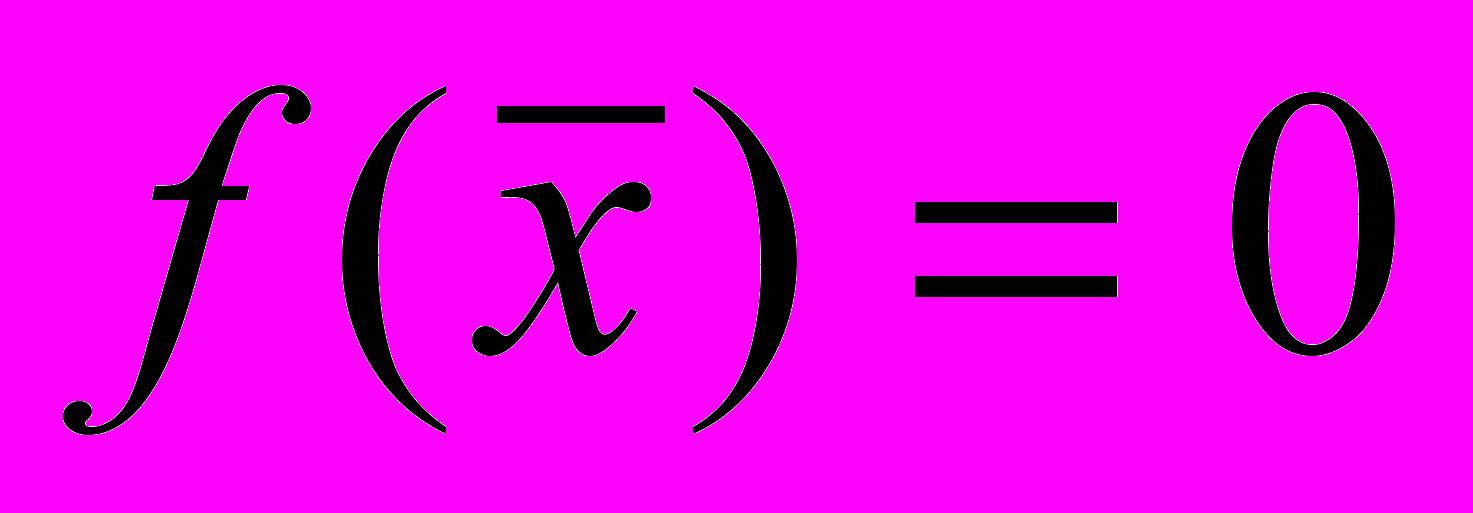 методом дихотомии с точностью
методом дихотомии с точностью 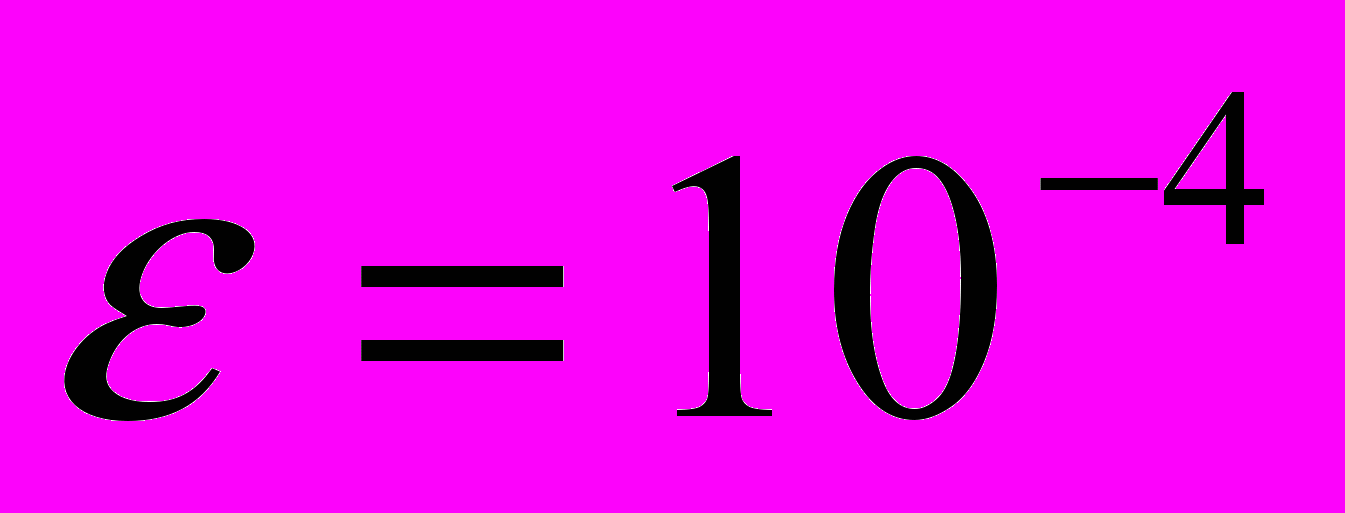 ,
, 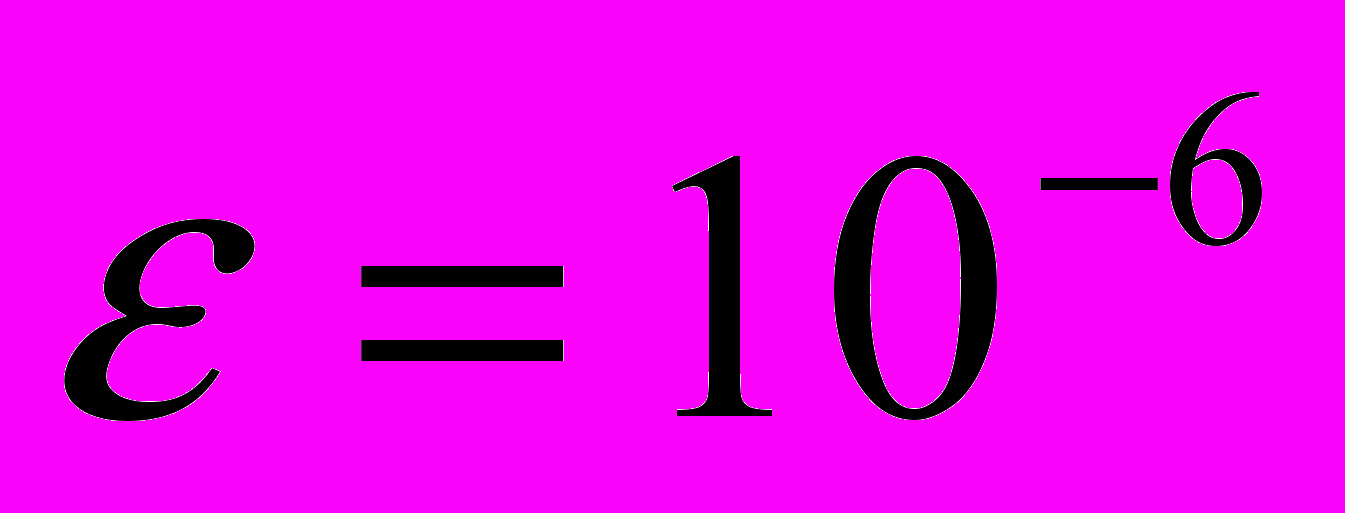 ,
, 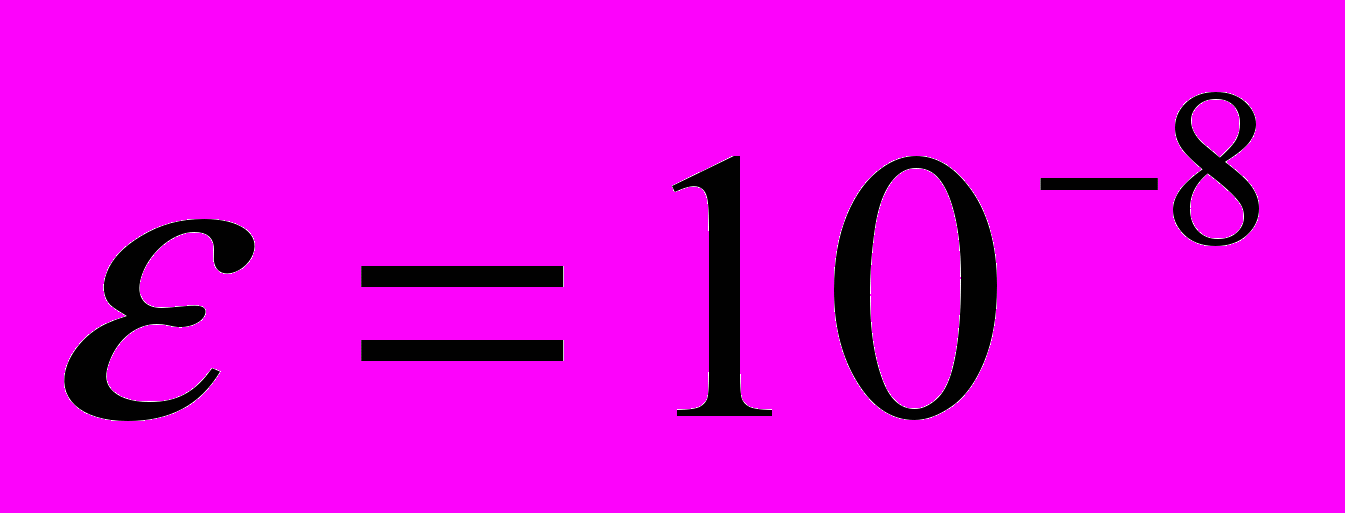 .
.1.2. Разработка алгоритма
За основу метода берется теорема Больцмана-Коши:
Если функция f(x) на концах принимает значения разных знаков: f(a)*f(b)<0, то тогда всегда существует такое значение x=c, что f(c)=0; cÎ[a,b], причем корень будет единственен, если производная на рассматриваемом интервале не меняет знака.
Таким образом, при решении нелинейных уравнений метом дихотомии, начальный отрезок разбивается на два равных отрезка, и проверятся теорема Больцмана-Коши (Лапчик М.П. «Численные методы»). Корень лежит либо на одном из отрезков либо в середине, потом еще раз делится на два отрезка отрезок, на котором находится корень, и т.д.
1.3. Структурограмма
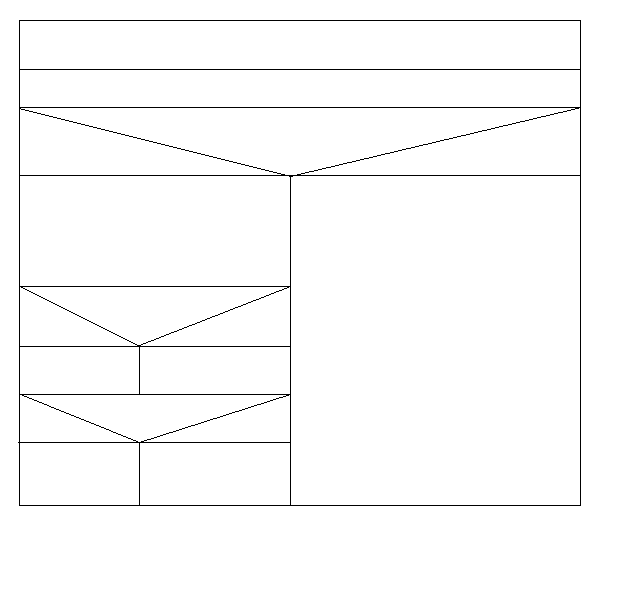
Ввод
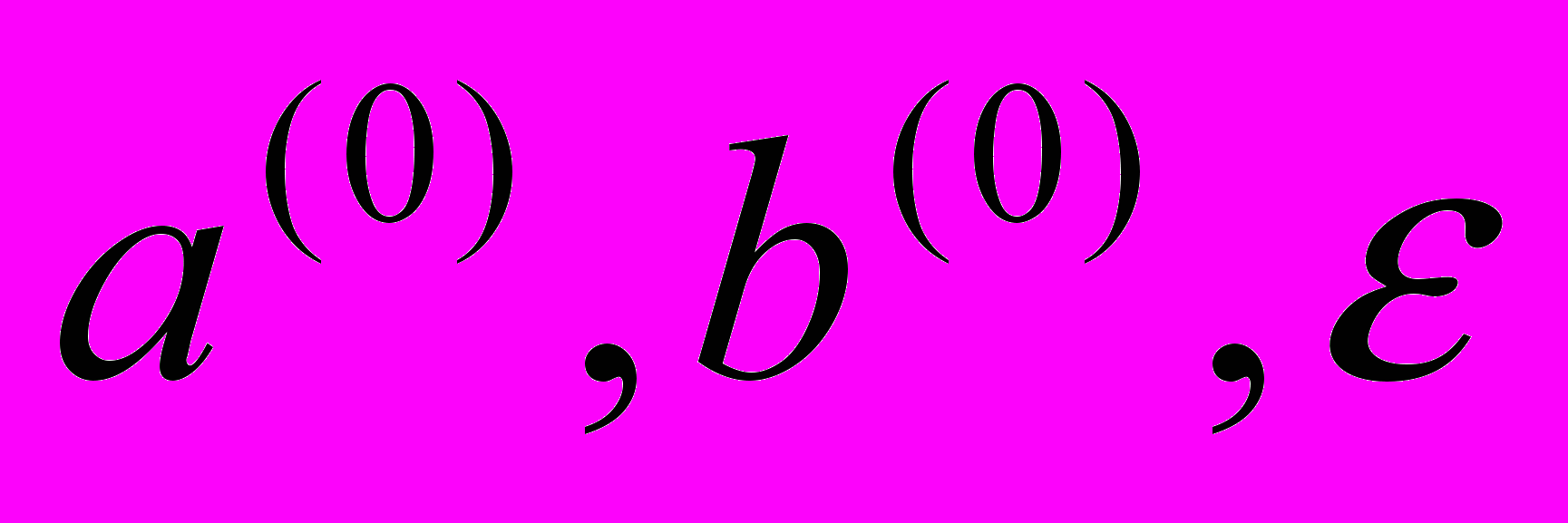
Вычисление
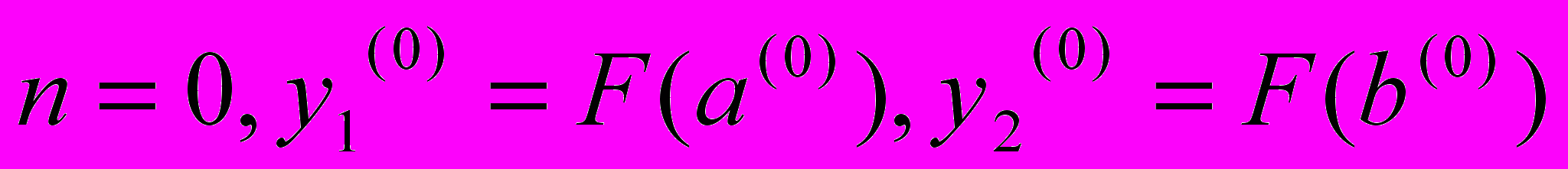
If
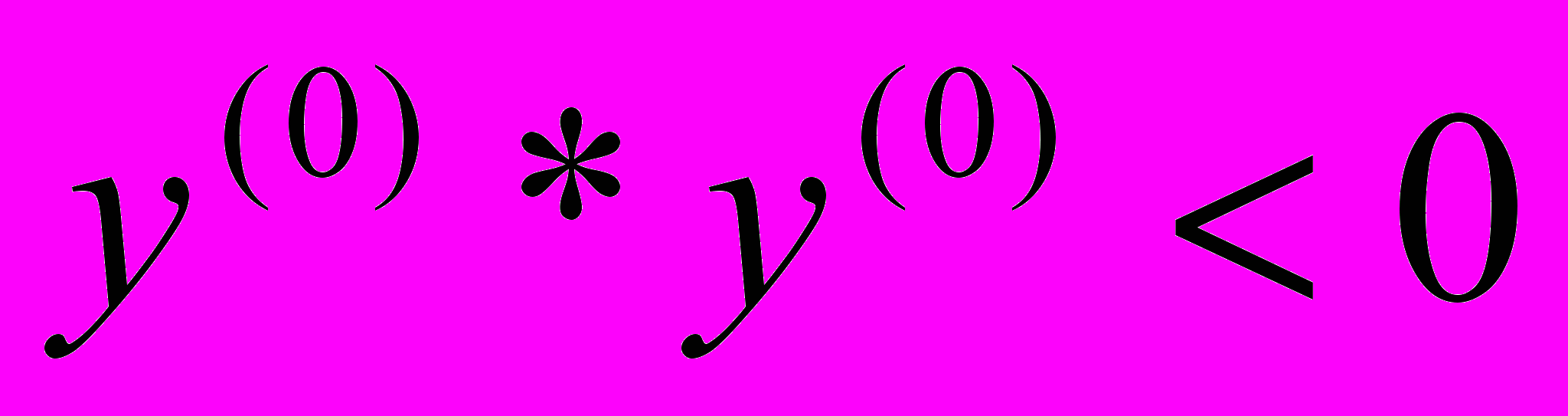
ДА НЕТ
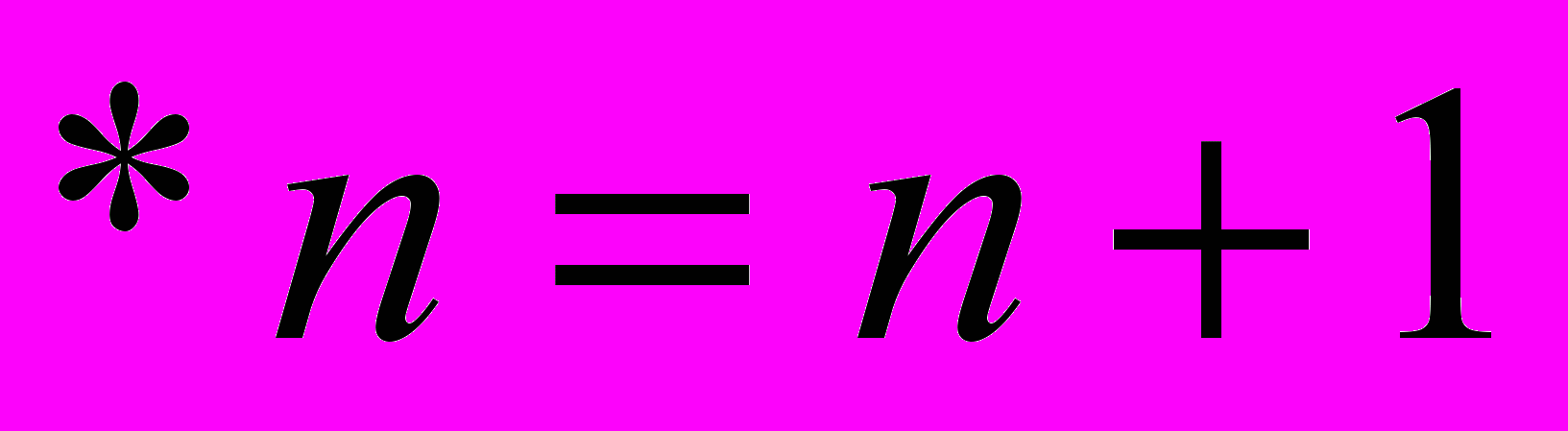 Вывод: интервал не содержит
Вывод: интервал не содержит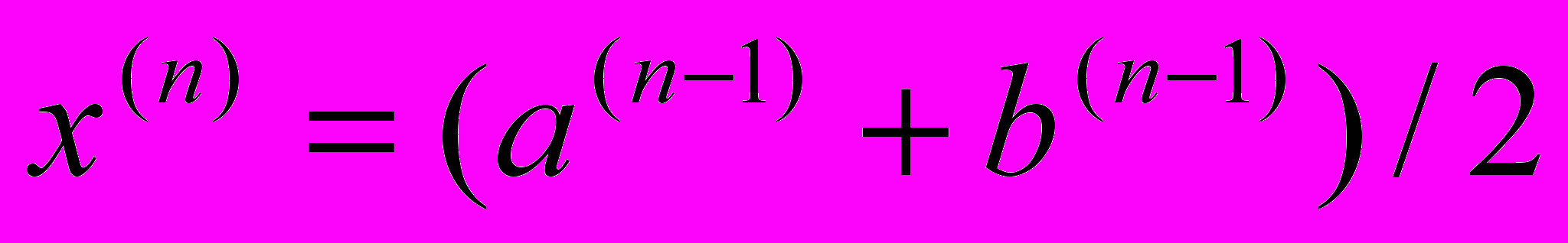 корней или четное количество
корней или четное количество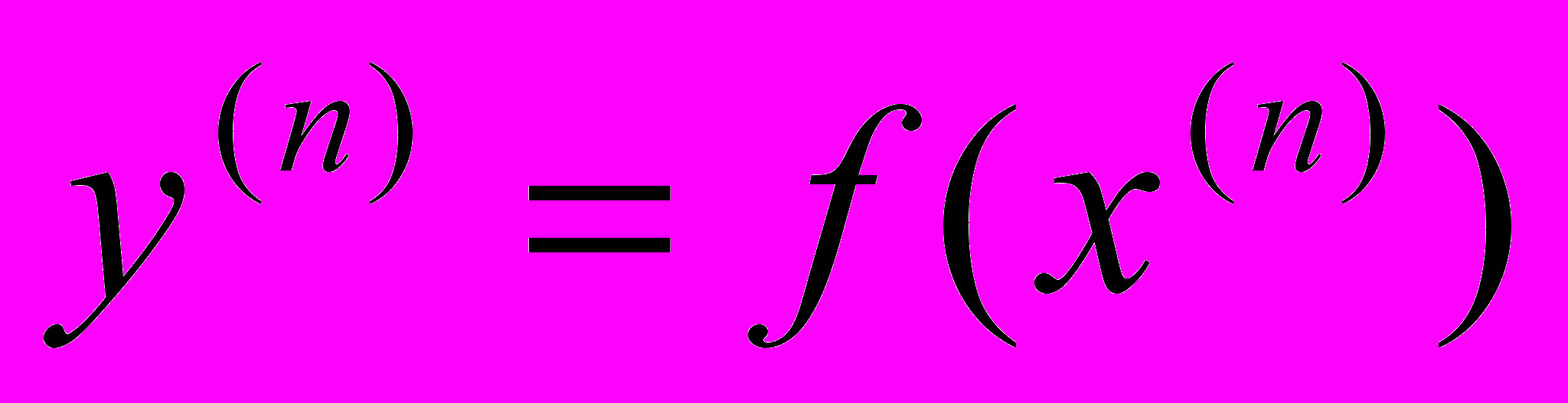 корней
корнейIf
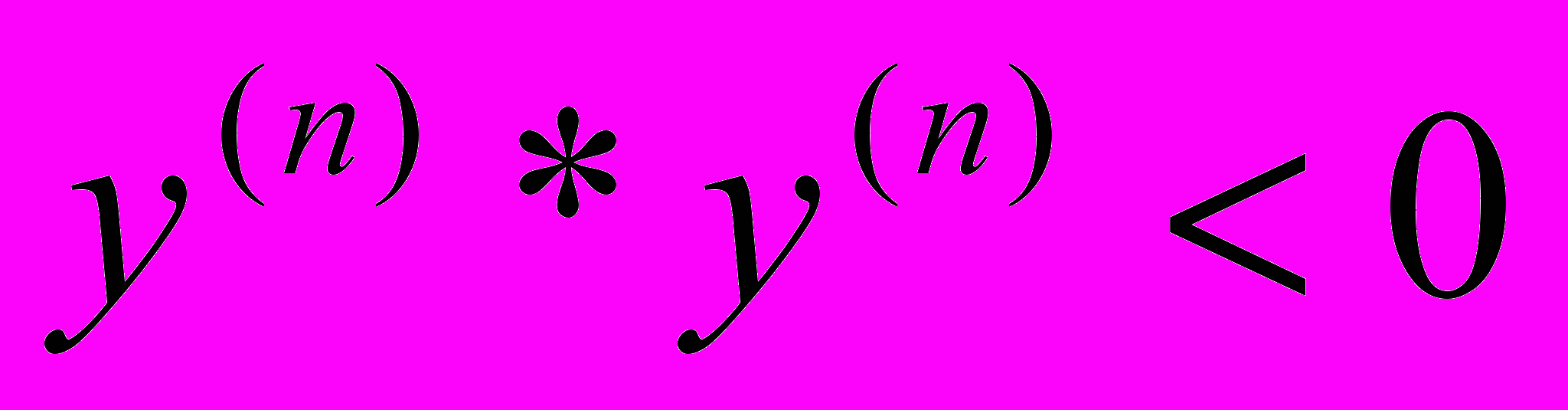
ДА НЕТ
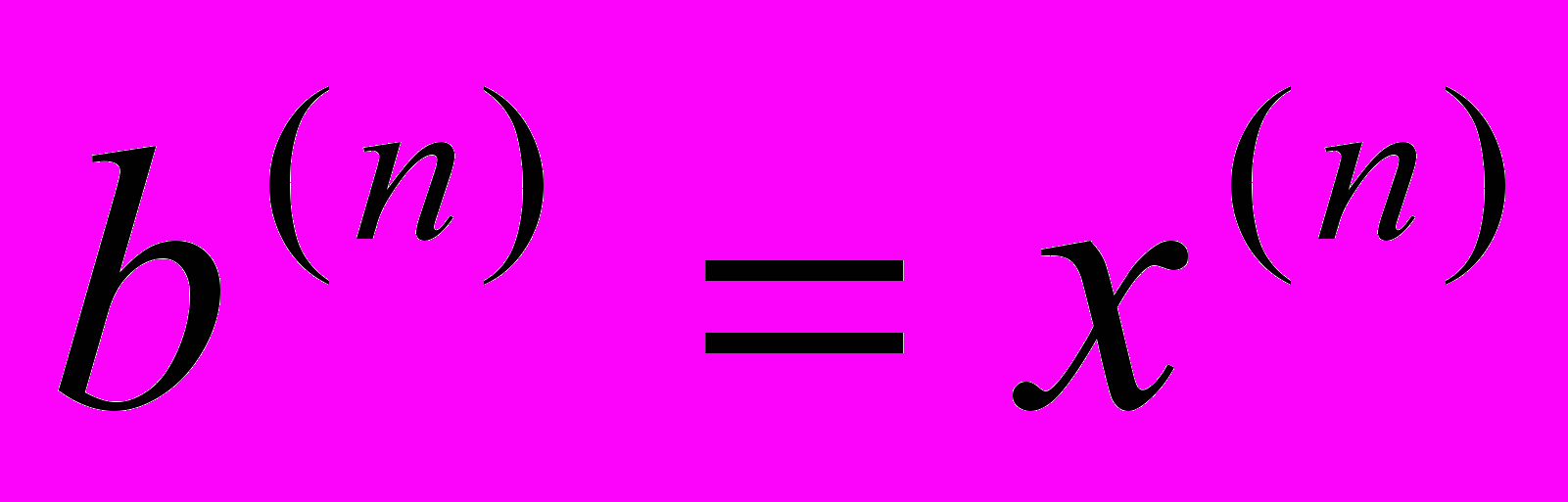
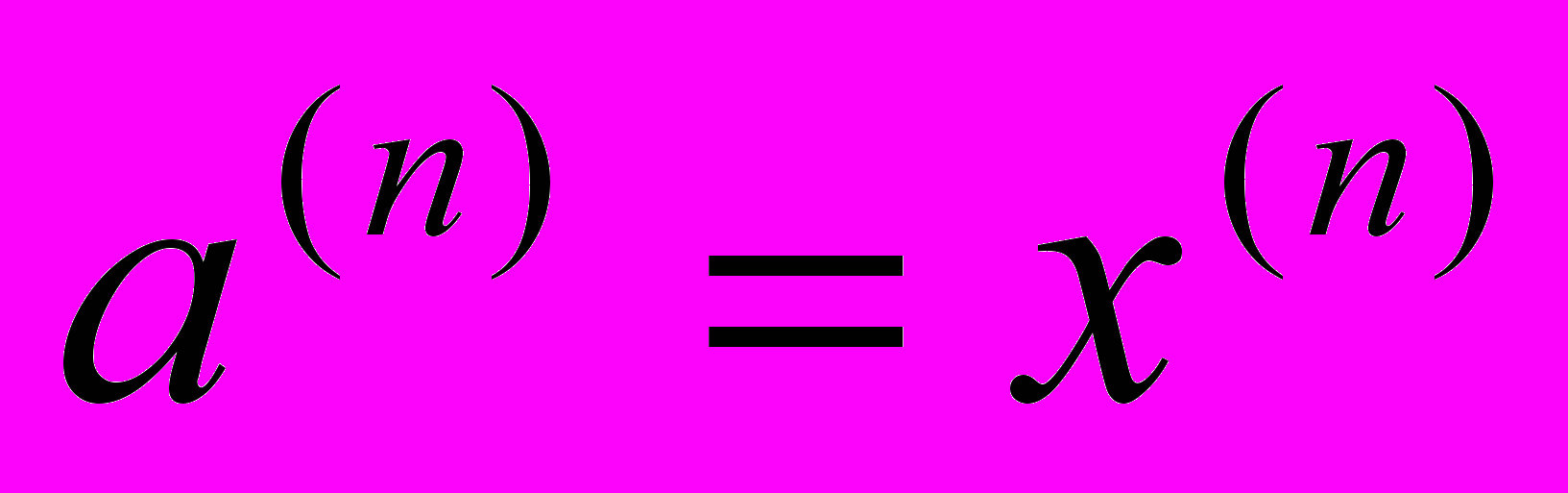
If
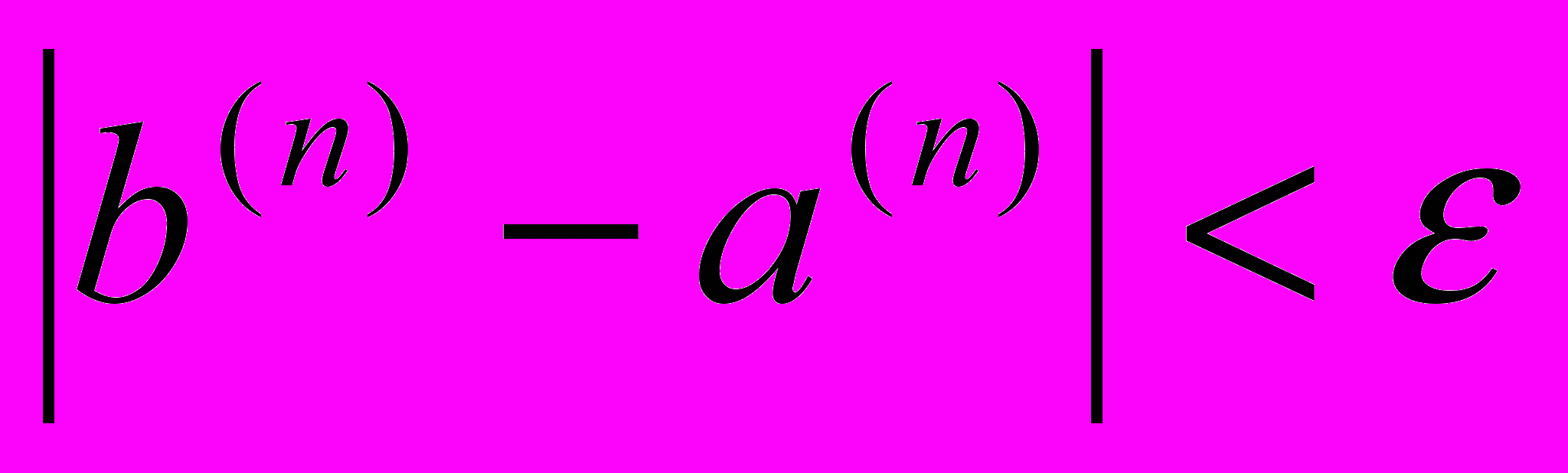
ДА НЕТ
Вывод
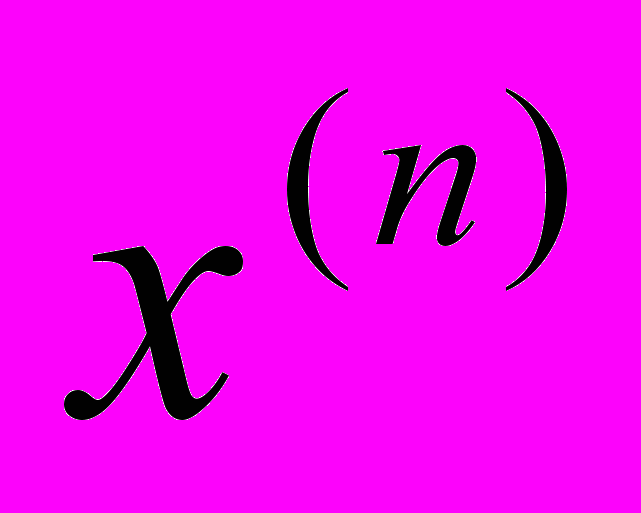 Возврат к *
Возврат к *1.4. Программа решения задания
Тело функции будет храниться в заголовочном файле func.h. Тело функции реализовано на языке программирования высокого уровня C++
#include
#include
float func (float x)
{
return 10*powf(x,3)+20*pow(x,2)-0.1*x-0.2;
}
float dfunc (float x)
{
return 30*powf(x,2)-40*x-0.1;
}
Программа обращается к заголовочному файлу func.h посредством директивы #include “func.h”
Текст программы
#include
#include
#include "func.h"
void main()
{
int i=0;
float a,b,x,fx,fa,fb,eps=0.000001;
m1:
printf("Vvedite granicy otrezka");
scanf("%f%f",&a,&b);
fb=func(b);
if(fa*fb>0)
{
printf("Na otrezke kornei net\n");
goto m1;
}
do
{
x=(b-a)/2+a;
fx=func(x);
if(fa*fx<0)
b=x;
else
{
if(fa*fx==0)
{
a=x;
b=x;
}
else
a=x;
}
i++;
}
while(fabs(b-a)>eps);
x=a+(b-a)/2;
printf("x= %f\nKol-vo iteraciy=%d\n",x,i);
}
1.5. Результат счета
x=-2.000000 на отрезке [-2.1;-1.9]
x=-0.100000 на отрезке [-0.2;0]
x=0.100000 на отрезке [0;0.2]
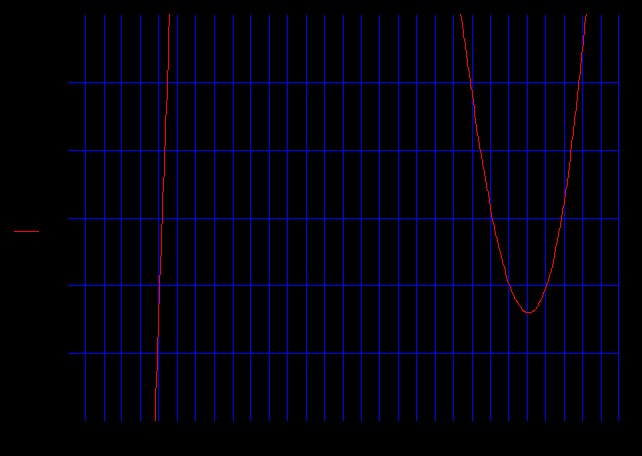 Проверка в MathCAD:
Проверка в MathCAD: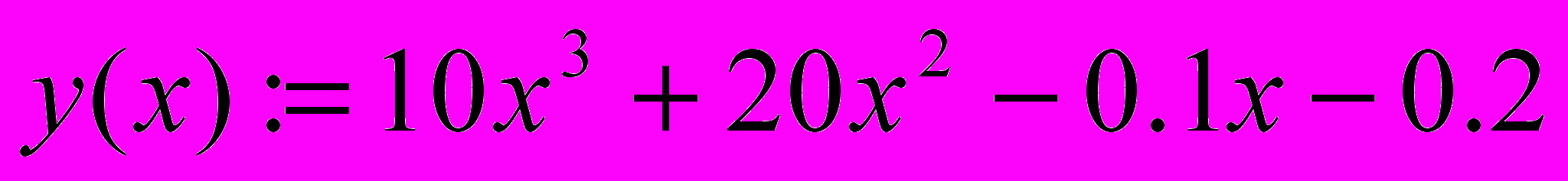
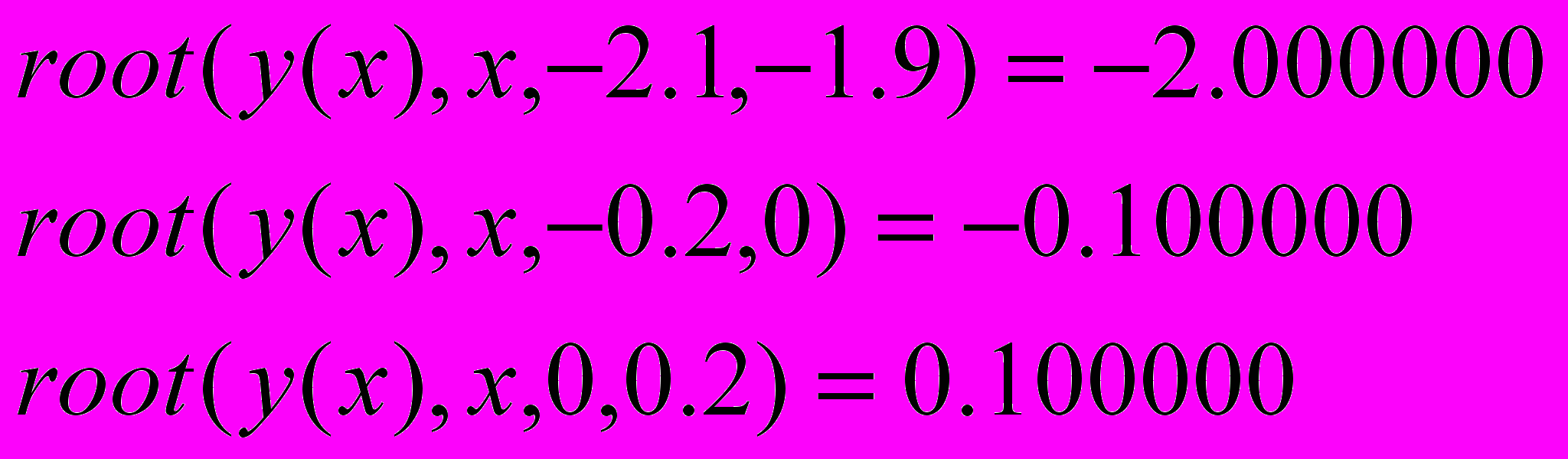
Задание II: Метод простой итерации
2.1. Постановка задачи
Задано нелинейное уравнение
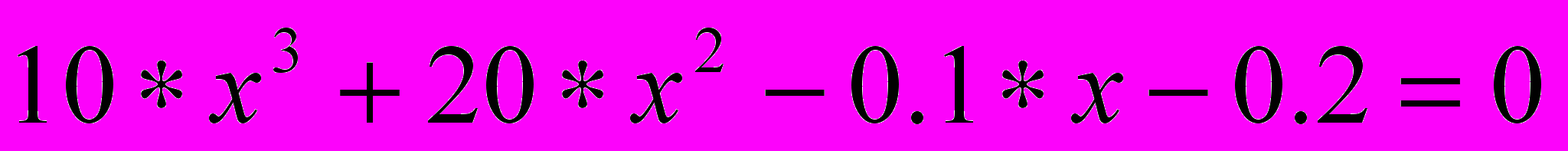
Требуется найти корни этого уравнения, т.е. те значения
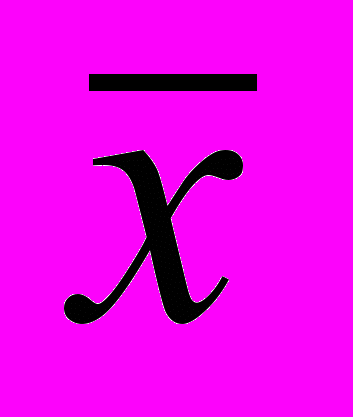 , при подстановке которых уравнение обращается в тождество
, при подстановке которых уравнение обращается в тождество 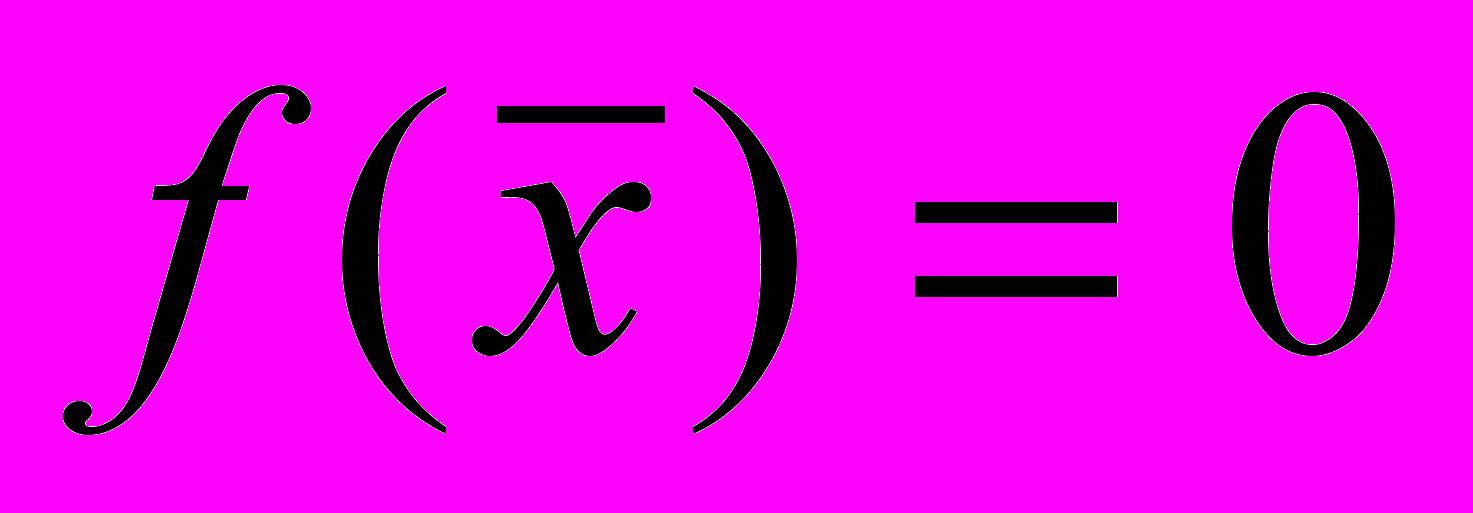 методом простой с точностью
методом простой с точностью 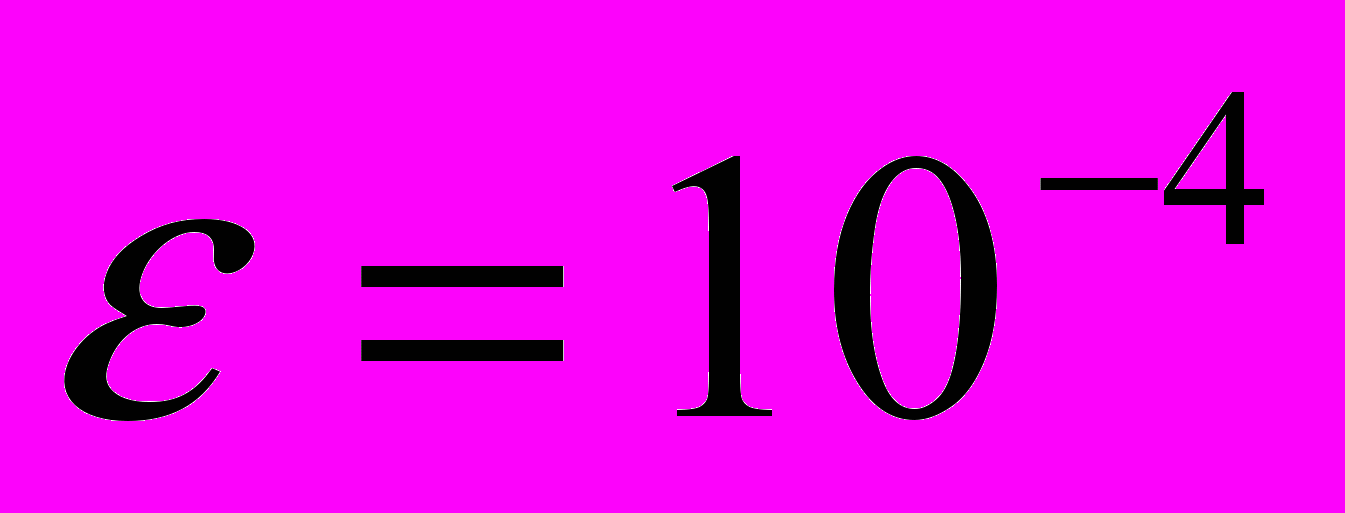 ,
, 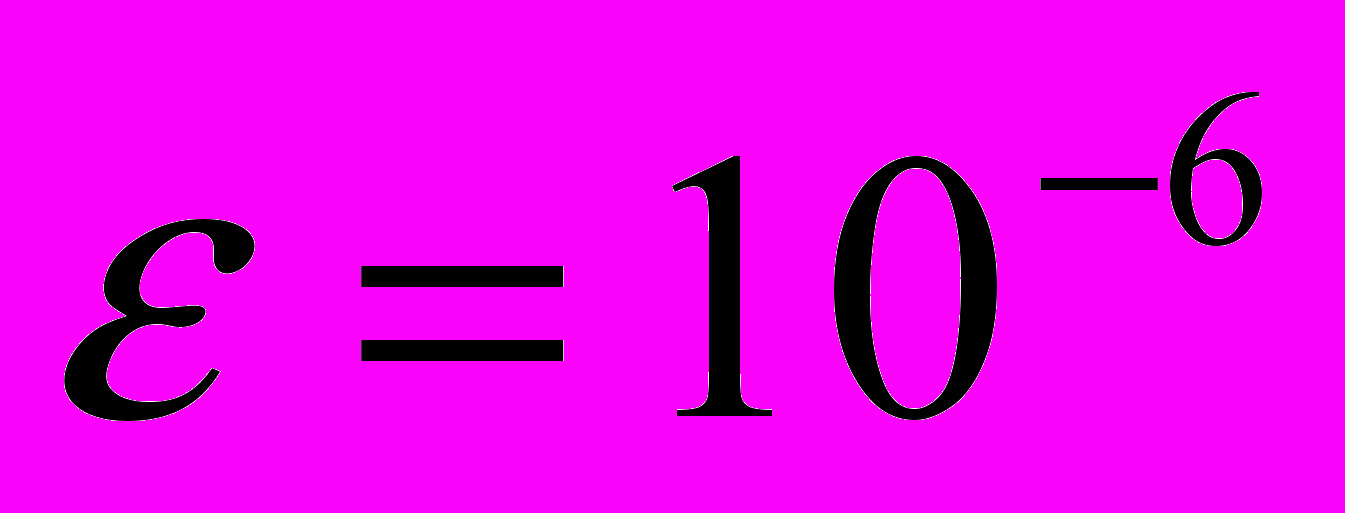 ,
, 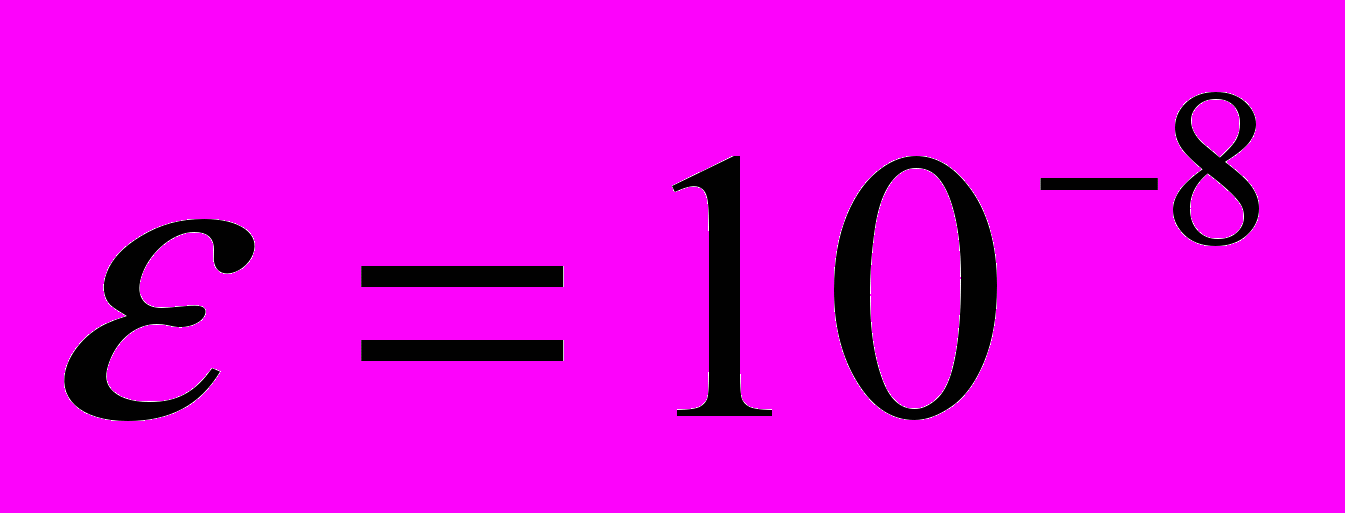 .
.2.2. Разработка алгоритма
Использование метода простой итерации для решения уравнения
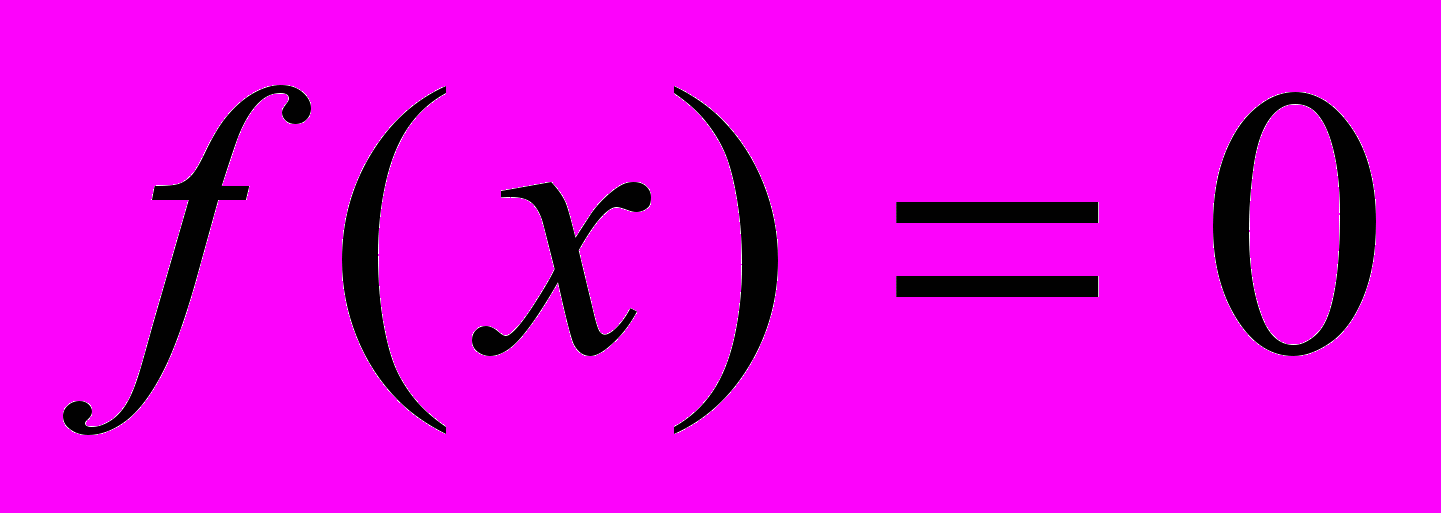 связано с преобразованием его к равносильному уравнению вида:
связано с преобразованием его к равносильному уравнению вида: 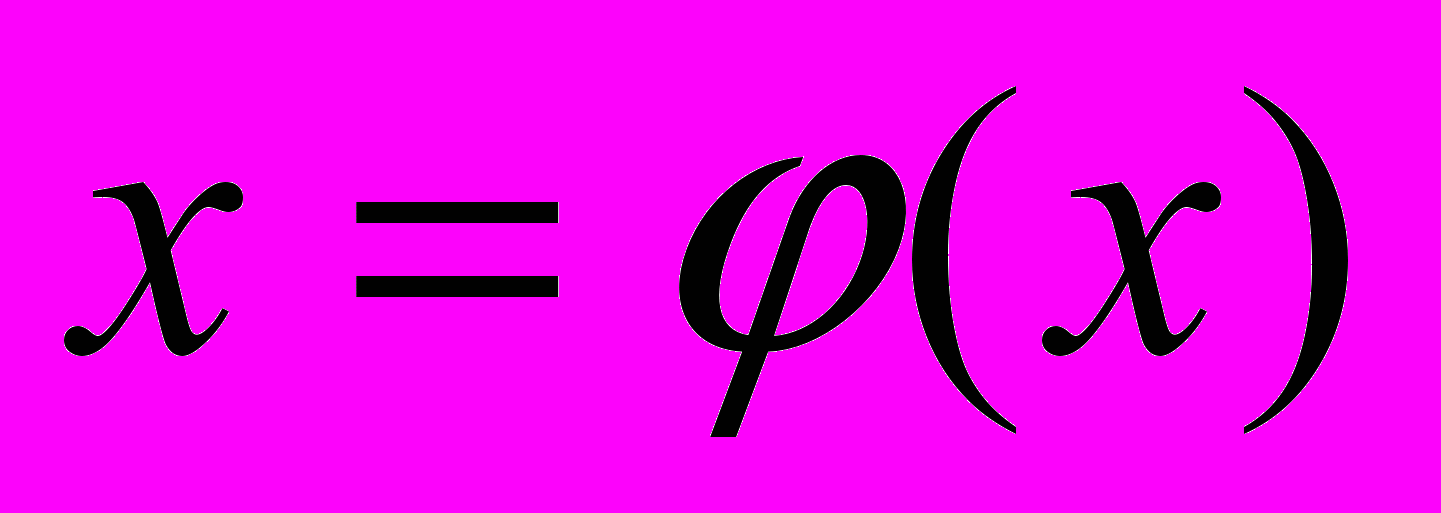 .
.Такое преобразование называется приведением уравнения к виду, удобному для итерации, и может быть выполнено различными способами. Функция
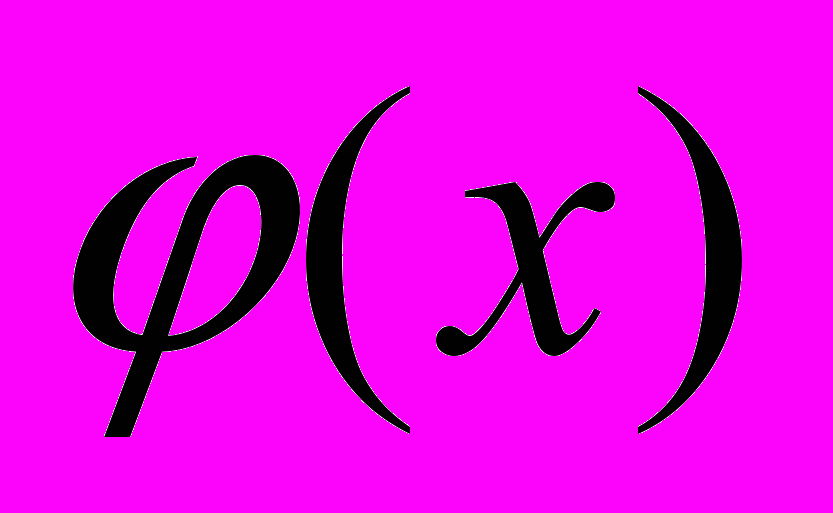 называется итерационной функцией.
называется итерационной функцией.Выберем начальное приближение к корню
 и подставим его в правую часть
и подставим его в правую часть 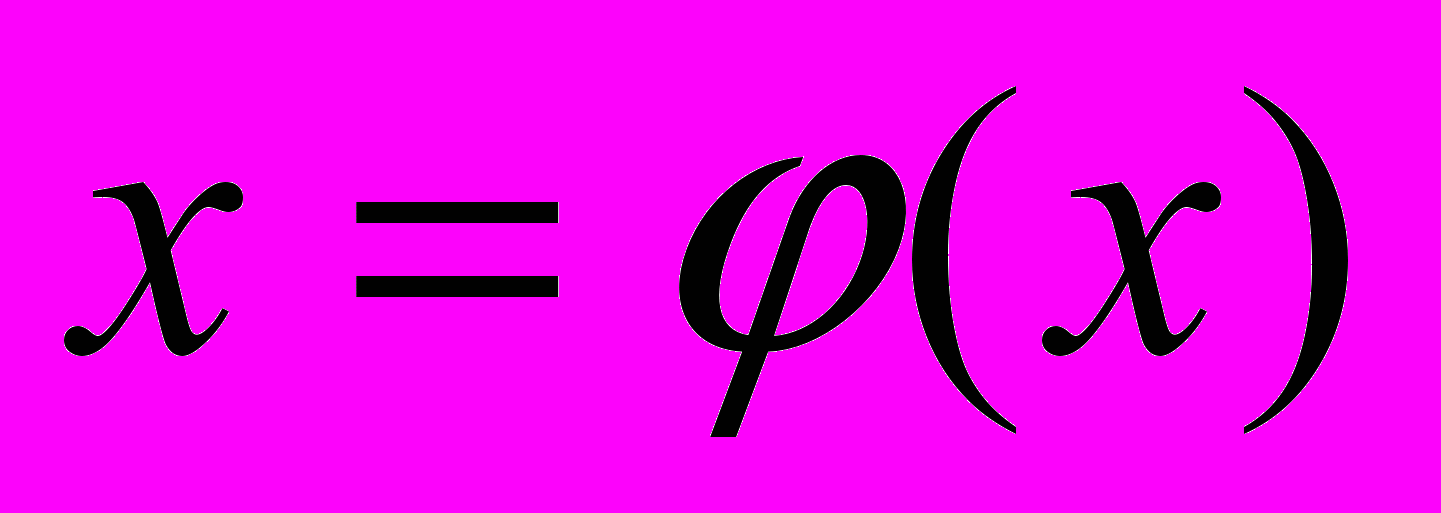 . Получим
. Получим 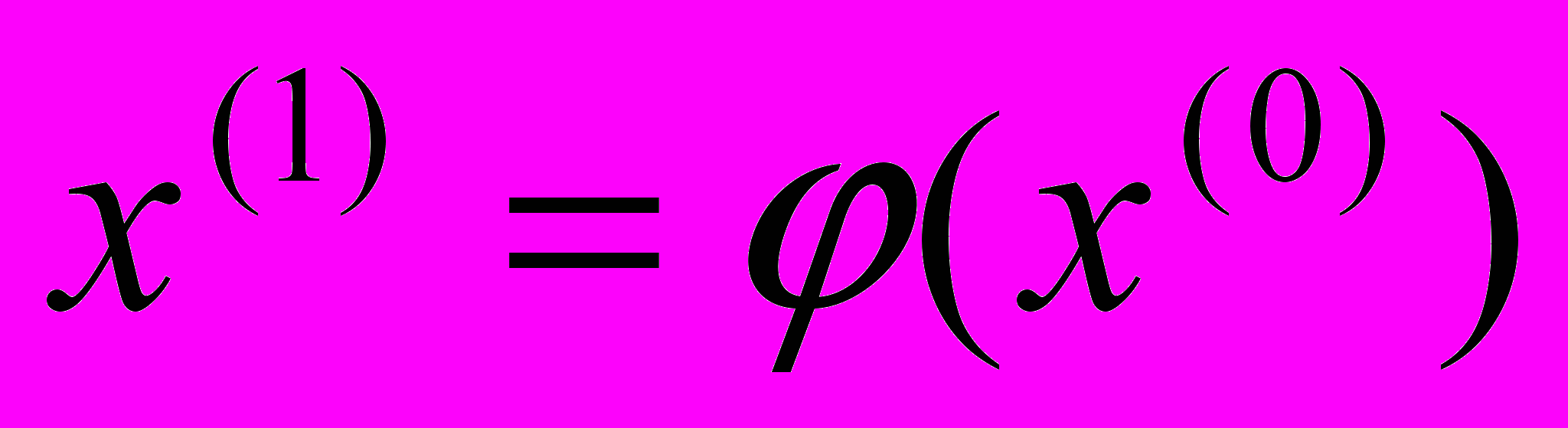 . Подставив
. Подставив 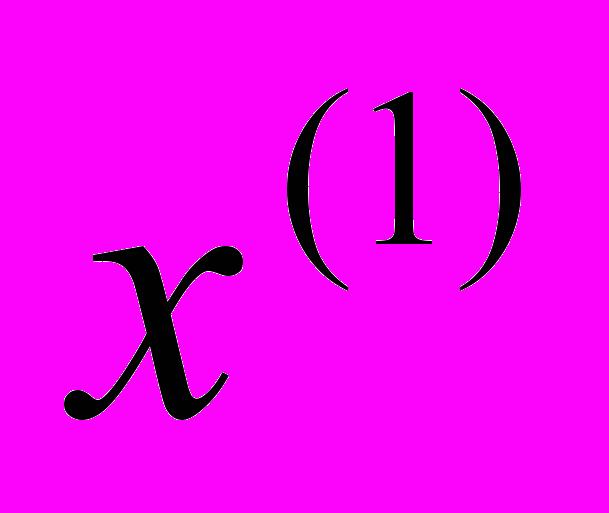 в правую часть
в правую часть 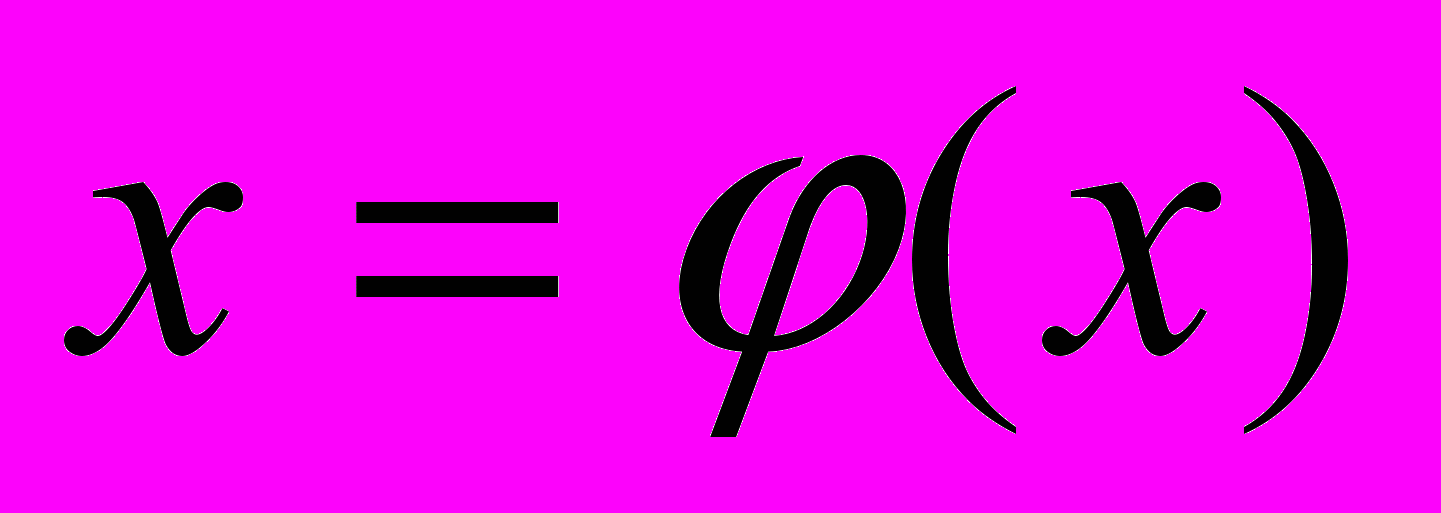 , получим
, получим 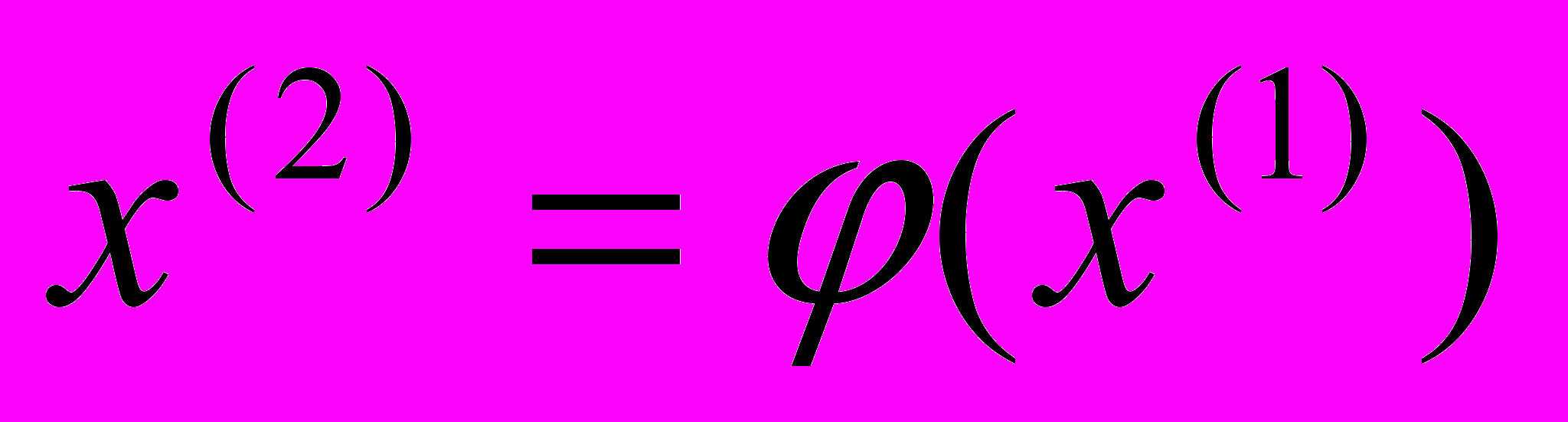 . Продолжая неограниченно этот процесс, получим последовательность приближений к корню, вычисляемую по формуле:
. Продолжая неограниченно этот процесс, получим последовательность приближений к корню, вычисляемую по формуле: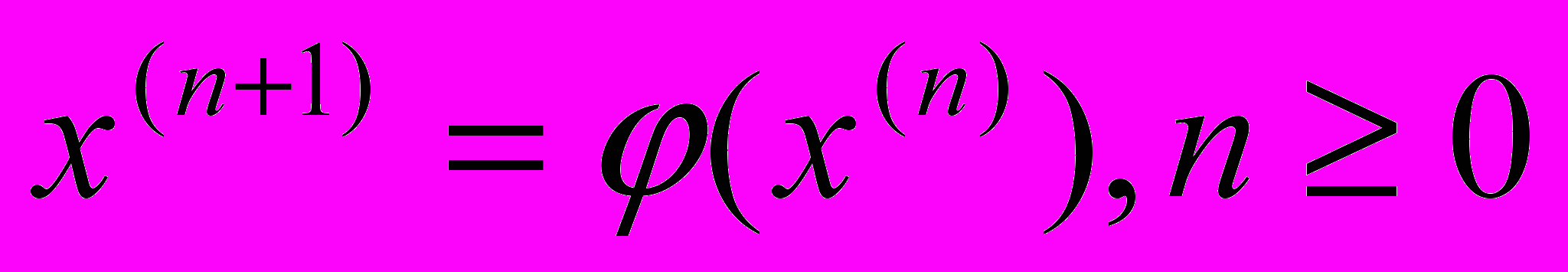 .
.Метод простой итерации является одношаговым. Если существует предел этой последовательности и, полагая функцию
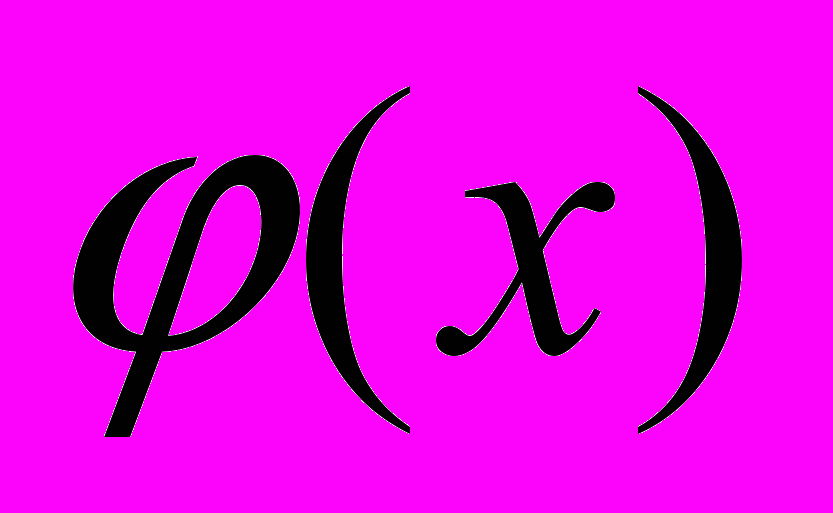 непрерывной, получим равенство
непрерывной, получим равенство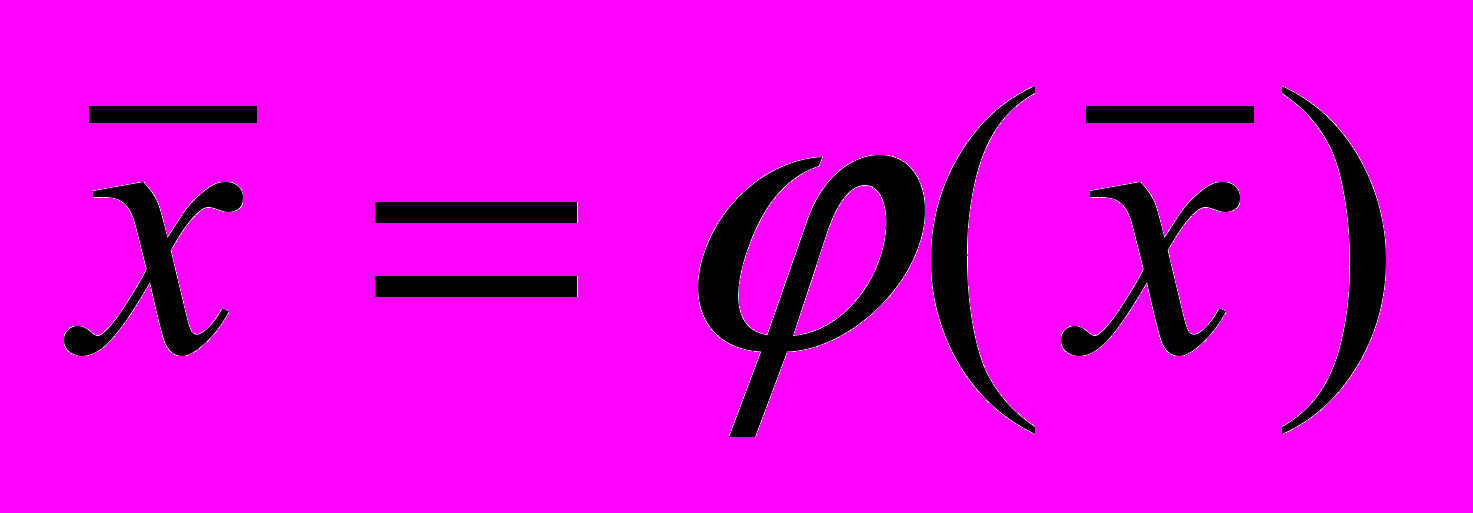 ,
,которое означает, что
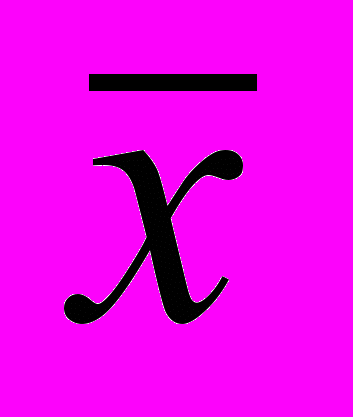 - корень уравнения.
- корень уравнения.2.3. Структурограмма
Ввод
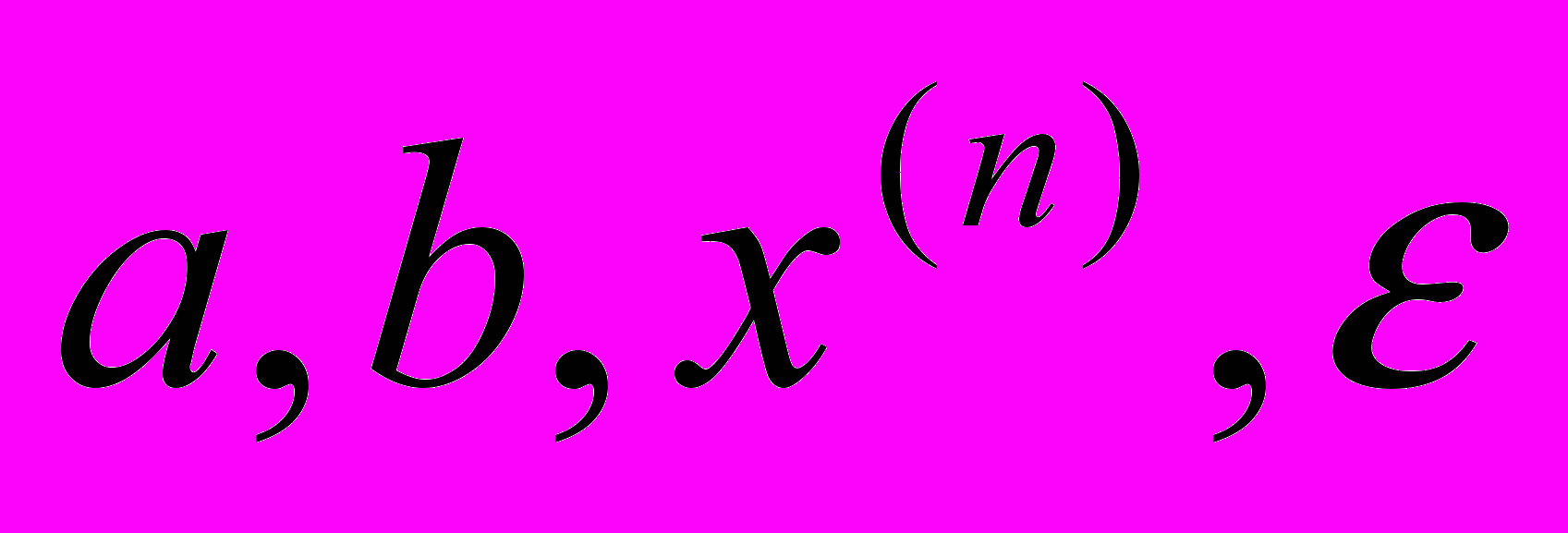
*
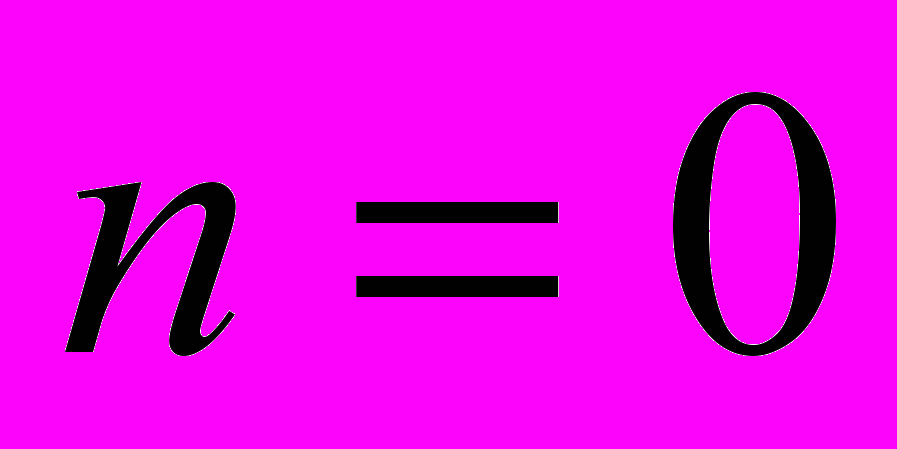
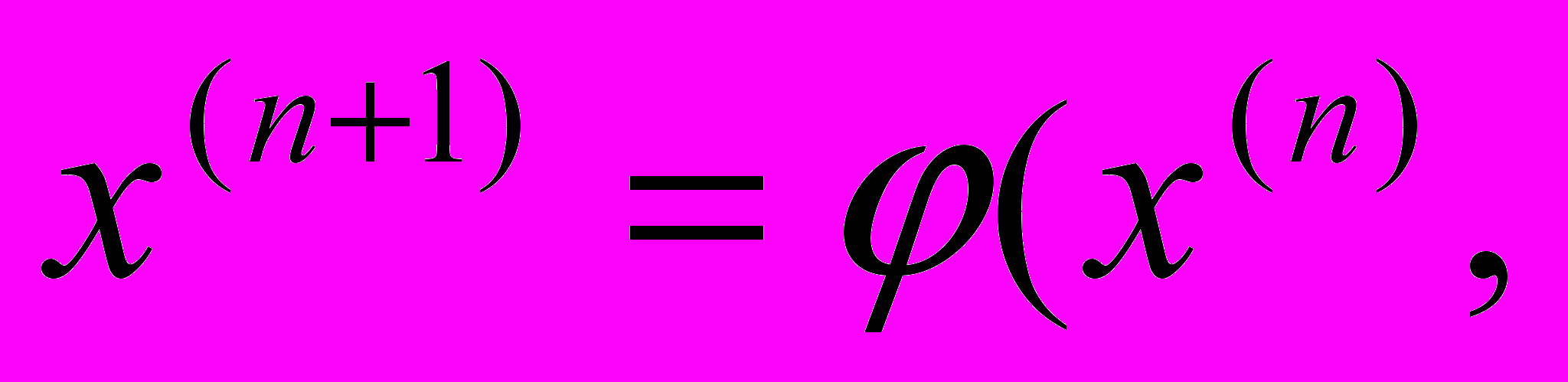
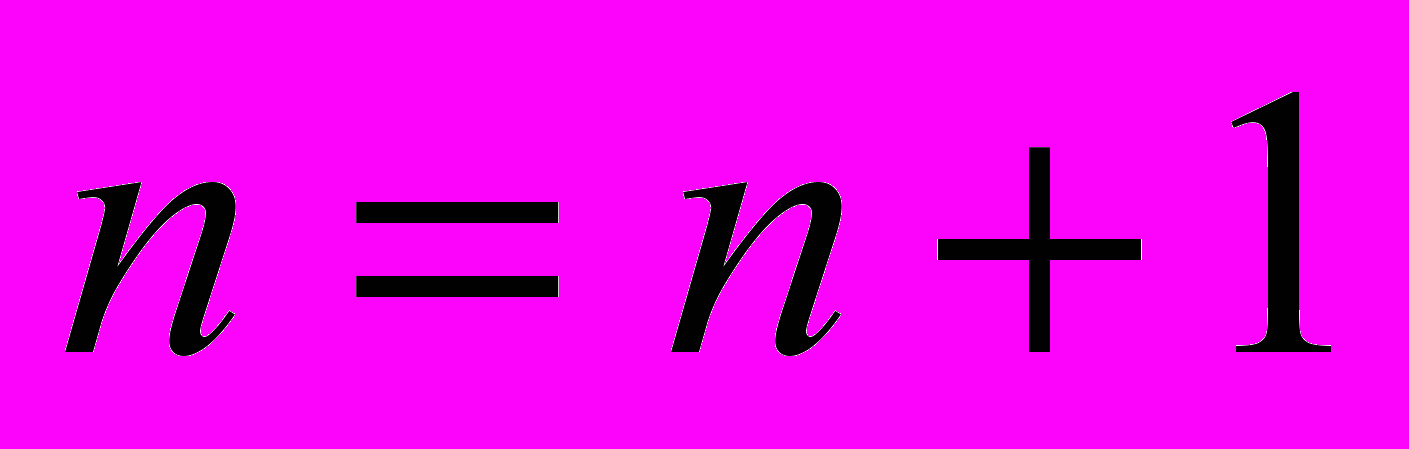
If
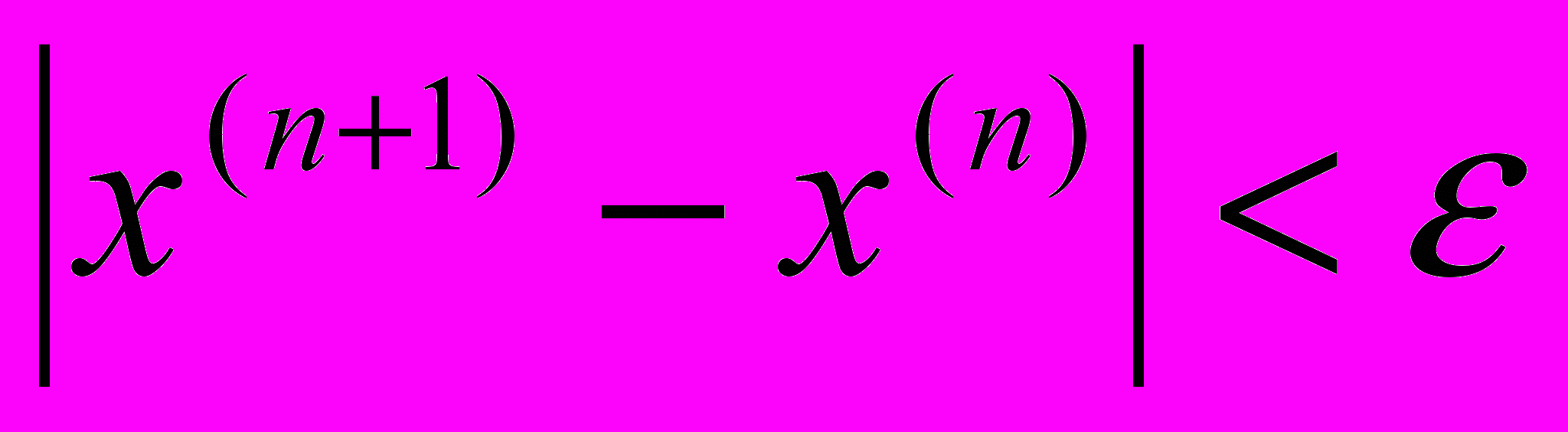
ДА НЕТ
Вывод
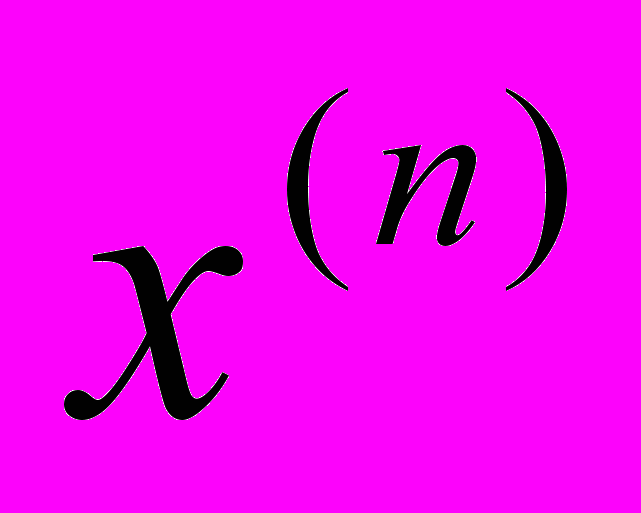 Возврат к пункту *
Возврат к пункту *2.4. Программа решения задания
#include
#include
#include "func.h"
void main()
{
int i=0,j=0,k=0;
float a=-1,b=0,x=0.,c,eps=0.000001,e1,e2,e,h,t,q,alpha,ymax=-1000,ymin=1000,xmax,xmin;
float q1[100];
puts("Vvedite ogranichenia na otrezok a,b i nachalnoe priblizhenie x0");
scanf("%f\t%f\n%f",&a,&b,&x);
e1=-2/dfunc(a);
e2=-2/dfunc(b);
h=(b-a)/100;
xmin=a;
xmax=b;
t=a;
for(i=0; i<100; i++)
{
q1[i]=dfunc(t);
t=t+h;
if(q1[i]
{
ymin=q1[i];
xmin=t-h;
}
if(q1[i]>ymax)
{
ymax=q1[i];
xmax=t-h;
}
}
q=fabs((ymax-ymin)/(ymax+ymin));
printf("\nq=%f",q);
if(fabs(e1)<=fabs(e2))
e=fabs(e1);
else
e=fabs(e2);
alpha=-2/(ymin+ymax);
printf("\nalpha=%f\n",alpha);
do
{
c=x;
x=x+alpha*func(c);
k++;
}
while((q/(1-q))*fabs(x-c)>eps);
printf("Koren uravnenia x=%f\n",x);
printf("Kol-vo iteraciy=%d\n",k);
}
2.5. Результат счета
x=-2.000000 на отрезке [-2.1;-1.9]
x=-0.100000 на отрезке [-0.2;0]
x=0.100000 на отрезке [0;0.2]
Задание III: Метод Ньютона
3.1. Постановка задачи
Задано нелинейное уравнение
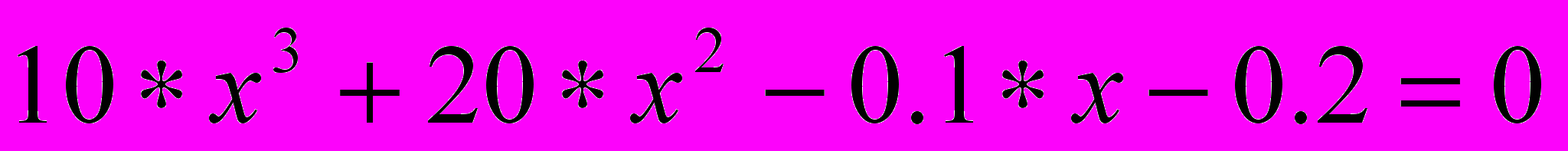
Требуется найти корни этого уравнения, т.е. те значения
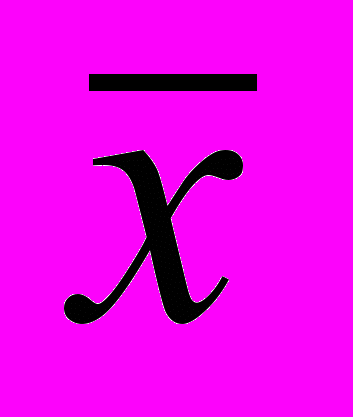 , при подстановке которых уравнение обращается в тождество
, при подстановке которых уравнение обращается в тождество 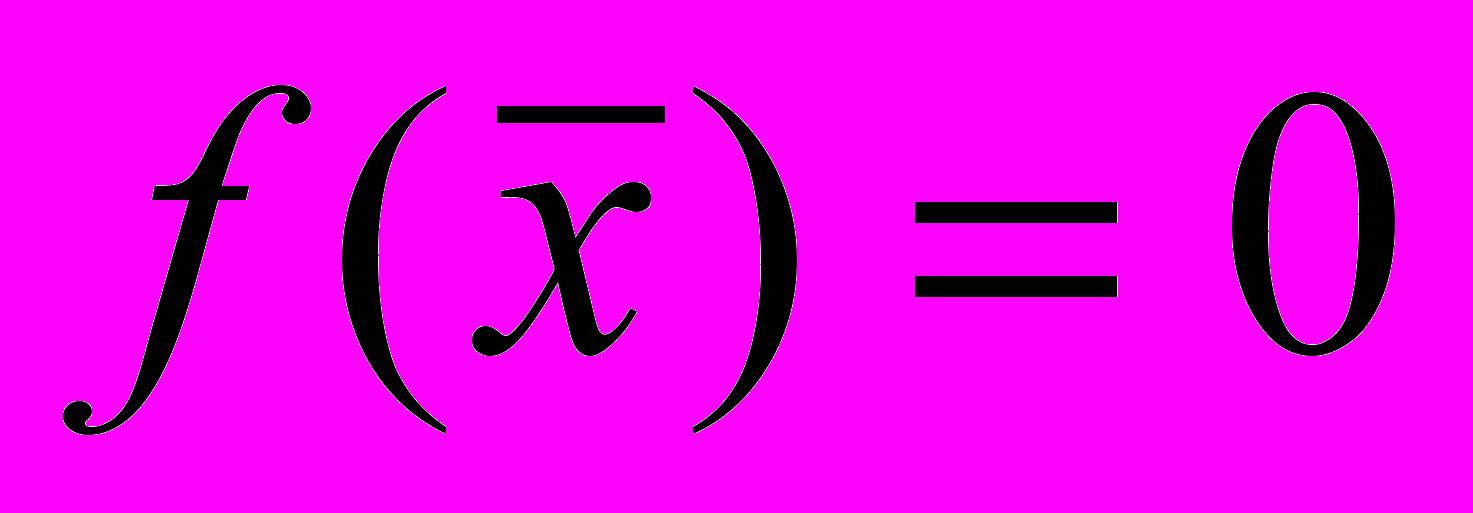 методом Ньютона с точностью
методом Ньютона с точностью 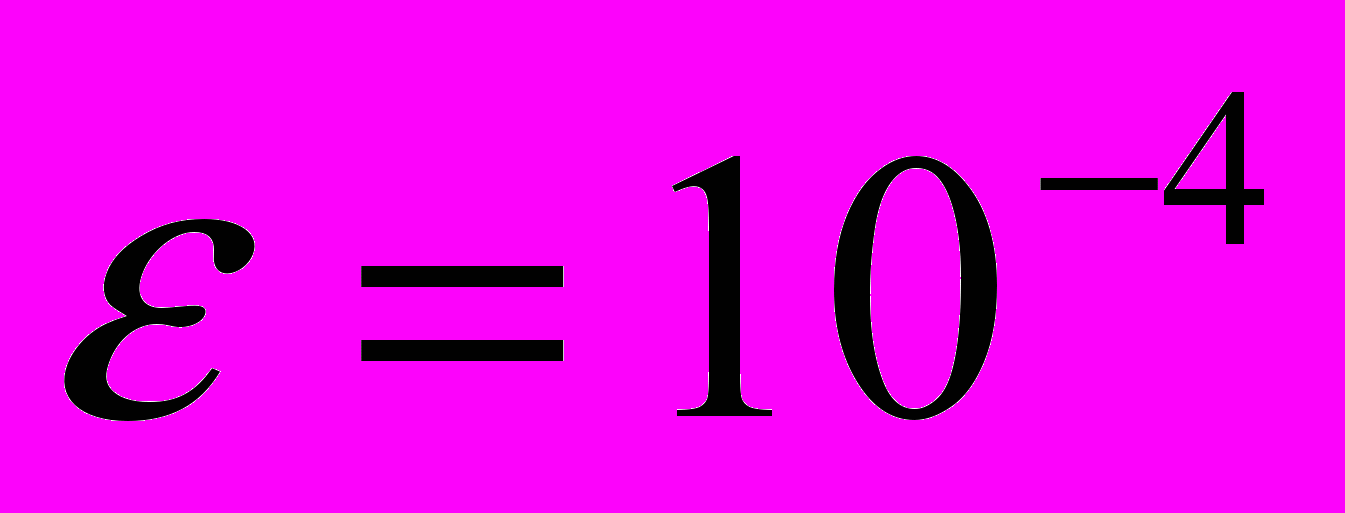 ,
, 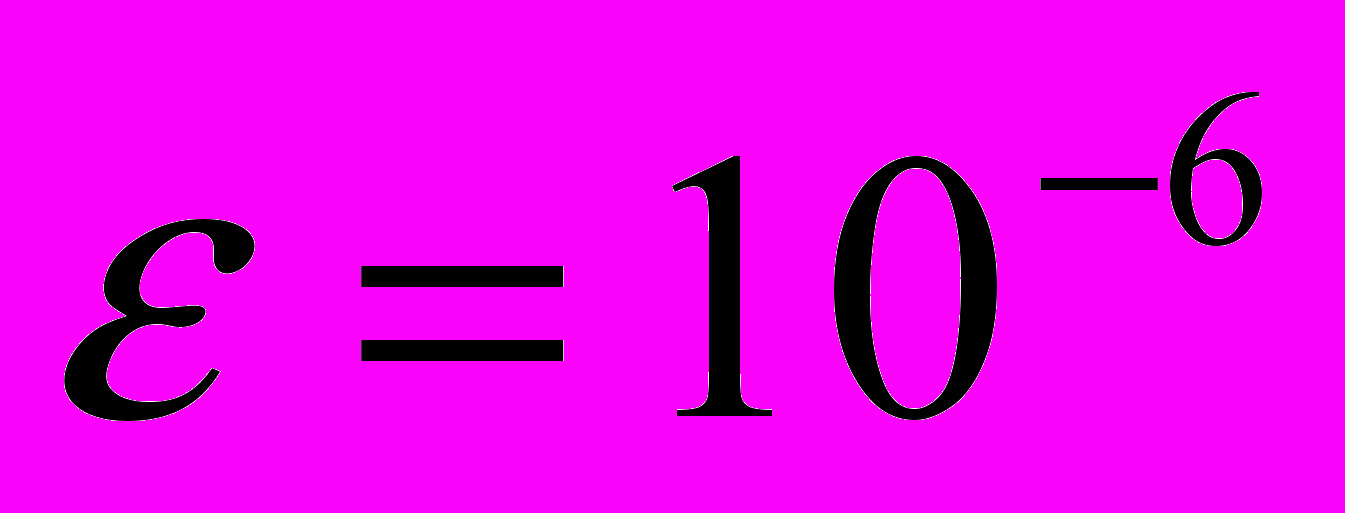 ,
, 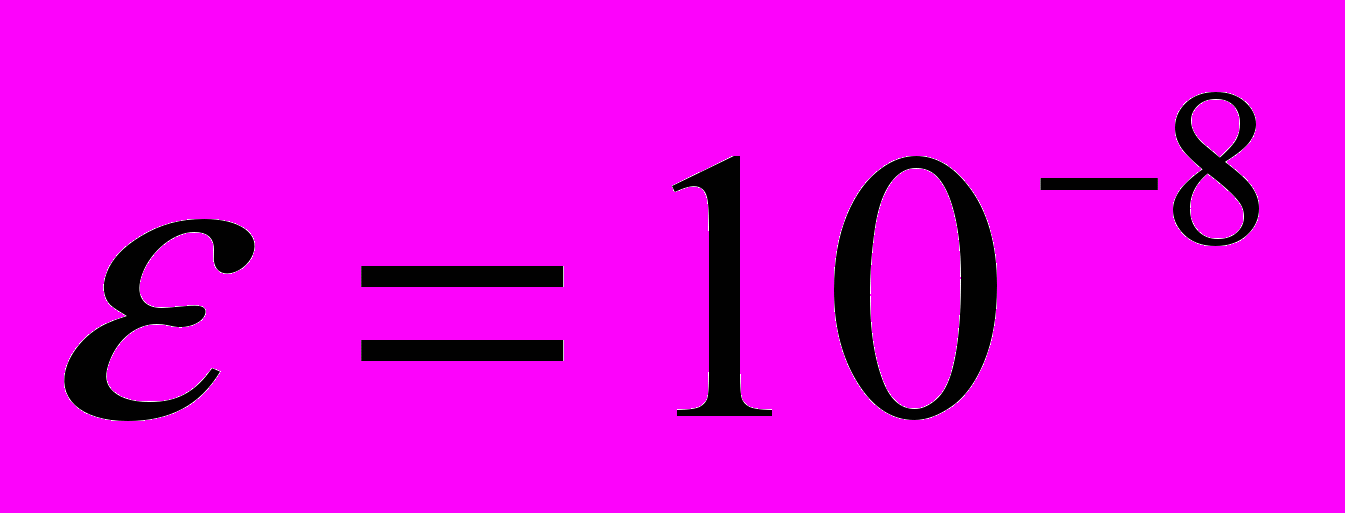 .
.3.2. Разработка алгоритма
Метод Ньютона можно рассматривать как один из вариантов метода простой итерации, который связан со специальным преобразованием уравнения f(x)=0 к виду х=φ(x), где φN(x)=х-(f(x)/f’(x)). Действительно, итерационная формула метода простой итерации x(n+1)= φ(x(n))= x(n)-(f(x(n))/f’(x(n))) совпадает с формулой метода касательных.
3.3. Структурограмма

Ввод
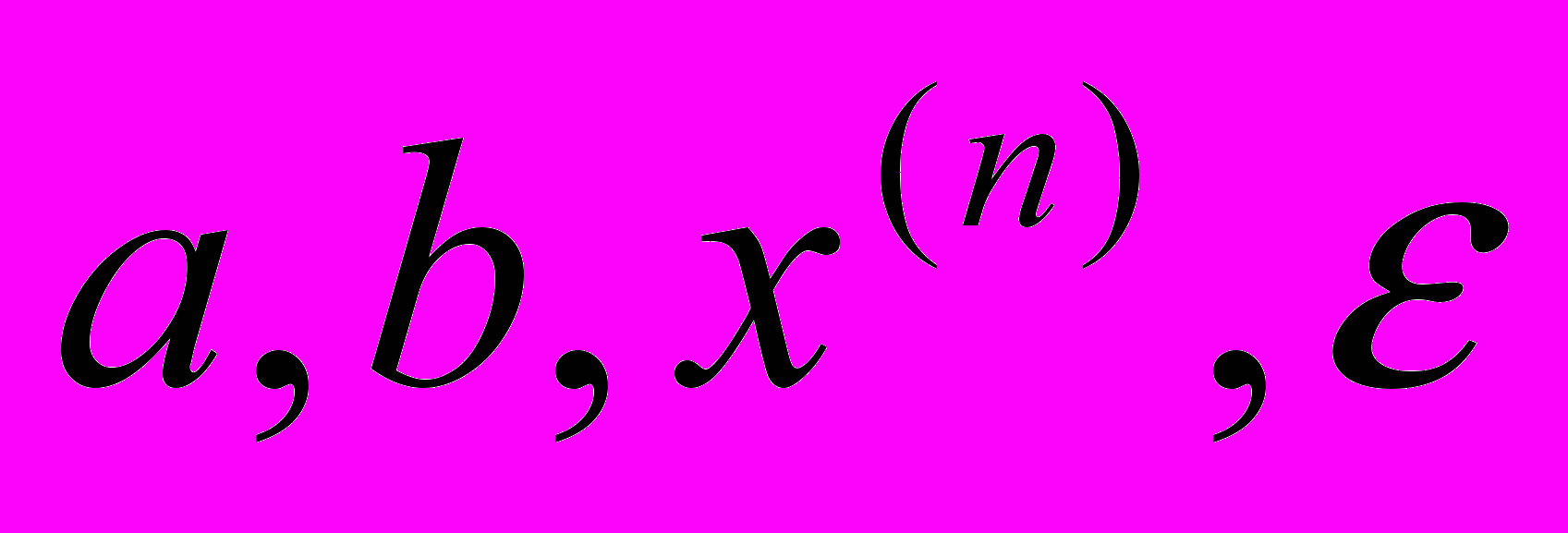
*
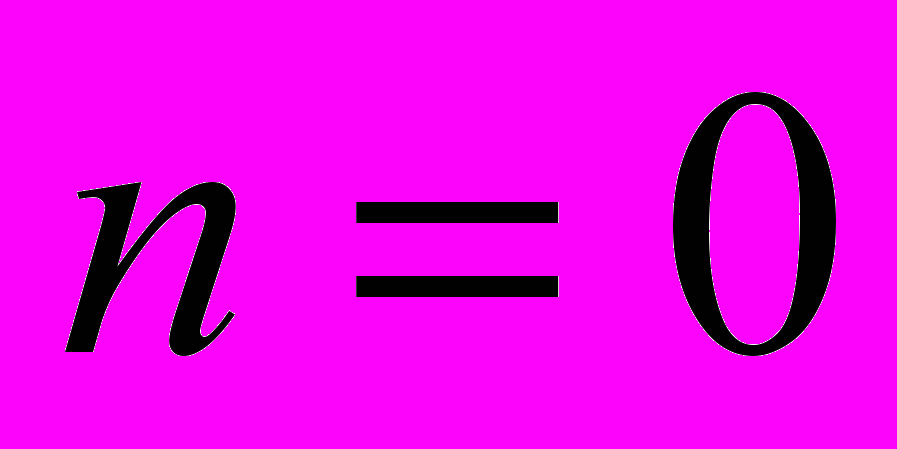
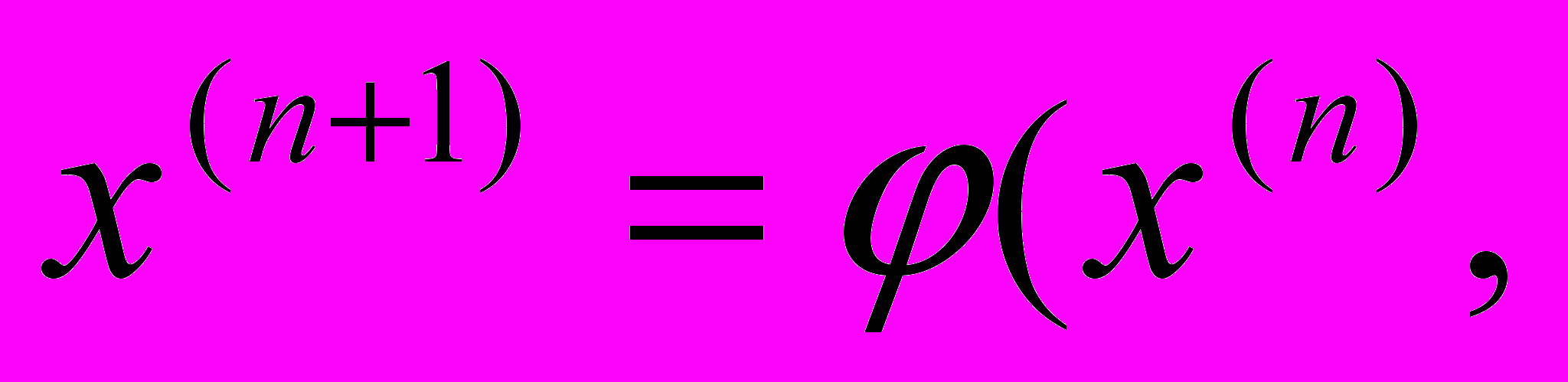
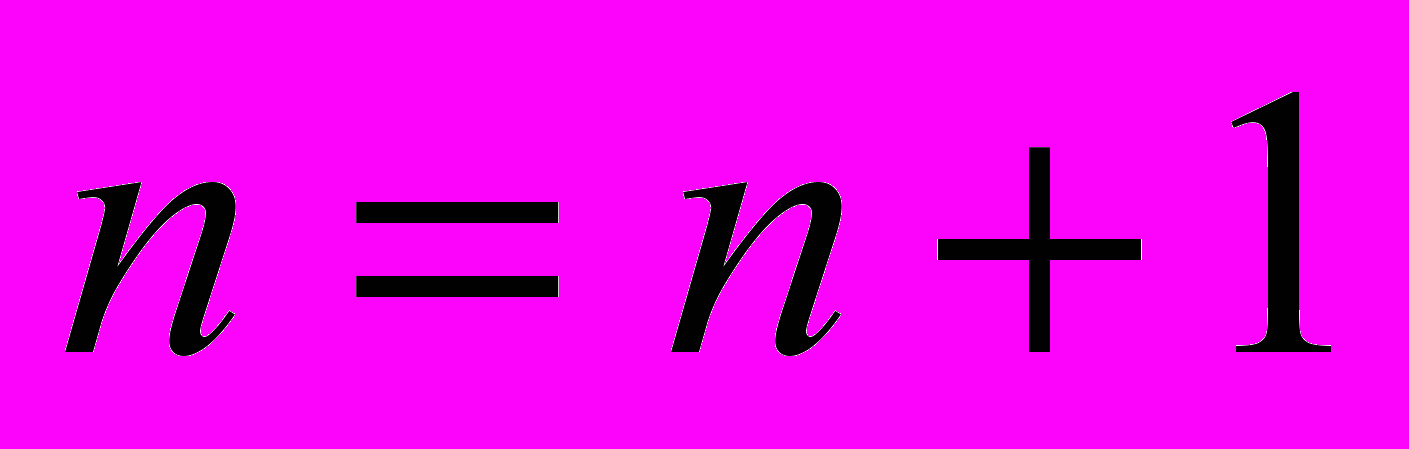
If
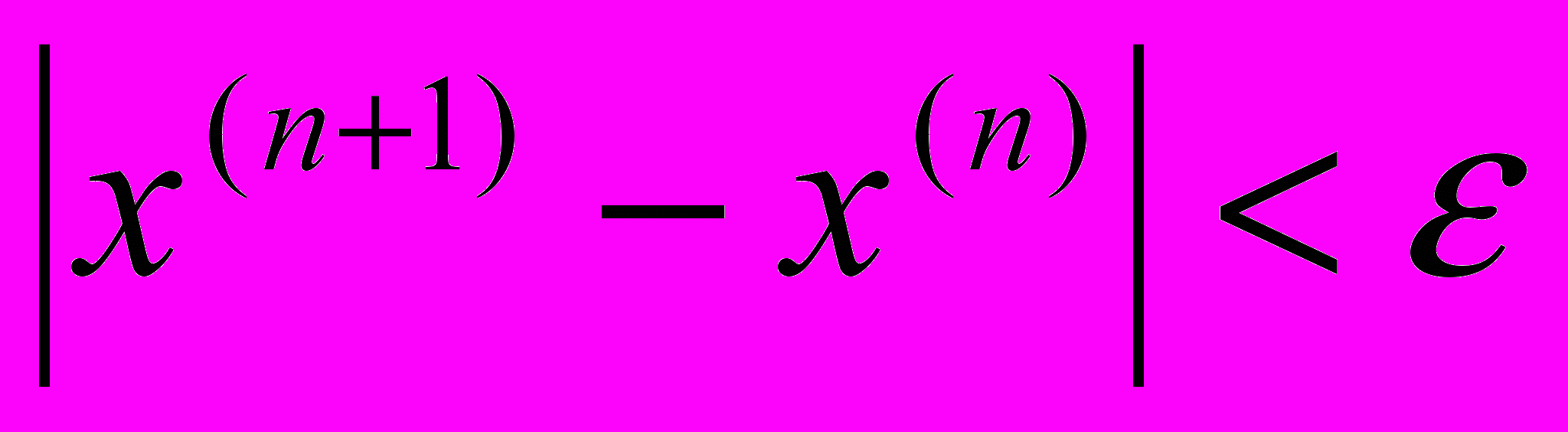
ДА НЕТ
Вывод
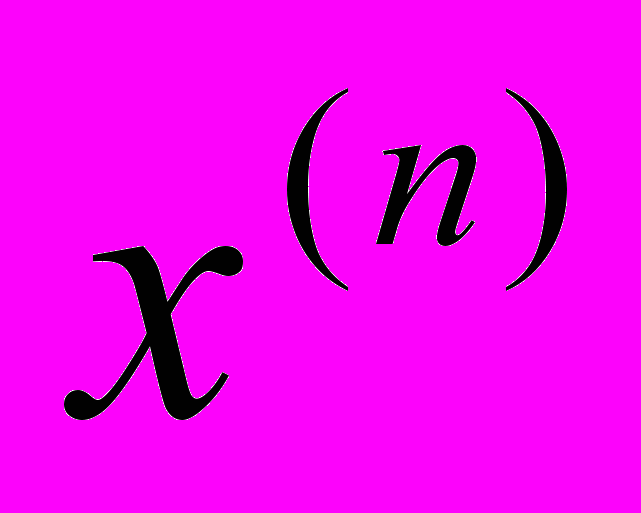 Возврат к пункту *
Возврат к пункту *3.4. Программа решения задания
#include
#include
#include "func.h"
void main()
{
int i=0;
float a,b,x,eps=0.000001,c;
puts("Vvedite granici otrezka a i b");
scanf("%f\n%f",&a,&b);
if(func(a)*d2func(a)>0)
x=a;
else
x=b;
do
{
c=x;
x=c-func(c)/dfunc(c);
i++;
}
while(fabs(x-c)>eps);
printf("x=%f\nkol-vo iteraciy=%d\n",x,i);
}
3.5. Результат счета
x=-2.000000 на отрезке [-2.1;-1.9]
x=-0.100000 на отрезке [-0.2;0]
x=0.100000 на отрезке [0;0.2]
Задание IV: Метод секущих
4.1. Постановка задачи
Задано нелинейное уравнение
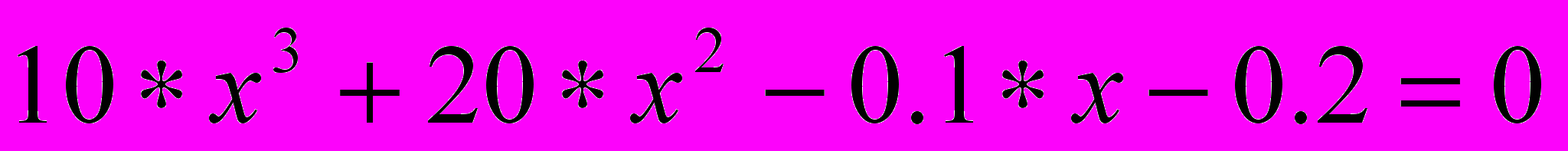
Требуется найти корни этого уравнения, т.е. те значения
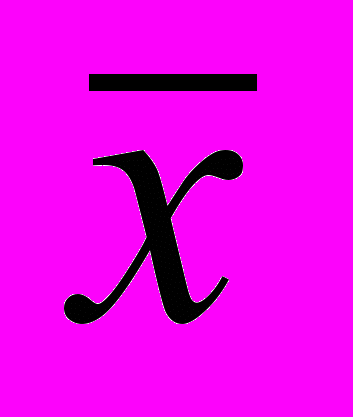 , при подстановке которых уравнение обращается в тождество
, при подстановке которых уравнение обращается в тождество 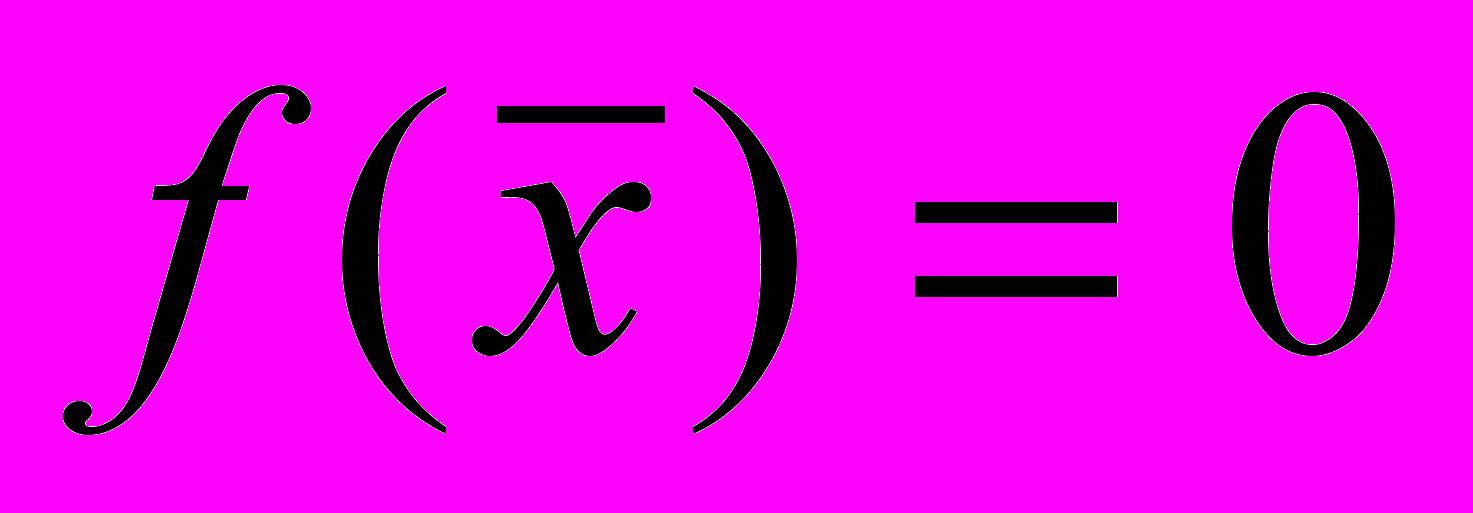 методом секущих с точностью
методом секущих с точностью 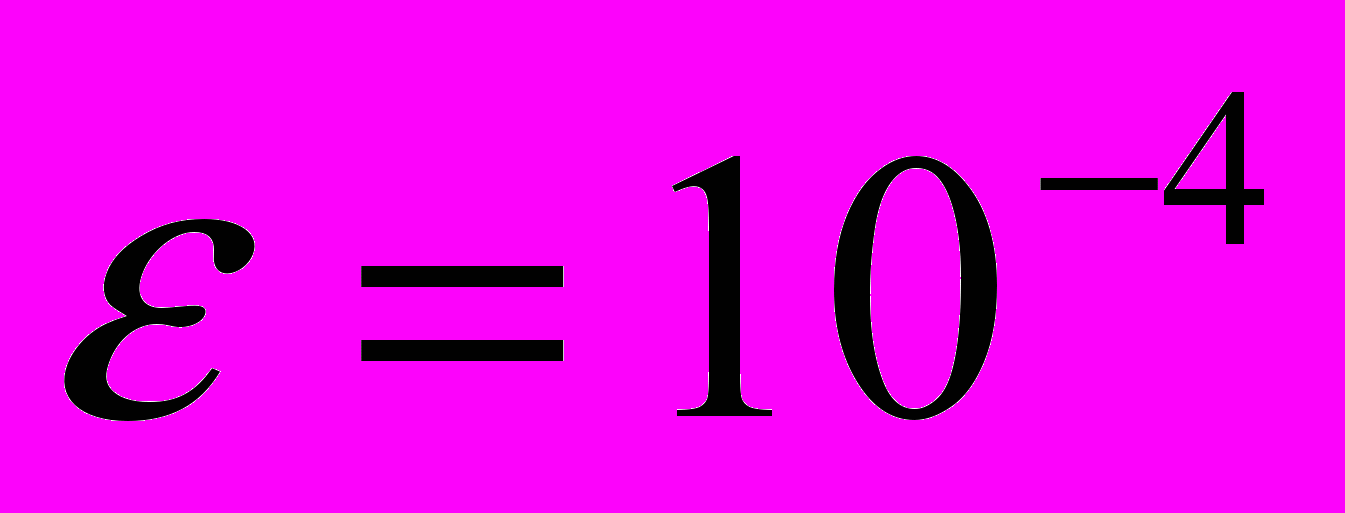 ,
, 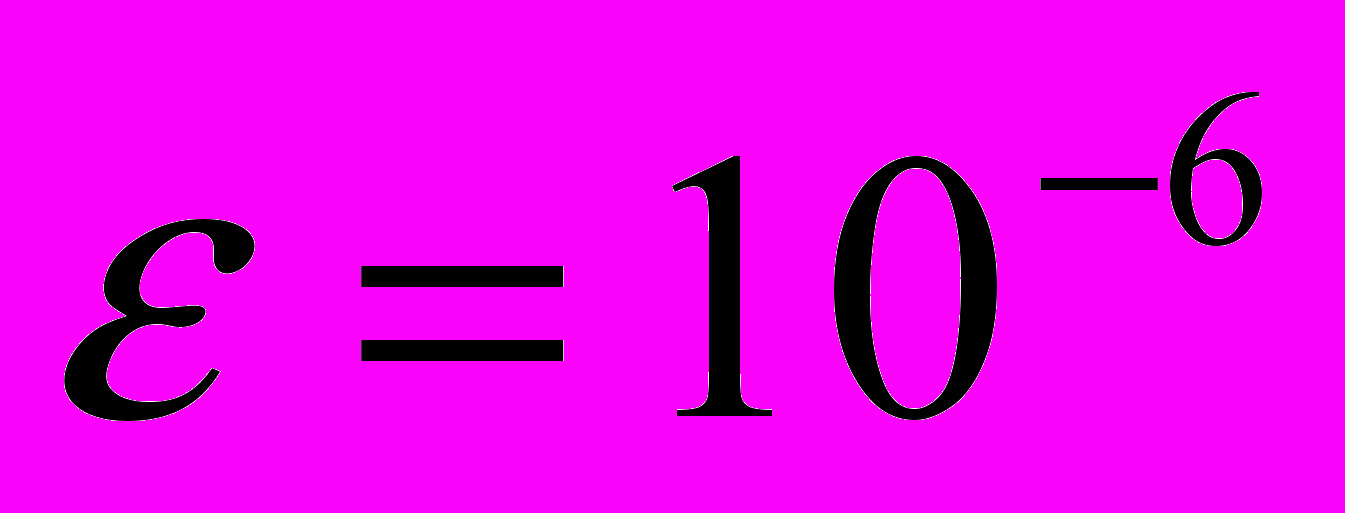 ,
, 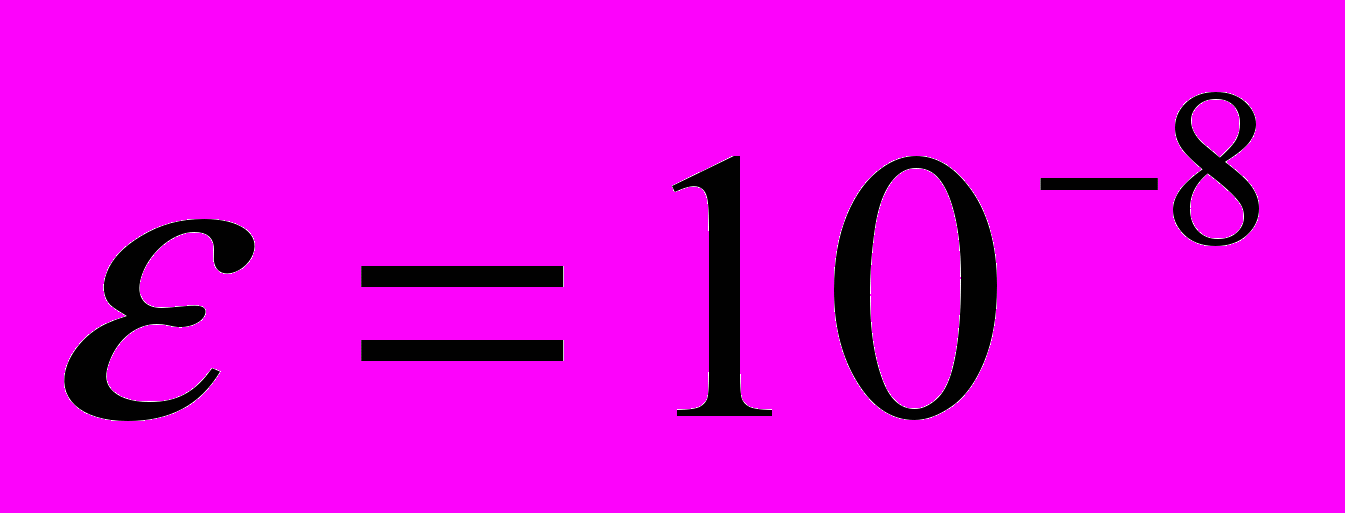 .
.4.2. Разработка алгоритма
Заменим производную
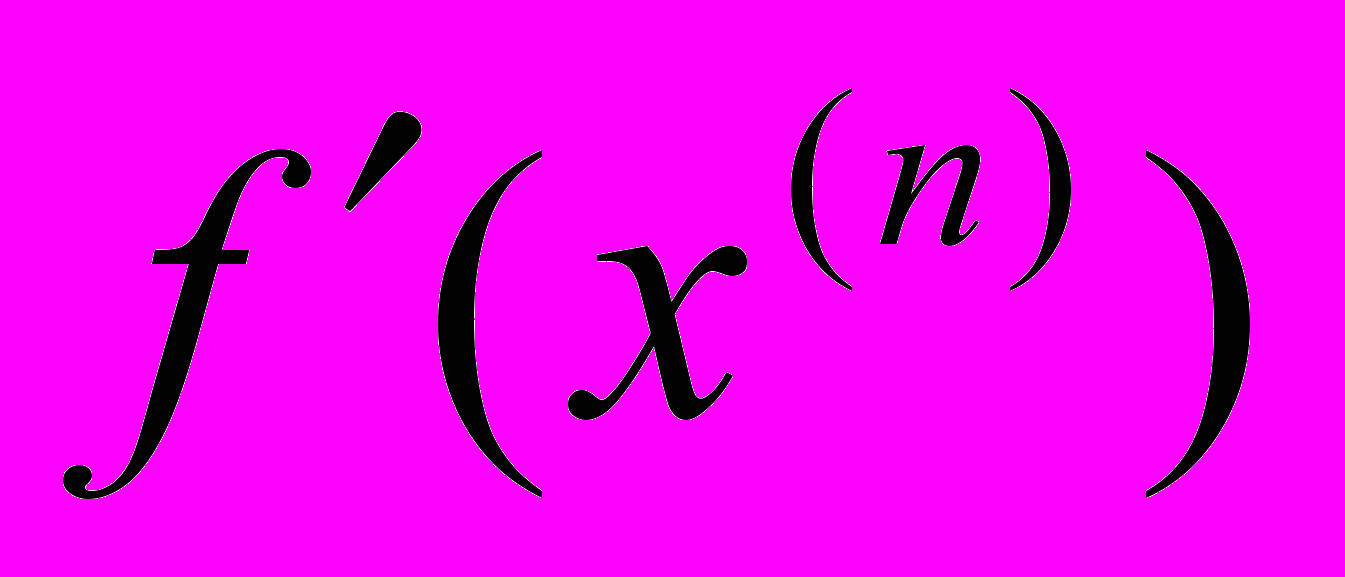 в формуле метода Ньютона приближением
в формуле метода Ньютона приближением 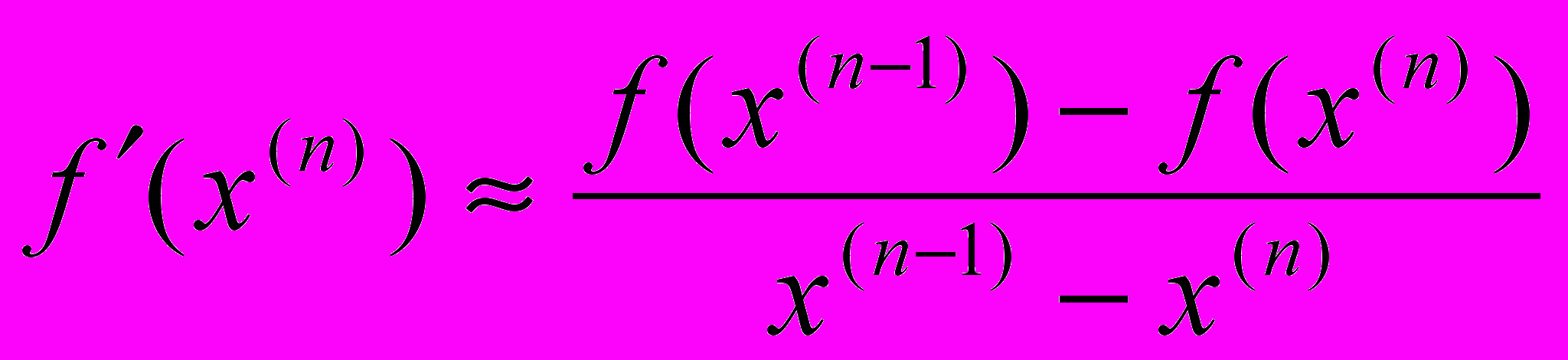 и получим расчетную формулу метода секущих:
и получим расчетную формулу метода секущих: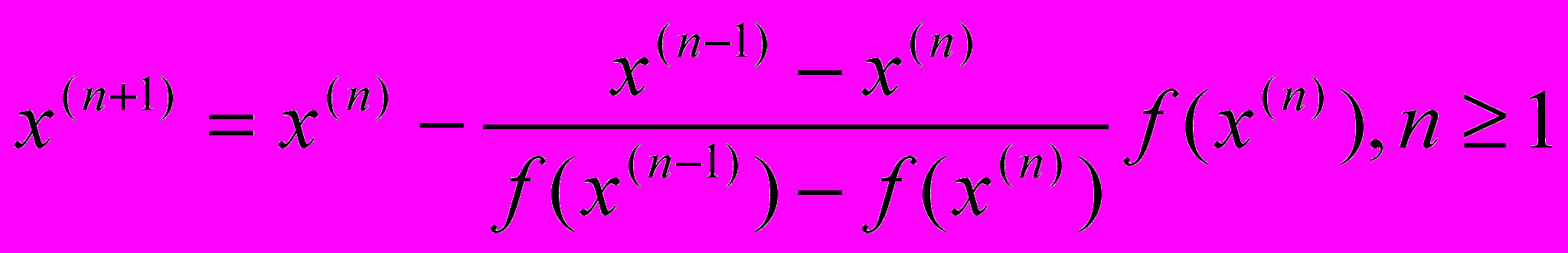
4.3. Структурограмма

Ввод
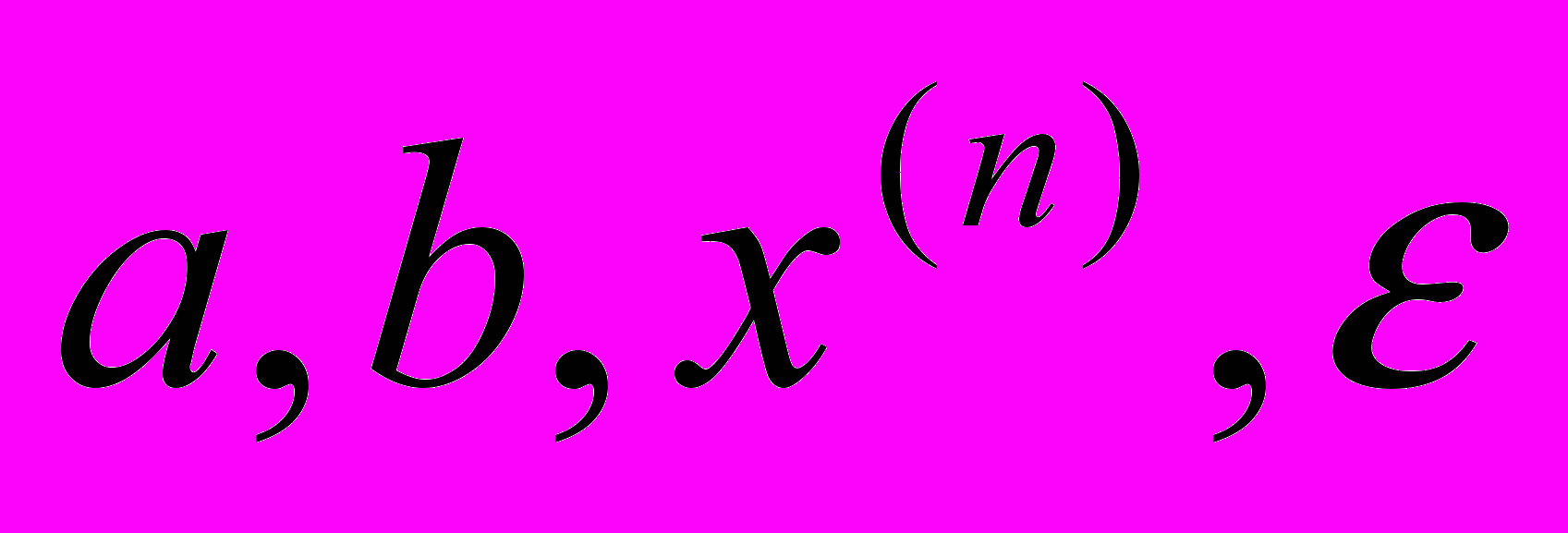
*
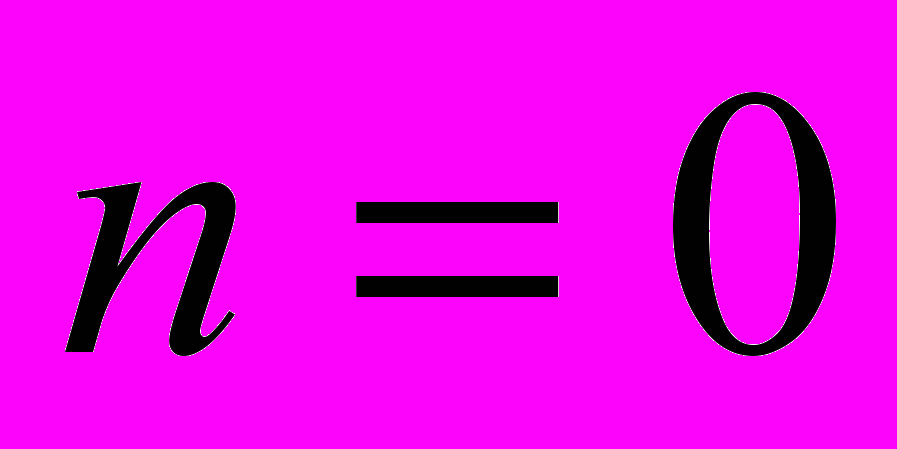
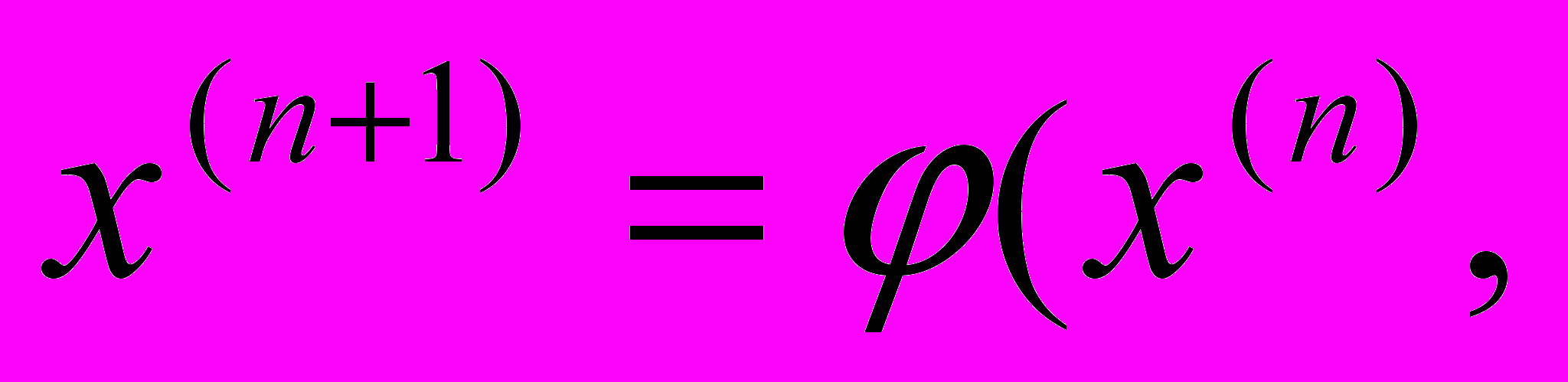
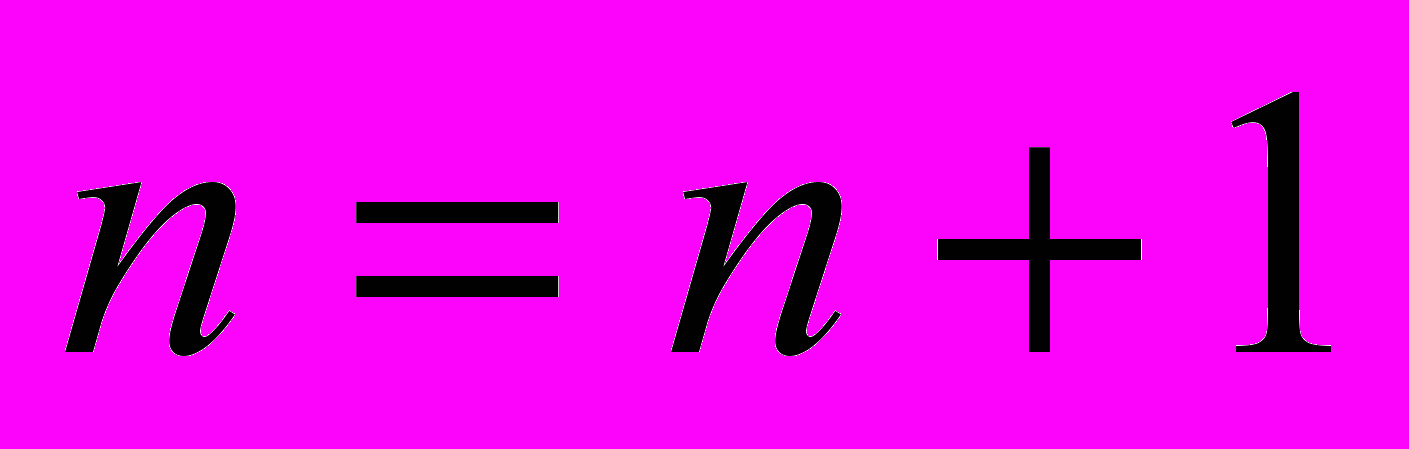
If
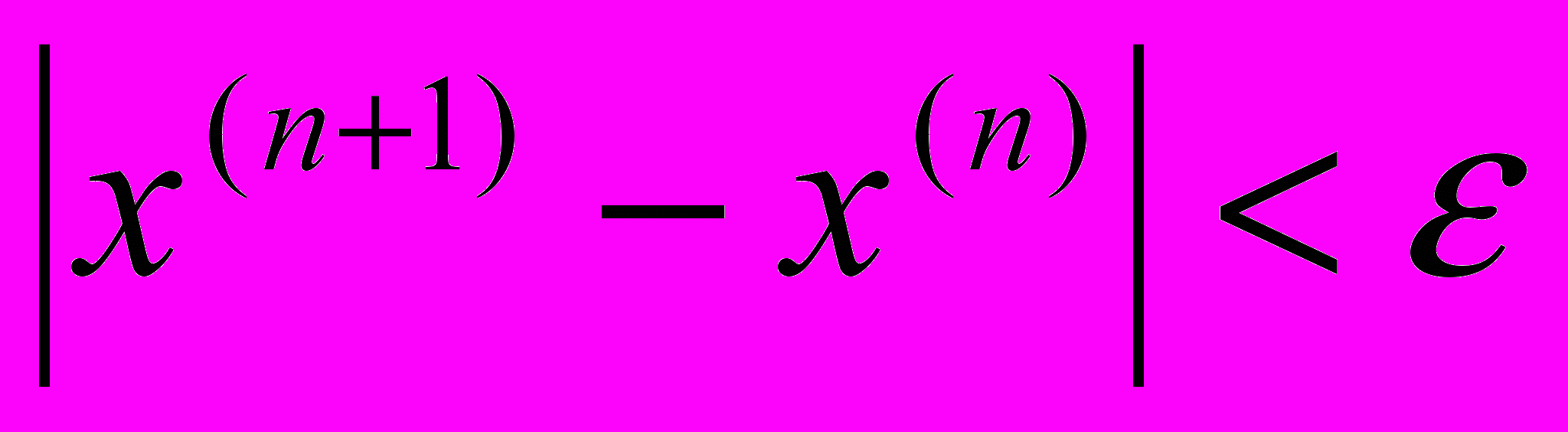
ДА НЕТ
Вывод
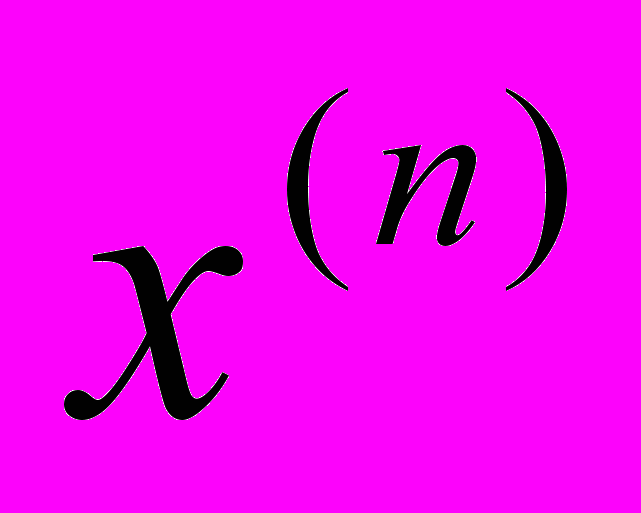 Возврат к пункту *
Возврат к пункту *4.4. Программа решения задания
#include
#include
#include "func.h"
void main()
{
int i=0;
float a,b,xp,xc,x,eps=0.000001;
puts("Vvedite granici otrezka a i b");
scanf("%f%f",&a,&b);
x=(a+b)/2;
if(dfunc(x)*d2func(x)>0)
{
xc=a;
xp=xc+(b-a)/100;
}
else
{
xc=b;
xp=xc+(a-b)/100;
}
{
}
do
{
xc=xp;
xp=x;
x=xp-((xc-xp)*func(xp))/(func(xc)-func(xp));
i++;
}
while(fabs(x-xp)>eps);
printf("x=%f\nkol-vo iteraciy=%d\n",x,i);
}
4.5. Результат счета
x=-2.000000 на отрезке [-2.1;-1.9]
x=-0.100000 на отрезке [-0.2;0]
x=0.100000 на отрезке [0;0.2]
Задание V: Гибридный метод
5.1. Постановка задачи
Задано нелинейное уравнение
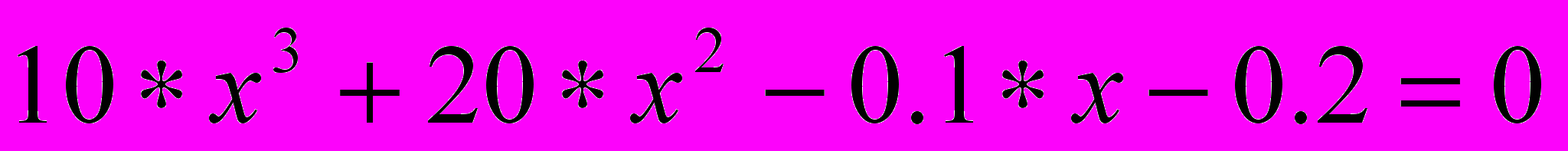
Требуется найти корни этого уравнения, т.е. те значения
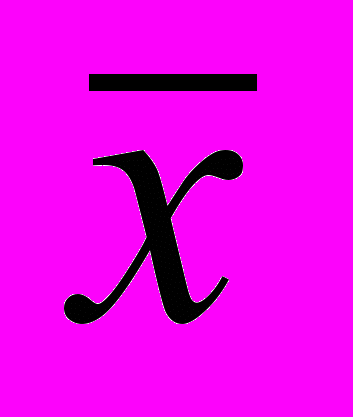 , при подстановке которых уравнение обращается в тождество
, при подстановке которых уравнение обращается в тождество 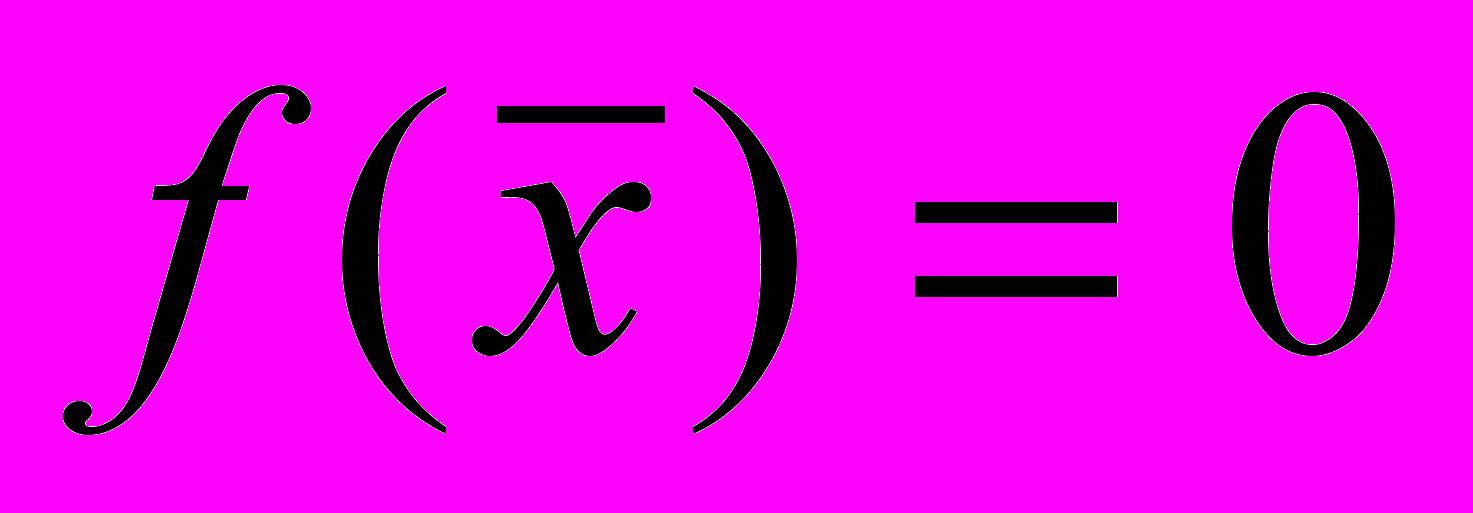 гибридным методом с точностью
гибридным методом с точностью 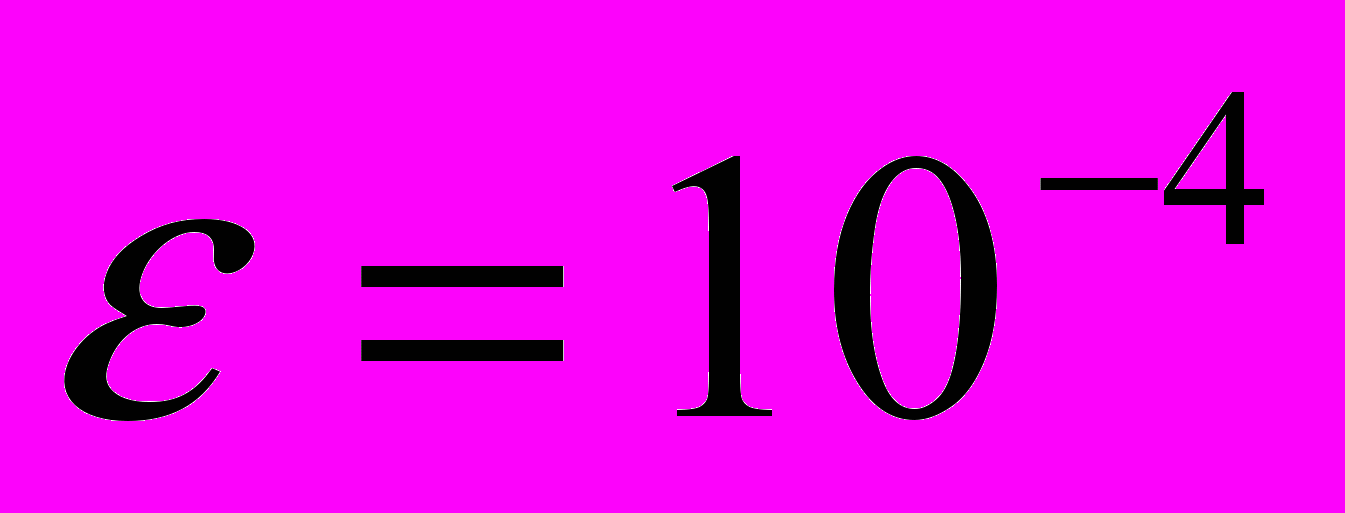 ,
, 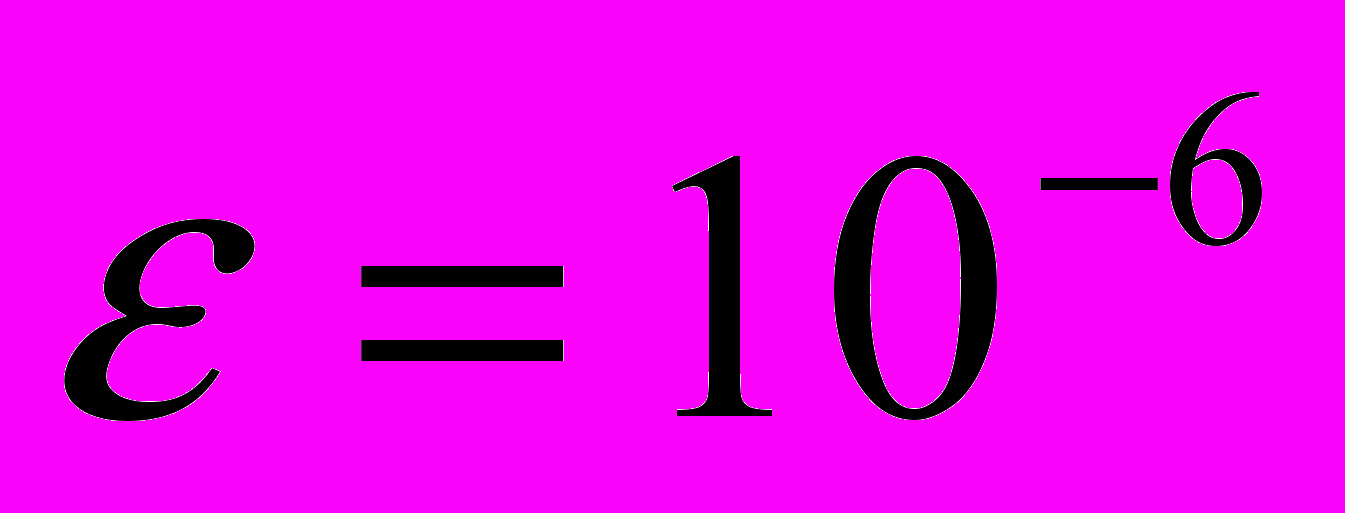 ,
, 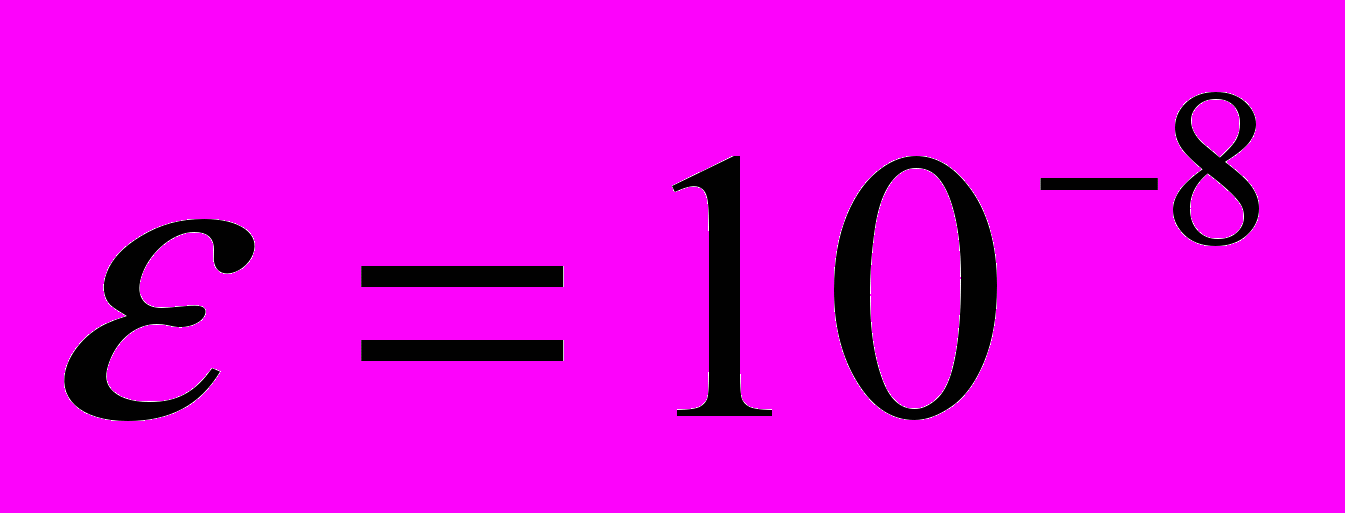 .
.5.2. Разработка алгоритма
Итерационная формула метода Стеффенсена записывается следующим образом:
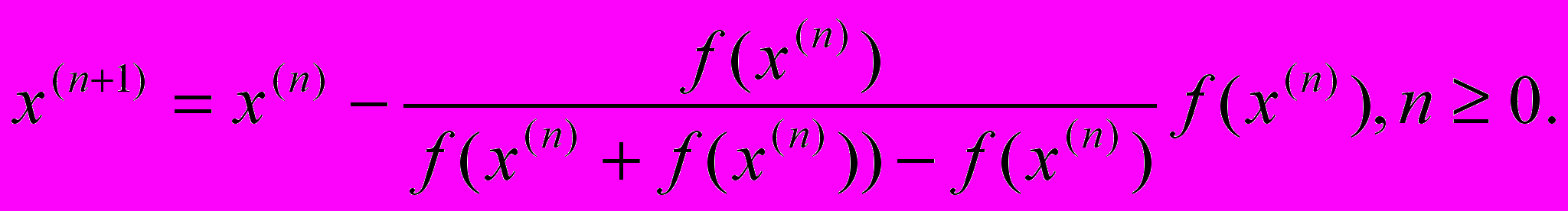
Можно считать, что она получена в результате замены производной
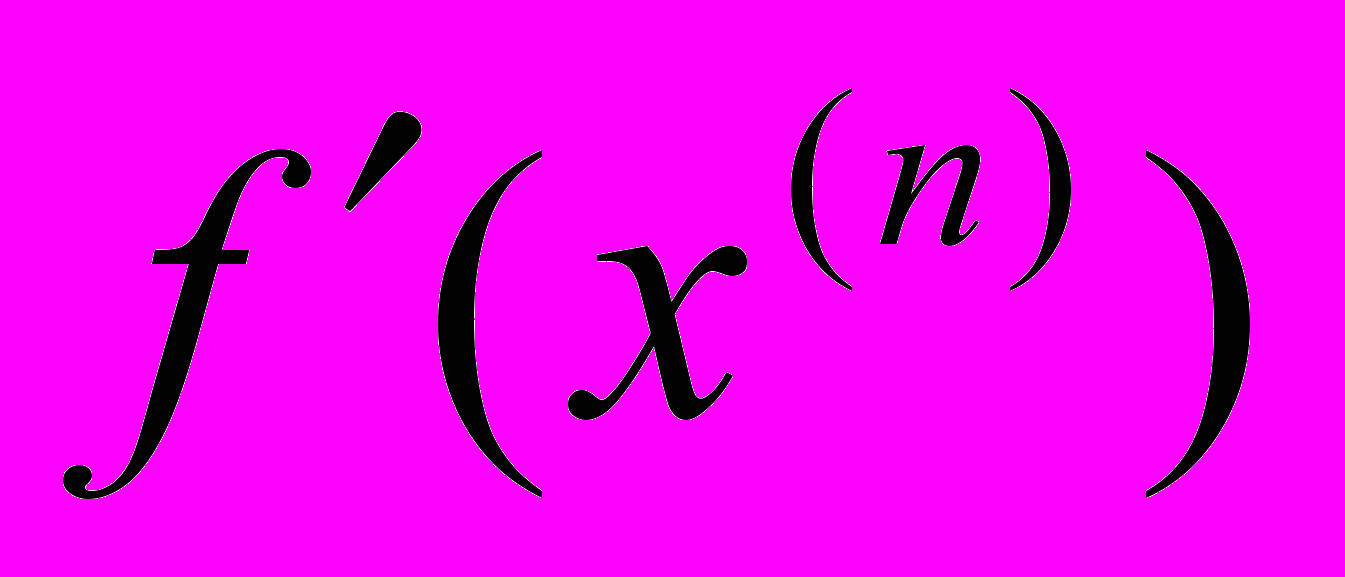 , входящей в расчетную формулу метода Ньютона, по формуле
, входящей в расчетную формулу метода Ньютона, по формуле 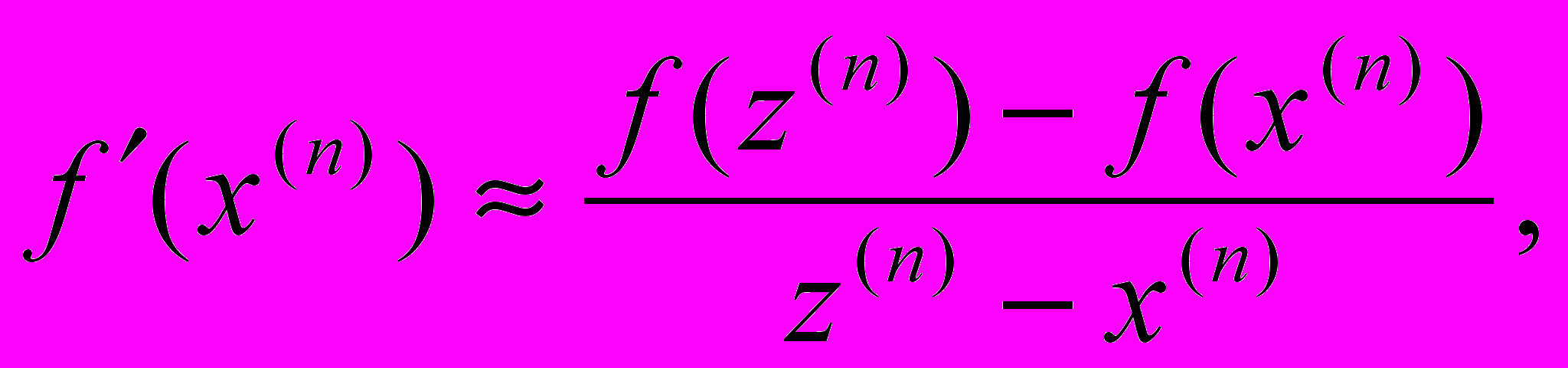 где
где 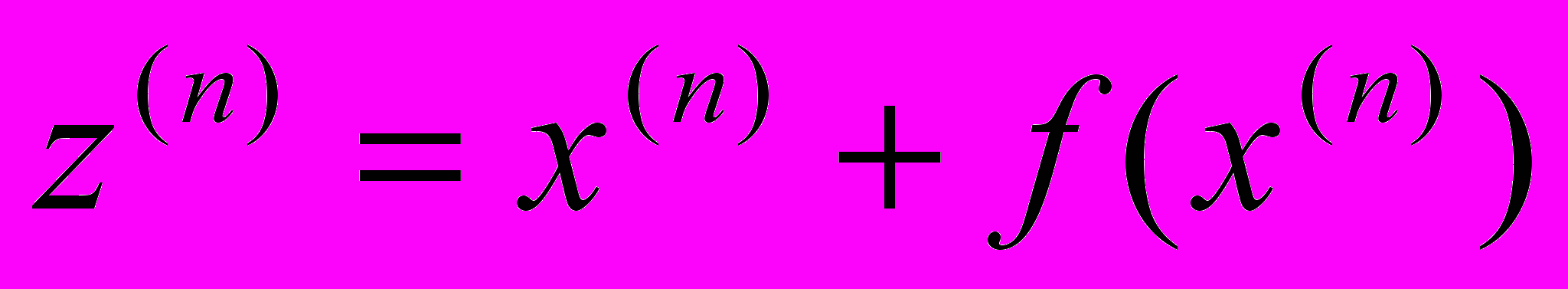
5.3. Структурограмма

Ввод
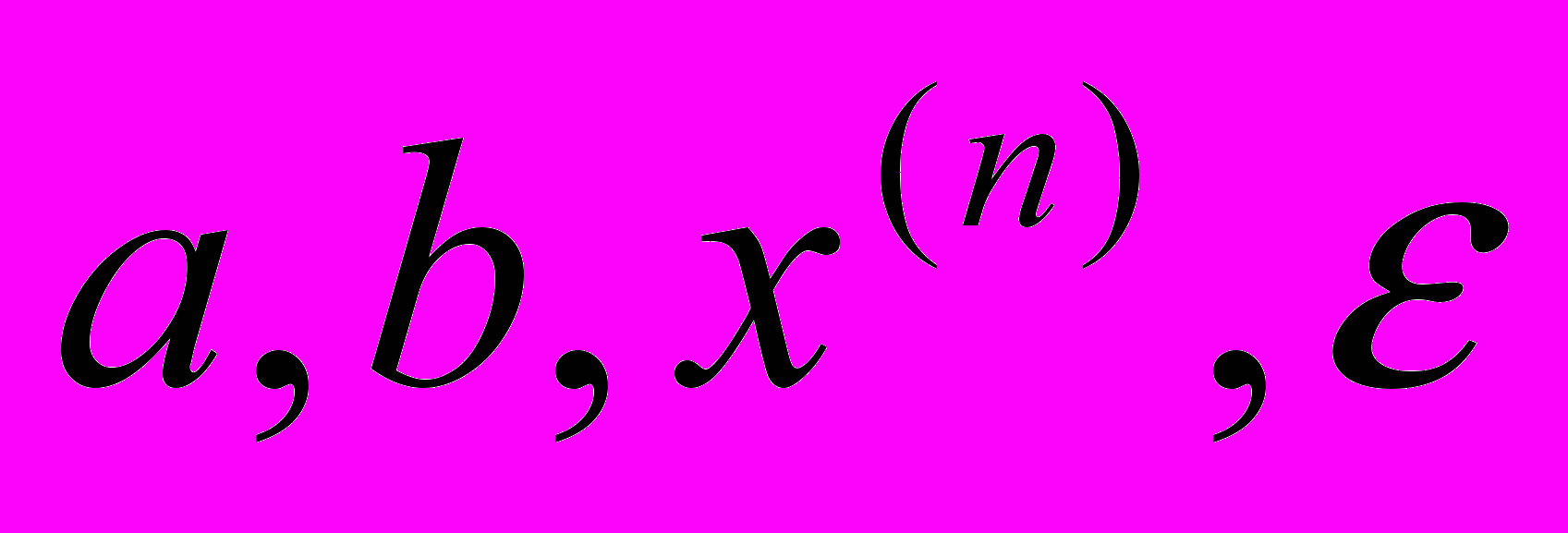
*
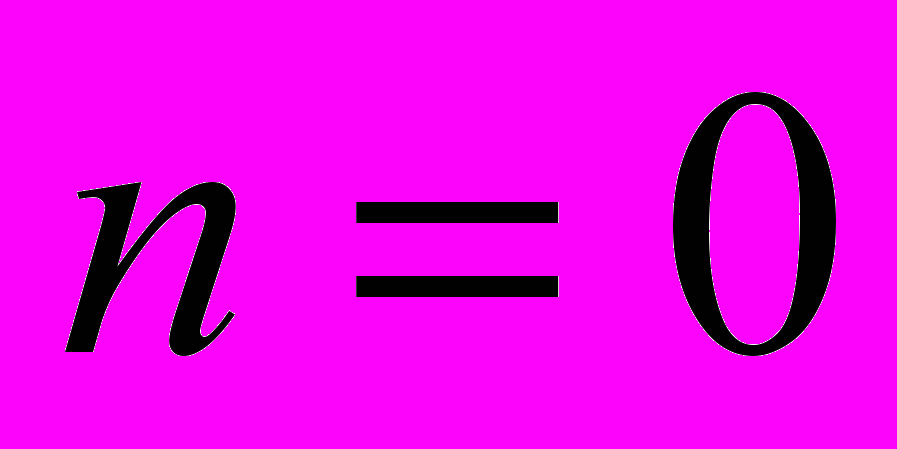
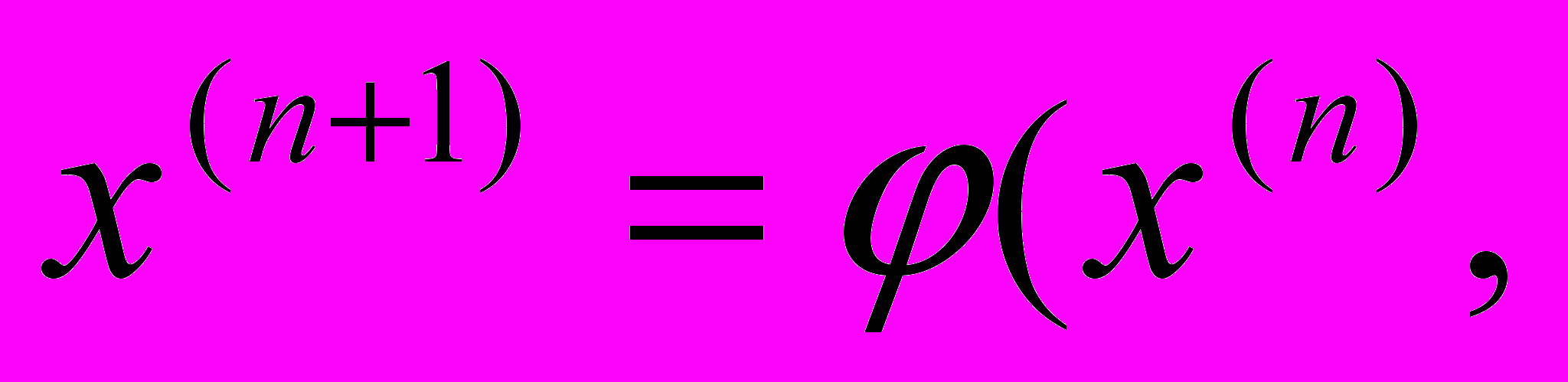
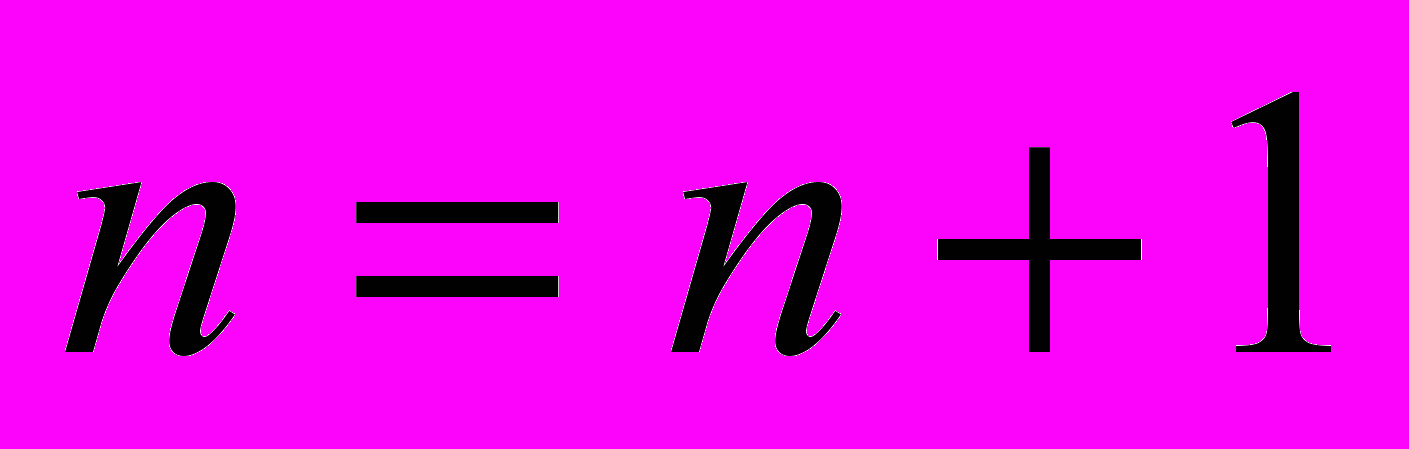
If
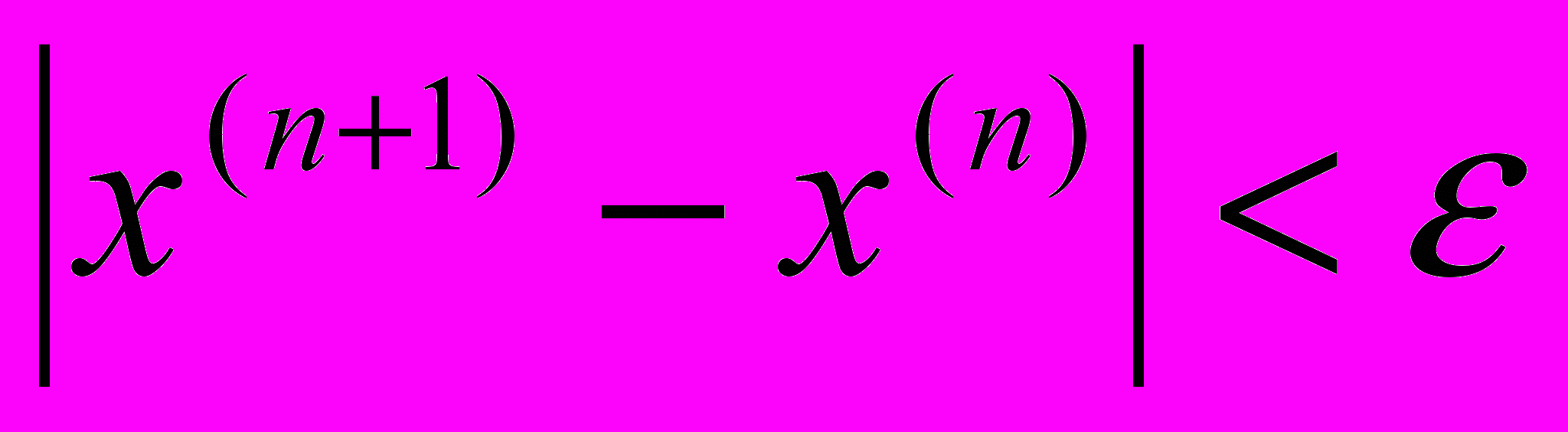
ДА НЕТ
Вывод
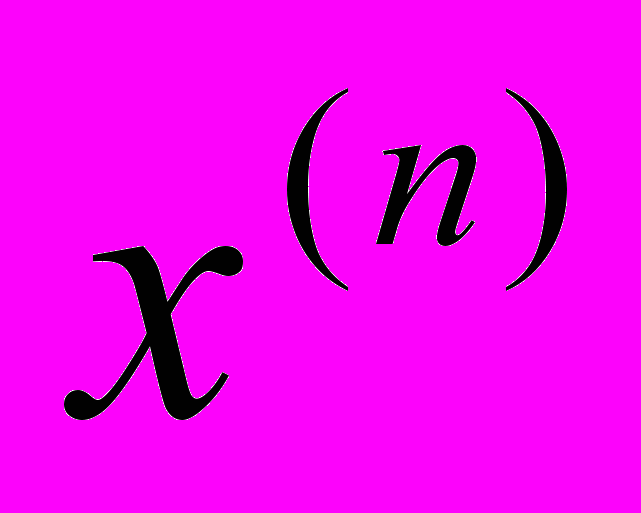 Возврат к пункту *
Возврат к пункту *5.4. Программа решения задания
#include
#include
#include "func.h"
void main()
{
int i=0;
float a,b,xp,x,eps=0.000001;
puts("Vvedite granici otrezka a i b");
scanf("%f%f",&a,&b);
x=(a+b)/2;
do
{
xp=x;
x=xp-func(xp)*func(xp)/(func(xp+func(xp))-func(xp));
i++;
}
while(fabs(x-xp)>eps);
printf("x=%f\nkol-vo iteraciy=%d\n",x,i);
}
5.5. Результат счета
x=-2.000000 на отрезке [-2.1;-1.9]
x=-0.100000 на отрезке [-0.2;0]
x=0.100000 на отрезке [0;0.2]
Задание VI: Решение системы линейных алгебраических уравнений (СЛАУ)
6.1. Постановка задачи
Задана система линейных уравнений
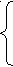
Требуется найти решение данной системы.
6.2. Разработка алгоритма
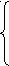
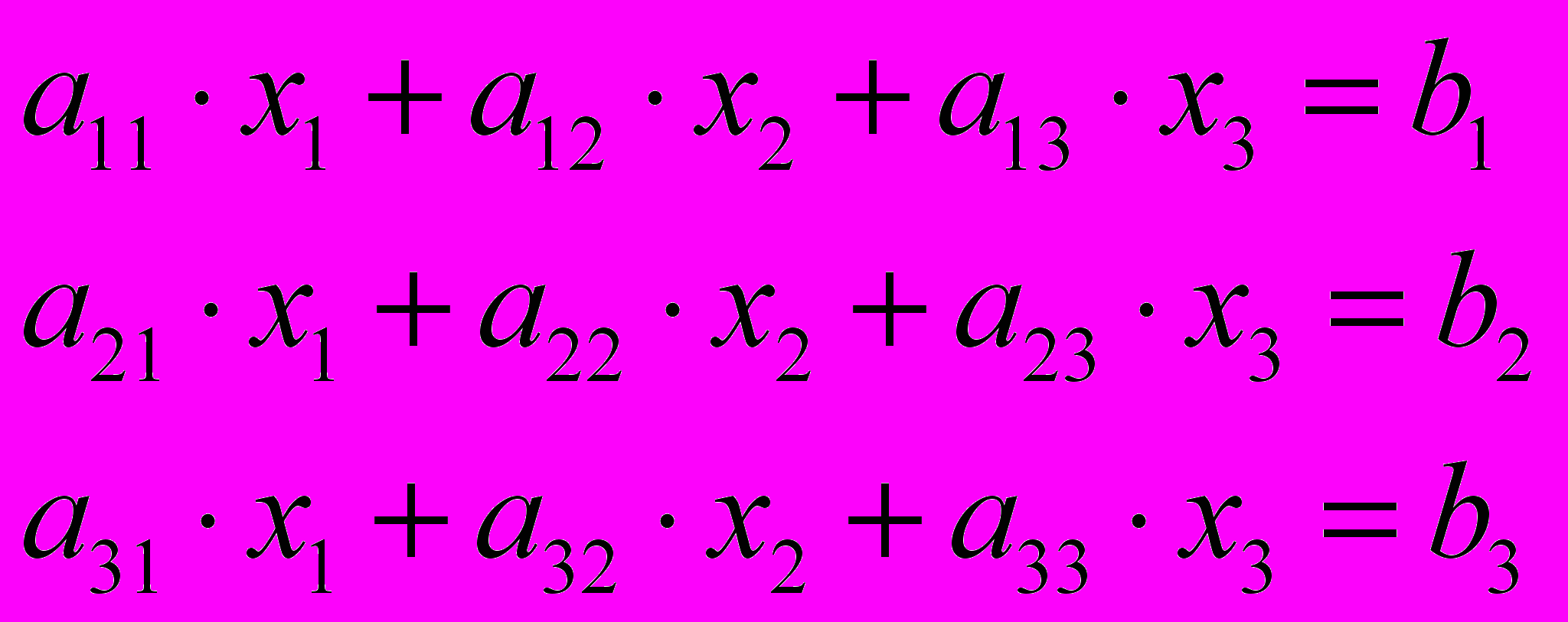
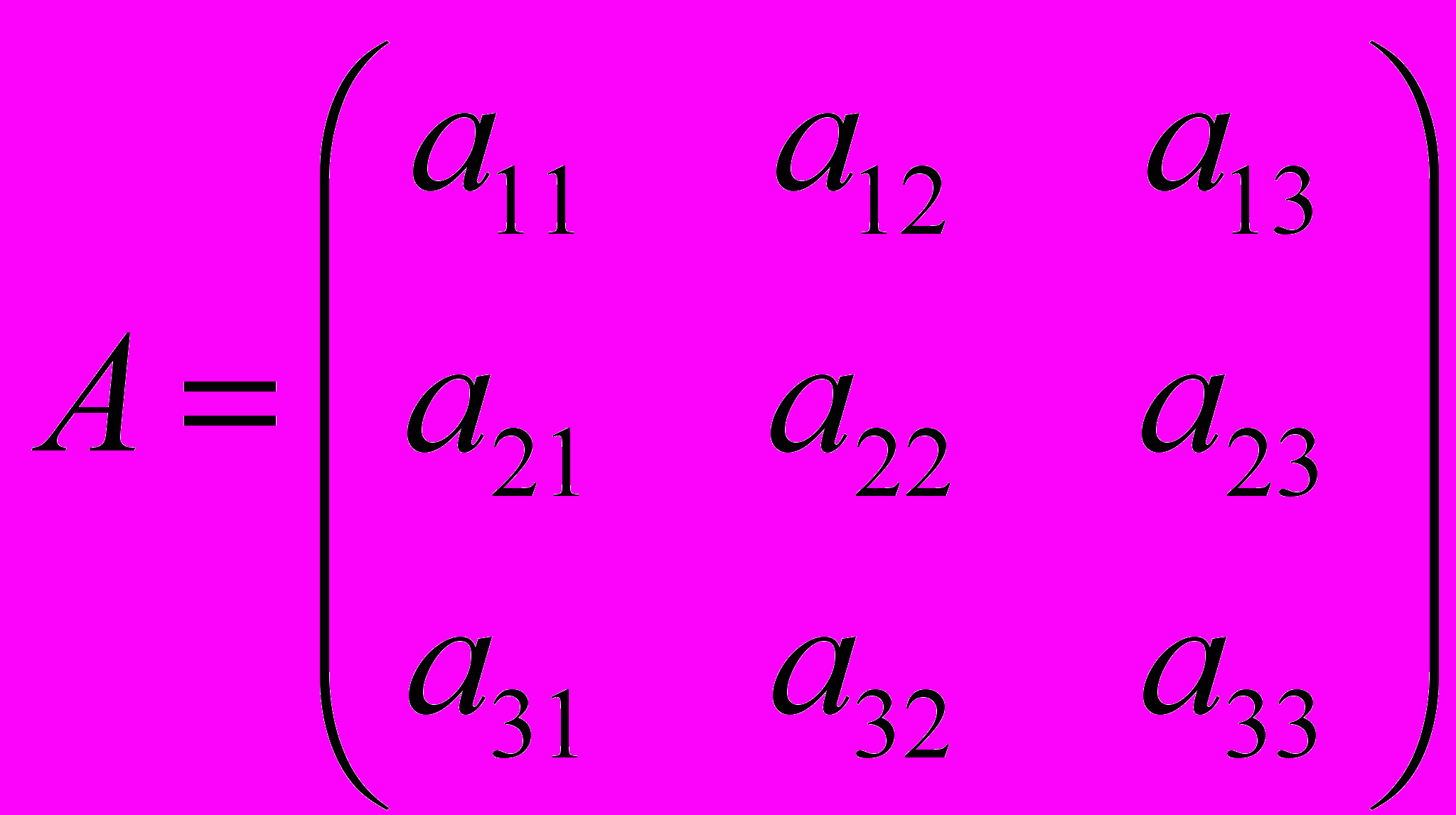 - квадратная матрица
- квадратная матрицаДля решения системы линейных уравнений необходимо найти главный определитель матрицы.
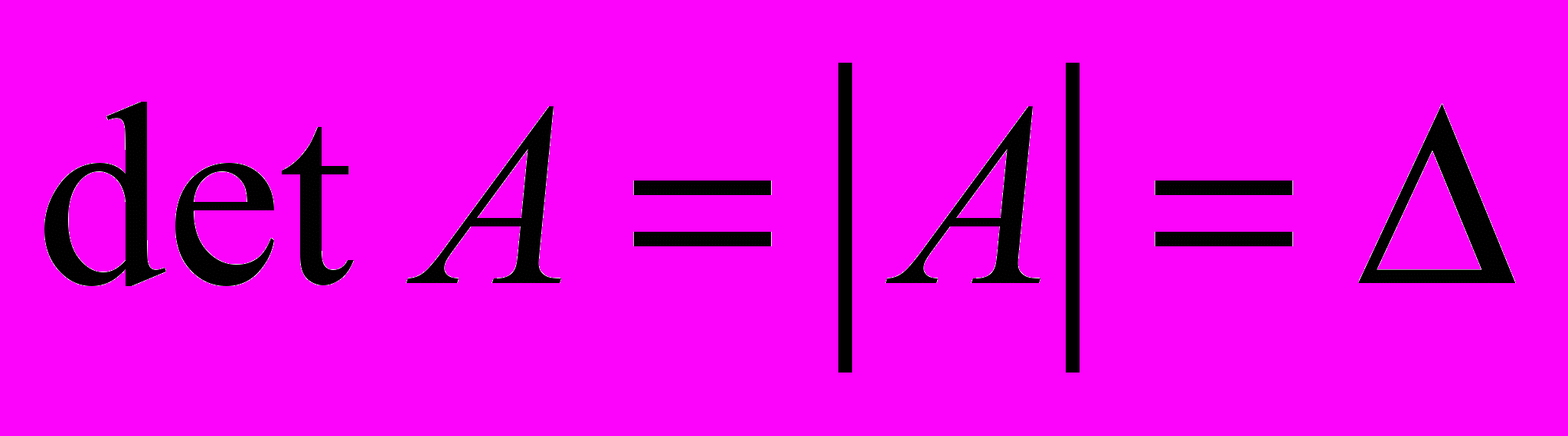
Далее определяем вспомогательные определители:
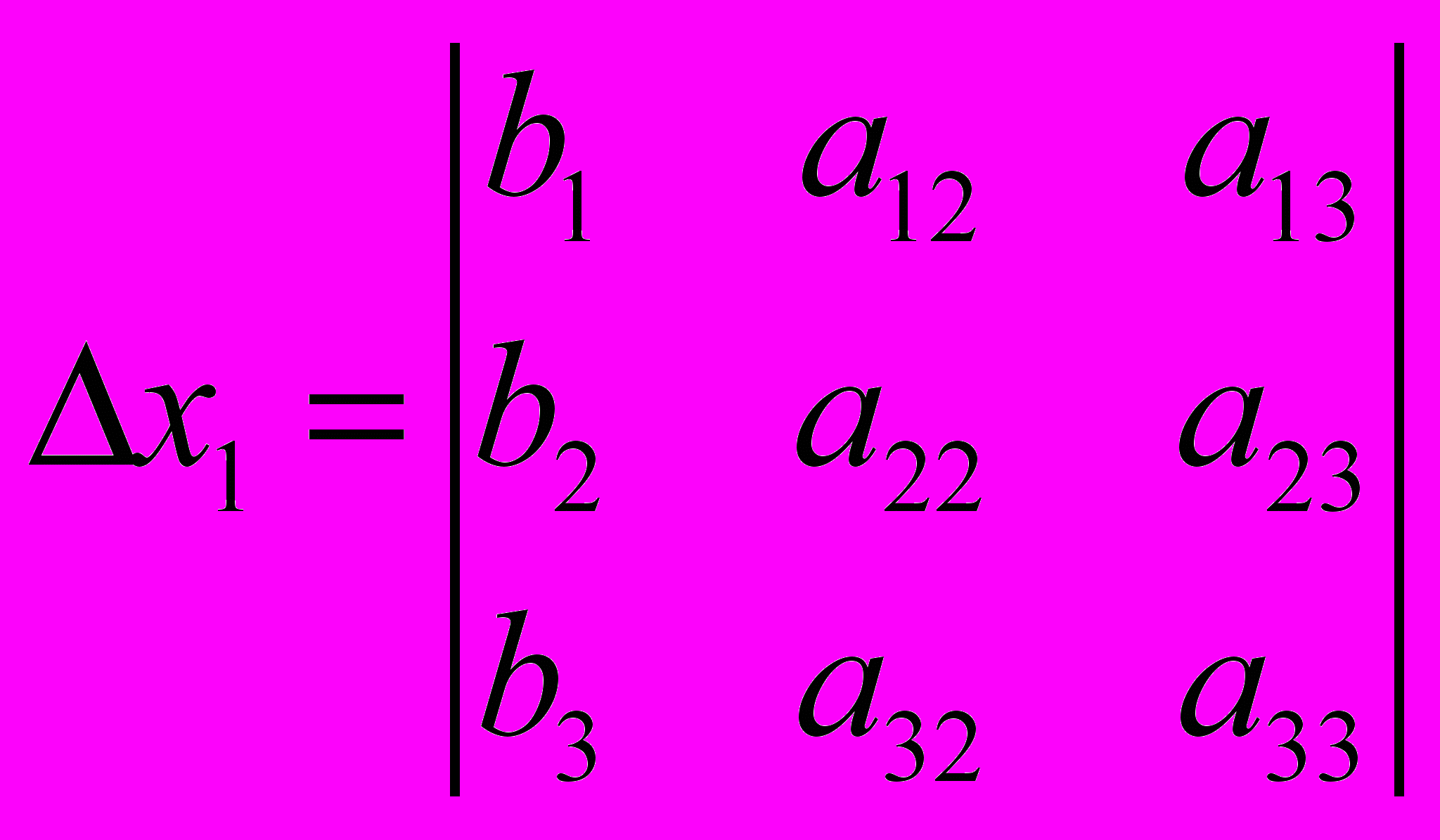
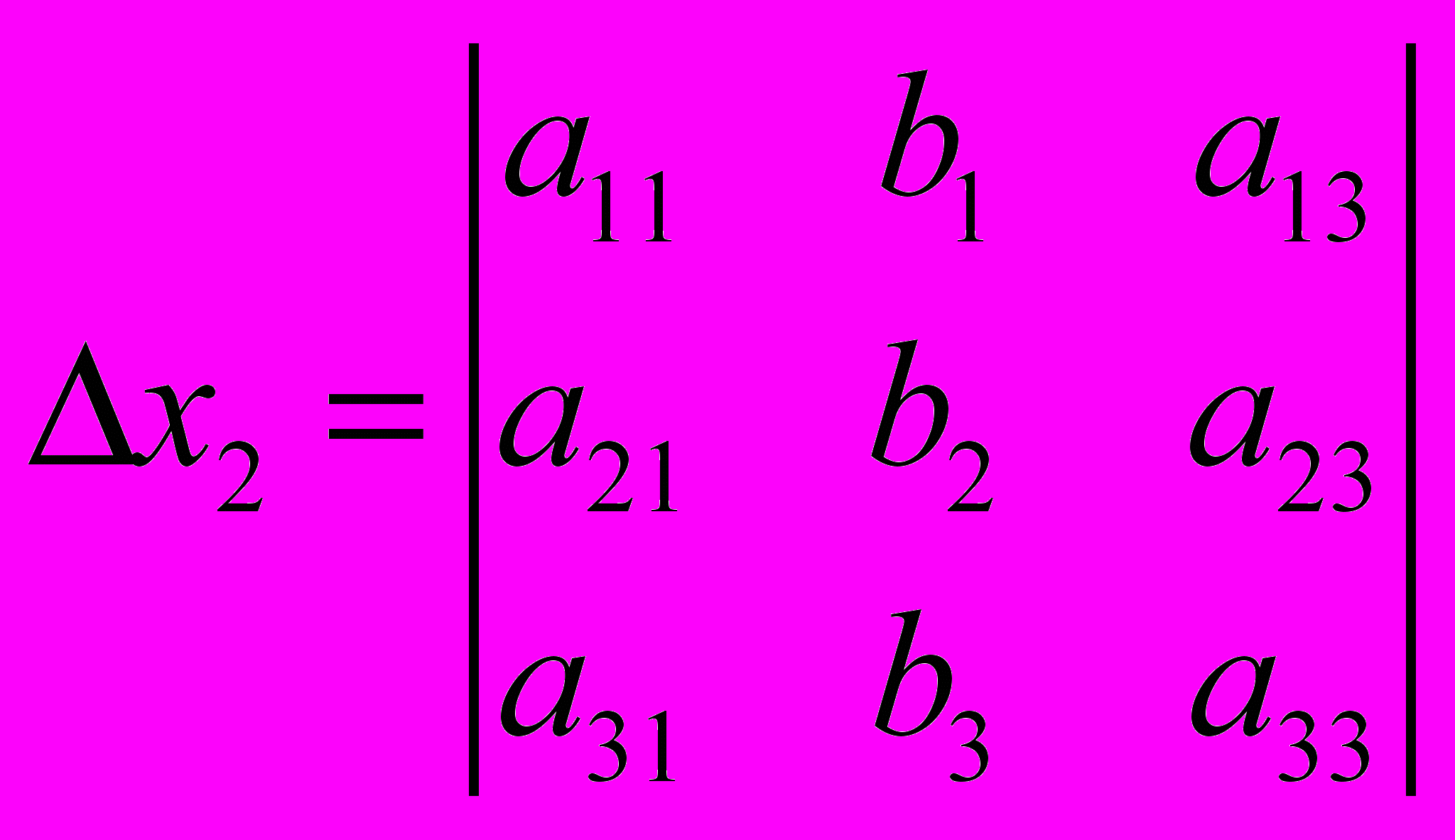
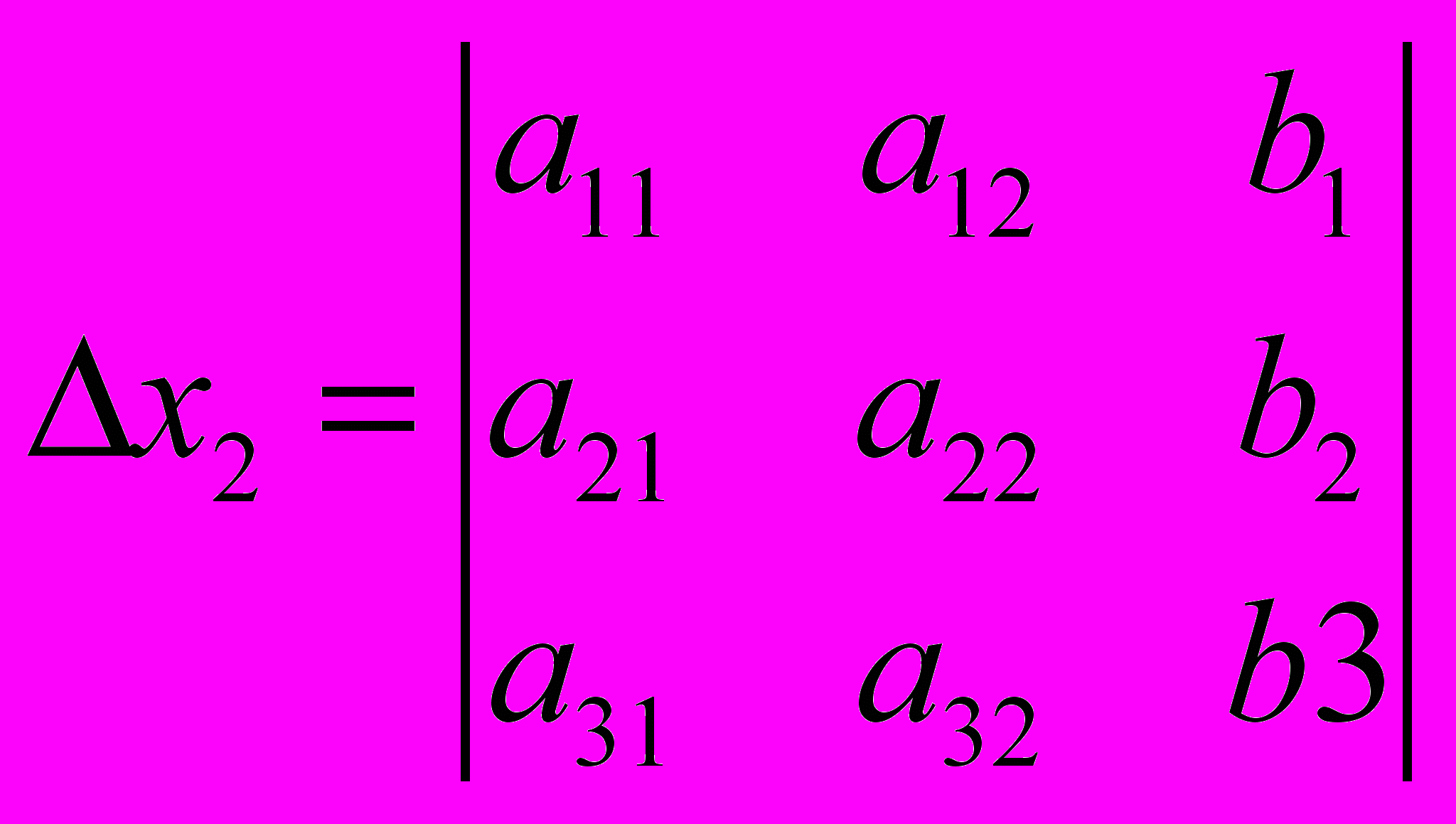
В том случае, если определитель матрицы равен нулю, то система линейных уравнений не имеет решения. Если определитель не равен нулю, то система имеет следующее решение:
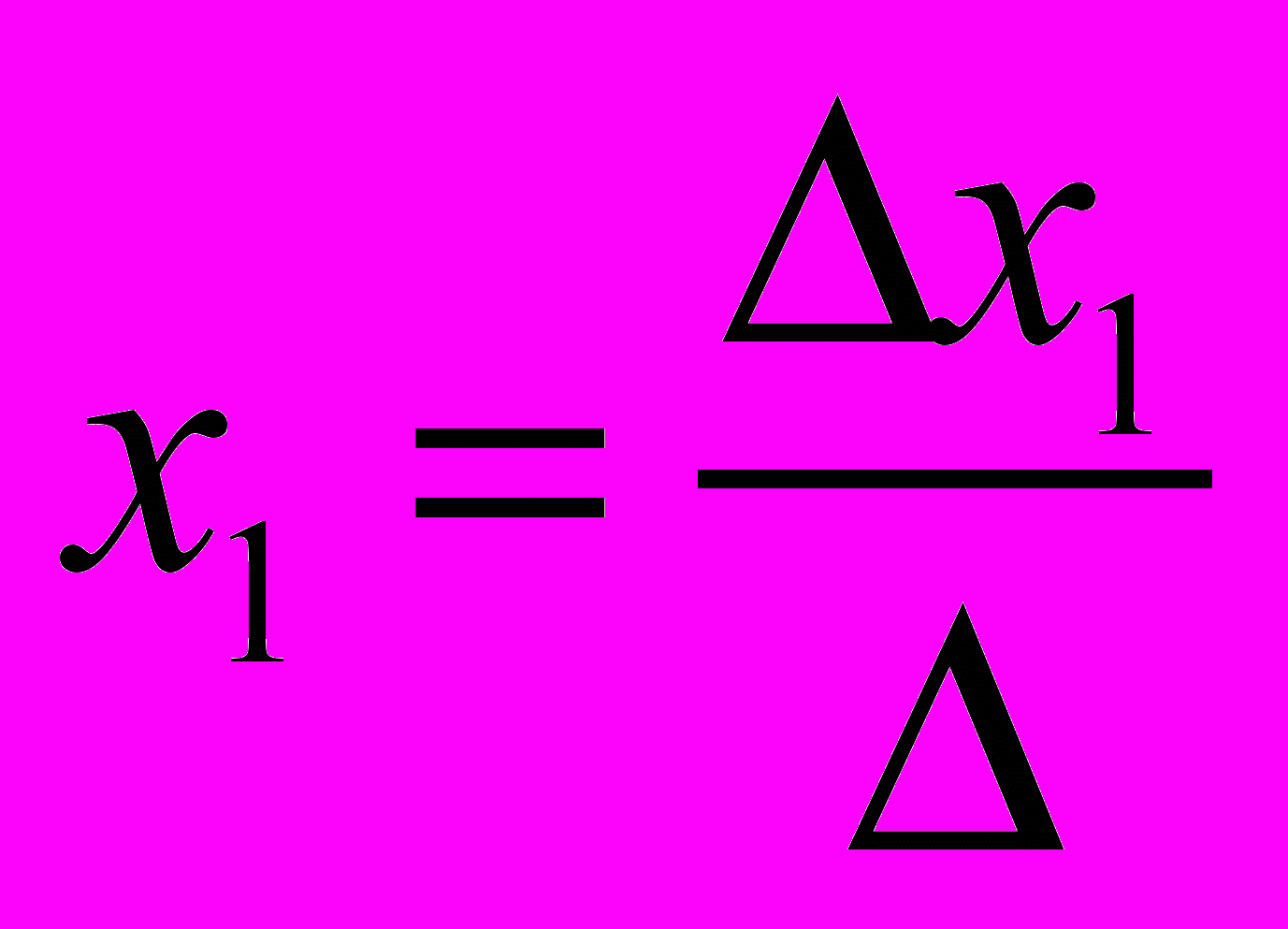
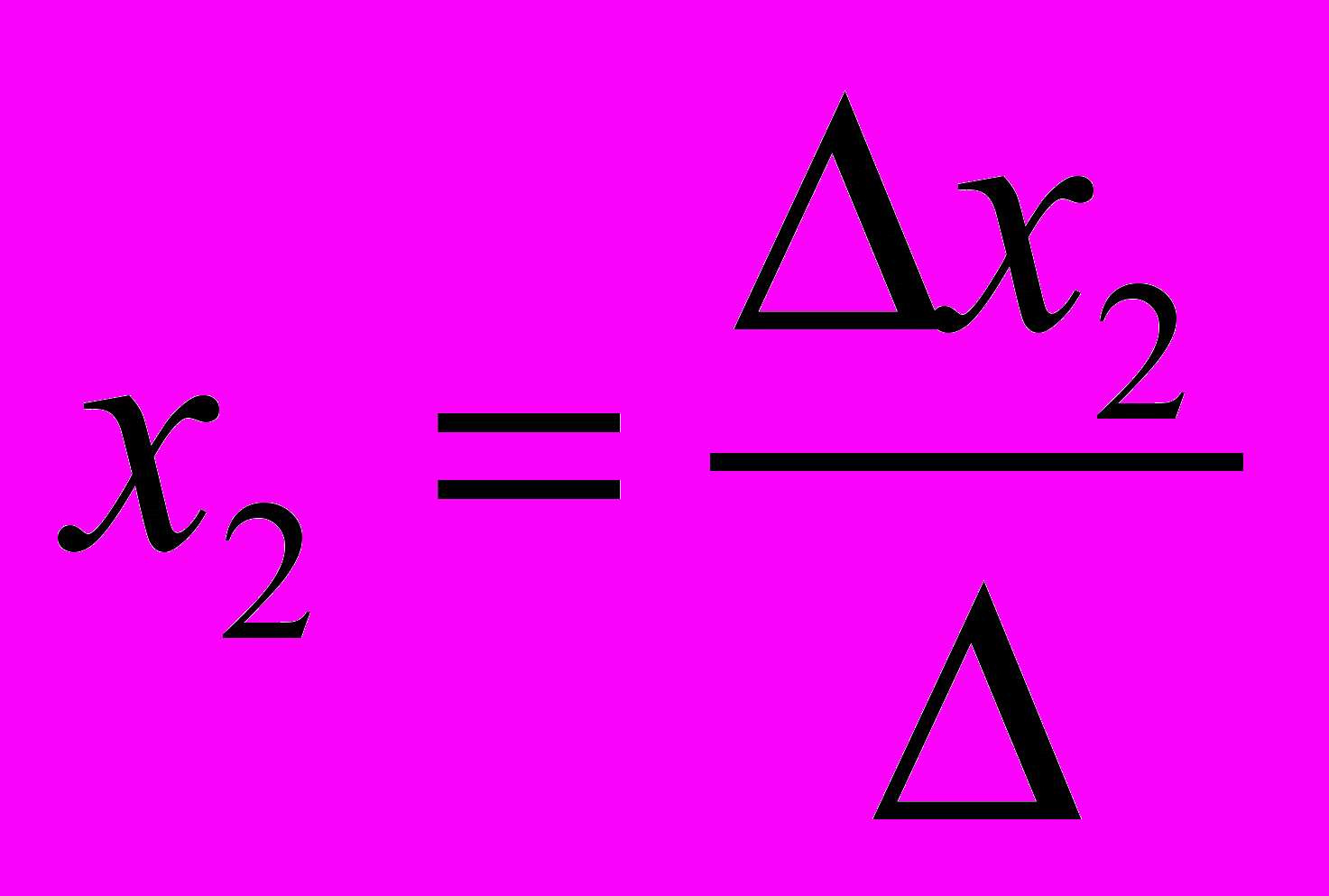
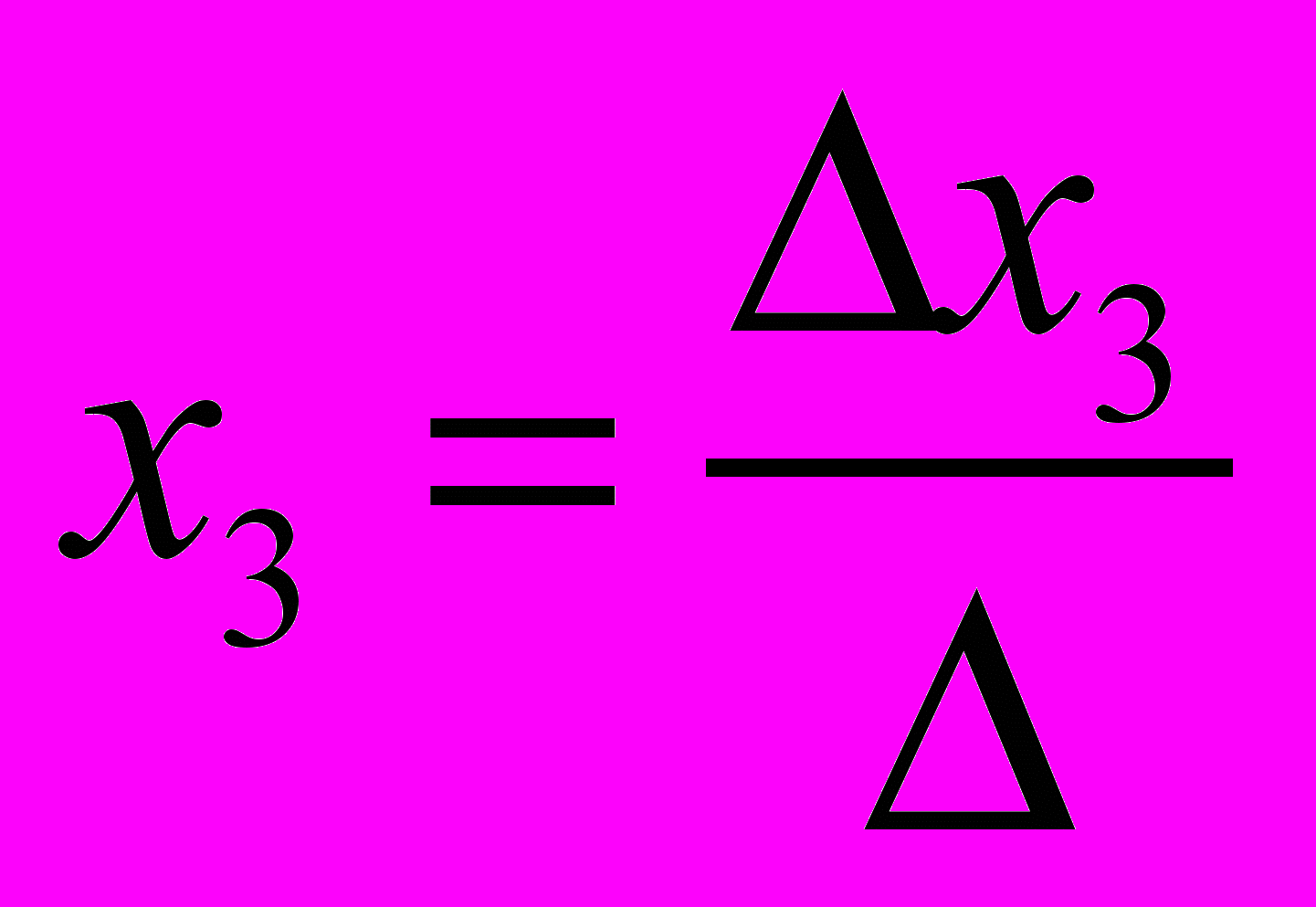
Если
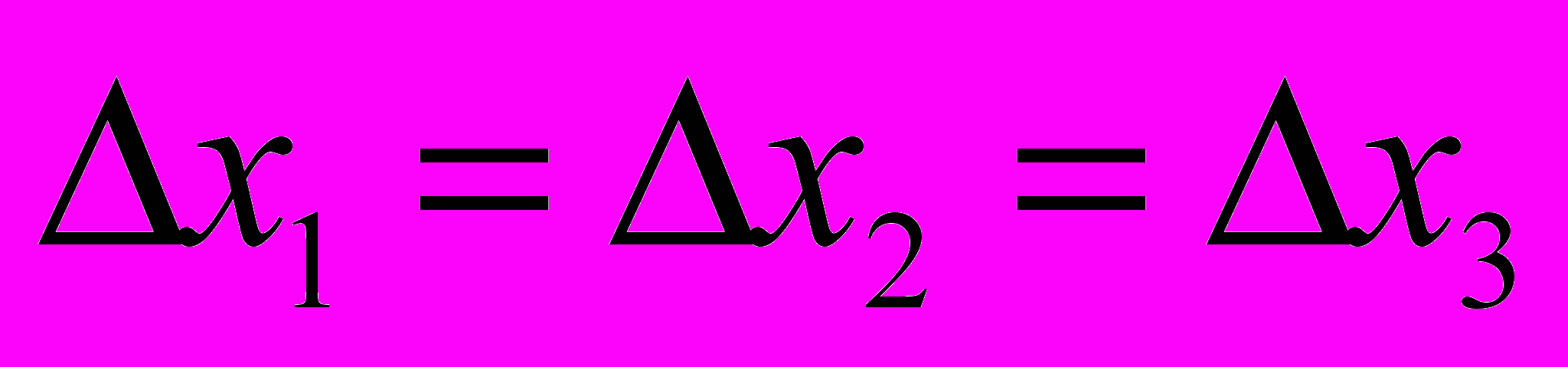 , то система линейных уравнений имеет бесконечно много решений.
, то система линейных уравнений имеет бесконечно много решений.6.3. Структурограмма
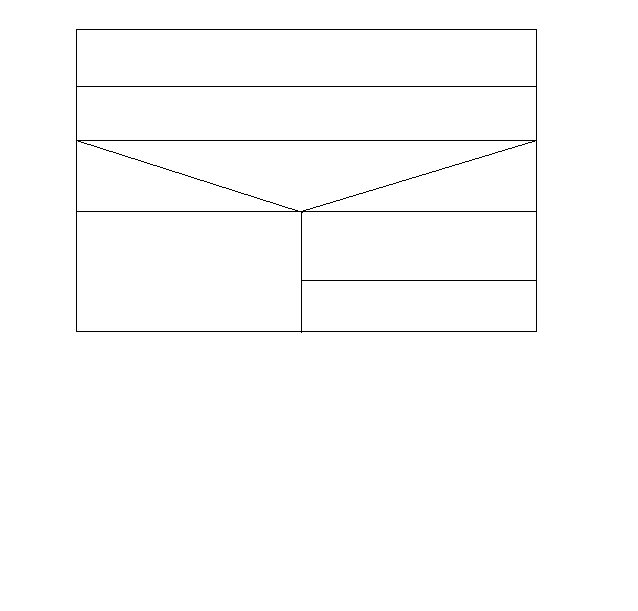
Ввод A,B
Вычисление определителя

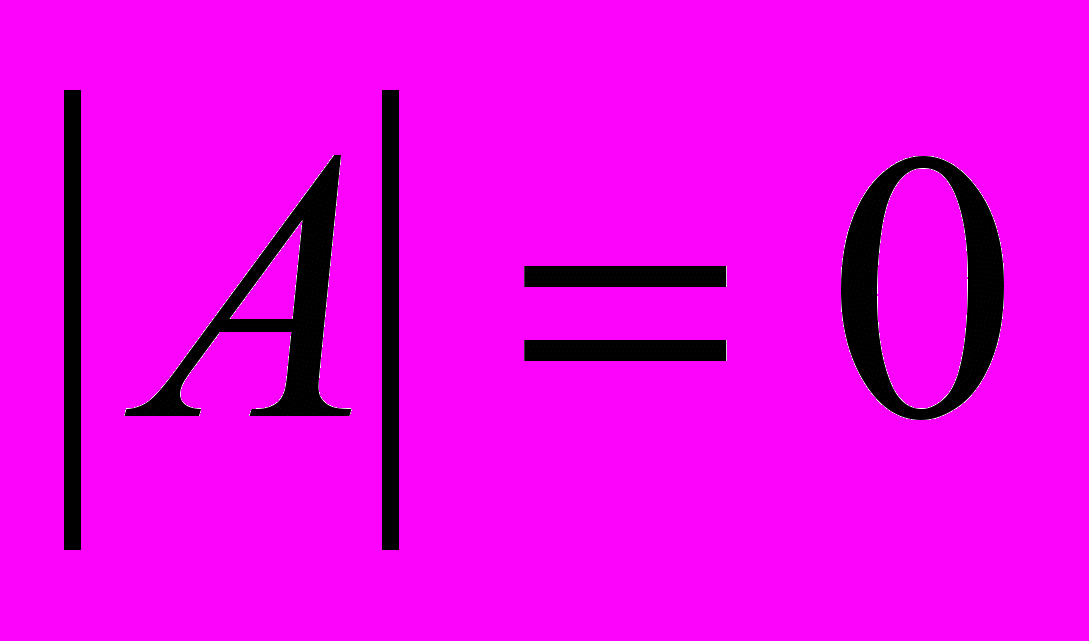
ДА НЕТ
Вывод: решений нет
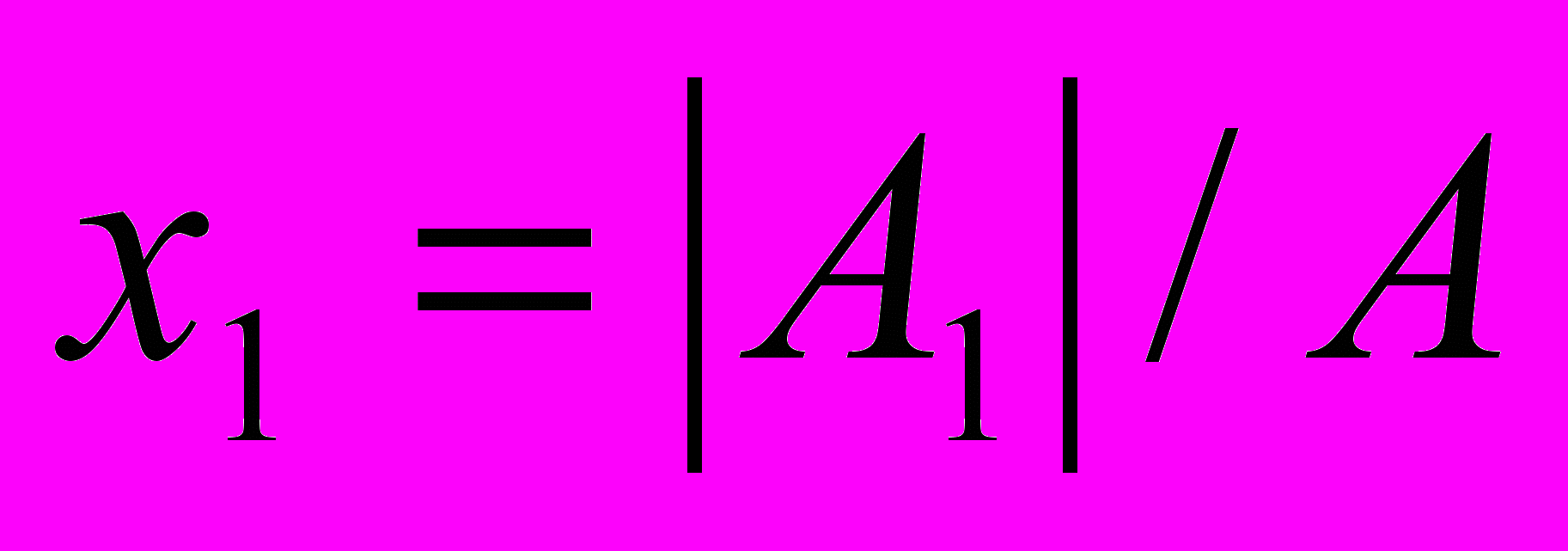
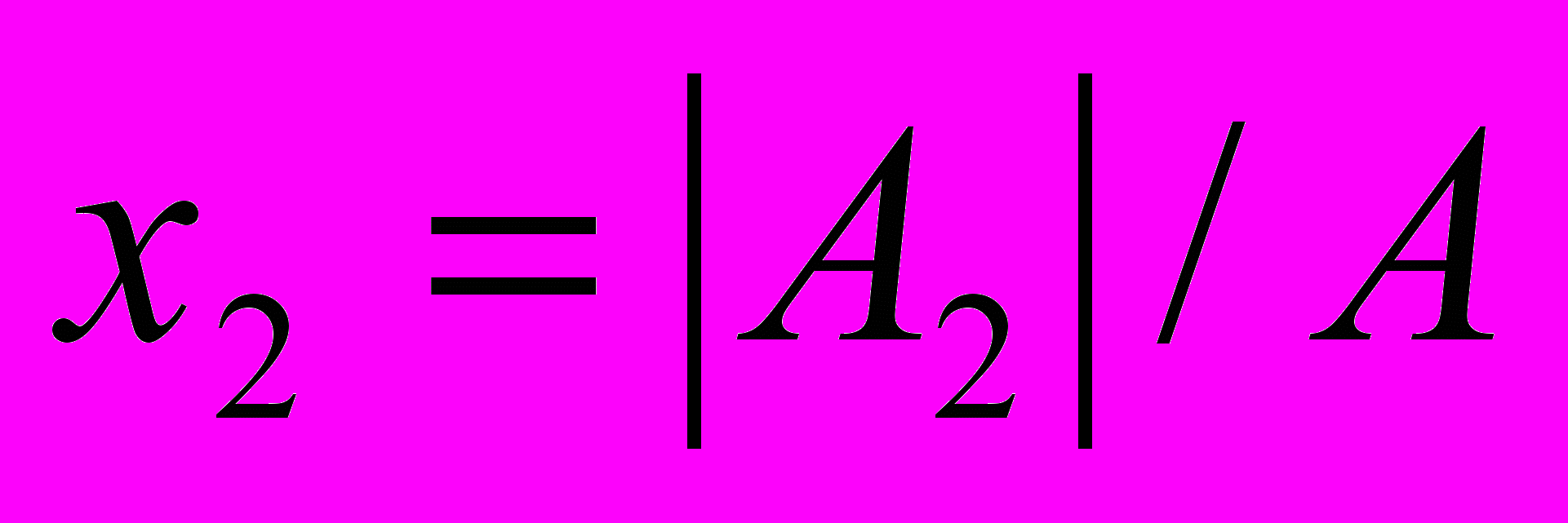
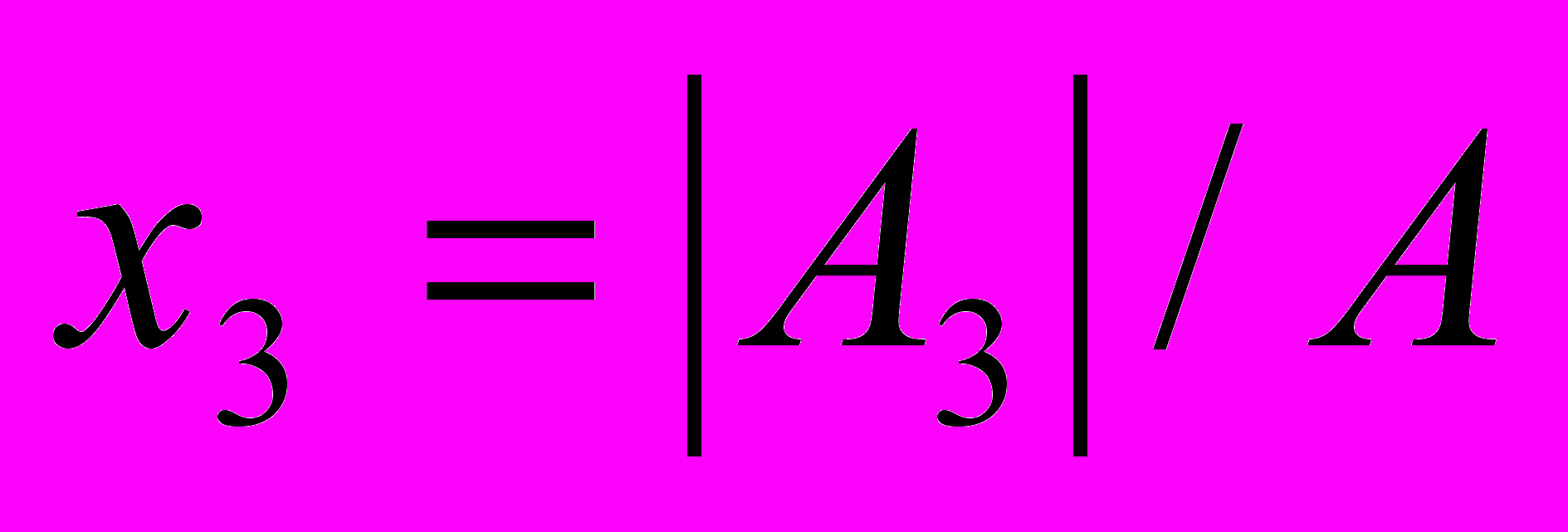
Вывод
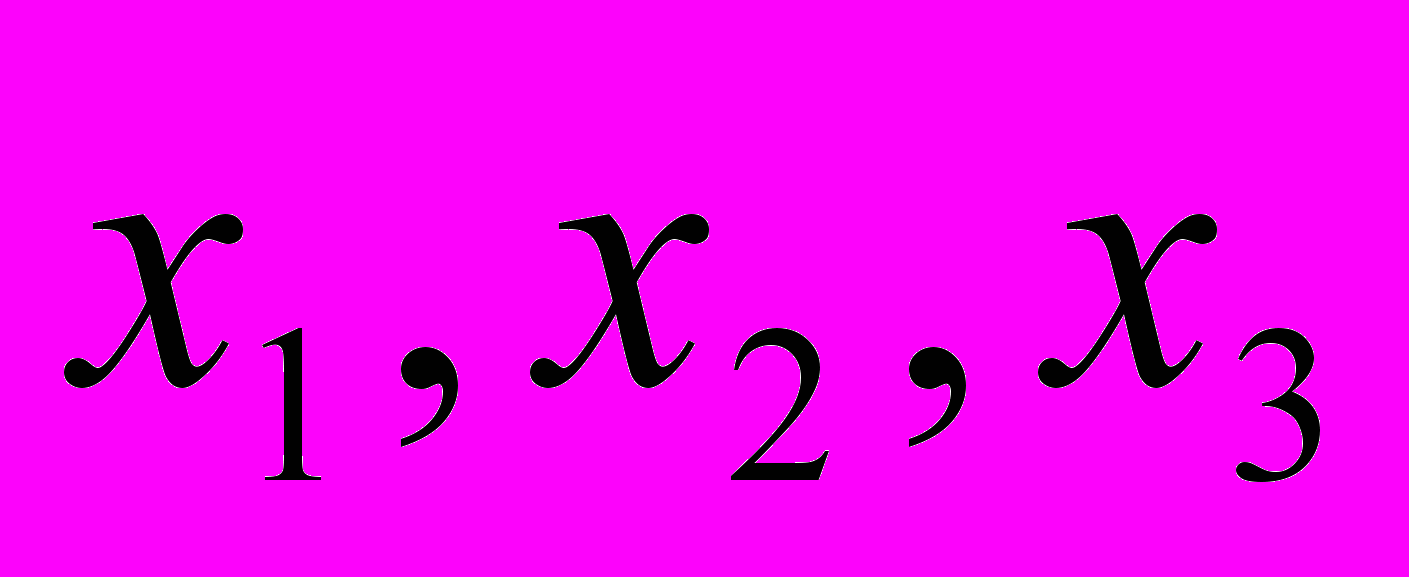
6.4. Программа решения задания
#include
#include
#include
#define L 9
int i,j,n=3,k,w,q;
float a[4][5],b[4][5],x,z,det,detA;
void determinant(void)
{
if(q!=0)
{
for(i=1;i<=n;i++)
{
for(j=1; j<=n+1; j++)
{
b[i][j]=a[i][j];
if(j==q)
{
b[i][j]=a[i][n+1];
}}}}
else
{
for(i=1;i<=n;i++)
{
for(j=1; j<=n+1;j++)
{
b[i][j]=a[i][j];
}}}
det=1.0;
for(k=1;k<=n;k++)
{
z=fabs(b[k][k]);
i=k;
for(j=k+1;j<=n;j++)//???
{
if(fabs(b[j][k])>z)
{
z=fabs(b[j][k]);
i=j;
}}
if(i>k)
{
det=det*(-1);
for(j=k;j<=n;j++)//???
{
z=b[i][j];
b[i][j]=b[k][j];
b[k][j]=z;
}}
z=b[i][n+1];
b[i][n+1]=b[k][n+1];
b[k][n+1]=z;
det=det*b[k][k];
for(j=k+1;j<=n+1;j++)
{
b[k][j]=b[k][j]/b[k][k];
}
for(i=k+1;i<=n;i++)
{
for(j=k+1;j<=n+1;j++)
{
b[i][j]=b[i][j]-b[k][j]*b[i][k];
}}}
q=q+1;
}
void main()
{
q=0;
printf("vvedite elementi rasshirennuyu matricu");
for(i=1;i<=n;i++)
{
for(j=1;j<=n+1;j++)
{
printf("a[%d][%d]=",i,j);
scanf("%f",&a[i][j]);
}}
printf("rasshirennaya matrica\n");
for(i=1;i<=n;i++)
{
for(j=1;j<=n+1;j++)
printf("%1.6f\t",a[i][j]);
printf("\n");
}
determinant();
detA=det;
for(w=1;w<=n;w++)
{
determinant();
printf("x%d=%1.6f",w,det/detA);
printf("\n");
}
}
6.5. Результат счета
Расширенная матрица:
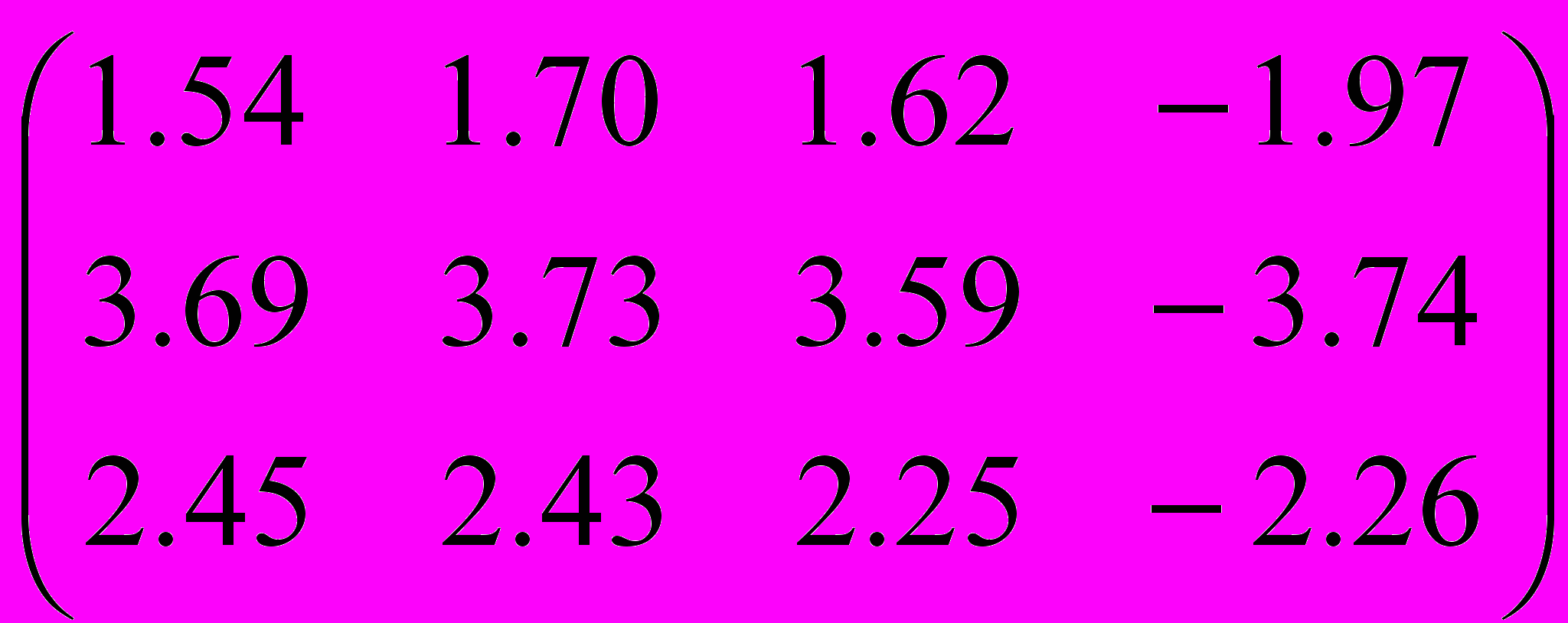
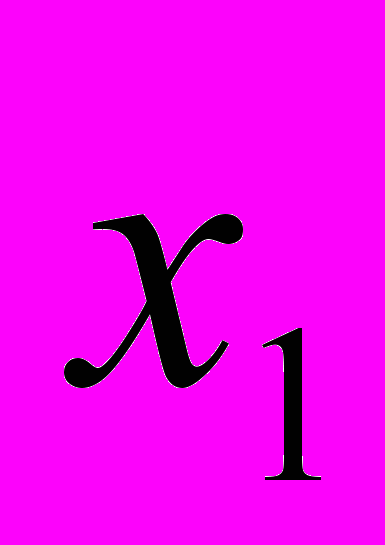 = 1.981984
= 1.981984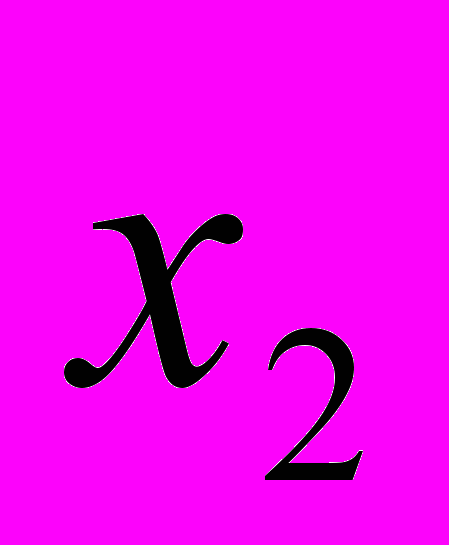 =-2.039600
=-2.039600 = -0.959834
= -0.959834Проверка в MathCAD:
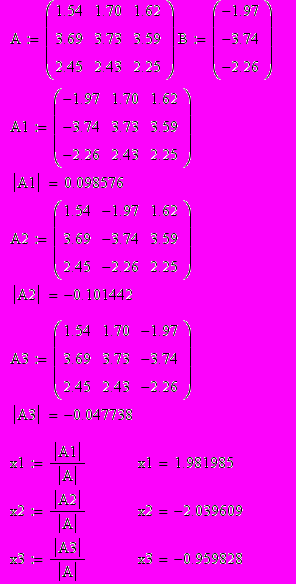
Задание VII: Решение системы нелинейных уравнений
7.1. Постановка задачи
Задана система линейных уравнений

Требуется найти решение данной системы с точностью
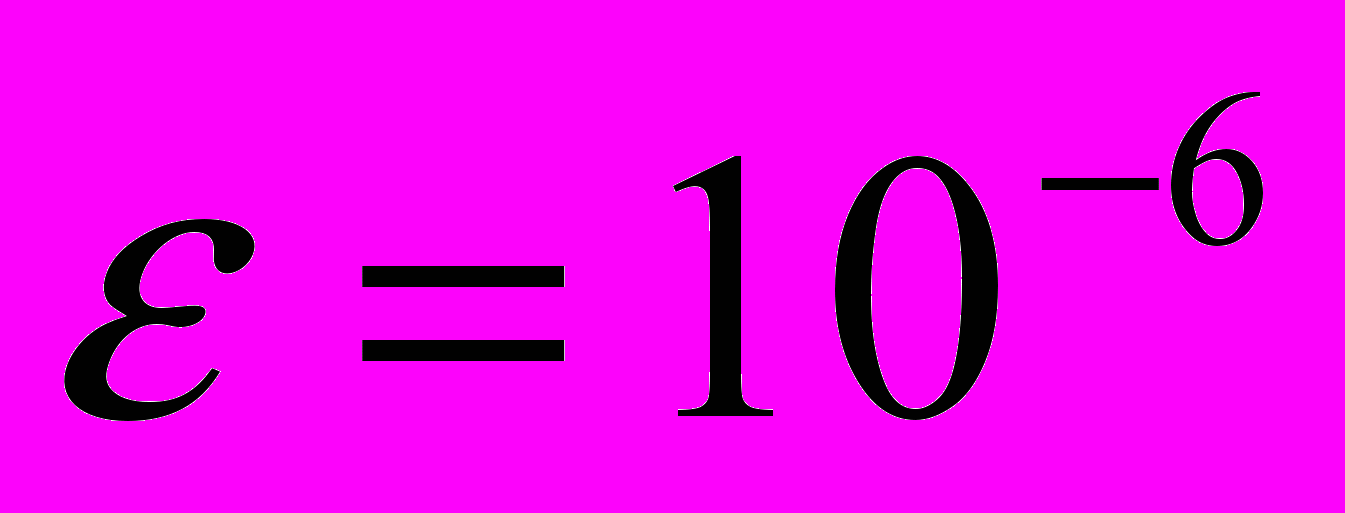
7.2. Разработка алгоритма
Для решения данной системы используем метод простой итерации, как самый общий из всех изученных.
Для метода простой итерации должны выполняться условия диагонального преобладания:
либо по строкам
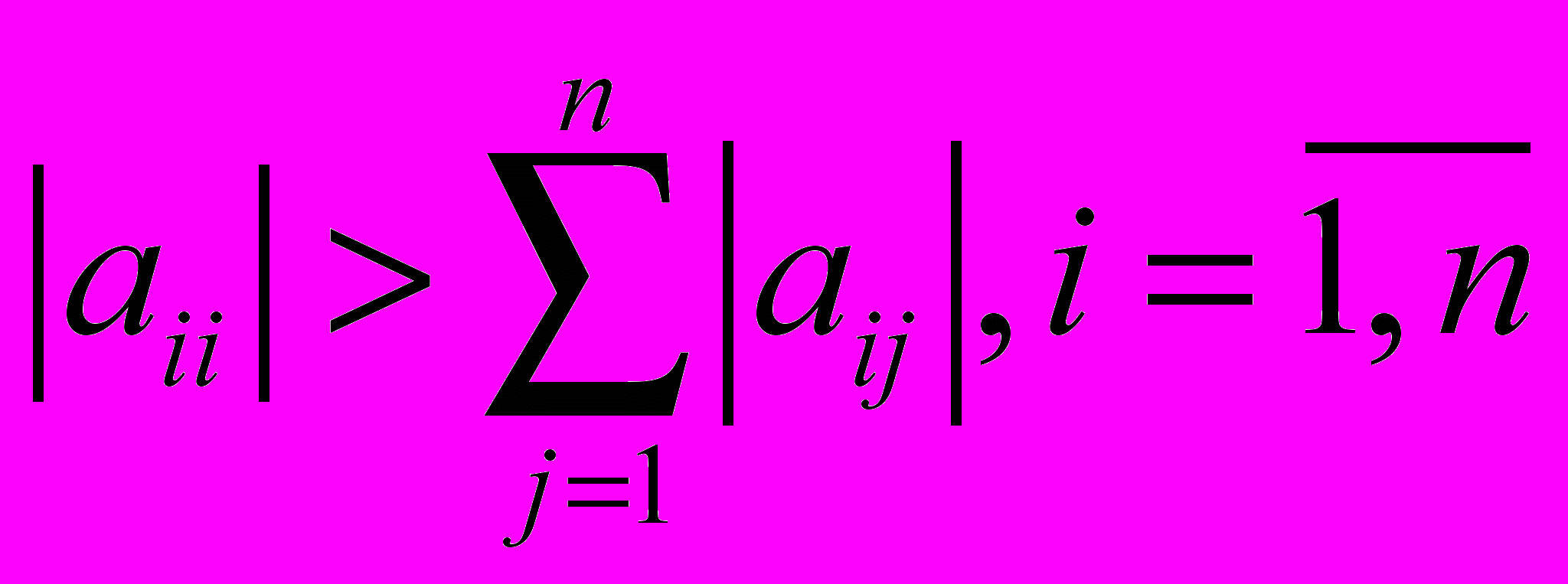
либо по столбцам
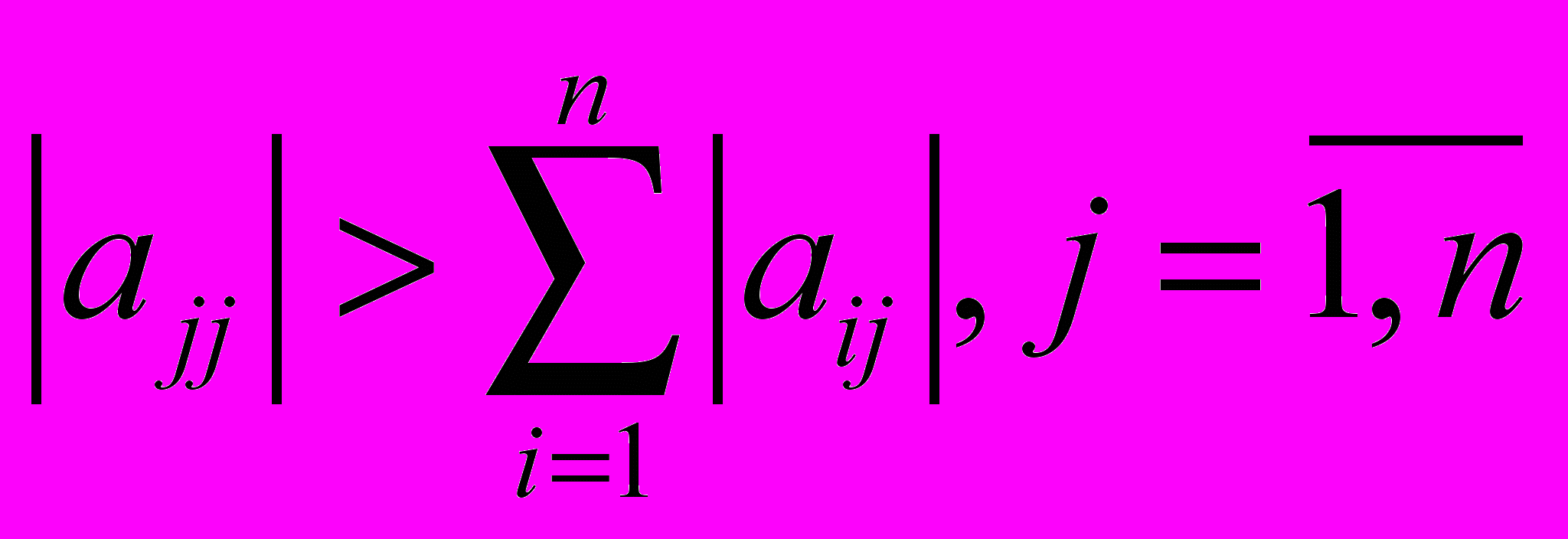
7.3. Структурограмма
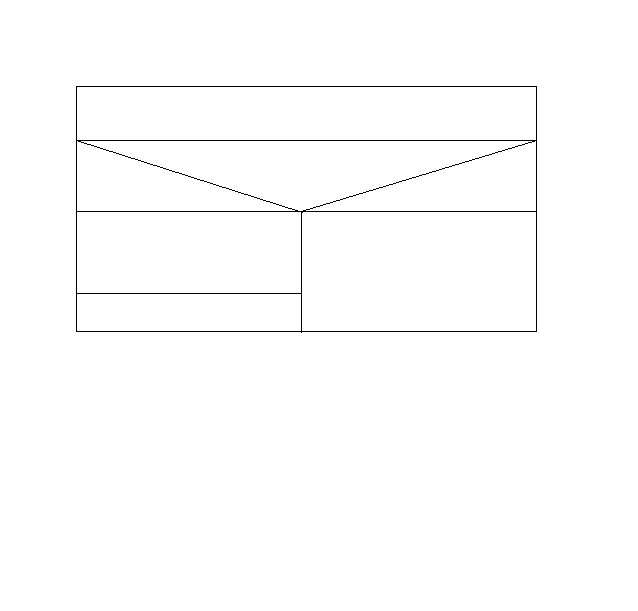
Ввод
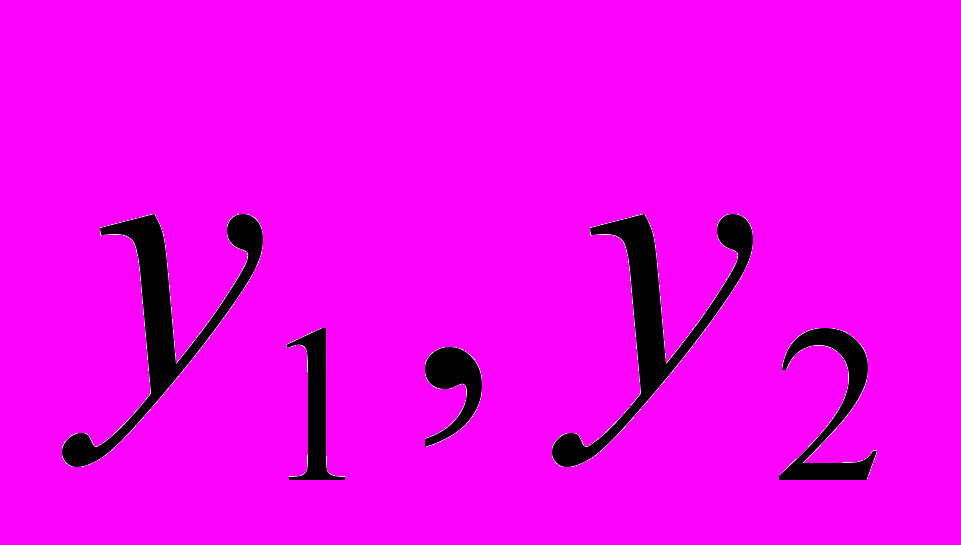
Есть ли точка пересечения
ДА НЕТ
Уточнения точки пересе- Вывод: корней нет
чения методом простой
итерации
Вывод x
7.4. Программа решения задания
#include
#include
#include "func.h"
void main()
{
int i=0,j=0,k=0;
float a=-1,b=0,x=0.,c,eps=0.000001,e1,e2,e,h,t,q,alpha,ymax=-1000,ymin=1000,xmax,xmin;
float q1[100];
puts("Vvedite ogranichenia na otrezok a,b i nachalnoe priblizhenie x0");
scanf("%f\t%f\n%f",&a,&b,&x);
e1=-2/dfunc(a);
e2=-2/dfunc(b);
h=(b-a)/100;
xmin=a;
xmax=b;
t=a;
for(i=0; i<100; i++)
{
q1[i]=dfunc(t);
t=t+h;
if(q1[i]
{
ymin=q1[i];
xmin=t-h;
}
if(q1[i]>ymax)
{
ymax=q1[i];
xmax=t-h;
}
}
q=fabs((ymax-ymin)/(ymax+ymin));
printf("\nq=%f",q);
if(fabs(e1)<=fabs(e2))
e=fabs(e1);
else
e=fabs(e2);
alpha=-2/(ymin+ymax);
printf("\nalpha=%f\n",alpha);
do
{
c=x;
x=x+alpha*func(c);
k++;
}
while((q/(1-q))*fabs(x-c)>eps);
printf("Koren uravnenia x=%f\n",x);
printf("Kol-vo iteraciy=%d\n",k);
}
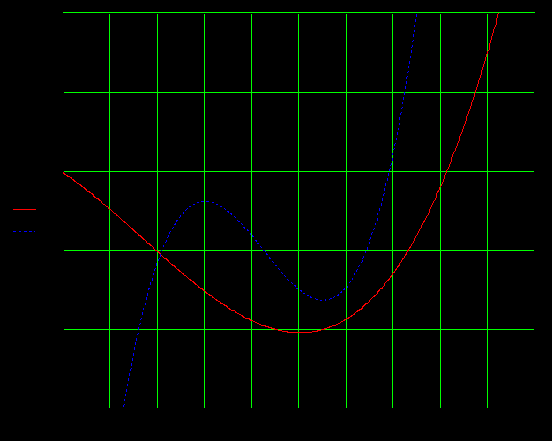
7.5.Результат счета
x=-0.589317
Проверка в MathCAD:
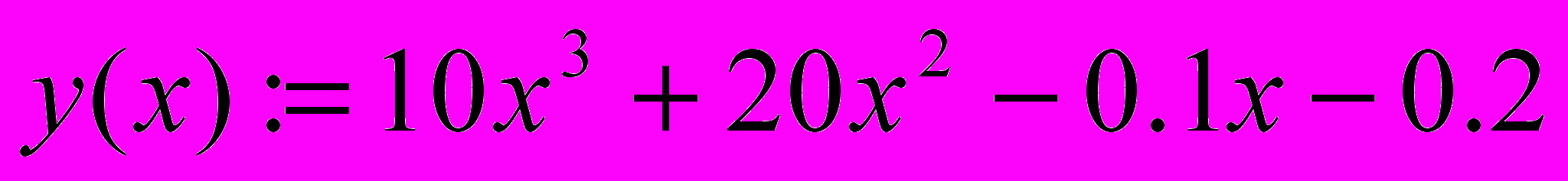
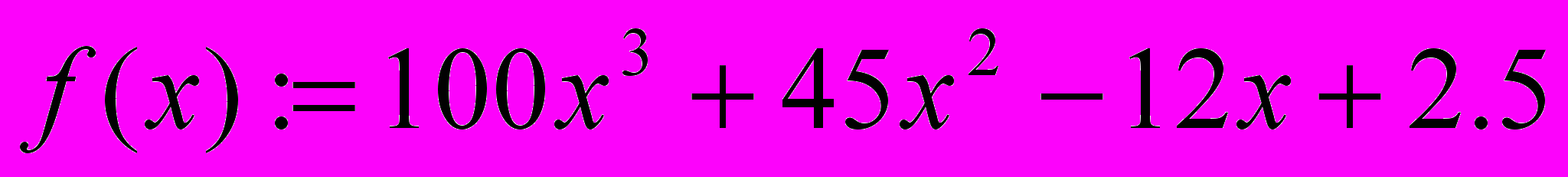
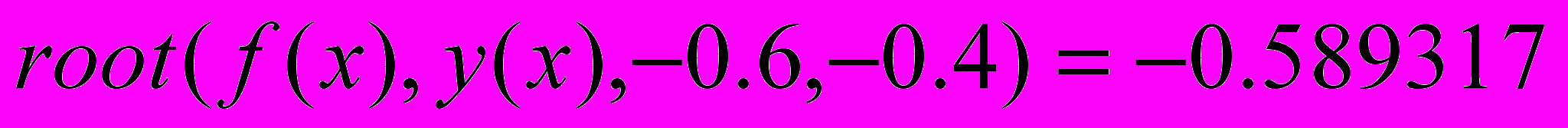
Список литературы
1. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа.- М.: Наука, 1967.-368 с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики.-М.:Наука, 1966.-664 с.
3. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Численные методы.- М.: Академия, 2005.- 384 с.
4. Азаров А. И., Басик В. А., Мелешко И. Н. и др. Сборник задач по методам вычислений . М.: Наука, ФМ, 1994.
5. Амосов А.А., Дубинская Ю.А., Копченов Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994.
6. Бахвалов Н.С., Жидков Н. П., Кобельков Г. М. Численные методы. М.: Лаборатория базовых знаний, 2000.
7. Волков Е. А. Численные методы. М.: Наука, ФМ, 1987.
8. Дьяконов В. П. MATHCAD 2000. Серия Учебный курс. СПб.: ПИТЕР, 2000.
9. Дьяконов В. П. MATHCAD 2001. Серия Учебный курс. СПб.: ПИТЕР, 2001.
10. Кирьянов Д. В. MATHCAD 12. Полное руководство. СПб.: БХВ - Петербург, 2005
