Geum.ru

Программа для подготовки к экзамену по математике вступительные испытания по предмету «Математика» проводятся в виде выполнения письменной работы по тестовым заданиям

Вид материалаПрограмма для подготовки

Содержание


Общие требования
Основные математические понятия и факты
П. основные формулы и теоремы
Iii. основные умения и навыки
Примерные варианты
Программа для подготовки к вступительному экзамену по информатике и информационно-коммуникационным технологиям
Темы для подготовки к экзамену по информатике и ИКТ
2) Алгоритмизация и программирование
3) Основы логики
5) Социальная информатика
2) Программные средства информационных и коммуникационных технологий
3) Технология обработки текстовой информации
4) Технология обработки графической и звуковой информации
6) Технология хранения, поиска и сортировки информации в базах данных
7) Телекоммуникационные технологии
Программа для подготовки к экзамену
При оценке сочинения учитывается
Приведем некоторые темы сочинений.
План должен
Подобный материал:
Направление 230700 ПРИКЛАДНАЯ ИНФОРМАТИКА


Квалификация – бакалавр


Форма обучения: очная, заочная (с сокращенным сроком обучения)


Срок обучения: 4 года (очная форма обучения), 2,5 года (сокращенная форма обучения)


Требования к предшествующему уровню образования абитуриента: среднее полное (общее) образование, среднее специальное образование.


ПРОГРАММА ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ

ПО МАТЕМАТИКЕ

Вступительные испытания по предмету «Математика» проводятся в виде выполнения письменной работы по тестовым заданиям.


Общие требования

На экзамене по математике поступающий в высшее учебное заведение должен показать:

а) четкое знание математических определений и теорем, предусмотренных программой, умение доказывать эти теоремы;

б) умение точно и сжато выражать математическую мысль в устном и письменном изложениях, использовать соответствующую символику,

в) умеренное владение математическими знаниями и навыками, предусмотренными программой, умение применять их при решении задач.

Программа по математике для поступающих в высшее учебное заведение предназначена для лиц, имеющих законченное среднее образование. Объем знаний и степень владения материалом, описанным в программе, соответствуют курсу математики средней школы.

Программа состоит из трех разделов.

В первом разделе перечислены основные математические понятия и факты, которыми должен владеть поступающий (уметь правильно использовать при решении задач, ссылаться при доказательстве теорем). Второй раздел представляет собой перечень вопросов теоретической части устного экзамена. В нем указаны теоремы, которые необходимо уметь доказывать, и формулы, которые надо уметь выводить. В третьем разделе охарактеризованы основные математические умения и навыки, которыми должен владеть экзаменуемый на письменном и устном экзаменах.

В связи с обилием учебников и регулярным их переизданием отдельные утверждения второго раздела могут в некоторых учебниках называться иначе, чем в программе, или формулироваться в виде задач, или вовсе отсутствовать. Такие случаи не освобождают поступающего от необходимости знать эти утверждения



  1. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ФАКТЫ



Арифметика, алгебра и начала анализа

Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель Наименьшее общее кратное.

Признаки делимости на 2, 3, 5,10.

Целые числа (Z). Рациональные числа (G), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.

Действительные числа (R), их представление в виде десятичных дробей. Сравнение действительных чисел.

Числовые промежутки. Модуль (абсолютная величина) действительного числа и его геометрический смысл.

Числовые выражения. Выражения с переменными. Тождественно равные выражения. Формулы сокращенного умножения. Степень с натуральным показателем. Арифметический корень.

Одночлен и многочлен. Стандартный вид многочлена. Многочлен с одной переменной. Корень многочлена на примере квадратного трехчлена.

Понятие функции. Способы задания функции. Область определения, множество значений функции.

График функции. Возрастание и убывание функции; периодичность, четность, нечетность

Достаточное условие возрастания (убывания) функции на промежутке. Понятие экстремума функции. Необходимое условие экстремума функции (теорема Ферма). Достаточное условие экстремума. Наибольшее и наименьшее значения функции на промежутке.

Определение и основные свойства функций: линейной (y=kx+b), квадратичной (у – ах2 + bх + с), степенной (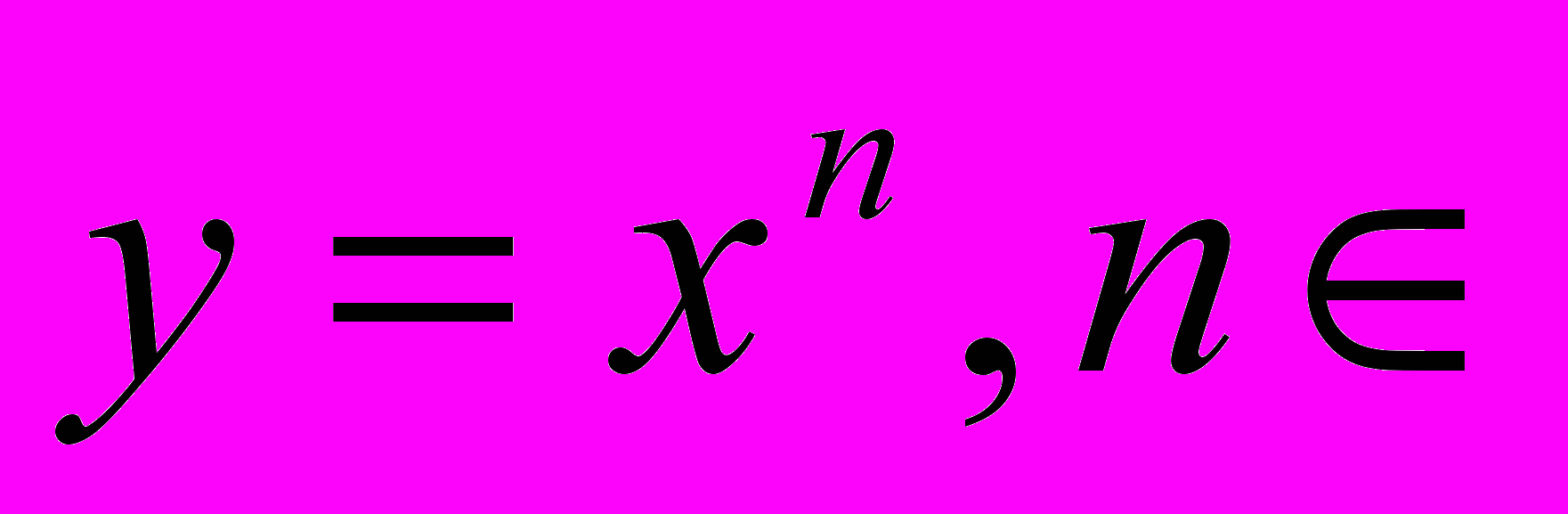Z), показательной (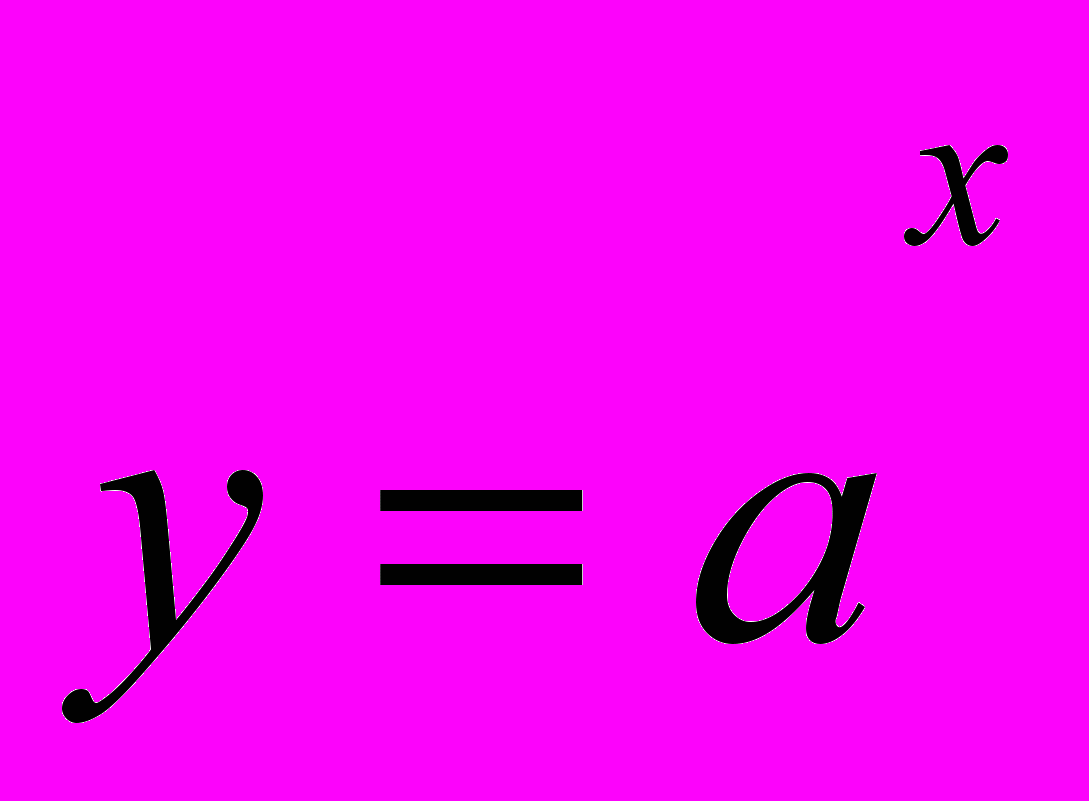), логарифмической 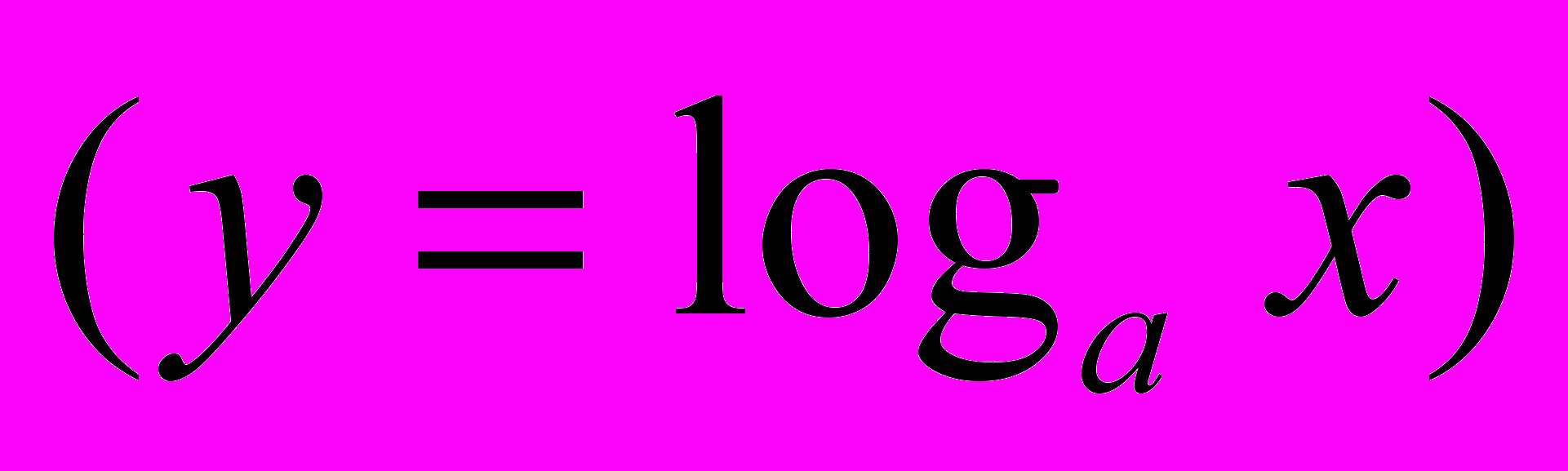, тригонометрических функции (y = sin x, y = cos x,

y = tg x, y = ctg x); арифметического корня

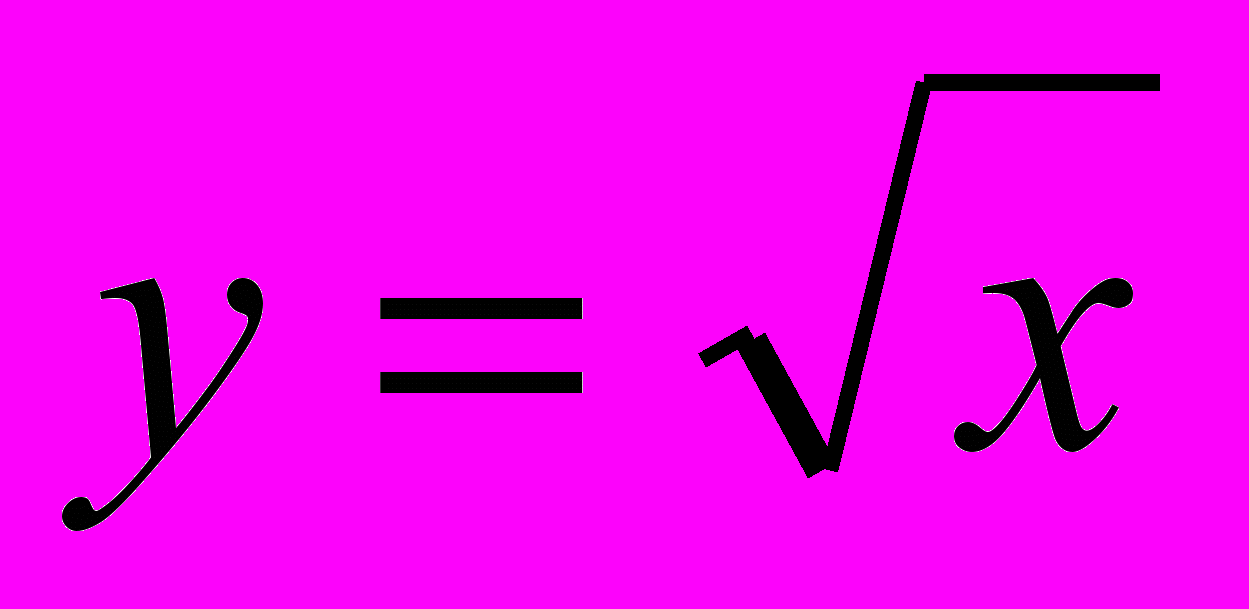
Арифметическая и геометрическая прогрессии. Формула n-го члена и суммы первых и членов арифметической прогрессии. Формула n-го члена и суммы первых п членов геометрической прогрессии.

Уравнение. Корни уравнения. Равносильные уравнения. Неравенства. Решения неравенства. Равносильные неравенства. Системы уравнений и неравенств. Решение системы. Производная. Ее физический и геометрический смысл. Производная сложной функции.

Производные функций y=sin x, y=cos x, y=tg x, y=ctg x, ,,

.


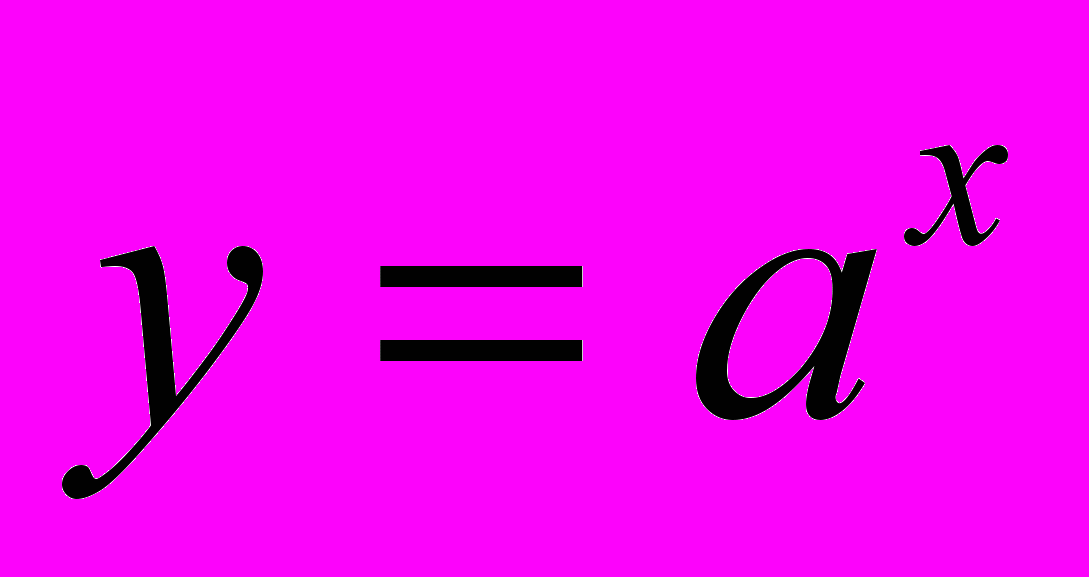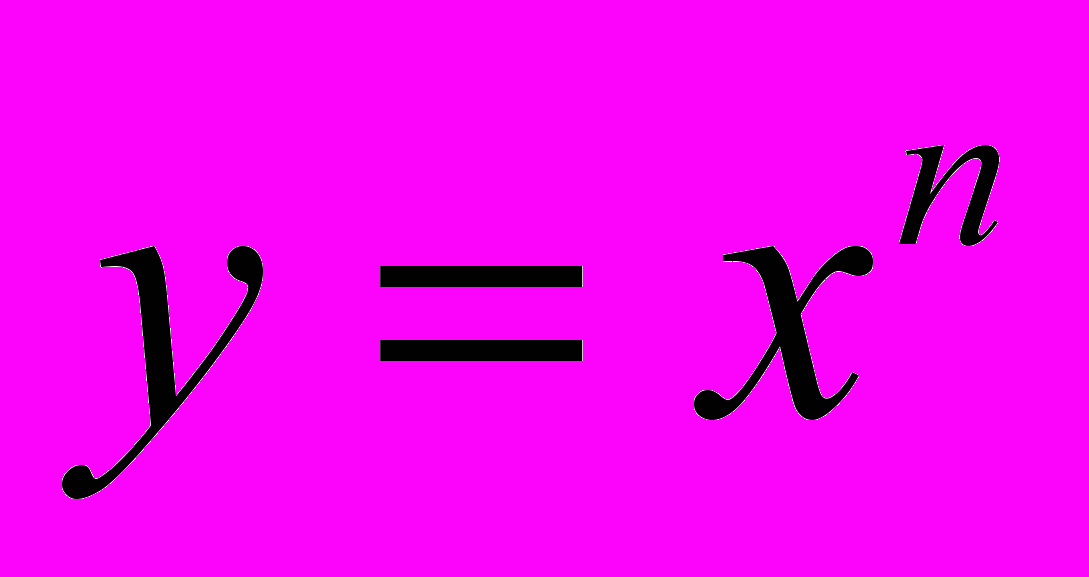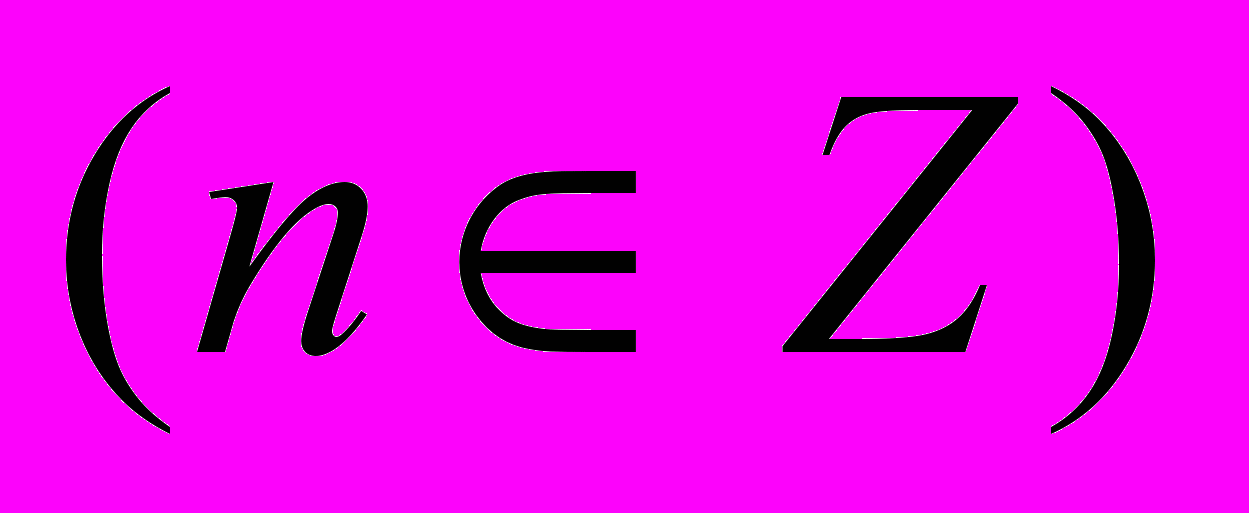Геометрия

Геометрическая фигура как множество точек. Прямая, луч, отрезок, ломаная; длина отрезка. Угол, величина угла. Вертикальные и смежные углы. Окружность, круг. Параллельные прямые.

Примеры преобразования фигур, виды симметрии. Преобразование подобия и его свойства.

Векторы. Операции над векторами.

Выпуклые фигуры. Многоугольник, его вершины, стороны, диагонали. Треугольник, его медиана, биссектриса, высота. Виды треугольников. Средняя линия треугольника. Соотношения между сторонами и углами прямоугольного треугольника.

Четырехугольники: параллелограмм, прямоугольник, ромб, квадрат, трапеция. Средняя линия трапеции.

Окружность и круг. Центр, хорда, диаметр, радиус. Касательная к окружности. Дуга окружности. Сегмент и сектор. Центральные и вписанные углы.

Вписанные и описанные многоугольники. Правильные многоугольники. Выражение стороны правильного многоугольника через радиус описанной около него окружности.

Площадь многоугольника. Формулы площади: треугольника, прямоугольника, параллелограмма, ромба, квадрата, трапеции, правильного многоугольника (через радиус описанной около него окружности).

Длина окружности и длина дуги окружности. Радиальная мера угла. Площадь круга и площадь сектора.

Подобие. Подобные фигуры. Отношение площадей подобных фигур. Плоскость. Параллельные и пересекающиеся плоскости.

Параллельность прямой и плоскости. Угол прямой с плоскостью. Перпендикуляр к плоскости. Двугранные углы. Линейный угол двугранного угла. Перпендикулярность двух плоскостей.

Многогранники. Их вершины, ребра, грани, диагонали. Прямая и наклонная призмы; пирамиды. Правильная призма и правильная пирамида. Параллелепипед, Прямоугольный параллелепипед. Куб.

Фигуры вращения: цилиндр, конус, сфера, шар. Центр, диаметр, радиус сферы и шара. Плоскость, касательная к сфере.

Формулы площади поверхности и объема призмы.

Формулы площади поверхности и объема пирамиды.

Формулы площади поверхности и объема цилиндра.

Формулы площади поверхности и объема конуса.

Формула объема шара.

Формула площади сферы.


П. ОСНОВНЫЕ ФОРМУЛЫ И ТЕОРЕМЫ


Алгебра и начала анализа

1. Свойства функции у = ах + b и ее график.

2. Свойства функции y = k/x и ее график.

3. Свойства функции у = ах2 + bх + с и ее график.

4. Формула корней квадратного уравнения.

5. Теорема Виета (прямая и обратная).

6. Разложение квадратного трехчлена на линейные множители.

7. Свойства числовых неравенств.

8. Формула n-го члена и суммы первых n членов арифметической прогрессии.

9. Формула n-го члена и сумм первых n членов геометрической прогрессии.

10. Сумма бесконечно убывающей геометрической прогрессии.

11. Определение и свойства показательной функции. График.

12. Определение и свойства логарифмической функции. График.

13. Логарифм произведения, степени, частного.

14. Определение и свойства функций у = sin x и cos x и их графики.

15. Определение и свойства функции y = tg x и ее график.

16. Решение уравнений вида sin x =a, cos x= a, tg x = a.

17. Зависимости между тригонометрическими функциями одного и того же аргумента.

18. Формулы приведения.

19. Формулы синуса, косинуса и тангенса суммы двух аргументов.

20. Тригонометрические функции двойного и половинного аргумента.

21. Производная суммы двух функций.

22. Производная частного двух функций.

23. Производные функций: y = sin x, y = cos x, y = tg x, , .


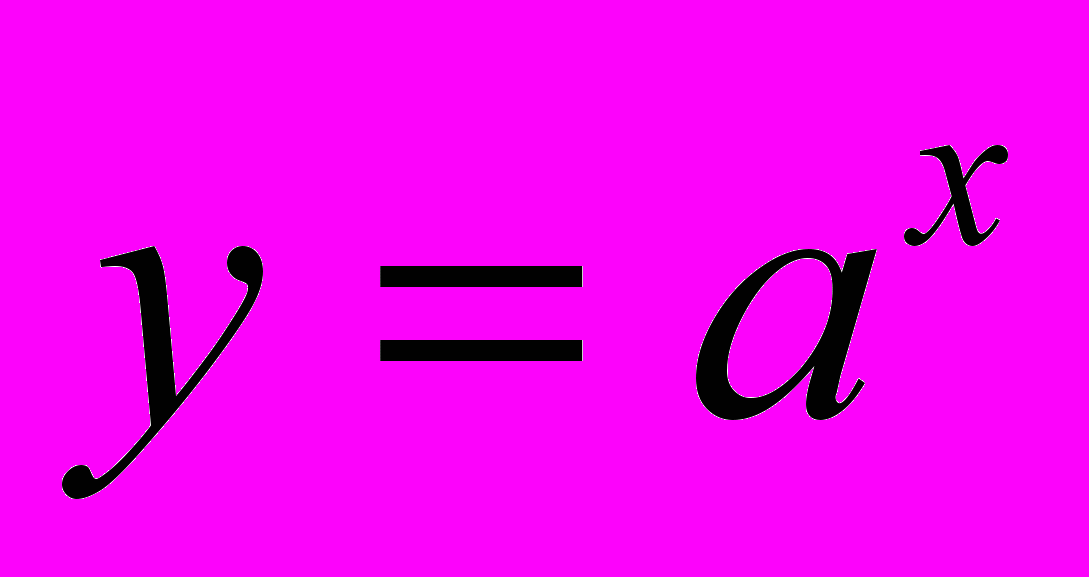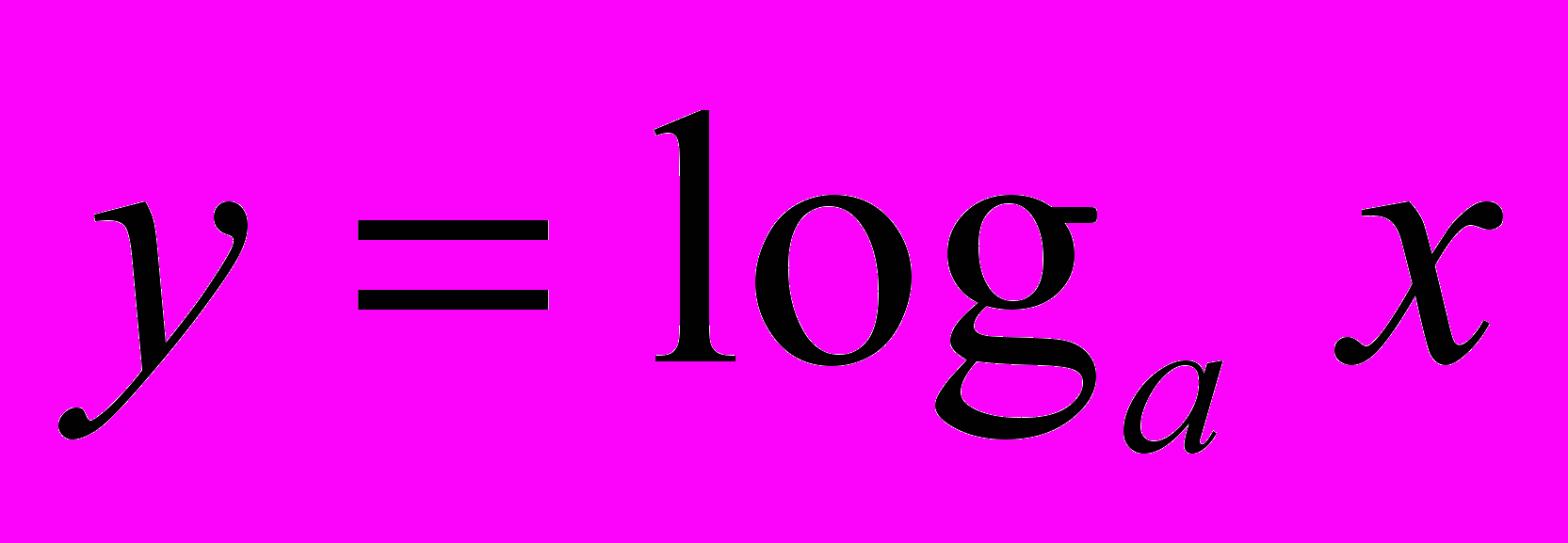Геометрия

1. Свойства равнобедренного треугольника.

2. Свойства точек, равноудаленных от концов отрезка.

3. Признаки параллельности прямых.

4. Сумма углов треугольника. Сумма внутренних углов выпуклого многоугольника.

5 Свойства средних линий треугольника и трапеции.

6. Признаки параллелограмма.

7. Существование окружности, описанной около треугольника.

8. Существование окружности, вписанной в треугольник.

9. Касательная к окружности и ее свойство.

10. Измерение угла, вписанного в окружность.

11. Признаки подобия треугольников.

12. Теорема Пифагора.

13. Теорема косинусов.

14. Теорема синусов.

15. Формулы площадей параллелограмма, треугольника, трапеции.

16. Формула расстояния между двумя точками плоскости. Уравнение окружности.

17. Признак параллельности прямой и плоскости.

18. Признак параллельности плоскостей.

19. Теорема перпендикулярности прямой и плоскости.

20. Перпендикулярность двух плоскостей.

21. Теорема о трех перпендикулярах.


III. ОСНОВНЫЕ УМЕНИЯ И НАВЫКИ


Экзаменуемый должен уметь:

– Производить арифметические действия над числами, заданными в виде десятичных и обыкновенных дробей; округлять числа с заданной точностью. Производить действия над приближенными значениями с использованием практических приемов; пользоваться таблицами;

– Проводить тождественные преобразования многочленов, дробей, содержащих переменные, выражений, содержащих квадратные корни, показательные, логарифмические и тригонометрические функции;

– Строить графики функций, указанных в программе; исследовать функции с помощью производной; решить задачи на нахождение экстремальных значений;

– Решать уравнения, неравенства первой и второй степени и уравнения и неравенства, приводящиеся к ним; решать системы уравнений и неравенств первой и второй степеней и уравнения и неравенства, приводящиеся к ним, решать системы уравнений неравенств первой и второй степеней и приводящиеся к ним;

– Решать задачи на составление уравнений и систем уравнений. Изображать геометрические фигуры на чертеже и производить простейшие построения на плоскости;

– Проводить операции над векторами (сложение, вычитание, умножение на число, скалярное умножение) и пользоваться свойствами этих операций;

– Использовать геометрические представления при решении алгебраических задач и задач из начал анализа; использовать методы алгебры и начал анализа при решении геометрических задач.

Примерные варианты:

вариант А – повышенной трудности;

вариант В – средней трудности.


Вариант А-11-05



  1. Решить уравнение .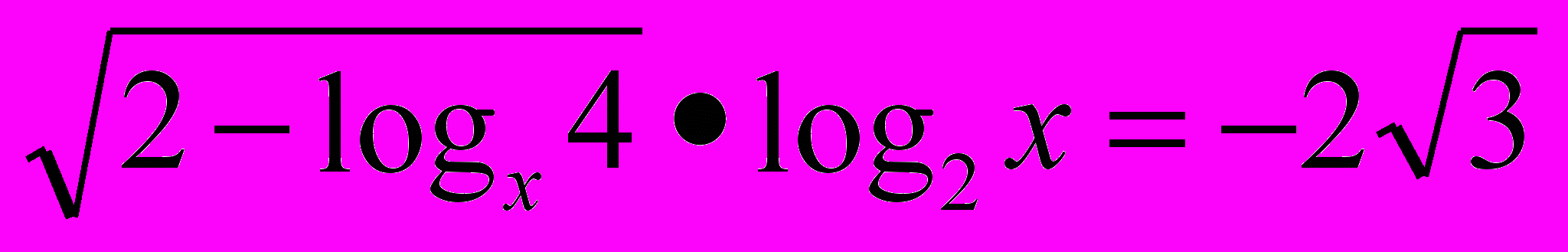
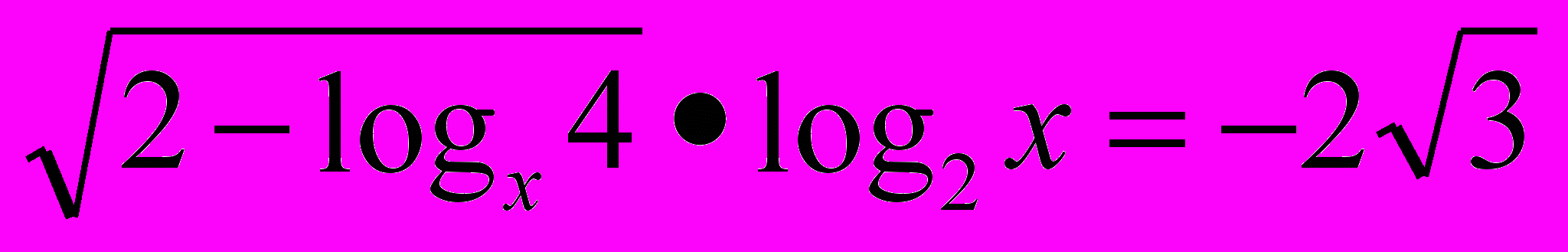  2. Решить неравенство .
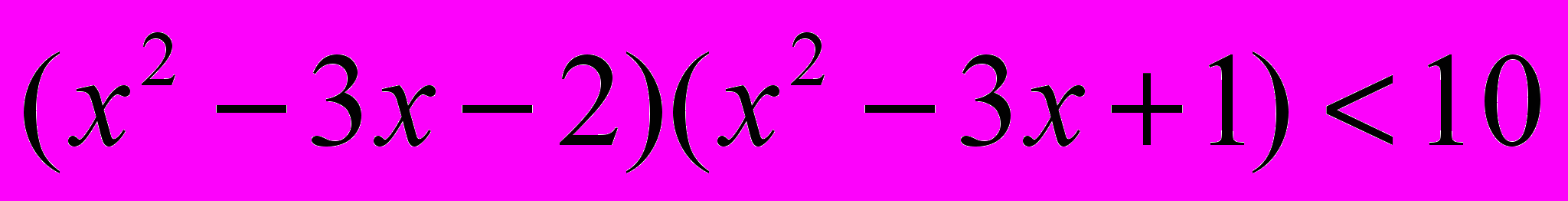  3. Вычислить 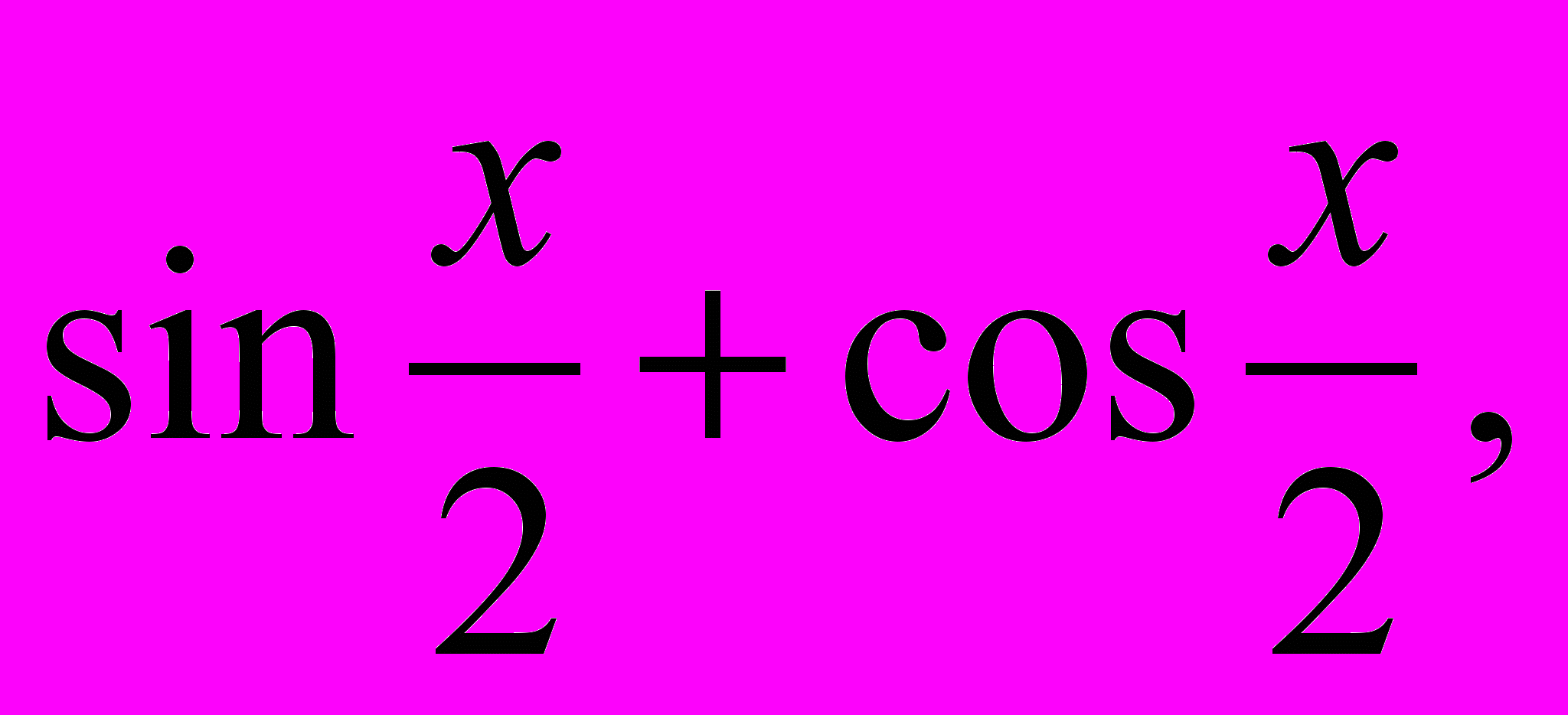если sin x = 0,21.
  4. Поезд должен был пройти 54 км. Пройдя 14 км, он был задержан на 10 мин. у семафора. Увеличив первоначальную скорость на 10 км/ч, он прибыл на место назначения с опозданием на 2 мин. Определить первоначальную скорость.
  5. Боковые ребра пирамиды наклонены к плоскости основания под углом 30˚. Основание пирамиды – треугольник со сторонами 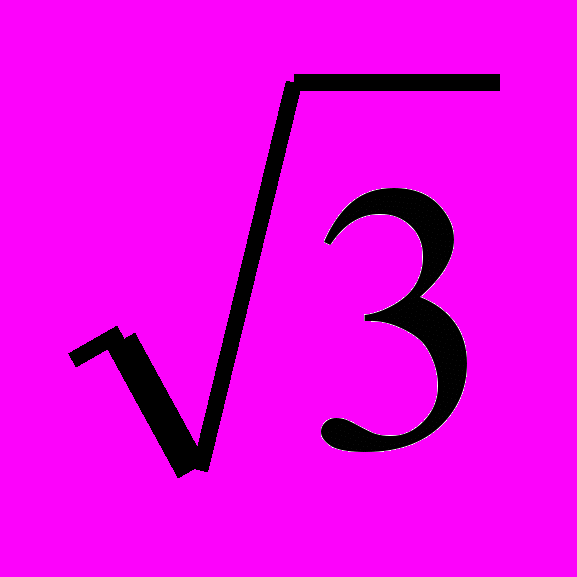, 2 и 3. Найти объем пирамиды.



Вариант А-12-05

  1. Решить уравнение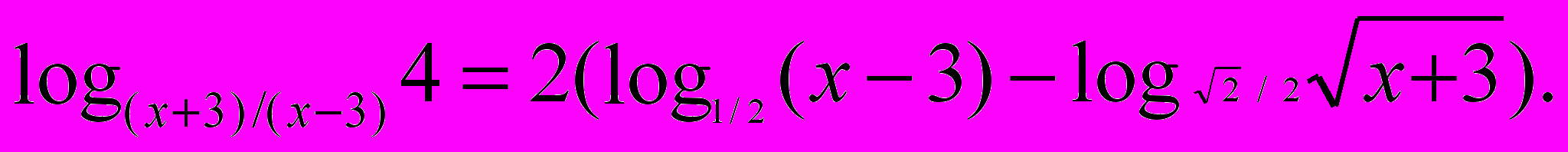
  2. Решить неравенство
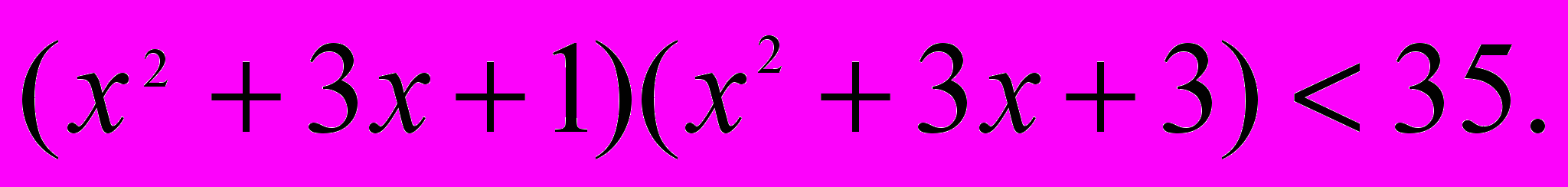
  3. Вычислить tg x, если .
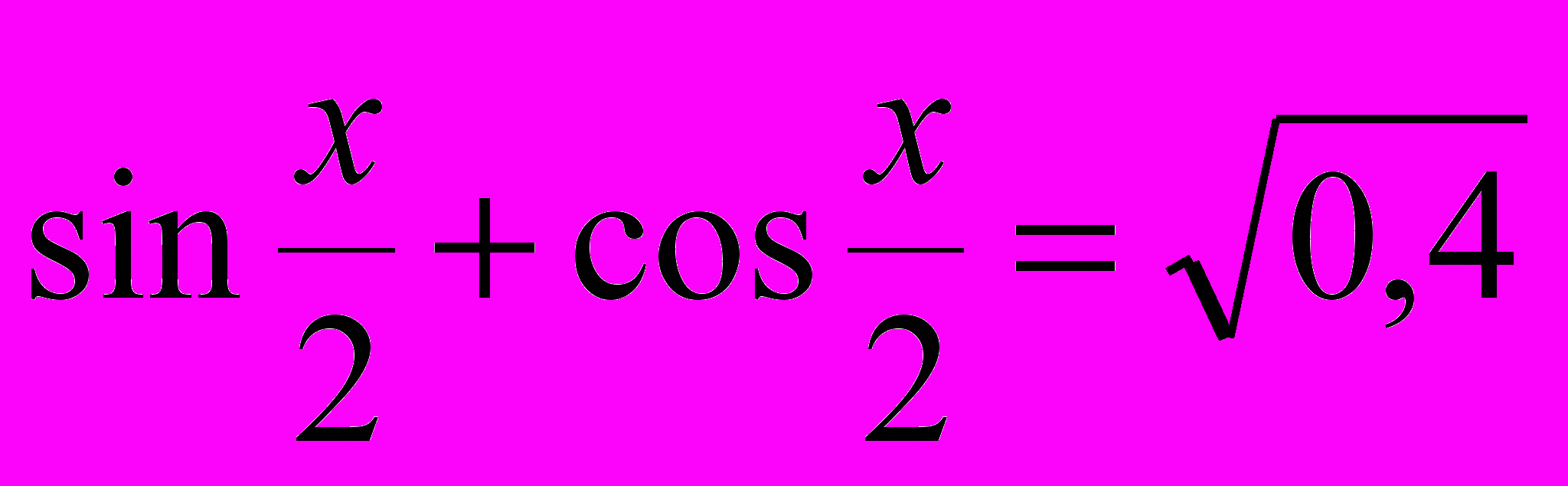
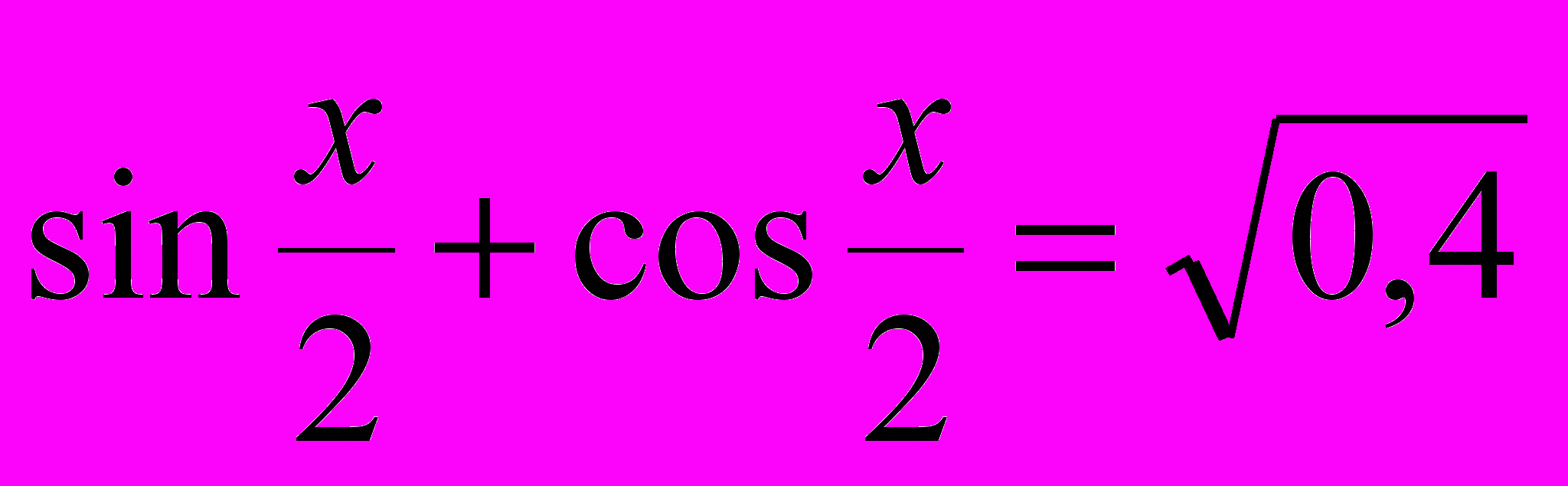  4. Две автомашины выехали одновременно из одного и того же пункта в одном и том же направлении: одна со скоростью 50 км/ч, другая – 40 км/ч. Спустя полчаса из того же пункта в том же направлении выехала третья машина, которая обогнала первую машину на 1 ч 30 мин. позже, чем вторую. Найти скорость третьей машины.
  5. Основанием пирамиды служит ромб с острым углом 60˚. Определить объем пирамиды, если радиус вписанного в ромб круга .



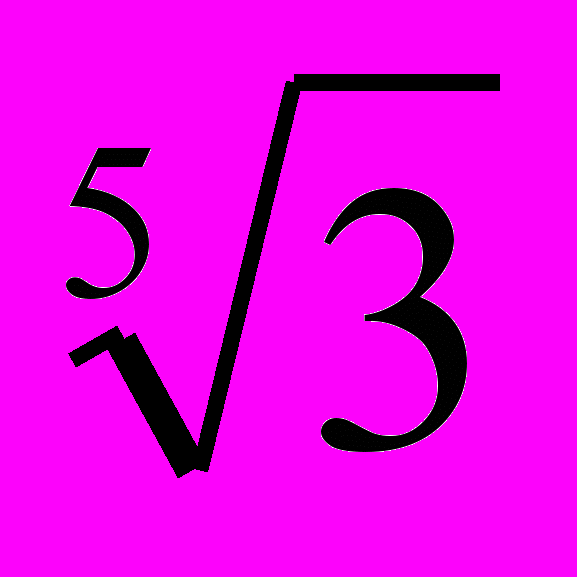Вариант А-21-05

  1. Решить уравнение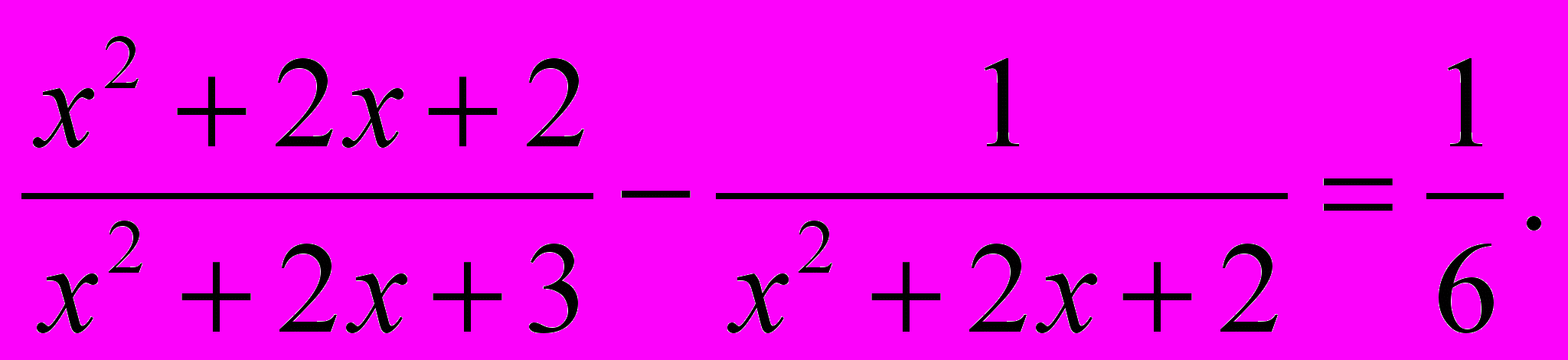
  2. Решить неравенство
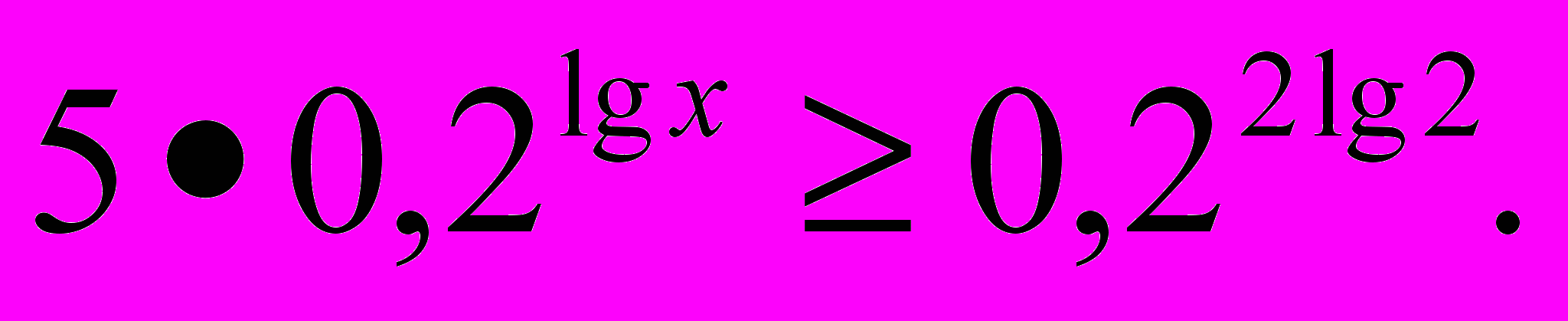
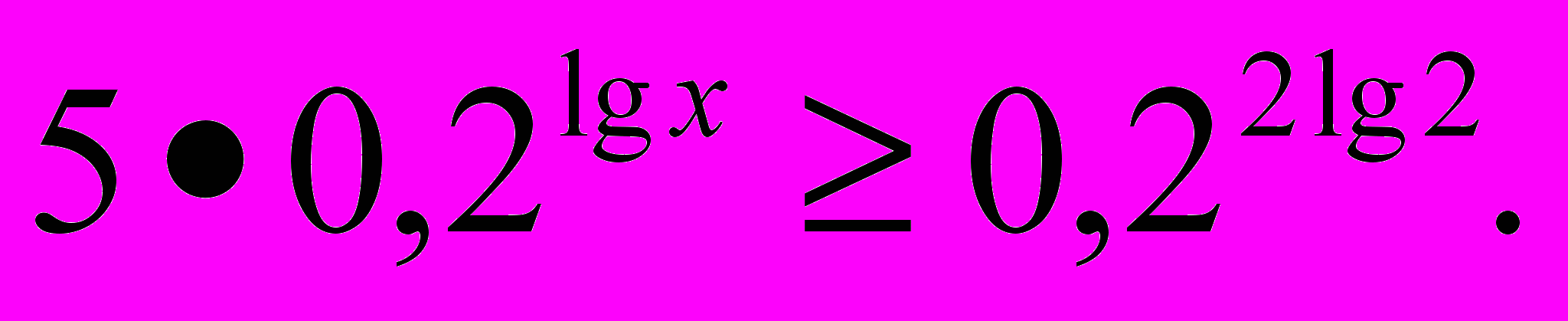
  3. Вычислить
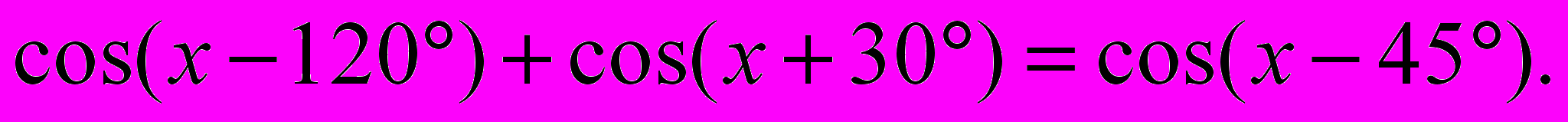
  4. Два поезда отправились одновременно из А и В навстречу друг другу. Скорость первого поезда на 10 км/ч больше скорости второго. Поезда встретились в 28 км от середины расстояния АВ. Если бы первый поезд отправился из А на 45 мин. позже второго, то они встретились бы на середине расстояния АВ. Найти расстояние АВ и скорости обоих поездов.
  5. Угол между высотой правильной пирамиды и боковой гранью равен 30˚. Найти длину стороны основания, если радиус вписанного в пирамиду шара равен 1.



Вариант А-22-05

  1. Решить уравнение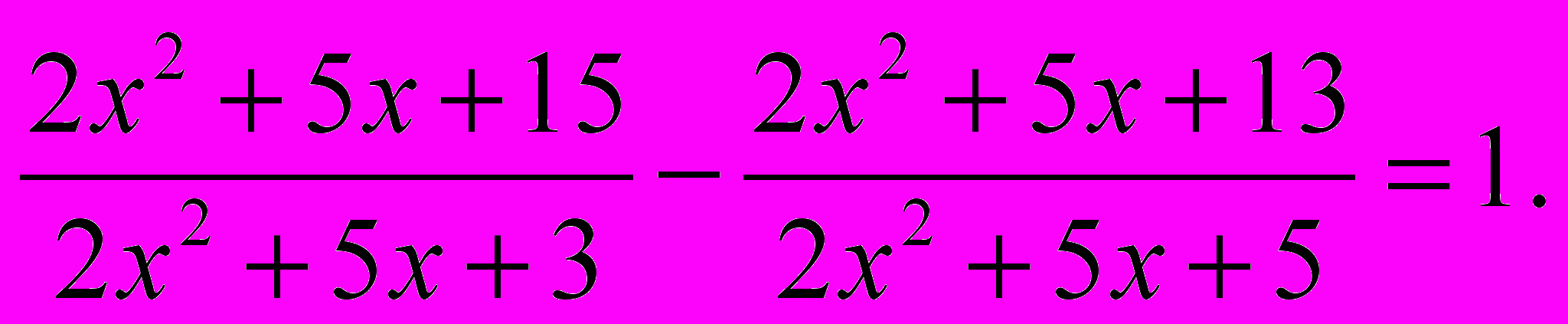
  2. Решить неравенство
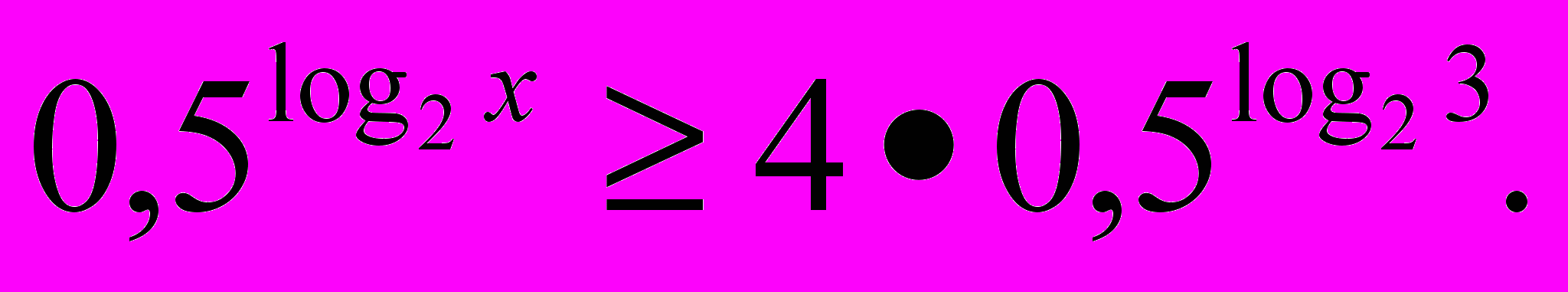
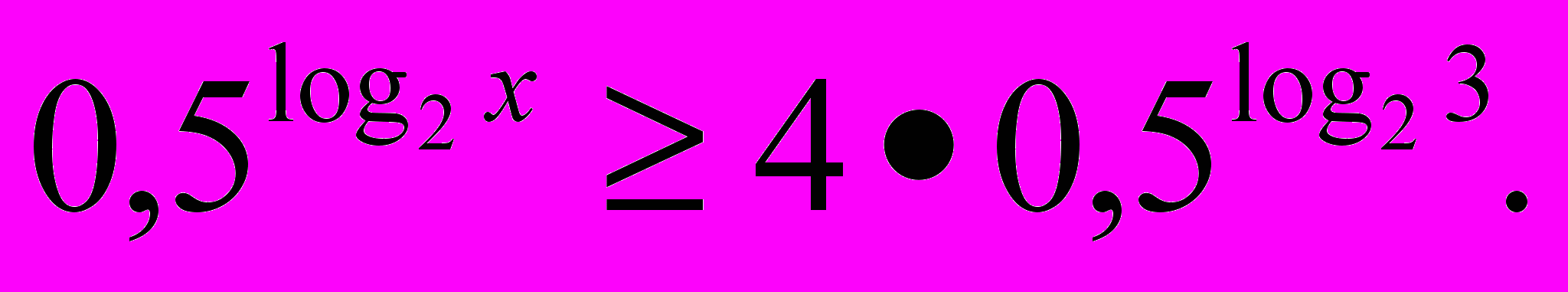
  3. Вычислить
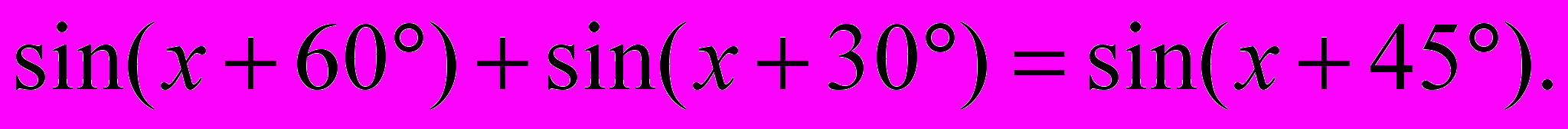
  4. Из двух городов навстречу друг другу вышли два поезда. Первый шел со скоростью 54 км/ч, а второй, выйдя на 2 ч позже первого, – со скоростью 75 км/ч и до встречи прошел на 102 км больше первого. Каково расстояние между городами?
  5. Угол между высотой правильной треугольной пирамиды и боковой гранью равен 30˚. Найти длину бокового ребра, если радиус вписанного в пирамиду шара равен .



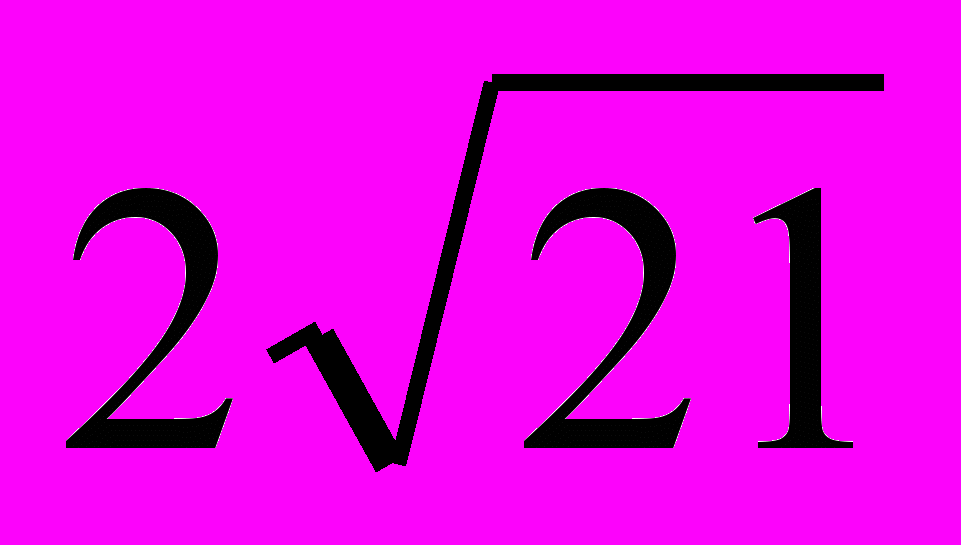Вариант А-23-05

  1. Решить уравнение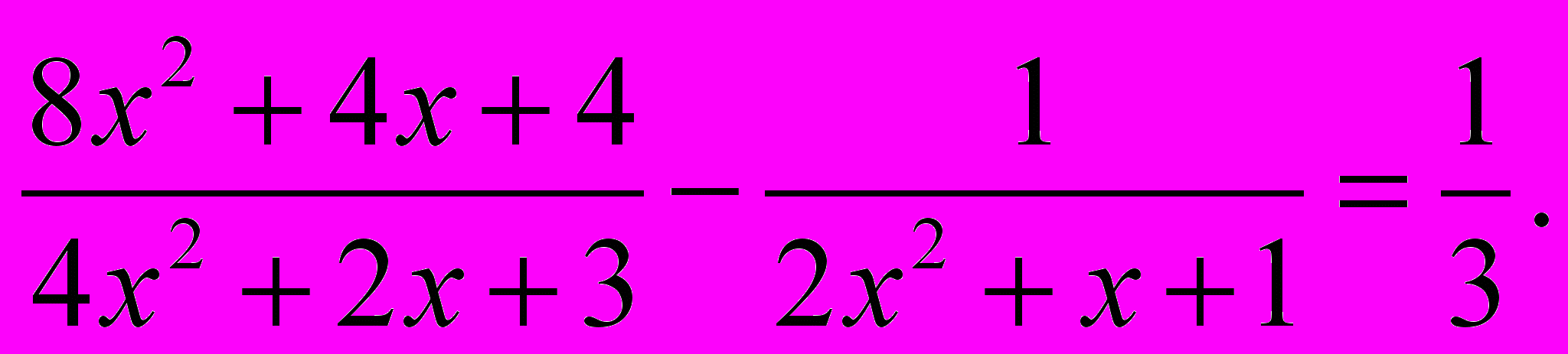
  2. Решить неравенство
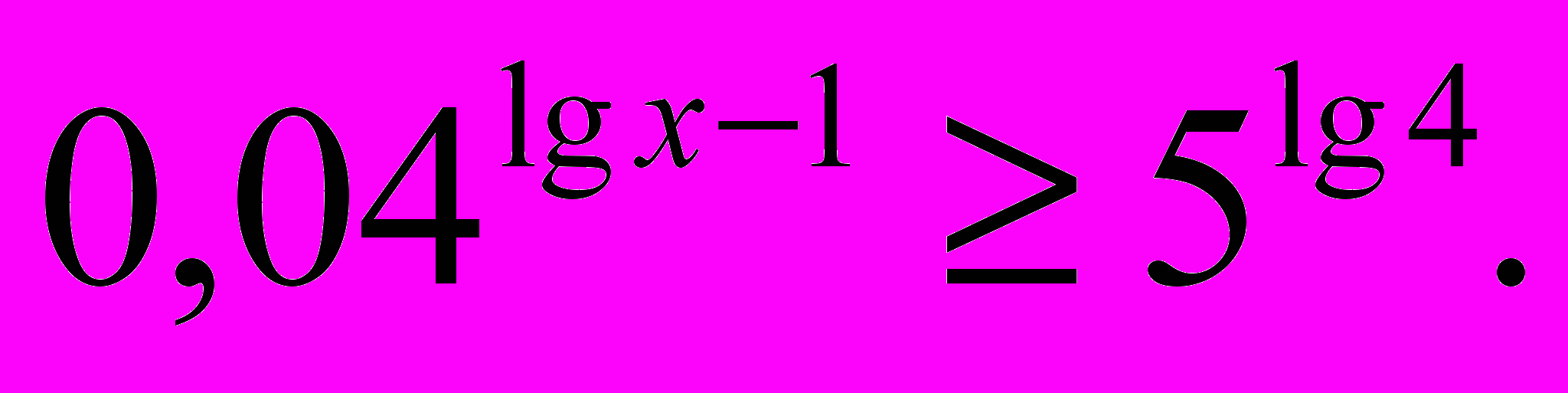
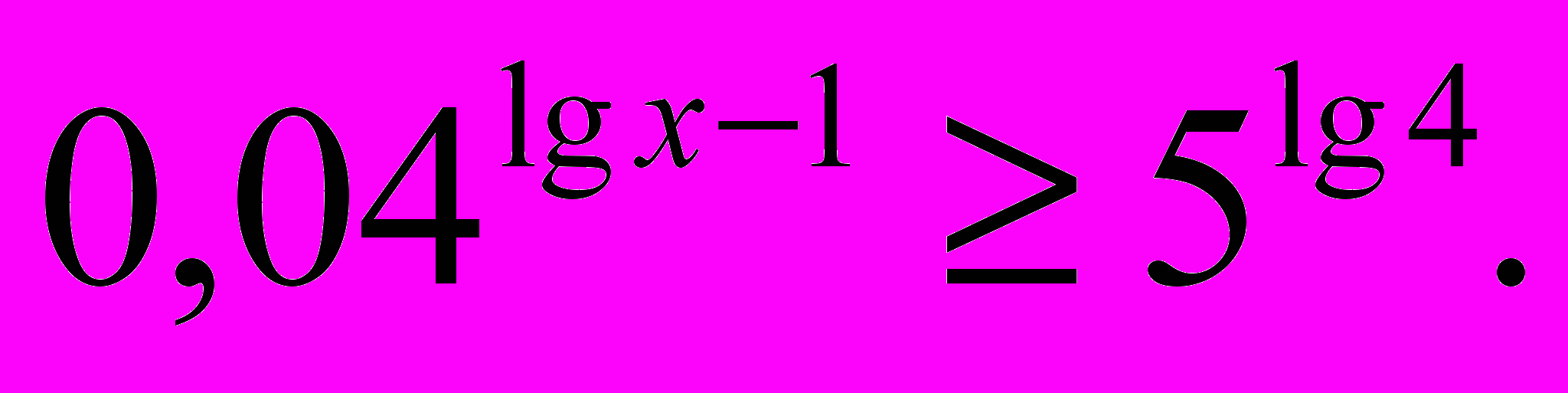
  3. Вычислить
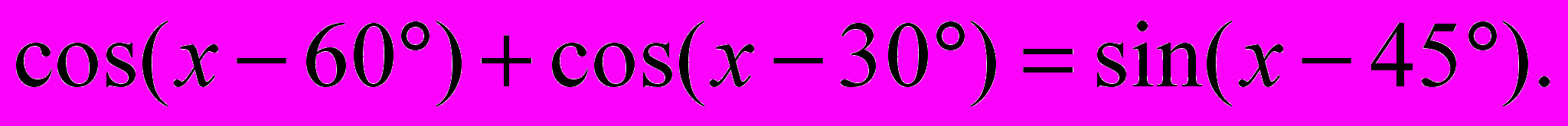
  4. Из города А в город В, расстояние между которыми 10 км, отправился пешеход. Через 30 мин. после него из А и В отправился велосипедист, скорость которого на 6 км/ч больше скорости пешехода. Велосипедист, обогнав пешехода и доехав до города В, возвратился обратно в А и приехал туда в тот момент, когда пешеход пришел в город В. Определить скорость пешехода.
  5. Угол между высотой правильной треугольной пирамиды и боковой гранью равен 30˚. Найти объем пирамиды, если радиус вписанного в пирамиду шара равен .



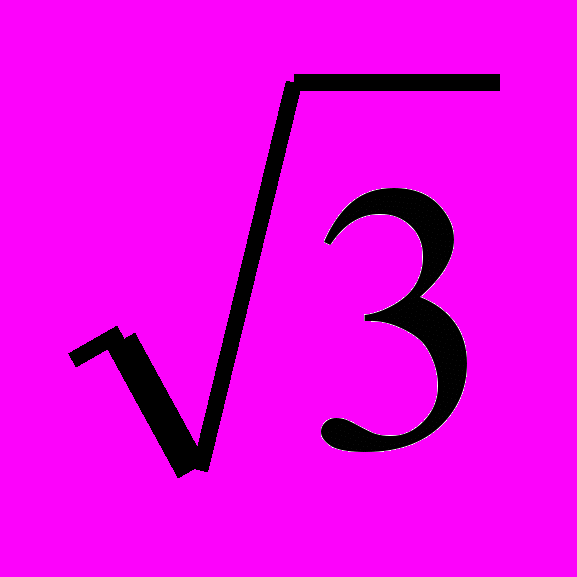Вариант А-24-05

  1. Решить уравнение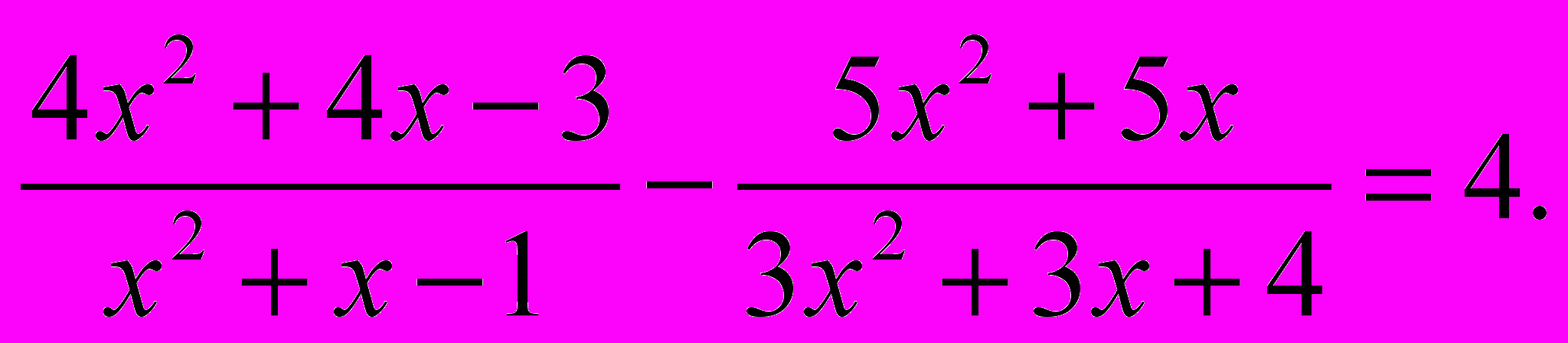
  2. Решить неравенство
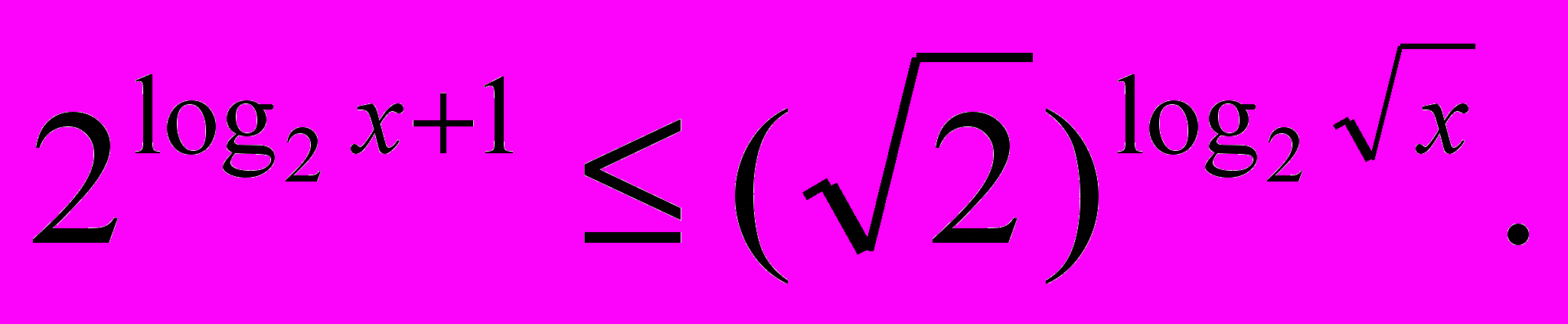
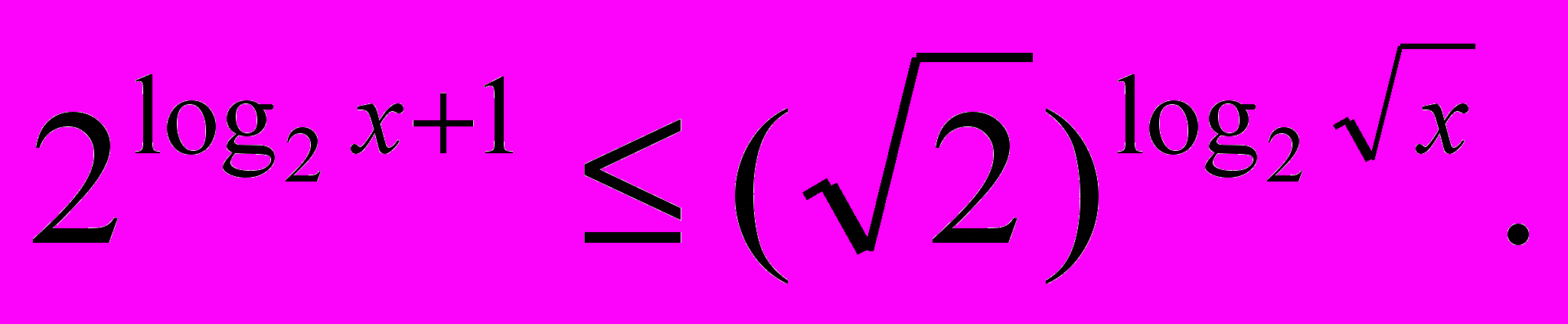
  3. Вычислить
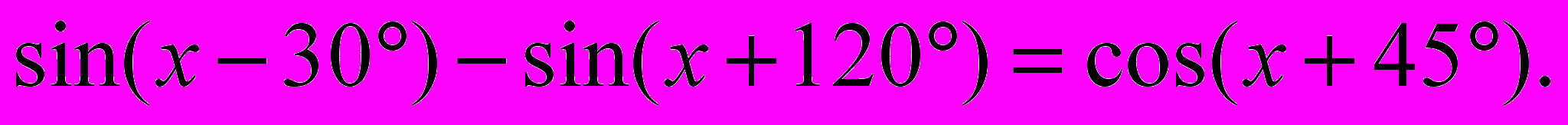
  4. Турист проехал 160 км, причем 5/8 этого пути он ехал на автомашине, а остальную часть – на катере. Скорость катера на 20 км/ч меньше скорости автомашины. На автомашине турист ехал на 15 мин. больше времени, чем на катере. Чему равны скорости катера и автомашины?
  5. Угол между высотой правильной треугольной пирамиды и боковой гранью равен 30˚. Найти площадь боковой поверхности пирамиды, если радиус вписанного в пирамиду шара равен



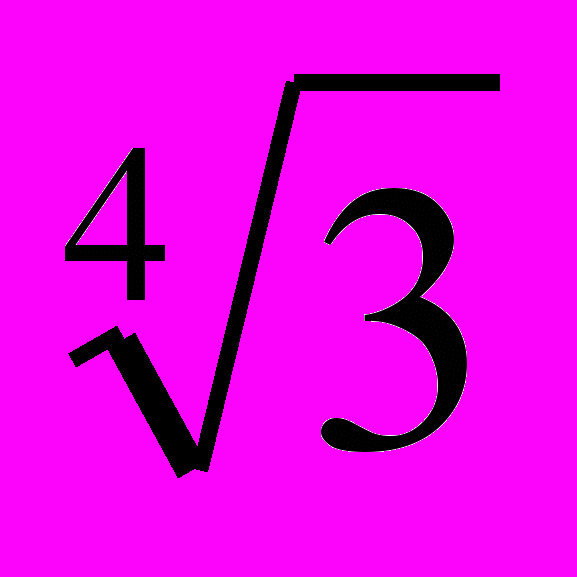
Вариант В-11-05

  1. Решить уравнение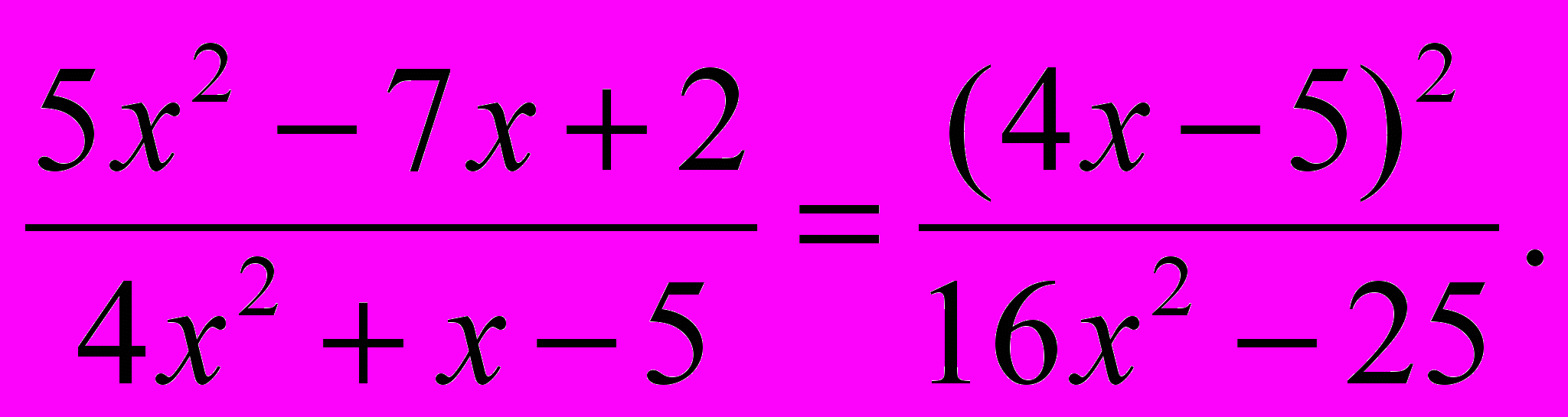
  2. Решить неравенство
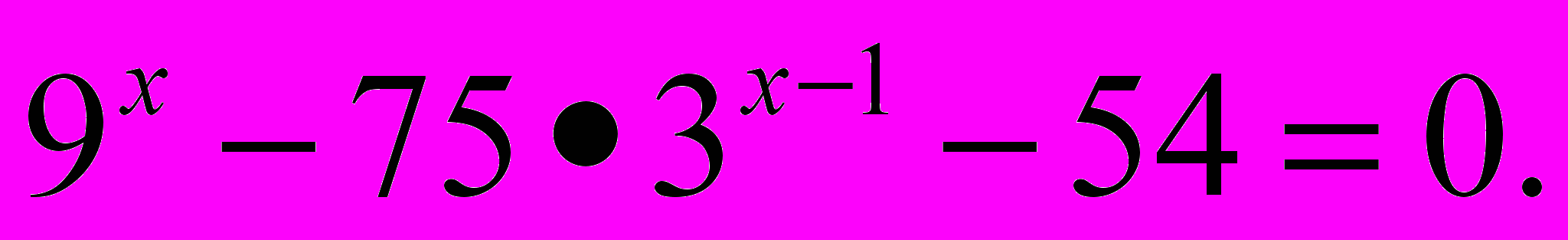
  3. Вычислить
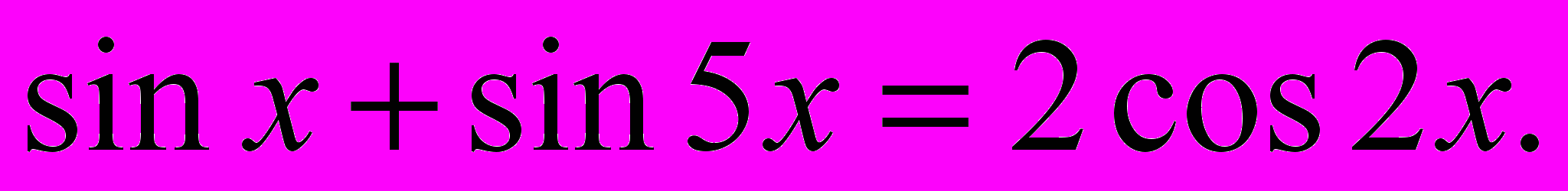
  4. В прямоугольном треугольнике АВС из вершины прямого угла В проведены медиана ВЕ и высота ВК. Величина угла ВСА равна 60˚. Найти величину угла КВЕ.
  5. Токарь и его ученик должны были изготовить за смену 65 деталей. Благодаря тому, что токарь перевыполнил план на 10%, а ученик – на 20%, они изготовили 74 детали. Сколько деталей по плану должны были изготовить за смену токарь и сколько – его ученик?



Вариант В-12-05

  1. Решить уравнение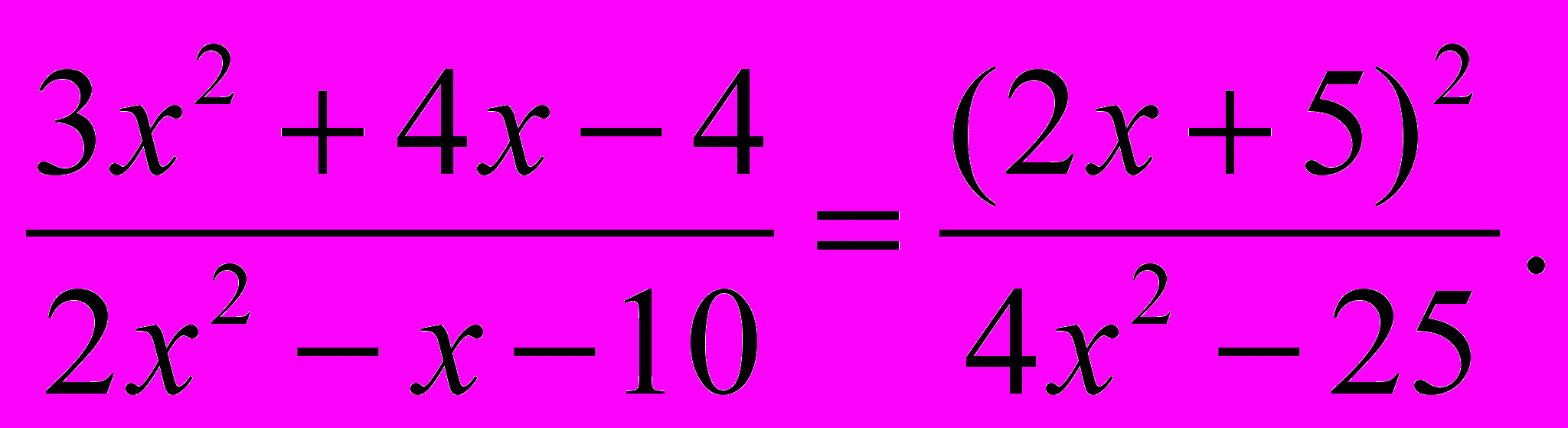
  2. Решить неравенство
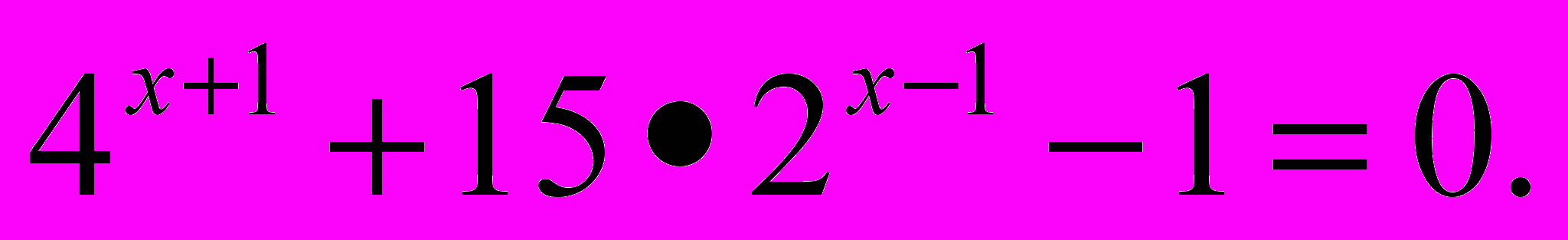
  3. Вычислить
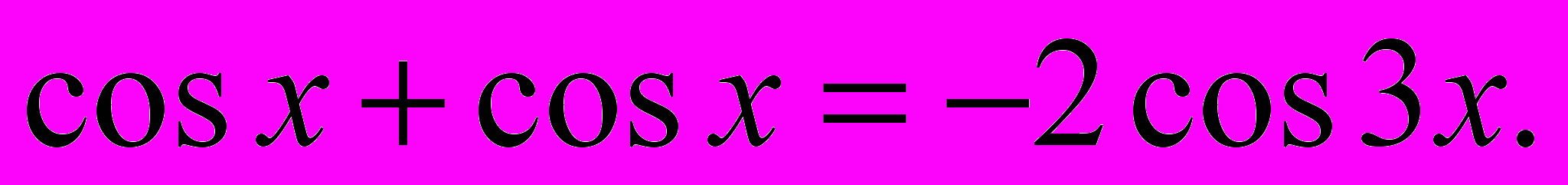
  4. В равнобедренном треугольнике длина боковой стороны равна 5, а площадь треугольника – 12. на основании треугольника взята точка М. Найти сумму расстояний от точки М до боковых сторон треугольника.
  5. Известно, что 5% первого числа и 4% второго составляют в сумме 44, а 4% первого числа и 5% второго составляют в сумме 46. Найти эти числа.



Вариант В-13-05

  1. Решить уравнение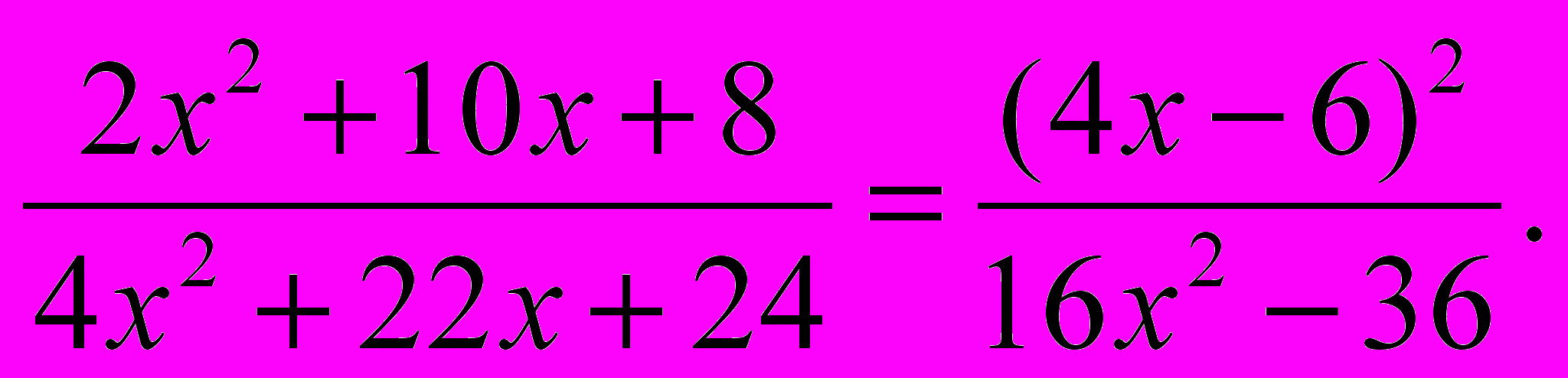
  2. Решить неравенство
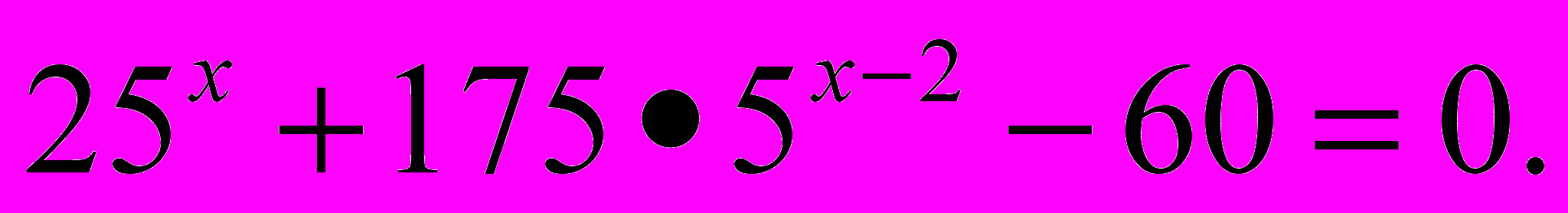
  3. Вычислить
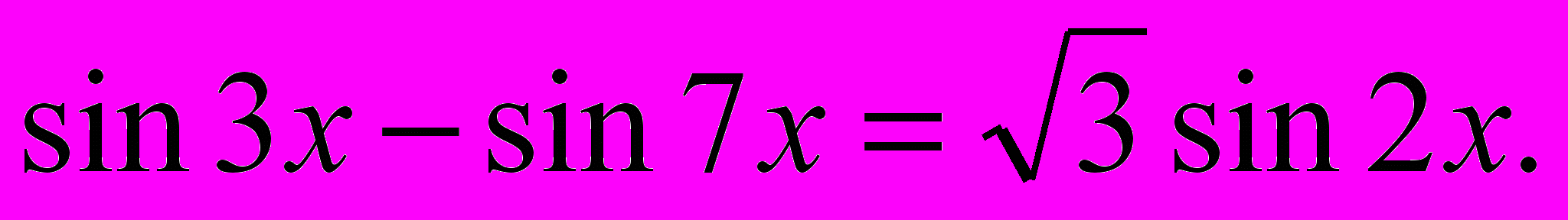
  4. В прямоугольном треугольнике величина угла, образованного медианой и высотой, проведенными к гипотенузе, равна 16˚. Найти меньший острый угол треугольника.
  5. Сумма двух чисел равна 2490. Найти эти числа, если 8,5% одного из них равна 6,5% другого.



Вариант В-14-05

  1. Решить уравнение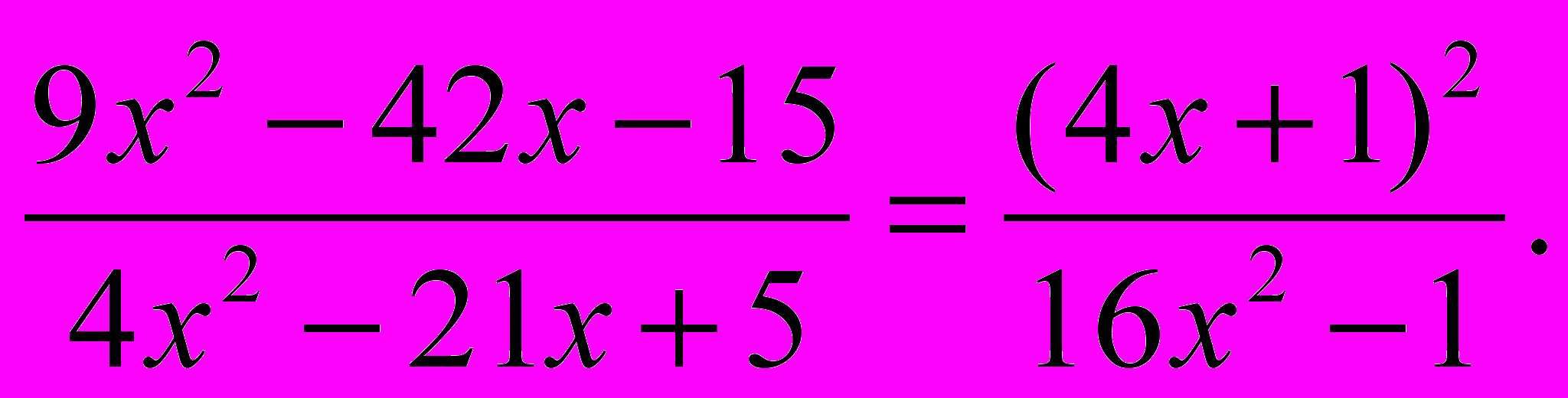
  2. Решить неравенство
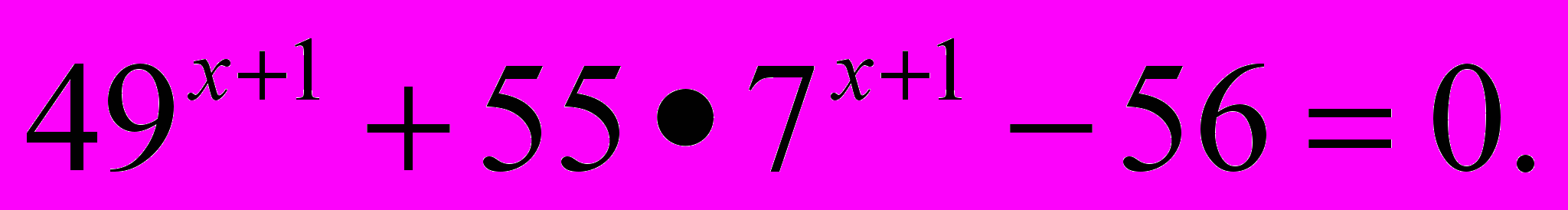
  3. Вычислить
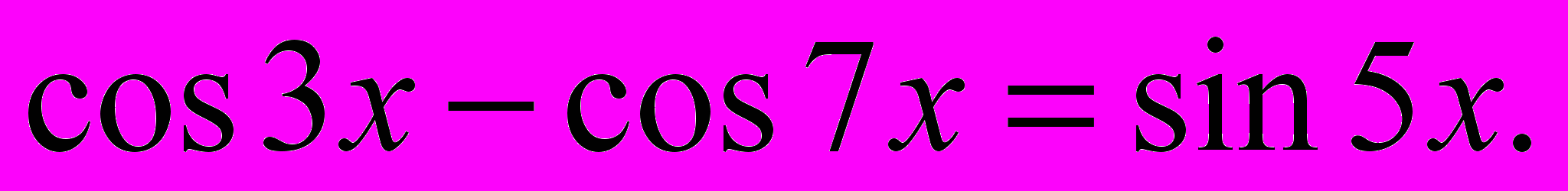
  4. В равнобедренном треугольнике длина боковой стороны равна 6. На основании треугольника взята точка М. Сумма расстояний от точки М до боковых сторон треугольника равна 5. Найти площадь треугольника.
  5. Известно, что 30% числа А на 10 больше, чем 20% числа В, а 30% числа В на 35 больше, чем 20% числа А. Найти числа А и В.


ПРОГРАММА ДЛЯ ПОДГОТОВКИ К ВСТУПИТЕЛЬНОМУ ЭКЗАМЕНУ ПО ИНФОРМАТИКЕ И ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫМ ТЕХНОЛОГИЯМ


Экзамен по информатике и ИКТ проходит в 2 этапа:

  1. первый этап экзамена — тестовое задание, направленное на проверку знаний в сфере информатики и ИКТ.
  2. второй этап экзамена организуется в форме собеседования.



Темы для подготовки к экзамену по информатике и ИКТ

Информационные процессы и системы:

1) Информация и ее кодирование.

Различные подходы к определению понятия «информация». Виды информационных процессов. Информационный аспект в деятельности человека; информационное взаимодействие в простейших социальных, биологических и технических системах. Язык как способ представления и передачи информации. Методы измерения количества информации: вероятностный и алфавитный. Единицы измерения количества информации. Числовые параметры информационных объектов и процессов: объем памяти, необходимый для хранения информации, скорость обработки информации. Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче. Скорость передачи информации и пропускная способность канала связи. Представление числовой информации. Сложение и умножение в разных системах счисления. Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы.


2) Алгоритмизация и программирование

Алгоритмы, виды алгоритмов, описания алгоритмов. Формальное исполнение алгоритма.

Использование основных алгоритмических конструкций: следование, ветвление, цикл.

Использование переменных. Объявление переменной (тип, имя, значение). Локальные и глобальные переменные. Работа с массивами (заполнение, считывание, поиск, сортировка, массовые операции и др.). Структурирование задачи при еѐ решении для использования вспомогательного алгоритма. Вспомогательные алгоритмы: функции и процедуры.


3) Основы логики

Алгебра логики. Логические выражения и их преобразование. Построение таблиц истинности логических выражений.


4) Моделирование и компьютерный эксперимент

Общая структура деятельности по созданию компьютерных моделей. Представление и считывание данных в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы). Математические модели (графики, исследование функций). Построение и использование информационных моделей реальных процессов (физических, химических, биологических, экономических).


5) Социальная информатика

История развития вычислительной техники. Нормы информационной этики (почта, публикации в Интернете и др.). Правовые нормы в области информатики (охрана авторских прав на программы и данные, электронная подпись и др.).


Информационные и коммуникационные технологии:


1) Основные устройства информационных и коммуникационных технологий

Типы компьютеров, их основные характеристики и области использования. Выбор необходимого для данной задачи компьютера. Основные периферийные устройства (ввода-вывода, для соединения компьютеров и др.). Обеспечение надежного функционирования средств ИКТ, устранение простейших неисправностей, требования техники безопасности, гигиены, эргономики и ресурсосбережения при работе со средствами ИКТ.


2) Программные средства информационных и коммуникационных технологий

Операционная система: назначение и функциональные возможности. Графический интерфейс (основные типы элементов управления). Файлы и файловые системы (файловые менеджеры и архиваторы). Оперирование информационными объектами с использованием знаний о возможностях информационных и коммуникационных технологий (выбор адекватного программного средства для обработки различной информации). Технологии и средства защиты информации от разрушения и несанкционированного доступа (антивирусные программы, межсетевые экраны и др.).


3) Технология обработки текстовой информации

Ввод, редактирование и форматирование текста (операции с фрагментом текста, одновременная работа с многими текстами, поиск и замена в тексте, изменение параметров абзацев). Внедрение в текстовый документ различных объектов (таблиц, диаграмм, рисунков, формул) и их форматирование. Автоматизация процесса подготовки издания. Верстка документа. Проверка орфографии и грамматики.


4) Технология обработки графической и звуковой информации

Растровая графика. Графические объекты и операции над ними. Векторная графика. Графические объекты и операции над ними. Компьютерное черчение. Выделение, объединение, перемещение и геометрические преобразования фрагментов и компонентов чертежа. Создание и редактирование цифровых звукозаписей. Компьютерные презентации: типы слайдов, мультимедиа эффекты, организация переходов между слайдами.


5) Технология обработки информации в электронных таблицах

Ввод и редактирование данных в электронных таблицах, операции над данными. Экспорт и импорт данных. Типы и формат данных. Работа с формулами. Абсолютная и относительная ссылки. Использование функций. Статистическая обработка данных. Визуализация данных с помощью диаграмм и графиков. Построение графиков элементарных функций.


6) Технология хранения, поиска и сортировки информации в базах данных

Структура базы данных (записи и поля). Табличное и картотечное представление баз данных. Сортировка и отбор записей. Использование различных способов формирования запросов к базам данных.


7) Телекоммуникационные технологии

Базовые принципы организации и функционирования компьютерных сетей. Локальные и глобальные сети. Адресация в сети. Услуги компьютерных сетей: World Wide Web (WWW), электронная почта, файловые архивы, поисковые системы, чат и пр. Поиск информации в Интернет. Методы и средства создания и сопровождения сайта (основы HTML).


ПРОГРАММА ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ

ПО РУССКОМУ ЯЗЫКУ

Сочинение

Цель любого экзаменационного сочинения не только проверить знания абитуриентов, но и установить, насколько каждый овладел умением излагать свои мысли, культурой письменной речи.

Готовясь к сочинению, необходимо помнить о следующих требованиях:

– надо правильно понять вопрос, содержащийся в формулировке темы, и дать на него развернутый доказательный ответ;

– показать знание текста анализируемого произведения и необходимых теоретико-литературных понятий;

– уметь использовать конкретный материал из текста художественного произведения и из литературно-критических статей;

– уметь анализировать не только содержание, но и художественную форму произведения;

– обнаружить понимание единства формы и содержания;

– в сочинении должна быть показана связь творчества писателя с исторической обстановкой;

– главная мысль сочинения должна развиваться по плану (хотя сам план писать необязательно).

При оценке сочинения учитывается:

– соответствие теме;

– понимание, что для данной темы является главным, что имеет второстепенное значение;

– расположение частей сочинения, их пропорциональность и связь. Главные вопросы должны стоять на первом месте, быть обоснованы и подтверждены фактическим материалом;

– содержание сочинения должно находиться в строгом соответствии с предложенной темой и отличаться логичностью построения, обоснованностью в переходе от одной части к другой, доказательностью суждений, умением использовать текст художественного произведения и сведения по теории литературы;

– в сочинении надо обнаружить не только знание содержания литературного произведения, но и понимание его художественного своеобразия;

– сочинение должно быть написано литературным языком. Абитуриент должен уметь свободно пользоваться различными речевыми оборотами и образными средствами языка, проявить орфографическую и пунктуационную грамотность;

– сочинение должно отличаться стилистической грамотностью, причем особое внимание обращается на правильность построения фразы, соответствие стиля речи содержанию сочинения, умение правильно и уместно цитировать.

В оценке сочинений экзаменационная комиссия по русскому языку и литературе руководствуется существующими нормами оценок. Однако при этом особо учитывается творческий характер сочинений, самостоятельность суждений, культура письменной речи, умение мыслить логически и передавать образность художественной речи.

Следует помнить, что задача абитуриента, пишущего экзаменационное сочинение, не только показать знания и умения, но и раскрыть свои убеждения, эстетическую и общую культуру, культуру мышления и речи. Следовательно, в сочинении должны раскрываться не только общеизвестные сведения, но и ваша индивидуальность, ваше отношение к литературе, читательская активность, самостоятельность мышления,

"Пакет" тем сочинений предусматривает следующее распределение материала:

I тема – по русской литературе I половины XIX в. (материал 9 кл.)

Анализ творчества А.С. Грибоедова, А.С. Пушкина, М.Ю. Лермонтова, Н.В. Гоголя.

II тема – по русской литературе 2-й половины XIX в. (материал 10 класса). Анализ творчества И.С. Тургенева, А.Н. Островского, Н.А. Некрасова, Ф.М. Достоевского, М.Е Салтыкова-Щедрина, Л.Н. Толстого, А.П. Чехова, Н.С. Лескова и др.

III тема – по русской классической литературе XX в. (материал 11 класса). От анализа творчества А. Блока, М. Горького до анализа произведений А. Твардовского, М. Шолохова и др.

IV тема – по внеклассному чтению (материал, изучаемый факультативно в 8–11 классах). Это и современная русская литература текущего процесса последних лет (А. Солженицын, В. Дудинцев и др.), и "возвращенная" литература (М. Булгаков, В. Шаламов, В. Войнович и др.). Эта тема предполагает (анализ литературного материала при этом обязателен) личностный подход в рассмотрении проблем экологии, политики, философских проблем бытия, моральных, этических и нравственных проблем.

Приведем некоторые темы сочинений.
    1. "Век нынешний" и "век минувший" в комедии А.С. Грибоедова "Горе от ума".
    2. Молодое поколение в драме А.Н. Островского "Гроза" и его представление о счастье и воле.

3. Сатира В. Маяковского.

4. "Ради жизни на земле" (по двум произведениям современной литературы о Великой Отечественной войне).

Основная задача, которая стоит перед абитуриентом, – не перечень литературных фактов или пересказ художественного произведения, а глубокий анализ этого произведения, объяснение фактов, которые подводят автора к выводам.

Обычная структура сочинения – трехчастная: вступление, содержание (главная часть), заключение (выводы).

Во вступлении указывается цель сочинения. В зависимости от темы можно кратко охарактеризовать эпоху, время создания художественного произведения, особенности творчества писателя, рассказать о прототипах героев художественного произведения и т.п.

В главной части раскрывается основное содержание темы, дается характеристика образов, художественного произведения, мастерства писателя, и т.п. Именно в основной части полностью раскрывается тема сочинения.

В заключительной части делаются выводы, подводятся итоги анализа.

Систематизации материала и его правильному последовательному изложению помогает предварительно составленный план сочинения.

План должен:

а) соответствовать теме сочинения;

б) максимально полно охватывать все вопросы, отражая тему;

в) быть целенаправленным, т.е. отражать основное содержание сочинения, и логически выстроенным, что предполагает четкое расположение всех его частей.

В процессе раскрытия темы план может изменяться, уточняться и конкретизироваться. Он обычно записывается в черновике и может не выноситься в беловик, выполняя, таким образом, служебную роль.

Сочинение пишут четыре часа. Очень важным является умение правильно распределить свое время. Обязательно следует оставлять не менее 20 минут на исправление ошибок.

Опыт работы на вступительных экзаменах не раз убеждал экзаменаторов в том, что ошибки экзаменующихся достаточно типичны: слабое знание художественных текстов и элементов теории литературы, изучаемых в школе; неумение раскрыть тему сочинения (отсюда пересказ содержания произведения). Часто недостаточно целенаправленно используется текст, допускаются отдельные фактические ошибки.

Часто встречаются орфографические и пунктуационные ошибки: на непроверяемые безударные гласные, тире между членами предложения, обособления приложения и оборотов со словом "как". Многие не умеют отличить сложное предложение от распространенного простого, не знают правил обособления. К сожалению, часто в сочинениях наблюдаются отклонения от нормы, связанные со словоупотреблением.


Изложение

В последнее время изложение все чаще становится письменным экзаменом по русскому языку и литературе в высшие учебные заведения. Работа над изложением учит понимать прочитанное, наблюдать языковые факты, устанавливать логические связи, отбирать главное, делать обобщения и выводы, самостоятельно и грамотно излагать в письменной форме свои мысли.

Когда абитуриент пишет экзаменационное изложение, он должен в течение трех часов передать содержание отрывка, по возможности близко к тексту, сохраняя его стилистические особенности.

Преподаватель дважды медленно зачитывает достаточно законченный и цельный отрывок текста. Во время чтения текста преподавателем абитуриент может сделать в черновике небольшое количество рабочих записей, форма этих записей свободная. Обычно фиксируется то, что человек не надеется запомнить: собственные имена, даты, прямая речь, цифры и прочие данные. Полезно конспективно записать последовательность изложения, но это стоит делать только в том случае, если абитуриент уверен, что записи не отвлекут его внимания от восприятия текста. Тексты изложений разнообразны по тематике, языку, знакомят с разными стилистическими пластами русского языка.