Николай филинов и светлана ручкина

Вид материала

Документы

Содержание Типы оценки и рейтингов высшего образования Существующие в россии методики рейтингов Общая характеристика предлагаемой методики рейтинга Оценка и измерение ошибок показателей

Подобный материал:

• Пономарева Светлана. Пономарёв Николай. Фото на развалинах, 1081.39kb.
• Подпрограмма «Земляки» «Николашин Николай Павлович Заслуженный учитель, энтузиаст лыжного, 195.85kb.
• Ручкина Галина Викторовна, моу гимназия №1 Программно-методическое обеспечение: программа, 54.66kb.
• Государственный университет – Высшая школа экономики протокол, 1118.25kb.
• Национальный исследовательский университет «Высшая школа экономики» протокол, 802.78kb.
• Ручкина Галина Викторовна, моу гимназия №1 г. Липецка 9 класс, право Правовое регулирование, 48.15kb.
• Личность в истории: Николай, 283.04kb.
• II. Николай Романов личность в истории, 289.05kb.
• Николай Раевский родился 14 сентября 1771 года, в городе Москве.  Николай был болезненным, 115.26kb.
• Направления повышения качества контента корпоративных сми светлана Криворучко, 30.73kb.

Высшее образование в Европе Том XXVII, №4, 2002

РЕЙТИНГИ РОССИЙСКИХ ВУЗОВ: НЕКОТОРЫЕ АСПЕКТЫ МЕТОДОЛОГИИ

 

НИКОЛАЙ ФИЛИНОВ И СВЕТЛАНА РУЧКИНА

 

Рейтинг вузов рассматривается в статье с двух точек зрения: как общественное явление и как многокритериальная задача принятия решения. Первая точка зрения вводит идею заинтересованных сторон, вторая – ряд принципов, на которых должна основываться рациональная система построения рейтинга.

 

ВВЕДЕНИЕ И ОБОСНОВАНИЕ

Рейтинг вузов весьма актуальная проблема. Для составления рейтингов вузов и учебных программ применяются чрезвычайно разнообразные методы и технологии. В некоторых странах эта деятельность ведется уже много лет, в других только начинается. В последние годы в России также ощущалась потребность в подобной информации, и она не замедлила появиться в русской прессе. В 2001 г. Министерство образования Российской Федерации инициировало разработку методики рейтинга университетов. Эти факты говорят об интересе к рейтингам со стороны поступающих в вузы, будущих работодателей и государства.

Проблема подбора или разработки правильной методики подготовки рейтингов в России столь же насущна, как и в других странах. Существующие методы имеют определенные недостатки как с точки зрения используемых данных, так и с точки зрения способов их обработки. В сущности, перед нами повсюду в мире стоят одни и те же проблемы.

В то время как есть общее понимание того, кому нужны рейтинги – абитуриентам, работодателям, государственным организациям и общественности в целом, – тем не менее существует множество различных, а зачастую и противоположных точек зрения на то, кто должен выполнять эту работу и как ее надлежит выполнять.

В чем же состоит трудность построения рейтинга университетов и образовательных программ? По мнению авторов, тому есть две основные причины. С одной стороны, образование - это услуга, качество которой нельзя впрямую ощутить или измерить инструментально – оно проявляется со временем (иногда, в течение всей жизни). С другой стороны, рейтинги и таблицы лиг являются значимыми рыночными инструментами, до некоторой степени влияющими на поведение всех заинтересованных в образовании сторон – будущих студентов, их родителей, промышленных предприятий, государственных организаций и собственно образовательного сообщества. Сторонние наблюдатели, не участвующие в повседневной образовательной деятельности, не могут в полной мере оценить ход образовательного процесса. В итоге складывается ситуация, когда оценку образовательной системы придется проводить работникам этой же системы, т.е. они будут оценивать самих себя, что неминуемо приведет к необъективности и недостоверности.

В результате сложились три модели рейтинга: (1) рейтинг СМИ; (2) рейтинг профессиональных ассоциаций и (3) правительственный рейтинг.

Сильной стороной рейтинга, подготавливаемого СМИ, является, несомненно, его независимость (оценку образования проводят незаинтересованные лица), но его справедливо критикуют за недостаточную научную обоснованность, низкий уровень профессионализма, пристрастность и возможный ущерб престижу оцениваемых вузов.

«Рейтинг профессиональных ассоциаций», возможно, будет не вполне корректным термином, т.к. многие ассоциации, действующие в сфере образования, отказались участвовать в подготовке рейтингов. Свое решение они объясняют по-разному, но совершенно очевидно, что в основном их тревожит тот факт, что, приняв участие в подготовке рейтинга, они из соратников и сотрудников превратятся в разжигателей конкурентной борьбы. Многие из этих профессиональных ассоциаций активно участвуют в деятельности по аккредитации. Однако аккредитация существенно отличается от рейтинга.

Хотя с технической точки зрения между рейтингом и аккредитацией много общего (что не всегда охотно признают противники рейтингов), две процедуры коренным образом различаются с политической точки зрения. Все аккредитованные учебные заведения равны, поскольку они аккредитованы. Все вошедшие в рейтинг заведения различны, поскольку они имеют разный рейтинг.

Подготовку рейтинга профессиональными ассоциациями можно охарактеризовать как совместную деятельность группы заинтересованных сторон. Сильной стороной этой модели является, безусловно, профессионализм, слабой – замкнутость и необъективность вследствие конфликта интересов.

Третья модель – правительственный рейтинг, подготавливаемый государственным органом, ответственным за лицензирование, аккредитацию и руководство образовательной деятельностью в стране. Это высокобюрократизированная процедура, в значительной степени опирающаяся на мнение квалифицированных экспертов, и еще сильнее – на различные количественные данные. В силу своей сущности подобный рейтинг сфокусирован, скорее, на образовательной стороне процесса, в меньшей степени учитывая интересы будущих работодателей.

Оценить качество образования – достаточно сложная задача. Сравнительно просто оценить знания, полученные студентами в той или иной области, и чрезвычайно сложно оценить потенциал выпускников отдельных университетов, особенно их способности к самообразованию. Все попытки охарактеризовать результаты образования сталкивались со значительными сложностями при формулировании критериев оценки. Более того, полученное образование во многом определяет дальнейший ход жизни человека. Возникает вопрос, насколько возможно учесть это влияние. Сложности оценки результата образования подразумевают необходимость оценки образовательного процесса.

Концепция качества образования носит комплексный, многокомпонентный характер, внимание привлекается к различным граням образования. Соответственно оценка должна быть многомерной, т.е. необходимо учитывать все возможные характеристики обучения. Оценку качества любой услуги нельзя сводить к оценке качества результата. Для полной и верной оценки качества образования необходимо оценить способность и потенциал оказания образовательных услуг: характеристики преподавательского состава, уровень технической оснащенности, финансирование вуза и т.д.

Все перечисленные выше трудности, возникающие при попытках оценить качество образования, приводят к осознанию важности разработки адекватной методики рейтингов. И здесь мы хотели бы предложить некоторые дополнительные фундаментальные положения, которые необходимо учесть при построении рейтинга:

• -         Рейтинг (как род деятельности, причем необязательно в ныне существующем виде) должен в первую очередь рассматриваться как источник информации для руководства вузов. Широкая общественность неспособна полностью воспринять эту информацию, т.к. неспециалисты, далекие от высшего образования, не обратят должного внимания на детали, представляющие особую важность для профессионалов. Профессионалы смогут отследить динамику и сделать подробные выводы. Поэтому именно они используют рейтинги в полной мере, и при разработке рейтингов следует ориентироваться в первую очередь на их потребности.
  
• -         Рейтинг представляет собой процесс принятия решения на основе многочисленных критериев. При разработке процедуры значительную пользу могут принести положения общей теории принятия решений при многих критериях.
  
• -         Несмотря на все усилия по обеспечению максимальной достоверности и надежности данных, ошибки (как случайные, так и преднамеренные) неизбежны. Поэтому представляется разумным предусмотреть их наличие и оперировать интервальными оценками параметров, а не точечными.
  
• -         При работе с таблицами лиг возникает проблема числа лиг и их пределов. Здесь возможны два подхода: заранее зафиксировать оба показателя или определить их в процессе обработки данных для конкретного рейтинга. С точки зрения авторов, второй подход предпочтителен.
  

 

ТИПЫ ОЦЕНКИ И РЕЙТИНГОВ ВЫСШЕГО ОБРАЗОВАНИЯ

Можно определить два основных уровня оценки вузов: оценка вуза как организации в целом и оценка образовательной программы.

Такой подход предполагает две модели оценки:

институциональную и специализированную.

На институциональном уровне производится общая целостная оценка образовательного учреждения, не сводящаяся к оценкам отдельных подразделений. Основным недостатком этого подхода является неконкретность, абстрактность полученной таким образом оценки. Как правило, при таком подходе сильные стороны вуза неким образом компенсируют его слабости (например, слабый преподавательский состав в одной программе зачастую компенсируется сильным в другой). С другой стороны, только такая процедура позволяет учесть все многообразие ресурсов, формирующих потенциал данного вуза, причем не всегда эти ресурсы можно отнести по принадлежности к отдельному подразделению или образовательной программе. Такие процедуры успешно применяются для оценки образования во многих странах: США, Франции, Израиле, Японии и др.

Специализированная оценка связана с наиболее важными подсистемами вузов, а именно с образовательными программами, качество которых непосредственно определяет качество образования выпускника. Как правило, оценка такого типа предполагает изучение процессов преподавания, обучения и научно-исследовательской деятельности. Специализированная оценка также имеет многолетнюю историю развития и широко распространена в Западной Европе и США.

Следуя такой логике, имеет смысл говорить о рейтингах университетов или отдельных программ. Очевидно, что рейтинг учебных заведений в целом представляет значительный интерес для руководства университетов, но с ростом независимости подразделений вузов он теряет свою важность. В системе высшего образования зонтичного типа, где отдельные школы (программы) обладают значительной самостоятельностью, рейтинги университетов в целом, возможно, окажутся вообще бессмысленными. Дополнительную трудность представляет то, что сравнивать можно только однотипные сущности. Можно предположить, что легче выделить однотипные программы, чем однотипные вузы, каждый из которых предлагает различный набор программ.

 

СУЩЕСТВУЮЩИЕ В РОССИИ МЕТОДИКИ РЕЙТИНГОВ

Рейтинг университетов, публикуемый журналом «Карьера»

Оценка университетов производится по трем классам показателей (Карьера. 1999. № 3):

1. 
   i.                    характеристика контингента студентов;
   
2. ii.                  характеристика профессорско-преподавательского состава;
   
3. iii.                характеристика программ и условий обучения
   

По каждому классу было выбрано 7–8 показателей. Статистические данные были предоставлены университетами.

Методика рейтинга

Этап 1. Получение оценок по каждому показателю.

Этап 2. Расчет показателей по каждому университету:

- вычисление натурального веса (V_i) одного пункта измерений по показателю i:

, где Р_ij – значение i-го показателя для j-го университета, i = 1, j = 1, …, n;

• -         нахождение балла (B_ij) по этому показателю для каждого вуза:
  

Этап 3. Определение итогового балла каждого вуза:

, где (100%)

Этап 4. Составление рейтинговой таблицы на базе полученных оценок W_j.

 

Методика рейтинга университетов утвержденая приказом Министра образования Российской Федерации № 631 от 26 февраля 2001 г. “О рейтинге высших учебных заведений”.

 

Показатели рейтинга разделены на следующие основные группы:

• -         профессорско-преподавательский состав (штатные сотрудники);
  
• -         профессорско-преподавательский состав (совместители и почасовики);
  
• -         студенты и аспиранты;
  
• -         деятельность университетских диссертационных советов;
  
• -         объем НИР (в денежном выражении);
  
• -         издательская деятельность;
  
• -         бюджетные ассигнования и основные фонды;
  
• -         финансовая деятельность;
  
• -         социально-бытовые условия.
  

Методика построения рейтинга

Этап 1. Получение оценок по каждому показателю.

Этап 2. По каждому университету вычисляется локальный критерий третьего (низшего) ранга:

, где - определенный поднабор из полного набора показателей j-го университета, на базе которого производится оценка данного критерия , а - функция, описывающая взаимозависимость показателей и данного критерия.

Этап 3. Перерасчет значений локальных критериев по каждому университету:

• -         вычисление нормирующего значения для каждого локального критерия третьего (низшего) ранга:
  

, где Р_ij – значение i-го показателя для j-го университета,

i = 1, m; j = 1, …, n;

• -         определение значения (B_ij) для показателя i-го каждого университета:
  

Этап 4. Последовательная свертка локальных критериев в критерии первого ранга: потенциал и деятельность

Этап 5. Вычисление специального показателя Е = К₁/К₂. В данной методике этот показатель используется для усиления влияния продуктивных целей на результат итоговой оценки, что достигается путем использования показателя Е для расчета критерия К₁₁ (интеллектуальный потенциал). Свертка повторяется до получения значения глобального критерия.

Этап 6. Составление рейтинговой таблицы по значению глобального критерия. В основе этой методики лежит разветвленная структура критериев, на которые раскладывается комплексная глобальная цель системы. Структура представлена на рис. 1.

 

Рис. 1. Структура критериев рейтинга Министерства образования




 

 

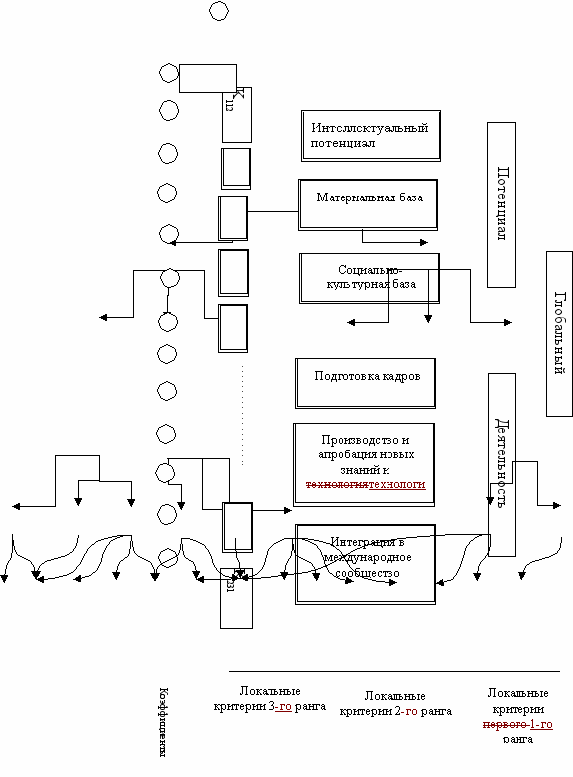
Анализ методик построения рейтингов университетов

 

Далее мы рассмотрим лишь некоторые аспекты упомянутых выше методик, чтобы наглядно доказать необходимость перемен, описанных в начале этой статьи.

Введение нормировочного коэффициента, определяемого максимальным значением показателя среди всех университетов, привело к тому, что интегрированная оценка университета, определяющая его положение в рейтинге, зависит от значений показателей других университетов. Так, для первого метода (применяемого журналом «Карьера») при подстановке всех введенных ранее коэффициентов, окончательная формула расчета глобального критерия будет выглядеть так:



 

Совершенно очевидно, что множители 10, будучи общими для всех университетов, не повлияют на итоговое значение рейтинга. Исключив их, получим формулу, позволяющую получить тот же самый рейтинг:

.

Приходим к выводу, что весовые коэффициенты, присвоенные показателям для вычисления итоговых баллов данного университета, зависят от значений показателей других университетов. Изменение весовых коэффициентов приведет к значительным изменениям баллов, а соответственно к изменениям в рейтинге вплоть до обратных.

Вторая методика также обладает подобной особенностью. Нормирование на третьем этапе (нормирование местного критерия третьего ранга) также приводит к нестабильности рейтинга.

При каких обстоятельствах меняются значения весов? Рассматривая две основные причины изменения весовых коэффициентов, мы охарактеризуем также их влияние на рейтинг.

1. 
   1.     Изменения в структуре университетов, предоставляющих данные
   

Оценим влияние этого фактора на результаты рейтинга. Представим себе три университета, оцениваемые по трем показателям:

	Университет 1	Университет 2	Университет 3
Показатель 1	5	2	10
Показатель 1 Показатель 2	2	4	1
Показатель 3	2	2	1

 

Предположим, что весовые коэффициенты, с которыми все показатели вводятся в интегрированную формулу, все равны 1/3. Тогда рейтинг примет следующий вид:

Университет	Значение интегрированного критерия	Положение
1	(3/8+1/3+1) /3=0,57	2
2	(0+1+1) /3=0,67	1
3	(1+0+0) /3=0,33	3

 

Если добавить четвертый университет:

	Университет 4
Показатель 1	1
Показатель 2	10
Показатель 3	1

рейтинг будет выглядеть так:

 

Университет	Значение интегрированного критерия	Положение
1	(4/9+1/9+1) /3=0,52	1
2	(1/9+3/9+1) /3=0,48	2
3	(1+0+0) /3=0,33	3-4
4	(0+1+0) /3=0,33	3-4

Первый и второй университеты поменялись местами.

Однако, этот методический недостаток не имеет решающего значения, если все университеты обязаны предоставлять данные. Соответственно, для рейтинга Министерства образования этот момент не является существенным.

 

2. 2.     Изменение значений показателей отдельного университета
   

Изменение значений показателей отдельного университета может привести к изменению положения других университетов в рейтинговой таблице

Для иллюстрации этого утверждения продолжим рассмотрение предыдущего примера. Представим себе, что значение второго показателя четвертого университета изменилось и равно не 10, а 5. В таком случае университеты расположатся в таблице так:

Университет	Значение интегрированного критерия	Положение
1	(4/9+1/4+1) /3=0,56	2
2	(1/9+3/4+1) /3=0,62	1
3	(1+0+0) /3=0,33	4
4	(0+1+0) /3=0,33	3

Итак, из-за изменения показателя четвертого университета первый и второй поменялись местами.

Приведенные выше рассуждения убедительно доказывают необходимость разработки методики, устойчивой к изменениям структуры университетов. Для этого следует избавиться от различных нормированных значений и зависимости весовых коэффициентов критериев от значений параметров.

Показатели, на основе которых готовятся оба рейтинга, в большинстве случаев невозможно рассчитать с абсолютной точностью. Данные неминуемо содержат ошибки, а соответственно и подготовленные по ним рейтинги будут не вполне точны. Незначительные неточности оценки показателей могут привести к неверному расположению университетов в рейтинге. Более того, если разница интегрированных оценок двух университетов незначительна, то нельзя с уверенностью утверждать, что один университет лучше другого. Эта проблема решается путем перехода от точечных оценок показателей к интервальным оценкам, что позволит учесть неточности измерения показателей. Финальный рейтинг будет представлять собой своего рода распределение университетов по лигам. В одну лигу войдут университеты, по качеству образования незначительно отличающиеся друг от друга, но при этом значительно отличные от университетов, вошедших в другие лиги.

 

ОБЩАЯ ХАРАКТЕРИСТИКА ПРЕДЛАГАЕМОЙ МЕТОДИКИ РЕЙТИНГА

 

Необходима новая методика рейтинга, свободная от описанных выше недостатков. Она должна удовлетворять следующим основным требованиям:

1. 
   i.                    Если отдельные группы образовательных учреждений объединяются для проведения совместного рейтинга, а также в случае, когда рейтинг разбивается на ряд отдельных рейтингов, соотношение приоритета между отдельными учебными заведениями должно остаться неизменным. Другими словами, если часть университетов отказывается от участия в рейтинге, взаимное расположение остальных университетов не должно меняться.
   
2. ii.                  Незначительные колебания предоставленных данных не должны менять результаты рейтинга.
   
3. iii.                Не следует определять весовые коэффициенты напрямую: подобная процедура ненадежна с точки зрения обеспечения достоверных результатов; скорее необходимо применять специальную процедуру с участием экспертов.
   

По результатам анализа существующих методик подготовки рейтингов университетов можно выделить основные этапы работы. При этом необходимо учитывать важнейший фактор – погрешности измерения показателей и строить интервальную интегрированную оценку, по которой формируется рейтинг.

Основные этапы подготовки рейтинга таковы:

Этап 1. Получение точечных оценок показателей

Этап 2. Получение интервальных оценок показателей

Этап 3. Получение интегрированной интервальной оценки по каждому университету.

Этап 4. Распределение университетов по лигам.

Такой подход может послужить основой для плана разработки методики рейтинга (рис. 2).

Рис. 2. Предлагаемая структура процедуры рейтинга и необходимых исследований

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

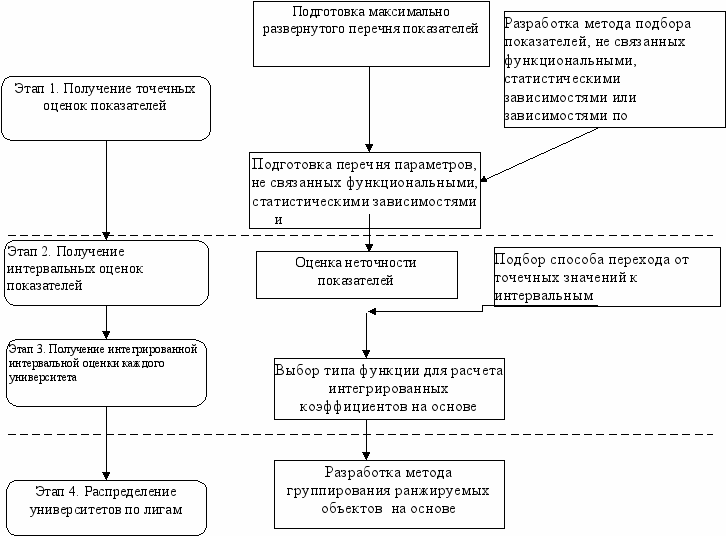
Разработка системы показателей

Европейское бюро качества (EQUAL) – Европейская ассоциация национальных органов аккредитации – издало документ, озаглавленный «Ответственный подход к таблицам лиг». В нем следующим образом описывается набор показателей, используемых для расчета рейтинга. «Диапазон показателей, по которым производится сравнение, должен быть широким и репрезентативным. С учетом желаемых результатов необходимо выбирать такие показатели, которые можно точно и независимо измерить количественно». В нашем понимании этот общий подход нуждается в конкретизации.

Для составления рейтинга необходимо подобрать набор показателей, который будет полным, декомпозируемым, функциональным, неизбыточным (минимальным) - не допускающим дублирования отдельных аспектов деятельности вузов. Обсудим эти свойства подробнее.

Набор показателей должен быть полным. Набор показателей является полным, если на его основе можно охарактеризовать уровень достижения глобальной цели и все представляющие интерес стороны процесса. Другой важной стороной этого требования является равномерность охвата всех аспектов качества образования. Если не уделить этому моменту достаточного внимания, то может сложиться ситуация, когда профессорско-преподавательский состав будет охарактеризован в мельчайших подробностях, а техническая оснащенность данного вуза будет освещена не полностью.

Набор показателей должен быть декомпозируемым. Другими словами, должна существовать возможность упростить процесс оценки, разбив его на части. Здесь может оказаться полезным иерархическое построение системы показателей, т.е. интегрированная оценка определенных аспектов деятельности каждого вуза посредством оценки их компонентов по системе надежно измеряемых показателей с последующим их агрегированием.

Набор показателей должен быть функциональным с управленческой и технической точек зрения. Набор показателей можно считать функциональным с управленческой точки зрения, если лицо, ответственное за принятие решений на уровне вуза, способно понять смысл показателей и контролировать их численные значения (хотя, разумеется, некоторые показатели могут выходить за пределы его или ее компетенции). Если же существенная часть показателей не поддается управлению, то весь процесс теряет смысл, поскольку невозможно извлекать уроки и выводы и предпринимать необходимые корректирующие действия.

С технической точки зрения первоочередным требованием к показателю является возможность его измерения. Наилучшей измеряемостью обладают документальные данные. В таком случае не возникает необходимости в услугах высококвалифицированных экспертов. Обработать такие данные могут административные работники, обладающие средним уровнем квалификации. С другой стороны, стремление собрать только такие показатели приводит к преобладанию формальных критериев – начинается подсчет количества публикаций без учета их качества и научного уровня и т.п. Поэтому в этом случае, как и во многих других, необходимо найти оптимальное соотношение.

Существует и другой аспект функциональности набора показателей, имеющий иную природу. Гораздо проще оперировать рейтингом, основанным на линейном объединении показателей, т.е. на аддитивной функции ценности. Этот механизм позволяет напрямую оценить влияние изменения отдельных показателей на общее положение данного университета или программы в рейтинге. Упомянутый выше документ EQUAL не приветствует применение такого подхода, а, напротив, рекомендует избегать применения дифференцированных весовых коэффициентов для каждого показателя. Если все же пользоваться ими, то необходимо их однозначно определять и подробно описывать их смысл и влияние. Тем не менее в России они применяются, и, насколько можно судить по публикациям в прессе, не только в России. Избежать использования весовых коэффициентов можно, но это повлечет за собой определенные дополнительные сложности. Поскольку оценка образовательных сущностей (учреждений и программ) носит многомерный характер и осуществляется посредством разложения, то процесс неминуемо будет содержать этап интегрирования. Интегрирование может осуществляться на основе целостной экспертной оценки или с учетом весов отдельных показателей. Если нежелательно применять схему с использованием весов, то придется полагаться на суждение экспертов, надежность которого во многих случаях вызывает сомнения.

Для того, чтобы их можно было представить в виде аддитивной функции ценности, показатели должны быть независимы друг от друга по предпочтению. Независимость по предпочтению предполагает, что решение о предпочтительности значения одного критерия зависит от значения, которое принимает в этот момент другой критерий. В теории принятия решений при многих критериях существует теорема о том, что для множества критериев Х₁, … , Х_n, n ³ 3, аддитивная функция ценности v(x₁,x₂, …, x_n) = Sv_i (x_i) (где v_i(x_i) – маргинальная функция ценности критерия x_i) существует тогда и только тогда, когда все x_i независимы по предпочтению.

Дебрё, Фишберн и др. (см. в Кини и Райфа, 1981) формально доказали эту теорему. Таким образом, появляется новое требование к показателям для составления рейтинга университетов: они должны быть взаимно независимы по предпочтению. Сколь бы важным и желательным ни было это свойство, его может быть весьма сложно проверить (это обстоятельство, в свою очередь, делает всю процедуру менее операциональной). Трудность заключается в том, что формально необходимо испытать все возможные комбинации показателей (пары, тройки и т.д.). Число таких комбинаций очень велико, даже если показателей всего 10–15. Для n показателей число комбинаций составит n×(n – 1)/2, если испытывать только пары. К счастью, было доказано, что достаточно испытывать только пары показателей на независимость от других подмножеств показателей. Тем не менее даже в таком усеченном виде задача вызывает значительные сложности. Чтобы упростить работу, можно ограничиться только теми комбинациями показателей, для которых мы можем подозревать наличие зависимости. Как известно из теории принятия решений, зависимость по предпочтению возникает, если в процессе принятия решения предпочтение отдается определенным пропорциям, отношениям или соотношениям значений данных критериев. Следовательно, задача решается в два этапа. Сперва выделяются «подозрительные» группы показателей, которые желательно проверить на наличие зависимости. На втором этапе проверка выбранных групп на зависимость от выбора производится хорошо известным диалоговым методом.

Набор показателей должен быть неизбыточным (минимальным). Показатели, характеризующие отдельные аспекты деятельности вузов, не должны дублировать друг друга. Для исключения избыточных данных, необходимо произвести причинно-следственный анализ, а также исследовать функциональные и статистические взаимозависимости показателей. Причинно-следственная связь между параметрами может проявляться в форме функциональной и статистической зависимости. Функциональная зависимость означает, что один или несколько показателей полностью определяют значение другого показателя. В случае статистической зависимости значение зависимого показателя определяется не полностью, а наблюдается только общая тенденция.

Чем может объясняться статистическая зависимость показателей? Одной из причин может быть наличие причинно-следственной связи между этими показателями. Есть и другое объяснение – т.н. явление ложной корреляции. Оно означает, что два или более показателей не связаны между собой причинно-следственными связями. Изменение одного показателя не приведет к изменению другого. Они оба зависят от третьего параметра, который и определяет на самом деле изменения обоих зависимых показателей, связанных между собой таким образом. И наконец, наблюдаемые статистические корреляции могут быть вызваны простым совпадением.

Можно ли включать в методику рейтинга показатели, сильно зависимые друг от друга? Ответ неоднозначен. В случае функциональной зависимости, возможно, будет разумным исключить один из вызывающих сомнения показателей, чтобы сделать ситуацию более управляемой. Так или иначе, в этом случае никакая информация не теряется – все можно вычислить. Однако что касается представления информации, то для принятия решений более удобным может оказаться анализ информации с помощью дополнительных производных показателей. Наглядным примером могут послужить показатели численности профессорско-преподавательского состава и контингента студентов. Оба параметра сами по себе важны, но их отношение обладает собственной значимостью, в то время как показатель численности студентов является знаменателем в некоторых других важных отношениях (коэффициентах). Поэтому нельзя исключить отношение численности преподавательского состава к численности студентов, но необходимо, кроме того, сохранить и сами показатели в исходном виде. В общем случае, если изменение значения показателя приводит к таким изменениям производных показателей, которые положительны (желательны) в одном случае, и отрицательны в другом, и существует по крайней мере одна нелинейная зависимость, необходимо оставить в наборе показателей оба производных показателя индикатора.

В случае статистической зависимости все приведенные выше соображения остаются в силе, за исключением одного: при исключении одного из статистически зависимых показателей часть информации теряется. С другой стороны, такое исключение уменьшает число показателей для обработки. Исключение статистически связанных показателей из рейтинга незначительно уменьшит пределы колебаний интегральных оценок ранжируемых вузов и, следовательно, не повлияет на окончательный рейтинг.

Особенную сложность представляют случаи ложной корреляции и чистого совпадения. При исключении одного из показателей не только теряется информация, но может нарушиться и вся логика модели.

Приходится признать, что создание идеального во всех отношениях набора показателей практически невозможно. Складывается довольно интересная ситуация: задача по подбору множества критериев представляет собой многокритериальную задачу! Приходится искать компромисс между противоречащими друг другу требованиями.

Целесообразно будет составить максимально развернутый перечень показателей и затем исключать из него некоторые показатели, связанные между собой различными зависимостями.

1. 
   i.                    Составление максимально развернутого перечня показателей.
   

Интегрированная оценка, на основе которой составляется рейтинг, представляет собой результат комплексного анализа качества образования. Интегрированная оценка вычисляется по отдельным показателям качества. Предлагается разделить показатели на три группы:

а. Показатели, характеризующие учебный процесс. К этой группе относятся показатели, основанные на сведениях о программах обучения, анализе его дифференциации и информации о деятельности университетов.

б. Показатели, характеризующие потенциал университета, или его способность давать образование. К ним относятся показатели объема инвестиций в образование (его финансирование, материальная база, и т.д.), показатели квалификации преподавательского состава, и т.д.

в. Показатели, характеризующие результат учебного процесса. К ним относятся результаты оценки качества знаний и общей культуры студентов, а также информация о судьбе студентов вуза после завершения определенной ступени образования.

2. ii.                  Разработка метода составления перечня показателей, не связанных функциональными и статистическими зависимостями, а также зависимостью по предпочтению. Исключение функциональных зависимостей представляет собой достаточно несложную задачу. Функциональная зависимость - это четкая и объективная концепция. Поэтому начинать второй этап следует именно с исключения функциональных зависимостей, соблюдая описанные выше меры предосторожности.
   

Выработать однозначное суждение о существовании статистической зависимости невозможно. Показатели могут быть связаны статистической зависимостью лишь в определенной степени. Равным же образом нельзя с уверенностью вычленить зависимость по предпочтению, в связи с субъективным характером оценки наличия этой зависимости. Могут отсутствовать мнения экспертов по определенным аспектам, что приведет к неоднозначности определения существования зависимости по предпочтению.

Следовательно, необходимо выбрать:

1. 
   i.                    показатель статистической зависимости;
   
2. ii.                  показатель зависимости по предпочтению.
   

Методы идентификации статистической взаимозависимости и зависимости по предпочтению существуют, однако их необходимо отобрать и адаптировать к нашему конкретному случаю.

Следующим этапом будет разработка методов проверки параметров рейтинга на наличие этих видов зависимостей. В рамках этой задачи необходимо решить следующие вопросы:

• -         Как работать с параметрами? Как правило, характеристики статистической взаимозависимости и зависимостей по предпочтению оценивают, анализируя пары показателей. Анализ всех возможных пар представляет собой огромную работу; следовательно, необходимо применять специальные методы, чтобы сократить число комбинаций, которые необходимо проверить.
  
• -         Какой метод использовать для принятия окончательного решения, при каких условиях мы считаем, что некоторые показатели взаимосвязаны?
  
• -         Следующим шагом после обнаружения взаимозависимостей будет решение о том, как учесть или исключить эти взаимосвязи. Возможны следующие варианты: соответствующие изменения интегрированной функции, исключение показателей из перечня, или соответствующие изменения показателей. Необходимо разработать алгоритм обработки взаимосвязанных показателей.
  
• -         Что произойдет, если исключить часть показателей? Исключение некоторых параметров может привести к неравномерности охвата различных аспектов качества образования. Поэтому на завершающем этапе обязательно должна проводиться проверка окончательного перечня параметров с точки зрения обеспечения равномерного охвата всех аспектов качества образования.
  

Ниже предлагается методика подготовки перечня показателей, учитывающих трудоемкость и техническую сложность выявления зависимости по предпочтению. Проверка наличия зависимости по предпочтению проводится только при необходимости после пересмотра перечня показателей с точки зрения статистических взаимозависимостей.

Этап 1. Составление максимально развернутого перечня показателей.

Этап 2. Выбор показателей, по которым имеются данные.

Этап 3. Классификация.

Этап 4. Определение степени статистической взаимозависимости между показателями.

Этап 5. Установка пороговых уровней статистических взаимозависимостей по каждому классу показателей.

Этап 6. Внесение изменений в перечень показателей.

Этап 7. Выбор пар показателей для проверки наличия зависимости по предпочтению. Осуществление проверки.

Этап 8. Установление пороговых уровней зависимостей по предпочтению по каждому классу параметров.

Этап 9. Внесение изменений в перечень показателей.

Этап 10. Проверка равномерности охвата всех аспектов качества образования. В случае неравномерного охвата необходимо изменить пороговые уровни важности – перейти к этапу 5. В случае равномерного охвата на этом работу можно завершить и принять существующий перечень как окончательный.

При таком подходе изменение пороговых уровней позволит создать перечень показателей, удовлетворяющих требованиям отсутствия взаимозависимости и однородности охвата различных аспектов качества образования.

 

Некоторые результаты вычислений

Рассмотрим задачу составления перечня показателей на практическом примере рейтинга образовательных учреждений в России.

В 1999 г. журнал «Карьера» опубликовал рейтинги высших учебных заведений, специализирующихся в области экономики и менеджмента. Для составления рейтинга использовались 22 показателя:

1. 
   1.     число абитуриентов на одно место;
   
2. 2.     средний балл аттестатов зрелости абитуриентов;
   
3. 3.     средний балл студентов во время летней сессии;
   
4. 4.     средний балл на итоговых выпускных экзаменах;
   
5. 5.     процент выпускников, получивших диплом с отличием;
   
6. 6.     процент поступивших в аспирантуру в том же вузе;
   
7. 7.     процент выпускников, нашедших работу не позже шести месяцев с момента окончания вуза;
   
8. 8.     количество преподавателей на 100 студентов;
   
9. 9.     процент обладателей кандидатских и докторских степеней среди преподавателей;
   
10. 10. доля учебной нагрузки, приходящаяся на преподавателей, работающих на полную ставку;
    
11. 11. число членов и членов-корреспондентов государственных академий;
    
12. 12. число диссертаций, защищенных преподавателями вуза за последние пять лет;
    
13. 13. число монографий, выпущенных преподавателями вуза за последние пять лет;
    
14. 14. число грантов на НИР, полученных преподавателями вуза за последние пять лет;
    
15. 15. число командировок за границу преподавателей, участвующих в НИР, за последние пять лет;
    
16. 16. бюджет вуза на одного студента;
    
17. 17. число единиц библиотечного хранения на одного студента;
    
18. 18. площадь учебных помещений (кв. м) на одного студента;
    
19. 19. площадь общежития (кв. м) на одного студента;
    
20. 20. площадь спортивных сооружений (кв. м) на одного студента;
    
21. 21. индекс международного признания;
    
22. 22. индекс общественного мнения.
    

 

Из 231 существующего коэффициента корреляции девять оказались значительными:

Показатель № 1	Показатель № 2	Корреляция
Средняя оценка летней сессии	Средняя оценка на итоговых выпускных экзаменах	1,00
Средняя оценка летней сессии	Процент выпускников, получивших диплом с отличием	0,88
Средняя оценка летней сессии	Процент выпускников, нашедших работу спустя полгода после окончания	0,98
Средняя оценка на итоговых выпускных экзаменах	Процент выпускников, получивших диплом с отличием	0.88
Процент выпускников, нашедших работу спустя полгода после окончания	Процент обладателей кандидатских и докторских степеней среди преподавательского состава	0,97
Процент выпускников, нашедших работу спустя полгода после окончания	Процент учебной нагрузки, приходящейся на долю преподавателей, состоящих в штате	0,95
Процент обладателей кандидатских и докторских степеней среди преподавательского состава	Процент учебной нагрузки, приходящейся на долю преподавателей, состоящих в штате	0,95
Площадь учебных помещений (кв. м) на одного студента	Площадь общежития (кв. м) на одного студента	0,79
Число абитуриентов на место	Площадь общежития (кв. м) на одного студента	0,74

 

Показатели «число абитуриентов на место» и «средняя оценка аттестатов зрелости абитуриентов» оказались зависимыми по предпочтению.

 

Оценка и измерение ошибок показателей

До сих пор мы вычисляли т.н. точечные значения всех показателей и аддитивной функции ценности. Однако совершенно очевидно, что большинство показателей будут измерены (оценены) с некоторой погрешностью, следовательно, функция ценности будет также иметь погрешность, что необходимо учесть при составлении рейтинга.

Согласно общей теории ошибок, погрешность значения функции n переменных, каждая из которых в свою очередь вычислена с погрешностью, можно вычислить следующим образом.

Если переменные имеют погрешности и используются для вычисления значений функции , погрешности носят случайный характер и являются независимыми тогда погрешность значения будет , и в любом случае не превышает обычной суммы: .

В случае аддитивной числовой функции есть не что иное, как весовой коэффициент.

 

БИБЛИОГРАФИЯ

Журнал «Карьера» [Career Journal] 3 (1999).

Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. – М.: Радио и связь, 1981

Keeny, R. L., and Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs. New York: John Wiley, 1981 [Russian edition].

 

Приказ Министра образования Российской Федерации № 631 от 26 февраля 2001 г. «О рейтинге высших учебных заведений» [Regulation No. 631 of the Ministry of Education of the Russian Federation, “On the Ranking of Higher Education Institutions”]. Moscow: Ministry of Education, 2001.