Пояснительная записка к курсовой работе «Динамическое программирование Задача об оптимальной триангуляции выпуклого многоугольника»
| Вид материала | Пояснительная записка |
- Пояснительная записка курсовой работы «Решение задачи о загрузке (задача о рюкзаке),, 608.78kb.
- Пояснительная записка к курсовой работе на тему: «Активный полосовой фильтр» по дисциплине, 342.06kb.
- Пояснительная записка к курсовой работе : 40 с., 6 рис., 2 приложения, 3 источника, 208.69kb.
- Курс является базовым как для изучения других математических дисциплин, так и для более, 36.89kb.
- Задача оптимального управления > 3 Критерии качества и оптимальное управление, 80.62kb.
- Аттестационное тестирование в сфере профессионального образования, 72.49kb.
- Курс является базовым как для изучения других математических дисциплин, так и для более, 39.9kb.
- Пояснительная записка Ккурсовой работе по дисциплине "Алгоритмические языки и программирование", 121.92kb.
- Пояснительная записка к курсовой работе по дисциплине: «Электроника и микросхемотехника», 171.54kb.
- Пояснительная записка к курсовой работе кр-080502-П60-11-12, 646kb.
ГОУ ВПО
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра АВТ
Структуры и алгоритмы обработки данных
Пояснительная записка к курсовой работе
«Динамическое программирование
Задача об оптимальной триангуляции выпуклого многоугольника»
Выполнил: _________________
Группа: ЭПО-21
Проверил: Андрианов И.А.
Вологда
2007
Содержание работы:
1. Описание заданной структуры данных или алгоритма
1.1 Описание работы алгоритма.
1.2 Строгое доказательство корректности алгоритма
1.3 Класс входных данных, для которых применим алгоритм или структура
1.4 Анализ временной и пространственной сложности алгоритма
1.5 Сравнение с аналогами
1.6 Примеры практических задач, где может использоваться данный алгоритм.
2. Разработка визуализатора
2.1 Выбор средств разработки
2.2 Определение отображаемых элементов, проектирование интерфейса
2.4 Разработка алгоритмов прямого пошагового выполнения визуализации и выполнения отката
2.5 Особенности программной реализации
3. Разработка задачи, системы тестов и проверяющей программы
3.1 Формулировка задачи
3.2 Собственное решение задачи
3.3 Анализ эффективности собственного решения
3.4 Обоснование неэффективности или сложности в реализации решений, не использующих предложенную структуру данных / алгоритм
3.5 Описание предложенной системы тестов
3.6 Доказательство, что предложенная система тестов охватывает все (или хотя бы большую часть) категории входных данных
3.7 Исследование сложности «лобовых» решений, обоснование их отсечения системой тестов. Реализация «лобовых» решений (не менее двух), экспериментальные результаты
3.8 Наиболее вероятные эвристические решения, обоснование их отсечения системой тестов. Реализация эвристических решений (не менее двух), экспериментальные результаты
3.9 Разработка проверяющей программы. Учет типовых ошибок в формировании подсказок проверяющей программой
1. Описание заданной структуры данных или алгоритма
1.1 Описание работы алгоритма.
Начиная с задачи S0N рекурсивно заполняется таблица стоимостей триангуляции с сохранением индексов вершин в которые проведены диагонали.
Cis = min1≤k≤s−2 {Ci,k+1 + Ci+k,s−k + D(vi, vi+k) + D(vi+k, vi+s−1)},
Далее рекурсивно выстраивается последовательность ребер триангуляции по сохраненным значениям концов ребер триангуляции.
Блок схема алгоритма вычисления стоимости триангуляции
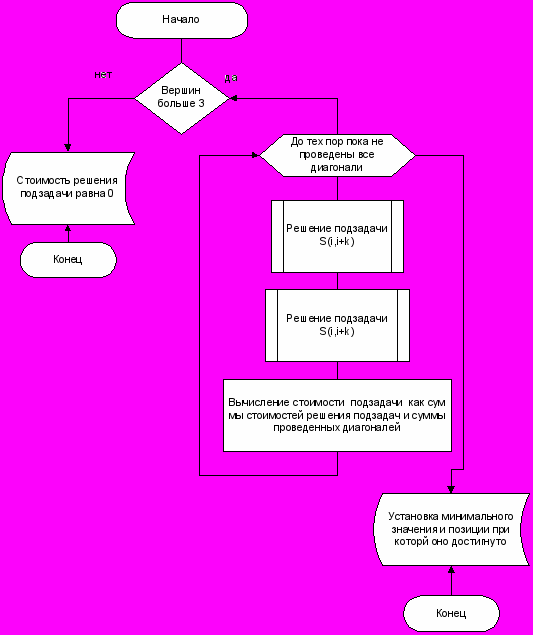
Блок схема процедуры вычисления ребер триангуляции.
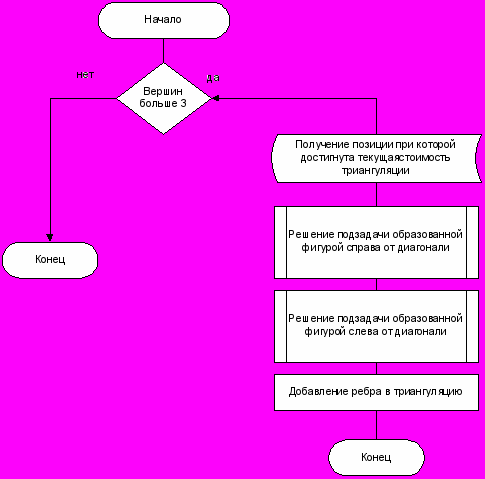
1.2 Доказательство корректности алгоритма
Предполагаем, что наш многоугольник имеет n вершин v0, v1, …, vn−1, перечисленных по часовой стрелке.
- В случае триангуляции любого многоугольника, содержащего более трех вершин, с каждой парой смежных вершин связана, по крайней мере одна хорда. Чтобы убедиться в этом, предположим, что ни vi, ни vi+1 не связаны ни с одной из хорд. В таком случае область, ограничиваемая стороной (vi, vi+1), должна бы включать стороны (vi−1, vi), (vi+1, vi+2) и по крайней мере еще одну дополнительную сторону или хорду. Но в таком случае это область не была бы треугольником.
- Если (vi, vj) является хордой в триангуляции, значит должна найтись, такая вершина vk что каждая из линий (vi, vk) и (vk, vi) либо стороной многоугольника либо хордой . В противном случае хорда (vi, vj), ограничивала бы область, не являющуюся треугольником.
Чтобы приступить к поиску минимальной триангуляции, выберем две смежные вершины, например v0 и v1. Из указанных выше фактов следует, что в любой триангуляции (а значит и в минимальной) должна найтись такая вершина vk, что (v1, vk) и (vk, v0) являются хордами или сторонами многоугольника. Необходимо рассмотреть, насколько приемлемую триангуляцию можно построить после выбора каждого значения k. Если в многоугольнике n вершин, то в нашем распоряжении имеется (n−2) возможных вариантов. Каждый вариант выбора k приводит к не более чем двум подзадачам, где мы имеем многоугольники образованные, одной хордой и сторонами исходного многоугольника. Например, могут возникнуть такие подзадачи при случае выбора вершины v3.
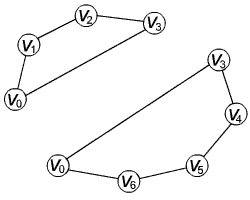
Далее нужно найти минимальную триангуляцию для многоугольников, полученных в результате появления новых подзадач. Правда, если мы будем решать все подзадачи, которые будут появляться, то мы получим алгоритм с экспоненциальной трудоемкостью. Но, имея треугольник, включающий хорду (v0, vk), нам никогда не придется рассматривать многоугольники, у которых более одной стороны являются хордами исходного многоугольника. «Факт 2» говорит о том, что при минимальной триангуляции хорда в подзадаче (например, хорда (v0, v3) на рис. 1) должна составлять треугольник с одной из остальных вершин многоугольника.
Определим подзадачу размера s, начинающуюся с вершины vi и обозначаемую Sis, как задачу минимальной триангуляции для многоугольника, образованного s вершинами, начинающегося с вершины vi и содержащего вершины vi, vi+1, …, vi+s−1, перечисляемые в порядке обхода вершин по часовой стрелке. В v0 хордой является замыкающая сторона (vi, vi+s−1). Чтобы решить подзадачу Sis необходимо рассмотреть три варианта:
- Можно выбрать вершину vi+s−2, чтобы составить треугольник с хордами (vi, vi+s−1), (vi, vi+s−2) и третьей стороной (vi+s−2, vi+s−1), а затем решить подзадачу Si,s−1.
- Мы можем выбрать вершину vi+1, чтобы составить треугольник с хордами (vi, vi+s−1), (vi+1, vi+s−1) и третьей стороной (vi, vi+1), а затем решить подзадачу Si+1,s−1.
- Для некоторого k из диапазона от 2 до s−3 можно выбрать вершину vi+k и образовать треугольник со сторонами (vi, vi+k), (vi+k, vi+s−1), (vi, vi+s−1), а затем решить подзадачи Si,k+1 и Si+k,s−k.
Если учесть, что решение подзадачи размером не более трех не требует вообще никаких действий, то рассматривая описанные варианты 1–3, следует предпочесть вариант 3, где нужно выбрать некоторое k из диапазона от 1 до s−2 и решить подзадачи Si,k+1 Si+k,s−k. Если для решения задачи размером более четыре и более воспользоваться очевидным рекурсивным алгоритмом, непосредственно вытекающим из перечисленных выше вариантов, то можно показать что общее число рекурсивных вызовов составляет 3s−4, если подсчитать лишь обращения к подзадачам размером четыре и более. Таким образом количество подзадач, которые необходимо решить, возрастает по экспоненциальному закону в зависимости от s. А следовательно общее количество шагов экспоненциально зависит и от n.
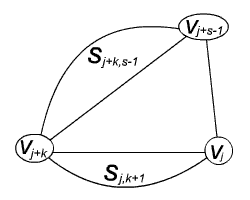
Но известно, что, помимо исходной задачи существует лишь n(n−4) различных подзадач, которые в любом случае необходимо решить. Значит в приведенном анализе что-то явно не совсем верно. Очевидно, что совсем не все подзадачи отличаются между собой, если действовать рекурсивно, как приведено выше, то у нас возникают ситуации, когда одни и те же ситуации приходится решать несколько раз. Именно это подсказывает нам эффективный способ вычисления триангуляции. Прежде всего, вычисления удобно организовать в виде таблицы. Назначим стоимость Cis триангуляции Sis для всех i и s. Поскольку решение любой данной задачи зависит от решения задач меньшего размера, то логичным порядком заполнения такой таблицы является порядок, основанный на размерах подзадач, т. е. для размеров s = 4, 5, …, n−1 мы указываем минимальную стоимость задач Sis для всех вершин i. Удобно включить и задачи размеров 0 ≤ s < 4, но при этом нужно помнить, что Sis имеет стоимость 0, если s < 4.
В соответствии с перечисленными выше вариантами действий 1–3 при определении подзадач формула вычисления Cis при s ≥ 4 должна иметь следующий вид:
Cis = min1≤k≤s−2 {Ci,k+1 + Ci+k,s−k + D(vi, vi+k) + D(vi+k, vi+s−1)},
где D(vp, vq) — это длина хорды между вершинами vp и vq, если vp и vq не являются смежными вершинами многоугольника; D(vp, vq) равняется 0, если являются смежными вершинами.
Отметим, что таким образом, мы вычислим всю таблицу, и определим стоимость минимальной триангуляции, но не саму триангуляцию. Поэтому для того, чтобы найти саму триангуляцию, мы должны еще также хранить информацию, о том, при каком значении k достигается минимум. И потом уже, по всем сохраненным значениям k мы можем легко восстановить минимальную триангуляцию. Ребрами триангуляции будут являться (vi, vi+k), (vi+k, vi+s−1) плюс ребра находимые решениями подзадач Si,k+1 + Si+k,s−k .
1.3 Класс входных данных, для которых применим алгоритм или структура
Алгоритм применим для совокупности точек с заданными координатами, образующими выпуклый многоугольник с количеством вершин большим 3-х.
Координаты вершин являются целыми числами. Количество точек не может быть больше 100.
1.4 Анализ временной и пространственной сложности алгоритма
Временная сложность алгоритма обусловлена рекурсивными функциями нахождения стоимости и соответствующих ребер.
O(N)=N*(N-4) – количество подзадач необходимых для решения
Таким образом можно сделать вывод, что для решения задачи минимальной триангуляции складывается из затрат времени на обработку массива расстояний между вершинами O(N)=N2 , расчет таблицы минимальной триангуляции O(N)=N*(N-4) и нахождения ребер по таблице стоимостей триангуляции (в худшем случае
O(N)=N*(N-4)).
Временная сложность алгоритма O(N)= N2
Пространственная сложность алгоритма складывается из массива координат вершин (2*N), массива ребер триангуляции (2*(N-3)), массива стоимостей триангуляции для подзадач (2*N2) и массива длин возможных хорд (N2). Таким образом суммарная пространственная сложность алгоритма равняется 4*N+3*N2
1.5 Сравнение с аналогами
Аналогичных результатов позволяет достичь полный перебор всех вариантов триангуляции заданного многоугольника, с последующей оценкой стоимости для каждого найденного варианта. Алгоритм полного перебора вариантов сравнительно прост в написании, что приводит к тому, что временная сложность вырастает по экспоненциальному закону в зависимости от количества вершин, что приводит к неприменимости данного алгоритма на практике.
Часто используемые алгоритмы триангуляции, например триангуляция Делоне, дают не единственно верное решение задачи об оптимальной триангуляции многоугольника, а лишь приближение к ней. В данном случае такой подход не возможен.
Использованный алгоритм работает в отличии от алгоритма полного перебора вариантов с временной сложностью равной O(N)= N2 что показывает его несомненное превосходство, и так же он дает истинно минимальную триангуляции многоугольника.
1.6 Примеры практических задач, где может использоваться данный алгоритм.
Алгоритмы триангуляции чаще всего используются при работе с трехмерными объектами. Например в статье [1] использовали обобщение задачи триангуляции для следующей цели. Рассмотрим задачу создания двумерной тени объекта, поверхность которого определяется совокупностью точек в трехмерном пространстве. Свет на объект падает из неподвижного источника, и яркость любой точки на поверхности зависит от углов между направлением света, положением наблюдателя и перпендикуляром к поверхности в этой точке. Чтобы определить нормаль к поверхности в какой-либо точке, надо найти минимальную триангуляцию точек, определяющих эту поверхность.
Каждый треугольник определяет некоторую плоскость в трехмерном пространстве, и поскольку ищется минимальная триангуляция, можно предположить, что эти треугольники будут очень малы. Нетрудно определить направление нормали к плоскости, что позволяет вычислить интенсивность освещения, общую картину можно улучшить путем локального усреднения.
Другой отраслью в которой применяются алгоритмы триангуляции является топология. В качестве вершин выступают высоты поверхности.
2. Разработка визуализатора
2.1 Выбор средств разработки
Для разработки визуализатора выбран Borland C++ Builder, т.к. данный программный продукт предоставляет наиболее удобные средства для визуальной разработки приложений, имеющих интерфейс, использующий стандартные элементы управления Windows.
2.2 Определение отображаемых элементов, проектирование интерфейса
Внешний вид визуализатора
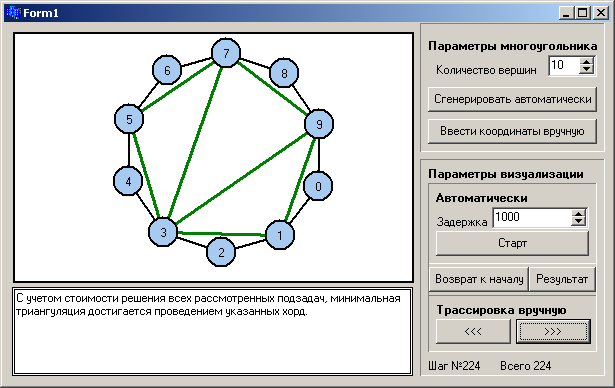
Для реализации функций визуализатора в интерфейс программы были включены:
- графическое поле предназначенное для наглядного изображения многоугольника и этапов его триангуляции.
- текстовое окно для вывода пояснений по шагам алгоритма и подсказок по настройке визуализации
- кнопки позволяющие сгенерировать многоугольник автоматически по количеству вершин или ввести все координаты вручную, путем указания позиций точек на рабочем поле. Проверка правильности ручного ввода координат не производится.
- реализована возможность пошагового выполнения алгоритма автоматически с заданной задержкой или по нажатию клавиш «<<<» и «>>>».
- так же добавлены кнопки возврата алгоритма в начало и просмотра результата применения алгоритма на исходных данных.
2.3 Разработка алгоритмов прямого пошагового выполнения визуализации и выполнения отката
Для реализации возможности пошагового выполнения при каждом изменении массива вершин многоугольника рассчитывается таблица стоимостей и ребер триангуляции. Промежуточные шаги сохраняются в массив. Для визуализации данного алгоритма необходимо сохранить значения указателя на начало решаемой подзадачи, размера подзадачи, и проводимой в данный момент диагонали, разбивающей решаему подзадачу на задачи меньшего размера.
Перемещение по массиву производится по внешнему событию (нажатие кнопки/сигнал таймера). Каждая строка массива позволяет наглядно изобразить действия алгоритма на текущем шаге. При использовании данного подхода реализация отката назад выполняется за минимальное время.
3. Разработка задачи, системы тестов
3.1 Формулировка задачи
Найти минимальную триангуляцию выпуклого многоугольника заданного координатами вершин в порядке обхода их по часовой стрелке. Триангуляцией многоугольника называется разбиение многоугольника на треугольники диагоналями, причем ни одна из диагоналей не пересекает ранее проведенную. Длина проведенных диагоналей должна быть минимальна среди всех возможных вариантов разбиения.
Входные данные – количество вершин, координаты вершин через пробел.
Выходные данные –стоимость оптимальной триангуляции (целое число).
Примечание: Все вычисления округлить до целых чисел.
3.2 Собственное решение задачи
Для решения задачи применен метод динамического программирования, основанный на вычислении текущего значения на основе предыдущих оптимально найденных значениях.
//---------------------------------------------------------------------------
#include
#include
#include
#pragma hdrstop
//---------------------------------------------------------------------------
#pragma argsused
int N;
float CIS[100][100][2];
int DC;
int **Vertexi
int **D;
int KPos;
int co;
void FillVertex(void)
{
cin >> N; Vertex=new int *[N];
for (int i=0;i
{
Vertex[i]= new int [2];
}
for (int i=0;i
cin >> Vertex[i][0] >> Vertex[i][1]; //
}
void FillD(void)
{
D=new int *[N];
for (int i=0;i
{
D[i]= new int [N];
}
for (int i=0;i
{
for (int k=0;k
{
if ((i+1==k)||(k+1==i)||((i==0)&&(k==(N-1)))||((i==(N-1))&&(k==0))) D[i][k]=0;
else D[i][k]=sqrt((Vertex[i][0]-Vertex[k][0])*(Vertex[i][0]-Vertex[k][0])
+(Vertex[i][1]-Vertex[k][1])*(Vertex[i][1]-Vertex[k][1]));
}
}
}
void CisArrayPrepare(void)
{
for (int s=1;s<=N;s++)
{
for (int i=0;i
{
if (s<4) CIS[i][s][0]=0;
else CIS[i][s][0]=-1;
}
}
}
int Chk(int Index)
{
if (Index>=N) Index=art-N;
return Index;
}
float Cis(int i, int s)
{
if (i>=N) i=i-N;
if (i<0) i=N+i;
int Ctmp;
int Min;
int Pos;
if (CIS[i][s][0]==-1)
{
for (int k=1;k<=s-2;k++)
{
k=k+i;
Ctmp=Cis(i,k+1)+Cis(i+k,s-k)+D[i][Chk(i+k)]+D[Chk(i+k)][Chk(i+s-1)];
if (k==1)
{
Min=Ctmp;
Pos=k;
}
else if (Min>Ctmp)
{
Min=Ctmp;
Pos=k;
}
}
CIS[i][s][0]=Min;
CIS[i][s][1]=Pos;
return Min;
}
else return CIS[i][s][0];
}
int main(int argc, char* argv[])
{
FillVertex();
FillD();
CisArrayPrepare();
DC=-1;
Cis(0,N);
cout << CIS[0][N][1];
return 0;
}
3.3 Анализ эффективности собственного решения
Эффективность решения легко видна при более подробном анализе задачи. Очевидно что общее число нуждающихся в решении подзадач равняется N*(N-4), следовательно для решения алгоритма применим алгоритм с квадратичной временной сложностью. Предложенный алгоритм удовлетворяет этому условию.
3.4 Обоснование неэффективности или сложности в реализации решений, не использующих предложенный алгоритм.
В случае, если не использовать методы динамического программирования, т.е. вычислять оптимальную триангуляцию, без опоры на ранее выбранные значения, то самым простым вариантом решения задачи будет использование полного перебора вариантов, что существенно увеличивает затраты времени.
Или же возможно использовать алгоритмы триангуляции Делоне, но они дадут лишь приближение к оптимальному решению, и для приведения к окончательному ответу, необходимо выполнить перестройку ребер триангуляции, что опять же сказывается на временной и пространственной сложности алгоритма.
3.5 Описание предложенной системы тестов
Предложенная система тестов последовательно проверят исследуемый алгоритм на правильность триангуляции многоугольников с 4, 5, 7 вершинами. При прохождении всех трех тестов можно сделать вывод что предложенный алгоритм работает верно.
3.6 Доказательство, что предложенная система тестов охватывает все (или хотя бы большую часть) категории входных данных
Т.к. рассматриваются только выпуклые многоугольники, то системы тестов основанной на оценке стоимости триангуляции многоугольников различной размерности достаточно для определения верности/неверности алгоритма и затрат времени и памяти для реализация.
3.7 Исследование сложности «лобовых» решений.
Одним из решений задачи «в лоб» является полный перебор, затраты времени O(n)=en-3 Т.к. система тестов построена так, что максимальным временем выполнения является время выполнения алгоритма реализованного с помощью методов динамического программирования, то можно с уверенностью сказать, что алгоритм полного перебора будет отсечен.
//---------------------------------------------------------------------------
#include
#include
#include
#pragma hdrstop
//---------------------------------------------------------------------------
#pragma argsused
// Глобальные переменные
int N; //Количество вершин заданного многоугольника
int **Vertex; //Указатель на начало массива координат вершин
int **D; // Указатель на начало массива длин хорд
/---------------------------------------------------------------------------
/* Заполнение массива вершин */
void FillVertex(void)
{
// Ввод координат вершин в порядке их обхода по часовой стрелке
// (вершины нумеруются с нуля)
cin >> N; // ввод количества вершин
//Организация в памяти динамического массива
Vertex=new int *[N];
for (int i=0;i
{
Vertex[i]= new int [2];
}
//Заполнение массива
for (int i=0;i
cin >> Vertex[i][0] >> Vertex[i][1]; // ввод координат X и Y соответственно
/*
// проверка правильности заполнения массива вершин
cout << " Vertex array:";
for (int i=0;i
cout << '\n' << Vertex[i][0] << " " << Vertex[i][1];
*/
}
/* Заполнение массива расстояний между вершинами */
void FillD(void)
{
// Организация в памяти
D=new int *[N];
for (int i=0;i
{
D[i]= new int [N];
}
// Заполнение массива
for (int i=0;i
{
for (int k=0;k
{
if ((i+1==k)||(k+1==i)||((i==0)&&(k==(N-1)))||((i==(N-1))&&(k==0))) D[i][k]=0;
else D[i][k]=sqrt((Vertex[i][0]-Vertex[k][0])*(Vertex[i][0]-Vertex[k][0])
+(Vertex[i][1]-Vertex[k][1])*(Vertex[i][1]-Vertex[k][1]));
}
}
}
/* Функция преобразовнания индекса вершины текущего многоугольника, для
доступа к исходному массиву вершин */
int Chk(int Index)
// Index - проверяемый индекс вершины
// Beg - первая вершина многоугольника при обходе по часовой стрелке
// n - количество вершин многоугольника
{
if (Index>=N) Index=art-N;
return Index;
}
//Рекурсивная функция вычисления стоимости триангуляции
float Cis(int i, int s)
{
// Закицкливание массива
if (i>=N) i=i-N;
if (i<0) i=N+i;
//Вспомогательные переменные
int Ctmp; // Промежуточное значение триангуляции
int Min; // минимальное значение
//Расчет стоимостей триангуляции
if (s>3)
{
// Поиск минимальной стоимости при 1<=K<=s-2
for (int k=1;k<=s-2;k++)
{
Ctmp=Cis(i,k+1)+Cis(i+k,s-k)+D[i][Chk(i+k)]+D[Chk(i+k)][Chk(i+s-1)];
if (k==1) // Выбор элемента для сравнения с минимальным
{
Min=Ctmp;
}
else if (Min>Ctmp) // Смена минимального элемента
{
Min=Ctmp;
}
}
return Min;
}
else return 0;
}
//------------------------------------------------------------------------------
int main(int argc, char* argv[])
{
FillVertex(); // Заполнение массива вершин
FillD(); // Рассчет расстояний между вершинами
cout << Cis(0,N); // Расчет таблицы стоимостей триангуляции
return 0;
}
//---------------------------------------------------------------------------
3.8 Наиболее вероятные эвристические решения.
Одним из вероятных решений является поиск минимальной суммы диагоналей основанный построении отсортированной последовательности длин диагоналей. С последующей проверкой возможности включения их в триангуляцию.
Предложенная система тестов осекает предложенное решение на 2 тесте.
Исходный код:
#include
#include
#include
#pragma hdrstop
int N; int Vertex[20][2];
int sides[20][3];
int trian[20]; int c;
float Triang[20][2];
int STr;
#pragma argsused
void Infill (void)
{
cin >> N;
for (int i=0;i
cin >> Vertex[i][1] >> Vertex[i][2];
}
void FindDiags (void)
{
c=0;
for(int i=0;i
{
for (int k=i+2;k
{
if (((i==0)&&(k!=(N-1))||(i!=0)))
{
sides[c][0]=(int)sqrt((Vertex[i][1]-Vertex[k][1])*(Vertex[i][1]-Vertex[k][1])+(Vertex[i][2]-Vertex[k][2])*(Vertex[i][2]-Vertex[k][2]));
sides[c][1]=i;
sides[c][2]=k;
c++;
}
}
}
return;
}
void Test(void) // Ïðîâåðêà ýòàïîâ âûïîëíåíèÿ ïðîãðàìû
{
for (int i=0;i
sides[0][0]=sides[0][0]+sides[i][0];
cout << (int)sides [0][0];
}
void PlaceDiags(void)
{
int min;
int pos;
float t0,t1,t2;
for (int i=0;i<=c;i++)
{
min=sides[i][0];
pos=i;
for (int k=i;k
if (sides[k][0]
{
min=sides[k][0];
pos=k;
}
t0=sides[i][0];
t1=sides[i][1];
t2=sides[i][2];
sides[i][0]=sides[pos][0];
sides[i][1]=sides[pos][1];
sides[i][2]=sides[pos][2];
sides[pos][0]=t0;
sides[pos][1]=t1;
sides[pos][2]=t2;
}
}
int main(int argc, char* argv[])
{
Infill(); FindDiags(); PlaceDiags();
Test();
}
3.9 Разработка проверяющей программы.
Проверяющая программа должна оценивать корректность ответа при предложенных входных данных.
Исходный код поверяющей программы:
#include
const int _WA=1; //wrong answer
const int _OK=0;
//argv[1] - input file
//argv[2] - student's output file
//argv[3] - right answer or special data file
int main(int, char *argv[])
{
ifstream f1(argv[2]),f2(argv[3]);
long x1,x2;
while (!f2.eof()) {
f1 >> x1;
f2 >> x2;
if (x1!=x2) return _WA;
}
return _OK;
}
При запуске проверяющей программе передаются параметры «имя файла входных данных» «ответ тестируемого алгоритма» «верный результат»
Реакция программы:
При верном ответе возвращается 0, при неверном - 1.
Проверка возможных решений с помощью предложенной системы тестов и проверяющей системы.
- Тест задачи решенной с помощью методов динамического программирования.
test N input file correct file result time worked memory usage.
1 1.in 1.out 0 0.015 sec 416 KB
2 2.in 2.out 0 0.015 sec 416 KB
3 3.in 3.out 0 0.031 sec 416 KB
4 4.in 4.out 0 0.015 sec 416 KB
5 5.in 5.out 0 0.031 sec 528 KB
- Тест задачи решенной полным перебором
test N input file correct file result time worked memory usage.
1 1.in 1.out 0 0.015 sec 340 KB
2 2.in 2.out 0 0.015 sec 340 KB
3 3.in 3.out 0 0.031 sec 340 KB
4 4.in 4.out 0 0.015 sec 340 KB
5 5.in 5.out 4 1 sec 452 KB
- Тест задачи решенной эвристически
test N input file correct file result time worked memory usage.
1 1.in 1.out 0 0.015 sec 392 KB
2 2.in 2.out 1 0.015 sec 344 KB
----------- output -----------
234
------- correct output -------
241
Заключение.
Результатом выполнения работы является реализация решения задачи об оптимальной триангуляции выпуклого многоугольника, спроектирован визуализатор иллюстрирующий особенности работы алгоритма и поддерживающий выполнение по шагам с возможностью отката назад на любое количество шагов.
Разработана система тестов и проверяющая программа, целью разработки которой являлось отсечение всех решений не использующих методов динамического программирования.
