Р. А. Тикиджи-хамбурьян нии нейрокибернетики им. А. Б. Когана Южного федерального университета, Ростов-на-Дону ischenko I. a@gmail com, vva@nisms krinc ru, rth@nisms krinc ru Исследование

Вид материала

Исследование

Подобный материал:

• International Scientific Events, 500.68kb.
• С программируемой архитектурой (мнмвс), 17.94kb.
• Южного Федерального Университета объявляет конкурс, 48.33kb.
• Актуальные теоретические вопросы языкознания, 326.51kb.
• Учебно-методический комплекс для студентов специальности 080102 «Мировая экономика», 1013.06kb.
• Программа ростов-на-Дону 2007 Конференция осуществляется при финансовой поддержке Российского, 406.02kb.
• Юридический адрес: 344082, г. Ростов-на-Дону, ул. Сиверса, 1 Фактический адрес: 344018,, 84.76kb.
• Южного Федерального Университета. Протокол №10 от 28 апреля 2007 г. Рецензент: программа, 335.17kb.
• Урушадзе Амиран Тариелович. Родился 11 марта 1985 г в Ростове-на-Дону. В 2002 г поступил, 39.77kb.
• Доктор технических наук, заведующий лабораторией физики прочности и механики разрушения, 418.09kb.

И.А. ИЩЕНКО, В.А. ВАСИЛЬКОВ,

Р.А. ТИКИДЖИ-ХАМБУРЬЯН

НИИ нейрокибернетики им. А.Б. Когана

Южного федерального университета, Ростов-на-Дону

ischenko.i.a@gmail.com, vva@nisms.krinc.ru, rth@nisms.krinc.ru


ИССЛЕДОВАНИЕ ВЛИЯНИЯ ВНУТРЕННИХ

СТОХАСТИЧЕСКИХ ПРОЦЕССОВ В НЕЙРОНАХ

ПЕРВИЧНЫХ ОТДЕЛОВ СЛУХОВОЙ СИСТЕМЫ

НА ВОЗНИКНОВЕНИЕ В НИХ ФАЗОВОГО ШУМА


Представлены результаты численного исследования нейронной сети, имитирующей промежуточную обработку сигнала в слуховом пути. Целью работы является исследование характеристик «фазового» шума, вызванного наличием внутренних стохастических процессов у нейронов периферических отделов слуховой системы. Показано существенное влияние амплитуды шумового тока, вызывающего стохастические флуктуации мембранного потенциала в модели единичного нейрона, на возникновение фазового шума в ответе нейронной сети. Оценена зависимость параметров фазового шума как от значения синаптической проводимости, так и от величины шумового тока.


Введение. Известно, что определение положения источника звука в горизонтальной плоскости возможно по интерауральной разности интенсивности и/или моментов прихода звукового сигнала. В середине ХХ века Джеффресс предложил модель локализации источника звука в горизонтальной плоскости на основе детекторов совпадения (биполярные E-E клетки) [1]. В модели детекторы образовывали некоторую матрицу, а местоположение источника звука определялось положением нейрона, либо локальной группы нейронов, проявивших импульсную активность. В настоящее время модель Джеффресса является общепризнанной и хорошо подтвержденной экспериментально. Значительный вклад в развитие идеи о механизмах пространственной локализации источника звука внесли работы Бекеши. Им была предложена модель, основывающаяся на двух параметрах: интерауральной разности интенсивности звука и разности моментов прихода сигнала на правое и левое ухо (также были использованы E-E нейроны) [1].

На данный момент нами проведен ряд исследований в области механизмов детектирования короткой временной задержки (КВЗ) искусственной нейронной сетью [2, 3]. В работах использовались так называемые E-I нейроны, то есть нейроны, которые активируются при стимуляции контралатерального уха и, напротив, тормозятся при ипсилатеральной стимуляции. Известно, что единичные E-I клетки являются достаточно грубыми детекторами определения местоположения источника звука (с левой или с правой стороны), однако результаты, полученные в работе [2], показали, что популяции медленных E-I нейронов могут детектировать межушные временные задержки с достаточно высокой точностью. В работах [2, 3] проводилась оценка влияния фазового шума во входном сигнале и амплитудного шума в активности единичного элемента сети на способность рассматриваемой модели детектировать КВЗ, однако источник фазового шума изучен не был. Позднее нами было рассмотрено поведение иерархической модели нейронной сети (содержащей два слоя нейронов), детектирующей короткие временные задержки, при наличии биполярного белого шума в активности единичной модели нейрона «первичного слоя» [4]. В качестве основного результата в работе [4] было показано влияние амплитудного шума в активности единичного элемента «первичного слоя» иерархической модели на возникновение дополнительного рассогласования при передаче бинаурального сигнала, то есть на возникновение так называемого фазового шума во «вторичном слое». В представленной работе рассматривается модель нейронной сети с целью определения вида зависимости влияния амплитудного шума на периферических отделах слуховой системы, являющихся возможными источниками фазового шума.

Модель. Исследуемая модель нейронной сети представлена рядом нейронов, каждый из которых получает возбуждающее синаптическое воздействие от входного элемента. Особенность данной модели заключается в том, что на все единичные модели нейронов подается биполярный белый шум, кроме первого элемента сети. В результате работы данной нейронной сети каждый нейрон генерирует потенциалы действия (ПД или spikes) с различной короткой временной задержкой относительно первой клетки, во входном сигнале которой нет шумовой компоненты (рис. 1).

Модель была построена из предположения, что сигнал от входного элемента появляется синхронно на всех моделях синапсов и до этого не претерпевает изменений ни по интенсивности, ни по длительности. В качестве единичного элемента сети используется нелинейная модель нейрона, которая была предложена Ижикевичем [5]. Выбранная модель приближена к биологически адекватной модели и хорошо применима для численного исследования.

Для модели Ижикевича характерны несколько режимов активности, каждому из которых соответствует определенный набор значений параметров. Был выбран режим активности модели нейрона «regular spiking», так как данный режим наиболее удобен для визуального анализа результатов. Для исследования поведения популяции нейронов использовалась реверсная модель синапса [6].





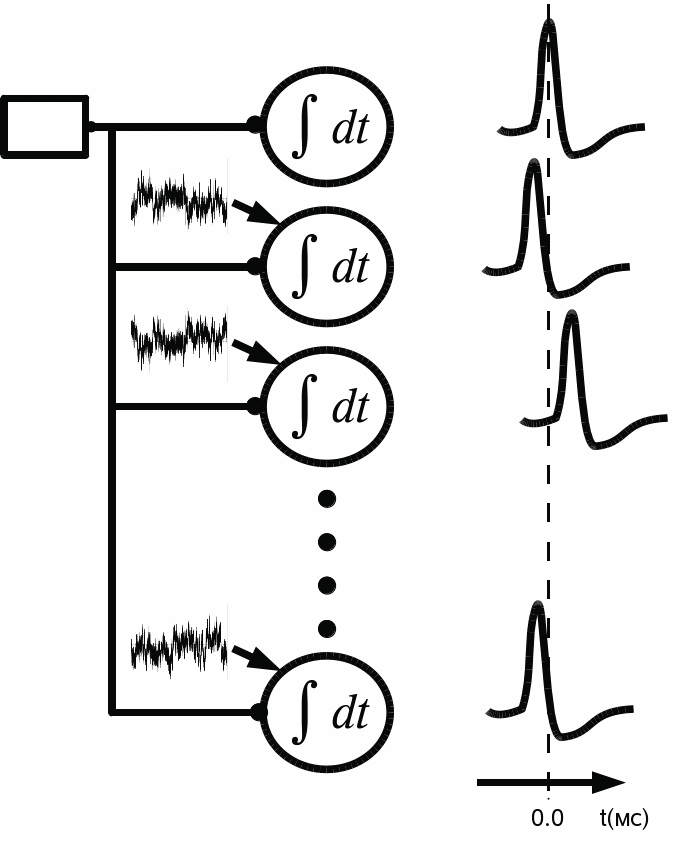
Рис. 1. Структура рассматриваемой модели


Для реализации данной модели нейронной сети было написано специализированное программное приложение на языке программирования высокого уровня С, являющееся оболочкой нейроимитационного пакета «NeuroCAD» [7], и с помощью специально разработанных bash-скриптов была проведена серия численных экспериментов.

Для решения дифференциальных уравнений, описывающих модель Ижикевича, в программном приложении был использован двухшаговый метод Эйлера, по рекомендации автора [5], а для решения уравнений, описывающих кинетику синаптических токов, был применен одношаговый метод Эйлера с экспоненциальной аппроксимацией, так как выбранный метод наиболее удобен для решения данных уравнений.

Результаты численного моделирования представлены в виде графиков ранжированных временных задержек с шагом накопления 0,2 мс.

В качестве задаваемых параметров исследуемой модели использовались:

• проводимости синапсов (мСм), которые выбирались таким образом, чтобы каждая клетка генерировала от 1 до 5 четко выраженных ПД (spike);
  
• значения амплитудного шума от 0.1 до 1 пА с шагом 0.1 пА и от 1 до 5 пА с шагом 0.5 пА;
  
• белый биполярный шум подавался с частотным диапазоном от 100 Гц до 1 кГц.
  

Результаты. В результате серии численных экспериментов были получены графики ранжированных временных задержек в интервале
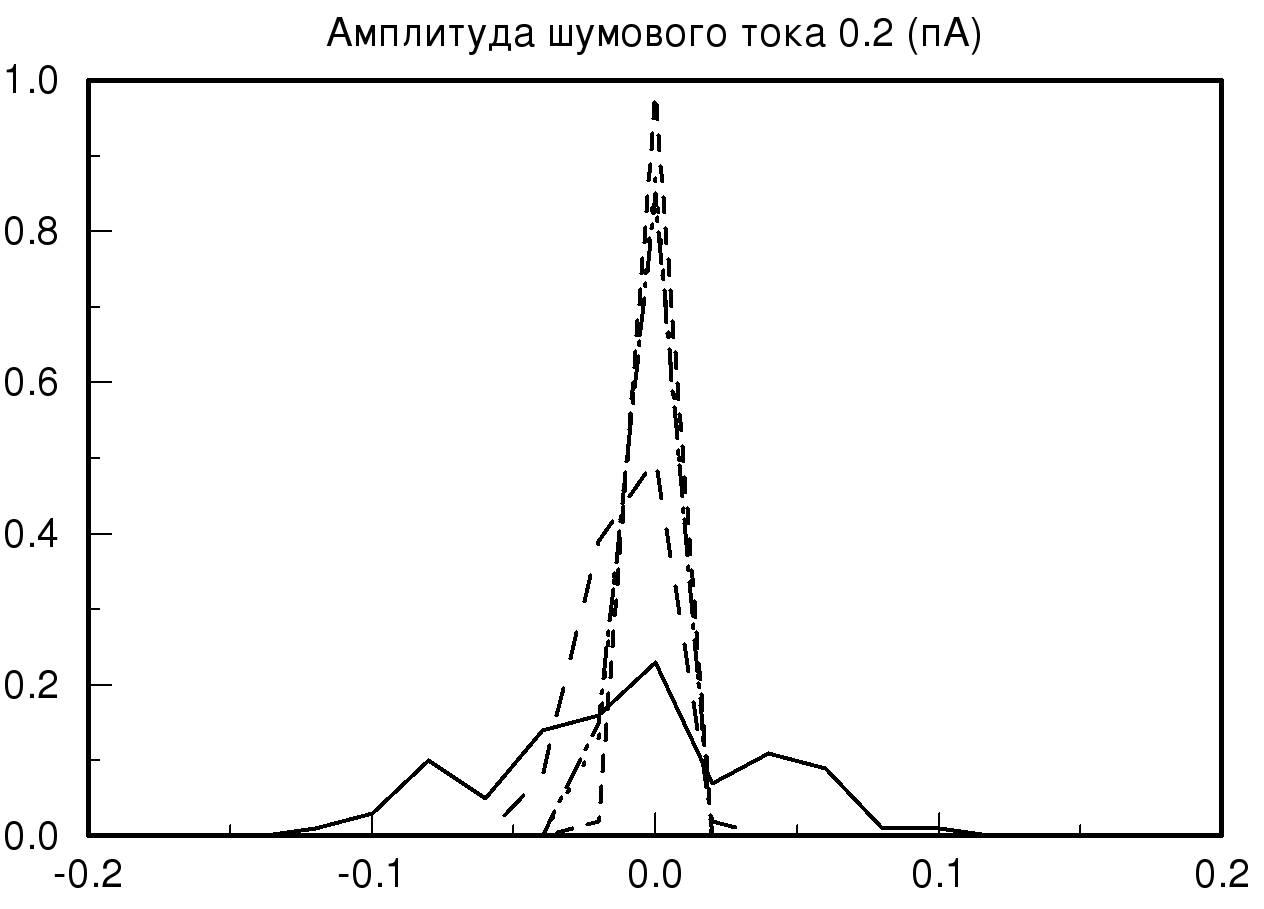
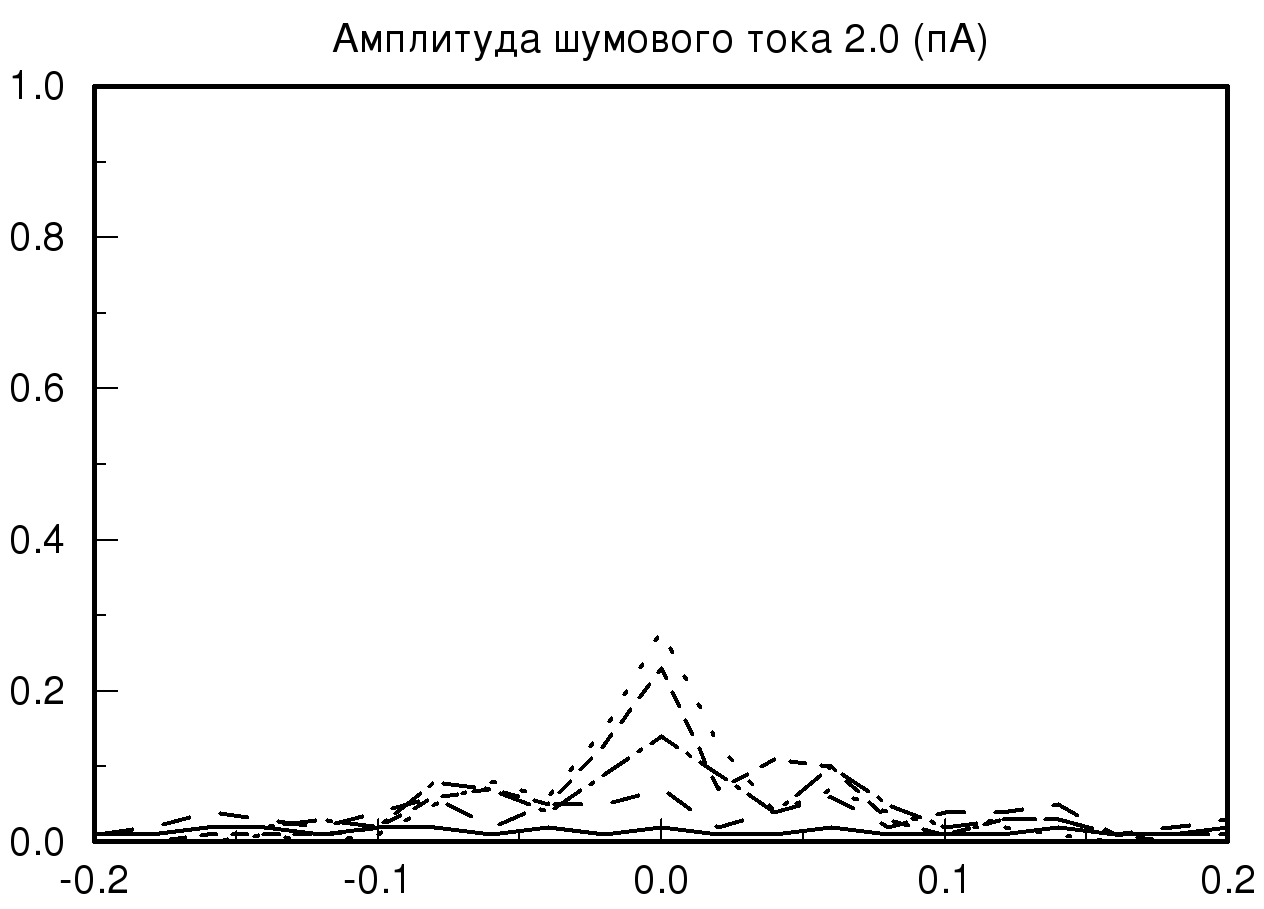
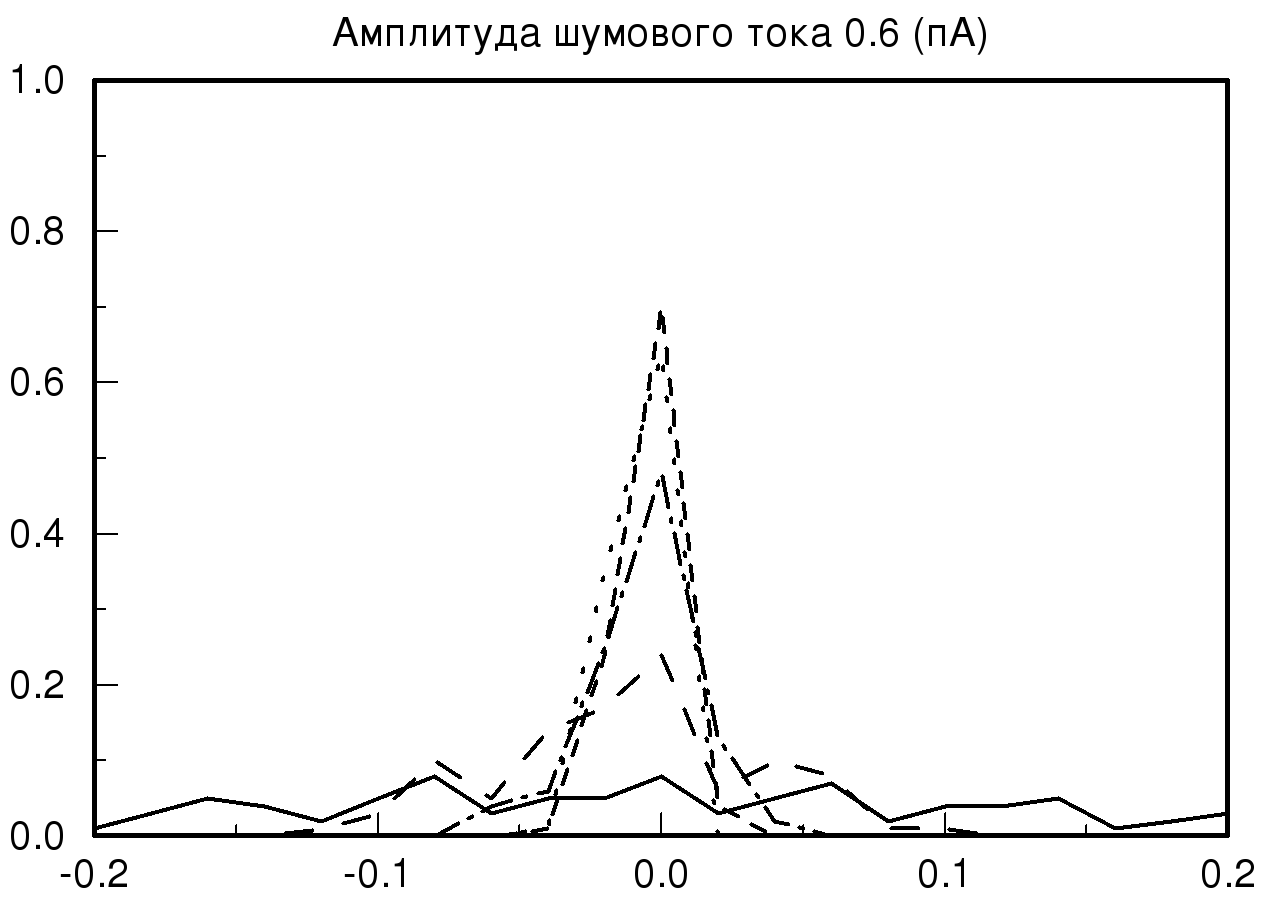
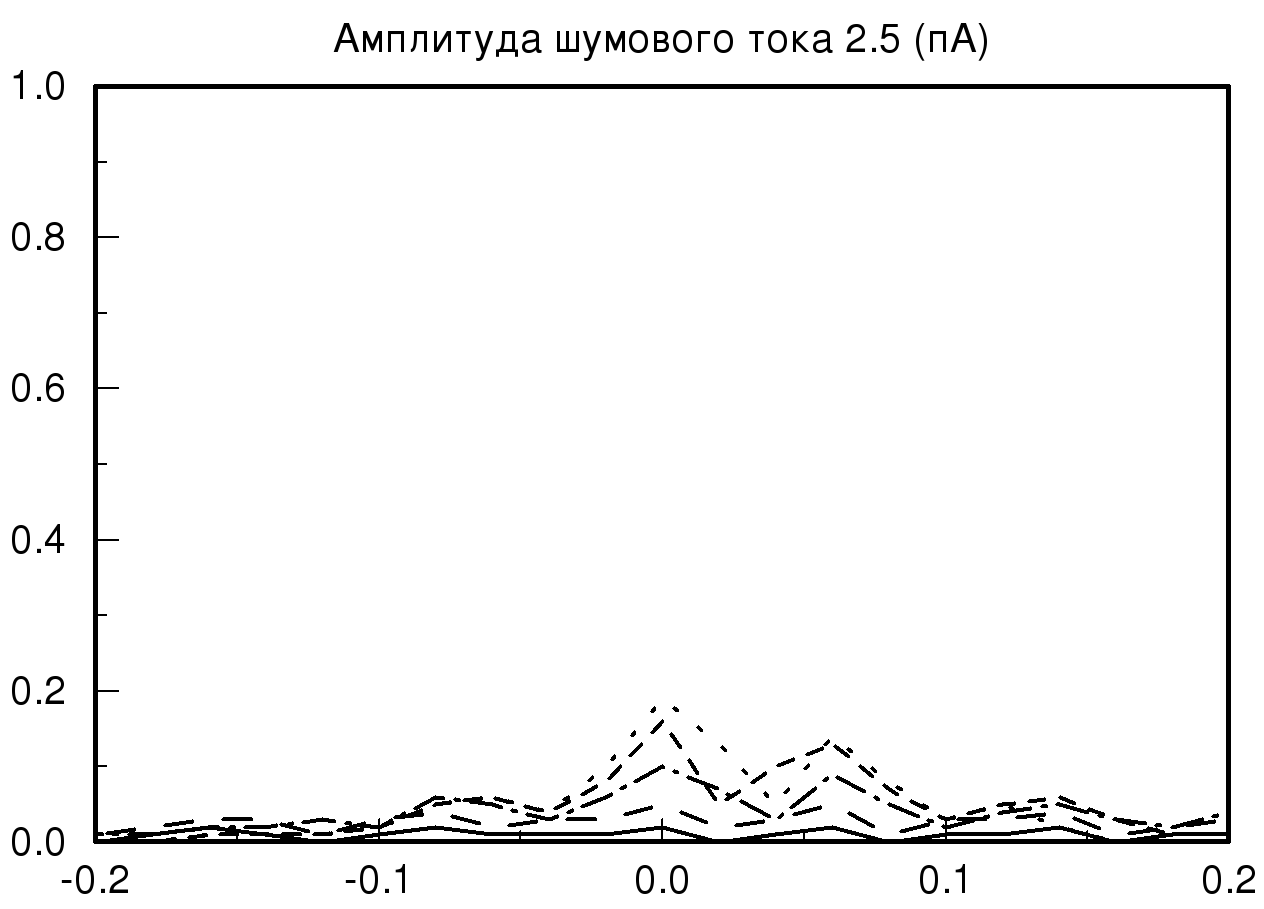
[-0.2;0.2] мс при различных значениях амплитуды шумового тока и синаптической проводимости. На рис. 2 представлены распределения временных задержек при различных значениях синаптической проводимости и одинаковой величине амплитудного шума. На представленных графиках хорошо видно, что при большом значении заданной проводимости и минимальном значении амплитудного шума разброса по значениям временных задержек практически нет, то есть при малых значениях амплитудного шума фазовый шум в модели отсутствует. В случае, когда значение проводимости не велико и задаются большие значения амплитудного шума, наблюдается существенное изменение на графике распределения временной задержки. На полученном распределении видно, что при значении амплитудного шума 2 пА график существенно уменьшается по амплитуде, это означает, что количество одинаковых значений временных задержек, детектируемых исследуемой моделью, уменьшается, таким образом, в модели популяции возникает фазовый шум. Важно отметить, что если мы продолжаем увеличивать амплитуду шумового тока, то на получаемых графиках наблюдается смещение пика распределения относительно значения нуля с последующим возможным нарастанием нового пика в новом временном интервале.

Также необходимо отметить, что на всех полученных графиках тип распределения близок по виду к нормальному распределению (распределению Гаусса) при условии, что на каждый единичный элемент модели, кроме первого элемента, подается биполярный белый шум.

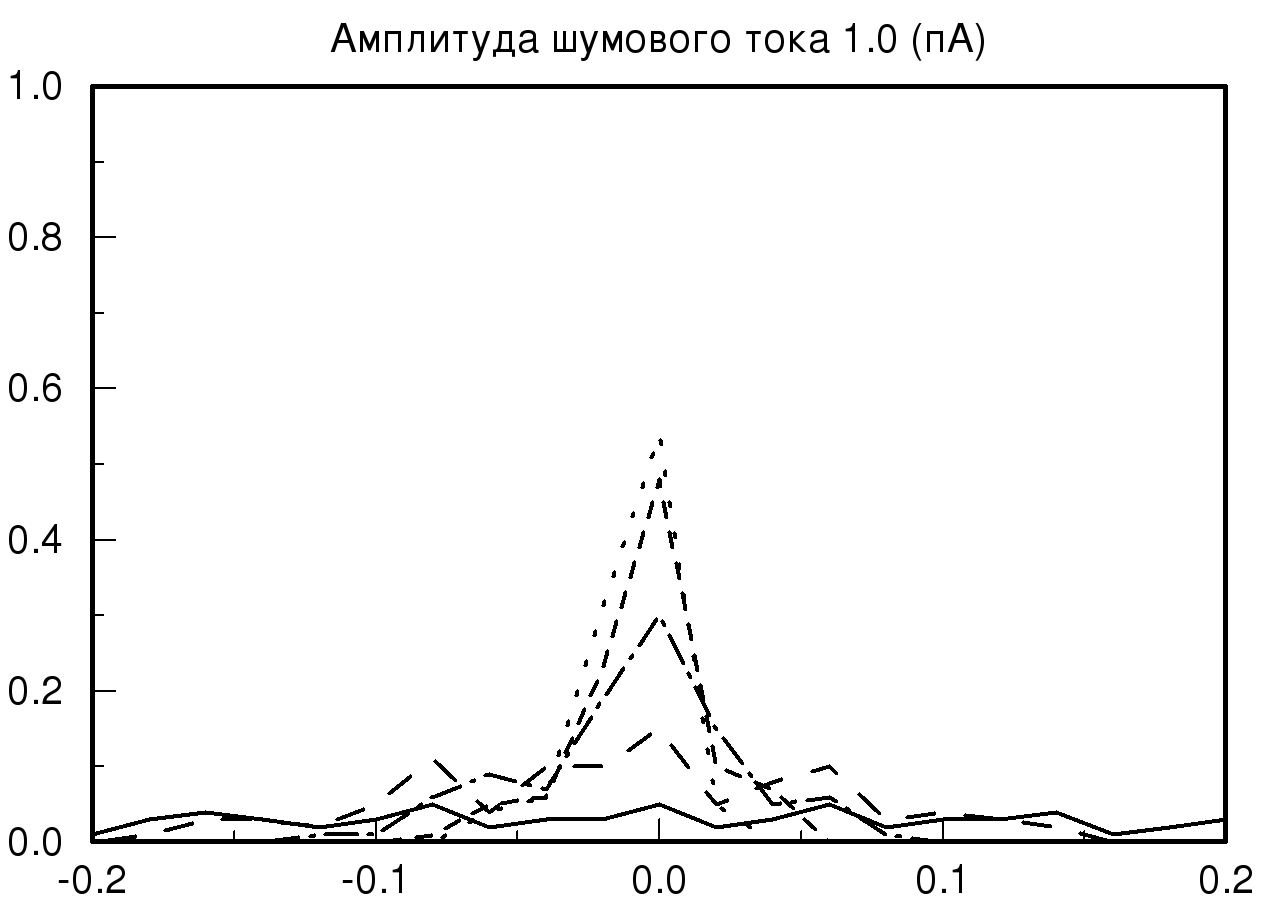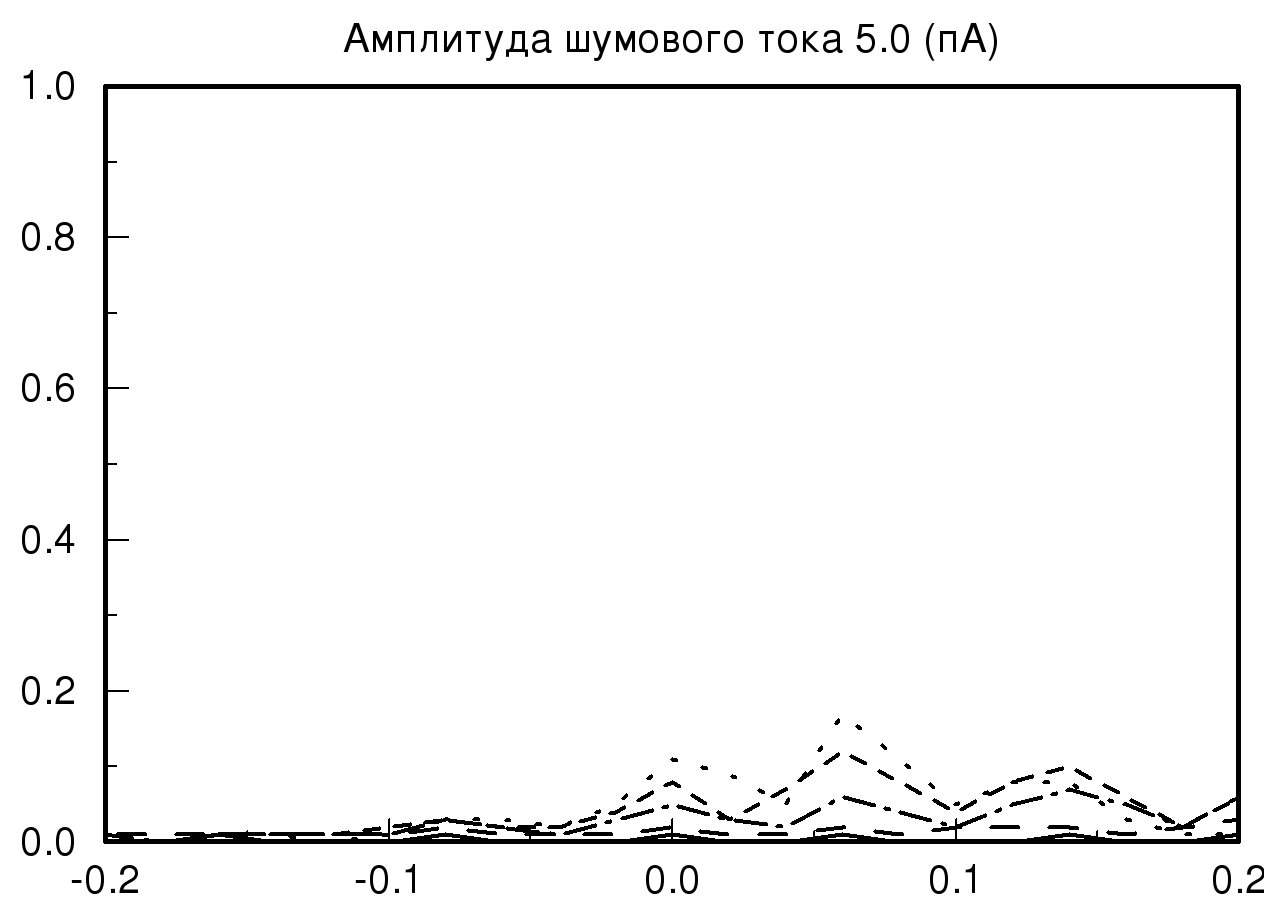Рис. 2. Распределения временных задержек при различных значениях синаптической проводимости и одинаковой величине амплитудного шума. На данных графиках прямой линией обозначено распределение при значении синаптической проводимости 10 мСм, пунктирной линией – 20 мСм, штрих пунктиром – 55 мСм и мелким пунктиром – 70 мСм

На рис. 3 показана зависимость максимальных величин значений временных задержек («пиков» полученных распределений, нормированных на количество клеток) от значений амплитудного шума при различных величинах синаптической проводимости и представлен вид этой зависимости в логарифмических координатах. На графике хорошо видно, что при увеличении величины амплитудного шума максимальные амплитуды фазового шума заметно уменьшаются. Так же на рис. 3 видно, что величина проводимости значительно влияет на наличие временных задержек. Из того, что в логарифмических координатах зависимость максимальных величин одинаковых значений временных задержек от амплитуды шумового тока при одиночном импульсе (проводимость 10 мСм) является графиком прямой, следует, что изменение величины амплитудного шума экспоненциально зависит от изменения количества значений возникающих временных задержек. При увеличении значения проводимости, то есть при наличии пачечной активности в ответе популяции, наблюдается изменение вида полученной зависимости на графике (рис. 3). В логарифмических координатах зависимость перестает быть линейной, что свидетельствует о том, что экспоненциальная зависимость изменения величины амплитуды шумового тока от изменения количества значений возникающих временных задержек ослабевает, и зависимость приближается по виду к линейной.





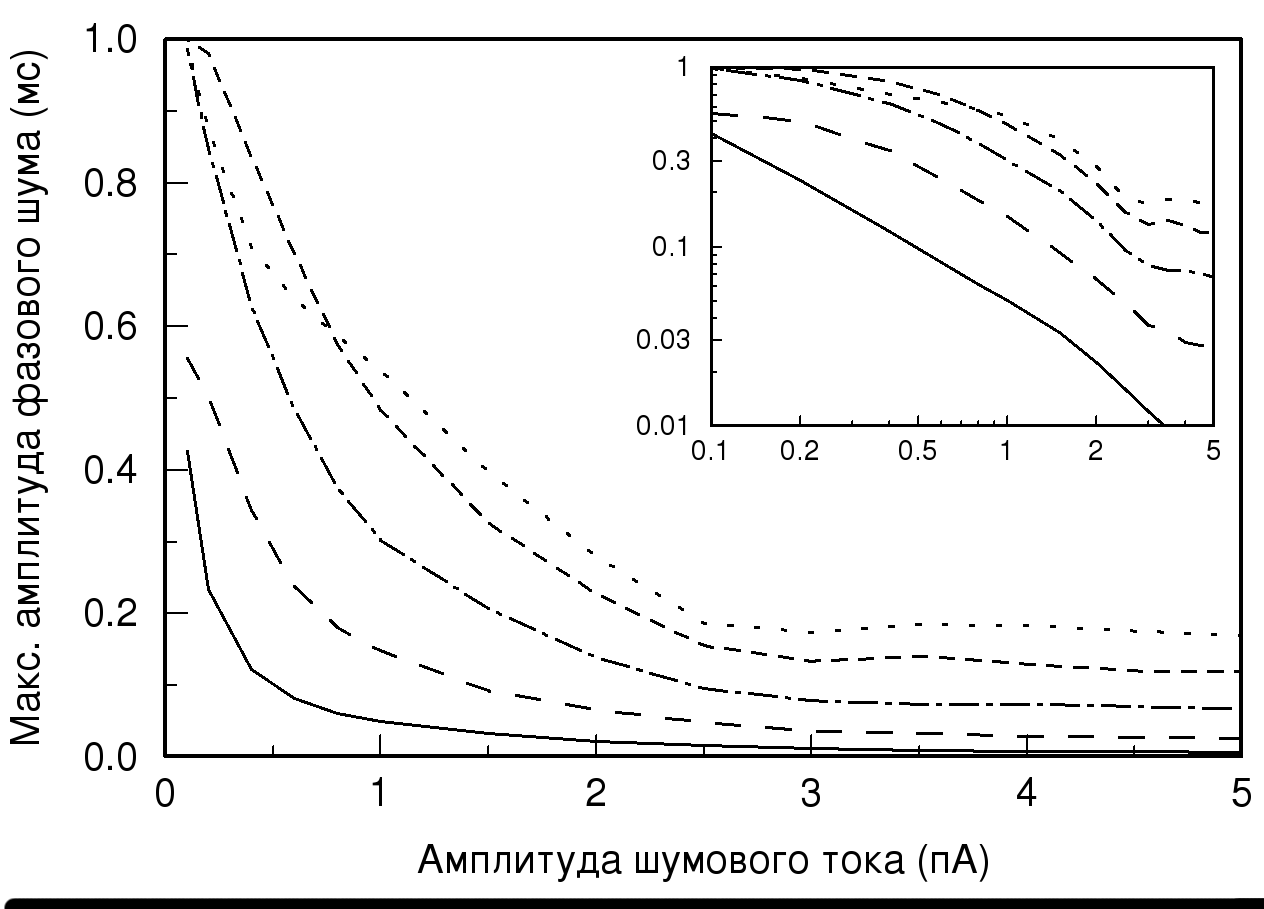
Рис. 3. Зависимость максимальных амплитуд фазового шума от значений

амплитудного тока. Обозначения линий те же, что и на рис. 2


На рис. 4 изображена зависимость ширины фазового шума на полувысоте получаемых распределений от величины подаваемого амплитудного шума при различных значениях проводимости. Как видно из графика, чем больше значения амплитудного шума и чем меньше величина проводимости, тем больше ширина фазового шума. При одиночном импульсе, то есть при минимальном значении синаптической проводимости и максимальном значении амплитудного шума, ширина распределения значительно увеличивается, что свидетельствует о наличии большого количества различных значений временных задержек. Из графика следует, что при малом значении проводимости ширина фазового шума практически линейно зависит от амплитуды шумового тока.





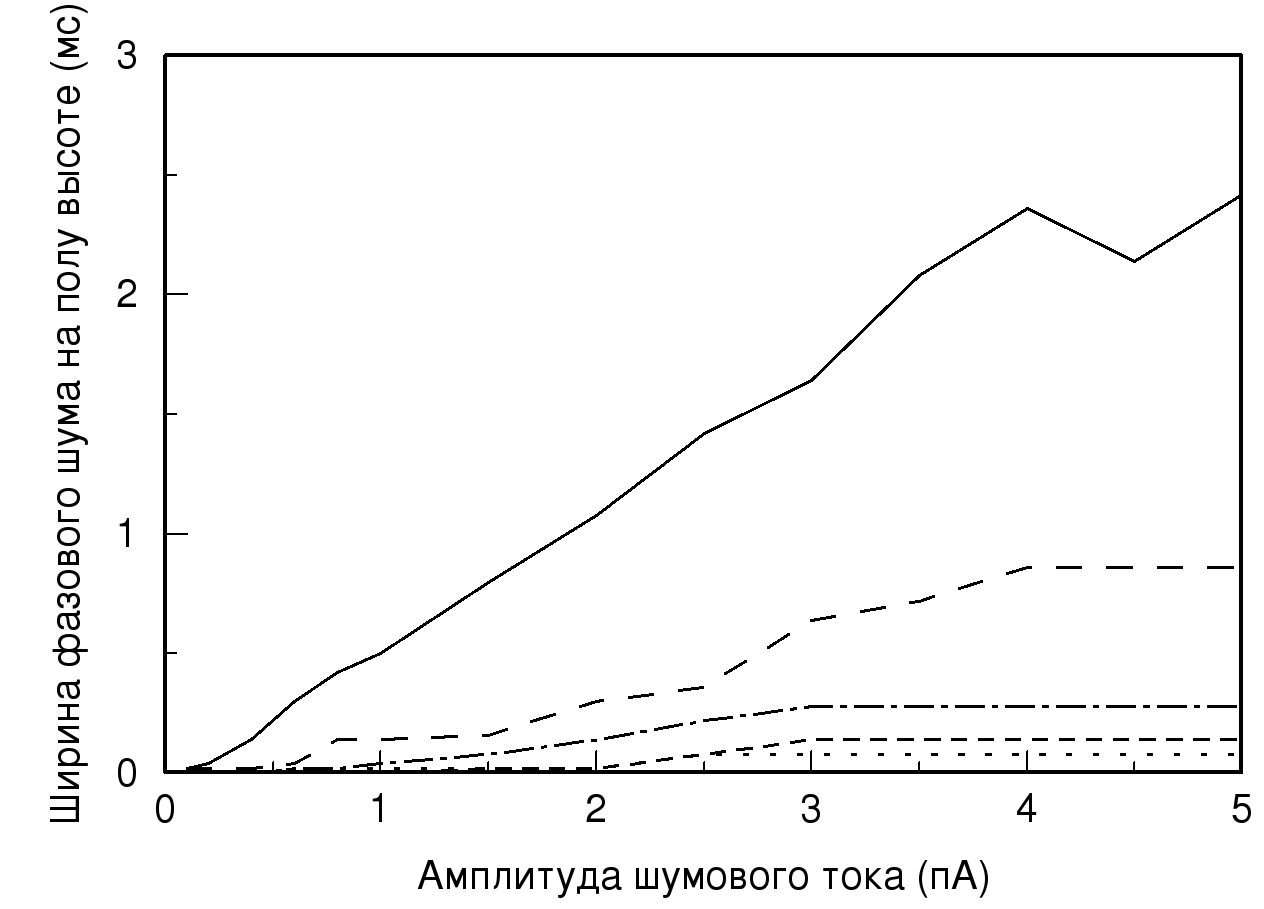
Рис. 4. Зависимость ширины фазового шума на полувысоте от значений

амплитудного шума. Обозначения линий те же, что и на рис. 2


Заключение. В представленной работе проведено численное исследование модели нейронной сети, имитирующей промежуточную обработку сигнала в слуховом пути. С помощью численного моделирования получены характеристики фазового шума, возникающего под влиянием амплитудного шума на промежуточных нейронах слуховой системы.

При увеличении значений амплитуды шумового тока и уменьшении величины проводимости в популяции амплитуда фазового шума растет. Отмечено, что при увеличении значений амплитудного шума пик получаемого распределения смещается относительно значения нуля и затем вновь нарастает в новом временном интервале.

Также выявлено, что при увеличении амплитудного шума и единичном импульсе количество возникающих временных задержек уменьшается экспоненциально, то есть амплитудный шум оказывает достаточно сильное влияние на возникновение «фазового шума» в модели популяции E-I нейронов. Была получена линейная зависимость ширины фазового шума на полувысоте от величины подаваемого амплитудного шума при минимальном значении проводимости и максимальном значении амплитуды шумового тока.

Было выявлено, что на графиках распределения временных задержек во временном интервале тип распределения близок по виду к распределению Гаусса, несмотря на то, что в модель подается биполярный белый шум. Полученные данные могут быть использованы для более детального биологически адекватного исследования системы бинаурального слуха.


Список литературы

1. Позин Н.В., Любинский И.А., Левашов О.В., Шараев Г.А. Элементы теории биологических анализаторов.- М.: Наука, 1978.
   
2. Васильков В.А., Тикиджи-Хамбурьян Р.А. Исследование возможных механизмов детектирования коротких временных задержек популяцией E-I нейронов. – Нейрокомпьютеры: разработка и применение, 2008, вып. 5-6, с. 46-53.
   
3. Тикиджи-Хамбурьян Р.А., Полевая С.А. Локализация источника звука искусственной нейронной сетью, основанной на модифицированных импульсных нейронах со следовой поляризацией. – Нейрокомпьютеры: разработка, применение, 2004, № 11, с. 41-45.
   
4. Vasilkov V., Ischenko I., and Tikidji - Hamburyan R. A hierarchical neural model sensitive to interaural time differences. Frontiers in Neuroinformatics. Conference Abstract: 2nd INCF Congress of Neuroinformatics. 2009.
   
5. Izhikevich E.M. Simple Model of Spiking Neurons. – IEEE Transactions on Neural Networks, 2003, vol. 14, № 6, P. 1569 – 1572.
   
6. Compte A., Sanchez-Vives M.V., McCormick D.A., Wang X.-J. Cellular and Network Mechanisms of Slow Oscillatory Activity (<1 Hz) and Wave Propagations in a Cortical Network Model. - J. Neurophysiol, 2003, P. 2707-2725.
   
7. Тикиджи-Хамбурьян Р.А., Маркин С.Н. Универсальный пакет прикладных программ для имитационного биологически адекватного нейромоделирования. – Научная сессия МИФИ-2007, IX Всероссийская научно-техническая конференция «Нейроинформатика-2007», 2007, т.3, с. 24-31.