Geum.ru

«Статистическое изучение национального богатства»

Вид материалаКурсовая
Подобный материал:
1   2   3   4   5

2.2.Выявление наличия корреляционной связи между признаками среднегодовой стоимости основных производственных фондов и выпуска продукции, установление направления связи и измерение ее тесноты.

2.2.1 Аналитическая группировка.


Для установления наличия и характера связи между среднегодовой стоимостью основных производственных фондов и выпуском продукции по данным исходной таблицы строим итоговую аналитическую таблицу. Факторным признаком является среднегодовая стоимость основных производственных фондов, а результативным – выпуск продукции.



























№ п/п
Группы предприятий по среднегодовой стоимости основных производственных фондов
Число предприятий
Среднегодовая стоимость основных производственных фондов
Выпуск продукции






всего
Средняя стоимость на одно предприятие
всего
средний выпуск продукции






А
Б
1
2
3
4
5






1
16,0-24,9846
3
59,737
19,912
56
18,667






2
24,9846-33,9692
4
117,521
29,380
117,31
29,328






3
33,9692-42,9538
11
447,974
40,725
480,886
43,717






4
42,9538-51,9384
7
330,329
47,190
382,504
54,643






5
51,9384-60,923
4
224,149
56,037
283,84
70,960















































































































Данные таблицы показывают, что с ростом среднегодовой стоимости основных производственных фондов предприятия, средний выпуск продукции тоже увеличивается. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость. Теснота связи может быть измерена коэффициентом корреляции, чтобы его найти строим таблицу .

 
№ п/п
Группы предприятий по среднегодовой стоимости основных производственных фондов
Число предприятий
х
y

 
А
Б
1
2
3

 
1,000
16,0-24,9846
3
59,737
56,000

 
2,000
24,9846-33,9692
4
117,521
117,310

 
3,000
33,9692-42,9538
12
447,974
480,886

 
4,000
42,9538-51,9384
7
330,329
382,504

 
5,000
51,9384-60,923
4
224,149
283,840

сумма
 
 
30
1179,710
1320,540

среднее
 
 
 
39,324
44,018



Достраиваем в таблице колонки для удобства дальнейших расчетов. Получаем следующую таблицу:


х
y
(х - хср)2
(у - уср)2
xy
x2
y2

2
3
4
5
6
7
8

59,737
56,000
1165,924
1968,897
1153,163
1225,027669
1086,16

117,521
117,310
403,716
877,011
3457,216
3461,026069
3454,1773

447,974
480,886
104,482
313,337
18036,341
16780,23332
19397,60491

330,329
382,504
452,336
853,971
18085,150
15607,37541
20965,0033

224,149
283,840
1154,693
3014,817
15969,552
12598,01101
20252,61805

1179,710
1320,540
3281,151
7028,034
56701,422
49671,67346
65155,564

39,324
44,018
 
 
 
 
 


Теперь вычисляем дисперсию, среднее квадратическое отклонение и коэффициент вариации по названным в п. 2.1 формулам, получаем следующие значения













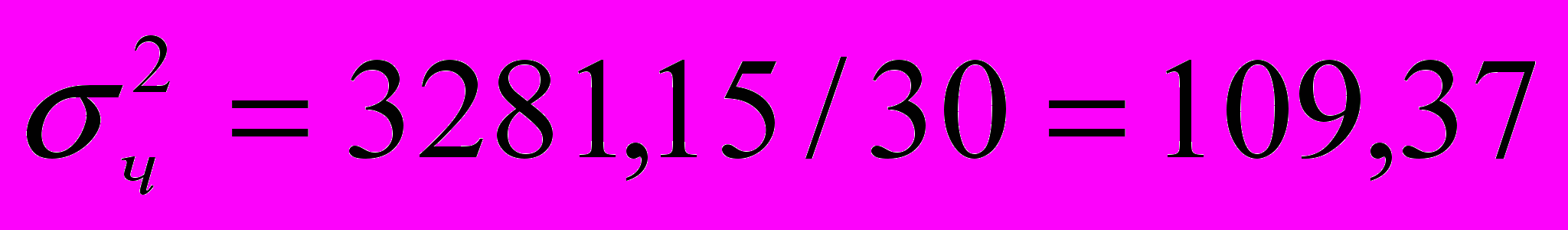
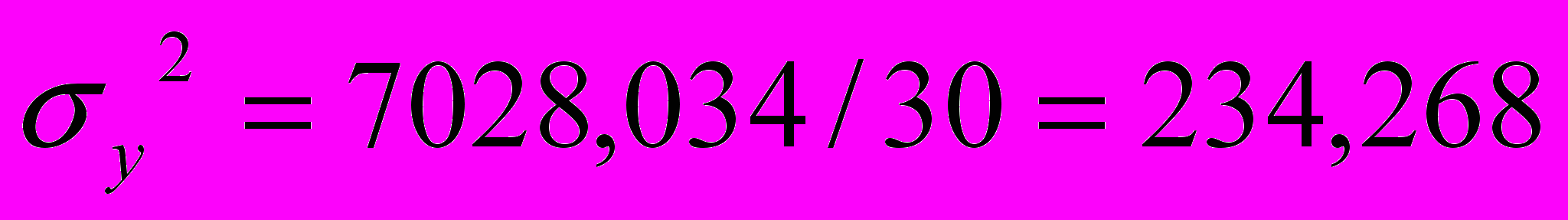
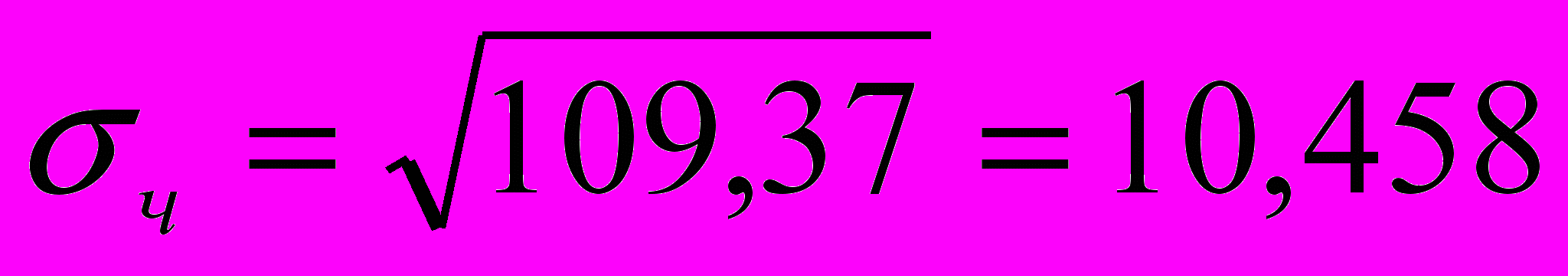
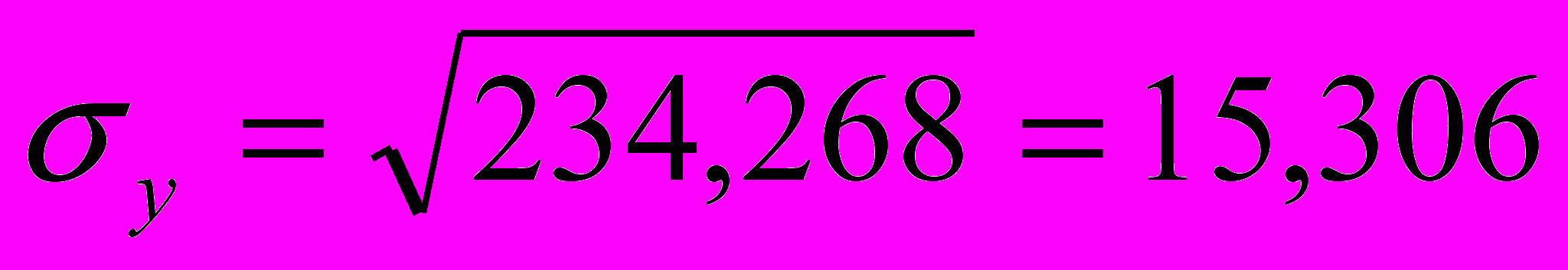
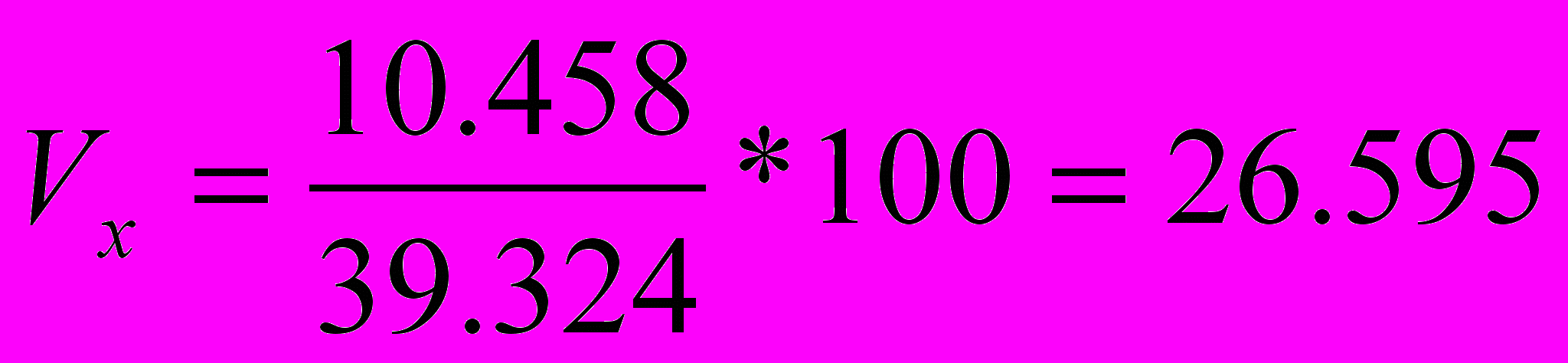
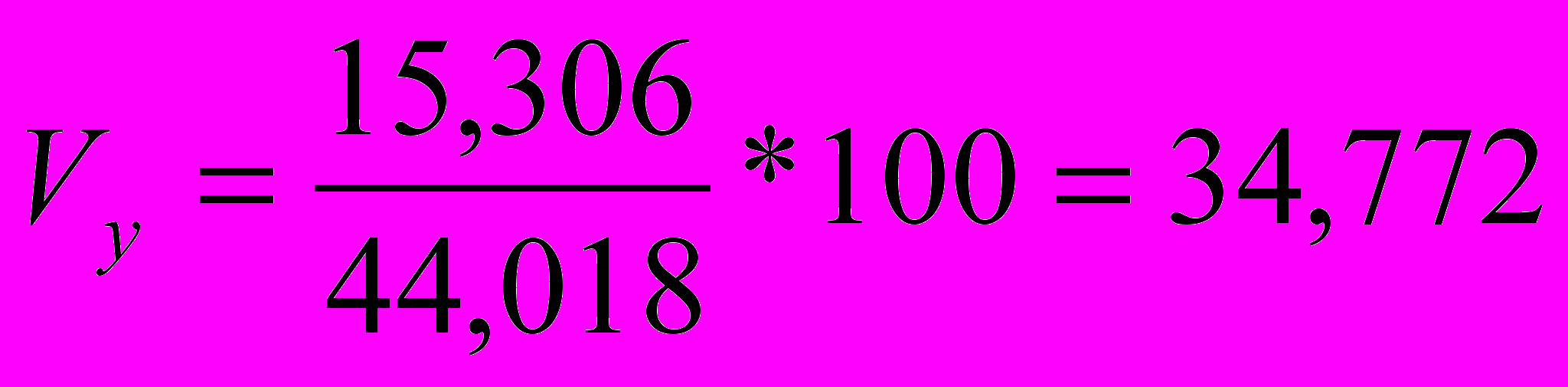
Далее вычисляем коэффициент корреляции r=((ху)ср-хср*уср)/ σx * σy , у нас r=0.994. Это говорит о том, что между х (среднегодовая стоимость основных производственных фондов) и у (выпуск продукции) существует корреляционная зависимость. Так как r=0,994 связь весьма тесная, а поскольку r=0,994>0, связь прямая.

Метод аналитического выравнивания ряда динамики по прямой. Уравнение прямой имеет вид



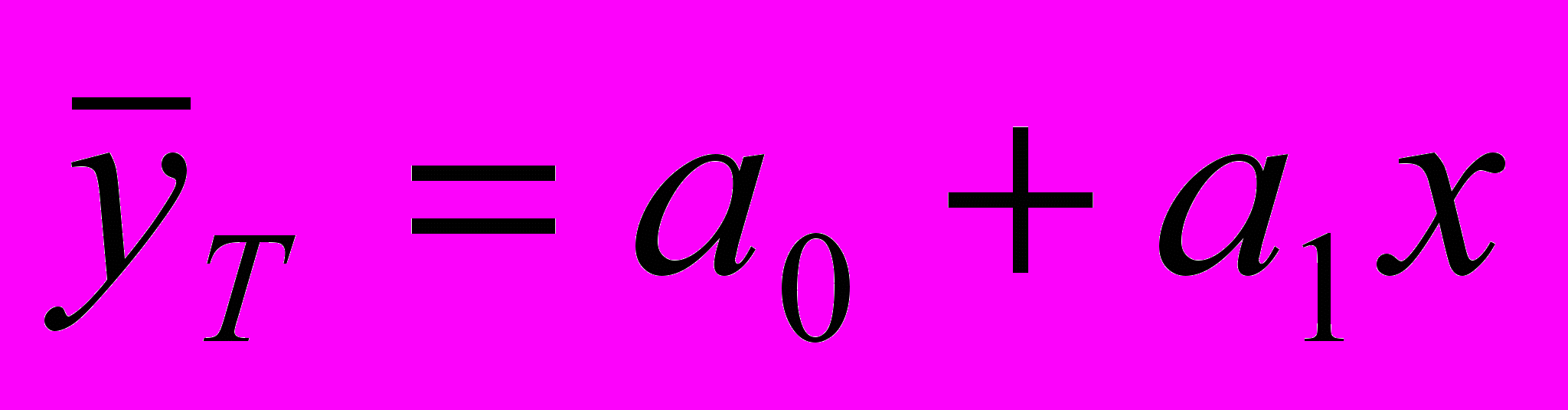
Коэффициенты уравнения регрессии находим по формулам:

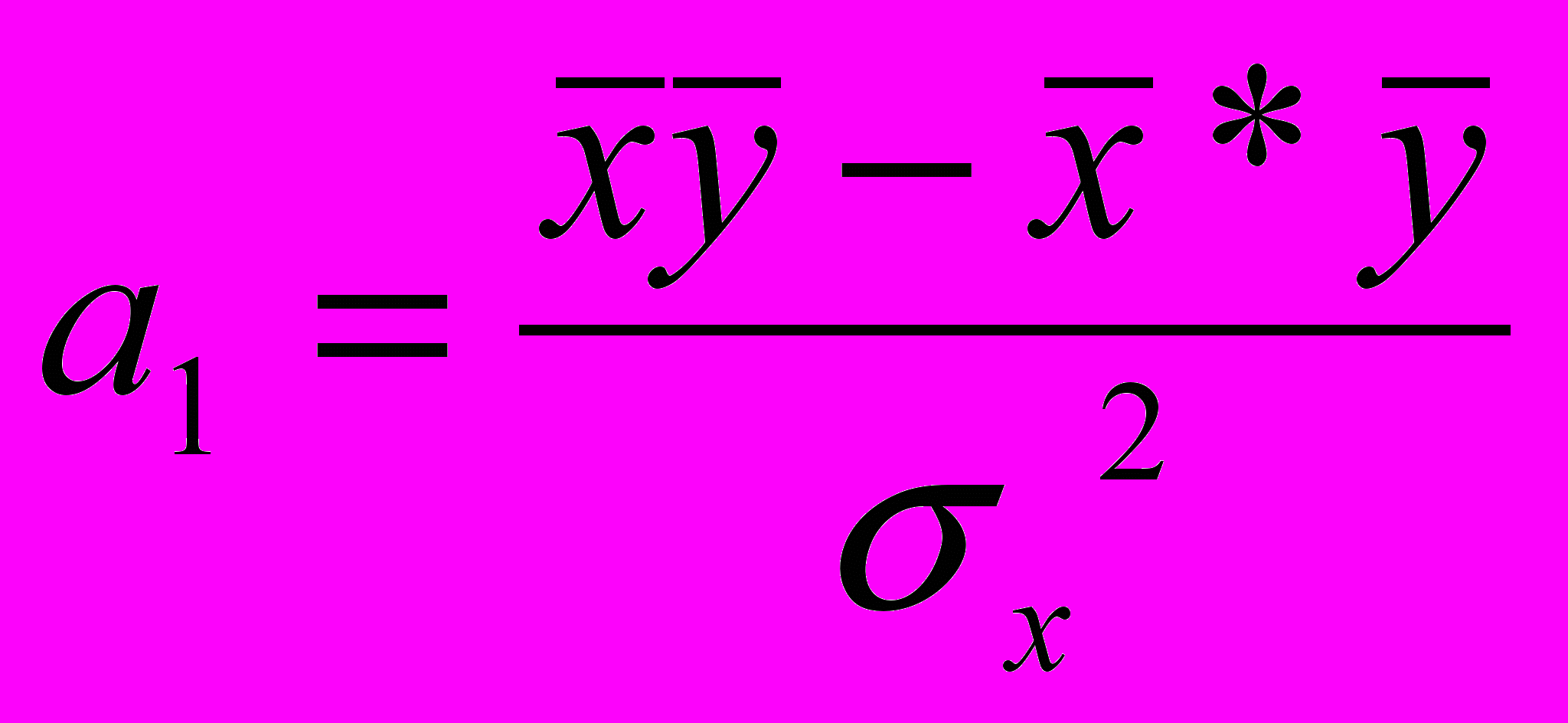- характеризует среднее изменение уровня результативного признака при изменении значения факторного признака на1.

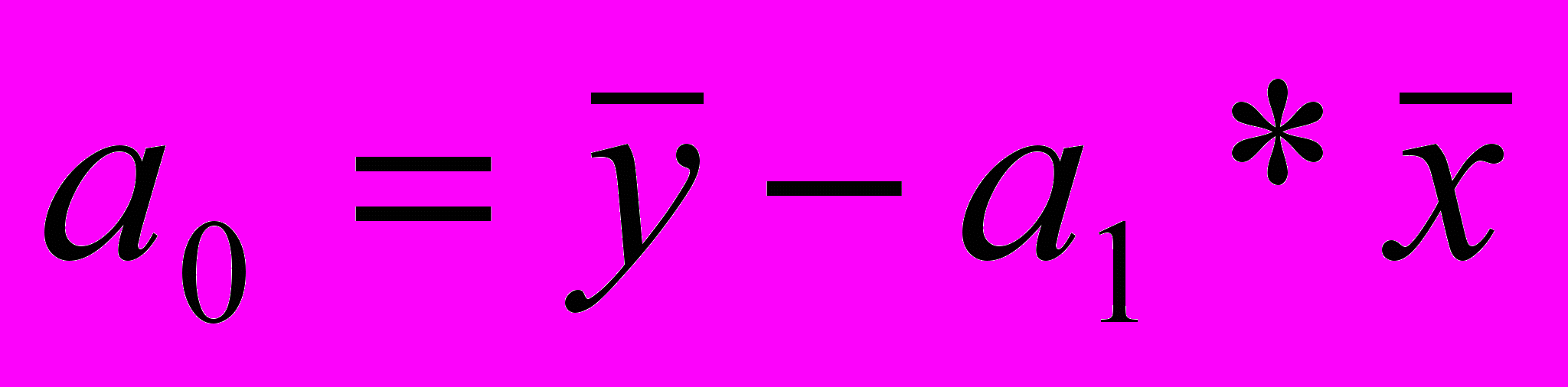- представляет собой среднее значение результативного признака при нулевом значении факторного признака

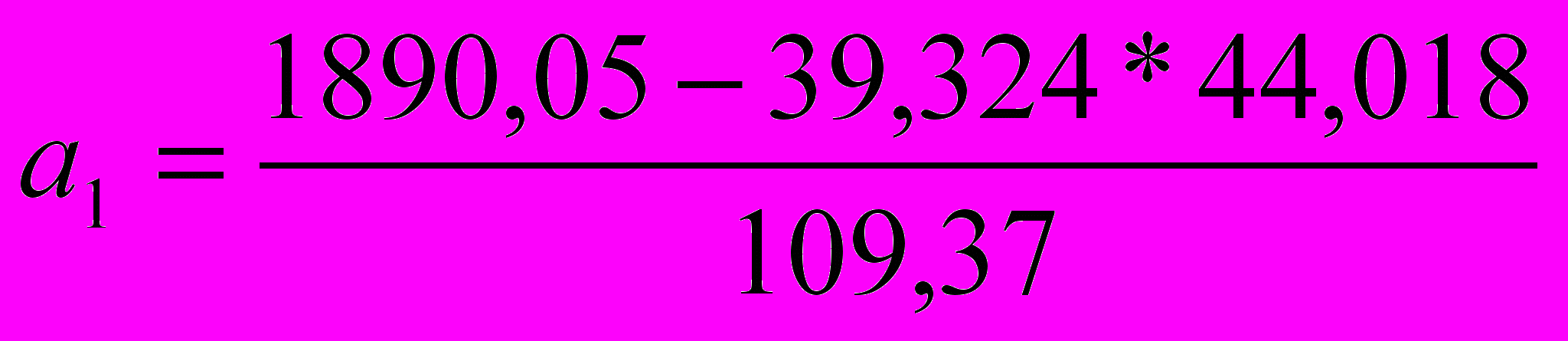=1,455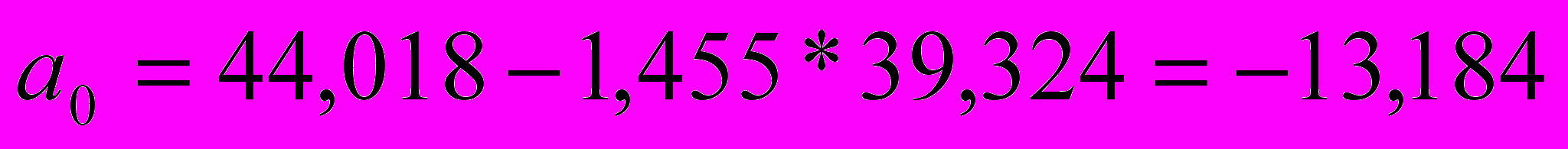



Значит, в общем виде уравнение регрессии выглядит следующим образом:



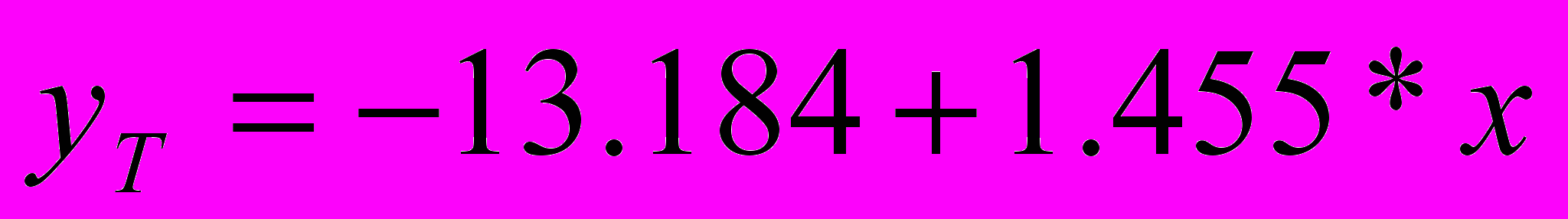
Подставив в это уравнение значение х, получим выровненные теоретические значения




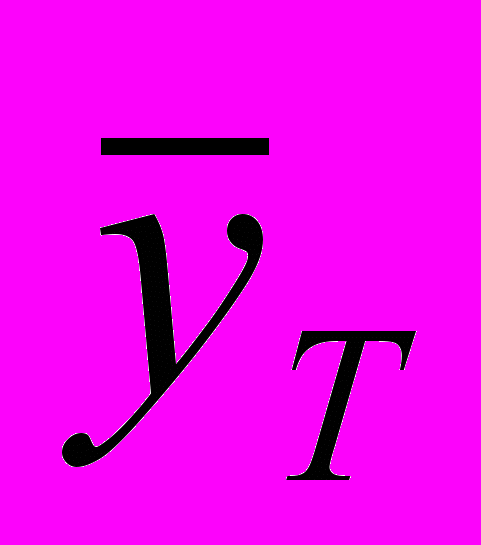
n
x
y
yt




1
16
14,4
 




2
19,362
18,2
10,090




3
24,375
23,4
14,981




4
27,408
26,86
22,273




5
28,727
28,44
26,685




6
30,21
30,21
28,603




7
31,176
31,8
30,761




8
34,388
35,42
32,166




9
34,522
35,903
36,838




10
34,714
36,45
37,033




11
34,845
36,936
37,313




12
36,985
39,204
37,503




13
37,957
40,424
40,616




14
38,318
41
42,030




15
38,347
41,415
42,555




16
38,378
41,832
42,597




17
38,562
42,418
42,642




18
39,404
43,344
42,910




19
41,554
46,54
44,135




20
44,839
50,22
47,262




21
45,674
51,612
52,041




22
46,428
53,392
53,256




23
47,172
54,72
54,352




24
47,59
55,68
55,435




25
48,414
57,128
56,043




26
50,212
59,752
57,241




27
52,5
64,575
59,857




28
55,25
70,72
63,185




29
55,476
69,345
67,185




30
60,923
79,2
67,514

сумма
 
1179,71
1320,54
1245,102

ср.знач.
 
39,32366667
44,018
42,935


После решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.



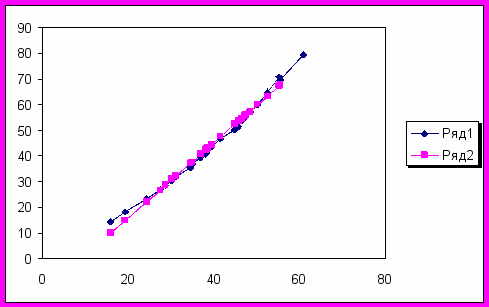
2.2.2.Корреляционная таблица


Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результатному. Концентрация частот около диагоналей матрицы данных свидетельствует о наличии корреляционной связи между признаками.

Построим корреляционную таблицу, образовав, пять групп по факторному и результативному признакам.

Среднегодовая стоимость основных производственных фондов
Выпуск продукции

14,4-27,36
27,36-40,32
40,32-53,28
53,28-66,24
66,24-79,2

16,0-24,9846
3
 
 
 
 

24,9846-33,9692
1
3
 
 
 

33,9692-42,9538
 
5
7
 
 

42,9538-51,9384
 
 
3
5
 

51,9384-60,923
 
 
 
1
3


Как видно из таблицы, распределение выпуска продукции произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, т.е. увеличение признака «Среднегодовая стоимость основных производственных фондов» сопровождалось увеличением признака «Выпуск продукции». Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии прямой весьма тесной связи между изучаемыми признаками.