Процесс нахождения производной функции называется дифференцированием. Существует обратный процесс интегрирование

Вид материала

Документы

Подобный материал:

• Лекция Производная функции, 30.86kb.
• Лекция №7 Применение производной, 42.29kb.
• Программа вступительного испытания (собеседование/устный экзамен) по дисциплинам «Математика», 59.58kb.
• В. Г. Белинского Кафедра бухгалтерского учета и аудита учебно-методический комплекс, 1401.74kb.
• Тема 1 Понятие психологии общения, 208.48kb.
• Тема урока : Применение производной исследованию функции, 18.03kb.
• Тема урока: «Исследование функции с помощью производной», 80.5kb.
• -, 2715.91kb.
• Теоретическое задание (тест) Согласно описанию эталонной модели взаимодействия открытых, 102.08kb.
• Процесс обучения как процесс познания нужно рассматривать в его противоречии, как процесс, 270.18kb.

Неопределенный интеграл


Процесс нахождения производной функции называется дифференцированием. Существует обратный процесс – интегрирование. Например, в задаче «Выяснить координату материальной точки в момент времени t,если известно, что скорость ее находится по формуле v(t)=5х²-4» необходимо, вспомнив, что скорость это первая производна от пути, фактически восстановить по производной саму функцию.


Определение 1.

Пусть F и f – функции, заданные на некотором промежутке Х. Если для любого хХ F'(x) = f(x), то функция F называется первообразной для функции f на промежутке Х.


Первообразную для функции можно попытаться найти по таблице производных. Например, в таблице производных написано, что (x²)’ = 2x, а значит, что первообразной для функции f=2x является функция F = x². Но вот ведь незадача!! Если мы найдем производную функции x²-10, то она тоже будет равна 2х. Что делать?! Какая из функций x² или x²-10 (или может быть еще какая-нибудь функция) является первообразной функции 2х? Ответ дает теорема на странице 8 в учебнике. Оказывается (о ужас!!!), если мы сможем найти одну первообразную F, то первообразными для данной функции будут ВСЕ функции вида F+C. Что делать с таким количеством первообразных для одной единственной функции? Ответ прост. Назовем мы все это множество первообразных одной и той же функции двумя словами: неопределенный интервал.


Определение 2.

Совокупность всех первообразных функции f называют неопределенным интегралом и обозначают .

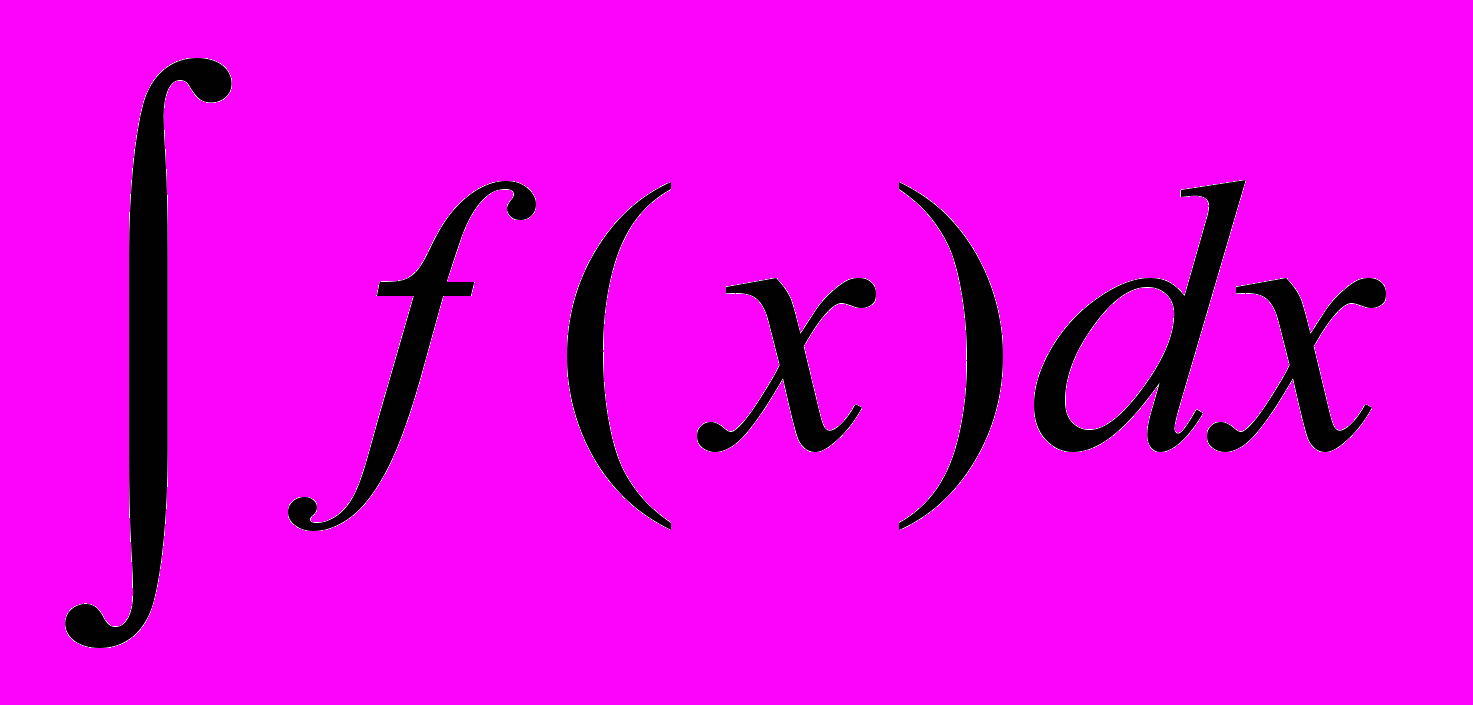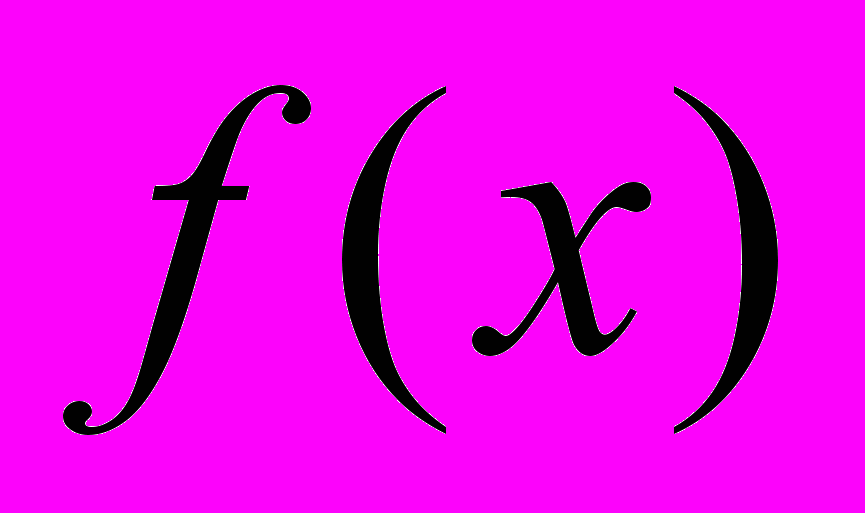- подынтегральная функция,

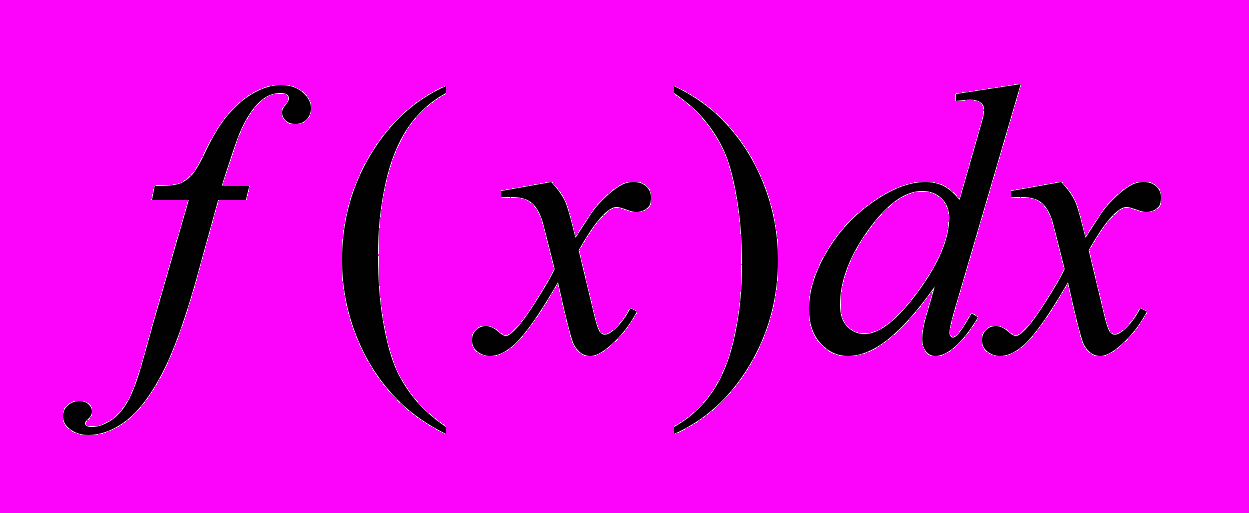- подынтегральное выражение.


Для неопределенного интеграла сформулированы 4 свойства (см. стр. 8-9), но главными из них для нас будут 3 и 4, которые позволяют находить эти самые интегралы или хотя бы существенно упрощать процесс интегрирования.

Свойство 3 говорит о том, что интеграл суммы двух (или более) функций можно расписать в суму интегралов, а 4 свойство говорит, что постоянный множитель можно выносить за знак интеграла. Запомним это!


Для нахождения неопределенных интегралов используется таблица, которая является следствием из таблицы производных. Вот она:

1)

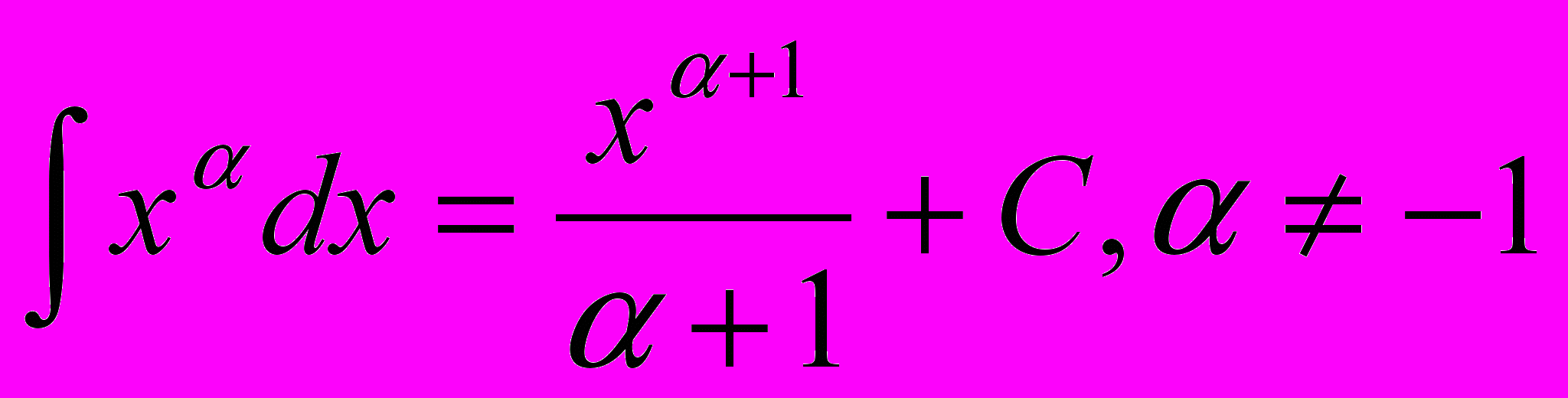
2)

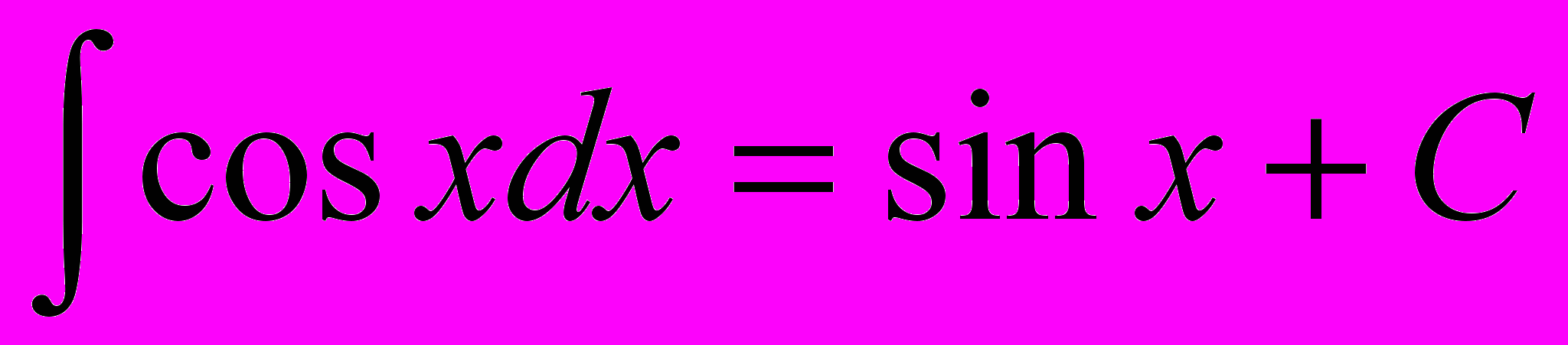
3)

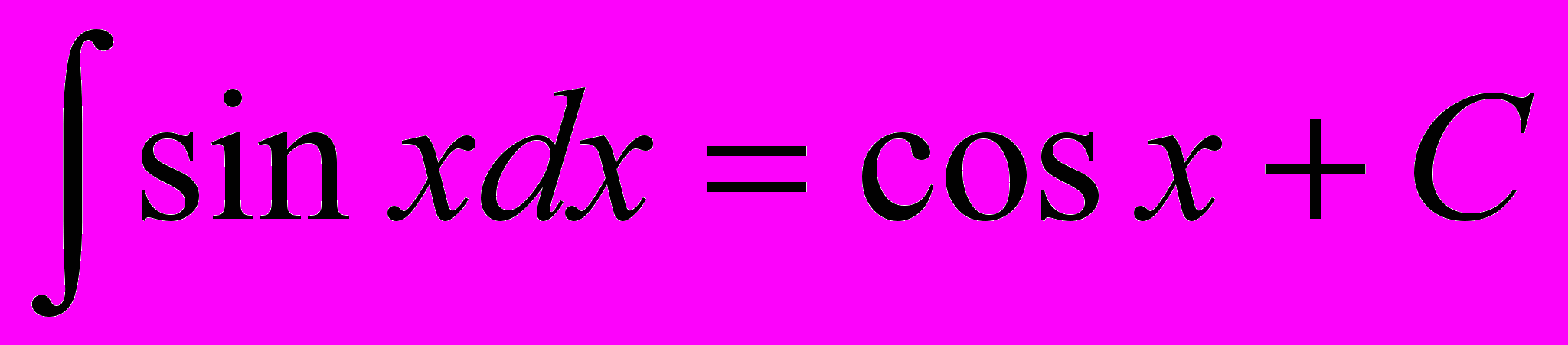
4)

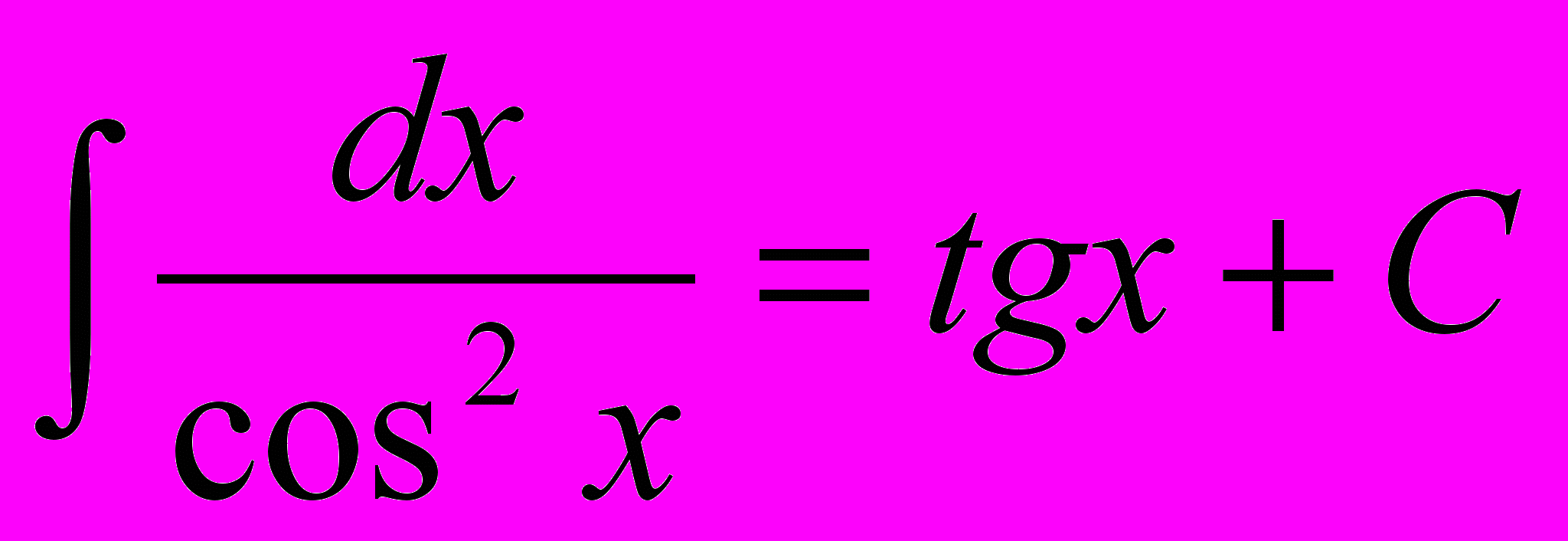
5)

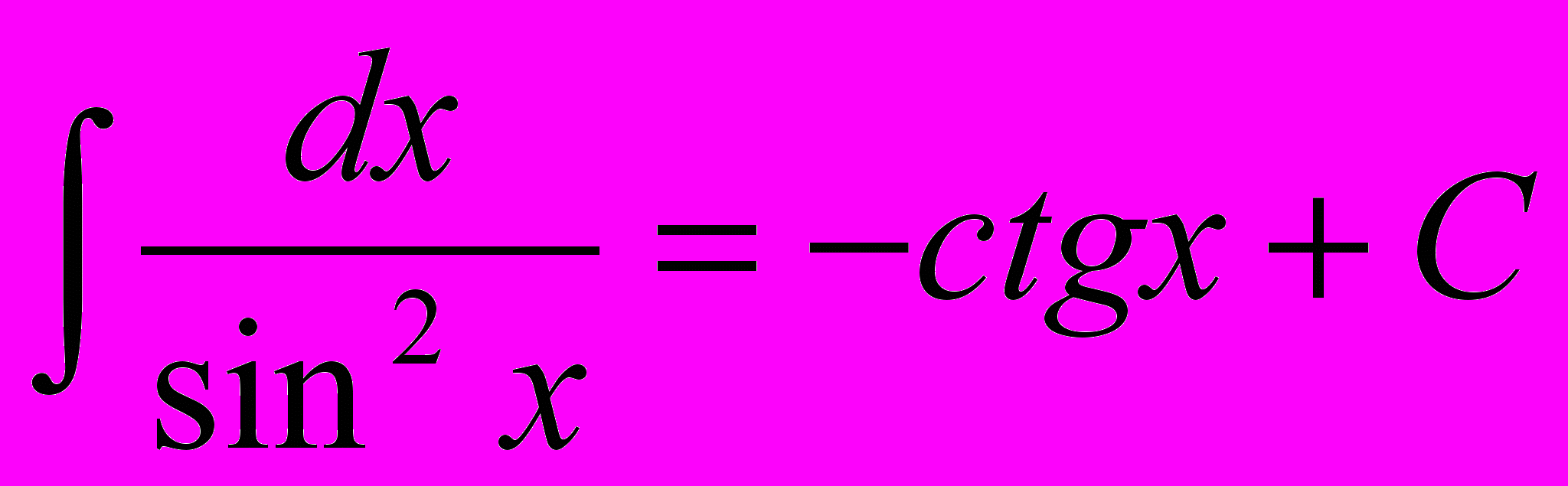
6)

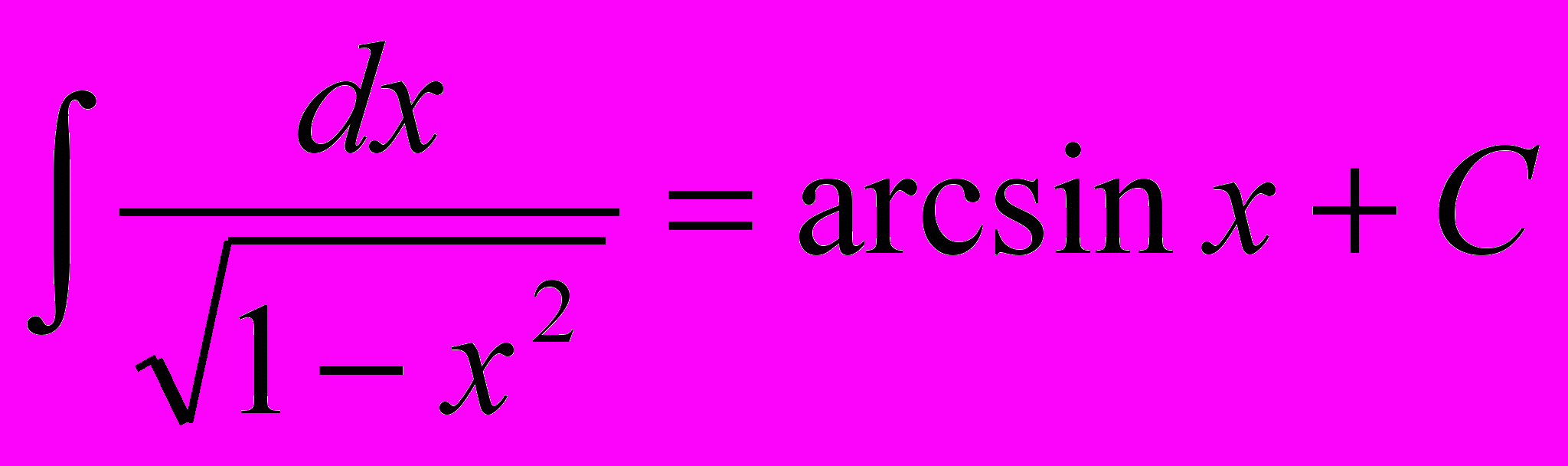
7)


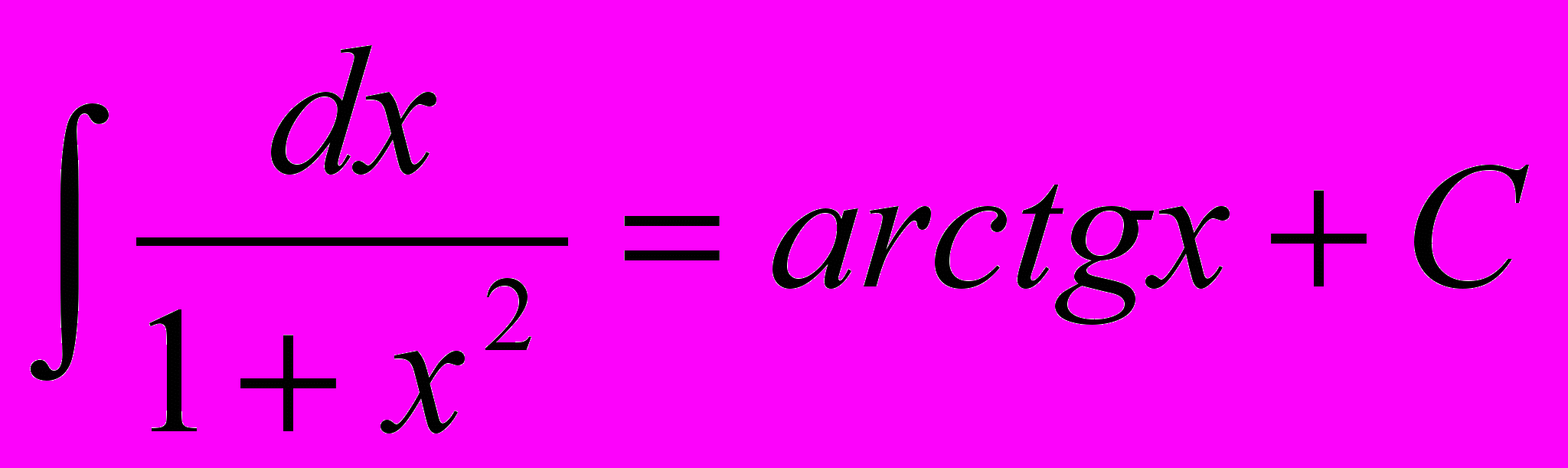
В итоге, задача нахождения неопределенного интеграла сводится к тому, что мы любыми возможными путями, например, используя тождественные преобразования или тригонометрические функции, а так же, свойства неопределенного интеграла, будем пытаться дойти до табличных интегралов.


Разберем пример:



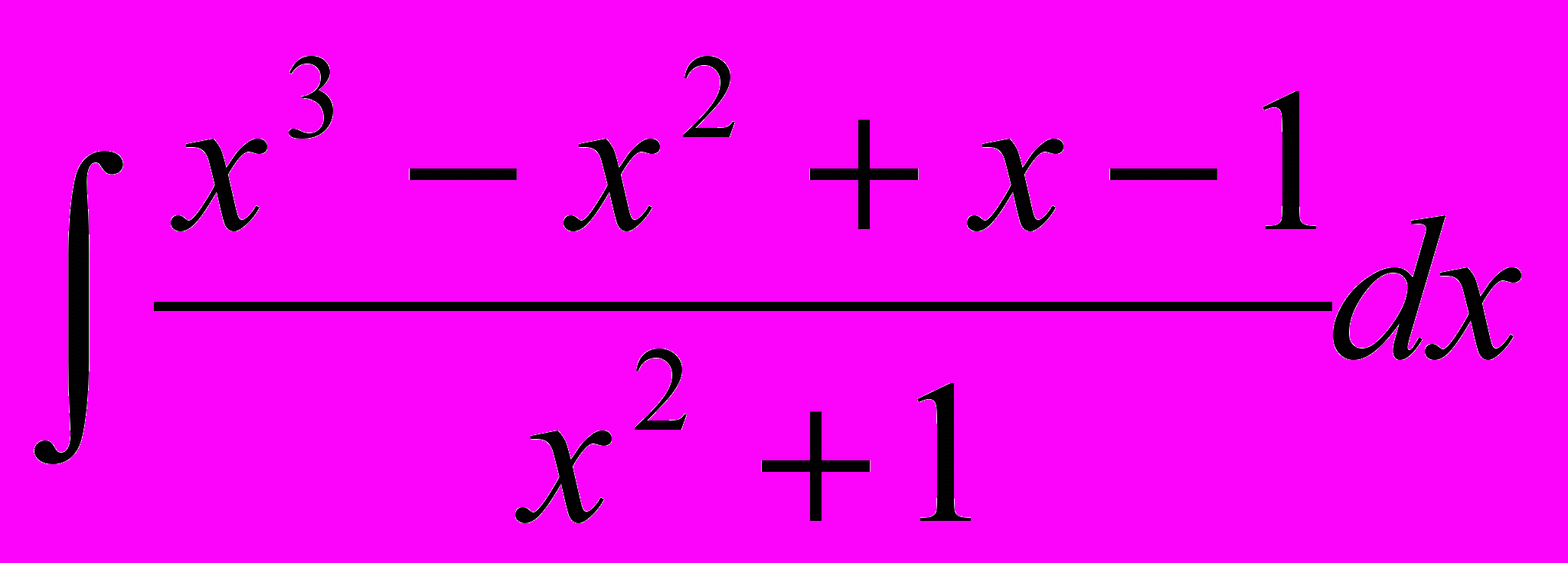
Ужас перед таким большим количеством слагаемых легко преодолеть, если вспомнить, что можно поделить числитель на знаменатель, когда в числителе и знаменателе многочлены. Делим уголком сами, для проверки выдаю результат деления:

.

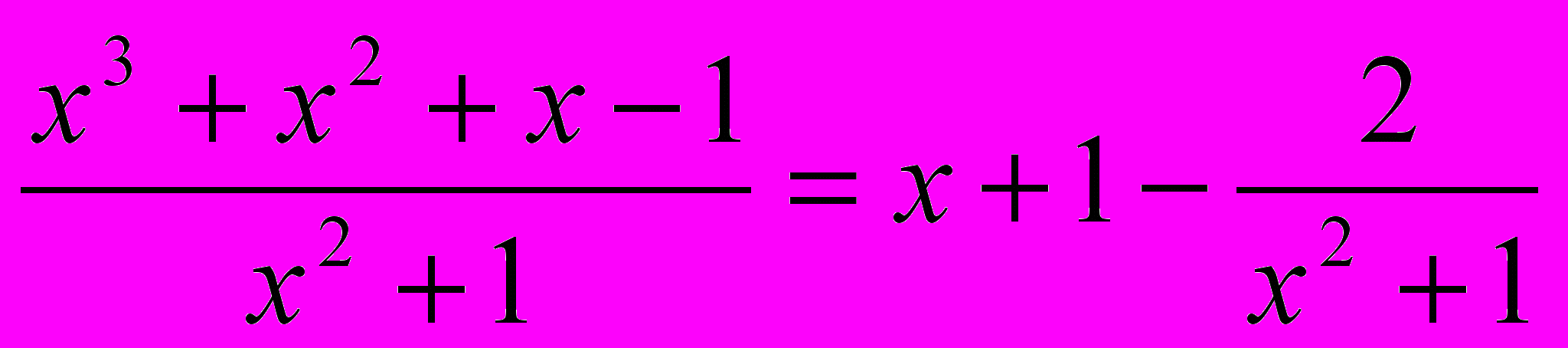Теперь, пользуясь 3 и 4 свойствами, исходный интеграл сводим к сумме трех интегралов:

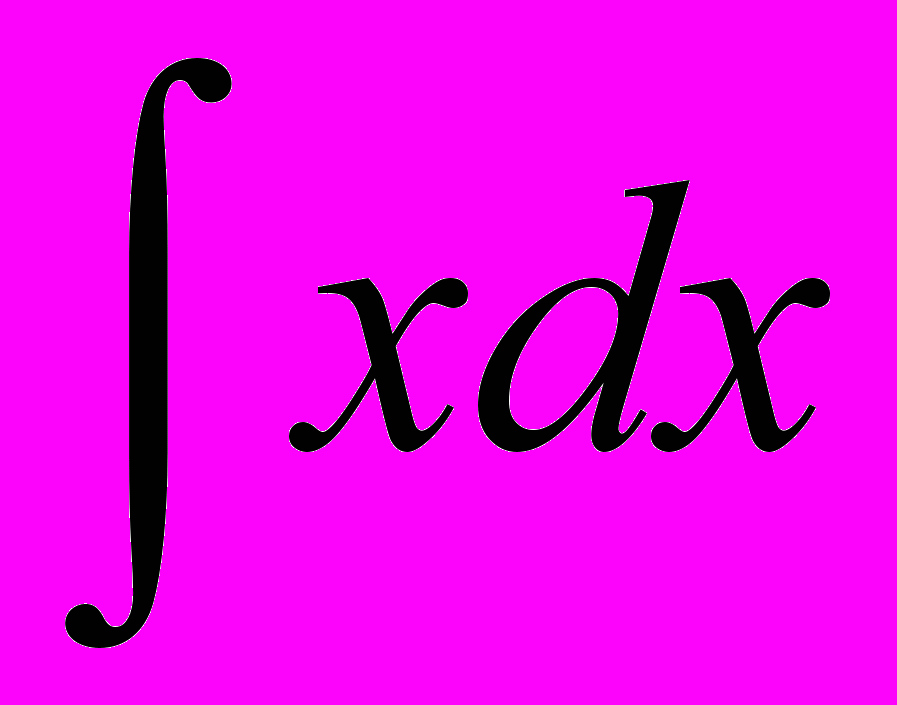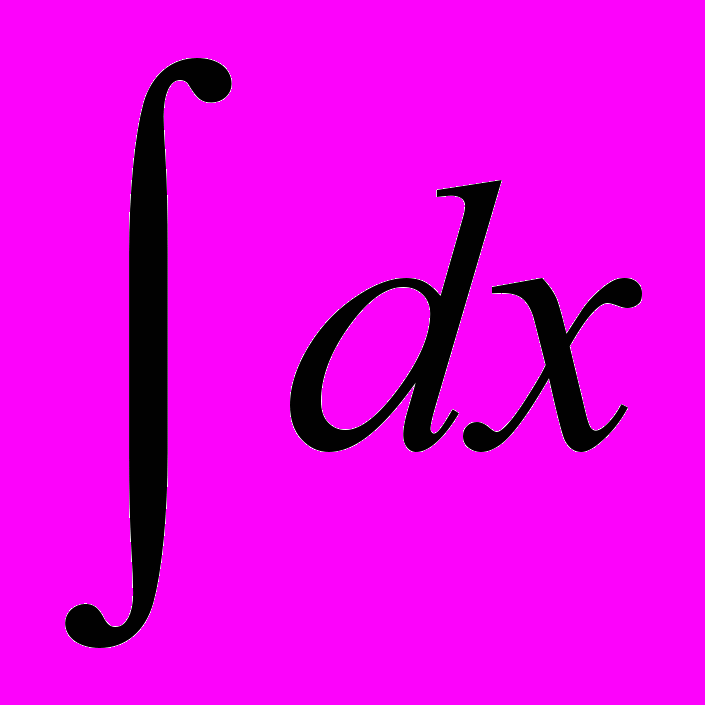+-2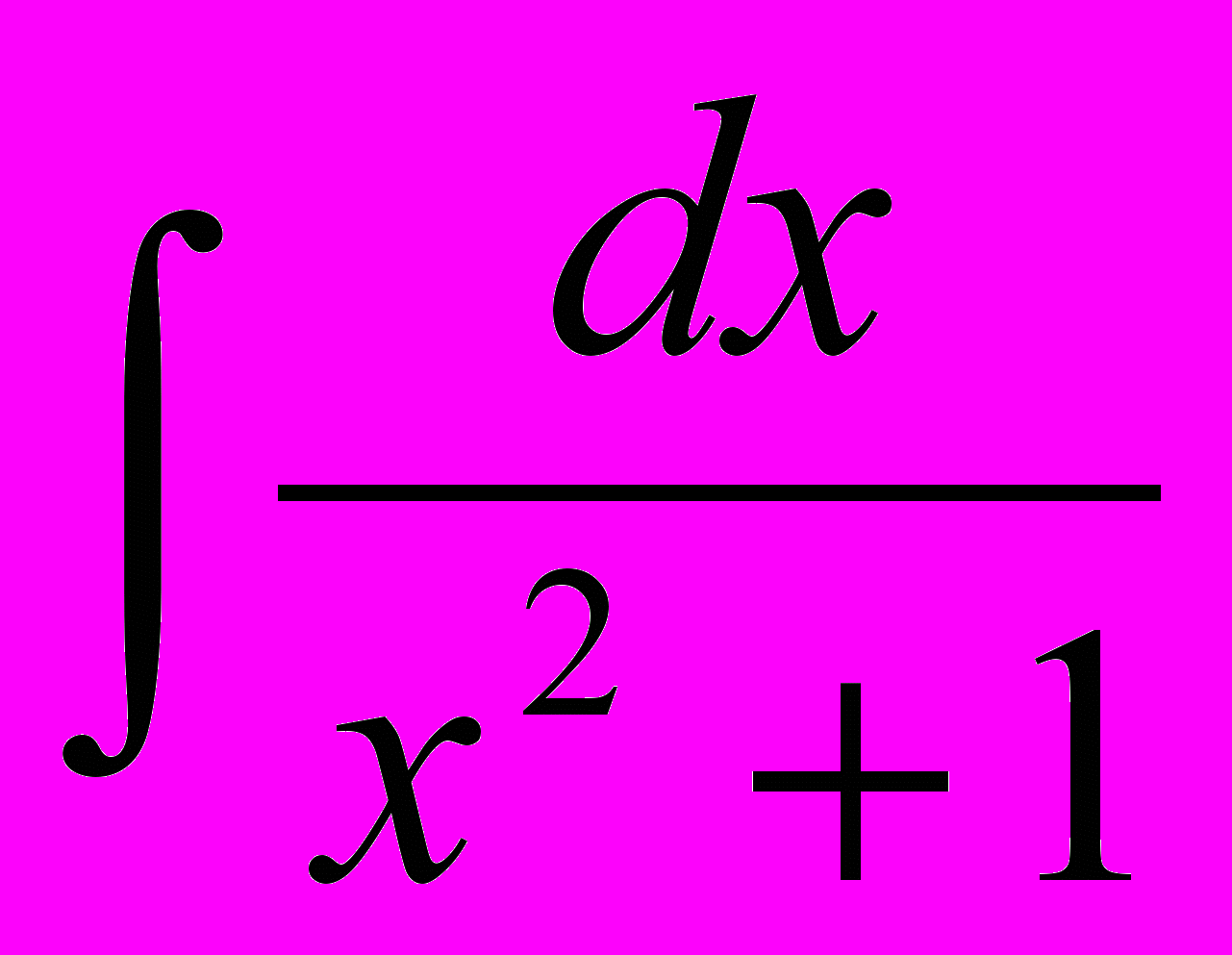

Каждый из этих интегралов табличный. Найдите)))

Важно!!! Не забыть, что неопределенный интеграл это не одна первообразная, а совокупность. Намекаю, что если вы забудете написать +С, то это будет ошибка! Ибо вы свели бесконечное множество функций к одной, что не может быть правильным.


Для тех, кто прочитал эту лекцию, рекомендую выполнить номера 3 и 4 на странице 12 учебника.


To be continued))