Докладов на ктф фф чну

Вид материала

Доклад

Содержание M1 = const

Подобный материал:

• Требования к оформлению докладов, 25.25kb.
• Оао "по "Уральский оптико-механический завод" г. Екатеринбурга заинтересован в молодых, 4.5kb.
• Ормы докладов на конференции, 68.07kb.
• Інформаційний бюлетень (липень-серпень 2011 р.). Вип. 16 Черкаси : Вид від. Чну ім., 533.23kb.
• Інформаційний бюлетень (травень-червень 2011 р.). Вип. 16 Черкаси: Вид від. Чну ім., 1337.24kb.
• Требования к оформлению докладов, 11.58kb.
• «Актуальные вопросы кардиологии», 58.59kb.
• Решение о публикации тезисов докладов принимает председатель секции. Тезисы докладов, 67.24kb.
• Правила оформления тезисов докладов Тезисы докладов предоставляются в электронном виде, 22.59kb.
• Требования к оформлению докладов, 57.52kb.

v в этот самый момент времени T


v_j = _j ((δx_0j)² - (δx_j)²)^½ (59)

v_0j = _j δx_0j (62)

v_j /V_j = π ((δx_0j)² - (δx_j)²)^½ /2x_j (63)

v_0i /V_j = π δx_0j /2x_j (64)


Интересно то, что соотношения (63) и (64) не зависят от величины упругости частиц, в то время как их составляющие (скорость волн и малая скорость частиц) зависят линейно. При больших амплитудах все зависит от явного вида функции a_j= f(x_j) и, соответственно, ее производной df(x_j) /dx_j. Например, при


f(x_j) = C₁ + C₂ /x_jⁿ (65)


и n=1 скорость волн не зависит от размеров частиц, а значит, и от величины деформации их упаковки


V_jn=1= 2x_j(-2df(x_j) /dx_j)^½ /π = 2x_j(+2C₂/x_j²)^½ /π = 2(2C₂)^½ /π = const (x_j) (66)


При других n1 скорость волн


V_jn>1= 2x_j(-2df(x_j) /dx_j)^½ /π = 2x_j(+2C₂n/x_jⁿ⁺¹)^½ /π = (8C₂n)^½ /πx_j^n-1  const (x_j) (67)


начинает зависеть от величины x_j, а значит, от деформации упаковки и амплитуды волн. Зависимость от деформации упаковки приводит к появлению разницы и анизотропии скоростей волн в по-разному деформированных частях упаковки и проявляется в явлениях изгиба-преломления ними потоков волн, похожего на отклонение света звезд окрестностями Солнца. Зависимость от амплитуды может проявляться в изменении (старении) формы волн со временем, причем продольные и поперечные волны ведут себя по-разному. Отличаются не только их скорости, но и зависимость скоростей от амплитуды и частоты. Наличие четкой частоты собственных колебаний приводит к тому, что упаковка ведет себя как резонансный механический фильтр-экран для волн с частотой большей, чем собственная. Так же упаковка реагирует на многомерные (не плоские, не линейные) волны, уменьшая их амплитуду (не пропуская) с расстоянием от источника из-за коллективности взаимодействия частиц. Количество вариантов довольно велико, поэтому анализировать их без потребности в кратком сообщении нет смысла из-за ограниченности времени. Важно отметить только то, что существуют процессы, содействующие стремлению упаковки к состоянию равновесия. И это волновые процессы.

При деформации первично однородная упаковка одинаковых у всех отношениях частиц становится неоднородной, а частицы – неодинаковыми по размерам. Однако к ним можно применить общее правило счета (4) и (6): вдоль любой фиксированной линии длиной L сумма размеров r_j частиц постоянна


L_АВ = ^MΣ_j=1L_j = ^MΣ_j=1r_j = const (68)

и

δL_АВ = ^MΣ_j=1δL_j = ^MΣ_j=1δr_j = 0 (69)


В многомерной упаковке каждая j-тая частица окружена многими M_o соседними частицами, которые можно также называть ее непосредственным окружением, и согласно (23)-(24) имеет по отношению к каждой k-той из них определенный u_jk и средний u_jс потенциал

u_jk = u_jс + δu_jk (70)


Для случаев упаковок самых низких измерений N = 0,1,2,3,... M_o= 0,2,6,12, .... По аналогии для большего количества измерений можно ожидать


M_o= N(N+1) (71)


Одинаковость частиц позволяет выражать суммарный потенциал u_jо окруженной частицы через сумму ее потенциалов, предопределенных окружающими частицами


u_jо = ^MоΣ_k=1 (u_jc + δu_jk) (72)


Геометрический потенциал из (23)


dU_i = - V_i dV_i = - d(V_i² /2) = - A_i dL_i (23)


Объем ^Nq_j, который приходится в плотной N-мерной упаковке на одну частицу (через проекции на оси координат ее линейных размеров x_ij и плотность m_ij)

^Nq_j = ^N_i=1 x_ij = ^N_i=11/m_ij (73)

d^Nq_j /^Nq_j = ^NΣ_i=1 dx_ij /x_ij = - ^NΣ_i=1 dm_ij /m_ij (74)


Объем ^Nq_j частицы, как выпуклого N-мерного многогранника (через его линейный размер - диаметр вписанной сферы r_jс)


^Nq_j = ^MоΣ_k=1 ^Nq_jk = ^MоΣ_k=1 C_qrk r_jс^N (75)

d^Nq_j /^Nq_j = ^NΣ _k=1 dr_jk /(r_jс) = N dr_jk /(r_jс) (76)


Очевидно равенство (73) = (75). Для изотропно деформированной упаковки все ^Nq_jk одинаковы


^Nq_j = ^MоΣ_k=1 ^Nq_jk = M_о ^Nq_jk (77)


Отклонение (флуктуация, вариация) суммарного потенциала δu_jо частицы от среднего значения u_jо при достаточно малых δr_jk


δu_jо = ^MоΣ_k=1 δu_jk = - ^MоΣ_k=1 a_jk δr_jk = - a_jkcr_jkc ^MоΣ_k=1δr_jk /r_jkc = - a_jkcr_jkc^MоΣ_k=1δ^Nq_jk /^Nq_jkcN =

= - a_jkcr_jkc M_о (^MоΣ_k=1δ^Nq_jk) /^Nq_jkcN M_о = - a_jkcr_jc (M_о /N) δ^Nq_j /^Nq_j =

= - f_ar(r_jc) r_jc (N+1) ^NΣ_i=1 δx_ij /x_ij = - (N+1) r_j f_ar(r_j) ^NΣ_i=1 δx_ij /x_ij =

= - u_jо ^NΣ_i=1 δx_ij /x_ij (78)

при условном обозначении

u_jо = (N+1) r_j f_ar(r_j) (79)

δu_jо /u_jо = - ^NΣ_i=1 δx_ij /x_ij = ^NΣ_i=1 δm_ij /m_ij (80)

δu_ijо /u_jо = - δx_ij /x_ij = δm_ij /m_ij (81)


То есть потенциал частиц упаковки оказывается прямо пропорционален плотности упаковки и обратно пропорционален размерам ее частиц в каждом направлении измерения. Потому любые частицы упаковки при перемещении в упаковке будут испытывать ускорение в направлении ее разрежения.

С другой стороны, например, при перемещении на ΔX плоского слоя частиц внутри и вдоль фиксированной части упаковки в форме стержня (Рис. 2) длиной X₀ количество частиц M₁, M₂ в частях 1, 2 упаковки не меняется, а их размеры x₁, x₂ в каждой части одинаковые в результате одинаковости частиц по условию, но разные в разных частях..

ΔX₁ = - ΔX₂







X₁ = M₁x₁ X₂ = M₂x₂




X₀




Рис. 2. Схема внутренней деформации стержня.


Это перемещение можно называть внутренней деформацией стержня


M₁ = const (ΔX) (82)

M₂ = const (ΔX) (83)

M₀ = M₁ + M₂ = const (ΔX) (84)

X₀ = X₁ + X₂ = M_x1x₁+ M_x2x₂= const (ΔX) (85)

x₀ = x_j + δx_j = const (ΔX) (86)

ΔX₀ = ΔX₁ + ΔX₂= M_x1δx₁ + M_x2δx₂ = 0 (87)

M_x1δx₁ = - M_x2δx₂ (88)


Но на границе раздела встречаются два слоя частиц, которые могут быть деформированы по разному не только за счет внешнего вмешательства, но и за счет разного количества частиц

δx₁  - δx₂ (89)


Любая неподвижная частица упаковки своей неподвижностью реагирует на равенство противоположных ускорений A_x1 і A _x2, которые она должна была бы получить от разного количества M_y1 и M_y2 соседок с противоположных сторон. Одинаковость-равноправие соседок требует одинаковости связанных с ними составляющих a_x1 и a_x2 ускорений, пропорциональных отклонением деформаций δx от средних значений


A_x1 = - A _x2 = M_y1a_x1 = - M_y2a_x2 (90)

M_x1δx₁ = - M_x2δx₂ (91)


что напоминает законы Ньютона и Гука и вместе с (88) позволяет выражать взаимную деформацию частей 1 и 2 упаковки суммой деформаций всех частиц M₁ и M₂ в их объемах


M₁δx₁ = - M₂δx₂ (92)


Если в поверхностный слой выделенной в упаковке сферы с радиусом R_с дополнительно к образовывающим его достаточно жестким M_с частицам добавить ΔM_с таких же частиц, то радиус ΔR_с этого слоя вырастет на

ΔR_с = ΔM_с τ_ji /2π (93)


Так же радиус уменьшится при исключении частиц. Радиальное расширение выделенной сферической части упаковки с радиусом R_с на ΔR_с приведет к перемещению в этом же направлении на меньшие пропорциональные величины ΔR_j всех других j-тых концентрических слоев упаковки из j₀. Из-за этого внутренние частицы растянутся в радиальном r_jвн и тангенциальных τ_jiвн i-тых направлениях на одинаковую величину (изотропно)


δr_jвн = ΔR_с /j_с = δτ_ji = 2πΔR_с /2πj_с (94)


и их потенциал упадет на одинаковую для всех них величину


δu_jовн /u_jо = δm_jо /m_jо = - ^NΣ_i=1 δx_ij /x_ij = - δr_jвн /r_j - ^NΣ_i=2 δτ_ji /τ_ij =

= - N δτ_ji /τ_ij = - N ΔR_с / x_ij j_с = - N ΔR_с /R_с = const (j) (95)


потому перемещение частиц внутри сферы не будет сопровождаться их ускорениями из-за отсутствия градиентов потенциала. Внешние слои в тангенциальных направлениях будут расширяться по тому же закону


δτ_ji = 2πΔR_j /2πj_нар = 2πτ₀ ΔR_j /2πR_jнар (96)


но из-за численности M_нар внешних ( наружных) частиц и


δL_АВ = ^MΣ_j=1δL_j = ^MΣ_j=1δr_j = 0 (59)

при

M = M_вн + M_нар =  (97)

M_вн << M_нар =  (98)

ΔR_j = ^MвнΣ_j=1δr_jвн = - ^MнарΣ_j=1δr_jнар (99)

δτ_ji >> δr_jнар  ΔR_с / M_нар  0 (100)


Поэтому потенциал частиц вокруг радиально растянутой (сжатой) сферы и, соответственно, плотность упаковки увеличиваются (уменьшаются) с расстоянием от центра


δu_jонар /u_jо = δm_jо /m_jо = - ^NΣ_i=1 δx_ij /x_ij = - δr_jнар /r_j - ^NΣ_i=2 δτ_ji /τ_ij  - (N-1) δτ_ji /τ_ij

 - (N-1) ΔR_с /R_jнар (101)


и подвижная частица при перемещении в этом окружении испытывает ускорение a_R к (от) центру сферы в направлении, противоположном ΔR_с


a_R = - d_Ru /dR_jзовн = - d_Rδu /dR_jзовн +(N-1) u_jо ΔR_с d(1/R_jзовн) /dR_j =

= - (N-1) u_jо ΔR_с /R²_jзовн = - (N-1) u_jо ΔM_с τ_ji /2πR²_jзовн = C_aMR (M,R) ΔM_с /R_j² (102)


Выражение (102) можно назвать законом обратных квадратов для радиальных ускорений подвижных частиц в радиально растянутых-сжатых упаковках. В тангенциальных направлениях размеры частиц одинаковы, потому градиент потенциала и ускорения подвижных частиц в этих направлениях равны нулю.

Количество перемещенных частиц для удобства можно условно называть зарядом соответствующего знака (избыток - “+”, недостачу “-”). Требование достаточной (для наблюдаемости) стабильности свойств упаковки приводит к сохранению общего количества частиц, а значит и общего заряда упаковки, при любых манипуляциях с ними


^MΣ_k=1 Δq_k = 0 (103)


В этих терминах (101)-(102) можно комментировать так: сближение одноименных зарядов энергетически выгодно при отсутствии других условий.




R_j ΔX_oсі







ΔX_j(R_j)













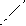
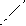
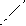
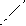
O₁ O₂ X





Рис. 3. Схема осевого сдвига частиц упаковки между разноименными зарядами.


Но в результате (103) создание избытка частиц в одной части упаковки всегда приводит к недостаче тождественно равного количества частиц в другой части упаковки, то есть к одновременному созданию не одного, а двух объектов, которые деформируют свое окружение в противоположных, по отношению к своим центрам, направлениях.

Если оба объекта являются концентрическими сферами, то деформации упаковки ними внутри них просто добавляются, но продолжают отвечать (101) -(102).

Если же центры этих объектов не совпадают, то смещения частиц общего окружения происходят на линии центров в одну сторону и тоже добавляются, но в результате деформация упаковки является деформацией цилиндрически-осевого сдвига вдоль конечного отрезка прямой, соединяющего центры количественно измененных (заряженных) частей упаковки (Рис.3). При этом величина осевой деформации δx_j частиц упаковки уменьшается с ростом расстояния R_j в направлении, перпендикулярном межцентровой (осевой) линии X, из-за одинаковости частиц противодействующих соседних коаксиальных колец приблизительно как


δx_j  C /M_τj = Cτ_j /2πR_j (104)

ΔX_j = ^Σ_k=j δx_k = C ^Σ_k=j τ_k /2πR_k (105)


Это же противодействие (своего рода торможение осевого смещения) делает неверным условие (100) из-за конечности М_12внеш<< и многомерности упаковки N_τ >>1. К тому же два разноименных заряда в значительной степени взаимно нейтрализуют тангенциальные смещения частиц окружения, поэтому в (101) уменьшается тангенциальная составляющая и растет осевая, которая может стать большей от тангенциальной. В таком случае, например, при

δr_j  const (X_j) = C = 2 ΔR_с /М_12внеш (106)

δu_jовнеш /u_jо = δm_jо /m_jо = - ^NΣ_i=1 δx_ij /x_ij = - δr_jвнеш /r_j - ^NΣ_i=2 δτ_ji /τ_ij 

 - 2 ΔR_с /R_12внеш (107)

a_R = - d_Ru /dR_внеш = - d_Rδu /dR_внеш 2 u_jо ΔR_с d(1/R_12внеш) /dR =

= - 2 u_jо ΔR_с /R²_12внеш = - 2 u_jо ΔM_с r_j /R²_12внеш = C_aMR (M,R) ΔM_с /R²₁₂ (108)


То есть, на больших расстояниях энергетически выгодным становится и сближение равных по величине разноименных зарядов по тому же закону обратных квадратов.


+Δq₁ δu_jо(X)



+Δq₁

+q₁ +Δq₁ +Δq₁

-Δq₂

-Δq₂ -q₂ X

-Δq₂




-Δq₂

а)


δ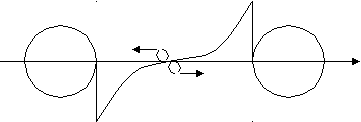u_jо(X)



+Δq₁

+q₁

-q₂ X

-Δq₂


б)


Рис. 4. Схема перемещения третьего малого заряда между двумя большими при отсутствии деформаций носителя-сферы: а - на больших расстояниях, б - на малых расстояниях. Стрелками показаны направления ускорений.


Для всех этих случаев формальные замены E₁ = C_Ea a_R, q₁ = C_Ea C_aMR ΔM_с, F₁₂ = q₂E₁ дают право переписать (102) и (108) в виде закона Кулона


F₂₁ = q₂E₁= q₂ q₁ /R² (109)

или одного уравнения Максвелла

div E = 4π (dM_с /d ^NQ) = 4π (110)


независимо от мерности частиц и упаковки. К сожалению, простые выражения (102)-(110) приблизительно верны только для случая двух зарядов с


|R| >> |R_c| >> |ΔR_c| (111)

q₁q₂ (112)


Третий заряд между этими двумя будет вести себя совсем иначе (Рис. 4)

Например, если от одного из двух образуемых равных противоположных зарядов q₁ ΔM₁ і q₂  ΔM₂ (q₁q₂) отщепить маленькую частицу q₃ Δq₁ и разместить на межцентровой линии О₁О₂ основных зарядов, то эта частица на средней части межцентровой линии будет перемещаться в сторону большего противоположного ей заряда, но в непосредственной близости от любого из зарядов будет ускоряться в обратном направлении из-за ослабления влияния другого заряда на тангенциальную составляющую потенциалов. Это вызвано возникшим непостоянством ΔR(R) и, соответственно, более сильным уменьшением δτ_ji(R), чем 1/R. Поэтому положение третьего малого заряда между двумя большими зарядами может иметь три особенных точки равновесия - одну точку неустойчивого равновесия ближе к одноименному заряду, вторую точку устойчивого равновесия почти симметричную первой ближе к противоположному за знаком заряду и третью точку устойчивого равновесия на поверхности одноименного заряда

Но может иметь и точку устойчивого равновесия, если его частицы закреплены на поверхности, поверхность будет достаточно жестка, а расстояния достаточно большие (Рис. 4а). На малых расстояниях более сильный рост потенциала за счет δτ_ji(R) перевесит противоположное изменение потенциала за счет δr_ji(R), и третий малый заряд будет иметь лишь одну устойчивую точку на поверхности одноименного большого заряда (Рис. 4б).

Если же избыточные частицы имеют возможность свободно двигаться по заряженным (ведущим) поверхностям, то в результате одинаковости они будут пытаться равномерно распределиться по этим поверхностям, потесняя другие частицы поверхности. В результате конечности (отличия от нуля) малой δr_jнар, пренебреженной в (100), все частицы заряженной сферы оказываются сжатыми на δτ_iс в тангенциальном направлении сравнительно с начальным состоянием x₀


τ_iс - τ₀ = δτ_iс << -δτ_ij (113)


В результате правил счета малых величин, связанных общей зависимостью


δτ_iс = C₁ δτ_ij = C₁τ_ij ΔR_с /R_с = C₂ ΔM_с /R_с (114)


Вследствие (92) сжатые частицы сферы будут иметь больший потенциал, чем частицы окружения

δu_jос = - u_jос ^NΣ_i=2 δτ_iс /τ_iс = u_jос (N-1) C₂ ΔM_с /R_сτ_iс= C_с q_c (115)


где коэффициент

C_с = C₃ /R_с (116)

можно назвать емкостью сферы.

Сжатие (113) меньше по величине, чем растяжение окружения δx_ij, но оно определяет неустойчивость сжатой сферы и потому играет решающую роль при ее перемещениях и неизотропных деформациях. Например, при прикосновении двух заряженных поверхностей подвижные частицы будут переходить из поверхности с большим потенциалом на поверхность с меньшим потенциалом, пока потенциалы частиц в точках прикосновения не уравняются. Этот же эффект обусловит перетекание подвижных частиц по любой замкнутой поверхности на линии между зарядами (поляризацию поверхности).

На линии между зарядами радиальная зависимость осевого сдвига (104) -(105) приводит к неизотропной деформации заряженной сферы. Поверхность сферического заряда q₃ +Δq₁ со стороны +q₁ окажется сплюснутой (сплощеной), а со стороны -q₁ выпуклой (заостренной) прогибом ΔX упаковки основными зарядами (Рис. 5). Сокращение сплющенной части сферы сопровождается увеличением, а удлинение выпуклой - уменьшением потенциалов частиц сферы и прилегающей упаковки. При наличии подвижных частиц это приводит к переходу некоторых из них из вогнутой к выпуклой части сферы и сохранению потенциалов частиц сферы. В свою очередь, это приводит к уменьшению разницы потенциалов между вогнутой частью сферы и прилегающей к ней частью упаковки и к увеличению разницы потенциалов между выпуклой частью сферы и