Докладов на ктф фф чну

Вид материала

Доклад

Подобный материал:

• Требования к оформлению докладов, 25.25kb.
• Оао "по "Уральский оптико-механический завод" г. Екатеринбурга заинтересован в молодых, 4.5kb.
• Ормы докладов на конференции, 68.07kb.
• Інформаційний бюлетень (липень-серпень 2011 р.). Вип. 16 Черкаси : Вид від. Чну ім., 533.23kb.
• Інформаційний бюлетень (травень-червень 2011 р.). Вип. 16 Черкаси: Вид від. Чну ім., 1337.24kb.
• Требования к оформлению докладов, 11.58kb.
• «Актуальные вопросы кардиологии», 58.59kb.
• Решение о публикации тезисов докладов принимает председатель секции. Тезисы докладов, 67.24kb.
• Правила оформления тезисов докладов Тезисы докладов предоставляются в электронном виде, 22.59kb.
• Требования к оформлению докладов, 57.52kb.

I потока включений через сечение конденсата-проводника может быть формально связан с приростом любого параметра деформации, например, разницы потенциалов dU

dI = СdU = dU /R (180)


что совпадает с известным законом Ома для токов, математически однотипным с законом Гука для деформаций сжатия-растяжения, законом Ньютона для ускорений и всеми другими подобными дифференциальными соотношениями, которые можно считать законами постольку, поскольку они больше являются отображением принятых и, потому, бесспорных правил счета, чем субъективных результатов наблюдений.

Продольный сдвиг окружения в направлении перемещения частиц упаковки приводит к появлению осесимметричного сдвига упаковки вокруг проводника с током в направлении потока частиц. Особенностью такой деформации упаковки является обратная пропорциональность осевого смещения X одинаковых частиц окружения упаковки от их расстояния R_оX от оси тока. Дифференциальная форма счета требует пропорциональности (и параллельности) приростов смещения d_iX частиц окружения и тока dI=j_cds_c


d_iX = C_IxdI /R_о (181)

R_о d_iX = C_Ixj_cds_c (182)

При малых I

X = C_IxI /R_о (183)

X R_о = C_Ixj_cs_c (184)

Допустимая замена переменних

X = C_IxH /2 (185)


при выборе условного направления HR_o і HX приводит к

H = 2[I /R_о] = [I2R_о] /R_о²

HR_о²= [IR_о] (186)


Для круглого контура радиусом R_о, площадь S і длина L


S = R_о²

L = R_о

HS = IL (187)

HL = 4 j_cs_c (188)

Из определения ротора

rot I dS = I dL

rot H ds_c = H dL

поэтому

H = rot I (189)

rot H = 4 j_c (190)


что совпадает с другими уравнениями Максвелла.


L_v=Vt

L_{ вак} L_вкл

L _вак L_вкл


X_{вкл,вак}


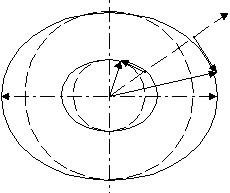
Рис. 10. Схема отклонения деформированного дефекта от направления скорости V


При деформации упаковки ее дефекты деформируются вместе с ней и принимают формы вытянутых или сплющенных эллипсоидов вращения в областях радиального сдвига или плоско сдвинутой сферы в области тангенциального сдвига. Во всех случаях они становятся неизотропными и имеют разные размеры осей симметрии и разную кривизну в разных направлениях, а потому и разную анизотропную подвижность. Причем дефект может двигаться прямолинейно (точнее, по спирали с прямой осью) только в случае, когда его оси параллельны или перпендикулярны к направлению движения (оси спирали движения). Если же направление движения не совпадает с осью оболочки, то ее частицы, которые находятся в лучших для перемещения условиях на концах осей оболочек (выпуклостях включений и вогнутостях вакансий) обусловят переупаковку дефекта в свою сторону и заставят уклониться его в сторону от траектории, которую бы имел недеформированный сферический дефект.

Величину тангенциального (бокового) отклонения L_ дефекта за единицу времени в первом приближении можно представить пропорциональными скорости V, деформации X (эксцентриситету ₁₂), знаку заряда e, размерному коэффициенту k_a и некоторой функции f, которая обнуляет ускорение при совпадении направления скорости с направлением осей деформированного дефекта, например, sin2((V;X))=2sin((V;X))cos ((V;X))


dL_ = dL_ = k_a e f((V;X)) dV dX = k_a e sin 2((V;X)) dV dX (191)


При стабильных значениях V и X


L_ = k_a e f((V;X)) VX = k_a e sin 2((V;X)) VX (192)


Численно длина пути L_ за единицу времени при постоянном ускорении A_ равна половине ускорения

 L_ = A_ /2 (193)

поэтому

A_ = 2 L_ = 2k_a e sin 2((V;X)) VX (194)


Реальная функция f((V;X) может иметь другой вид, но это несущественно повлияет на результат.

Тангенциальное (боковое) отклонение (“сбочивание”) (191) предопределяет возможность ускорения дефектов не в направлении градиента плотности упаковки, которая приводит, например, к прецессии их эллиптических орбит в плоскости (V;X). Траектория дефекта искривляется до тех пор, пока одна из осей дефекта не станет параллельной, а другие – перпендикулярными направлению движения. Если же деформация вдоль траектории сама имеет ненулевую кривизну, то оси дефекта возвращаются нею, и траектория не может стать прямой. Потому при постоянной кривизне деформации, характерной для областей деформаций радиального сдвига и осевого скручивания, траектория может стать круговой. При непостоянной кривизне вместо того, чтобы стать эллиптическими, как того требуют упрощенные правила движения в потенциальных полях, траектории дефектов и их скоплений в областях деформаций радиального сдвига начинают прецессировать и превращаются в розетки, как орбита Меркурия вокруг Солнца.

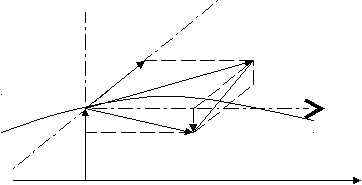
Если деформация дефекта обусловлена осе-цилиндрическим сдвигом упаковки током I, то X(I;R) всегда лежит в плоскости (I;R). При этом X никогда не параллельный ни I, ни R, но при малых I угол между I и X тоже будет малым и пропорциональным I. В обозначениях (182)-(190) направления I, R и H взаимно перпендикулярны и удобны для ориентации прямоугольной системы координат (Рис. 11).

У мимобежной траектории L всегда есть точки, в которых скорость V лежит в плоскости HI^/ или близкая к ней. Радиальная составляющая R отклонения при постоянных V и X зависит от угла (V;X), который при малых деформациях X близок к (V;I^/) в окрестностях таких точек. Эта составляющая имеет максимум при (V;I^/)= 0 и равна нулю при (V;I^/) = /2, потому безразмерную функцию f можно приблизить, например, косинусом этого угла, ровным синусу дополняющего угла (V;H). При


X = C_IxH /2 (195)

k_a e = e^*/C_Ixm^* (196)

sin ((V;H)) VH = [VH] (197)

 R = k_a e f((V;X)) VX = k_a e cos ((V;I^/)) V C_IxH /2 =

= e^*sin ((V;H)) C_IxVH /2C_Ixm^* = e^*[VH] /2m^* (198)

Из (167)

m^*A_ = 2m^* L_ = e^*[VH] (199)





H V


L I^/||I

R R

X

I


Рис. 11. Схема отклонения дефектов деформацией осевого сдвига


что по виду (форме) совпадает с формулой Лоренца для мнимой “силы”, действующей на подвижные “заряженные” частицы в “магнитных” полях. Отличие по содержанию обусловлено отличием принятых представлений. В частности, (199) требует пропорциональности ускорения косинусу угла между вектором скорости и осью деформированного дефекта. Любое отклонение реальной зависимости ускорения от этого угла автоматически требует коррекции (199) для компенсации ошибок. При фиксированных e^*, v, H и a_ весь груз компенсации ложится на параметр m*, делая его зависимым от всех других параметров, в первую очередь, от “наблюдаемых” параметров v и H, и делая не всегда удобным “взвешивание” и сравнение частиц по кривизне траекторий. Неоднородность деформаций сдвига-кручения практически не изменяет принятых представлений.

Несколько отличается перемещение дефектов в неоднородных деформациях сжатия-растяжения через изменение не только направлений, но и величин скоростей дефектов.

В случае неоднородного плоского (одномерного) сжатия-растяжения упаковки размер r частиц упаковки становится переменным, что требует изменения скорости dv (ускорения da) подвижной частицы пропорционально изменению размеров dr частиц упаковки в направлении изменения радиуса R и в первом приближении приводит к


da = k dr = k (dr /dR) dR (200)


Допустимая при малых значениях формальная замена переменных на пропорциональные им величины

da = a (201)

(dr /dR) dR = dE = E (202)

k = e^*/m^* (203)

приводит к

m^*a = e^*E (204)


что по виду похоже на выражение для мнимой “силы”, действующей на “заряды” в “электрических” полях.

Величина каждого прыжка дефекта равна его радиусу R_d = rM_d, а частота f_d прыжков равна частоте инициирующих переходов оболочковых частиц, пропорциональной величине деформации

f_d = v_r /r = V_d /R_d =k_f (dr /dR) (205)

V_d = R_d f_d = rM_d k_f (dr /dR) = k_Vf (dr /dR) M_d = M_dv_r (206)

A_d = M_d a_r= k_Af (dr /dR) M_d (207)

Из (204)

m^*A_d = e^*E = m^*k_Af (dr /dR) M_d = m^*a_r M_d (208)

m^*= e^* /k_Af M_d (209)


Нелинейная зависимость длительности прыжка от средней скорости дефекта


v_r = r /(t₁ + t₂) (210)


тоже приводит к уменьшению ускорения-подвижности дефекта при увеличении его скорости, которая требует внимательности при сравнении частиц по кривизне траекторий.

Учет проявленной мерности n деформации и N упаковки приводит к представлению об ускорении дефекта, как о векторной сумме составляющих одномерных ускорений. В свою очередь, это позволяет представить направление суммарного ускорения a_r частиц и A_d дефектов (с точностью до знака) как направление градиента многомерной плотности m упаковки и потенциала u ее частиц


dm /m = du /u = - n dr /r (211)

A_d = M_d a_r= k_Am (n dr /dR) M_d = - k_Am (dm /dR) M_d (212)


Боковое ускорение (отклонение) подвижных дефектов деформациями сдвига упаковки приводит к соответствующему ускорению проводника с током, заключенного в зону такой деформации упаковки первым током


d_RA₂ = C₂ dI₂ dX = C₂ dI₂ C₁dI₁ /R_о (213)

A₂= C₃ I₁I₂ /R_о= C₄ I₁I₂ cos(I₁I₂) /R_о (214)

A₁= C₃ I₂I₁ /R_о= C₄ I₂I₁ cos(I₂I₁) /R_о = - A₂ (215)


В принятых обозначениях C₄ достаточно сложно зависит от угла между осями токов (точнее, угла между проекциями осей на плоскость, перпендикулярную кратчайшему расстоянию между ними), потому общепринятое простое математическое представление о скалярном произведении векторов не исчерпывает зависимость ускорения от угла между токами, однако делает ее достаточно простой и наглядной. Тем более, что нормальное желание максимализации возводит техническое использование по большей части к крайним случаям параллельных или перпендикулярных токов. Симметрия выражений отвечает представлению о равенстве и противоположности ускорений обоих проводников в полном соответствии с представлениями о симметрии процессов в упаковке и постулатами Ньютона.

Элементы одного тока всегда параллельны, потому всегда пытаются сближаться и сойтись на оси тока, вызывая эффект “шнурования”. Потому густота постоянного тока на оси проводника всегда выше, чем на поверхности. Разница плотностей пропорциональна величине тока.

Направления тока в диаметрально противоположных частях замкнутого проводника (витка) противоположны, потому виток растягивается током и пытается принять кольцевую форму. Два витка проворачиваются и притягиваются или отталкиваются в зависимости от направления токов. Каждый виток создает характерную деформацию сдвига-скручивания окружения.

При быстром изменении величины тока в одном из двух параллельных проводников смещаемая током окружающая упаковка смещает с собой и малоподвижные относительно нее вакансии второго проводника на X. Более слабо связаны с упаковкой более подвижные относительно нее включения отстают и накапливаются в его задней части, поднимая ее потенциал на U сравнительно с передней частью. Возникший вдоль проводника градиент потенциала dU/dL предопределяет их ускорение A_вкл вперед, пока оно не станет равно ускорению A_уп упаковки и не прекратит рост отставания и потенциала отставших включений, которые начинают двигаться с постоянным ускорением вместе с проводником и упаковкой. С использованием обозначений (182)-(190) градиент потенциала отставших частиц можно считать пропорциональным ускорению проводника с обратным знаком и, соответственно, смещению L₁=X₁=C_IxH₁/2 и изменению I₁ и H₁ за единицу времени


dU /dL = E = - A_вкл = - 2L₁ = - 2C_IxI₁ /R_о (216)

HdS = IdL (217)

dU = E dL = - 2C_IxI₁ dL /R_о = - 2C_IxH₁ dS /R_о=

= - 2C_Ix dS dH/dt R_о = rot E dS (218)

При обозначении

B = 2C_IxH/R_о (219)

rot E = - dB/dt (220)


что совпадает еще с одним уравнением Максвелла. В результате сохранения частиц упаковки любые их потоки через замкнутые поверхности уровни нулю и


div I = 0 (221)


поэтому для всех пропорциональных І функций, включая L, H и B


div I = div L = div H = div B = ...= 0 (222)


Вместе (110), (190), (220) и (222) составляют известную систему уравнений Максвелла


div E = 4 (223)

div H = 0 (224)

rot E = - dB/dt (225)

rot H = 4j (226)


Процесс появления потенциала можно назвать индукцией. При замыкании проводящей перемычкой концов второго проводника часть отставших дефектов может стекать через нее, преодолевая ее сопротивление. Измерение тока через известное сопротивление дает возможность измерять индуктируемую разницу потенциалов. Из-за малых размеров частиц смещение проводника на размер одного включения позволяет перейти в обратном направлении большому количеству частиц, потому при обычных условиях насыщения индуктируемого тока не может наблюдаться. Вследствие отставания внутренних слоев проводника от ускоренных поверхностных с наибольшей амплитудой колеблются и, соответственно, больше всего разогреваются поверхностные слои, что можно считать поверхностным эффектом высокочастотной индукции.

Пропорциональность сдвига упаковки количеству частиц, которые двигаются в одном направлении, приводит к зависимости этого сдвига от произведения количества проводников на величину тока в них. В частичном случае катушки-соленоида - от количества “ампер-витков”. И наоборот, величина индуктируемой разницы потенциалов является пропорциональной длине проводника и количеству “ампер-витков” w


dU = C₁ dI dL dw (227)


Можно было бы привести еще много примеров свойств упаковки и ее частей, для которых есть аналоги в других разделах физики, описываемые очень похожими математическими выражениями. Но для этого нужно намного больше времени, чем можно позволить для короткого сообщения. Но это и нецелесообразно, потому что много из них опубликованы в Интернете на сайте SciTecLibrary.com и записаны в компьютере на кафедре теорфизики, где с ними можно легко ознакомиться или скопировать и распечатать для удобства. А все свойства невозможно описать в принципе.

Как видно из изложенного, свойства плотной упаковки упругих частиц и ее частей очень подобны свойствам других известных физических объектов - вакуума-эфира, гравитационных, электромагнитных и ядерных полей, элементарных частиц вещества и их скоплений. Настолько подобные, что не исключается возможность тождественности описываемых объектов. Сугубо математическое происхождение основных выражений, которые описывают эти свойства, позволяет считать законным (несомненным) их приложение к любым физическим объектам, включая как рассматриваемую плотную упаковку упругих частиц и любые ее части и частицы, так и другие известные объекты с похожими свойствами. Однако модель плотной упаковки упругих частиц имеет существенное преимущество перед всеми другими моделями известных объектов с похожими свойствами в виде внутренней логической цельности (единства), которая позволяет непрерывным образом предусматривать поведение всех частей упаковки, исходя только из очень ограниченного количества свойств ее частиц. Такое преимущество делает заманчивым использование модели плотной упаковки упругих частиц в качестве общей теоретической модели всех других известных физических объектов, общее моделирование которых до сих пор вызывало трудности. Следует заметить также, что сравнительно с множеством других возможных общих теоретических моделей, существование которых допускает известная теорема Геделя, такая новая модель согласно принципу Оккама имеет еще одно преимущество, потому что является самой простой из них. Эти преимущества вместе делают модель плотной упаковки упругих частиц перспективной и в качестве основы общей теории строения, как минимум, известной части Вселенной.

Можно, по-видимому, только дополнительно вспомнить некоторые интересные, по моему мнению, предвидения такой новой теории. Например, возможность существования низкотемпературных невзрывных спокойных термоядерных реакций с