Лекомцева екатерина николаевна

Вид материала

Содержание

Уроки математики с использованием ИКТ
Цель урока
Ход урока
Помните, что увидеть необычное в простом – это признак мудрости!
Форма урока: урок с использованием компьютера
Ход урока
2. Актуализация знаний
3. Закрепление изученного материала при решении задач.
Тема урока: « Распределение простых чисел. Графическая обработка данных »
Ход урока
Ответ: Простые числа – это числа, которые имеют только два делителя, а составные – более двух делителей)
Учитель информатики
Мастер диаграмм
Таблица распределения простых чисел по диапазонам
V. Поведение итогов практической работы и изучение нового материала
Интегрированный урок геометрии и информатики в 7 классе ( 2 ч )
Тип урока: урок изучения нового материала
Учитель математики
Учитель информатики
Учитель математики
...
Полное содержание

Подобный материал:

ЛЕКОМЦЕВА ЕКАТЕРИНА НИКОЛАЕВНА,

учитель математики

МОУ средней общеобразовательной школы № 289

с углубленным изучением отдельных предметов г. Заозерска

Образование: высшее, Калининградский государственный университет, 1980 г., преподаватель математики.

Стаж педагогической работы: 23 года.

Квалификационная категория: высшая категория по должности «учитель».

Награды, звания: Почетная грамота комитета по образованию Мурманской области (2004 г.), Почетная грамота Министерства образования и науки Российской Федерации (2005 г.).

Почтовый адрес места работы, контактный телефон:

184310 г. Заозерск Мурманской области, ул. Мира, д. 5А, раб. тел. 8-815-56-3-25-95.

Адрес электронной почты: lek-ekaterina@yandex.ru

Уроки математики с использованием ИКТ

Математика является одной из ведущих школьных дисциплин и это не случайно. Во все времена общество двигалось вперед благодаря людям, которые умели независимо мыслить, людям которые умели видеть задачи, требующие нестандартных решений в различных областях жизни. Перед учителем математики стоит задача организации процесса обучения таким образом, чтобы ученик, приобретая навыки самостоятельной деятельности, объективно оценивая знания и умения, ставил перед собой задачи и находил их решения.

Для развития самостоятельности в получении знаний можно и должно использовать ИКТ. Уроки с использованием ИКТ делятся на:

Урок с использованием компьютера (демонстрация CD-дисков или презентаций к уроку)
Медиаурок или интерактивный (использование электронных энциклопедий и электронных учебных пособий)
Интегрированный

Мною были проведены уроки:

- с использованием компьютера по темам: «Теорема Пифагора и ее применение» (8кл.), «Площади многоугольников» (8кл.), «Применение теорем синусов и косинусов при решении практических задач» (9кл.), «Правильные и полуправильные многогранники» (10кл.), «Осевая и центральная симметрия» (11кл.), «Увидеть необычное в простом – признак мудрости» и др.;

- медиауроки по темам: «Преобразование графиков функций» (9,11кл.), «Построение правильных многоугольников» (9кл.), «Углы в окружности» (8кл.) и др.

- интегрированные уроки математики и информатики по темам: «Прогрессии» (9кл.), «Решение прямоугольных треугольников по двум катетам в среде электронных таблиц с использованием стандартных функций в формулах» (8кл.), «Распределение простых чисел. Графическая обработка данных» (8кл.), «Деление отрезка пополам» (7кл.)

Для проведения уроков использую CD-ROM диски: «Открытая математика 2.5 Планиметрия. Стереометрия. Функции и графики» (Продукт ООО «Физиков»), «Виртуальная школа Кирилла и Мефодия. Уроки алгебры 7- 8,9 класс. Уроки геометрии 7, 8, 9, 10 класс», «Интерактивная математика. Электронное учебное пособие, 5-9 классы» (Продукт издательства «Дрофа»). Для проведения учебных исследований при изучении геометрии и алгебры и выдвижения гипотез и их проверки использую виртуальную математическую лабораторию «Живая математика» (4-я версия «Живой геометрии». Русская версия ИНТ).

Урок геометрии в 9 классе по теме: «Длина окружности. Число π»

Конкурсный урок: « Увидеть необычное в простом – признак мудрости».(30 мин)

Тип урока: урок изучения нового материала

Форма урока: урок с использованием компьютера

Цель урока: Показать учащимся, как простая окружность открывает путь в мир познания

законов математики и физики.

Оборудование: мультимедийный проектор, экран, компьютер, мультимедийная презентация, раздаточный материал для измерений, калькуляторы.

Ход урока:

на экране: "…Задача состоит не в том, чтобы видеть то, что никто не видел; а в том, чтобы думать так, как никто не думал о том, что все видят" - Эрвин Шредингер. (слайд 1)
на экране: окружности (слайд 2)

Учитель: Что такое окружность?
Дети: отвечают
Учитель: Это такое простое понятие и так часто встречается в нашей жизни, что мы даже не задумываемся о его определении. Напомните, где нам встречаются окружности.

на экране: картинки предметов (слайд 3)
- Учитель: Вам уже давно известно, что все действительные числа располагаются на координатной прямой. ( Взять веревку, растянуть с помощью учеников, изобразить на ней числа)
- Учитель: А как вы думаете, ребята, можно ли все числа расположить на окружности?
- Отвечают.
- Учитель: Давайте попробуем это сделать. (Учитель накручивает веревку на макет окружности. Ставит на ней точку жирным маркером. Раскручивает веревку)
- Учитель: Что вы заметили в расположении точек на прямой? Какие особенности?
- Точки располагаются через одинаковые промежутки.
- Учитель: Значит одна и та же точка окружности изображает различные числа. А чему равно расстояние между этими точками?
- Длине окружности.
- Учитель: Вы уже умеете находить длину окружности. Как ее вычислить?
- Отвечают.
на экране: формулы длины окружности (слайд 4)

Учитель: Чему равна длина окружности, радиус которой равен 1?
2.
Учитель: А что такое ? Давайте найдем значение этого интересного числа и сделаем это необычным способом.
Учитель: перед Вами инструкция по выполнению практической работы:

на экране и на партах у учащихся инструкция по выполнению практической

работы (слайд 5):

Измерь с помощью нитки и линейки длину предложенной окружности С.
Измерь с помощью линейки диаметр окружности d.
Вычисли число  по формуле 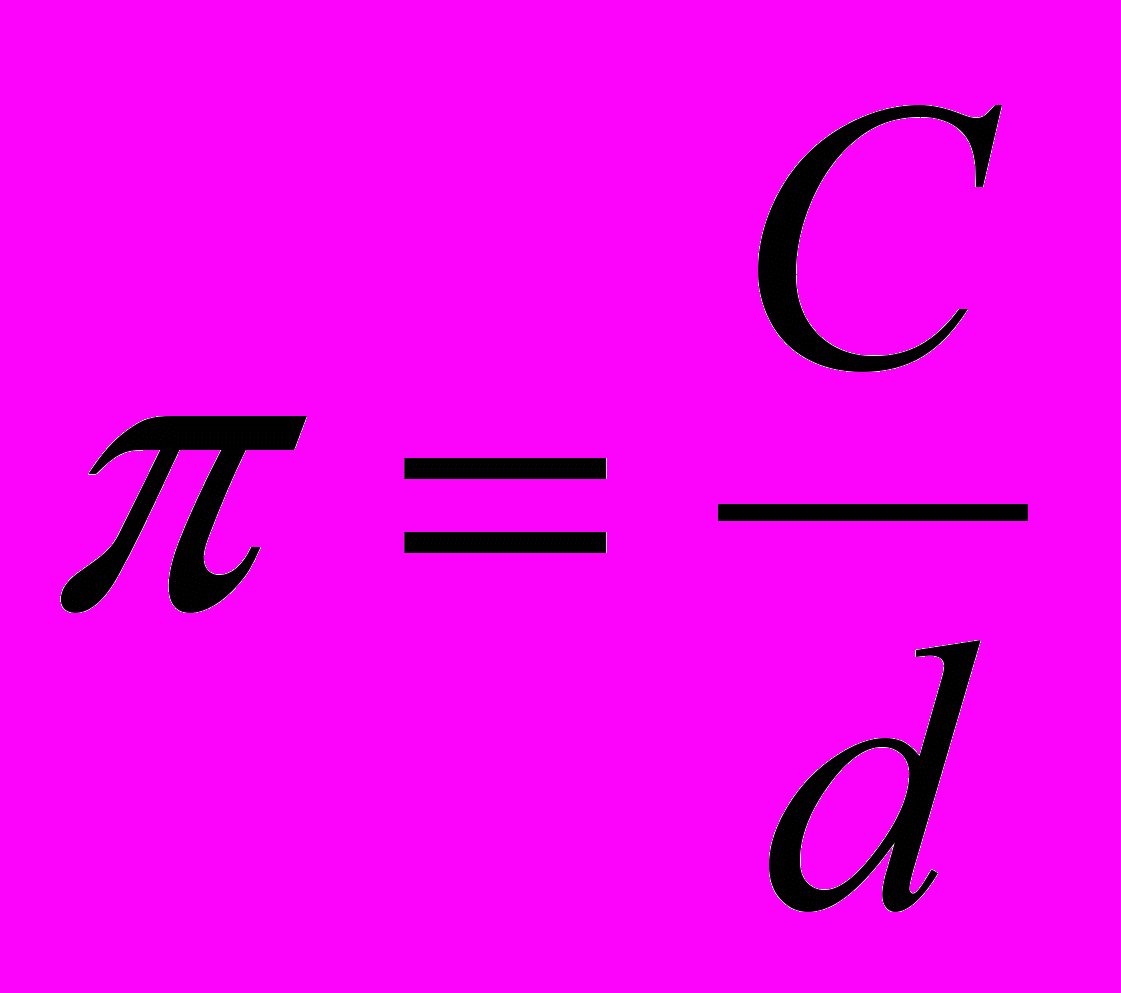с помощью калькулятора с точностью до сотых.

Учитель: сообщите, пожалуйста, полученные результаты. ( Записывает на доску результаты опытов)
Учитель: Найдите среднее арифметическое этих чисел с точностью до сотых, используя калькулятор.
Полученный результат выписать на доску.
Учитель: А теперь сравним свои результаты с известным значением числа «пи»

на экране: 3, 1415926….. (слайд 6)
на экране: картинка и сообщение об истории числа (слайд 7)

"Письменная история числа

начинается с египетского папируса, датируемого примерно 2000 годом до нашей эры, но оно было известно еще древним людям. Тогда оно ещё не обозначалось одной из букв греческого алфавита и его роль играло число 3.

"Обозначение числа

происходит от греческого слова

("окружность"). Впервые это обозначение использовал в 1706 году английский математик У.Джонс.

Учитель: А как же запомнить число ? Попробуйте с помощью стихотворения (слайд 8)

Стихи отпечатаны детям на партах.

Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь,
Чтобы нам не ошибаться,
Чтоб окружность, верно, счесть,
Надо только постараться
И запомнить все как есть
Три - четырнадцать - пятнадцать - девяносто два и шесть!

Учитель: Кстати, число  имеет свой день рождения. 14 марта его отмечают все фанаты числа . Встретить это число можно и в очень необычных местах:

8. на экране: (слайд 9)

Христиан Крюзер, давний любитель числа пи не только взял это число с собой в полет, но и заставил его (наверняка не спросив) совершить прыжок вместе с группой парашютистов.

9. (слайд 10)

Он же установил памятный знак пи на одной из высочайших вершин мира - пике Ленина.

10. (Слайд 11)

Другой энтузиаст Вернер Лехманн выложил на земле мозаику, цвета плиток в которой соответствуют цифрам числа пи, и гордо на ней восседает. Вот уж кто прочувствовал цифры пи буквально своими руками.

11. Слайд 12

Сама природа постоянно напоминает нам о числе :

Учитель:

Пи, несомненно, одна из наиболее универсальных и фундаментальных констант, известных Человечеству. В силу своей универсальности Пи используется в вычислениях для микро- и макрокосмоса и входит в формулы, описывающие движение комет, астероидов, космических кораблей и другие физические и химические процессы.

Учитель: Я уверена, что после сегодняшнего урока вы станете хоть немного мудрее и полюбите это удивительное простое, и в то же время необычное число . Сегодня я предлагаю вам вступить в члены клуба «Почитателей числа ». (раздать всем карточки членов клуба, ручки «Пилот»)

Помните, что увидеть необычное в простом – это признак мудрости!

Всем спасибо!

Урок геометрии в 8 классе (1 ч)

Тема: «Площади многоугольников»

Тип урока: урок повторения и систематизации знаний

Форма урока: урок с использованием компьютера

Цели:

образовательные: - повторить и закрепить знания учащихся по теме: «Площади многоугольников»

воспитательные: - формировать умения аккуратно и грамотно выполнять математические записи;

- воспитывать самостоятельность и творчество;

развивающие: - развивать мыслительную деятельность учащихся на уроке;

- развивать интуицию и наблюдательность;

- способствовать развитию умения делать выводы и обобщения;

- формировать у учащихся навыки исследовательской деятельности при решении геометрических задач

Оборудование: компьютер, мультимедийная презентация, мультимедийный проектор,

большой экран

Ход урока

I. Организация начала урока

- Здравствуйте, ребята! Пожелаем, друг другу удачи на уроке и вдохновения т.к. как говорил А.С.Пушкин: «Вдохновение нужно в геометрии не меньше, чем в поэзии». Садитесь.

- Площади каких фигур мы научились находить на прошлых уроках?

(Ответ: квадрата, прямоугольника, параллелограмма, треугольника и трапеции)

Какой класс образуют эти фигуры?

( класс многоугольников)

Какова же тема урока?

(Площади многоугольников)

Запишите в тетрадях дату и тему урока.

Тема записана на экране (Слайд 2).

- Сегодня у нас урок повторения и обобщения знаний по данной теме.

Для успешной работы на уроке повторим известные формулы, которые мы сегодня будем использовать.

2. Актуализация знаний

Все учащиеся работают вместе, проговаривая алгоритм нахождения площадей многоугольников, и записывают формулы площадей на доске и в тетрадях.

- Найдите площади фигур, изображенных на чертежах:

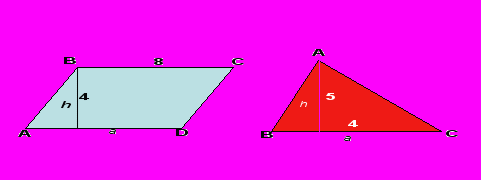
Решение:

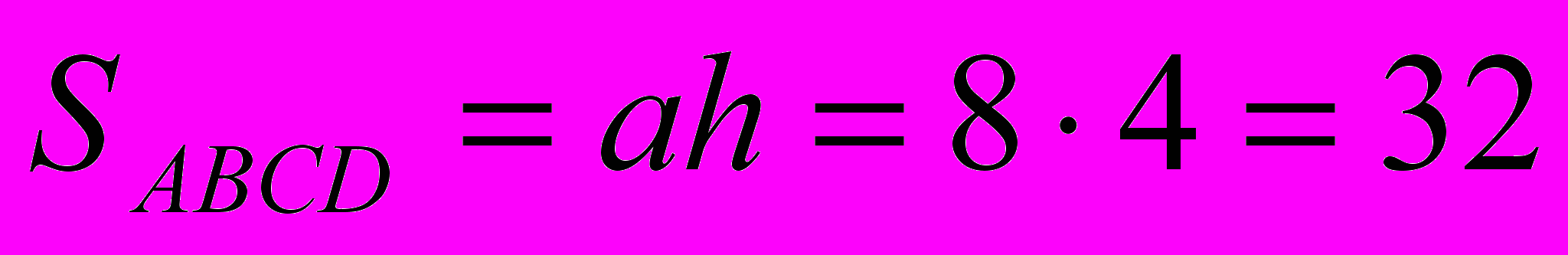
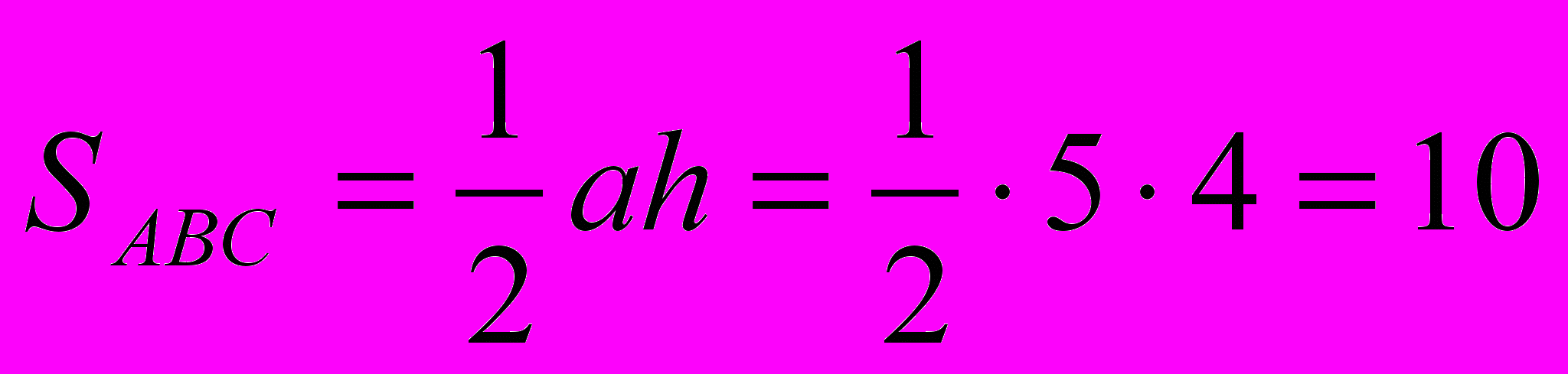
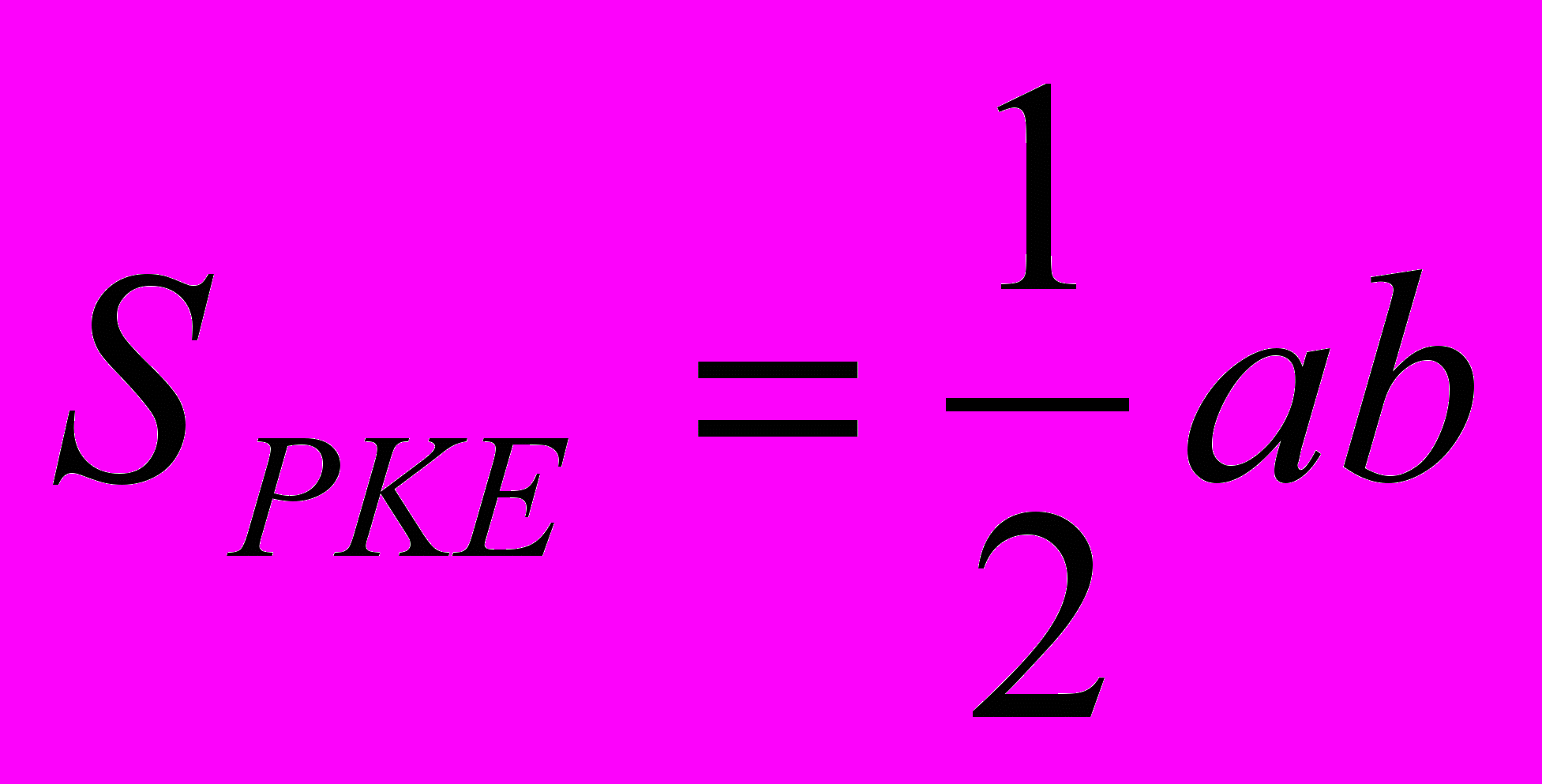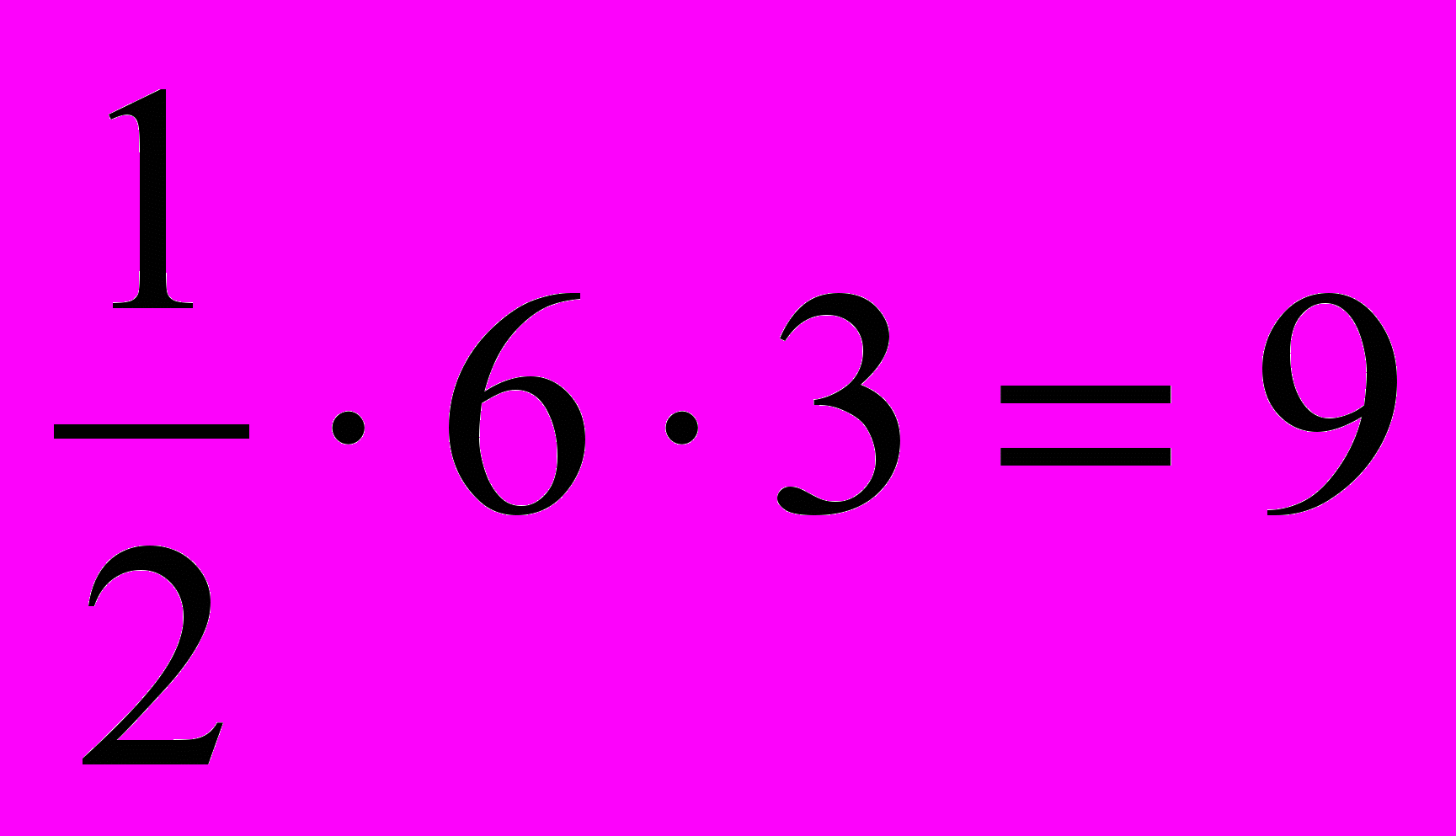
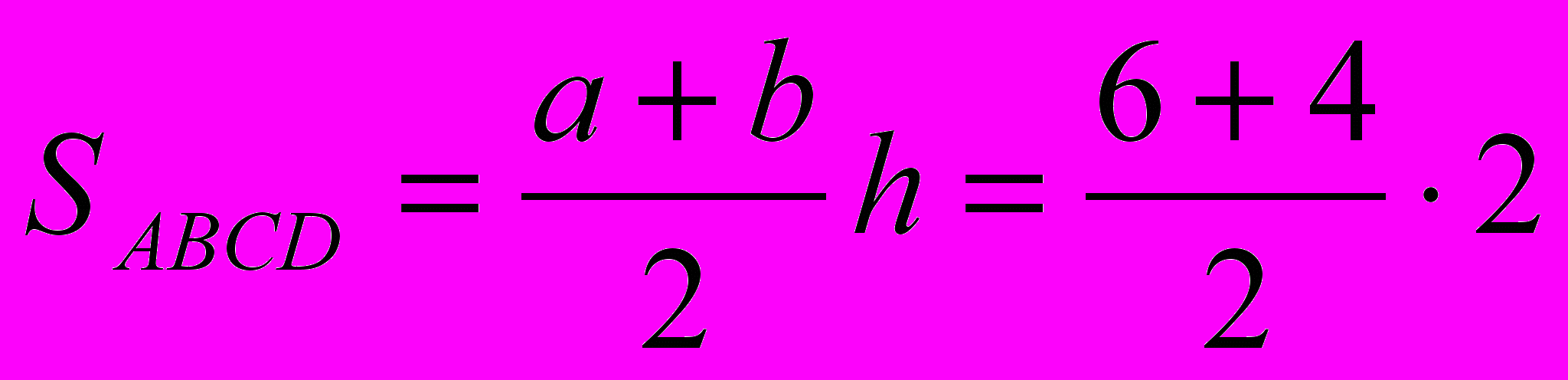= 10

- Площади каких фигур получились равные?

(Ответ: Площади треугольника АВС и трапеции ABCD равны.)

- Как называются фигуры, имеющие одинаковые площади?

(Ответ: равновеликими)

Какую величину можно вычислить по формуле ?

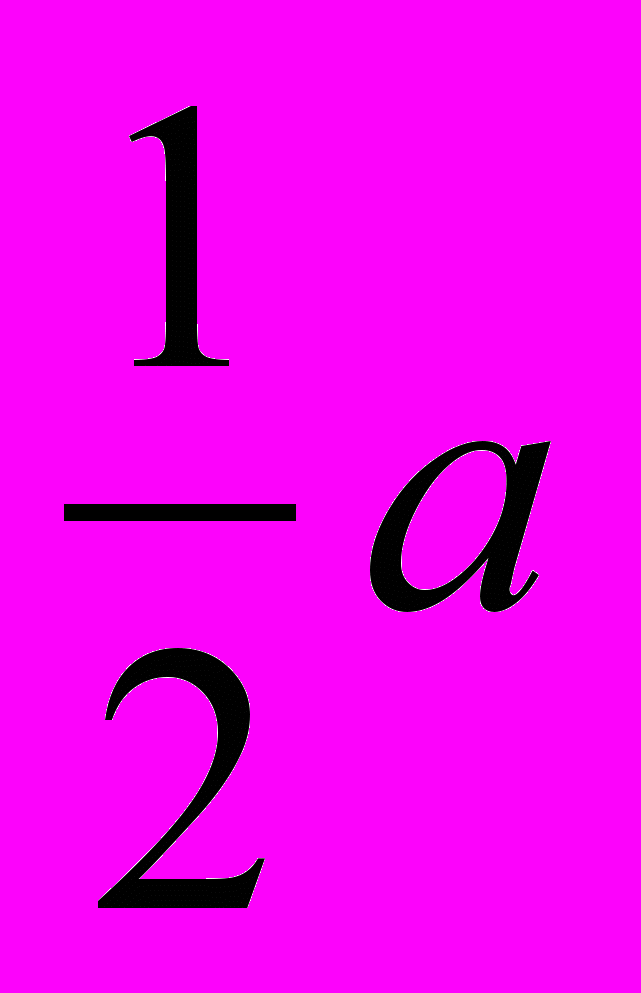(Ответ: среднюю линию треугольника)

- Что называется средней линией треугольника?

(Ответ: Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.)

Как найти площадь треугольника, зная среднюю линию и высоту, перпендикулярную этой средней линии?

(Ответ: Площадь треугольника равна произведению средней линии на высоту.)

Какую величину можно вычислить по формуле ?

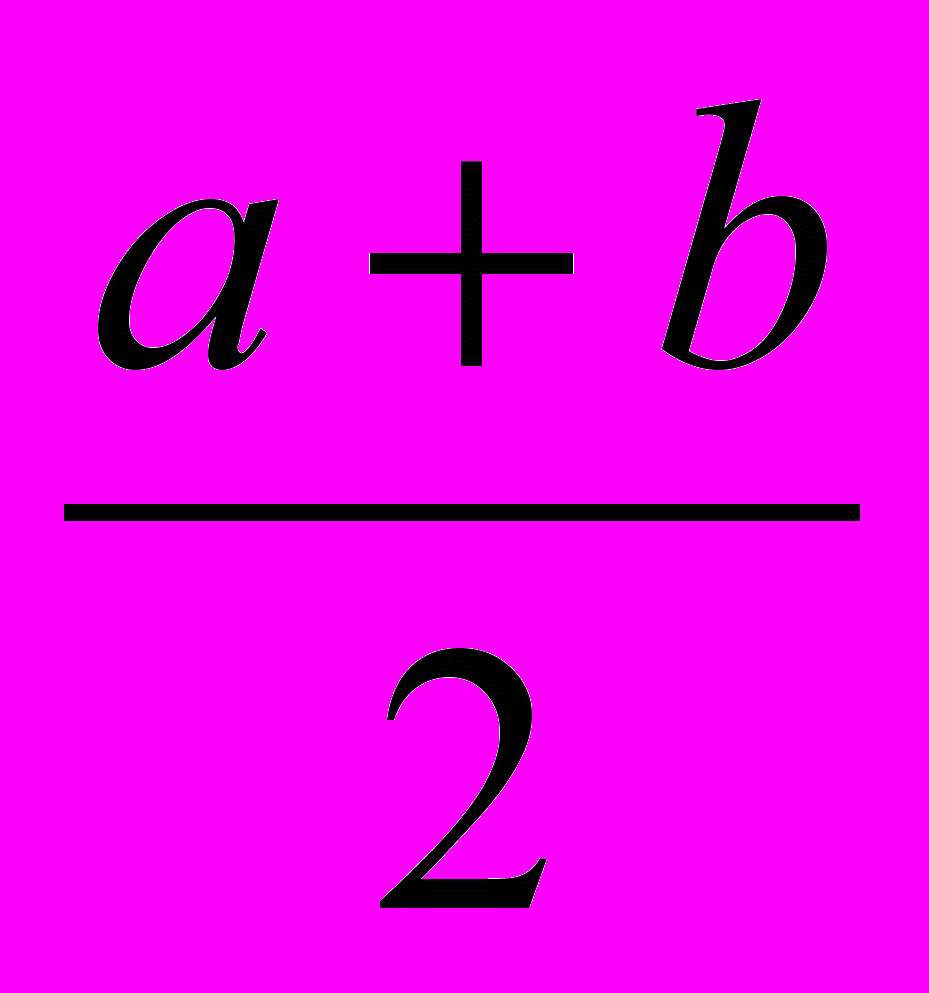(Ответ: среднюю линию трапеции)

- Что называется средней линией трапеции?

(Ответ: Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.)

Как найти площадь трапеции, зная среднюю линию и высоту?

(Ответ: Площадь трапеции равна произведению средней линии и высоты.)

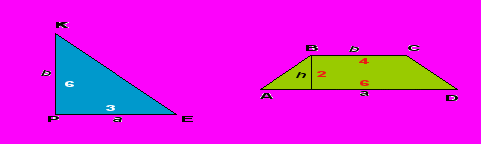
В

ычислите длины средних линий по готовым чертежам

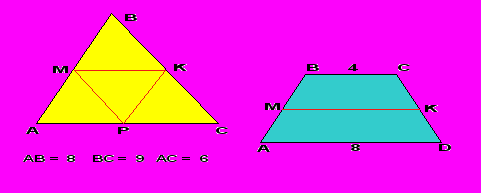
(Ответ: МК = АС : 2 = 5 МК = (4 + 8 ) : 2 = 6 )

МР = ВС : 2 = 4,5

КР = АВ : 2 = 4

3. Закрепление изученного материала при решении задач.

- Метод площадей используется при решении многих геометрических задач.

Р

ассмотрим параллелограмм ABCD

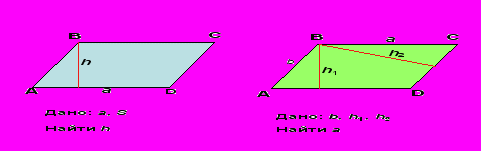
(Решение: h = S : а S = bh, a = )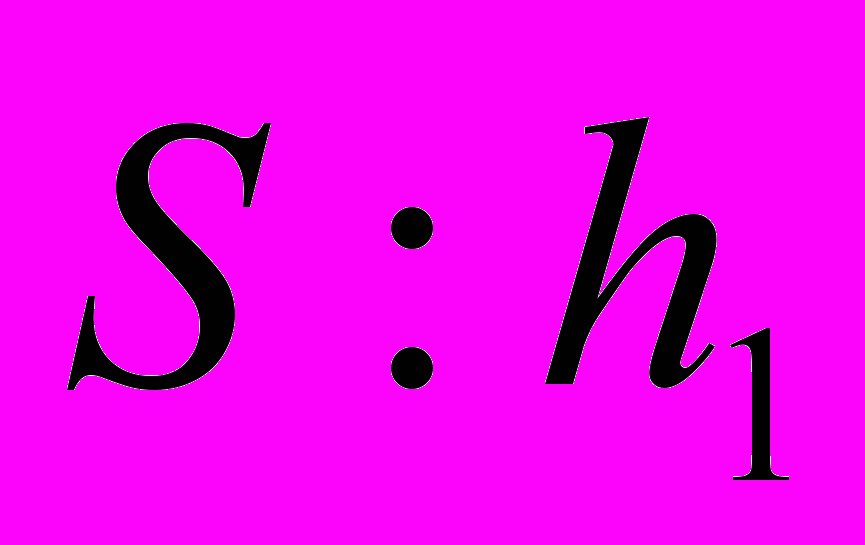

Р

ассмотрим треугольник АВС.

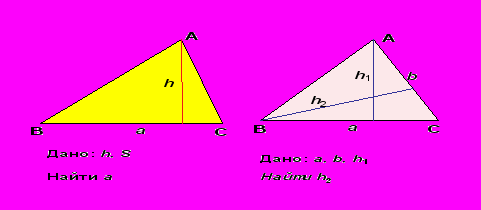
(Решение:

)

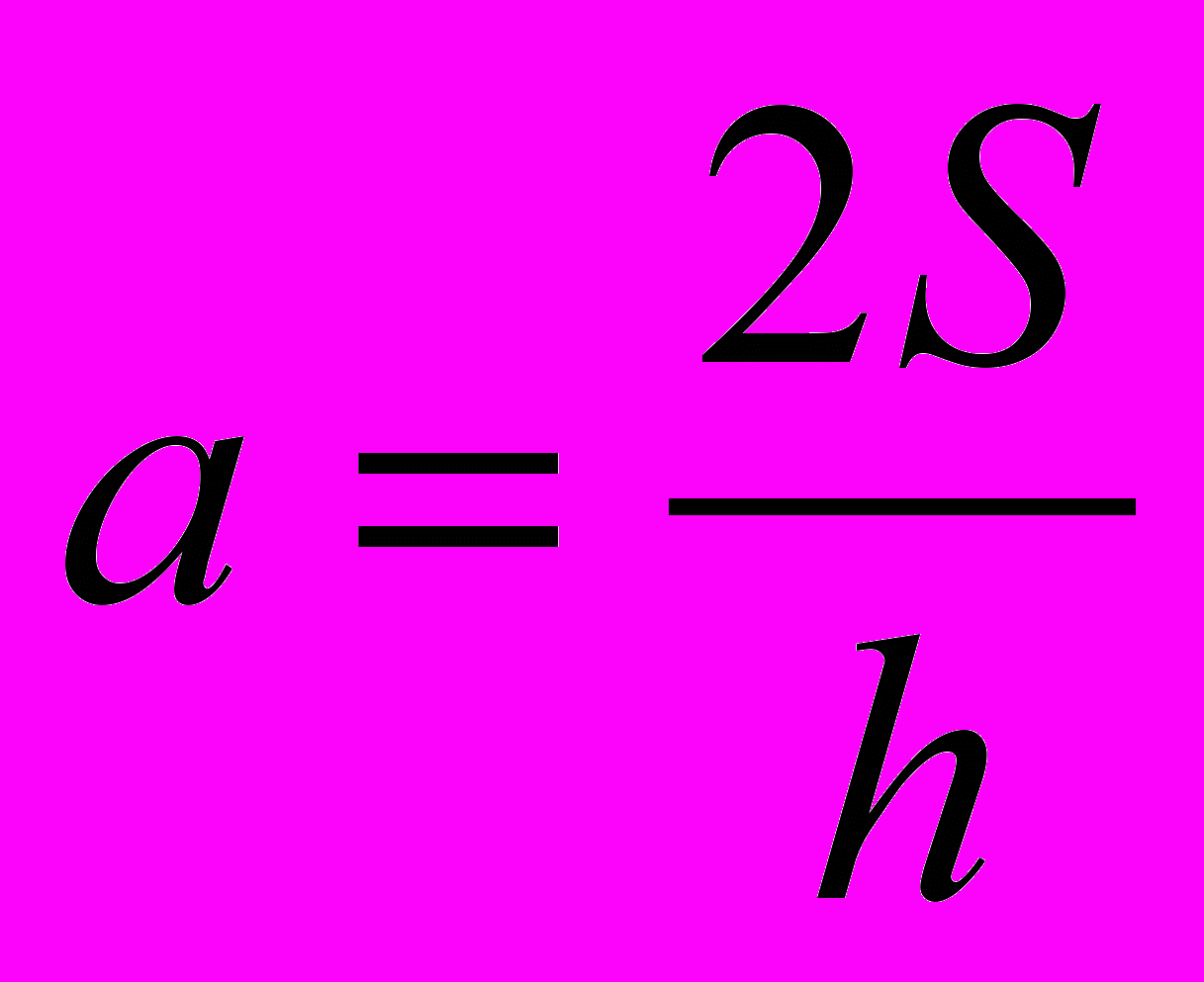
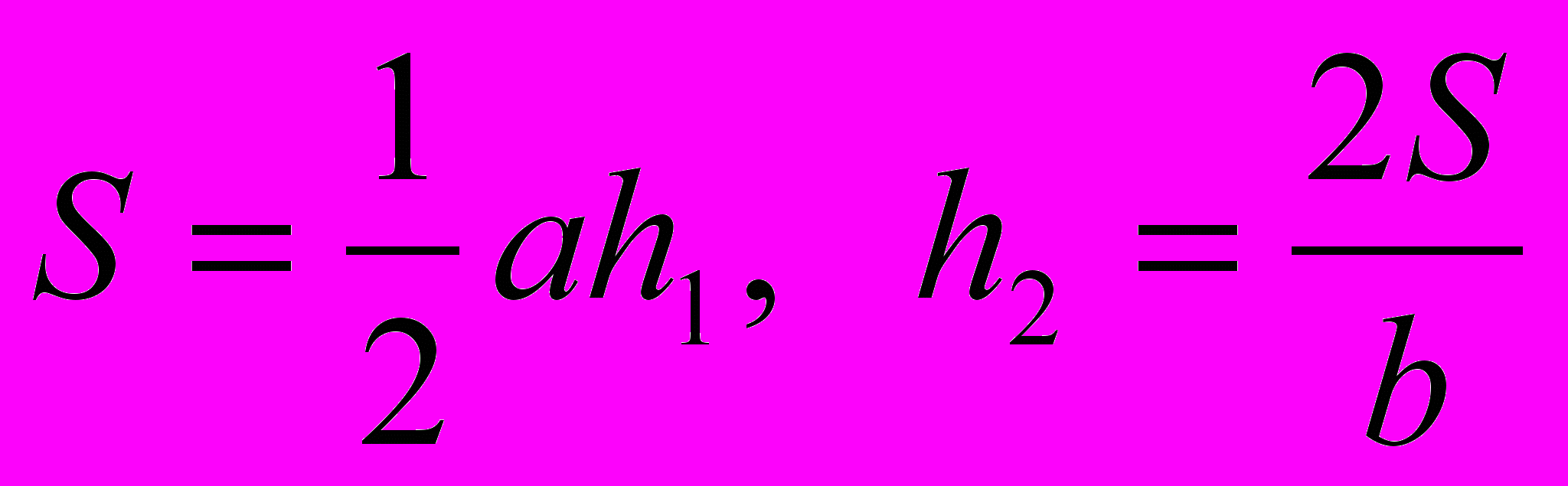Рассмотрим трапецию АВСD.

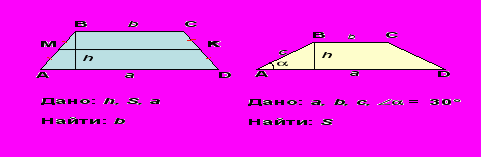
(Решение: МК = S : h, b = 2MK – a h = )

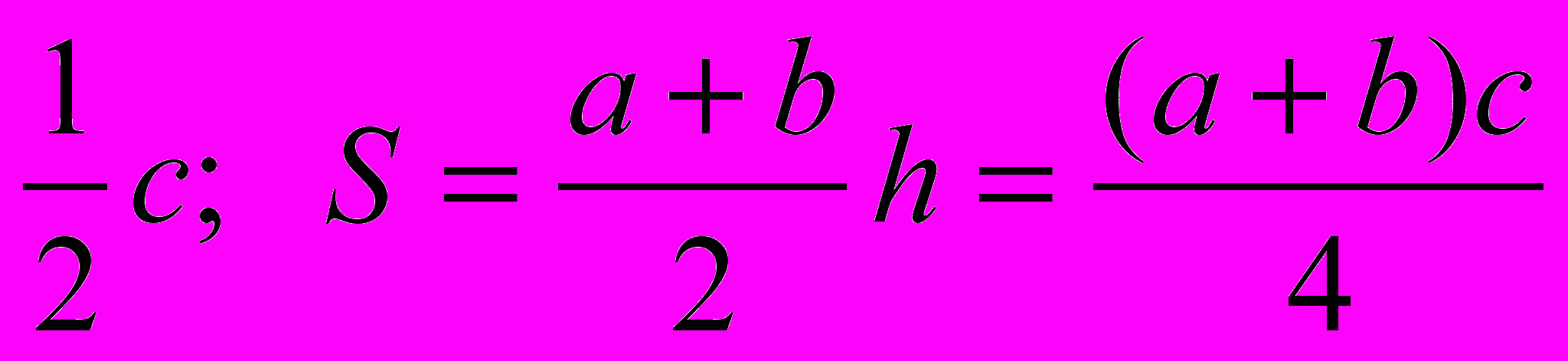Получим еще одну формулу площади трапеции.

Д

окажите, что площадь трапеции равна произведению боковой стороны на перпендикуляр, опущенный на нее из середины второй боковой стороны.

Решение:

B

C

E
Проведем ЕК АВ. Получим параллелограмм АВЕК.

S₁

∆ СЕО = ∆ DKO (по второму признаку). Значит площади

этих треугольников равны.

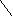
O

d

q
Следовательно,

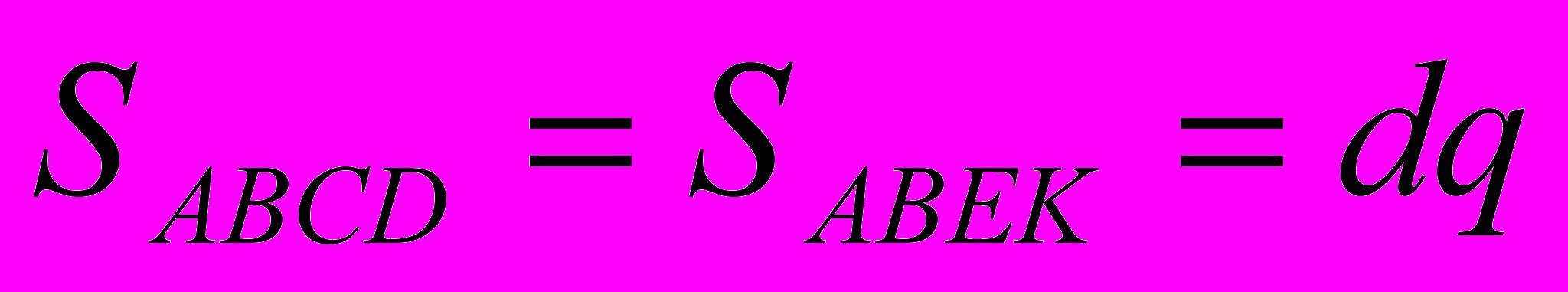
S₂

A

D

K

Укажите равновеликие фигуры на чертежах.

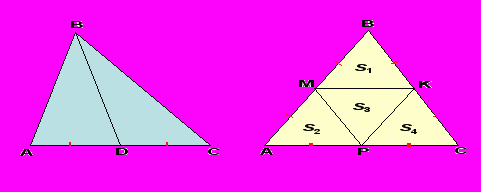
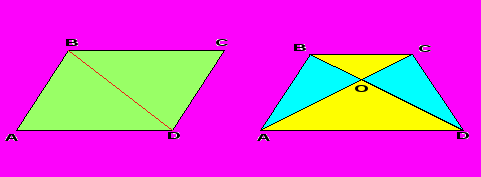
Почему они равновелики?

(Ответ: Треугольники равновелики, т.к. имеют равные основания и высоты.)

- Как доказать, что треугольники АВО и СОD равновелики?

Решение:

S_ABD = S_ACD

S_ABO = S_ABD - S_AOD

S_CDO = S_ACD - S_AOD

Значит, S_ABO = S_CDO

Докажите, что прямоугольник и треугольник АВЕ равновелики (Слайд 12).

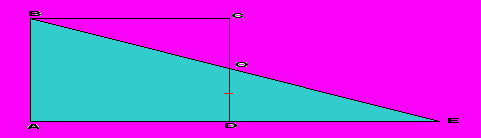
Ответ:

 ВСО =  ЕDO (по второму признаку). Значит,

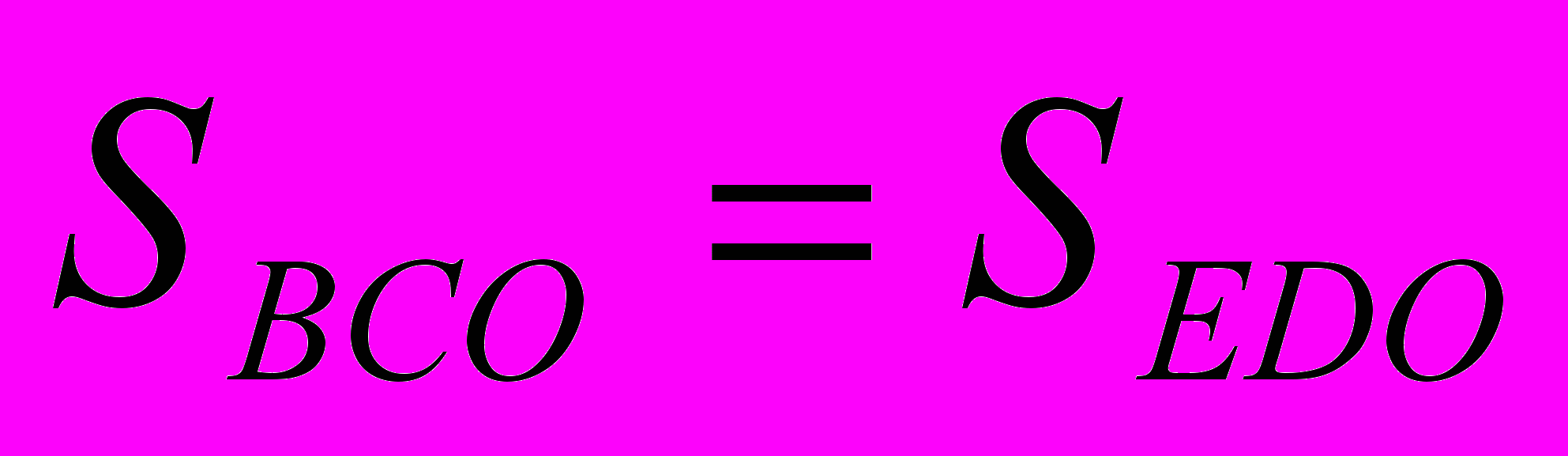
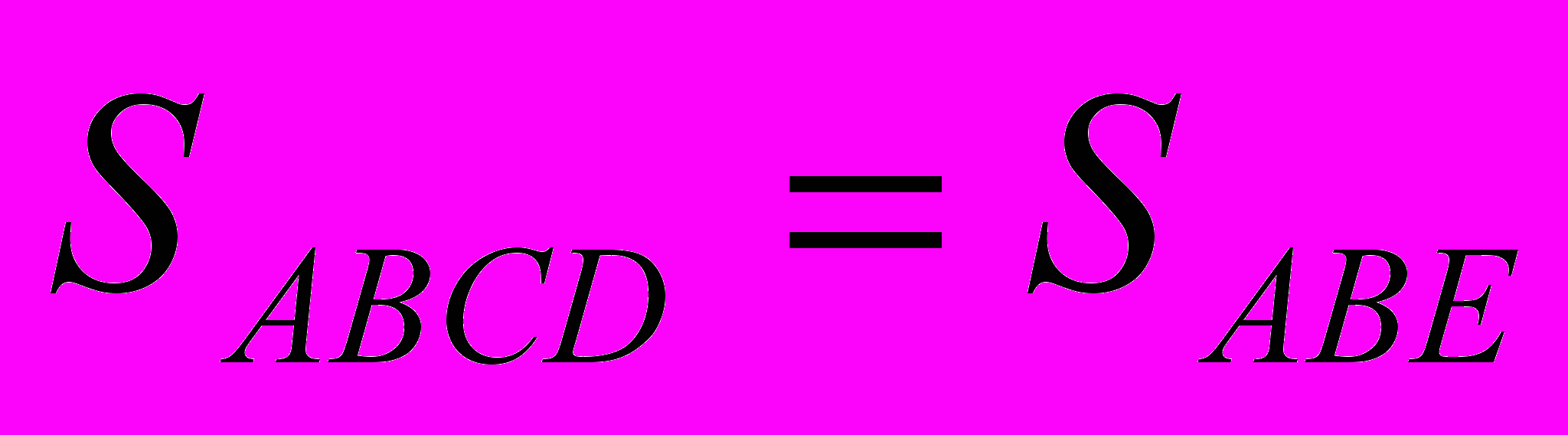
Как изменится площадь треугольника, если основание увеличить в 2 раза? Как изменится площадь треугольника, если высоту уменьшить в 3 раза?
Дан равнобедренный треугольник АВС.

-Как передвинуть одну из его вершин, чтобы получить тупоугольный треугольник втрое меньшей площади?

-Как передвинуть одну из его вершин, чтобы получить прямоугольный треугольник вдвое большей площади?

Аристотель говорил: «Ум заключается не только в знании, но и в умении приложить знание на деле».

Примените имеющиеся знания для решения практической задачи.

Задача

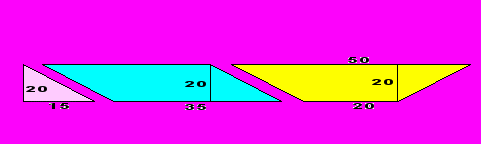
Требуется выполнить работу по настилке полов строящегося детского сада. Предлагается произвести настилку паркетного пола в игровом зале размером 5,75  8 (м)

Паркетные плитки имеют форму прямоугольных треугольников, параллелограммов и равнобоких трапеций. Размеры плиток в см указаны на рисунке. Нужно рассчитать необходимое количество плиток, чтобы после настилки пола не осталось лишних плиток и число треугольных плиток было минимальным, а плиток в форме параллелограммов и трапеций – одинаковое количество.

Решение

Паркет укладывается в ряды так, что параллелограммы и трапеции чередуются, а треугольников всего два.

Площадь одной полосы шириной 20 см и длиной 575 см будет 11500 см

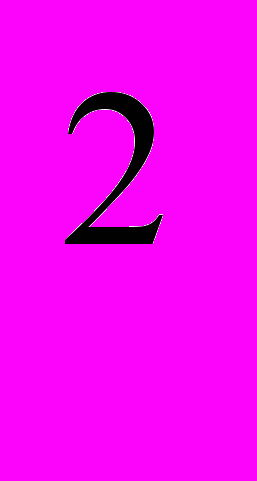
Площадь двух треугольников 300 см

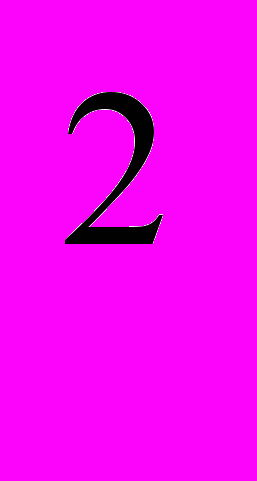
Площадь параллелограмма или трапеции 700 см

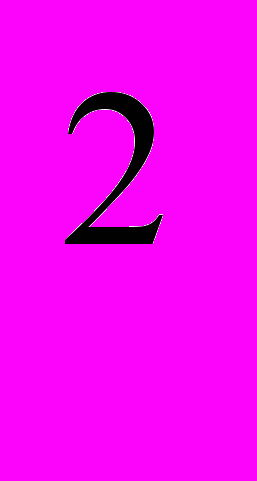
( 11500 – 300) : 700 = 16

Значит, в одной полосе по ширине игрового зала поместится по 8 параллелограммов и трапеций. Таких полос в длине комнаты поместится 800 : 20 = 40.

Следовательно, для настилки пола понадобится 80 треугольников и по 320 параллелограммов и трапеций.

Формулы площадей фигур вы применяете также на уроках географии при работе с планом местности, на уроках труда при изготовлении различных фигур.

Домашнее задание: пп.51 - 53. № 503, № 511

Итоги урока:

По какой формуле находят площадь прямоугольника? Параллелограмма? Треугольника?
По каким формулам находят площадь трапеции?
Какие фигуры называются равновеликими?
Где используются формулы площадей многоугольников?
Что необходимо повторить для успешной работы на следующем уроке?

Интегрированный урок алгебры и информатики в 8 классе ( 2 ч )

(Урок можно провести при изучении темы: «Простые и составные числа»)

Тема урока: « Распределение простых чисел. Графическая обработка данных »

Тип урока: урок изучения нового материала

Форма урока: интегрированный урок

Цели урока:

образовательные – изучить характер распределения простых чисел и

выяснить есть ли закономерности в распределении

простых чисел,

научить учащихся строить графики и диаграммы;

развивающие - развивать мыслительную деятельность учащихся на уроке

и развивать у учащихся навыки исследовательской

деятельности;

развивать умение анализировать, сравнивать, используя

знания математики;

воспитательные - прививать учащимся интерес к математике посредством

применения информационных технологий;

прививать информационную культуру.

Оборудование: компьютеры, мультимедийный проектор, большой экран,

презентации по математике и информатике, таблицы

простых чисел

Ход урока:

I. Организация начала урока

Учитель математики:

Сегодня мы проведем необычный урок – интегрированный урок алгебры и информатики по теме « Распределение простых чисел». (Слайд 1)

Вам придется работать сразу в двух тетрадях – сначала по алгебре, потом по информатике. Запишите тему урока в тетрадь по алгебре.

На прошлых уроках вы познакомились с простыми и составными числами и решали задачи, связанные с понятиями простого и составного числа. В начале урока проверим, как вы усвоили учебный материал.

Затем выясним, имеются ли закономерности в характере распределения простых чисел и увидим это с помощью построения диаграмм и графика в среде электронных таблиц.

II. Актуализация знаний

Учитель математики:

- Какие числа называются простыми, а какие – составными?

( Ответ: Простые числа – это числа, которые имеют только два делителя, а составные – более двух делителей)

- Назовите самое маленькое простое число

(Ответ: Число 2)

- Существует ли самое большое по величине простое число?

(Ответ: нет)

- Хотя самого большого простого числа не существует вообще, но самое большое из тех, что нам известны, все же есть.

Слайд 2:

Простое число Количество цифр Когда

2^6 972 593 – 1 2 098 960 1999

2^3 021 377 – 1 909 526 1998

2^2 976 221 – 1 895 932 1997

На экране вы видите 3 самых больших из известных на сегодня простых чисел.

- Существует ли формула простого числа?

( Ответ: нет)

- Как же составить таблицу простых чисел?

( Ответ: с помощью перебора одного за другим всех чисел и вычеркивания составных)

- Процедура поиска простых чисел с помощью компьютера по существу не отличается от процедуры, предложенной около 2000 лет назад астрономом и географом из Александрии Эратосфеном.

Слайд 3:

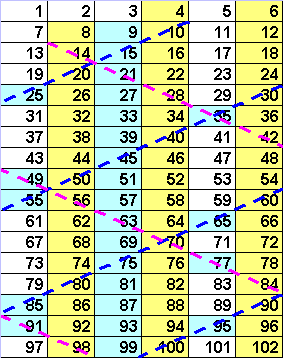
Сначала вычеркнем все четные числа, кроме двойки, 3 столбика с желтым фоном. Потом вычеркнем числа кратные трем, кроме самой тройки – это голубой столбик. Столбик с шестеркой уже вычеркнут как четный. Теперь избавляемся от чисел, кратных пяти, проводя синие пунктирные линии. Также делаем и с семеркой – проводим розовую пунктирную линию.

Больше проверять ничего не нужно, т.к. делители проверяются только до квадратного корня из количества проверяемых чисел. Первым математиком, указавшим на это, был Фибоначчи.

Оставшиеся числа и есть простые числа, меньшие 100, или, точнее 102.

III. Изучение нового материала

Упорядоченный алгоритм решета Эратосфена наводит на мысль, будто найти формулу, позволяющую хотя бы указать число простых чисел на любом интервале числовой оси, - дело не такое уж трудное. Но сколько ни бились математики, им так и не удалось найти желанную формулу. В начале позапрошлого века была высказана ( подкрепленная наблюдением за простыми числами) гипотеза, согласно которой число простых чисел меньших данного числа п, приближенно выражается соотношением, зависящим от п ( п/ln n).

На сколько же быстро разряжаются простые числа при увеличении промежутка рассматриваемых чисел?

С помощью построенных диаграмм в среде электронных таблиц вы ответите на этот вопрос и построите график, показывающий, сколько простых чисел меньших данного числа п, находится на отрезке

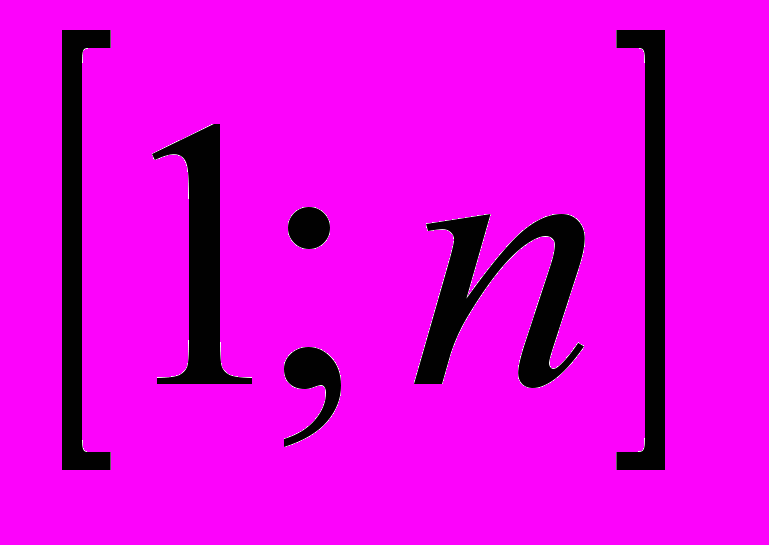
Учитель информатики:

Проведем небольшое повторение.

Первый ряд задаст два вопроса второму ряду по теме ЭТ. Потом вы поменяетесь ролями. За ответы сразу учащиеся получают оценки.

(Проходит самоопрос среди учащихся).

Слайд № 1. Запишем в тетрадь тему урока.

Наша задача сегодня – научиться строить графики и диаграммы.

Слайд № 2.

- В чем преимущество графической обработки данных?

Наглядное отображение зависимостей;
Облегчение восприятия информации;
Помощь при анализе и сравнении

Типы диаграмм:

Линейчатые, использующиеся для наглядного сравнения величин (Слайд № 4)
Круговые, которые служат для отображения частей от целого (Слайд № 5)
Типа «график», использующиеся для отображения изменения величин в зависимости от времени и построения графиков функций (Слайд № 6).

Слайд № 7.

Располагать диаграмму можно на листе с данными или на отдельном листе.

Для создания диаграмм служит МАСТЕР ДИАГРАММ, пиктограмма которого находится на стандартной панели электронных таблиц.

Алгоритм работы:

Выделить диапазон ячеек с данными
Запустить мастер диаграмм
Выбрать тип диаграммы
Далее выбирать нужное из предлагаемого

IV. Практическая часть

Файл Простые числа.

Вам предстоит заполнить таблицу распределения простых чисел по диапазонам и построить для каждой строки диаграмму различного вида. Чтобы выделить два не связанных между собою диапазона, нужно нажимать клавишу Ctrl. Далее действуете по алгоритму.

Таблица распределения простых чисел по диапазонам

Диапазон	Простые числа
1 – 10	4
1 – 100	25
1 – 1000	168
1 – 10 000	1 229
1 – 100 000	9 525

V. Поведение итогов практической работы и изучение нового материала

Учитель математики:

- Какие выводы можно сделать, посмотрев на диаграммы и график?

(Ответ: Доля простых чисел с увеличением промежутка падает, а количество простых чисел на отрезке 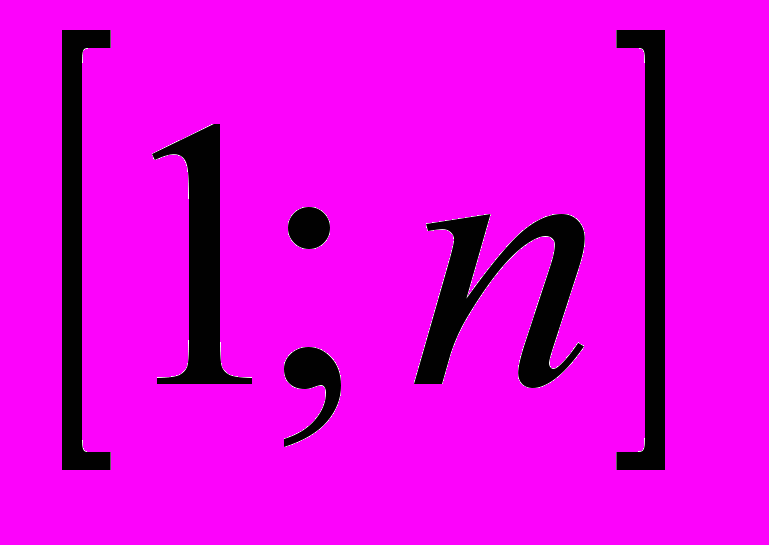с увеличением п растет)

- Плавность, с которой поднимается эта кривая, следует отнести к числу удивительнейших фактов математики.

В зависимости от расположения целых чисел простые числа могут образовывать тот или иной узор. Однажды математику Станиславу Уламу пришлось присутствовать на одном очень длинном и очень скучном, по его словам, докладе. Чтобы развлечься, он начал писать на клетчатой бумаге числа, поставив в центре 1 и двигаясь по спирали против часовой стрелки, без всякой задней мысли он обводил все простые числа кружками. Вскоре к его удивлению, кружки с поразительным упрямством стали выстраиваться вдоль прямых. Слайд 4:

На приведенном рисунке, полученном на компьютере, продублировано то, что Улам сделал от руки. Простые числа выделены черными точками, а составные – белые квадраты. Выделяющиеся темные линии – это залежи простых чисел. Вблизи центра выстраивания простых чисел вдоль прямых еще можно было ожидать, поскольку плотность простых чисел вначале велика. Однако не было оснований ожидать, что и в области больших чисел, где плотность простых чисел значительно меньше, те так же будут выстраиваться вдоль прямых. Улама заинтересовало, как же будет выглядеть его спираль, если ее продолжить до нескольких тысяч простых чисел. Разработав программу, он получил рисунок для чисел от 1 до 65 000

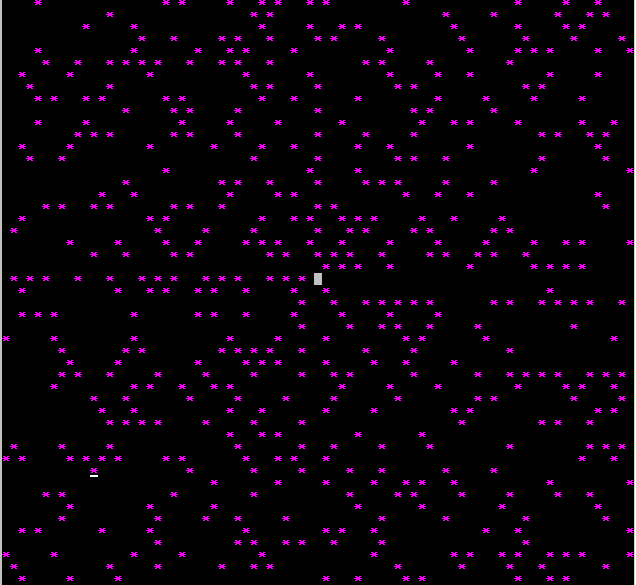
Слайд 5

(иногда его называют «скатертью Улама», из которого видно, что даже у края картины простые числа продолжают послушно укладываться на прямых. Участкам прямых соответствуют квадратные трехчлены, порождающие простые числа, например найденный Эйлером х² + х + 41, у которого первые 39 решений простые.

Простые числа могут сгенерировать музыку или создавать разные картины, например такую

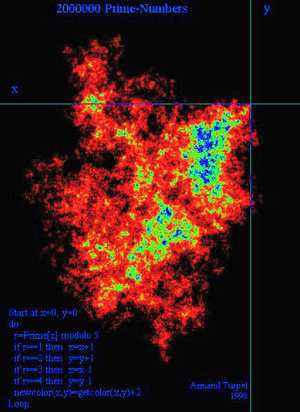
Слайд 6

Алгоритм создания этой картины незатейлив: берется простое число, определяется его остаток от деления на 5, в зависимости от его (остатка) значения происходит сдвиг от текущей точки в одном из четырех направлений и новая точка подсвечивается с учетом ее предыдущей яркости. Цикл повторяется 2 миллиона раз.

О сложности структуры множества простых чисел свидетельствует тот факт, что в ряду простых чисел встречаются сколь угодно большие пробелы; так, например, среди м и л л и о н а идущих подряд чисел может не оказаться ни одного простого числа. Математикам до сих пор не удавалось обнаружить какой-либо системы в характере распределения простых чисел. Так, считается, что в окрестности целого числа х среднее расстояние между последовательными простыми числами пропорционально некоторой функции от х и оно растет с увеличением х. Тем не менее, уже давно известны так называемые парные простые числа (простые числа-близнецы, разность между которыми равна 2). Иногда они образуют целые скопления. Например: 101, 103, 107, 109, 113. У математиков давно существовало подозрение, что такие скопления существуют и в области очень больших простых чисел, однако ни доказать, ни опровергнуть это утверждение до сих пор не удавалось. Если такие скопления будут найдены, стойкость криптографических ключей, используемых в настоящее время, может оказаться под очень большим вопросом.

VI. Итог урока и домашнее задание

- Как изменяется доля простых чисел с увеличением промежутка рассматриваемых чисел?

- Как изменяется количество простых чисел меньших п с увеличением п?

- Какие промежутки между соседними простыми числами могут быть?

- Есть ли какая-либо система в характере распределения простых чисел?

Д/З – выучить конспекты по математике и информатике

Интегрированный урок геометрии и информатики в 7 классе ( 2 ч )

(Урок можно провести при изучении темы: «Примеры задач на построение»)

Тема урока: «Деление отрезка пополам»

Тип урока: урок изучения нового материала

Форма урока: интегрированный урок

Цели и задачи урока:

образовательные –	отработать этапы решения задач на построение; научить выполнять эти построения на экране компьютера, используя панель инструментов и приемы работы с мышью; научить работать с электронным учебником;
развивающие –	развивать мыслительную деятельность учащихся на уроке и сформировать у учащихся начальные навыки исследовательской деятельности при решении задач на построение; развивать алгоритмическое мышление;
воспитательные –	прививать учащимся интерес к математике посредством применения информационных технологий; прививать информационную культуру; воспитывать аккуратность и точность при выполнении геометрических построений.

Оборудование: компьютеры; мультимедийный проектор; большой экран; CD-ROM диск «Открытая математика 1.0. Планиметрия» (Продукт ООО “Физикон”, 1997-2001).

Ход урока:

Организация начала урока.

Учитель математики:

Сегодня мы проведем необычный урок - интегрированный урок геометрии и информатики по теме: «Деление отрезка пополам». На прошлых уроках мы с вами познакомились с различными задачами на построение. Сегодня более подробно поговорим об одной из них – о делении отрезка пополам. На этом уроке вы впервые познакомитесь с электронным учебником «Открытая математика 1.0», его разделом «Планиметрия», а также научитесь выполнять построения на экране компьютера, используя панель инструментов и приемы работы с мышью. Процесс построения, выполненный учителем, вы сможете увидеть на большом экране с помощью мультимедийного проектора.

Актуализация знаний.

Учитель математики:

С древнейших времен для построений используется линейка, а циркуль примерно с I в. стал применяться в Древней Греции. С помощью электронного учебника познакомьтесь с тем, какие построения позволяют выполнить эти инструменты и что значит решить задачу на построение. Учитель информатики объяснит вам, как пользоваться электронным учебником.

Учитель информатики:

Для работы с электронным учебником необходимо использовать навыки работы с мышью. Алгоритм работы с учебником достаточно прост. Внимательно следите за моими действиями и читайте пояснения на экране компьютера. Можно включить звук для прослушивания информации. При работе с электронным учебником мы переходим от одной страницы текста к другой. Вернемся к предыдущему параграфу и выберем тему «Циркуль и линейка». Внимательно прочитайте этот материал.

Учитель информатики демонстрирует принцип работы с электронным учебником на компьютере. Учащиеся наблюдают за его действиями на большом экране.

После прочтения текста учитель математики задает вопросы ученикам.

Учитель математики:

Вопрос 1:

Что значит решить задачу на построение?

(Ответ: Это значит найти способ построения фигуры, осуществить это построение и доказать, что построенная фигура – фигура, обладающая требуемыми свойствами).

Вопрос 2:

Какие построения позволяет выполнить линейка?

(Ответ:

провести произвольную прямую;
провести прямую, проходящую через данную точку;
построить произвольный луч;
построить луч с заданным началом, проходящий через заданную точку;
построить отрезок с заданными концами).

Вопрос 3:

Какие построения можно выполнить с помощью циркуля?

(Ответ:

построить произвольную окружность;
построить окружность с заданным радиусом;
построить окружность с заданным центром и радиусом;
отложить данный отрезок на прямой от данной точки).

Любая задача на построение состоит из нескольких частей. Прочитайте, из каких частей состоит задача о делении отрезка пополам и для чего нужна каждая часть.

Учитель информатики:

Перейдем к следующему параграфу нашего электронного учебника «Деление отрезка пополам». Внимательно прочитайте этот материал.

Учитель информатики выполняет необходимые действия на компьютере, учащиеся наблюдают за его действиями на большом экране.

После прочтения информации учитель математики задает ученикам вопросы.

Учитель математики:

Вопрос 1:

Для чего нужен анализ построения?

(Ответ: для того, чтобы составить план построения).

Вопрос 2:

Каков план построения середины отрезка?

(Ответ: из точек А и В провести окружности радиусом, равным АВ и точки пересечения этих окружностей соединить отрезком СС

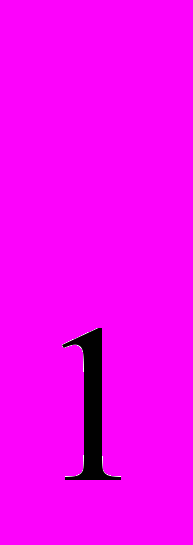. Точка пересечения отрезков АВ и СС

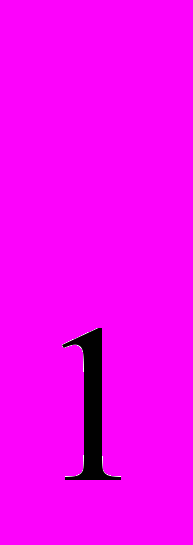- точка О является серединой отрезка АВ).

Вопрос 3:

Как доказать, что О – середина АВ?

(Ответ: Треугольники АСС

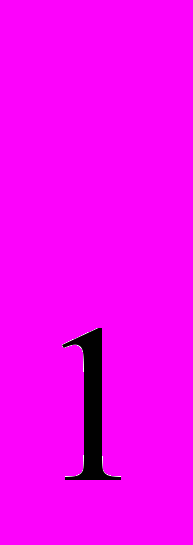и ВСС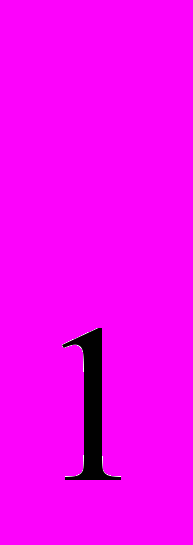

равны по третьему признаку равенства треугольников, значит

1=2. В равнобедренном треугольнике АВС биссектриса СО будет медианой).

Это доказательство рассказывают по готовому чертежу на доске.

Практическая часть.

Учитель информатики:

Сейчас вы посмотрите ролик о выполнении построения середины отрезка.

Вы будете использовать некоторые инструменты, применяемые при выполнении данного построения, выбирая их на панели инструментов, - это циркуль, карандаш, линейка, ластик.

Вопрос:

Для чего используют каждый из этих инструментов при работе за компьютером?

(Ответы: циркуль нужен для построения дуг и окружностей, карандаш нужен для изображения точек и произвольных линий, линейка нужна для построения отрезка прямой, ластик стирает изображение).

Перед нажатием кнопки «Старт» учитель информатики показывает на панели инструментов, где располагаются инструменты, применяемые при выполнении данного построения (циркуль, карандаш, линейка, ластик). Учащиеся отвечают на вопросы о назначении этих инструментов.

После просмотра ролика учитель математики задает ученикам вопросы о шагах построения.

Учитель информатики:

Теперь я покажу вам, как нужно выполнять построение. Шаги построения с помощью мультимедийного проектора будут спроецированы на большой экран. Смотрите на экран и слушайте меня внимательно.

Учитель информатики медленно выполняет построение на компьютере, комментирует его, заостряя внимание учащихся на сложных моментах построения.

Учитель информатики:

Выбираем на панели инструментов циркуль. Появляется дополнительная панель с изображением окружностей.
Нажимаем на  для выбора радиуса окружности.
Выбираем радиус окружности, нажав на концы отрезка АВ.
Выбираем дугу окружности в правом нижнем углу - это дуга окружности с фиксированным радиусом.
Нажимаем на точку А – центр окружности, делаем засечку вверху и фиксируем её щелчком мыши. Аналогично делаем засечку из точки А внизу.
Аналогично делаем две засечки из точки В.
Выбираем на панели инструментов карандаш.
В окне «имя» присваиваем первой точке имя С (буква С – латинская заглавная) и фиксируем первую точку щелчком мыши.
Второй точке также присваиваем имя С и в соседней ячейке указываем индекс 1, фиксируем вторую точку щелчком мыши.
Выбираем на панели инструментов линейку, появляется другая дополнительная панель.
Выбираем отрезок и соединяем точки С и С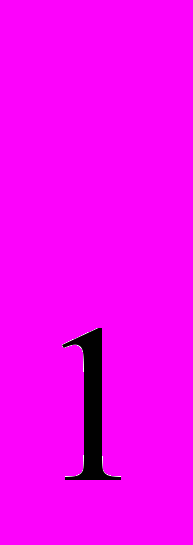, фиксируя эти точки.
Выбираем на панели инструментов карандаш и выбираем имя для точки, являющейся серединой отрезка (имя О без индекса), фиксируем точку щелчком мыши.

Учитель математики:

Для выполнения задания на компьютере класс необходимо разбить на группы. Первая группа учащихся выполняет задание на компьютере самостоятельно. Выполнение вашей работы сегодня будет оценивать не учитель, а компьютер. Вторая группа учащихся выполняет это же задание с помощью циркуля и линейки традиционным способом на листочках, записывает план построения и доказательство. Затем эти группы учащихся меняются местами.

Учитель информатики:

Сегодня для выполнения работы на компьютере вам необходимо будет вспомнить, что алгоритм – это организованная последовательность действий и свойствами алгоритма являются правильность и результативность.

На уроках информатики вы применяли словесный способ записи алгоритма. Прежде, чем вы начнете выполнять работу на компьютере, запишите в своих тетрадях алгоритм построения. Построение будет выполнено правильно, если вы не нарушите порядок действий.

Алгоритм:

Выбрать циркуль, на появившейся панели нажать .
Выбрать радиус (концы отрезка АВ).
Выбрать дугу в правом нижнем углу.
Сделать засечки из точки А, фиксируя их (щелчок мыши).
Аналогично сделать засечки из точки В.
Выбрать карандаш. В окне «имя» - латинская заглавная буква С, фиксируем точку.
Выбрать для второй точки - имя С, в соседней ячейке - индекс 1, фиксируем.
Выбрать линейку, выбрать отрезок, соединить точки С и С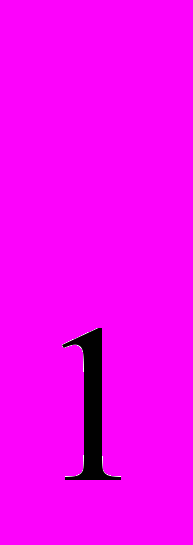, фиксируя.
Выбрать карандаш и имя О для точки, фиксируем.

Чтобы перейти с кириллицы на латиницу, необходимо нажать компьютерный аккорд Shift + Alt (слева).

Выполнив построение по алгоритму, с помощью кнопки «Проверить» получить ответ компьютера о правильности вашего построения.

Проверка выполнения задания и итог урока.