Программа по курсу: введение в искусственный интеллект (базовый) по направлению: 511600 факультет

Вид материала

Программа

Содержание Всего часов: 122 Введение в искусственный интеллект Задачи для практикума А - конечный алфавит, F Р (нужно записать в виде «если ... то...»): p Список литературы

Подобный материал:

• Программа по курсу: практикум по трёхмерной машинной графике (базовый) по направлению:, 91.42kb.
• Программа по курсу: Основы выпуклого анализа и линейного программирования по направлению:, 31.8kb.
• «Искусственный интеллект», 622.01kb.
• Software Project Management ) (базовый) по направлению: 511600 факультеты: фупм кафедра:, 41.85kb.
• Прагина Л. Л. Мозг человека и искусственный интеллект, 1498.79kb.
• Ю. А. Самарский 17 июня 2006 г. Программ а по курсу вычислительная математика по направлению, 137.08kb.
• Рабочая программа курса «Искусственный интеллект и нейросетевое управление», 131.7kb.
• ) состоится V всероссийская конференция студентов, аспирантов и молодых учёных «искусственный, 29.67kb.
• Программа по курсу: современные технологии параллельного программирования (по выбору), 69.72kb.
• Ix национальная конференция с международным участием "Искусственный интеллект-2004",, 147.79kb.

Министерство образования и науки Российской Федерации

Московский физико-технический институт

(Государственный Университет)


УТВЕРЖДАЮ

Проректор по учебной работе

___________ Самарский Ю.А.

«______» _______________2008 г.

ПРОГРАММА

по курсу: ВВЕДЕНИЕ В ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ (базовый)

по направлению: 511600

факультет: ФУПМ

кафедра: ИНФОРМАТИКИ

курс: 4 курсовая работа: 7 семестр

семестр: 7 экзамен: 7 семестр

лекции: 34 часа

практические занятия: 34 часа

ВСЕГО ЧАСОВ: 122

Программу составил: профессор Л.Н. Столяров


Программа обсуждена на заседании

кафедры информатики

28 августа 2008 г.


Заведующий кафедрой И.Б. Петров

профессор


ВВЕДЕНИЕ В ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ

1. Мифы и реалии искусственного интеллекта. Концепция Тьюринга. Эшби и его «конструкция мозга». Психология мышления и автоматы. Лабиринтная модель мышления и эвристическое программирование. Генетические алгоритмы.
   
2. Формальные дедуктивные системы. Исчисление высказываний и аристотелева логика. Правильные рассуждения и аристотелевы правила вывода. Правило резолюции. Исчисление предикатов. Силлогистика Аристотеля и ее современные модификации. Универсум Эрбрана.
   
3. Нечеткая логика. Правдоподобные рассуждения. Схема Пойа. Схема Шафера.
   
4. Автоматные модели поведения. События и действия. Рефлекторное поведение и автономные автоматы. Условные рефлексы и автоматные сети. Дискретные нейронные сети. Сети Петри и модели кооперативного поведения. Моделирование типов поведения человека. Ритуальное, подражательное и ролевое поведение. Ситуационное поведение.
   
5. Экспертные системы. Система продукций. Пополнение и обобщение знаний.
   
6. Мозговой штурм для решения сверхсложных проблем методом группового экспертного анализа. Методика FACTION.
   
7. Система Battle for Money. Формальные прогнозные сценарии в политической, социальной, экономической и финансовой средах. Тренажеры и имитационные модели. Распределенные потоковые сети (CFN).
   
8. Практикум по составлению прогнозных сценариев и написанию имитационных моделей CFN
   

Задачи для практикума


I. Формальные системы и доказательство теорем

Формальная система FS =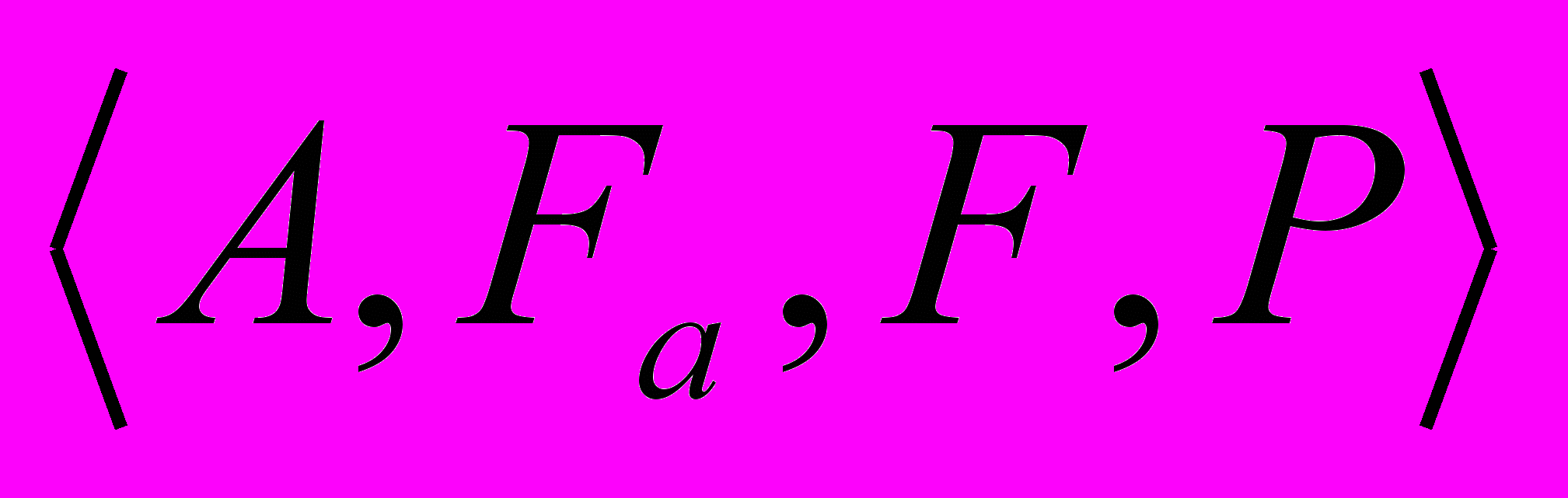, где А - конечный алфавит, F - правильно построенные формулы, выводимые в FS, F_a формулы, которые являются выводимыми по определению (аксиомы), Р - конечное множество правил вывода; 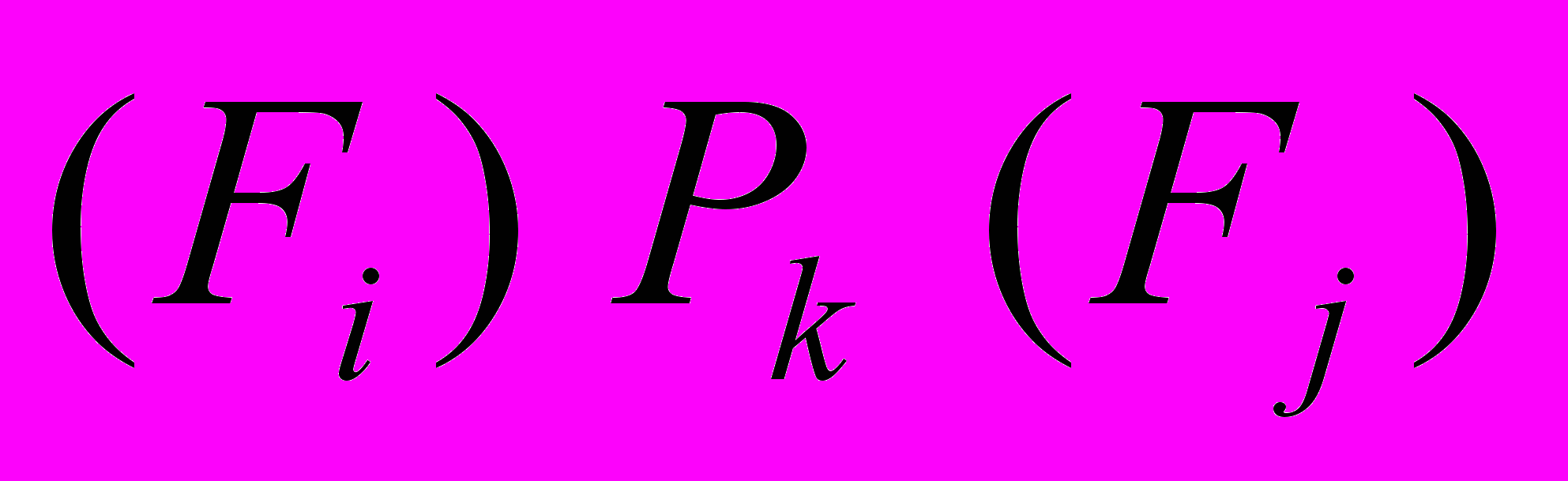- читается «формула , выводима из по правилу 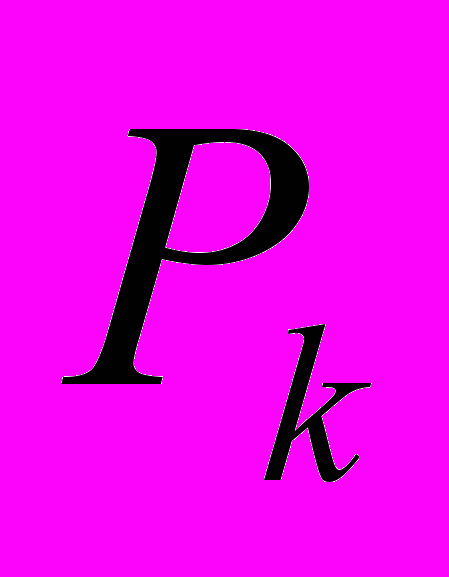» (если к , применить 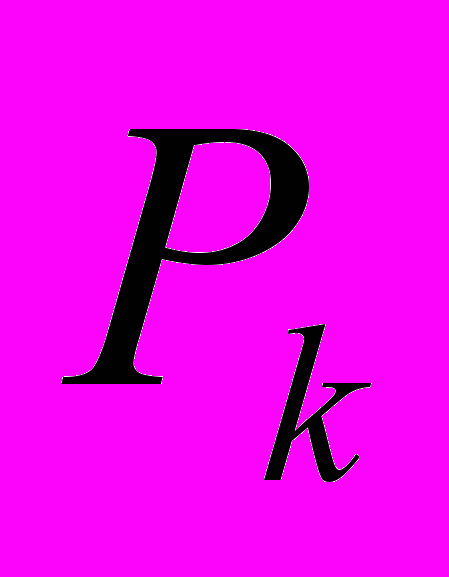, то получится ).

Типовая задача. Задана FS, заданы исходные формулы 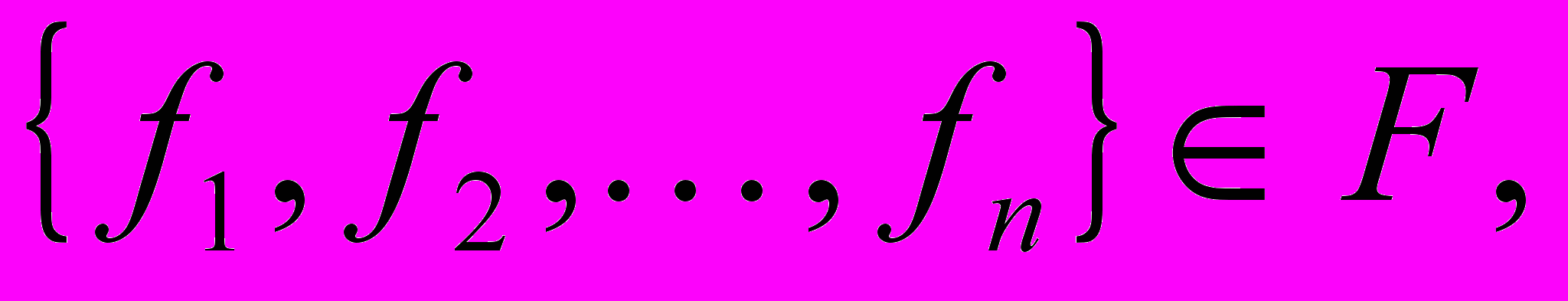найти решающее дерево (дерево вывода) для формул 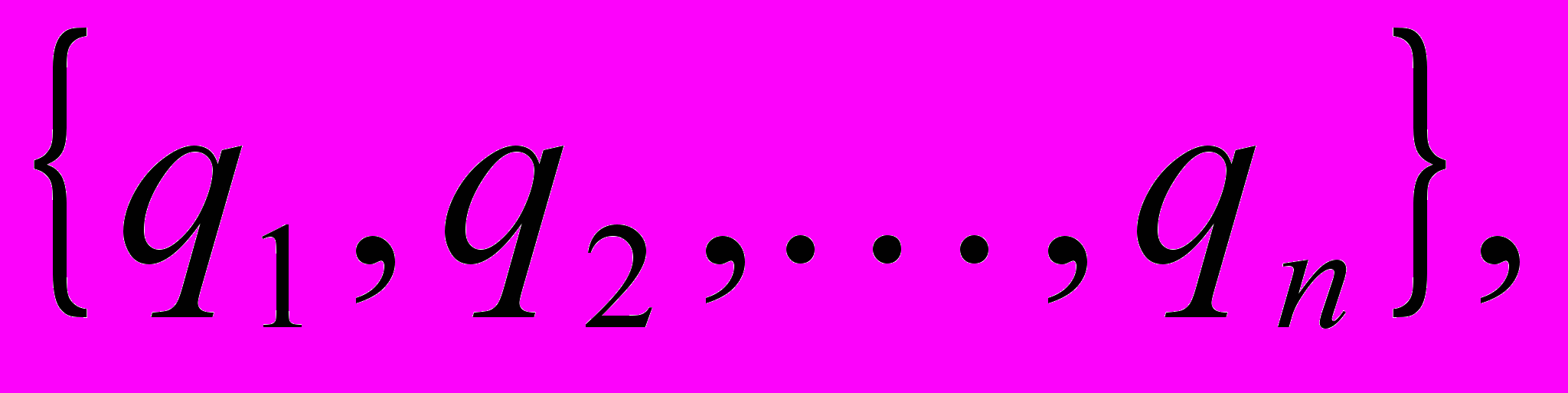обладающих заданным свойством.

1.1. Доказать теорему: любая точка биссектрисы равноудалена от era сторон.

Дано: 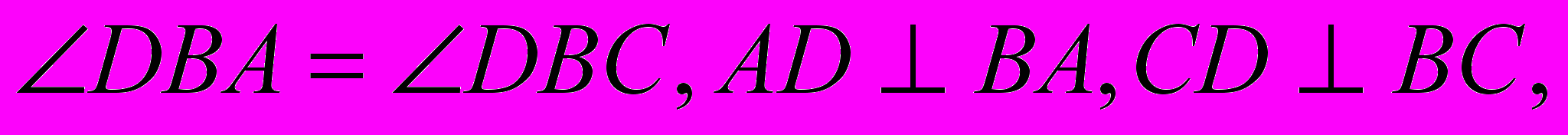где DB – отрезок, 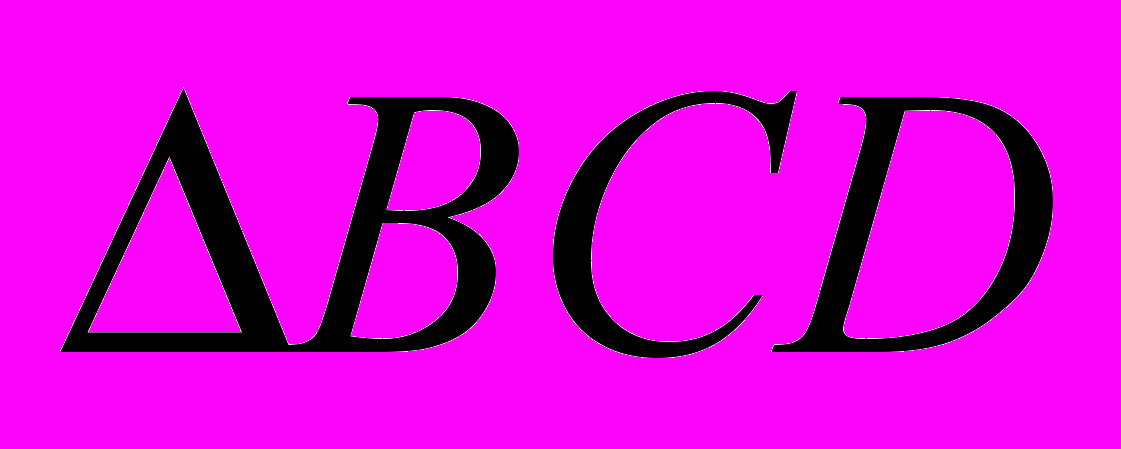- треугольник.

Доказать:

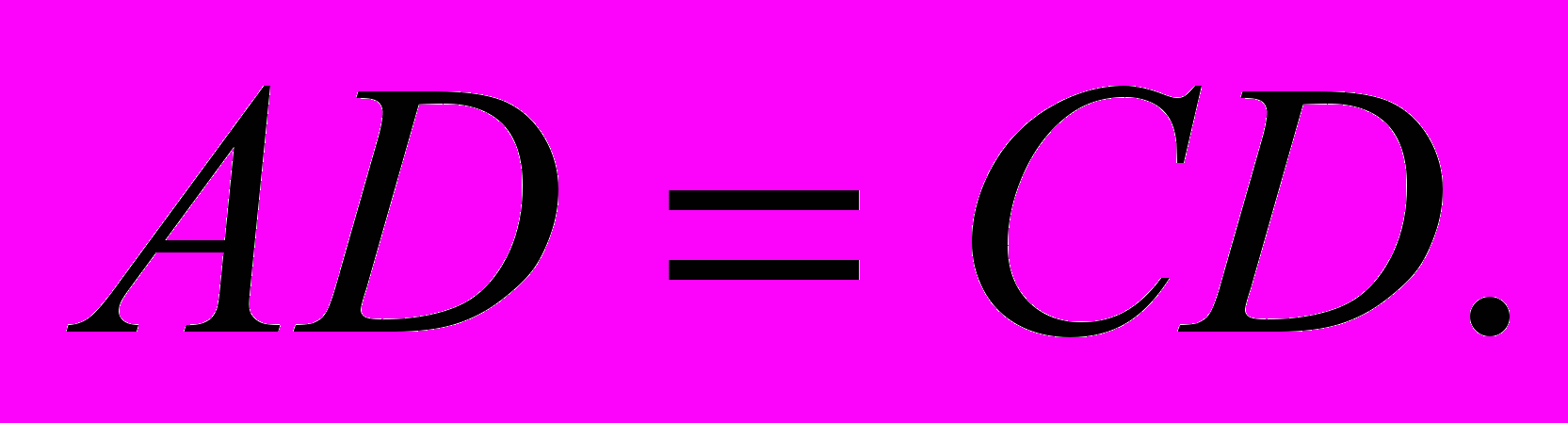
Правила Р (нужно записать в виде «если ... то...»):

p₁ (прямые углы равны между собой);

Р₂ (отрезок равен самому себе);

P₃ (угол равен самому себе),

P₄ ({сторона, угол, угол = сторона, угол, угол J);

Р₅ (два пересекающихся перпендикулярных отрезка определяют прямой угол):

Р₆ (соответствующие стороны равных треугольников равны).

Построить решающим граф (дерево) для доказательства теоремы и прокомментировать его с точки зрения построения алгоритма перебора по дереву.

1.2. Игра – «последний проигрывает». Число игроков – п, количество монет в куче m, единственное правило р. из кучи можно взять 1, 2, ... k монет. Каждый игрок имеет сноп номер 1,
2,..., п Построить решающие деревья, которые показывают для m, k такой помер игрока, которым всегда выигрывает.

1.3. Игра - «крестики-нолики». Построить все возможные решающие деревья, которые приводят к выигрышной ситуации (формуле). Проанализировать эффективность 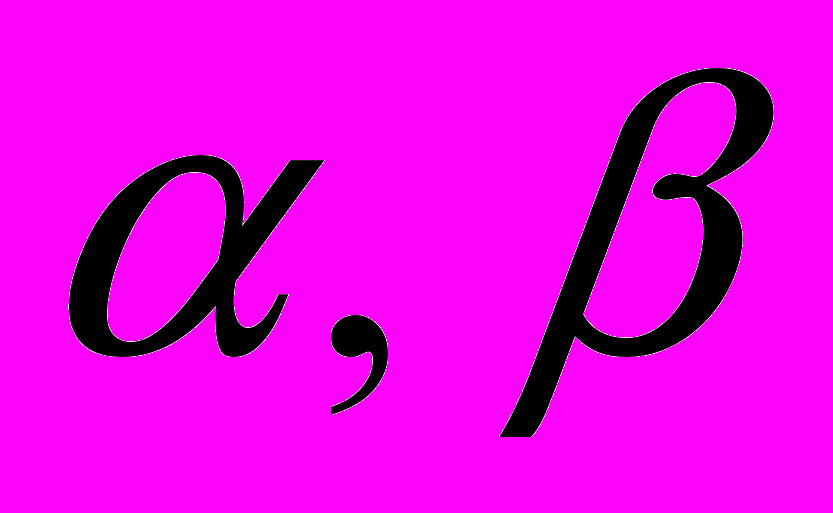– процедуры перебора при поиске выигрышей.


//. Формирование понятий и кластеризация


Задано конечно множество признаков 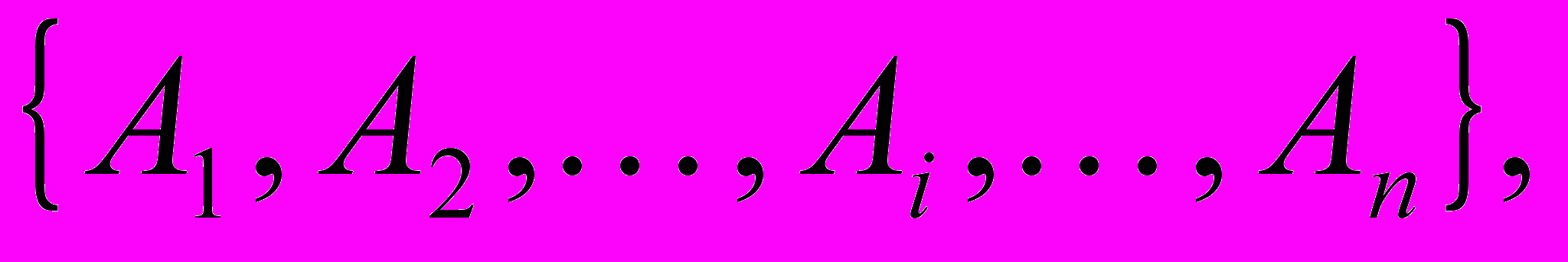каждый признак A_i, определен па конечном множестве значений 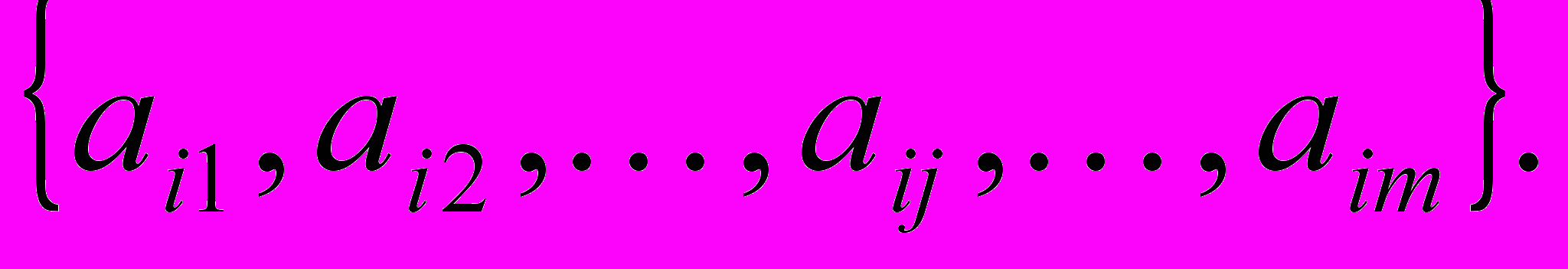Определено конечное множество отношений 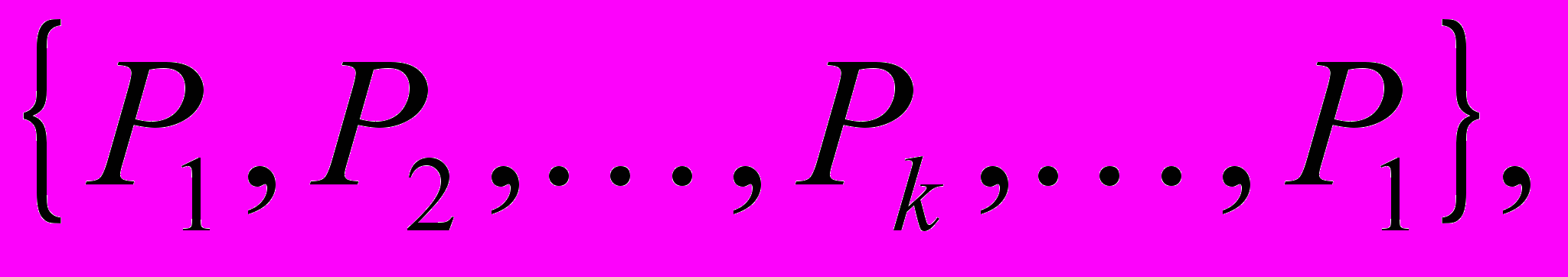на декартовом произведении 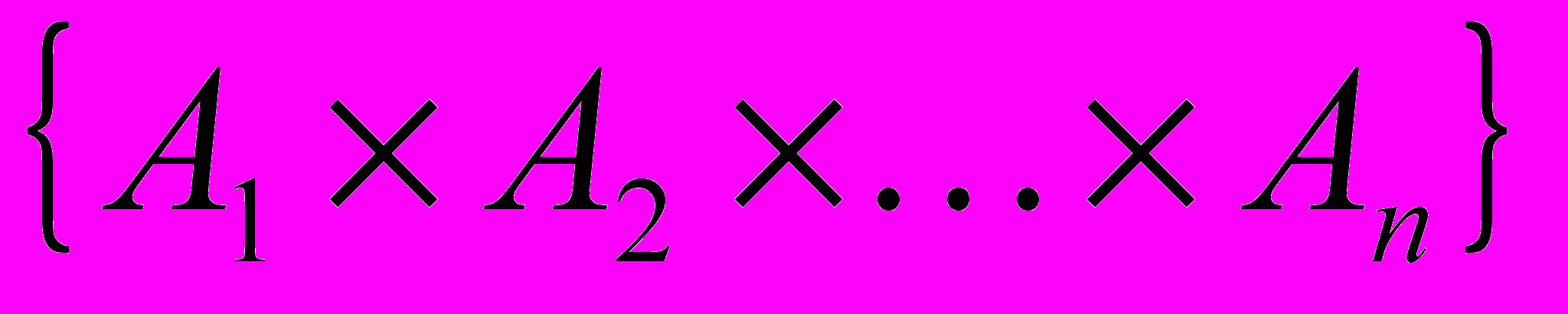. Понятием называется утверждение о правиле идентификации нахождения отношения (предиката) Р_k..

2.1. Для анализа произвольного текста выбраны два признака A₁ (нахождение буквы х в некотором слове) со значениями (а₁₁ на первой позиции, а₁₂: на 2-й позиции, ..., а₁₇ на 7-й позиции); A₂ (нахождение буквы y, идущей после буквы x на a₂₁: 1-й позиции, a₂₂: 2-й позиции, а₂₃: 3-й позиции).

Построить понятия, которые задаются утверждениями: если x будет на r – й позиции, то у будет на 1-й позиции (предикат 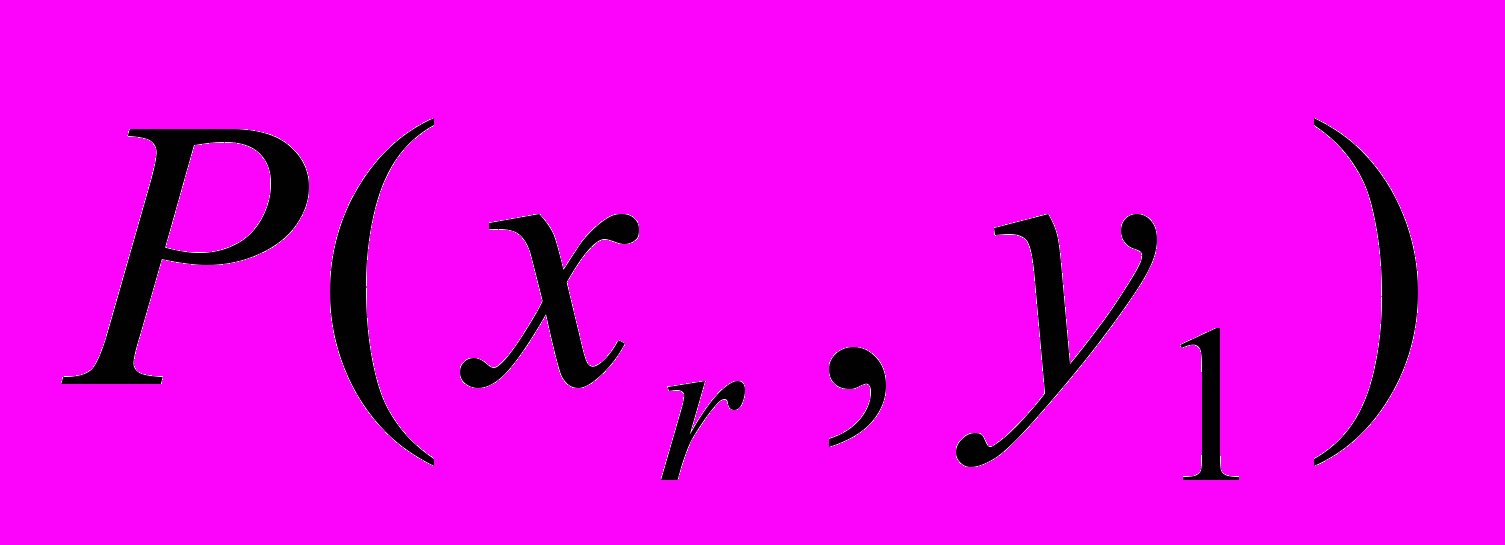) с уверенностью 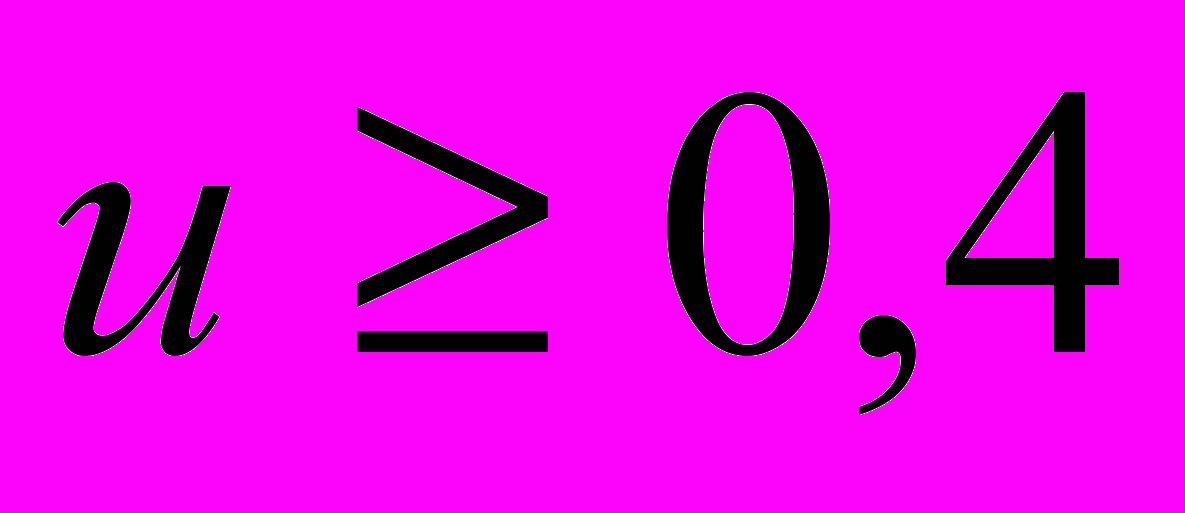, где 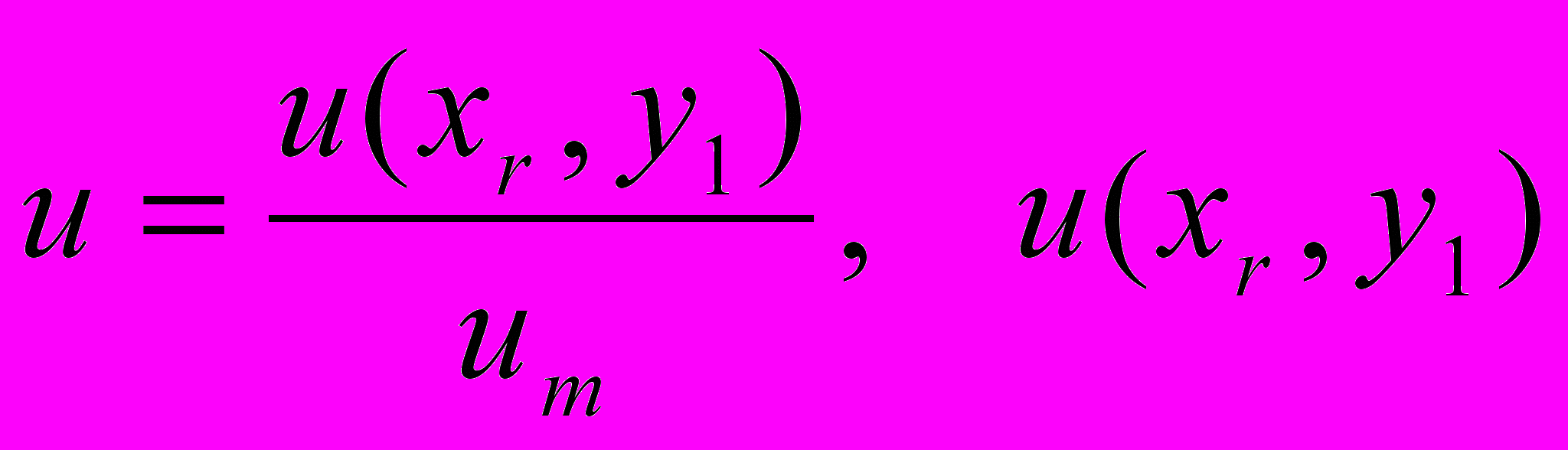- число случаев истинности предиката 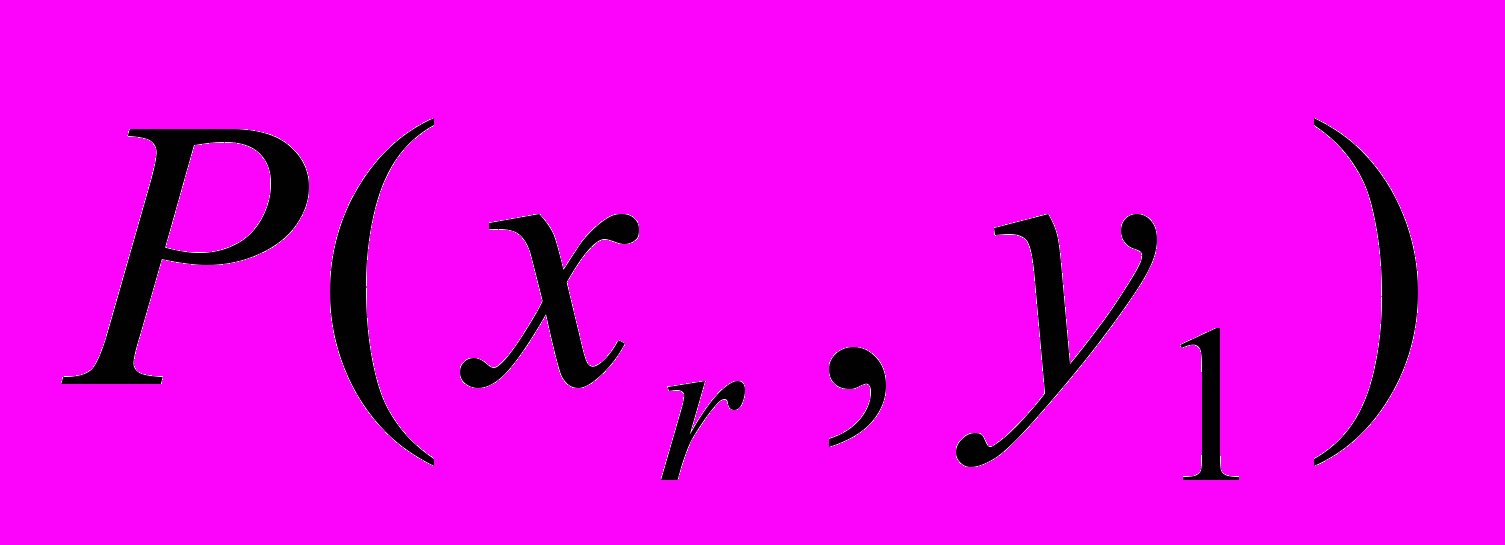при анализе текста, 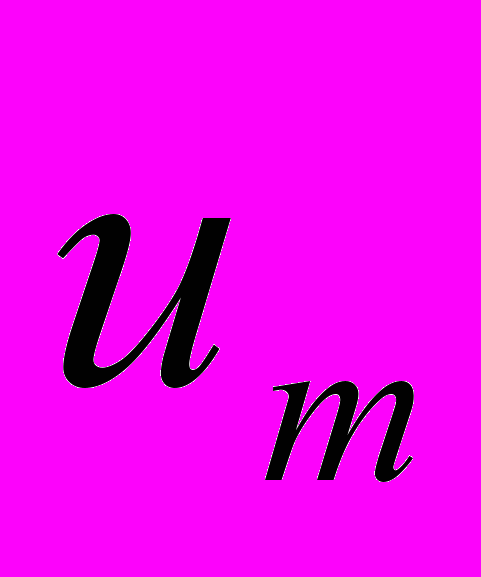- число слов в анализируемом тексте. Так построенное утверждение называется кластером.

Построить программу, анализирующую произвольный текст на русском языке не менее 1000 слов.

2.2. Поиск разумных существ во Вселенной.

Предложить идею построения двух понятий и соответствующих им утверждений и кластеров, таких, что одно из них является посылкой к инопланетянам, а другое ответом инопланетян на эту посылку.


III. Структурное распознавание образов


Структурный образ 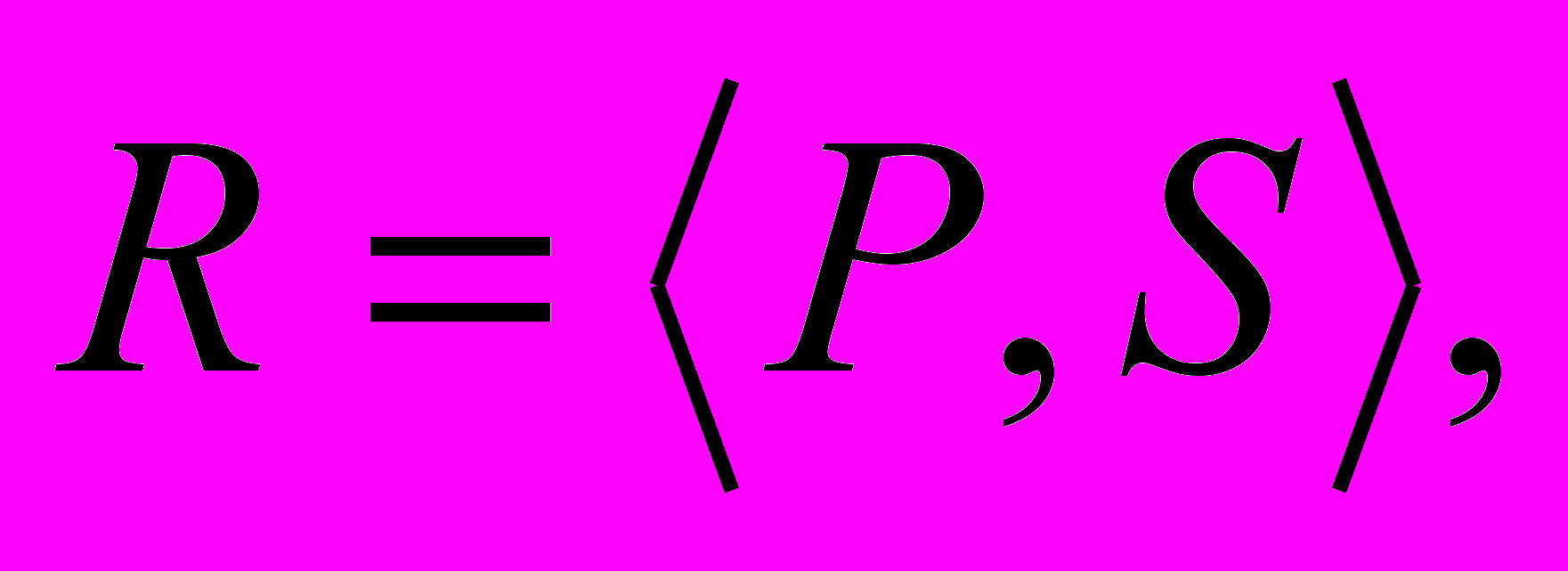где P – отношение (обычно бинарное), определённое на конечном множестве базовых (составляющих) признаков 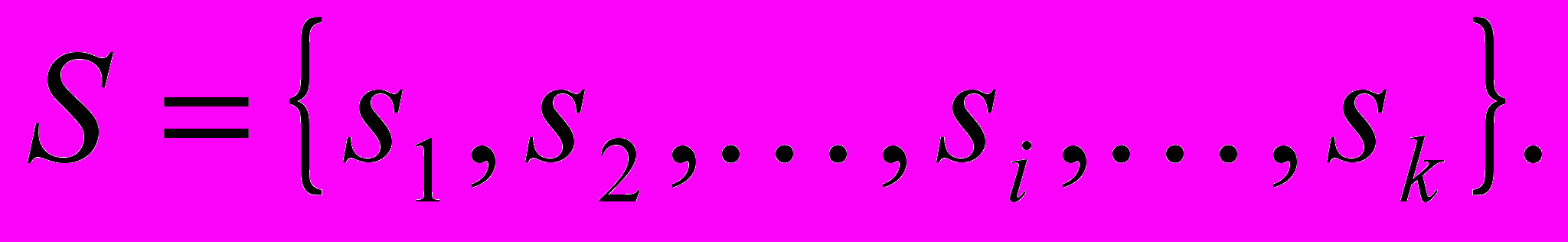Каждому признаку 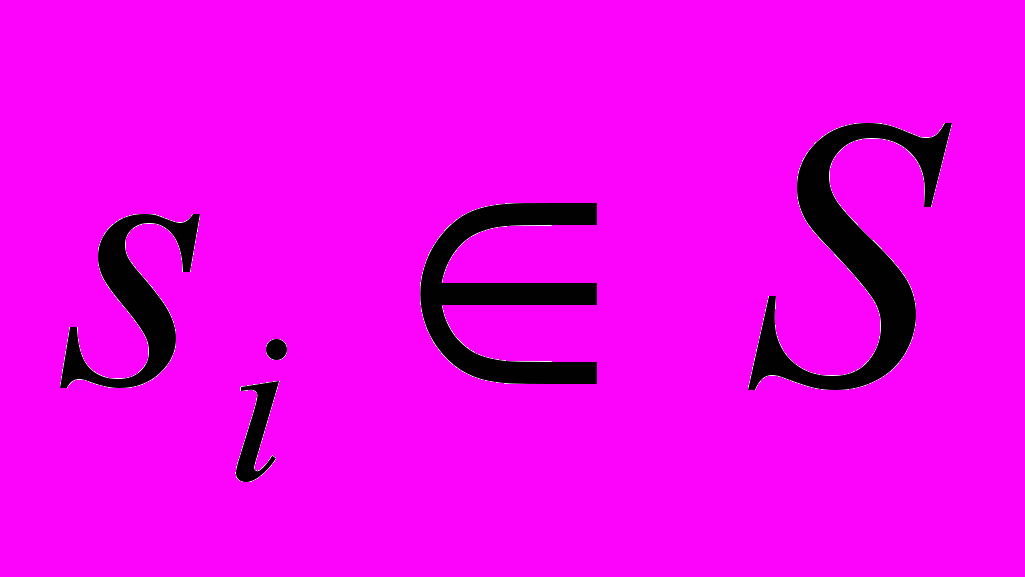поставлена в соответствие распознающая процедура. Считается, что реализация 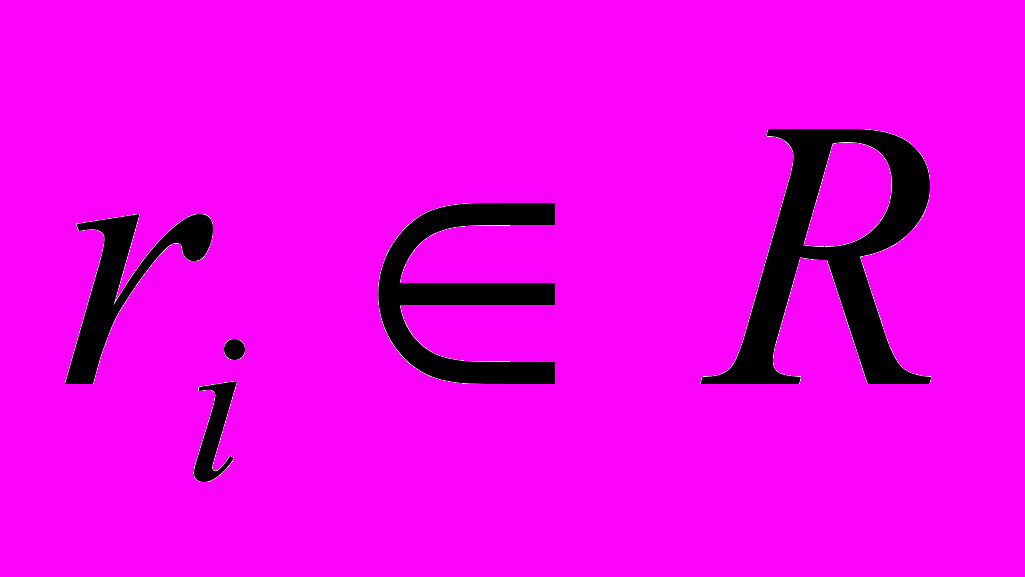сохраняет отношение P (отношение Р считается инвариантным для всех реализаций образа). Алгоритм структурного распознавания представляет собой процедуру (правила) нахождения инвариантного отношения Р. Обычно алгоритмы структурного распознавания имеют 2-шаговую процедуру:

1. Обработка реализации и получение последовательного кода (кодирование реализации).
   
2. Сравнение полученного кода с эталонным кодом образа.
   

3.1. Распознавание букв русского алфавита.

1. Выбрать конечное множество признаков, характеризующих букв.
   
2. Составить описание каждой буквы в виде бинарного отношения на множестве признаков.
   
3. Поставить в соответствие каждой букве T – код (код «Тезея», который получается алгоритмом «Тезея» обхода графа бинарного отношения Р).
   
4. Написать программу структурного распознавания букв русского алфавита.
   

3.2. Распознавание радиолокационной картины местности.

Принцип ориентирования крылатой ракеты состоит в следующем. Целевая траектория задаётся в виде полетного задания, состоящего из последовательности образов, которые получаются при обработке радиолокационных покадровых съёмок местности. Каждый кадр представляет собой структуру вложенных друг в друга контуров. Кадру сопоставляется D – код (слово скобочного языка Дика).

1. Построить алгоритм обработки кадра и получения соответствующего D – кода.
   
2. Ввести меру сходства (расхождения) между эталонным D – словом и D – словом, полученным в реальном полете.
   
3. Написать программу кодирования радиолокационных кадров в слова языка Дика и вычисления значения меры расхождения полученного D – слова с эталонным.
   

СПИСОК ЛИТЕРАТУРЫ

1. Пойя Д. Математика и правдоподобные рассуждения. – М: ИЛ. 1957.
   
2. Журавлев Ю.И. и др. Дискретная математика и математические вопросы кибернетики. – М. Наука. 1974.
   
3. Shafer G. Mathematical Theory of Evidence. – Princeton Univ. 1976.
   
4. Кнут Д. Искусство программирования, т.2. – М.: Вильямс, 2000.
   
5. Новиков Ф.А. Дискретная математика для программистов. – СПб., Питер, 2000.
   
6. Ахо А. Структуры данных и алгоритмы. – М.: Вильямс. 2000.
   
7. Кормен Т. Алгоритмы, построение и анализ. – М.: МУНМО, 2000.
   
8. А. Тей и др. Логический подход к искусственному интеллекту. М.: Мир, 1990.
   
9. Новиков Д.А., Чхартишвили А.Г. Рефлексивные игры. М.: СИНТЕГ, 2003.
   
10. Непейвода Н.Н. Прикладная логика. Новосибирск. Из-во Новосибирского университета, 2000.
    
11. Гладков Л.А. и др. Генетические алгоритмы. М.: Физматлит, 2006.