Ю. А. Самарский 17 июня 2006 г. Программ а по курсу вычислительная математика по направлению 511600 факультет факи, ффкэ кафедра вычислительной математики курс III семестр 5 лекции
| Вид материала | Лекции |
СодержаниеСписок литературы Задача №20. Задача № 10. |
- Курс 2 Семестр 3 Лекции: 36 (часа) Лабораторные работы: 18(часов) Составитель, 725.91kb.
- Программа по дисциплине вычислительная математика, 44.55kb.
- Н. И. Лобачевского Факультет Вычислительной математики и кибернетики Кафедра Математического, 169.45kb.
- Рабочая программа по курсу «Высокопроизводительные вычислительные системы» по направлению, 95.97kb.
- Н. И. Лобачевского Факультет Вычислительной математики и кибернетики Кафедра Математического, 172.6kb.
- Курс IV семестры 8 (весенний) лекции 16 часов Экзамен 8 семестр (весенний), 30.19kb.
- Программа по курсу: современные технологии параллельного программирования (по выбору), 69.72kb.
- Н. И. Лобачевского Факультет Вычислительной математики и кибернетики Кафедра Математического, 123.69kb.
- Курс, 3-й семестр лекции (48 часов), экзамен практикум на ЭВМ (64 часа), зачет с оценкой, 60.04kb.
- Н. И. Лобачевского Факультет Вычислительной Математики и Кибернетики Кафедра иисгео, 4000.54kb.
УТВЕРЖДАЮ
Проректор по учебной работе
Ю.А. Самарский
17 июня 2006 г.
П Р О Г Р А М М А
по курсу ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
по направлению 511600
факультет ФАКИ, ФФКЭ
кафедра вычислительной математики
курс III
семестр 5
лекции – 34 часа Экзамен – нет
практические (семинарские)
занятия – нет Диф. зачет – 5 семестр
лабораторные занятия – 34 часа Самостоятельная работа –
2 часа в неделю
ВСЕГО ЧАСОВ 68
Программу составил д.ф.-м.н., профессор В. В. Демченко
Программа обсуждена на заседании
кафедры вычислительной математики
12 апреля 2006 года.
Заведующий кафедрой А.С. Холодов
I. Погрешности при решении прикладных задач. Классификация погрешностей, особенности возникновения и накопления ошибок.
II. Системы линейных уравнений высокого порядка. Неустранимая погрешность. Число обусловленности.
II.1. Точные методы решения.
- Метод Гаусса.
- Метод ортогонализации.
II.2. Итерационные методы.
- Метод простой итерации.
- Метод Зейделя.
Теорема о необходимых и достаточных условиях сходимости.
III. Нелинейные уравнения и системы уравнений.
III.1. Задача локализации корней. Алгебраические уравнения. Теоремы Декарта, Бюдана–Фурье, Штурма.
III.2. Численные методы нахождения корней скалярных уравнений с заданной точностью. Принцип сжимающих отображений. Условие Липшица.
- Метод половинного деления.
- Метод простой итерации.
- Метод секущих.
- Метод Ньютона.
- Методы высших порядков сходимости.
Условия сходимости. Порядок сходимости итерационного процесса. Условия достижения заданной точности.
III.3. Решение нелинейных систем уравнений.
- Метод простой итерации.
- Метод Ньютона.
- Метод наискорейшего спуска.
Условия сходимости итерационного процесса.
IV. Приближение функций, заданных в конечномерных
пространствах.
IV.1. Интерполяция. Понятие об обобщенном интерполяционном многочлене. Существование и единственность интерполяционного многочлена, представление его в форме Ньютона. Конечные и разделенные разности. Интерполяционный многочлен в форме Лагранжа, Эрмита. Остаточный многочлен интерполяции.
Сплайн-интерполяция.
IV.2. Среднеквадратичное приближение. Ортонормирванные системы в гильбертовом пространстве. Переопределенные линейные системы уравнений.
IV.3. Равномерное приближение. Многочлены Чебышева.
- Численное дифференцирование. Вывод формул численного дифференцирования. Оценка погрешности.
Оптимальный шаг численного дифференцирования.
- Численное интегрирование. Квадратурные формулы Ньютона–Котеса. Метод Гаусса. Метод Монте-Карло. Оценка погрешности.
- Обыкновенные дифференциальные уравнения (ОДУ). Метод Эйлера. Сходимость, невязка, аппроксимация, устойчивость. Теорема о сходимости, являющейся следствием аппроксимации и устойчивости.
- ОДУ. Задача Коши. Нежесткие уравнения.
VIII.1. Вывод формул метода Рунге–Кутты. Таблицы Бутчера. Оценка погрешности и выбор длины шага интегрирования. Неявные методы Рунге–Кутты.
VIII.2. Вывод формул метода Адамса. Особенности численной реализации и сохранения порядка.
VIII.3. Системы уравнений. Уравнения второго и более высоких порядков.
СПИСОК ЛИТЕРАТУРЫ
1. Рябенький В.С. Введение в вычислительную математику. — М.: Наука–Физматлит, 1994. —335 с.
2. Годунов С.К., Рябенький В.С. Разностные схемы. — М.: Наука, 1977.
3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные
методы. — М.: Наука, 1987.
4. Косарев В.И. 12 лекций по вычислительной математике. Вводный курс. — М.: Изд-во МФТИ, 1995. — 175 с.
5. Хайрер Э., Нёрсетт С.,Ваннер Г. Решение обыкновенных дифференциальных уравнений (Нежесткие задачи). — М.: Мир, 1990.
6. Демченко В.В. Распад произвольного гидродинамического разрыва. — М.: изд. МФТИ, 1998. — 54 с.
7. Сборник задач для упражнений по курсу вычислительной математики / Под ред. Рябенького В.С. – М.: МФТИ, 1988.
8. Дробышевич В.И., Дымников В.П., Ривин Г.С. Задачи по вычислительной математике. — М.: Наука, 1980.
9. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. — М.: Высшая школа, 2000.
ЗАДАНИЕ 1
- Погрешности – задачи: [7] – (I.1);
Задача № 2.

Пусть приближенное значение производной функции
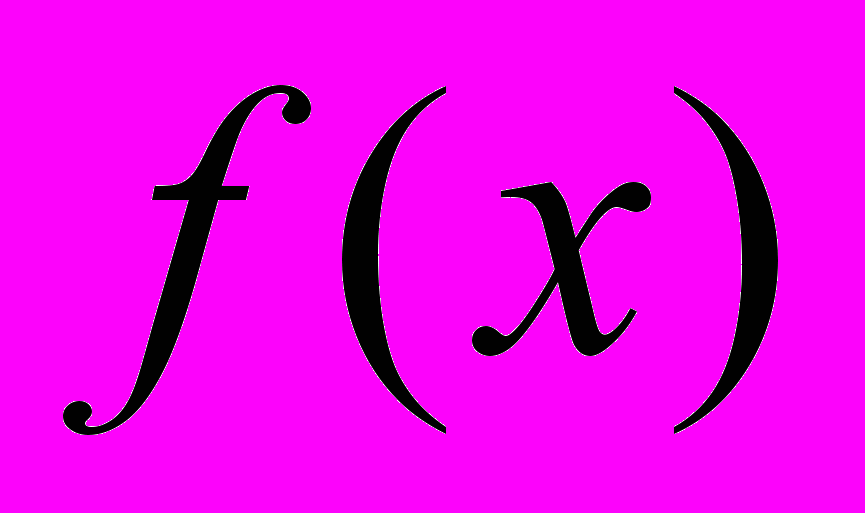 определяется при
определяется при 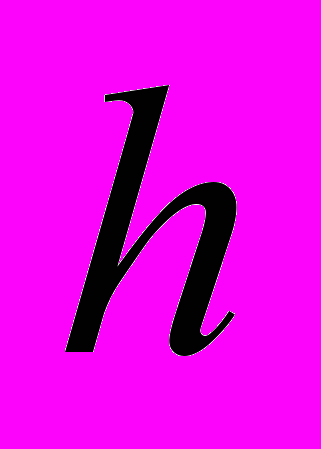 << 1 по одной из формул:
<< 1 по одной из формул: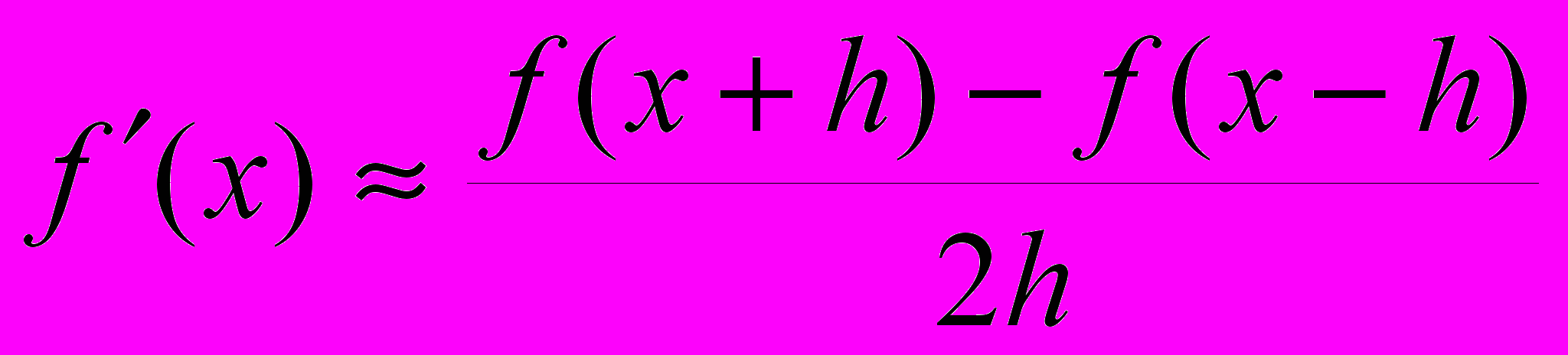
или
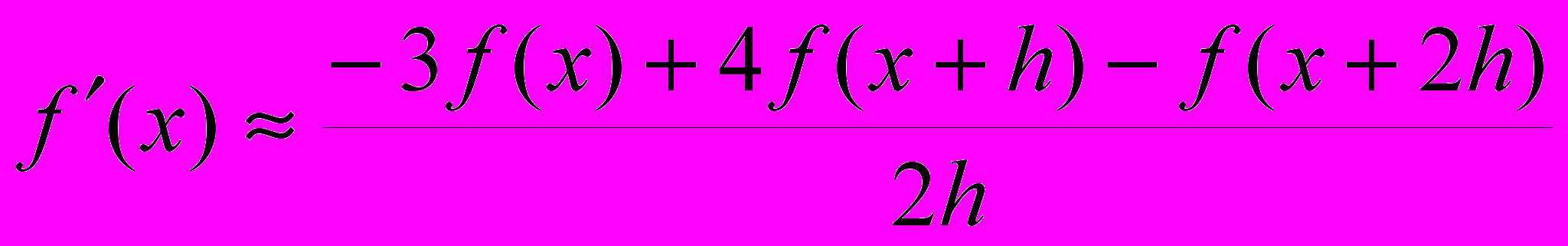 ,
,а сами значения
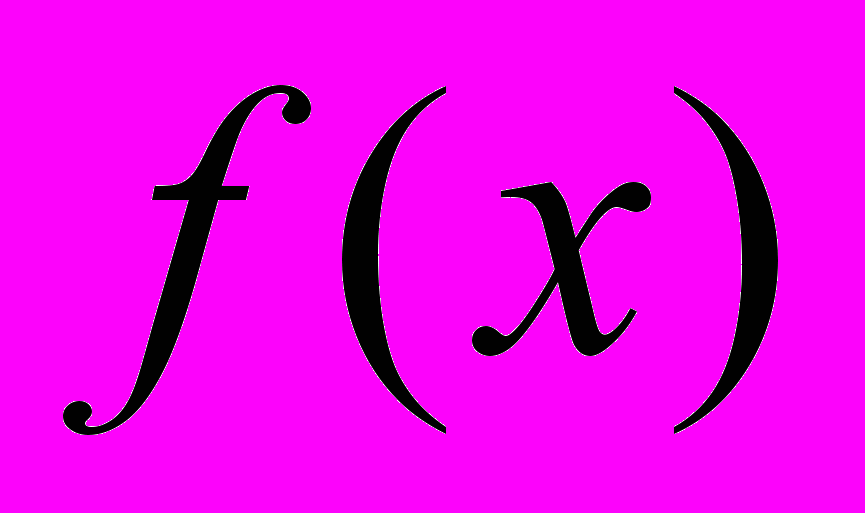 вычисляются с абсолютной погрешностью
вычисляются с абсолютной погрешностью  . Какую погрешность можно ожидать при вычислении производной, если
. Какую погрешность можно ожидать при вычислении производной, если 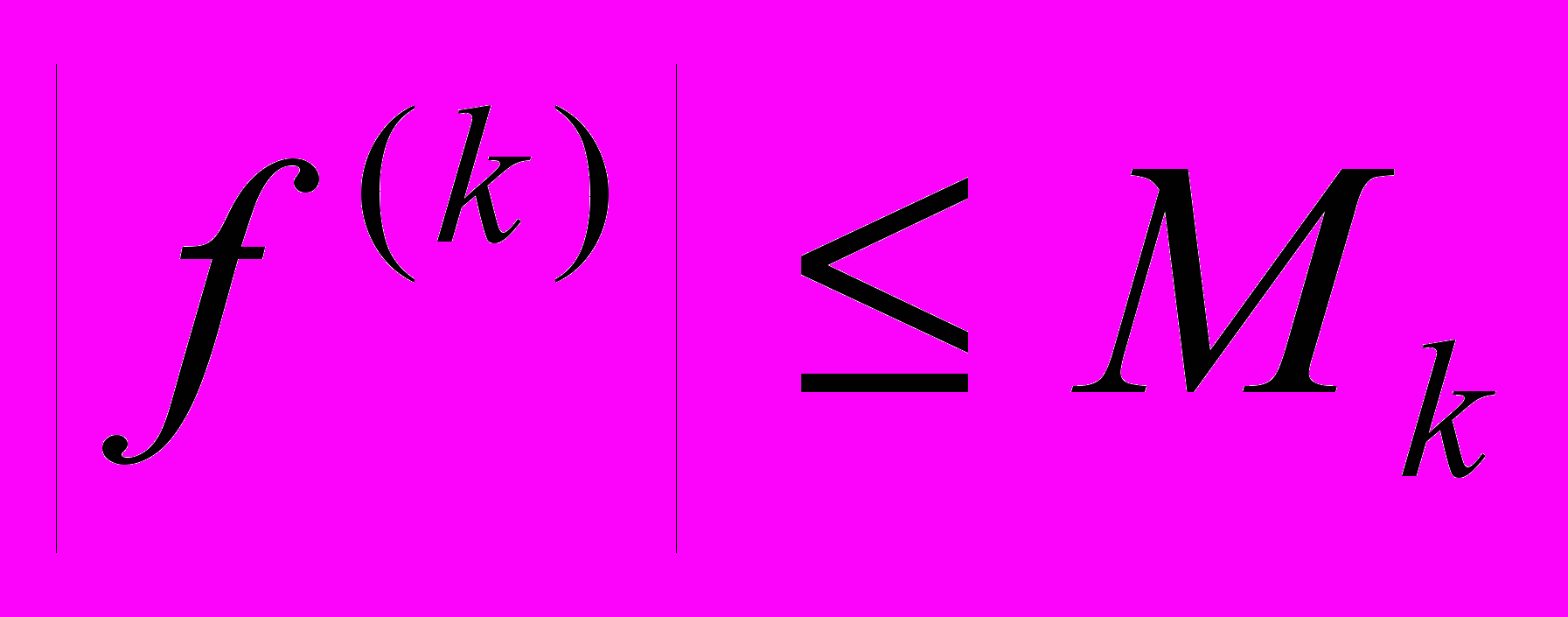 ,
, k = 0, 1, … ?
- Линейные системы — задачи: [7] – (II.2), (II.4), (II.9);
Задача № 6.
Доказать, что если С – симметричная положительно определенная матрица, то
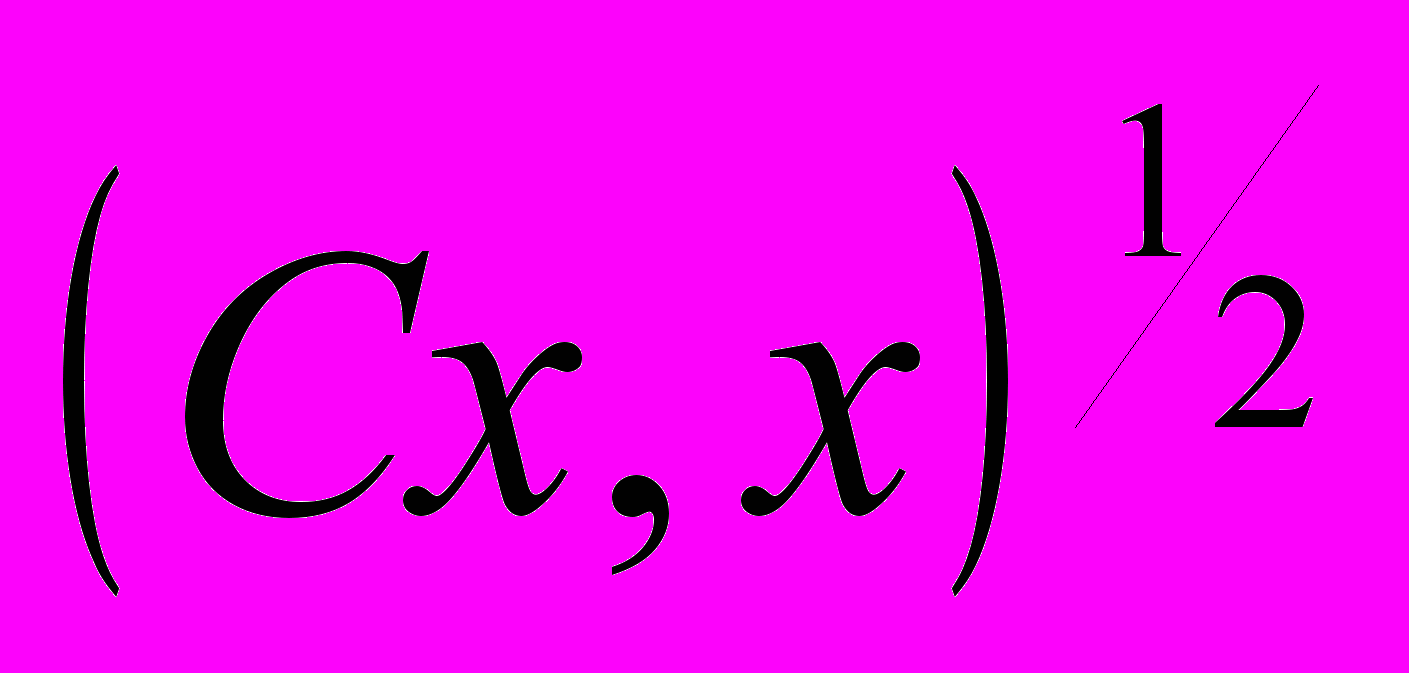 есть норма вектора x.
есть норма вектора x. Задача № 7.
Доказать, что всякая норма матрицы согласована с некоторой нормой вектора.
Задача № 8.
Доказать, что норма
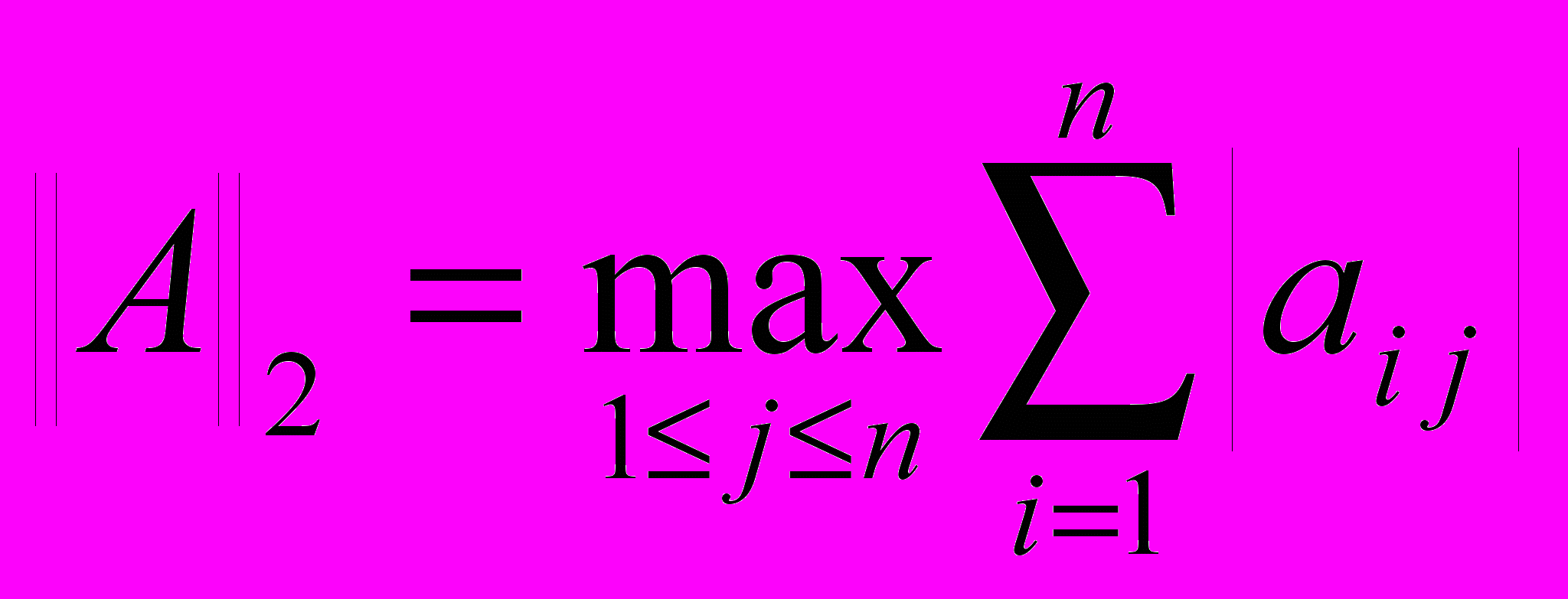 подчинена норме
подчинена норме  .
.Задача № 9.
Доказать, что норма
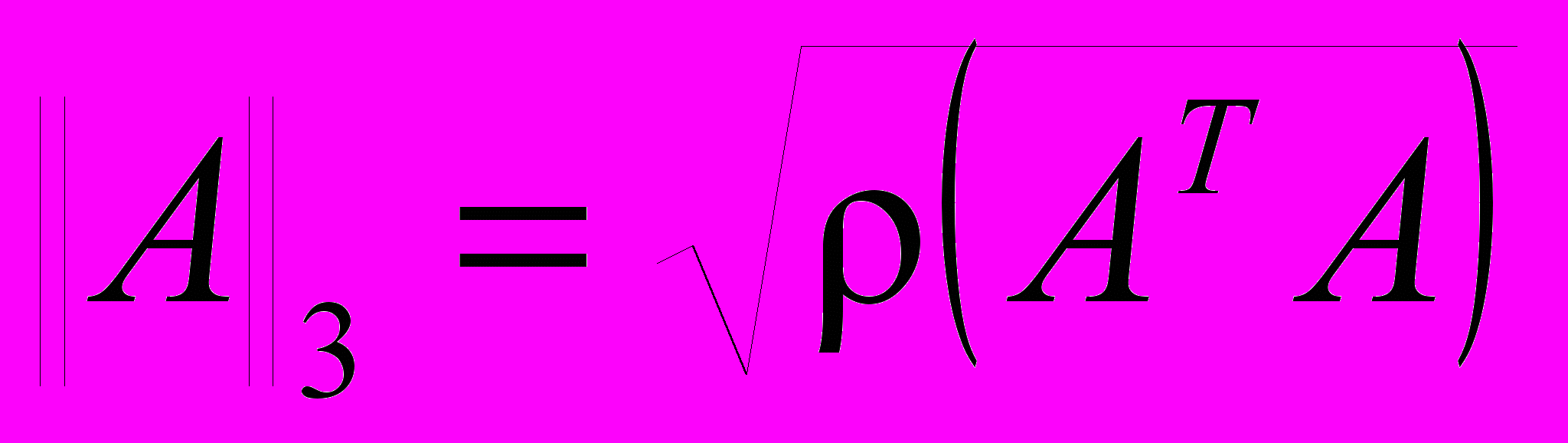 подчиненa норме
подчиненa норме 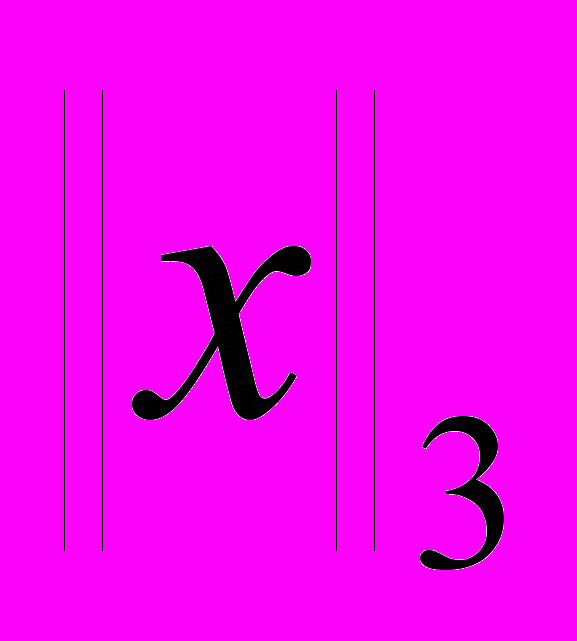 .
.Задача № 10.
При каком векторе
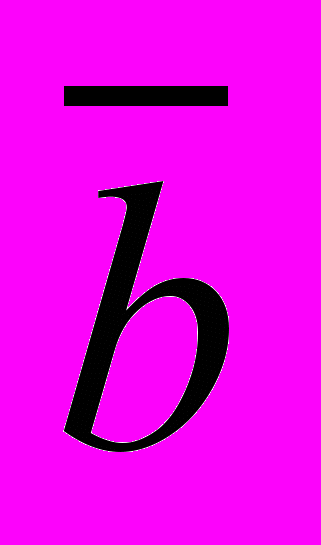 и произвольной погрешности
и произвольной погрешности  , допущенной при его задании, максимальна величина
, допущенной при его задании, максимальна величина  в оценке относительной погрешности решения
в оценке относительной погрешности решения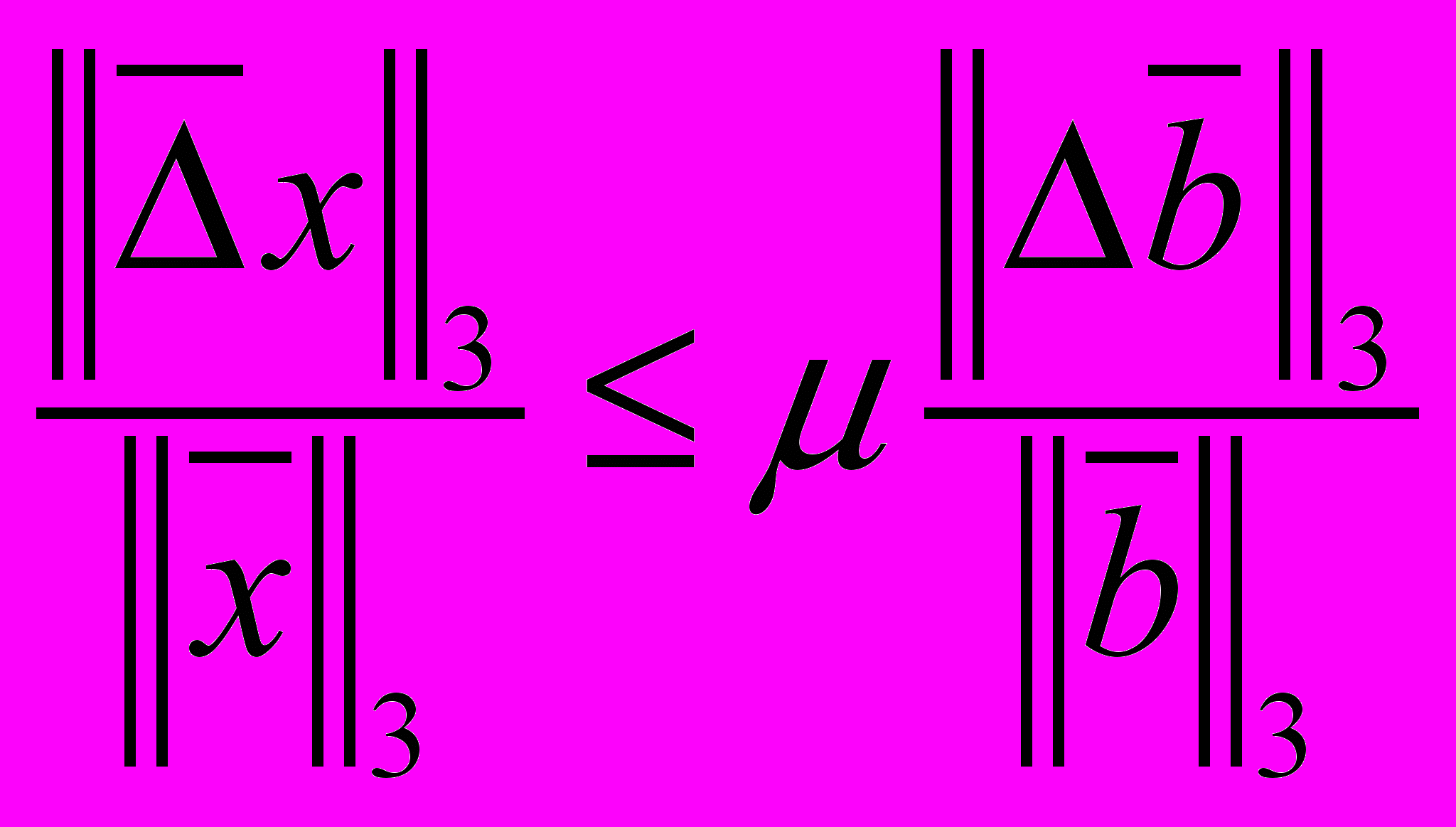
для системы линейных уравнений
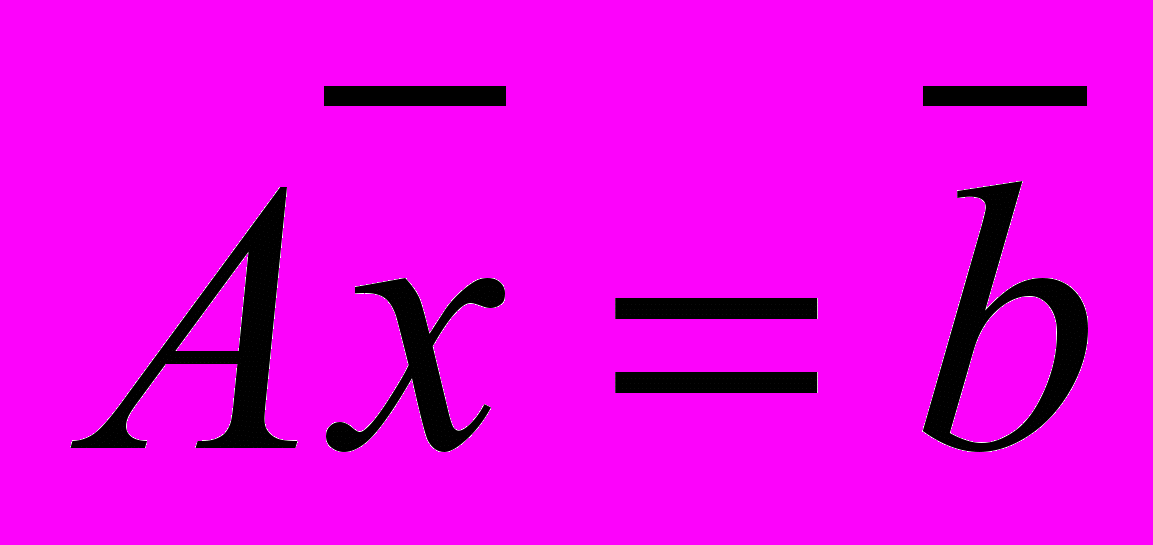 , где
, где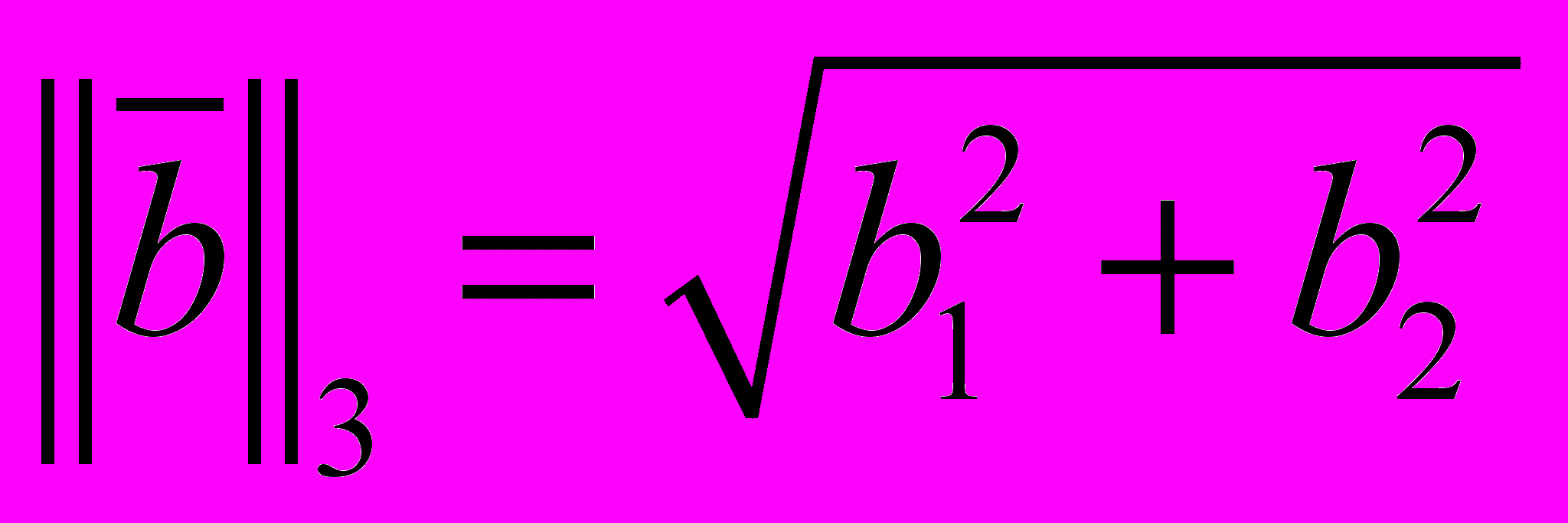 , и чему равна
, и чему равна  ?
?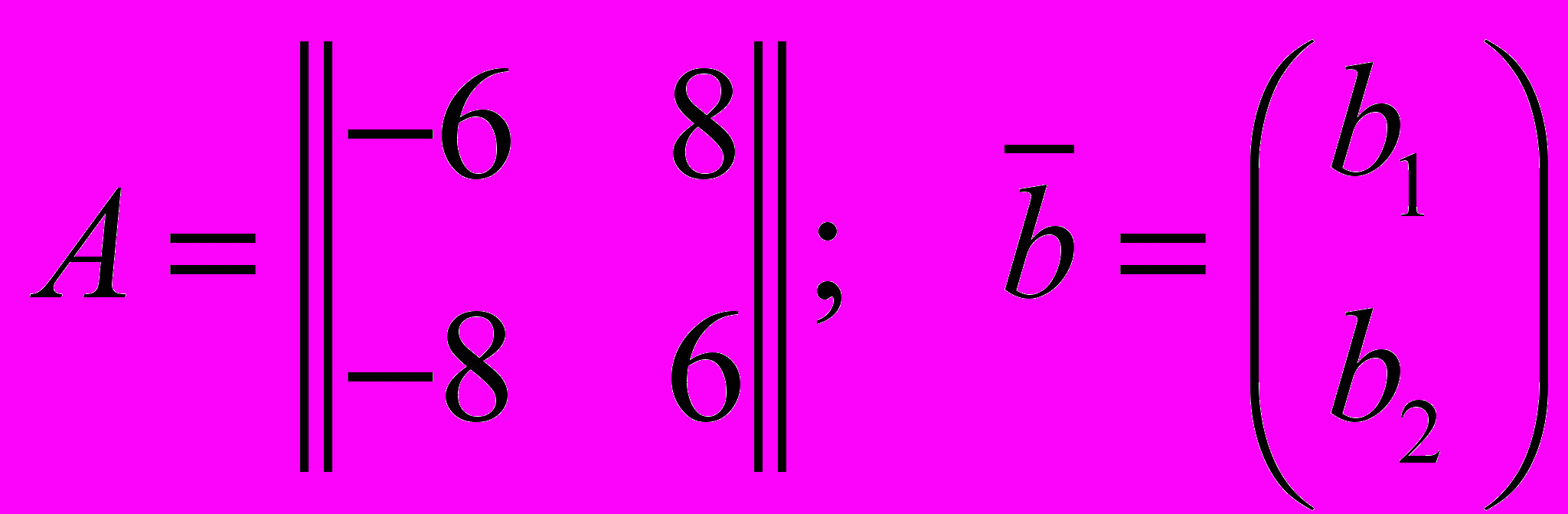 .
.Задача № 11.
При каких значениях параметра
 метод
метод 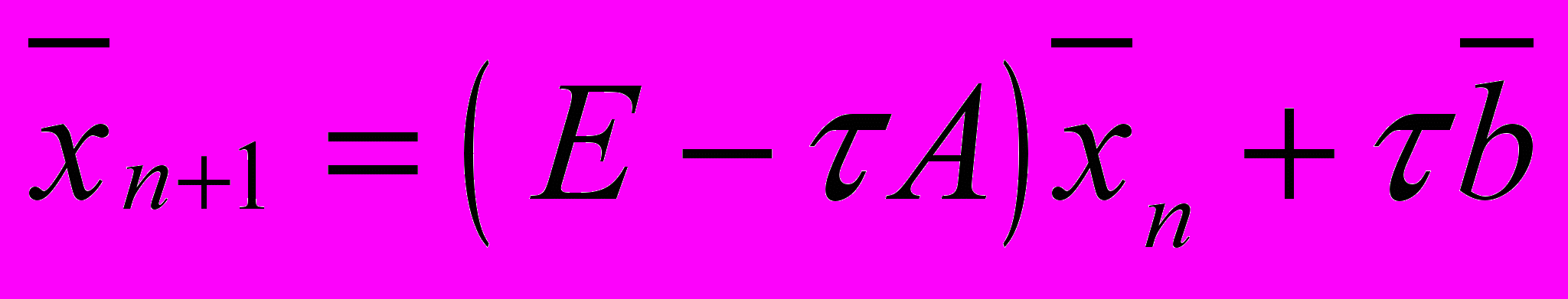 сходится с произвольного начального приближения для системы линейных уравнений
сходится с произвольного начального приближения для системы линейных уравнений 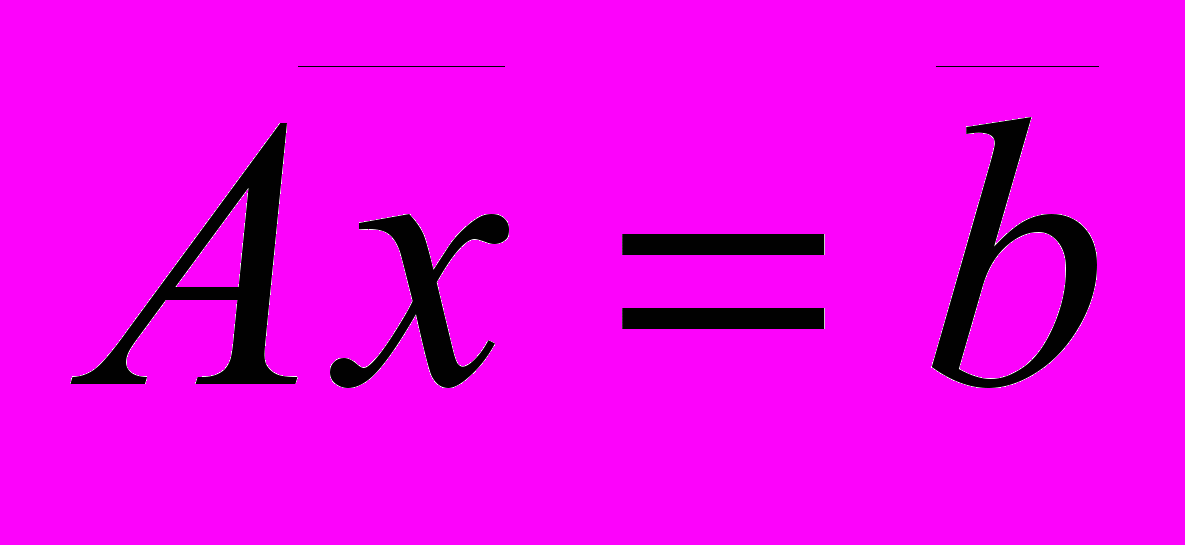 с матрицей
с матрицей 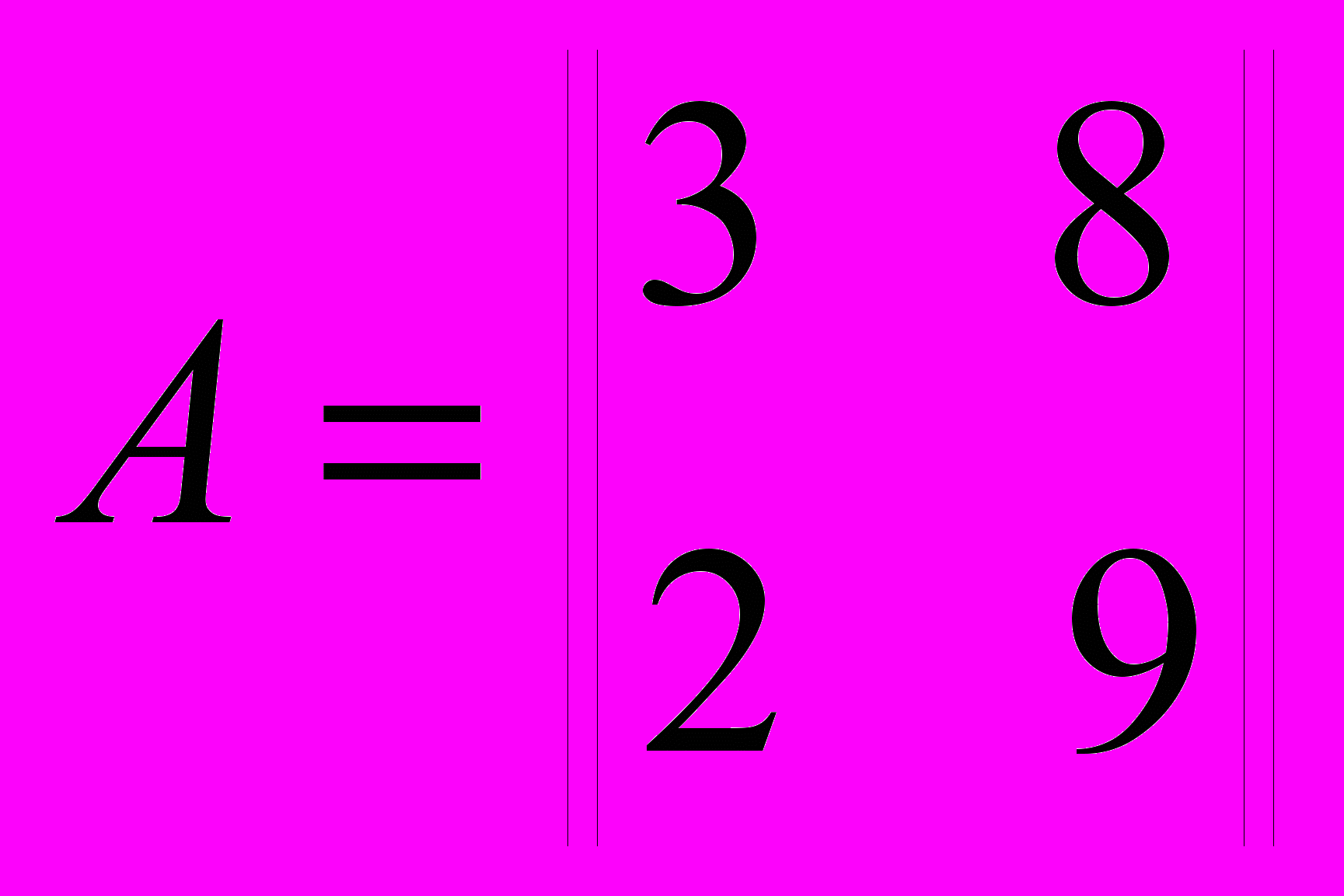 .
.Задача № 12.
Найти
 , при которых метод Гаусса–Зейделя будет сходящимся для систем уравнений с матрицами:
, при которых метод Гаусса–Зейделя будет сходящимся для систем уравнений с матрицами: .
.- Нелинейные уравнения и системы — задачи: [7] – (IV.8 в, м), (IV.12 б, г);
Задача № 15.
Отделить действительные корни, выбрать точку начального приближения, написать итерационную формулу метода Ньютона для уточнения одного из действительных корней уравнения, проверить выполнение условий сходимости метода и привести оценку достижения заданной точности при вычислениях
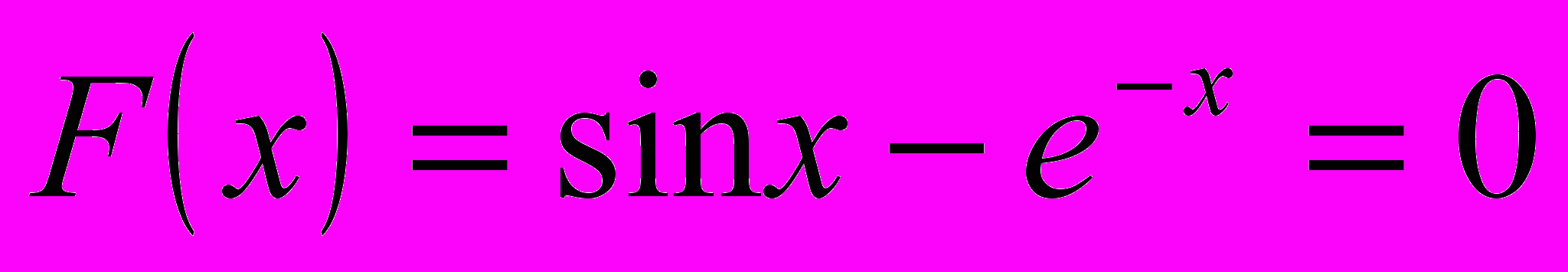 .
.Задача № 16.
Локализовать действительные корни алгебраического уравнения
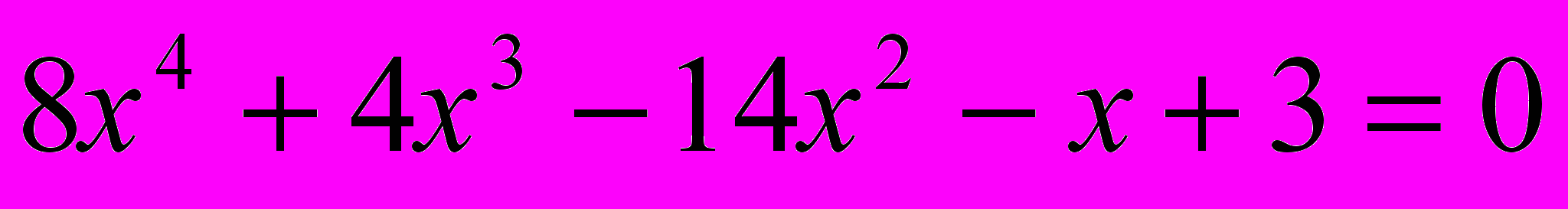 .
.Задача № 17.
Определить порядок сходимости итерационного метода при вычислении корня
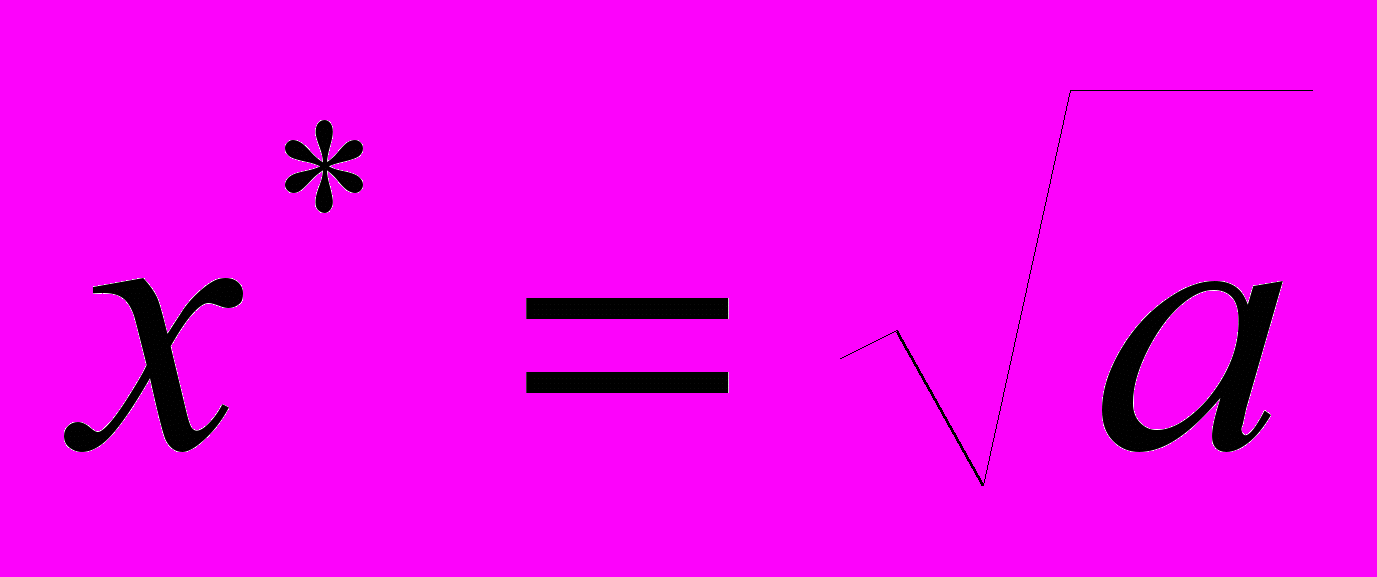 по формуле
по формуле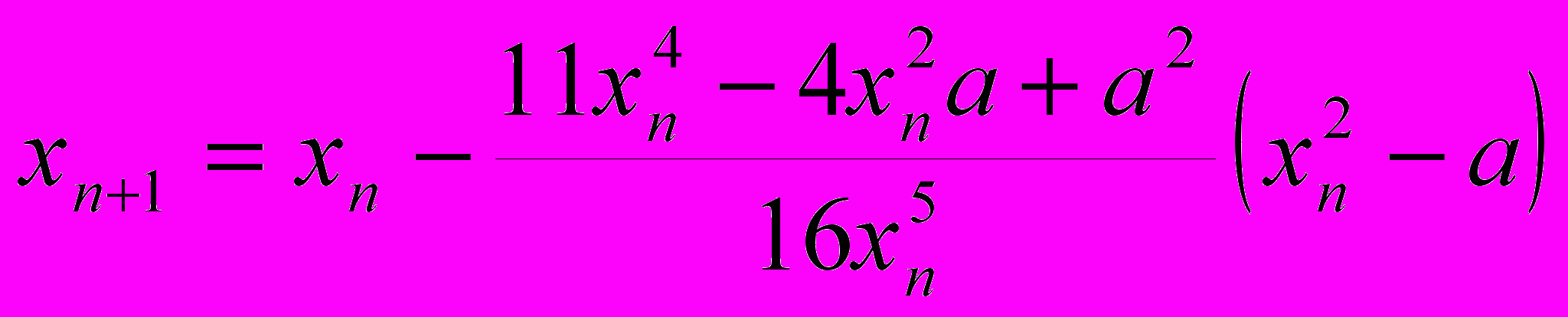 .
.Задача № 18.
Предложить метод простой итерации и определить область его сходимости для решения уравнения
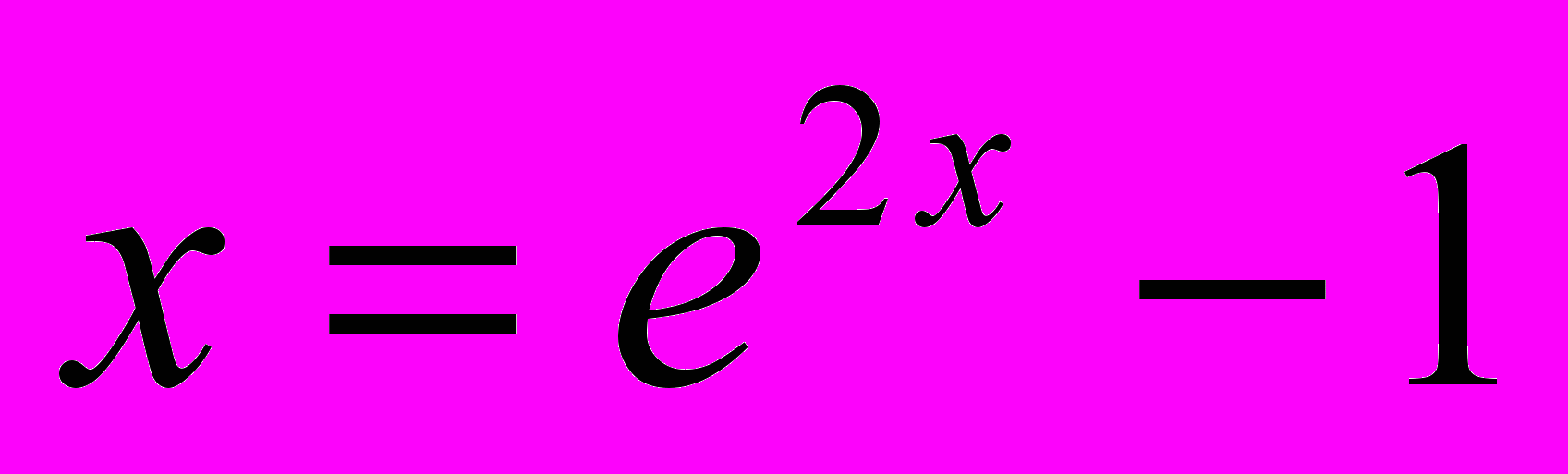 .
.Задача № 19.
Уравнение
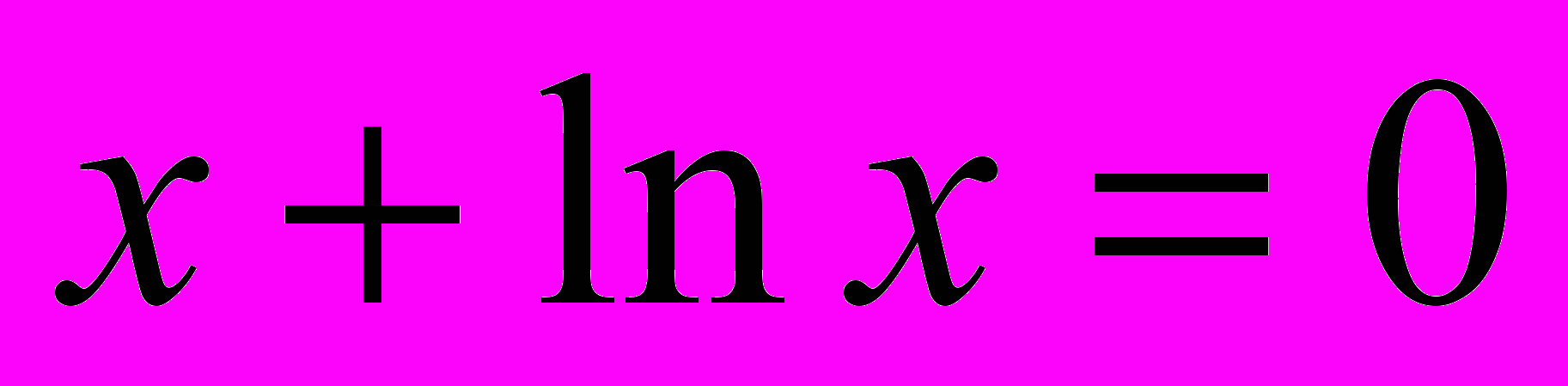 , имеющее корень
, имеющее корень 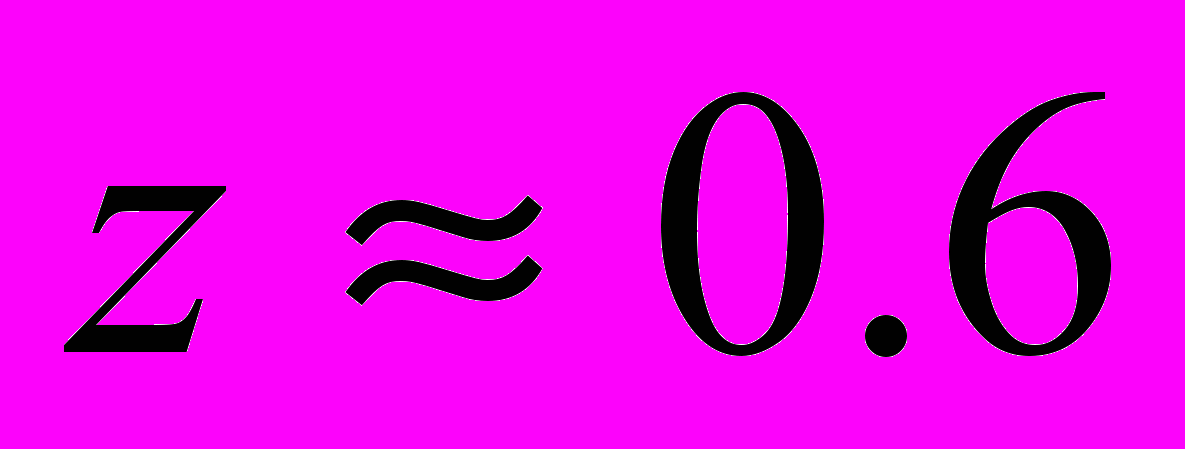 , предлагается решить одним из методов простой итерации:
, предлагается решить одним из методов простой итерации:1)
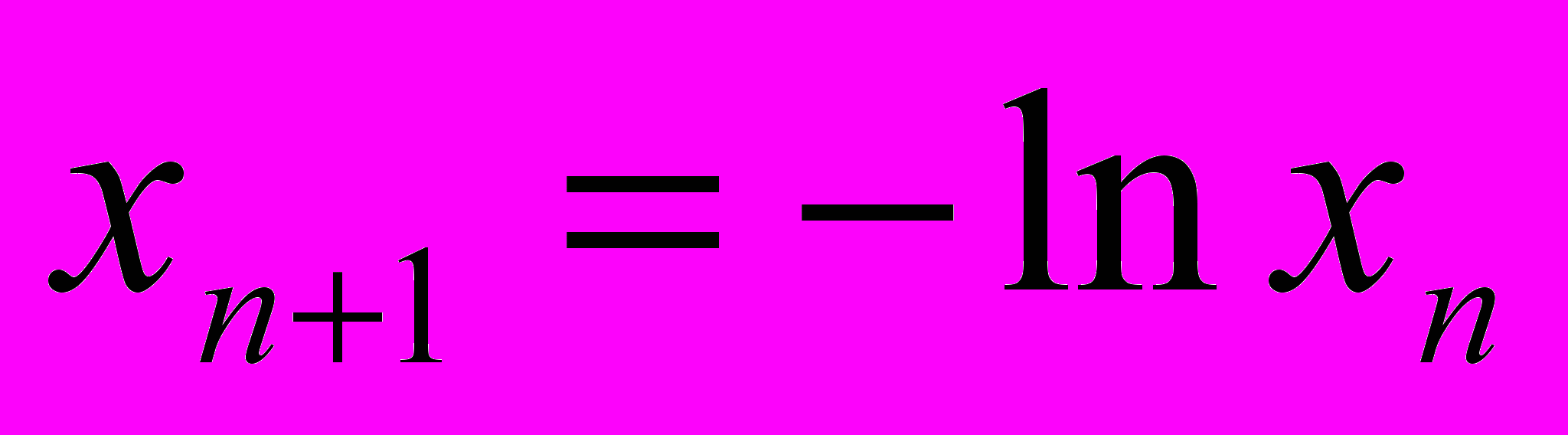 ; 2)
; 2) 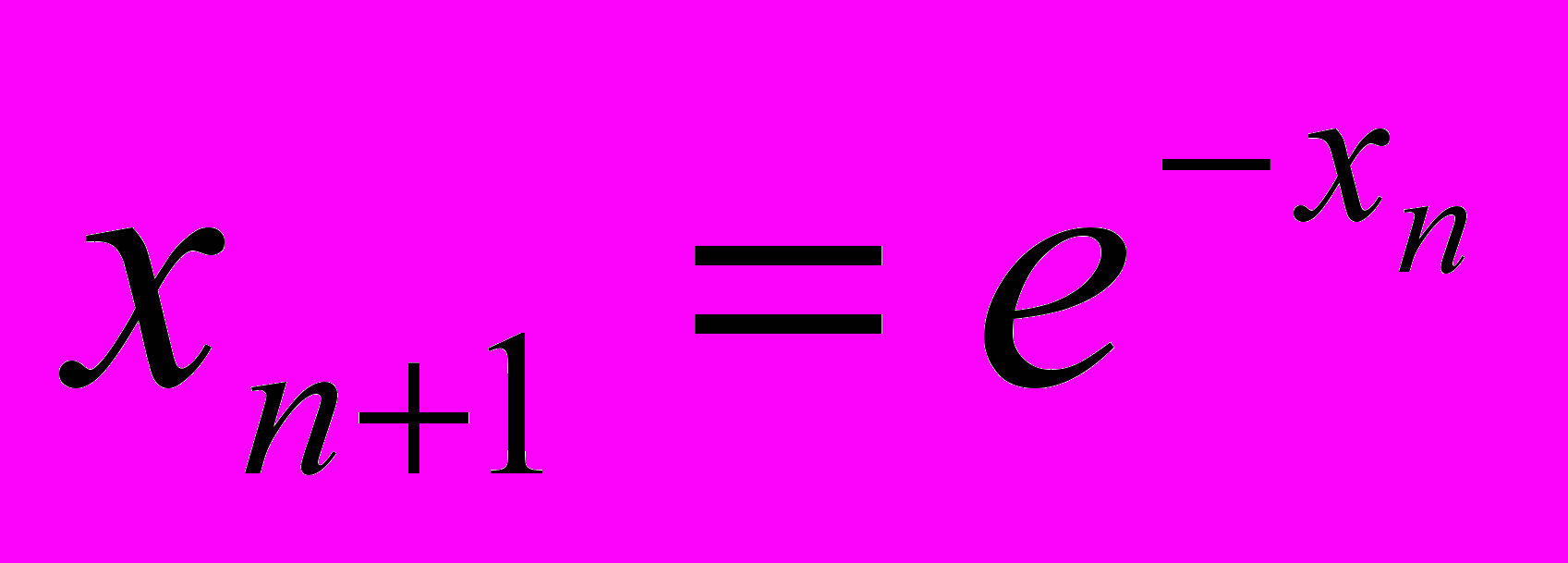 ;
;3)
 ; 4)
; 4) 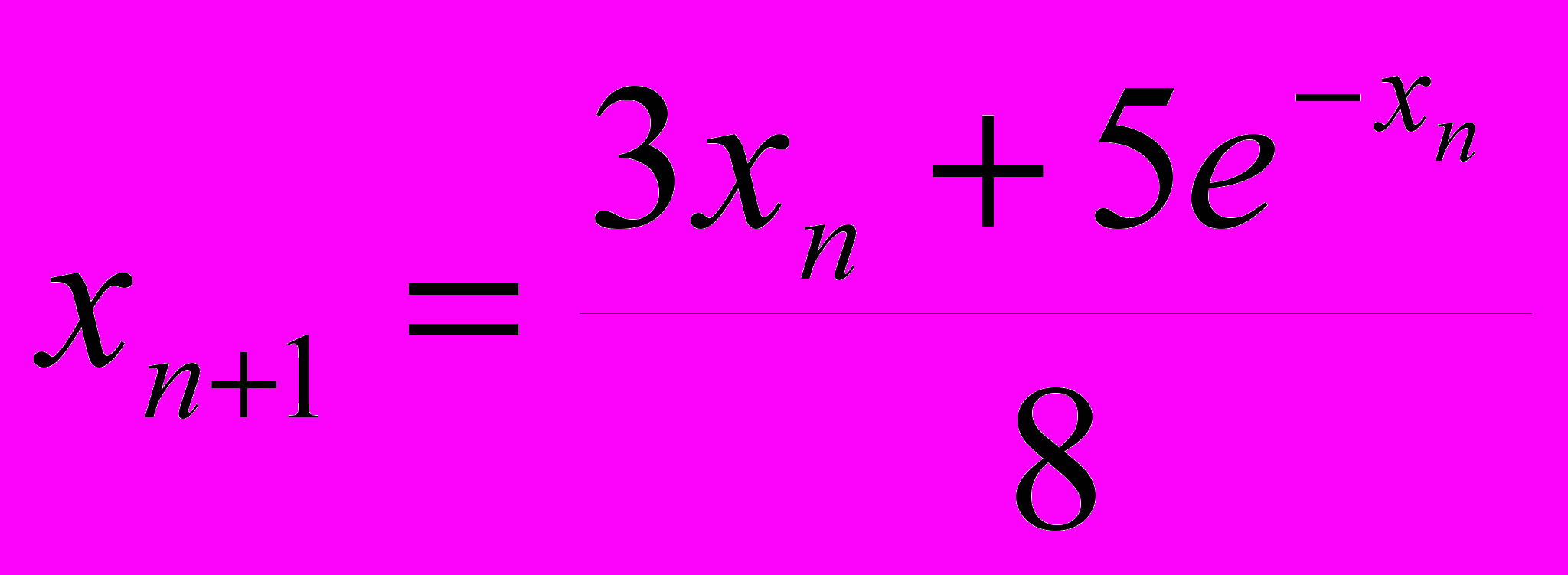 .
.Исследовать эти методы и сделать выводы о целесообразности использования каждого из них.
Задача №20.
Указать начальное приближение и оценить число итераций в методе Ньютона, требующихся для достижения точности
 для системы уравнений:
для системы уравнений: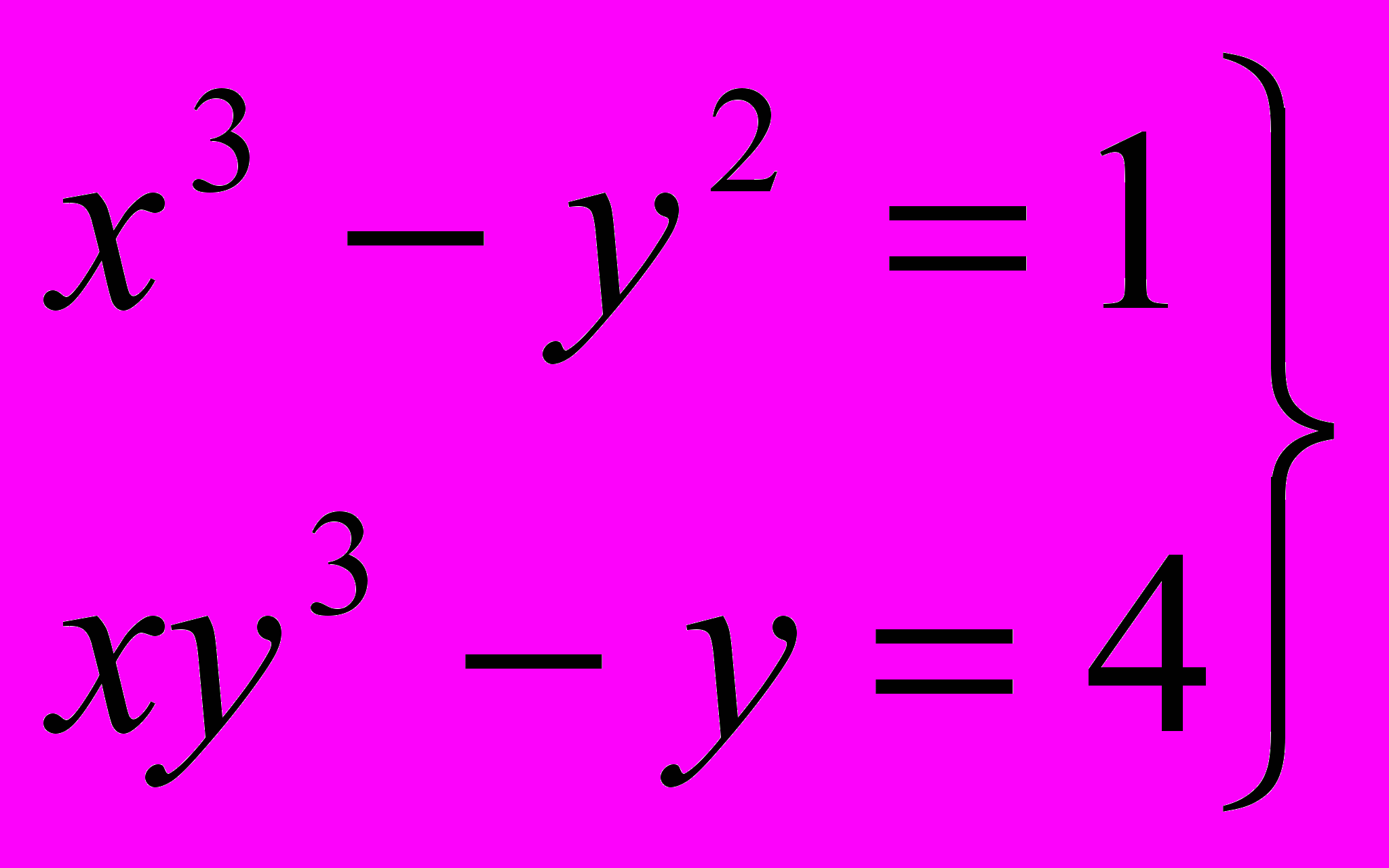 .
.ЗАДАНИЕ 2
- Приближение функций.
IV.1. Интерполяция — задачи: [7] – (V.1), (V.3), (V.5).
Задача №4.
Для заданной таблицы значений достаточно гладкой функции построить интерполяционный многочлен, обеспечивающий погрешность интерполяции, соответствующую точности задания таблицы, и вычислить его значение при
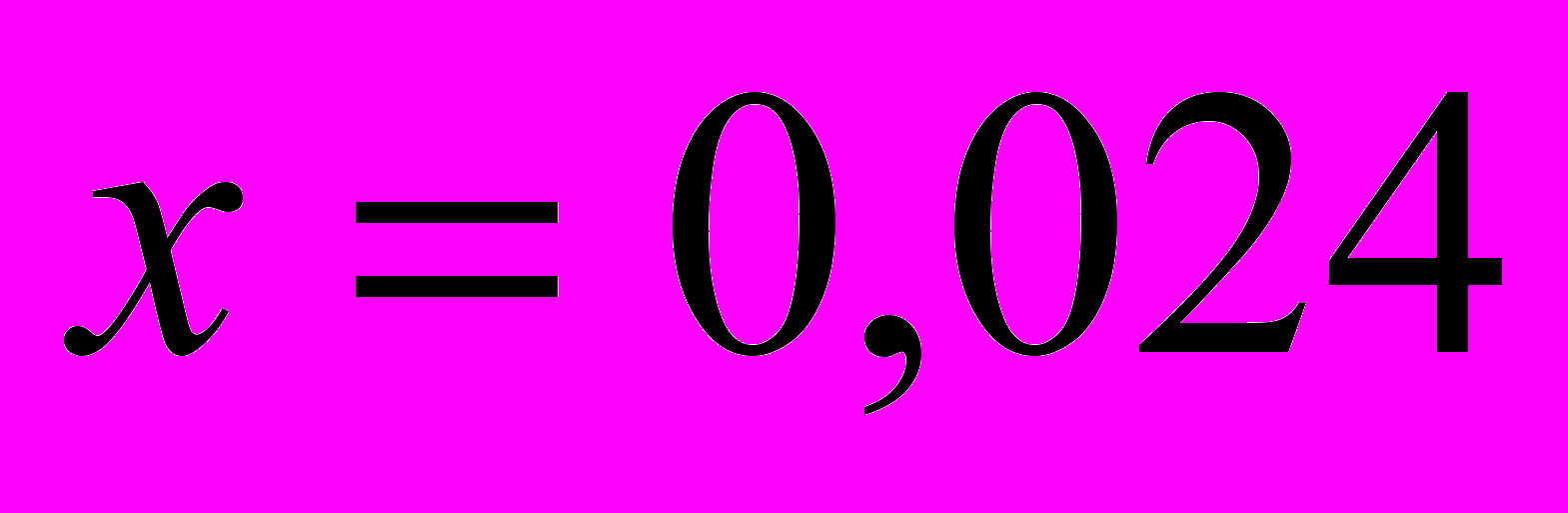 .
.-
x
0,0000
0,0100
0,0200
0,0300
0,0400
0,0500
y
1,0000
1,0101
1,0202
1,0305
1,0407
1,0513
-
x
0,0600
0,0700
0,0800
0,0900
0,1000
y
1,0618
1,0725
1,0833
1,0942
1,1053
Задача № 5.
Для заданной таблицы значений достаточно гладкой функции оценить погрешность квадратичной (линейной) интерполяции при
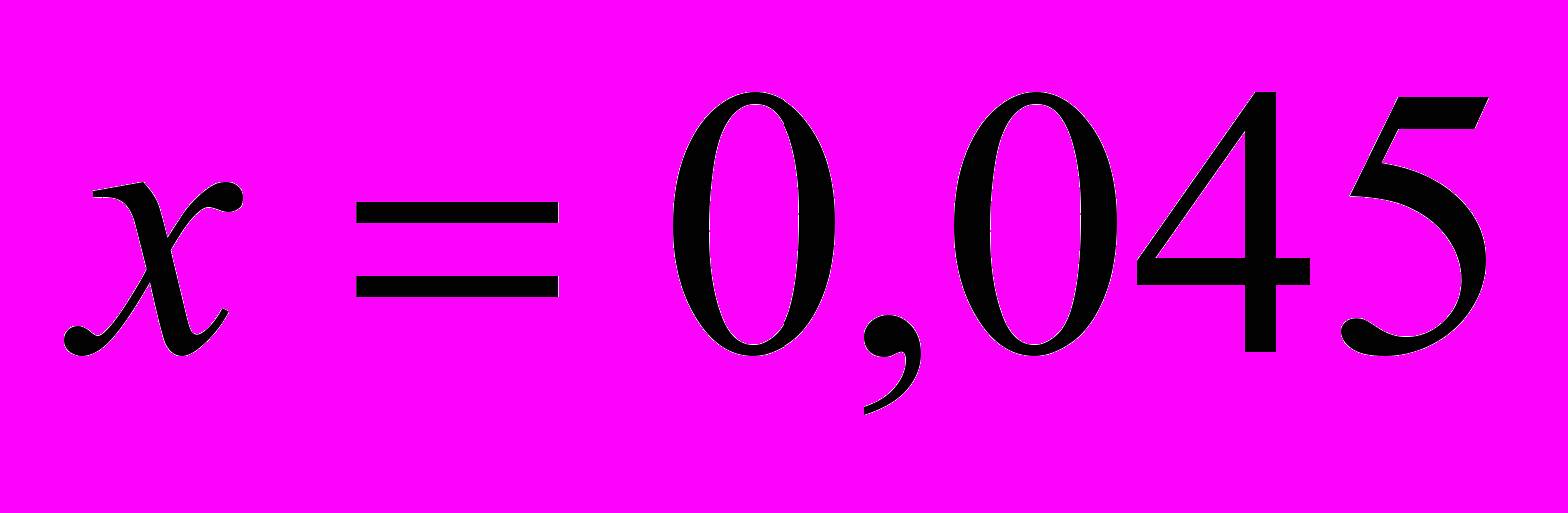
-
x
0,0000
0,0100
0,0200
0,0300
0,0400
0,0500
y
1,0000
1,0101
1,0202
1,0305
1,0407
1,0513
-
x
0,0600
0,0700
0,0800
0,0900
0,1000
y
1,0618
1,0725
1,0833
1,0942
1,1053
IV.2. Cреднеквадратичное приближение — задачи: [7] – (III.1), (III.9).
Задача № 8.
Задана таблица приближенных значений функции
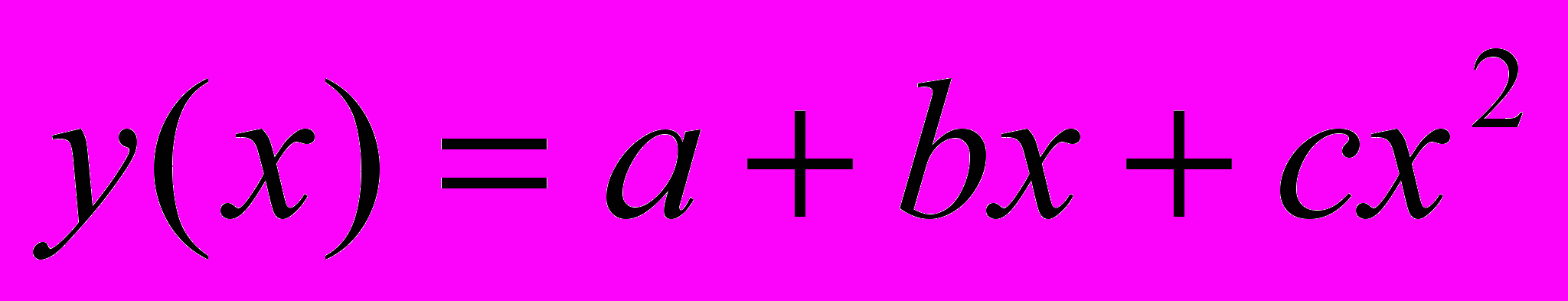 . Определить коэффициенты
. Определить коэффициенты 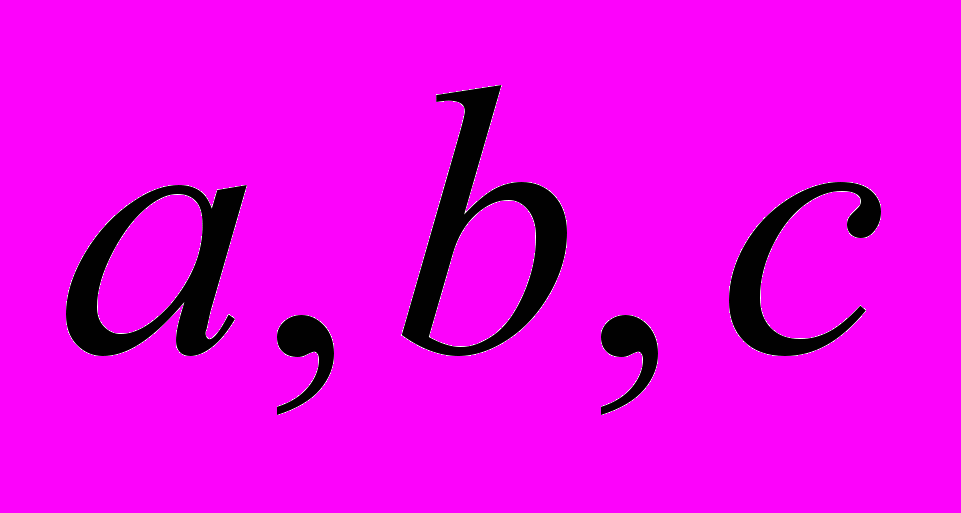 методом наименьших квадратов
методом наименьших квадратов-
x
-3
-2
-1
0
1
2
3
y
-10
-5
-2
0
2
5
10
Задача № 9.
Для заданной таблицы значений функции, где в качестве узлов
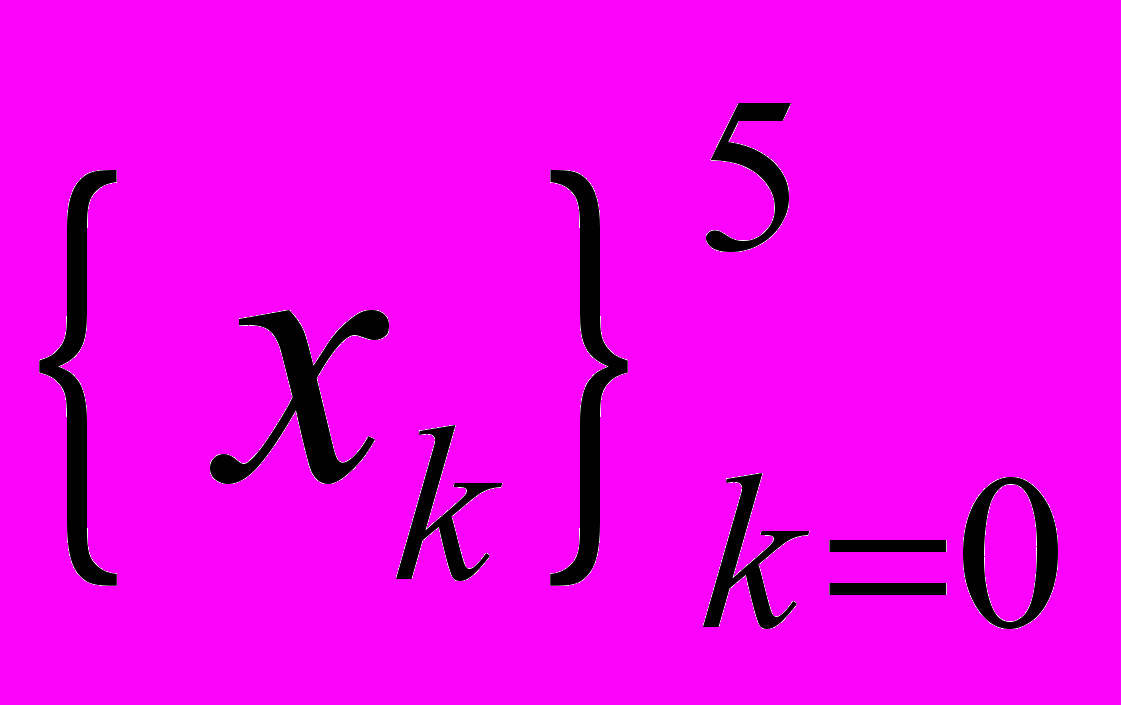 выбраны нули многочлена Чебышева
выбраны нули многочлена Чебышева 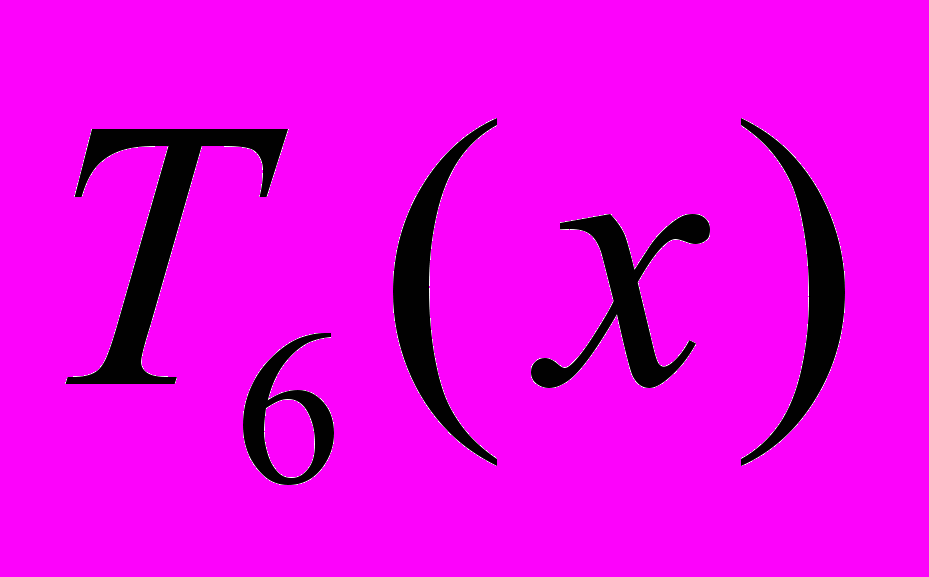 , определить элемент
, определить элемент 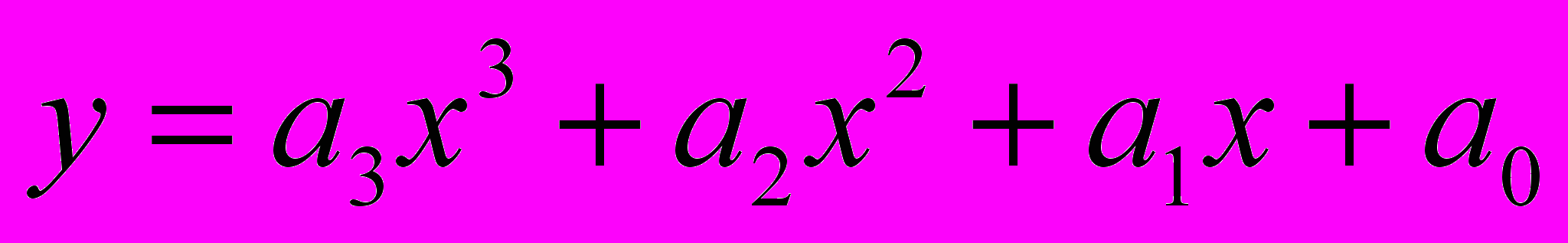 (
(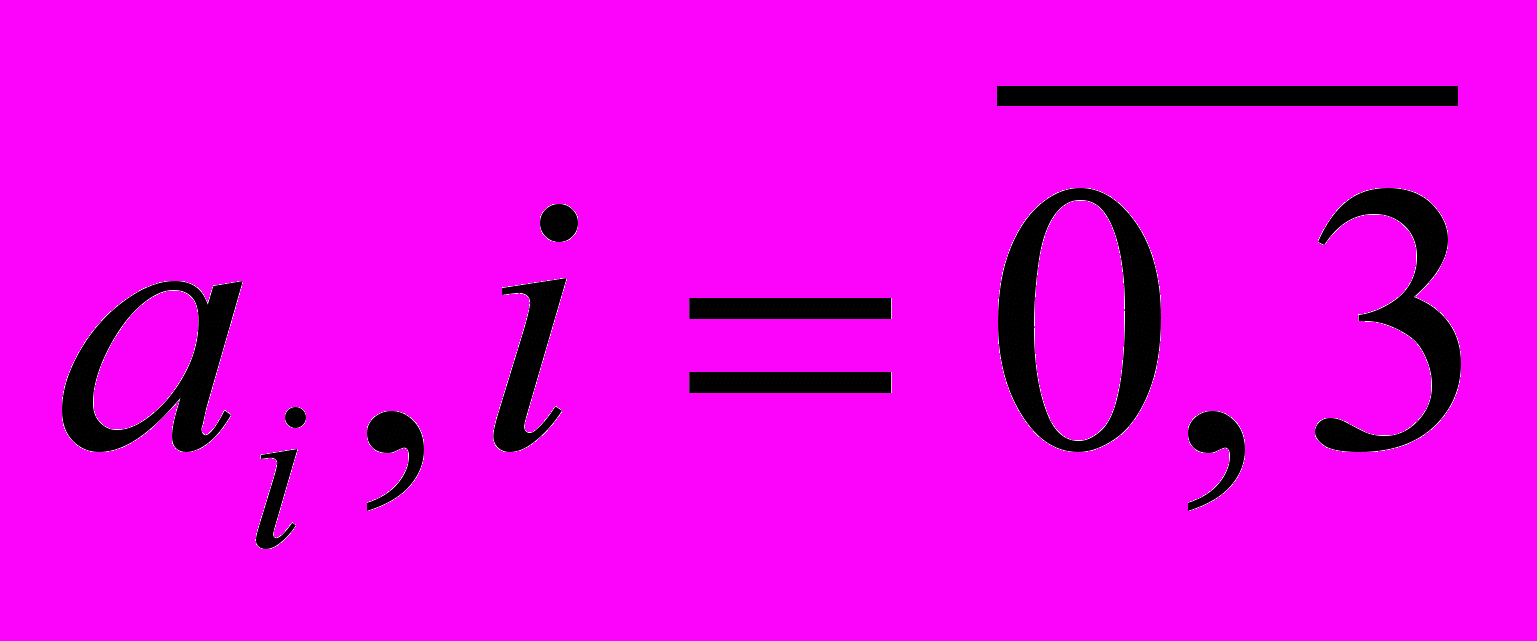 –постоянные) наилучшего среднеквадратичного приближения
–постоянные) наилучшего среднеквадратичного приближения-
x
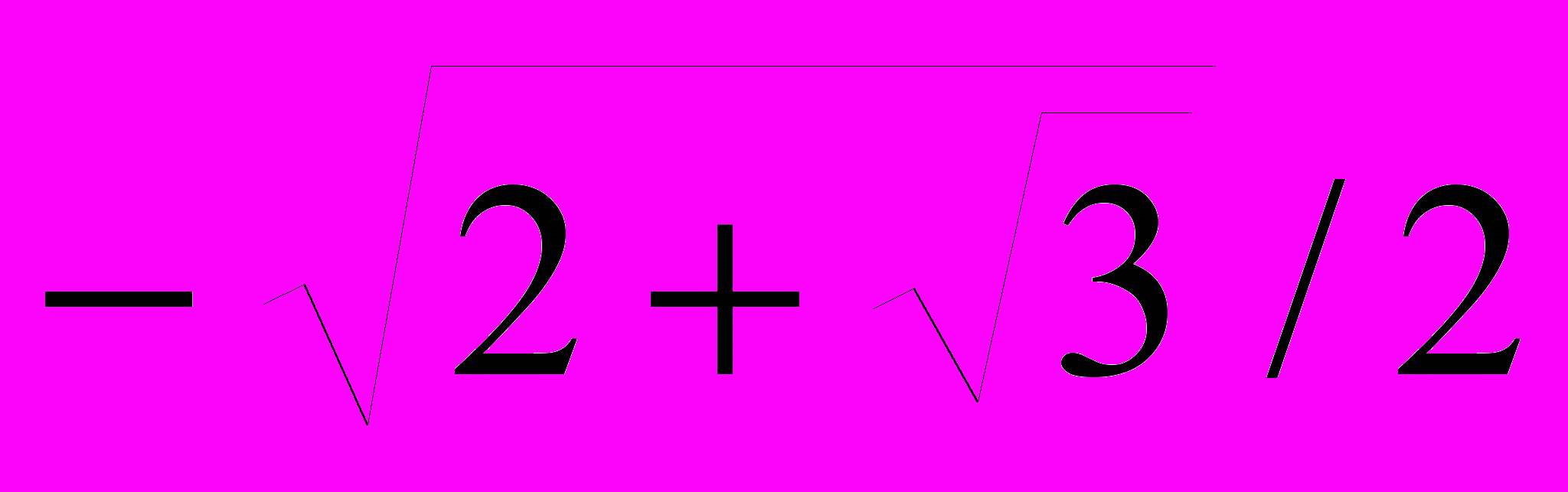
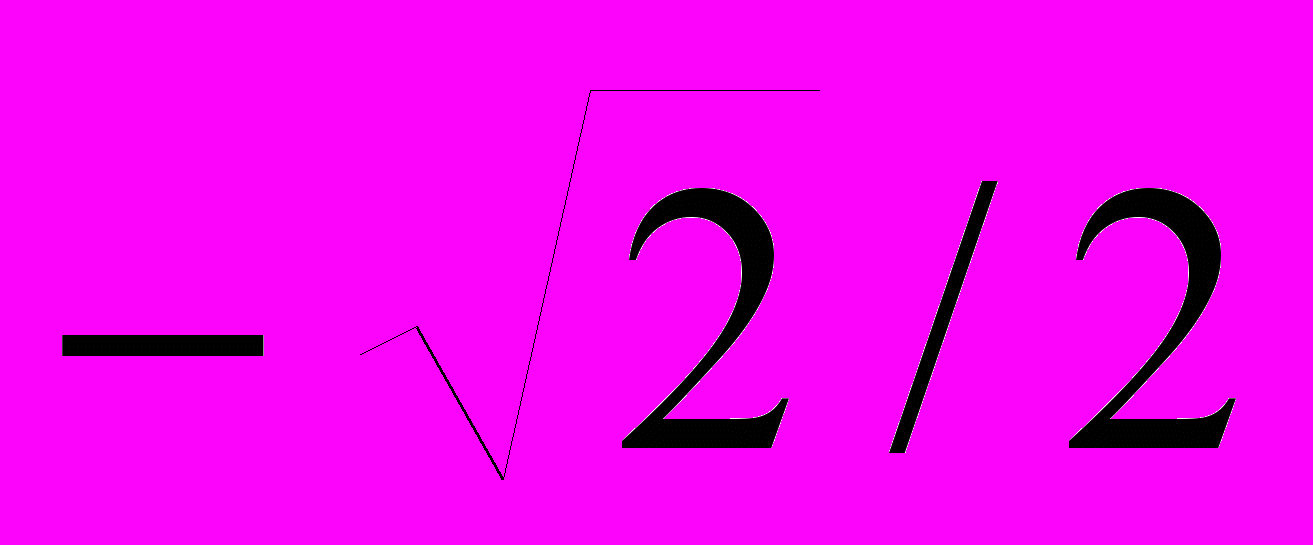


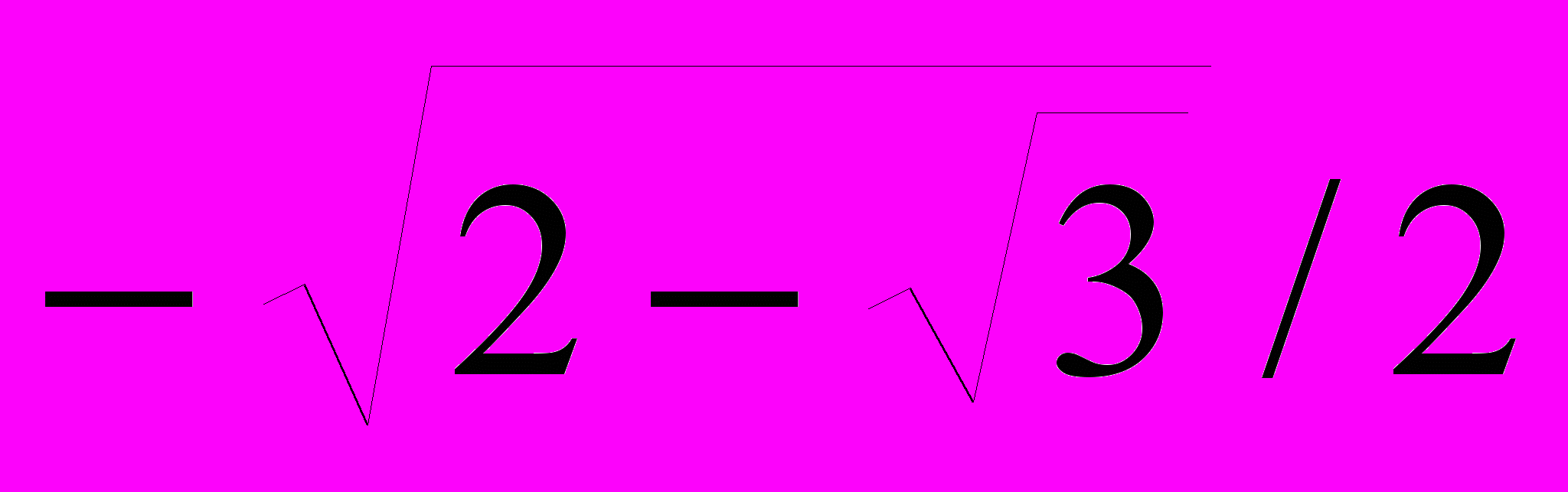
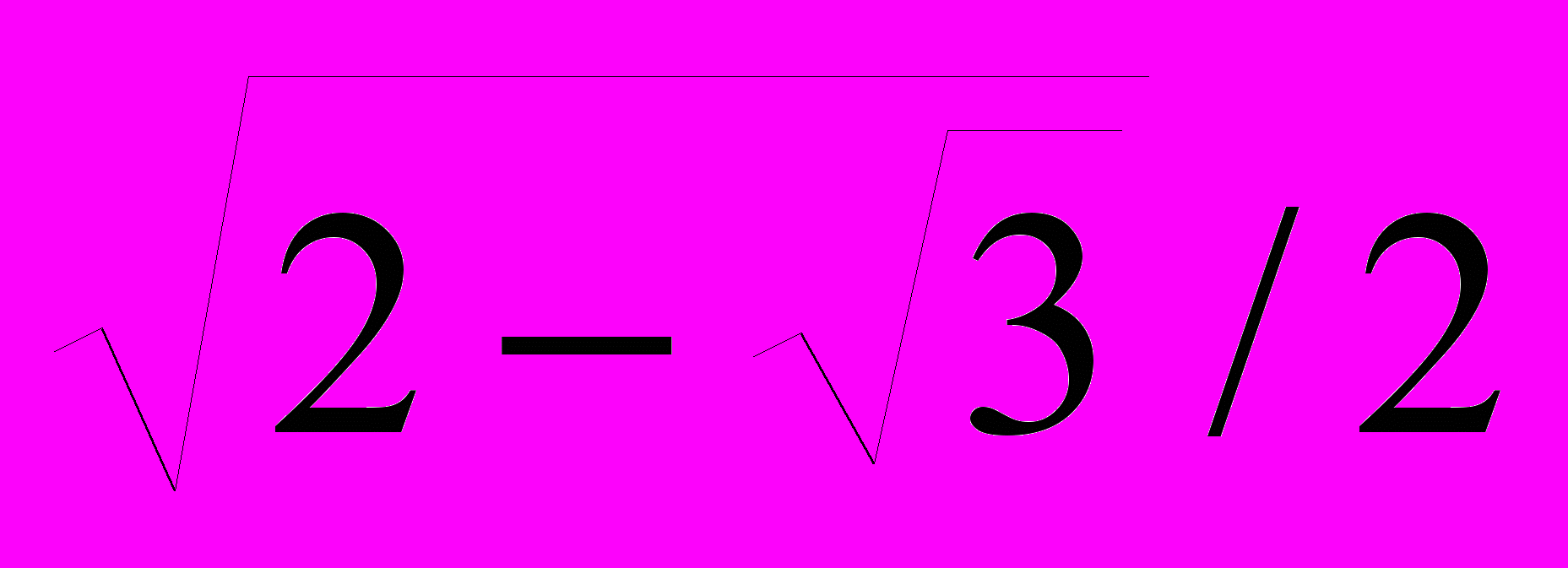
y
0,0000
-1,0000
0,0000
0,0000
x
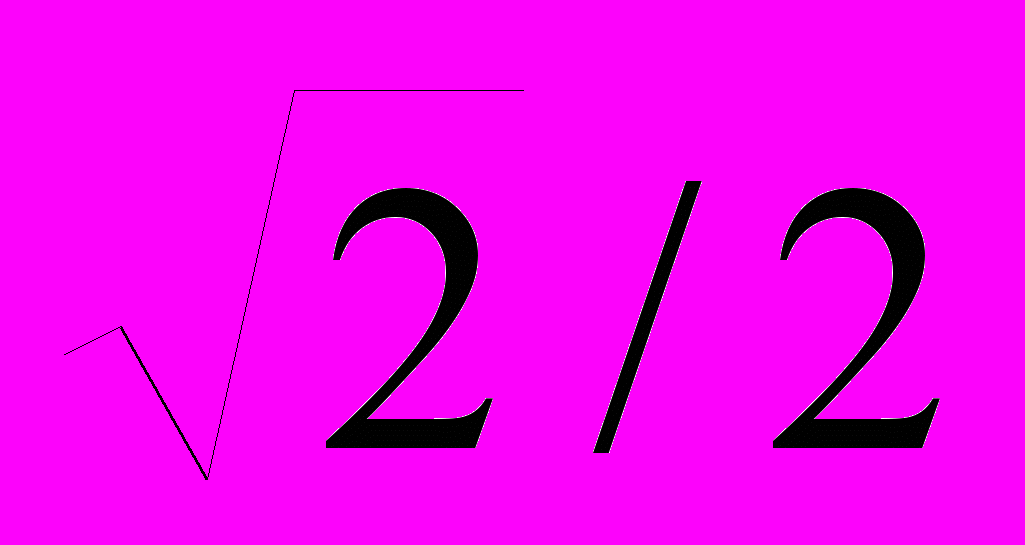
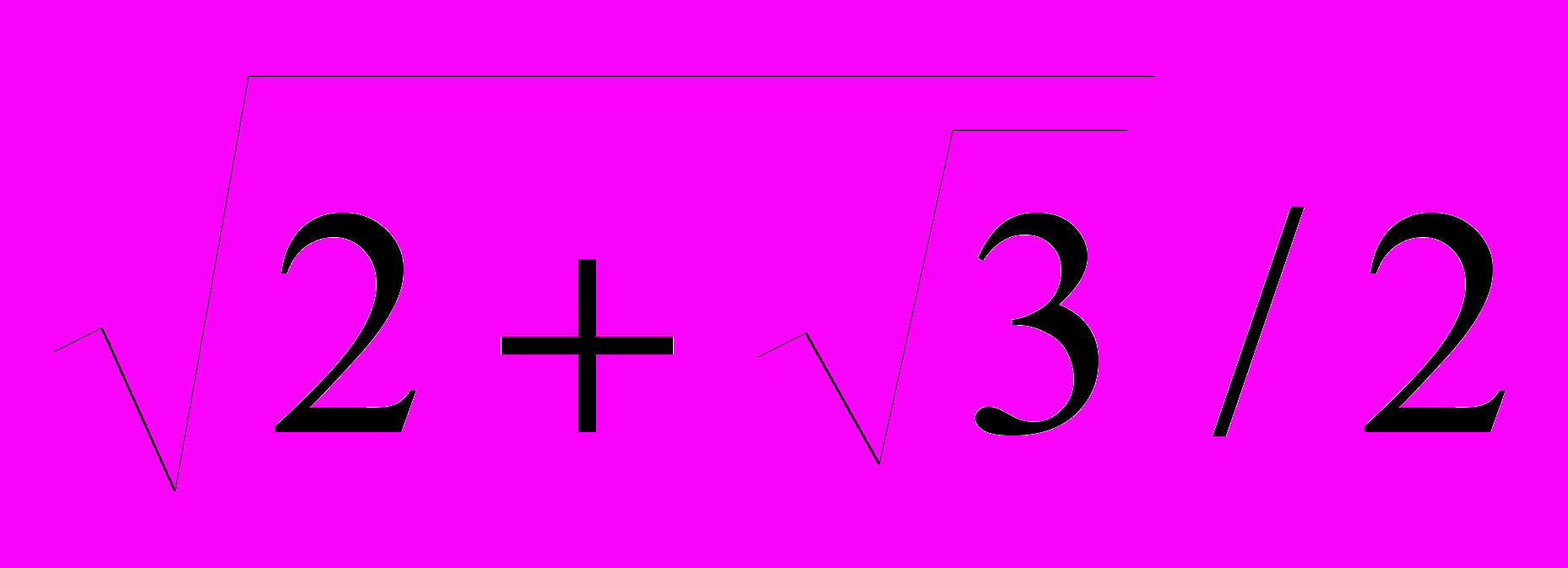
y
1,0000
0,0000
Задача № 10.
Для заданной таблицы значений функции, где в качестве узлов
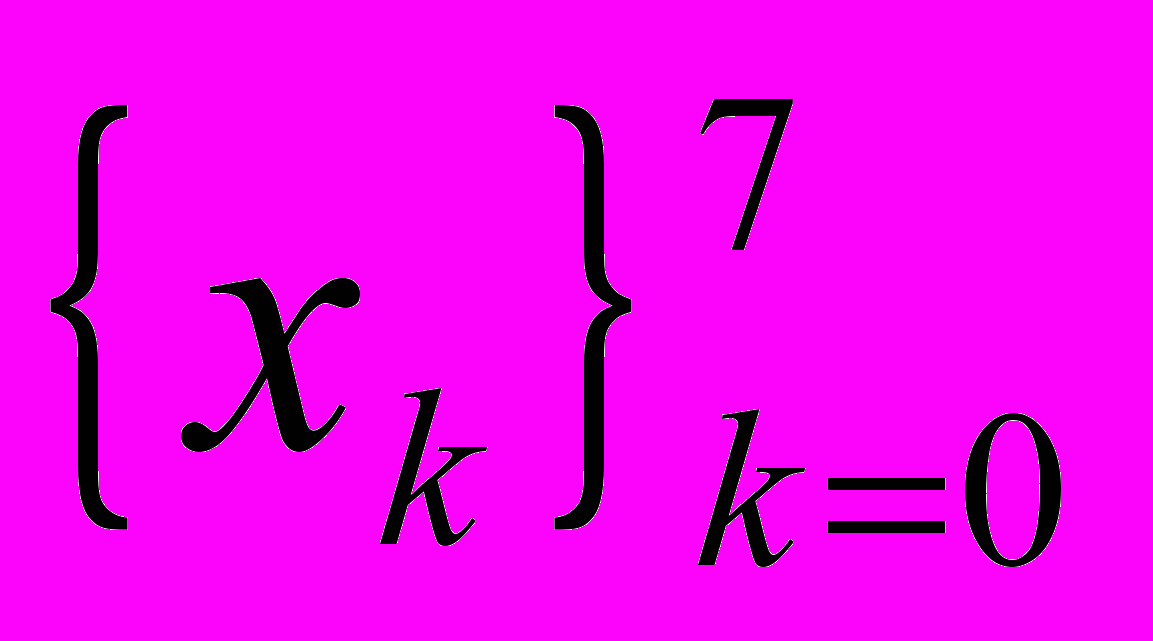 выбраны точки
выбраны точки 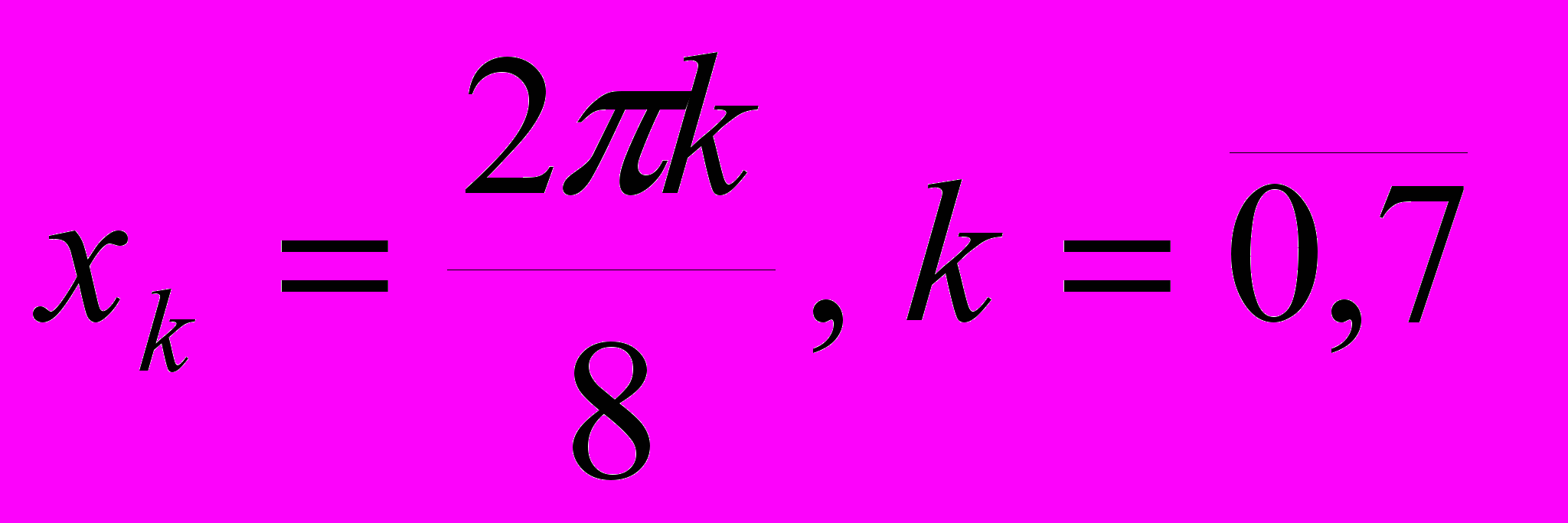 , построить обобщенный многочлен
, построить обобщенный многочлен 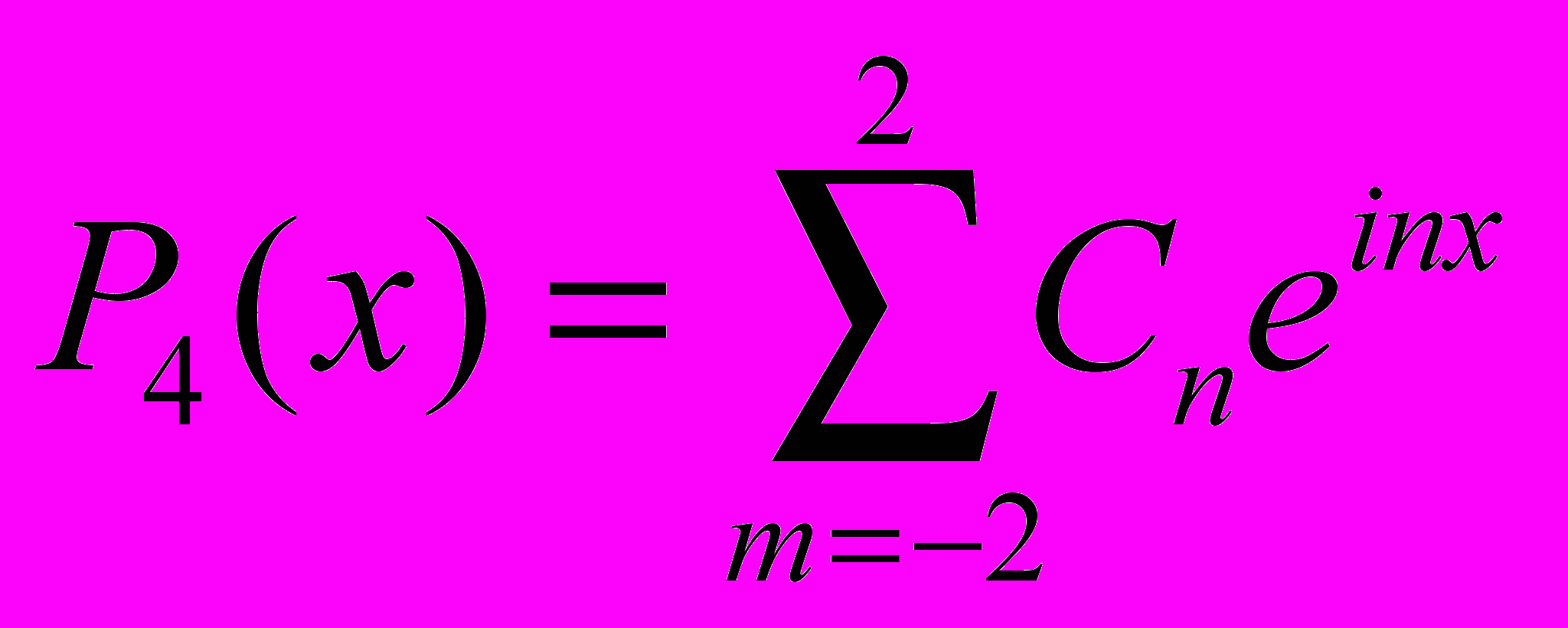 наилучшего среднеквадратичного приближения
наилучшего среднеквадратичного приближения| x | 0 | π/4 | π/2 | 3π/4 | π | 5π/4 | 3π/2 | 7π/4 |
| y | 1 | 0,000 | 5,000 | 2,000 | -1,000 | 2,000 | 5,000 | 0,000 |
IV.3. Равномерное приближение.
Задача № 11.
Найти все экстремумы многочлена Чебышева на отрезке [– 1, 1].
Задача № 12.
Среди всех многочленов вида
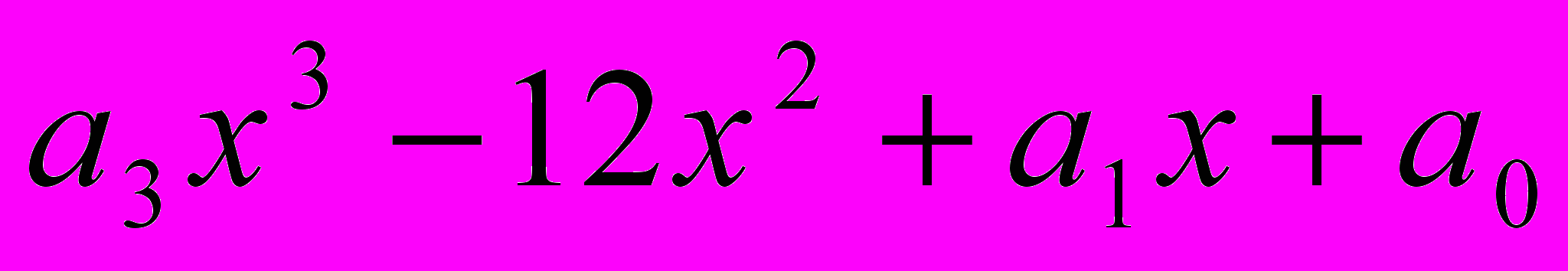 найти многочлен, наименее уклоняющийся от нуля на [0, 2].
найти многочлен, наименее уклоняющийся от нуля на [0, 2].V, VI. Численное дифференцирование и интегрирование — задачи: [7] – (VI.1а, в), (VI.з).
Задача № 15.
Определить порядок точности формулы численного дифференцирования, приближающей первую производную в точке
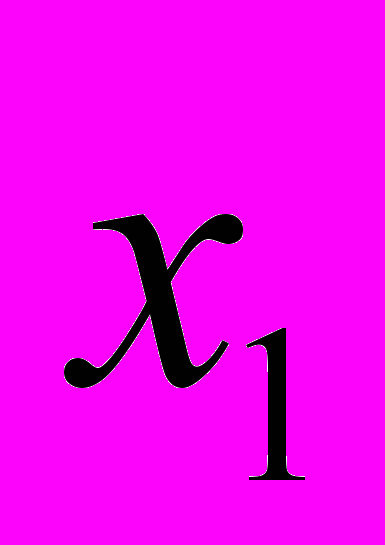
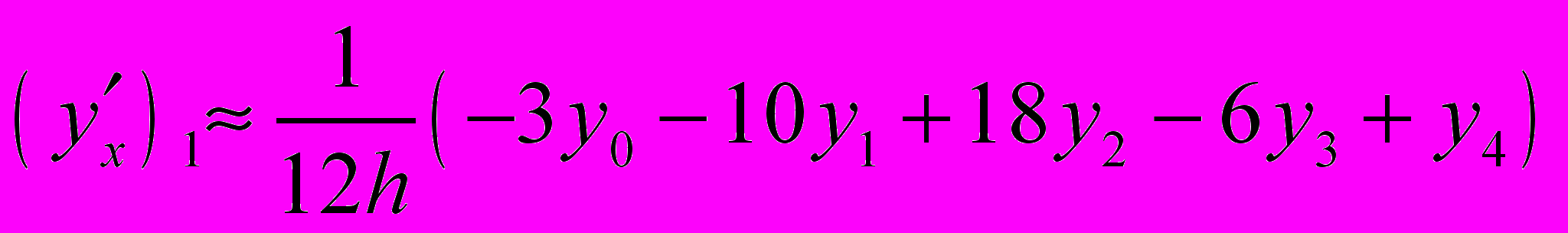
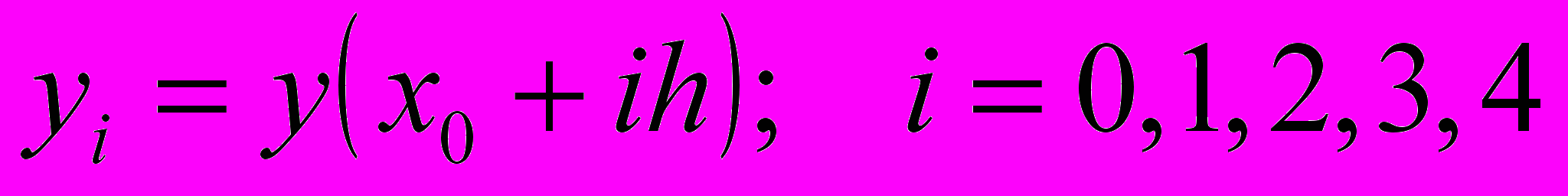 .
.Задача № 16.
Оценить минимальное число разбиений N отрезка интегрирования для вычисления по методу трапеции с точностью
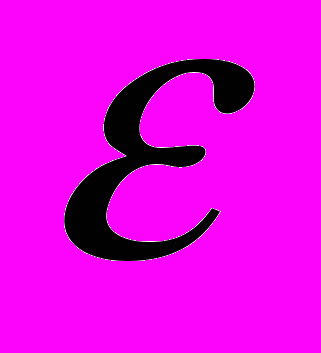 интеграла
интеграла 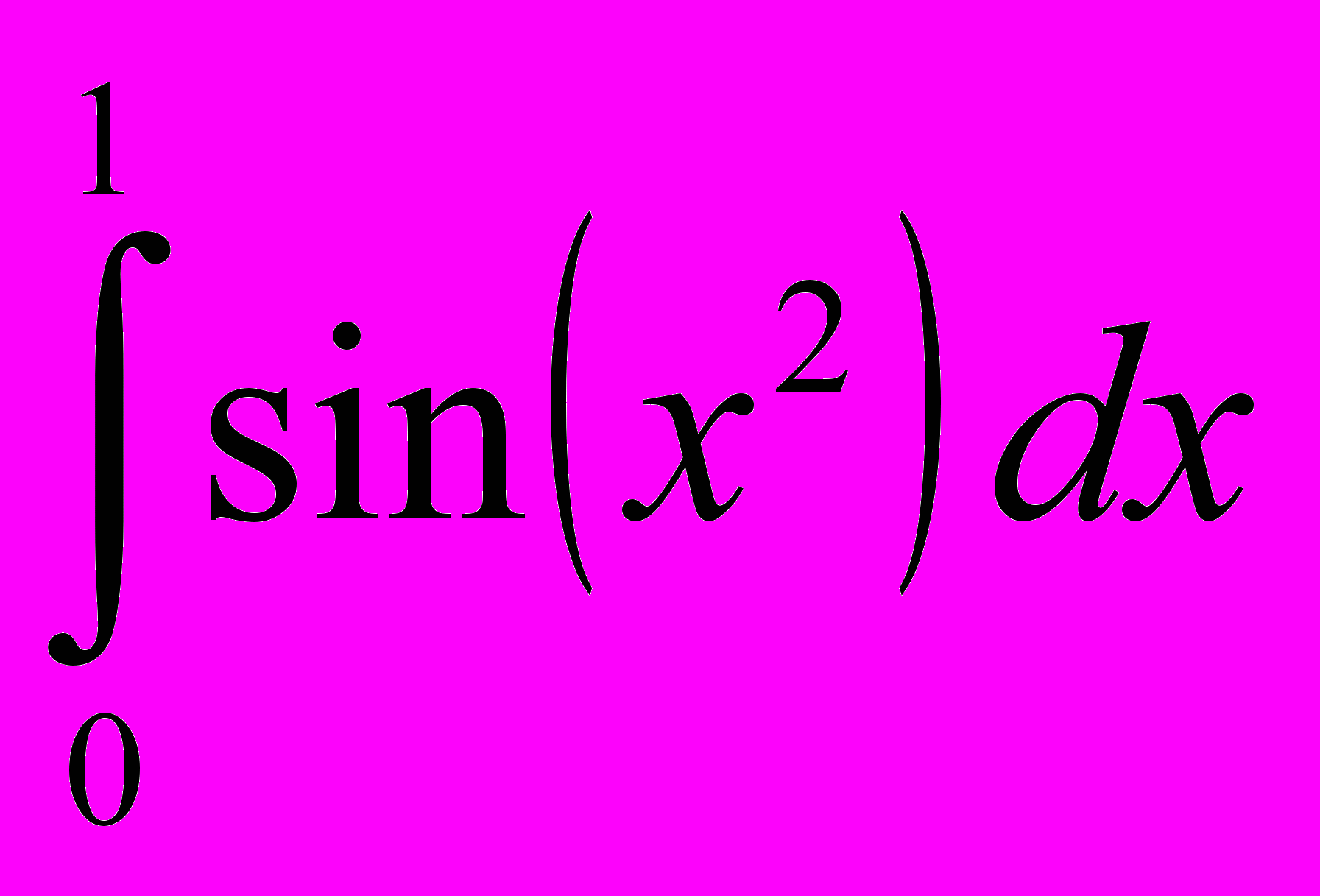 .
.Задача № 17.
Вычислить приближенное значение интеграла
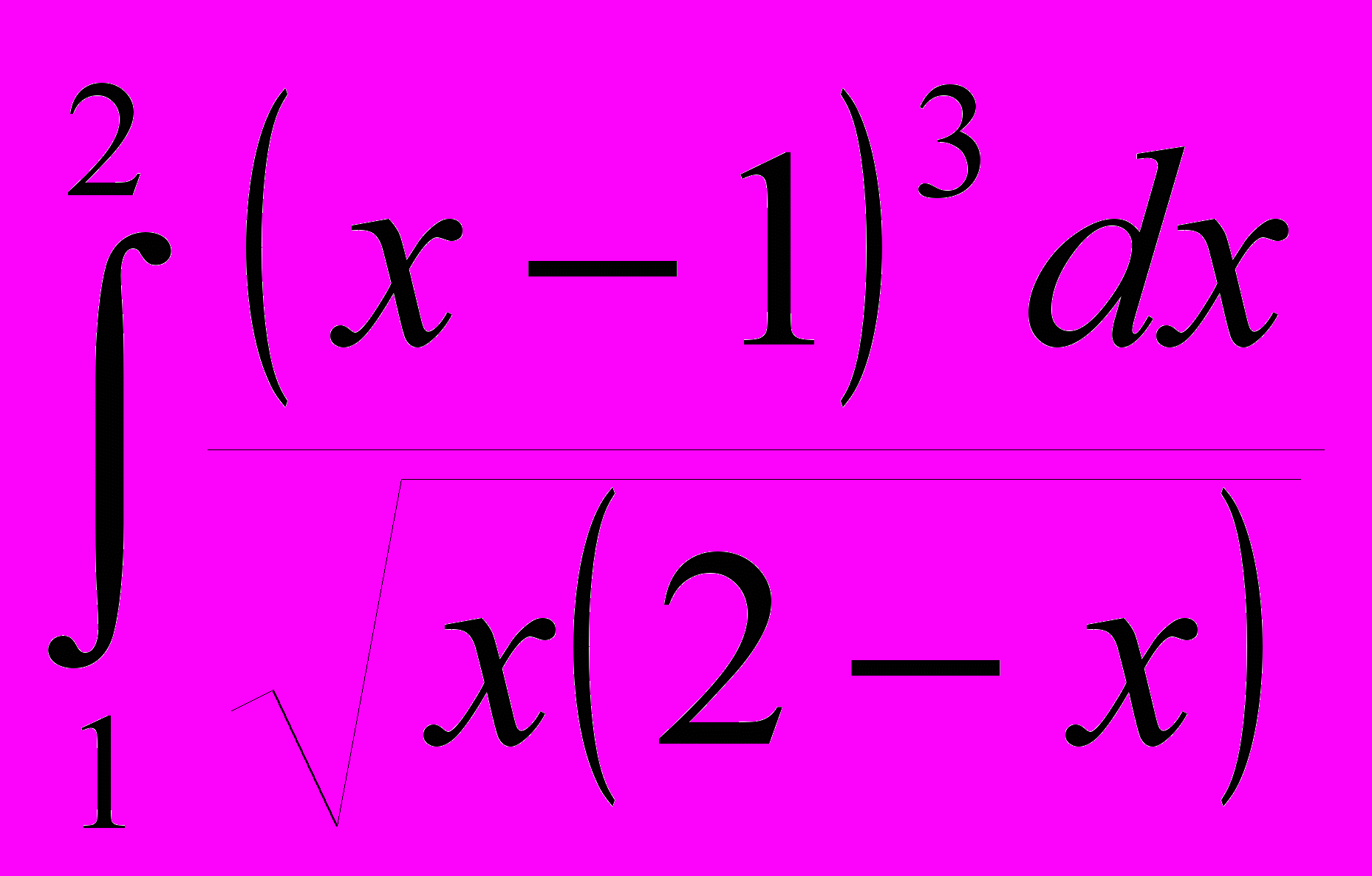 , используя квадратурную формулу Гаусса с двумя узлами.
, используя квадратурную формулу Гаусса с двумя узлами.- Обыкновенные дифференциальные уравнения (ОДУ): [7] – (VII.1).
Задача № 19.
Для решения задачи Коши а) на (0,1) предложена разностная схема б). Исследовать разностную задачу на аппроксимацию и определить порядок сходимости ее решения к решению дифференциальной задачи при
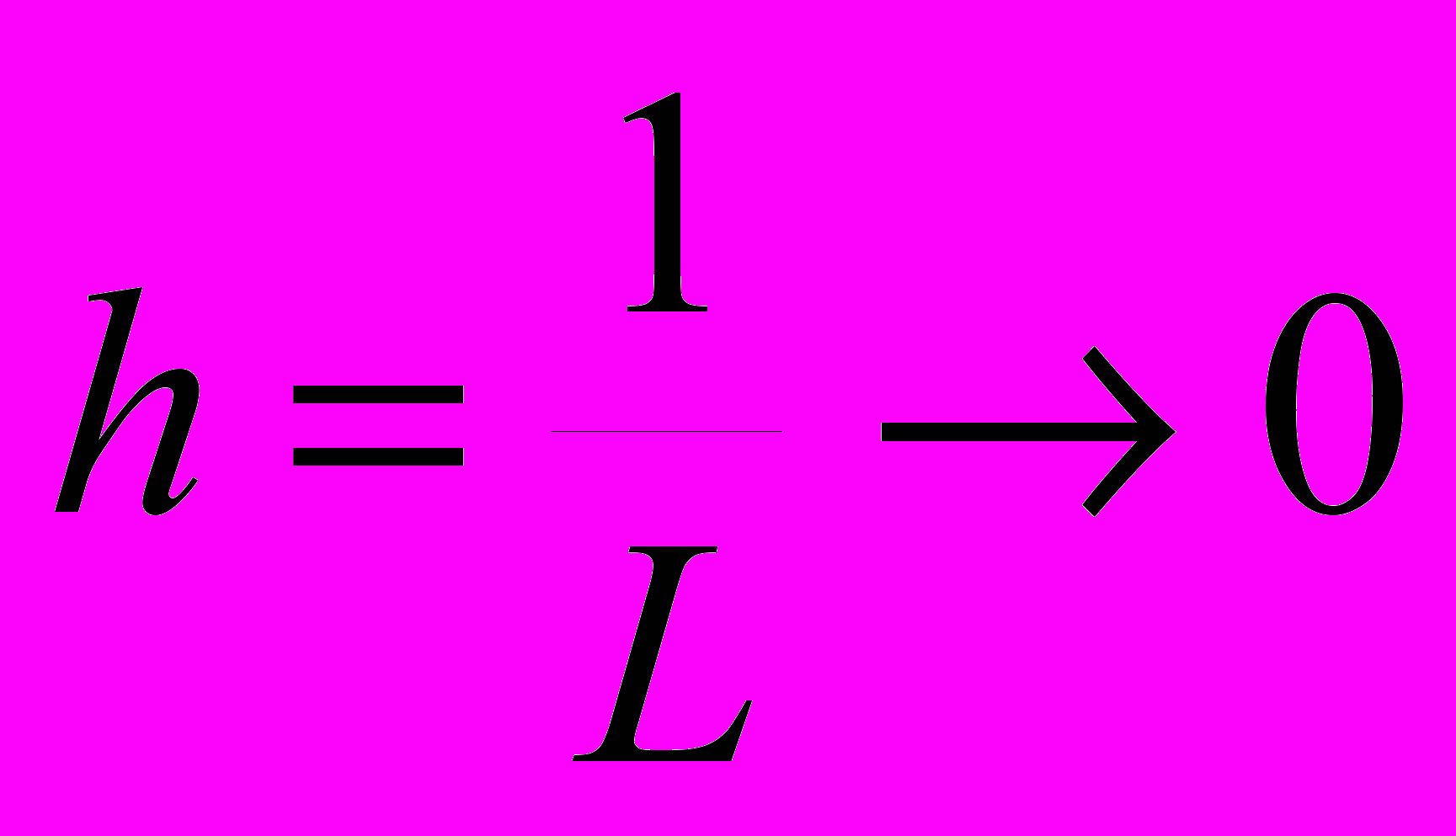 .
.а)
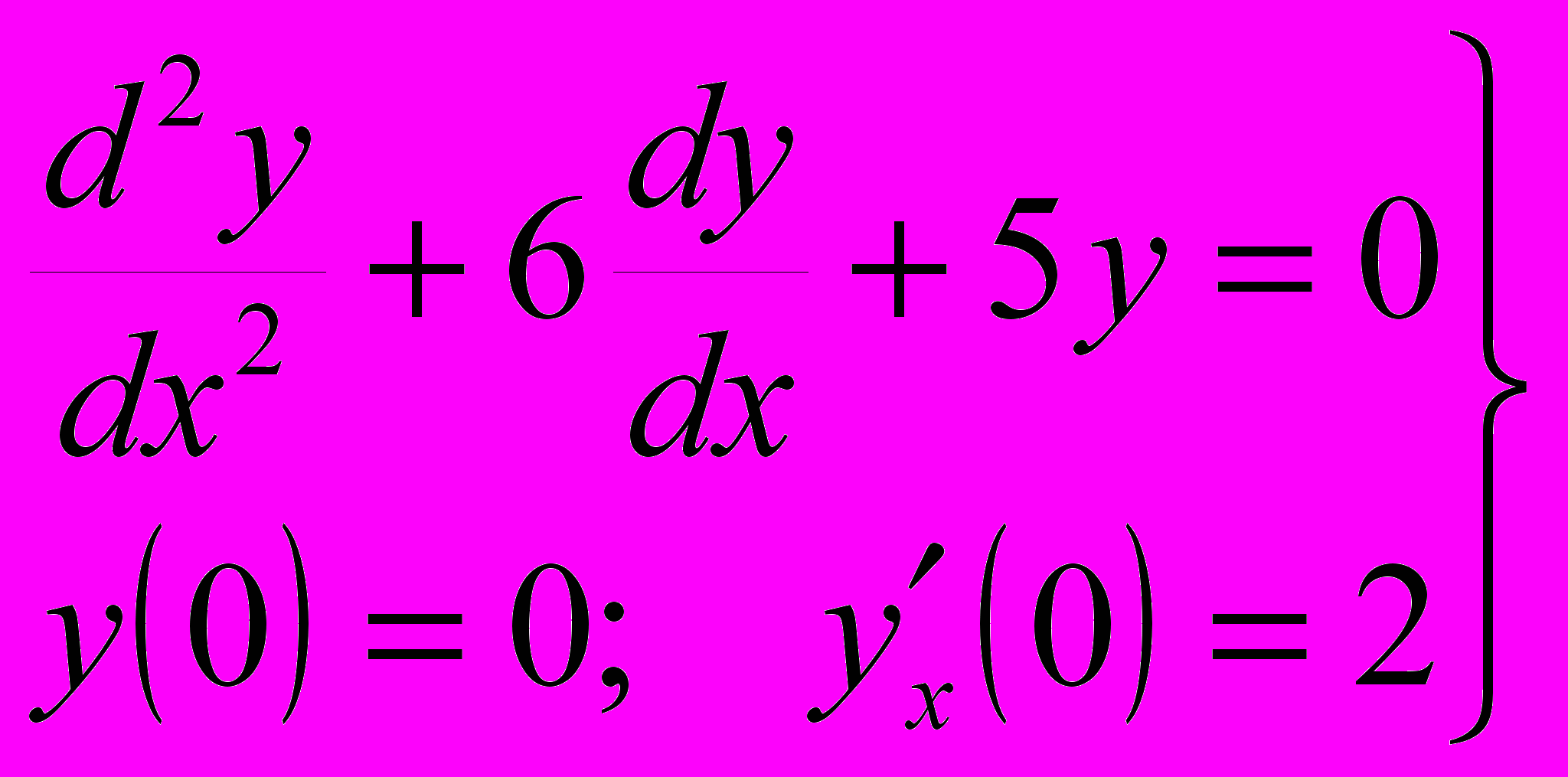
б)
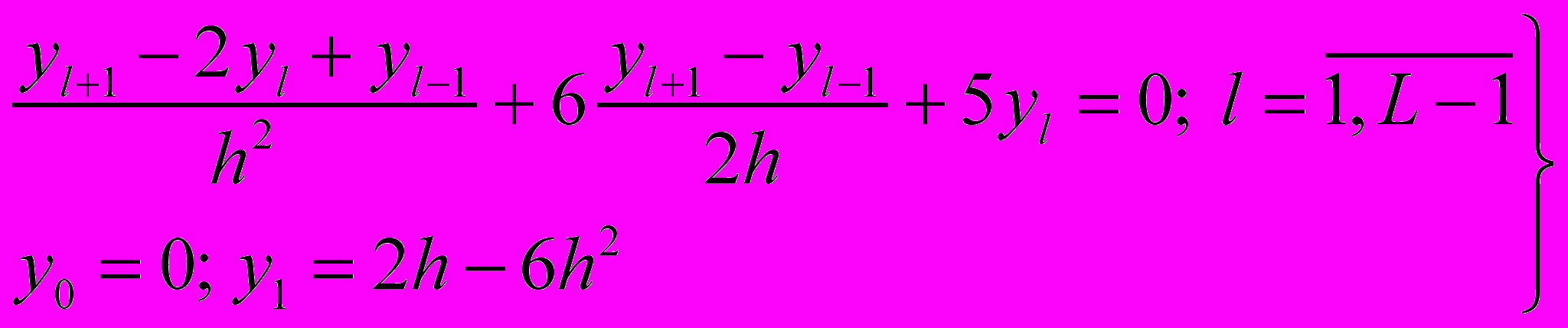 .
.VIII. ОДУ. Задача Коши: [7] – (VII.3).
Задание для практического решения на ЭВМ дается преподавателем и состоит из трех задач:
- по первому заданию – одна задача;
- по второму заданию – две задачи.
Срок сдачи: первого задания – 2-ая неделя октября;
второго задания – 2-ая неделя декабря.
Семестровая потоковая
контрольная работа – 2-ая неделя декабря.
Усл. печ. л. Тираж экз.
