Государственный технический университет (мади) Т. М. Александриди, Б. Н. Матюхин, Е. Н. Матюхина организация ЭВМ и систем
| Вид материала | Учебное пособие |
Содержание2.1. Иерархическая структура функциональных модулей 2.2. Физические способы представления информации |
- Дорожный Технический Университет (мади) г. Москва, Ленинградский проспект, д. 64, программа, 39.53kb.
- Конспект лекций по курсу «Организация ЭВМ и систем» Организация прерываний, 576.86kb.
- Дорожный Государственный Технический Университет (мади) Научно-образовательный материал, 127.07kb.
- Математическое моделиРование процессов регулирования движения транспортных потоков, 234.61kb.
- Осрб 1-36 04 02-2008, 702.53kb.
- «Астраханский государственный технический университет», 377.57kb.
- Косинова, 736.96kb.
- Самарский государственный технический университет научно техническая библиотека, 378.58kb.
- Культурные репрезентации в структуре этнической идентификации, 255.68kb.
- -, 1043.2kb.
2.1. Иерархическая структура функциональных модулей
При проектировании и построении ЭВМ и систем используют модульный принцип. Он состоит в том, что проектирование и построение схем и устройств в ЭВМ выполняют на основе некоторых наборов стандартных модулей (рис.2.1). Эти модули, как правило, выпускаются в промышленности серийно.
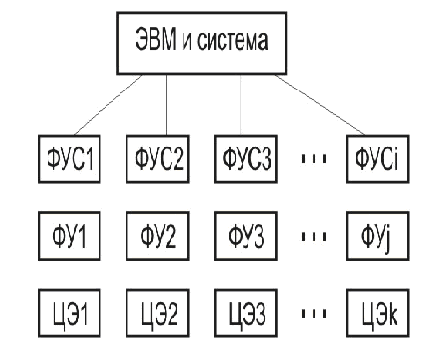
Рис.2.1.Иерархическая структура представления стандартных модулей в составе ЭВМ
Цифровой элемент (ЦЭ) – простейший функциональный модуль, который обеспечивает несложный алгоритм по обработке и хранению информации.
Функциональные узлы (ФУ)- функциональные модули, которые выполняют более сложные стандартные операции по обработке информации. Например, регистры, счетчики.
Функциональные устройства (ФУС) – функциональные модули, которые могут использоваться в качестве самостоятельных устройств.
2.2. Физические способы представления информации
Логические сигналы в электрических схемах представляются (кодируются) в виде различных значений токов и напряжений в различных точках схемы.
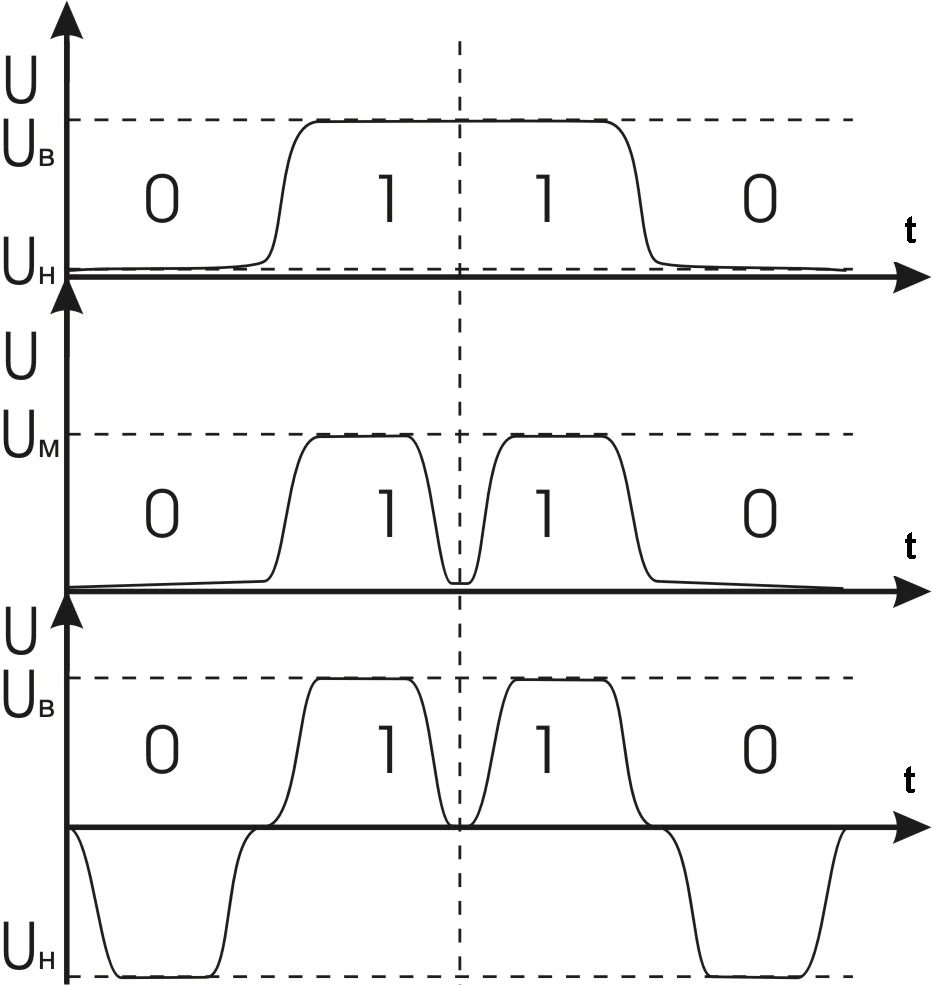
Рис. 2.2. Временные диаграммы представления логических сигналов
Используют два основных способа представления логической информации: в виде потенциальных сигналов и в виде импульсных сигналов (рис. 2.2).
На первой временной диаграмме представлено изображение потенциальных логических сигналов. Его характеристиками являются высокий и низкий потенциальные уровни, которым соответственно присвоены значения “1” и “0”.
На второй временной диаграмме представлено изображение логических сигналов в виде импульсов напряжения, при этом отсутствие импульса в данном временном такте означает “0”, а наличие импульса представляет “1”.
На третьей временной диаграмме представлено изображение логических сигналов в виде импульсов напряжения разной полярности, при этом отрицательный импульс в данном временном такте означает “0”, а положительный –“1”.
2.3. Общие сведения об алгебре логики
В схемотехнике возникают задачи анализа и синтеза логических схем. При этом используют специальный математический аппарат, который называется алгеброй логики (алгебра Буля) или исчислением высказываний. Высказывание - это любое утверждение, в отношении которого можно сказать истинно оно или ложно. В вычислительной технике принято принимать за “истину” –“1”, за “ложь –“0”. В основу булевой алгебры положены три логические операции: инверсия, конъюнкция, дизъюнкция. Правила выполнения логических операций задаются с помощью таблиц истинности. Условные графические обозначения (УГО) логических элементов определяются по ГОСТ 2742-82.
2
 .3.1. Основные логические операции
.3.1. Основные логические операции1) Инверсия (“НЕ”) F = Х
Таблица 2.1
| X | F |
| 0 | 1 |
| 1 | 0 |
В табл. 2.1 показана таблица истинности операции инверсия. На рис.2.1 – УГО логического элемента.
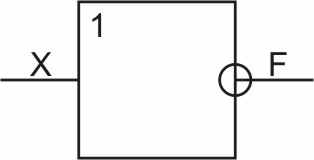
Рис. 2.3. Логический элемент- инвертор
2) Дизъюнкция (“ИЛИ”) F = X1 V X2 V ... V X n.
Таблица 2.2
-
Х1 Таблица 2.2Х1
Х2
……
Хn
F
0
0
0…
0
0
1
0
0…
0
1
0
1
0…
0
1
0
0
0…
1
1
В табл. 2.2 показана таблица истинности операции “ИЛИ”, которая иногда называется “логическое сложение”. На рис.2.4 – УГО соответствующего логического элемента “ИЛИ”.
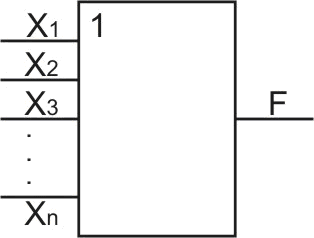
Рис.2.4. Логический элемент- дизъюнктор
3) Конъюнкция ( “И” ) F = X1 & X2 & X3 ...& Xn .
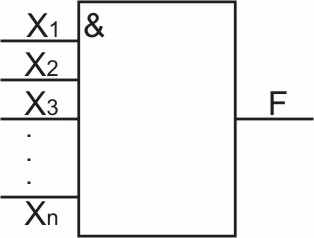
Рис.2.5. Логический элемент – конъюнктор
Таблица 2.3
| X1 | X2 | … | Xn | F |
| 0 | 0 | 0… | 0 | 0 |
| 1 | 0 | 0… | 0 | 0 |
| 1 | 1 | 0… | 0 | 0 |
| … | ||||
| 1 | 1 | 1… | 1 | 1 |
В табл. 2.3 показана таблица истинности операции “И”, которая иногда называется “логическое умножение”.
На рис.2.5 – УГО логического элемента “И”.
4) Штрих Шеффера
Таблица 2.4
| X1 | X2 | F |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
В табл. 2.4 представлена таблица истинности логической операции “штрих Шеффера”.
F
 = X1 & X2 = X1 │ X2 .
= X1 & X2 = X1 │ X2 .5) Стрелка Пирса
В табл. 2.5 представлена таблица истинности логической операции “стрелка Пирса”.
Таблица 2.5
| X1 | X2 | F |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
