Методичні рекомендації обласного семінару з проблеми «Робота з обдарованими учнями в контексті підготовки до олімпіади з інформатики» для вчителів інформатики, які ведуть питання підготовки учнів до олімпіади з інформатики

Вид материала

Содержание

Доолімпіадний період
Методист М.В. Кирилюк
Методист М.В. Кирилюк
Організація роботи з обдарованими і здібними учнями

Подобный материал:

Методичні рекомендації

обласного семінару з проблеми «Робота з обдарованими учнями в контексті підготовки до олімпіади з інформатики»для вчителів інформатики, які ведуть питання підготовки учнів до олімпіади з інформатики

Процес підготовки учнів до олімпіад безпосередньо пов'язаний з наявністю у навчальному закладі вчителів, які готові і здатні взяти на себе відповідальність за роботу з обдарованими учнями. У педагогічній діяльності творчість вчителя займає особливе місце. Адже, лише неформальне, творче ставлення до своїх обов’язків може дати позитивні результати.

Можна виділити такі складові готовності вчителя до роботи з обдарованими учнями:

відповідний рівень і постійна підтримка фахово-інформаційного рівня роботи з обдарованими учнями (курси, семінари, конференції тощо);
володіння методиками роботи з обдарованими учнями (індивідуальна робота, робота в групах тощо);
володіння психологічними аспектами роботи з обдарованими учнями.

Робота вчителя з обдарованими учнями не повинна носити хаотичний, епізодичний характер, а має бути системною, неперервною, спланованою на перспективу.

Доолімпіадний період:

Цей період починається на початку навчального року. Протягом цього часу передбачається робота безпосередньо в навчальних закладах, а також позашкільні форми занять (гуртки, заняття окремих груп тощо).

Підготовка включає:

Вирівнювальні підготовчі заняття щодо повторення задач минулого олімпіадного сезону, уведення в групу олімпіадників нових учнів. Ця робота включає як індивідуальні, так і диференційовані форми. Обов’язковою є також робота в групах.
Розв’язування завдань І та ІІ етапів попередніх олімпіад.
Проведення занять у формі «міні олімпіад» для поступового психологічного налаштування учнів.

І етап олімпіади:

Шкільні олімпіади. Проводяться в навчальних закладах вчителями інформатики. Особливості проведення:

Участь беруть всі бажаючі.
Підбір завдань повинен бути диференційованим, тобто включати завдання 3-х рівнів:
- нескладні завдання репродуктивного характеру, які може розв’язати більшість учасників;
- завдання, які потребують творчого підходу до розв’язання;
- завдання, рівень яких відповідає ІІ (ІІІ) етапу олімпіади.
Умови проведення олімпіади повинні максимально відповідати умовам олімпіади наступного етапу.

Завдання, що пропонуються на шкільній олімпіаді, повинні враховувати той матеріал, що був засвоєний на момент проведення даної олімпіади за навчальною програмою, однак, складність цих завдань повинна носити олімпіадний характер, визначаючи вміння учнів логічно мислити, застосовувати програмний матеріал до більш складних завдань.

ІІ етап олімпіади:

Районна (міська) олімпіада. Для того, щоб учасники ІІ етапу олімпіади, до яких відносяться й учителі, були в максимально однакових підготовчих умовах, рекомендується попередньо провести такі заходи:

семінари-практикуми для вчителів щодо ознайомлення з вимогами виконання завдань ІІ етапу та рівнем складності завдань;
заочну олімпіаду, що проходить у декілька етапів та передбачає ознайомлення учнів з авторськими розв’язками запропонованих завдань.

ІІІ етап олімпіади:

Обласна олімпіада. Цьому етапу олімпіади можуть передувати такі заходи:

семінари-практикуми для вчителів-тренерів районних та міських команд для ознайомлення з вимогами виконання завдань ІІІ етапу та рівнем складності завдань;
участь вчителів у курсах з розв’язування задач олімпіадного рівня.

Виходячи з вище зазначеного, рекомендуємо:

1. Вчителям інформатики в роботі з обдарованими учнями:

застосовувати проблемний метод у навчанні;
проводити самостійні роботи творчого характеру;
застосовувати індивідуальний підхід у навчанні;
впроваджувати розвивальні творчі ігри;
розв’язувати творчі завдання.

Також є широкий спектр позакласної роботи на виявлення та розвиток творчих здібностей учнів:

це підготовка і участь школярів в олімпіадах з інформатики;
дослідницька робота в МАН;
участь у гуртках, факультативах;
участь в інтелектуальних іграх;
робота над проектом;
участь у науково-практичних конференціях;
участь в Інтернет-олімпіадах.

2. Методистам районних (міських) методичних кабінетів провести у першому півріччі 2008 року районний (міський) семінар-практикум для вчителів інформатики з проблеми «Організації роботи з обдарованими учнями по підготовці до олімпіади з інформатики», де обговорити досвід вчителів інформатики, які мають переможців ІІ, ІІІ етапів олімпіад; ознайомити з досвідом роботи вчителів інформатики Кременчуцького ліцею № 30, Полтавського обласного ліцею-інтернату для обдарованих дітей із сільської місцевості при Кременчуцькому педагогічному училищі ім. А.С. Макаренка, Кременчуцького ліцею № 4, Полтавського ліцею № 1 (за матеріалами обласного семінару).

3. Керівникам навчальних закладів знаходити можливість відзначати працюючих творчо вчителів, які готують переможців конкурсів, олімпіад тощо.

Методист М.В. Кирилюк

Талант і творча обдарованість особистості стають сьогодні запорукою інтенсивного економічного розвитку країни і сприятливим фактором національного престижу. Як з’ясувалось, інтелектуала з високим рівнем розвитку творчих здібностей не можна замінити ні кібернетичною машиною, ні колективом індивідуумів із середніми інтелектуально-творчими здібностями. Тому проблема творчості в наші дні стала настільки актуальною, що вона по праву вважається проблемою століття.

Обдаровані діти – майбутній цвіт нації, її інтелектуальна еліта, гордість і честь України, її світовий авторитет. І завдання учителя на етапі модернізації змісту освіти в умовах особистісно орієнтованого підходу полягає в тому, щоб дбайливо ростити нові таланти, починаючи з молодшого шкільного віку.

Створення класів з поглибленим вивченням предметів дає хороший результат. Зрозуміло, якщо немає можливості створити класи з поглибленим вивченням предмету, роботу із здібними і обдарованими дітьми треба проводити на уроці і в позаурочний час.

Шляхи розвитку творчості учнів на уроці бачимо у реалізації:

проблемного підходу у навчанні;
проведенні самостійних робіт творчого характеру;
індивідуального підходу у навчанні;
впровадження розвивальних творчих ігор;
розв’язування творчих завдань.

Також є широкий спектр позакласної роботи на виявлення та розвиток творчих здібностей учнів. Сприяння самореалізація творчої особистості відбувається також завдяки широкому спектру позакласної роботи:

це підготовка і участь школярів в олімпіадах з інформатики;
дослідницька робота в МАН;
участь у гуртках, факультативах;
участь в інтелектуальних іграх;
робота над проектом;
участь у науково-практичних конференціях.

Виходячи з вище зазначеного, рекомендуємо:

1. Методистам районних (міських) методичних кабінетів:

провести у першому півріччі 2008 року районний (міський) семінар для вчителів інформатики з пробрели «Організації роботи з обдарованими учнями в контексті підготовки до олімпіади з інформатики».
вивчити та узагальнити досвід вчителів інформатики району по організації роботи з обдарованими учнями.
створити необхідні умови (участь у роботі МАН, організація конкурсів, олімпіад, факультативів, гуртків тощо) для залучення творчо обдарованих учнів до вивчення інформатики .
на засідання методичних об’єднань вчителів інформатики району (міста) проаналізувати роботу щодо участі дітей у позакласних заходах, спрямованих на розвиток творчих здібностей учнів.
на засіданнях методичних об’єднань вчителів інформатики району (міста) ознайомити з досвідом роботи з обдарованими дітьми Кременчуцького ліцею № 30, Полтавського обласного ліцею-інтернату для обдарованих дітей із сільської місцевості при Кременчуцькому педагогічному училищі ім. А.С. Макаренка, Кременчуцького ліцею № 4, Полтавського ліцею № 1.

Керівникам навчальних закладів знаходити можливість відзначати працюючих творчо вчителів, які готують переможців конкурсів, олімпіад тощо.

Методист М.В. Кирилюк

Метою проведення Всеукраїнських учнівських олімпіад з інформатики є стимулювання творчого самовдосконалення учнів, зацікавлення їх у якісному і поглибленому вивченні інформатики; виявлення та розвиток обдарованих учнів, сприяння розвитку алгоритмічного мислення у школярів, підвищення інтересу до програмування.

Організація роботи з обдарованими і здібними учнями

Талант і творча обдарованість особистості стають сьогодні запорукою інтенсивного економічного розвитку країни і сприятливим фактором національного престижу. Як з’ясувалось, інтелектуала з високим рівнем розвитку творчих здібностей не можна замінити ні кібернетичною машиною, ні колективом індивідуумів із середніми інтелектуально-творчими здібностями. Тому проблема творчості в наші дні стала настільки актуальною, що вона по праву вважається проблемою століття.

Обдаровані діти – майбутній цвіт нації, ії інтелектуальна еліта, гордість і честь України, ії світовий авторитет. І завдання учителя на етапі модернізації змісту освіти в умовах особистісно орієнтованого підходу полягає в тому, щоб дбайливо ростити нові таланти, починаючи з молодшого шкільного віку.

Під обдарованістю розуміється «сукупність високого рівня природних задатків і схильностей як передумова розвитку здібностей до певних видів діяльності».

Для обдарованих дітей характерними є: висока активність розуму, підвищена схильність до розумової діяльності, прояв самостійності в процесі пізнання. Тому головним завданням учителя в цьому напрямку є розкриття дитячої обдарованості, створення системи роботи з обдарованими учнями, використання різноманітних методик виявлення інтересів і розвитку здібностей дітей.

Ольшанська школа працює над проблемною темою: «Реалізація саморозвитку пізнавальних і особистих здібностей учнів через творче застосування сучасних освітніх технологій та інтерактивних методів. Забезпечення умов індивідуального навчання та розвитку учнів, реалізація їхніх нахилів та інтересів заходами виховної системи школи»

Для організації роботи з обдарованими дітьми в школі виробили алгоритм діяльності з цього питання.

1. Виявляємо здібності та обдарування учнів. Для цього використовуємо спеціальні методики розвитку:

оперативної пам'яті;
пам'яті на образи;
проводимо тести для визначення інтелектуального потенціалу дитини.

2. Запроваджуємо діагностики для вивчення інтересів особистості: створюємо банк даних «Обдарованість».

3. Проводимо мотиваційну роботу з обдарованими учнями для орієнтації їх на досягнення високих результатів.

4. Організуємо системну роботу :

Створюємо класи з поглибленим вивченням предметів (9А – математика, 11А – фізико-математичний профіль, 10Б – універсальний профіль, 11Б – універсальний профіль. Випустили: 11А – філологічний, 11Б – природничий профіль).
Робота з обдарованими учнями за індивідуальним планом.
Взаємодія вчителя з психологом та класним керівником.
Відбувається дослідницька діяльність учнів, які навчаються в МАН.
Участь у міжнародному математичному конкурсі «Кенгуру».
Проводиться робота наукових гуртків.
Випуски газет, брошур.
Турнір юних математиків, конкурси, олімпіади з математики (районні, обласні).
Здійснюється самоосвітня діяльність учнів.
Діє змістовна позакласна робота.
Стимулювання саморозвитку.

Створення класів з поглибленим вивченням предметів дає хороший результат. Якщо один – два здібних учня вчаться у звичайному класі, вони порівнюють себе з іншими учнями класу, вважають, що дуже багато вже знають і вміють. І в них зникає стимул, щоб працювати більше і краще на уроці. А також в деяких класах доводиться спостерігати, коли слабкі учні підколюють, насміхаються над тими учнями, які піднімають руку, відповідають на запитання вчителя. Згодом ці учні стають пасивними, щоб не виділятися в класі. А в класі з поглибленим вивченням предмету навпаки, всі стараються не відстати від учнів, що мають високий результат.

Поглиблене вивчення предметів починається , як правило, з 8-го класу. На мій погляд, поглиблене вивчення предмету краще починати з 6-го або з 7-го класу і щоб учні мали змогу без перешкод змінити клас, якщо у цьому класі вчитися їм буде важко.

Зрозуміло, якщо немає можливості створити класи з поглибленим вивченням предмету, роботу із здібними і обдарованими дітьми треба проводити на уроці і в позаурочний час.

Шляхи розвитку творчості учнів на уроці я бачу у реалізації:

Проблемного підходу у навчанні;
Проведенні самостійних робіт творчого характеру;
Впровадження технічних засобів навчання;
Індивідуального підходу у навчанні;
Впровадження розвивальних творчих ігор;
Розв’язування творчих завдань.

На уроці створюю ситуацію успіху. Використовую проблемний підхід у навчанні а також використовую метод доцільних задач.

Проблемне навчання – така організація навчальних занять, яка сприяє створенню під керівництвом учителя проблемних ситуацій і активній самостійній діяльності учнів з метою їх вирішення, внаслідок чого й відбувається розвиток розумових здібностей та творче оволодіння знаннями, навичками, вміннями. Наприклад, у 9-му класі з поглибленим вивченням математики розглядаються методи розв’язування ірраціональних рівнянь. Якщо рівняння містить корені квадратні, то обидві частини рівняння підносимо до другого степеня. Якщо рівняння містить корені третього степеня, то обидві частини рівняння підносимо до третього степеня. Це рівняння виду:

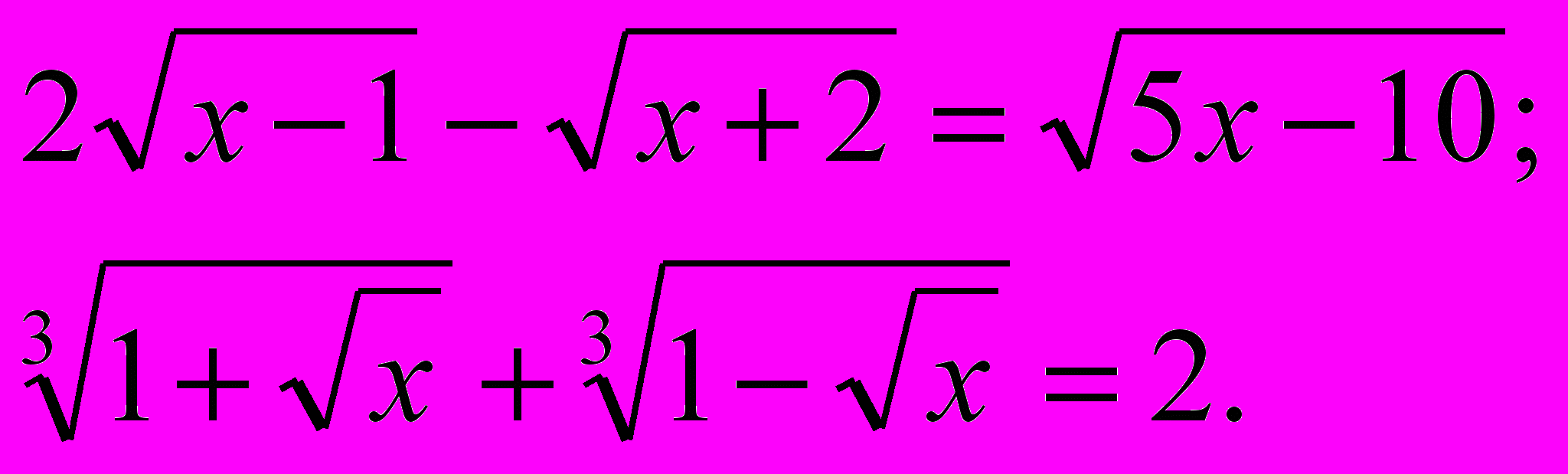
А що будемо робити, якщо дається рівняння, яке містить корені четвертого степеня? Учні припускають, що треба обидві частини рівняння піднести до четвертого степеня. Пропоную їм спробувати розв’язати рівняння

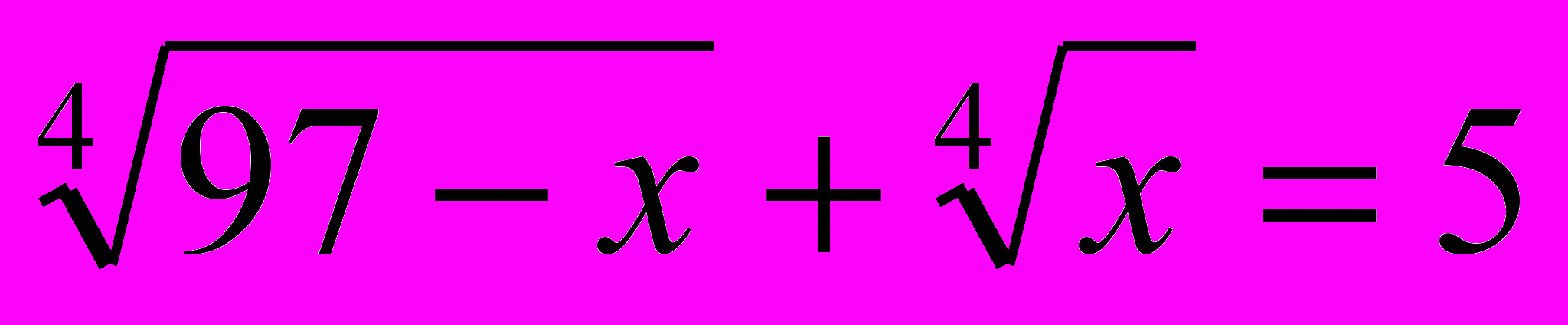таким способом. Загальними зусиллями учні розв’язують це рівняння і впевнюються, що розв’язання дуже складне. А як можна спростити роботу?

Тоді раджу їм зробити заміну змінної:

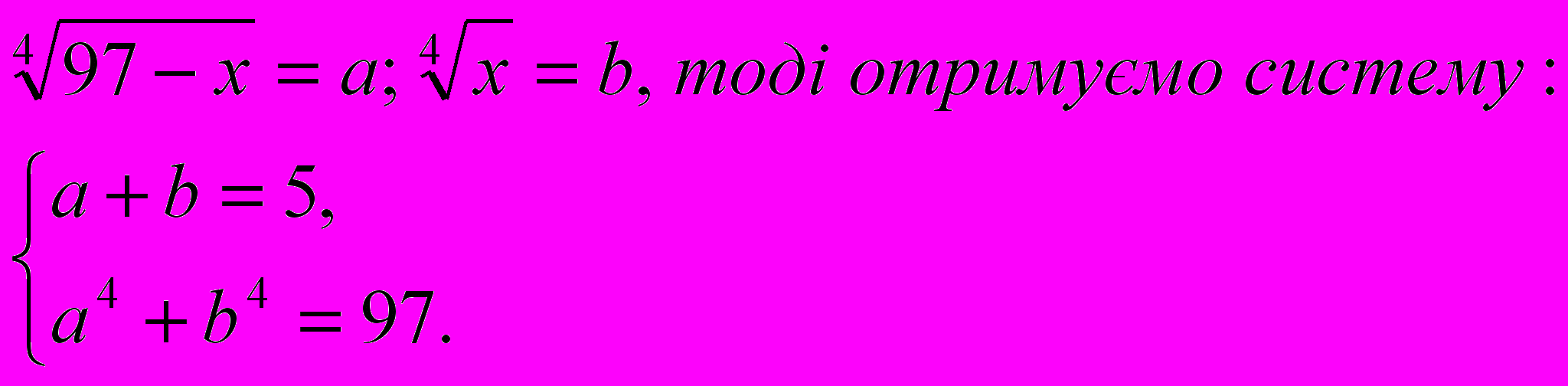
Звідси підбором знаходимо, що а = 2, b = 3 або а = 3, b = 2. Тоді х = 16 і x = 81.

Метод доцільних задач є корисним, коли потрібно підвести учнів к виявленню нової математичної закономірності, яка потім обґрунтовується. Під час розв’язування задач, що передують новому матеріалу, учні вчаться робити самостійні спостереження, експериментальні відкриття залежностей, що вивчаються. При цьому широко використовуються логічні засоби мислення: конкретизація і узагальнення. Учитель підводить учнів до розуміння того, що нові знання можна отримати на основі набутого досвіду. Цей досвід вони застосовують для обґрунтування виводу нової формули або доведення тільки що зробленого припущення.

Наприклад, на уроці алгебри у 7-му класі, коли вивчаються формули скороченого множення, пропоную серію завдань на множення двочленів. Розв’язав такі завдання, учні помічають певну закономірність, яку потім доводять у загальному вигляді. Або коли у 8-му класі вивчаються дії з алгебраїчними дробами, учні на уроці спочатку виконуються дії із звичайними дробами. Формулюють правила дій із звичайними дробами. Роблять припущення, що ці правила будуть правильними і для алгебраїчних дробів. Доводять їх у загальному вигляді, повторюючи ті кроки, які щойно були зроблені із звичайними дробами. Таких прикладів можна навести багато.

Метод доцільних задач дуже корисний і на уроках геометрії. Попередня робота при вивченні нової теореми підводить учнів до свідомого сприйняття нового матеріалу і кожен крок строгого доведення теореми стає зрозумілим. Наприклад, при вивченні у 7-му класі теми «Сума кутів трикутника», спочатку пропоную задачі для розв’язання за готовим малюнком: обчисліть величини кутів x, y, z, якщо a||b.

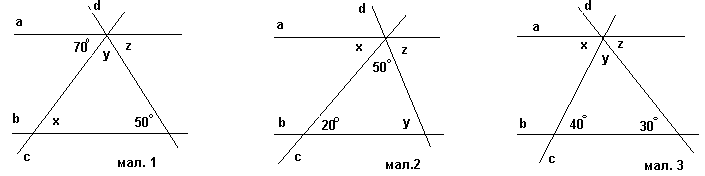
Розв’язав задачі, учні висловлюють припущення, що сума кутів трикутника дорівнює 180^о і з допомогою вчителя доводять цей факт. Причому доводять майже самостійно, тому що вони вже підготовлені для цього попередньою роботою.

Добрий результат дає використання на уроці самостійних робіт творчого характеру, індивідуальний підхід у навчанні. Індивідуальний підхід реалізується завдяки різним рівням подачі нового матеріалу, використанню чотирирівневих завдань за ступенем складності та самостійним вибором учнем свого рівня. Навчальний матеріал та умови задач, як правило, подаються у двох видах: із використанням схем, знаків і картинок з урахуванням провідного типу мислення учнів. Для цього використовую також картки із завданнями по кожній теми. Головна мета – всі учні повинні працювати на уроці і кожен на своєму рівні.

Наприклад, на уроці алгебри з теми «Квадратична функція» у 9-му класі пропоную такі завдання для фронтальної роботи:

Який квадратний тричлен задає графік даної функції (рис. а)?

Якому з графіків відповідає даний квадратний тричлен (рис. б)? Учні пояснюють свій вибір.

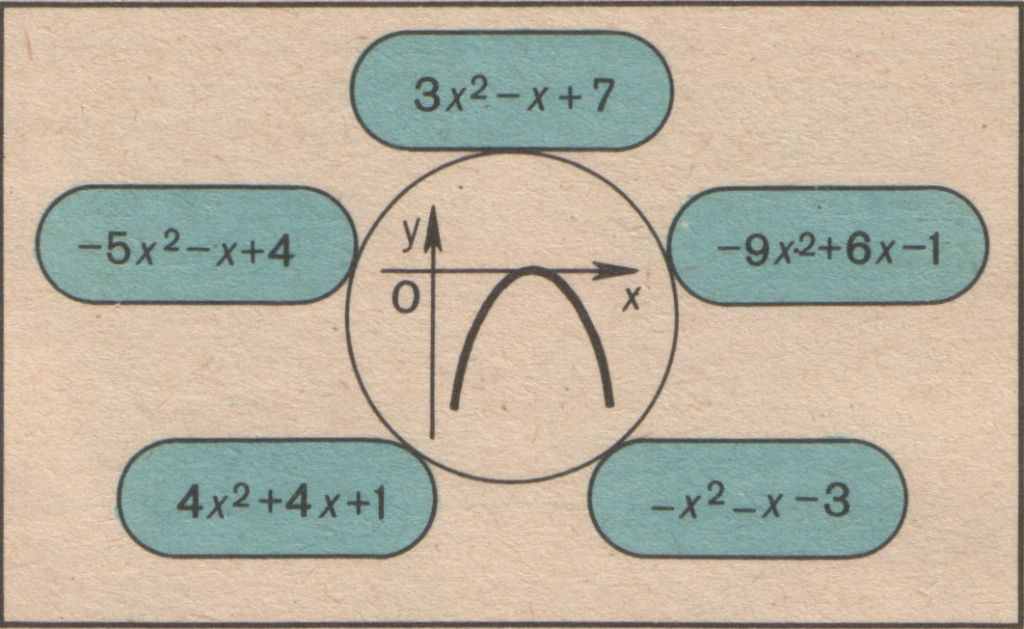
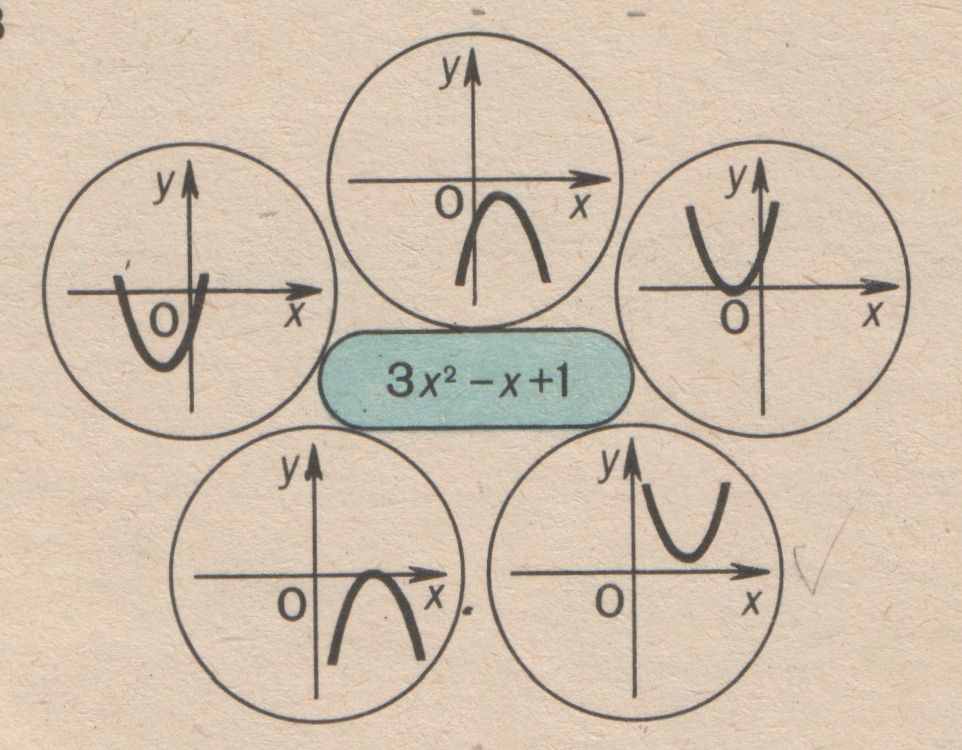
а) б)

На уроці з теми «Теорема Піфагора» у 8 – му класі, коли доведено теорему Піфагора, пропоную учням завдання з метою закріплення вмінь формулювати ії:

Згадайте, як ходе кінь на шахівниці, обійдіть клітинки, в які вписані частини слів і назвіть властивість, яку вивчили на уроці.

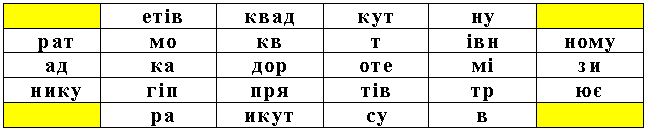
Відповідь. Квадрат гіпотенузи в прямокутному трикутнику дорівнює сумі квадратів катетів.

Для індивідуальної роботи з учнями використовую тести з кожної теми, що вивчається; картки із умовами логічних задач для усного розв’язування; картки із умовами задач для усного розв’язання на закріплення нової теми. Вони призначені для учнів з різним рівнем навченості.

Я працюю у класах з поглибленим вивчення математики, це 9-А, 11-А класи. Коли учні цих класів навчалися ще у 5 – 7 класах, я готувала їх до поглибленого вивчення математики і використовувала на уроках додатковий посібник «Збірник задач з математики. 5 – 6 класи», автори Мерзляк А.Г., Полянський В.Б., Рабинович Ю.М., Якір М.С.. Цей посібник містить понад 1 200 задач і вправ. Серед них немало простих і однотипних. Тому його зручно покласти на парту кожному учню і провести самостійну роботу контролюючого характеру. А також цей посібник містить складні, нестандартні задачі (вони помічені знаком *, а особливо важкі - **). Це дозволяє використовувати його для індивідуальної роботи, роботи гуртка, для підготовки учнів до олімпіад.

Додатково до основного підручника використовую на уроках такі посібники:

у 7–9 класах «Алгебраический тренажер», автори Мерзляк А.Г., Полонський В.Б., Якір М.С. , «Збірник задача з геометрії для 7 – 9 класів», автор Лоповок Л.М.

у 10-11 класах «Вчимося розв’язувати задачі з початків аналізу», автори Мерзляк А.Г., Полонський В.Б., Рабінович Ю.М., Якір М.С., «Алгебра та початки аналізу». 10 клас, автори Ковтонюк М.М., Ясінський В.А., Ковтонюк Г.М.

Підручники з алгебри для 8 і 9-х поглиблених класів потребують оновлення. По перше, деяких тем передбачених програмою в них немає. По друге, завдання не розбити по рівням складності і занадто важкі (в більшості це стосується підручника для 8-го класу). Відповіді в рівняннях часто є складними ірраціональними виразами. Хоча мета теми: виробити навички розв’язання рівнянь певного виду. У 9-му класі на уроці розв’язування ірраціональних рівнянь пропонувала учням завдання із підручника для 11-го класу (розділ А і Б), тому що ті рівняння, що є у підручнику для 9-го занадто складні. Можна сказати, що це просто набір завдань високої складності. По третє, багато помилок. Іноді урок розв’язування завдань перетворюється в урок «Знайди помилку».

Для тематичного оцінювання перевагу віддаю збірникам завдань для тематичного оцінювання знань із серії «Контроль на 12» авторів Прокопенко Н.С., Мерзляк А.Г., Полонський В.Б., Якір М.С. В кожній роботі завдання розміщені за рівнем складності і це відмічено знаками ^о, *, **. Виконав роботу, учень бачить, на якому рівні він працює. Коли ж учням пропонується інший вид тематичних робіт, де спочатку потрібно обрати рівень складності, часто бувають суперечки. Учні або переоцінюють свої можливості або сподіваються десь підглянути, тому обирають, як правило, більш високий рівень, ніж вони здатні розв’язати.

Застосовую на уроках математики інформаційні технології. Вивчення деяких розділів шкільного курсу з використанням традиційних засобів навчання викликають певні утруднення в учнів щодо їх сприйняття та практичного застосування. Це переважно тоді, коли навчальний матеріал є великим за обсягом, насиченим і вимагає додаткових наочно-демонстраційних засобів навчання. Такими є, наприклад, теми: «Теорема Фалеса» - 8-ий клас, «Розв’язування рівнянь і нерівностей з параметром графічним методом» - 9-й клас (з поглибленим вивченням математики), «Функція», «Перетворення графіків елементарних функцій», «Розв’язування рівнянь вищих степенів», «Розв’язування нерівностей вищих степенів», «Обернені тригонометричні функції», «Розв’язування найпростіших тригонометричних рівнянь», «Зображення просторових фігур на площині» - 10-ий клас (з поглибленим вивченням математики).

Матеріал, що пропонується розглянути протягом уроку, є досить великим за обсягом. Його виклад традиційними методами вимагатиме більше навчального часу. Застосування ж інформаційних технологій дає змогу оптимально використати час на вивчення теми, а також підвищити рівень сприйняття і розуміння учнями матеріалу, робити навчальну інформацію доступнішою для сприйняття, зрозумілою за допомогою відеосупроводу, інтерактивності навчальних систем.

У минулому навчальному році відбулася апробація електронного підручника з алгебри у 8-му класі «Терм». Застосування програмних засобів також передбачає більш самостійну роботу учня над вивченням нового матеріалу, ніж на звичайному уроці. Учителю відводиться роль консультанта, помічника. На жаль таких електронних підручників з математики українською мовою поки ще обмаль.

На уроках із застосуванням інформаційних технологій пояснення учителя супроводжується інформацією на слайдах, що є не тільки яскравою динамічною ілюстрацією, а й способом фіксації найсуттєвішого у новому матеріалі. Межпредметні зв’язки , що стають у процесі такого викладу тіснішими, роблять границі навчальних дисциплін прозорішими і сприяють їх інтеграції. А для учнів елементи навчального процесу складаються в цілісну, логічно оформлену систему.

Застосування програмних засобів дає змогу проводити таки види робіт:

Комп’ютерне спостереження – після пояснення нового матеріалу або під час пояснення пропоную учням 1-2 спостереження. Наприклад, у 10-му класі при вивченні теми «Екстремуми функції», «Обернені функції» учні спостерігають дану властивість по графікам функцій на екрані монітора. Вчитель економить час на побудову на дошці відомих учням функцій. Такі спостереження дозволяють учням на інтуїтивному рівні зрозуміти, що таке екстремум або властивість обернених функцій. Після цього їм буде зрозуміле і строге математичне означення.

Експериментальні задачі – дослідження – задачі, для розв’язання яких необхідно підставити відповідні параметри змінних і спостерігати, які зміни відбуваються із графіком. Наприклад у 9-му класі з поглибленим вивченням математики, коли вивчається тема «Квадратична функція», учням пропонується розв’язати рівняння ах² + bх + с = 0 для заданих значень коефіцієнтів а, b, с. Побудувати графік відповідної функції з допомогою комп’ютерної програми і заповнити картку – звіт. На перший погляд такі завдання здаються дуже прості. Але вони дуже корисні. Тому що дозволяють учням побачити живий зв'язок комп’ютерного експерименту і аналітичного розв’язування завдань.

Розрахункові задачі із послідуючою комп’ютерною перевіркою – задачі, які спочатку необхідно розв’язати без використання комп’ютера, а потім перевірити отриману відповідь. Ті задачі, що вимагають тривалого часу для розв’язання пропоную учням для попередньої роботи додому.

Лабораторні роботи – дозволяють проводити роботи, які носять творчий дослідницький характер. При виконання лабораторної роботи учневі необхідно провести побудову графіків функцій, зробити самостійні дослідження ії властивостей , спробувати помітити якісь закономірності, висловити у зв’язку з цим свої припущення, експериментально перевірити їх правильність. Наприклад, в 11-му профільному класі , коли вивчається тема «Степенева функція, ії властивості та графік», учні досліджують графіки, які будуються за допомогою комп’ютерної програми і заповнюють картку – інструкцію. Потім відбувається обговорення цікавих особливостей графіків степеневої функції, які учням вдалося помітити.

Все більш поширюються інтерактивні технології навчання, коли навчальний процес відбувається за умов постійної, активної взаємодії всіх учнів. Це співначання, взаємонавчання (колективне, групове, навчання в співпраці) де учень і учитель є рівноправними, рівнозначними суб’єктами навчання. Відбувається моделювання життєвих ситуацій, використання рольових ігор, спільне розв’язання проблем. Воно ефективно сприяє формуванню вмінь, навичок і цінностей, створює атмосфери співробітництва.

«Інтерактивний» означає здатність взаємодіяти, або знаходитися в режимі бесіди, діалогу з будь-чим (наприклад, з комп’ютером) або з будь-ким (людиною). Інтерактив виключає домінування однієї думки над іншими і будується на позитивному діалоговому спілкуванні.

Після розв’язання задачі або завдання, обговорюємо з учнями, чи не знайшов хтось з них інший розв’язок. Чи буде інший розв’язок кращим за розглянутий і чим саме? Пошук раціональних шляхів розв’язання задач дуже важливі для розвитку творчих здібностей учнів.

Інтерактивне навчання вможливлює різке збільшення відсотка засвоєння матеріалу, оскільки впливає не лише на свідомість учня, але й на його почуття, волю. Так на уроці в 8-му класі з теми «Теорема Піфагора», підготовлені учні доводили теорему Піфагора різними способами. Доповіді учнів були доповнені демонстрацією презентацій, які учні готували на протязі вивчення цієї теми.

Після доповідей учнів відбувається робота в парах. Учні обирають картку із завданням того рівня, на якому вони працюють. Таким чином відбувається повторення і закріплення знань теореми Піфагора, підвищується зацікавленість учнів у вивченні математики.

Щоб застосування інтерактивних технологій було ефективним, попередньо планую свою роботу:

даю завдання учням для попередньої підготовки: прочитати, продумати, виконати самостійні підготовчі завдання;
відбираю для уроку або заняття такі інтерактивні вправи, які дали б учням «ключ» до засвоєння теми;
під час самих інтерактивних вправ даю учням час подумати над завданням, щоб вони виконували його серйозно, а не механічно або «граючись»;
дуже важливо провести спокійне глибоке обговорення за підсумками інтерактивної вправи, зокрема, акцентуючи увагу на іншому матеріалі, що безпосередньо не порушувався в інтерактивній вправі;
проводжу швидкі опитування, самостійні домашні роботи з різноманітних матеріалів теми, що не були пов’язані з інтерактивними завданнями.

Лекцію теж намагаюсь зробити більш результативною. Пояснюючи матеріал короткими частинами, блоками пропоную учням обговорити кожну таку частину, а потім продовжувати пояснення. Унаслідок такого навчання засвоєння матеріалу може бути вдвічі більшим, ніж монологічне пояснення.

Ще краще, якщо ми можемо щось зробити з інформацією, аби мати зворотний зв'язок, дізнатися, чи добре ми ії зрозуміли. З цією метою пропоную учням: викласти інформацію своїми словами; навести свої приклади; показати подібні вияви, схожі ознаки в інших явищах і процесах; знайти зв'язок із іншими процесами або явищами, відомими раніше; передбачити деякі наслідки; знайти протилежності.

Використання наочності під час лекцій також збільшує запам’ятовування матеріалу від 14 до 38%.

Коли завершується вивчення деякої теми і необхідно повторити із класом і узагальнити вивчений матеріал, даю завдання класу: обговорити в парах, що в даній темі найважливіше? Кожна пара формулює свою тезу (означення, пункт плану), причому тільки одну. Потім це ж питання обговорюється в четвірках, з двох пропозицій обирається одна, найважливіша. Кожна четвірка записує свою тезу на дошці, пояснює, чому вони вважають саме так. Потім учням пропонується розмістити висунути тези в порядку їх важливості.

Необхідно використовувати інтерактивні методи навчання. Але це не означає, що потрібно використовувати тільки інтерактивне навчання. На одному уроці можна використовувати 1 (максимум 2) інтерактивні вправи, а не цілий калейдоскоп. Для навчання важливі всі рівні пізнання й усі види методик. Тип навчання обирається в залежності від завдань і умов роботи.

А також є широкий спектр позакласної роботи на виявлення та розвиток творчих здібностей учнів.

Сприяння самореалізація творчої особистості відбувається також завдяки широкому спектру позакласної роботи:

це підготовка і участь школярів в олімпіадах з математики;
дослідницька робота в МАН;
участь у гуртках, факультативах;
участь в інтелектуальних іграх;
участь в міжнародному математичному конкурсі «Кенгуру»;
робота над проектом;
участь у науково практичних конференціях;
самореалізація учнів під час проведення дня учнівського самоврядування. Щороку на день вчителя в нашій школі проводиться такий захід. Учні, які мають здібності до викладацької роботи, мають змогу проявити себе. Потім, як правило, такі учні обирають професію учителя.

Кожен вчитель математики нашої школи веде гурток, на якому відбувається підготовка учнів до участі в олімпіадах, готуються і проводяться інтелектуальні ігри («Брейн-рінг», «Самий розумний», математичні КВК та інше).

Улюбленою грою учнів нашої школи є міжнародна математична гра – конкурс «Кенгуру». Якщо на олімпіаді три призових місця, то за участь у «Кенгуру» весь клас може мати високі результати. Учням це дуже подобається, вони пишаються, коли отримують сертифікати а також книжки, в яких надруковані їх прізвища. Коли учні нашої школи вперше взяли участь у цьому конкурсі, то було всього 6 учасників. У минулому році було вже 80, серед них 40 мали відмінний результат, 28 – добрий результат. Треба сказати, що результати учнів нашої школи вищі, ніж середні по «Кенгуру». Агітаційну компанію починаємо з лютого. Ми вивішуємо стенд «Я люблю цю гру», щоб учні мали змогу дізнатися про умови конкурсу, його мету. Підготовка до конкурсу йдеться по паралельним класам. Коли конкурс закінчується, ми обговорюємо завдання, розв’язки. Від деяких задач (особливо геометричних) просто в захваті. Є такі красиві задачі, які мають дуже прості розв’язки, залишається тільки здогадатися, яку саме властивість треба застосувати. Їх потім використовуємо на уроці. Така робота сприяє розвитку інтересу до математики і розвитку творчих здібностей школярів.

Новою, цікавою, дослідницькою формою роботи є робота над проектом. Знайомство з цією формою роботою відбувається в межах програми Intel. Робота над проектом нагадує дослідницьку роботу в МАН, але вона значно менша за обсягом. Складність в цій роботі є як для вчителя, так й для учнів.

Для вчителя – це придумати цікаву тему для роботи, за якою можливо провести хоча б невеличку дослідницьку роботу.

Для учнів – це провести дійсно дослідницьку роботу. Бо вони намагаються виконати реферат, причому переписують у нього все, що тільки знайдеться, що хоч віддалено відноситься до даної теми, або відповідають зовсім не на те запитання.

Учні 7-го класу працювали над проектом «Як алгебра застосовується у реальному житті», «Чи багато геометричних фігур навколо нас?», «Як мені допомогли лінійні рівняння?», «Чи дійсно, створена людиною цивілізація повна паралелей.». Учні 9-го класу працювали над проектом «Як мені допомогла теорема Піфагора», вимога сучасності саме у тому, щоб вчити учнів дійсно дослідницькій роботі: вмінню спостерігати, виділяти головне, суттєве у вивчаємому матеріалі, вміння формулювати свою думку.

В нашій школі розроблено та постійно вдосконалюється система заохочень, стимулювання відповідно до досягнутих результатів, учні працюють за рейтинговою системою. По закінченню семестру класні керівники обчислюють середній бал успішності кожного учня, потім разом із заступником директора по виховній роботі додають бали за участь в різних конкурсах, олімпіадах, змаганнях тощо. За результатами визначаються учні, які набрали більшу кількість балів. Так у 2005-2006 н.р. двічі на рік підводили підсумки, за якими було визначено посеместрово по 25 переможців–стипендіатів та 25 призерів, які отримали по 25 гривень. 20 учнів за підсумками року отримали від районного відділу освіти Миколаївської райдержадміністрації стипендії в розмірі 200 гривень

Це дуже стимулює творчу активність учнів. Кожен учень намагається проявити себе там, де він може: один – в художній самодіяльності, другий – в спорті, третій – в предметних олімпіадах, четвертий – усюди встигає.

Тільки ось такий системний підхід до виявлення і розвитку творчої активності учнів може дати позитивний результат.

Які ж результати такої роботи з обдарованими дітьми? В школі 622 учня. Серед них :

15 учнів стали переможцями районних предметних олімпіад;
27 стали призерами районних предметних олімпіад;
12 учнів брали участь в обласних предметних олімпіадах. Серед них: Андрущенко Аліна – з географії стала призером і учасником республіканської олімпіади (вчитель Дзюба О.П.), Сосинюк Тетяна – з англійської мови – ІІ місце (вчитель Руденко С.А.). Федорова Тетяна – з української мови – ІІІ місце (вчитель Долженіцина В.М.).
16 учнів є членами наукового товариства МАН за трьома напрямками: філологічний, історико-географічний, фізико-математичний. Двоє учнів стали призерами наукових робіт в області.
12 учнів стали переможцями районного конкурсу ім. Петра Яцека.
80 учнів взяли участь у Міжнародному математичному конкурсі «Кенгуру». З них 68 виконали завдання на високому рівні.
12 учнів брали участь в міжнародному фізичному конкурсі «Левеня» та в конкурсі з природознавства «Колосок».
12 учнів школи брали участь в обласному форумі юних шанувальників фізики.

Відмінник освіти України, вчитель-методист,

вчитель математики Ольшанської зош І-ІІІ ступенів

Фірсіна Світлана Іванівна

навчити учнів визначати, розуміти, а потім самостійно ставити перед собою завдання;
вчити учнів використовувати найраціональніші способи роботи, які сприяють успішному оволодінню матеріалом;
формувати в учнів навчальні мотиви, пізнавальний інтерес, бажання вчитися, відповідально та свідомо ставитися до процесу навчання.

Blog

Содержание