Geum.ru

Питання до колоквіуму І мі

Вид материалаДокументы
Подобный материал:
  1   2   3

Питання до колоквіуму

І МІ
  1. Предмет і метод математики.
  2. Множина. Операції над множинами.
  3. Множина дійсних чисел.
  4. Взаємно однозначна відповідність між елементами множин. Аксіома Кантора.
  5. Властивості множини дійсних чисел.
  6. Аксіома Архімеда. Принцип вкладених відрізків.
  7. Числові проміжки.
  8. Модуль дійсного числа. Геометричний зміст, властивості модуля.
  9. Обмеженість числових множин.
  10. Теорема про існування точної верхньої (нижньої) грані числової множини.
  11. Функції. Означення. Способи задання функції.
  12. Елементарні функції.
  13. Деякі класи функцій (монотонні, парні та непарні, періодичні).
  14. Числова послідовність та її границя.
  15. Властивості збіжних послідовностей.
  16. Теорема Больцано-Вейерштрасса. Критерій Коші.
  17. Теорема про проміжну змінну. Нескінченно великі послідовності.
  18. Нескінченно малі послідовності та їх властивості. Нескінченно великі.
  19. Представлення збіжної послідовності у вигляді суми її границі та нескінченно малої послідовності. Теореми про границю суми і добутку двох послідовностей.
  20. Теореми про границю частки двох послідовностей.
  21. Теорема про існування граней монотонно зростаючої і обмеженої зверху послідовності. Число e. Натуральні логарифми.
  22. Границя функції в точці. Означення за Коші. Геометричне тлумачення границі функції в точці. Означення границі функції за Гейне.
  23. Властивості функцій, що мають границю функції в точці.
  24. Границя функції та нескінченності. Властивості границь. Нескінченні границі
  25. Перша важлива границя.
  26. Друга важлива границя.
  27. Нескінченно малі функції та їх властивості. Порівняння нескінченно малих.
  28. Теорема про еквівалентні нескінченно малі.
  29. Однобічні (односторонні) границі функції в точці. Їх зв’язок з границею. Приклади.
  30. Неперервність функцій в точці і на проміжку. Однобічна (одностороння) неперервність.
  31. Точки розриву функцій та їх класифікація.
  32. Властивості функцій, неперервних на відрізку.
  33. Границя точки. Означення границі числової послідовності через граничну точку. Теорема про збіжність.
  34. Теорема про існування і неперервність обмеженої функції.
  35. Первісна функція та невизначений інтеграл. Властивості невизначеного інтеграла.
  36. Таблиця основних невизначених інтегралів.
  37. Основні методи інтегрування. Метод розбивки. Метод підстановки.
  38. Метод інтегрування частинами у невизначеному інтегралі.
  39. Інтегрування раціональних функцій. Прості дроби. Інтегрування простих дробів перших трьох типів.
  40. Інтегрування четвертого типу простих дробів. Рекурентна формула.
  41. Представлення правильного алгебраїчного дробу у вигляді скінченного числа простих дробів.
  42. Метод невизначених коефіцієнтів інтегрування раціональних функцій.
  43. Метод М.В.Остроградського інтегрування алгебраїчних дробів.
  44. Інтегрування деяких класів ірраціональних функцій.
  45. Підстановки Ейлера.
  46. Інтегрування біноміального диференціала. Підстановки Чебишева.
  47. Інтегрування тригонометричних функцій.
  48. Задачі, що приводять до поняття визначеного інтеграла.
  49. Визначений інтеграл та його геометричний зміст.
  50. Необхідні і достатні умови інтегровності функції.
  51. Класи інтегровних функцій.
  52. Властивості визначеного інтеграла.
  53. Теореми про середнє для визначеного інтеграла.
  54. Інтеграл із верхньою змінною межею. Формула Ньютона – Лейбніца.
  55. Основні способи обчислення визначеного інтеграла. Метод розбивки. Метод підстановки.
  56. Метод інтегрування частинами у визначеному інтегралі.
  57. Невласні інтеграли. Інтеграли на нескінченних проміжках. Ознаки збіжності та розбіжності.
  58. Інтеграли від необмежених функцій. Ознаки збіжності та розбіжності.
  59. Застосування визначеного інтеграла в геометрії. Обчислення площ плоских фігур.


І МФ, МЕ
  1. Поняття множини, її елемента, підмножини, рівних множин.
  2. Означення перерізу, об’єднання і різниці множин та доповнення множини.
  3. Основні властивості операцій над множинами.
  4. Аксіоми множини дійсних чисел.
  5. Різні форми аксіоми неперервності (Дедекінда, Кантора, Вейєрштрасса) та їх рівносильність.
  6. Раціональні та ірраціональні числа. Їх зображення десятковими дробами. Приклади ірраціональних чисел.
  7. Обмежені та необмежені числові множини. Їхні межі і точні межі. Найбіль­ший та найменший елементи множини.
  8. Теорема Вейєрштрасса про існування точних меж.
  9. Критерій точних меж.
  10. Модуль дійсного числа, його геометричний зміст.
  11. Властивості модуля.
  12. Принцип і метод математичної індукції.
  13. Нерівність Бернуллі.
  14. Формула бінома Ньютона.
  15. Загальне поняття функції. Приклади функціональних і нефункціональних відповідностей.
  16. Сюр’єкція, ін’єкція та бієкція.
  17. Обернена функція.
  18. Суперпозиція функцій.
  19. Послідовність точок деякої множини.
  20. Функції дійсної змінної. Способи їх задання. Графік.
  21. Основні елементарні функції та вигляд їхніх графіків.
  22. Елементарні функції та їх класифікація.
  23. Найпростіші властивості функцій дійсної змінної (парність, непарність, монотонність, періодичність та обмеженість).
  24. Ціла та дробова частини дійсного числа.
  25. Поняття границі послідовності. Його суть і геометричний зміст.
  26. Нескінченні границі послідовності.
  27. Властивості збіжних числових послідовностей.
  28. Теорема про границю монотонної обмеженої послідовності.
  29. Теорема про число е. Наслідок про оцінку логарифма.
  30. Поняття часткової границі послідовності. Теорема про зв’язок між границею і частковими границями.
  31. Критерій часткової границі на мові околів.
  32. Теорема Больцано – Вейєрштрасса про існування часткових границь.
  33. Теорема про множину всіх часткових границь деякої послідовності.
  34. Верхня та нижня границі послідовності. Їх існування.
  35. Поняття фундаментальної послідовності, його зв’язок з обмеженістю.
  36. Критерій фундаментальності послідовності.
  37. Критерій Коші збіжності послідовності.
  38. Поняття околу і проколеного околу скінченної або нескінченно віддаленої точки.
  39. Поняття граничної точки множини. Різні способи його означення.
  40. Критерій граничної точки множини.
  41. Теорема Больцано – Вейєрштрасса про існування граничних точок множини.
  42. Поняття границі функції в точці. Його суть та геометричний зміст.
  43. Означення границі функції в точці за Коші, за Гейне та мовою околів. Їх еквівалентність.
  44. Означення мовою ε-δ границі функції в точці у випадках, коли точка або границя є нескінченною.
  45. Властивості функцій, які мають границю в точці.
  46. Ліва та права границі функції в точці. Критерій існування границі.
  47. Теорема про ліву та праву границі монотонної функції.
  48. Деякі важливі границі.
  49. Нескінченно малі функції в точці та їх порівняння між собою.
  50. Еквівалентні нескінченно малі. Застосування їх до обчислення границь.
  51. Поняття функції, неперервної у точці. Означення неперервності за Коші, за Гейне та мовою околів.
  52. Неперервність у точці за множиною, зліва та справа. Неперервність та рівномірна неперервність функції на множині.
  53. Критерій рівномірно неперервної функції.
  54. Властивості функцій, неперервних у точці.
  55. Точки розриву та їх класифікація.
  56. Властивості функцій, неперервних на відрізку.
  57. Теорема про існування, монотонність і неперервність оберненої функції.
  58. Означення і властивості степеня з натуральним, цілим та раціональним показником.
  59. Теорема про існування арифметичного кореня п-го степеня.
  60. Теорема про неперервність показникової функції в нулі за множиною раціональних чисел.
  61. Степінь з ірраціональним показником. Теорема про обгрунтування його означення.
  62. Поняття логарифма числа. Теорема про існування логарифма.
  63. Властивості логарифмів.
  64. Загальна степенева функція.
  65. Неперервність елементарних функцій.
  66. Поняття первісної і невизначеного інтеграла. Необхідні умови існування первісної. Приклади.
  67. Поняття первісної і невизначеного інтеграла. Теорема про множину всіх первісних, її геометричний зміст.
  68. Поняття первісної і невизначеного інтеграла. Інтегрування у скінченному вигляді.
  69. Таблиця невизначених інтегралів та її обґрунтування.
  70. Інтегрування функцій методом розкладання. Приклади.
  71. Інтегрування функцій методом підстановки. Приклади.
  72. Інтегрування функцій частинами. Приклади.
  73. Раціональні дроби, виділення цілої частини. Елементарні дроби. Леми про розкладання многочлена на множники та правильного дробу на елементарні. Приклади.
  74. Інтегрування елементарних дробів І – ІІІ типів у загальному випадку. Приклади.
  75. Інтегрування елементарного дробу IV типу. Рекурентна формула. Приклад.
  76. Алгоритм інтегрування довільної раціональної функції. Приклад.
  77. Інтегрування найпростіших ірраціональностей. Приклади.
  78. Інтегрування дробово-лінійних ірраціональностей. Приклад.
  79. Інтегрування квадратичних ірраціональностей. Перша підстановка Ейлера. Приклад.
  80. Інтегрування квадратичних ірраціональностей. Друга підстановка Ейлера. Приклад.
  81. Інтегрування квадратичних ірраціональностей. Третя підстановка Ейлера. Приклад.
  82. Окремі прийоми інтегрування квадратичних ірраціональностей. Приклади.
  83. Біноміальний диференціал і підстановки Чебишова. Випадок 2). Приклад.
  84. Біноміальний диференціал і підстановки Чебишова. Випадок 3). Приклад.
  85. Інтегрування тригонометричних функцій за допомогою універсальної підстановки. Приклад.
  86. Інтегрування деяких тригонометричних функцій без універсальної підстановки. Приклади.
  87. Інтегрування функцій, що містять показникову функцію. Приклади.
  88. Задача про площу криволінійної трапеції. Висновки.
  89. Означення визначеного інтеграла. Приклади інтегровних та неінтегровних функцій.
  90. Необхідна умова інтегровності. Чи є вона достатньою?
  91. Суми Дарбу та їхні властивості.
  92. Нижній і верхній інтеграли Дарбу. Теорема Дарбу про границі сум Дарбу.
  93. Критерій інтегровності Дарбу.
  94. Коливання функції. Лема про коливання. Критерій інтегровності мовою коливань.
  95. Критерій інтегровності Рімана.
  96. Критерій інтегровності мовою послідовностей.
  97. Інтегровність монотонної функції.
  98. Інтегровність неперервної функції.
  99. Інтегровність функції, розривної на кінцях відрізка.
  100. Властивості визначеного інтеграла. Довести лінійну і адитивну.
  101. Властивості визначеного інтеграла. Довести властивості монотонності та невід’ємності.
  102. Властивості визначеного інтеграла. Довести властивість про інтегровність модуля.
  103. Властивості визначеного інтеграла. Довести властивість про інтегровність добутку.
  104. Властивості визначеного інтеграла. Довести теорему про середнє інтегрального числення.
  105. Орієнтовані інтеграли. Деякі їхні властивості.
  106. Інтеграл із змінною верхньою межею. Його неперервність.
  107. Інтеграл із змінною верхньою межею. Його диференціювання.
  108. Існування первісної для неперервної функції.
  109. Формула Ньютона – Лейбніца. Приклади.
  110. Формула заміни змінної для визначеного інтеграла. Приклад.
  111. Формула інтегрування частинами для визначеного інтеграла. Приклад.


І ФІА
  1. Предмет та метод математики. Множини дії над множинами.
  2. Множини дійсних чисел. Аксіоматична теорія дійсних чисел.
  3. Наслідки з аксіом додавання та множення.
  4. Модуль дійсного числа. Властивості модуля.
  5. Основні числові множини. Межі числових множин. Обмежені множини.
  6. Метод математичної індукції. Приклад.
  7. Числова функція. Способи задання функції.
  8. Елементарні функції.
  9. Монотонні функції.
  10. Парні та непарні функції.
  11. Періодичні функції.
  12. Числова послідовність та її границя.
  13. Властивості збіжних послідовностей.
  14. Нескінченно малі та нескінченно великі послідовності.
  15. Властивості нескінченно малих послідовностей.
  16. Теореми про границі числових послідовностей.
  17. Обмежені числові послідовності. Теорема про існування границі монотонно-зростаючої (спадної) і обмеженої зверху (знизу) послідовності.
  18. Теорема Больцано-Вейерштрасса.
  19. Критерій Коші.
  20. Деякі види невизначеності. Число e. Натуральні логарифми.
  21. Границя функцій в точці. Означення за Коші. Геометричний зміст. Означення границі за Гейне.
  22. Властивості функції, що має границю в точці.
  23. Властивості границь.
  24. Границя функції на нескінченності. Геометричний зміст. Нескінченні границі.
  25. Перша важлива границя.
  26. Друга важлива границя.
  27. Теореми про границі функцій (в точці і на нескінченності).
  28. Нескінченно малі функції та їх властивості.
  29. Теорема про зв’язок функції, що має границю, з нескінченно малою функцією.
  30. Порівняння нескінченно малих функцій.
  31. Однобічні (односторонні) границі функції в точці. Зв’язок границі функції в точці з однобічними границями.
  32. Неперервність функції в точці. Означення. Геометричний зміст. Неперервність функції на проміжку.
  33. Теорема про неперервність складеної функції. Односторонні неперервності.
  34. Первісна функція та її властивості.
  35. Невизначений інтеграл та його властивості.
  36. Таблиця інтегралів.
  37. Основні методи інтегрування.
  38. Інтегрування елементарних раціональних дробів.
  39. Інтегрування раціональних функцій.
  40. Інтегрування в скінченному вигляді.
  41. Інтегрування ірраціональних функцій 1-го і 2-го типу.
  42. Інтегрування ірраціональних функцій. підстановки Ейлера.
  43. Інтегрування диференціальних біномів.
  44. Інтегрування тригонометричних функцій.
  45. Задача про площу криволінійної трапеції.
  46. Поняття визначеного інтеграла. Необхідна умова інтегровності функції.
  47. Достатні умови інтегровності функції.
  48. Властивості визначеного інтегралу.
  49. Теореми про середнє значення визначеного інтеграла.
  50. Визначений інтеграл із змінною верхньою межею. Теорема.
  51. Формула Ньютона-Лейбніца.
  52. Замінна змінної та формула інтегрування частинами для визначеного інтеграла.
  53. Застосування визначених інтегралів до обчислення площ плоских фігур.
  54. Застосування визначених інтегралів до обчислення довжини дуги кривої.
  55. Застосування визначених інтегралів до обчислення об’єму тіл обертання.


ІІ МІ
  1. Ортогональна система функцій. Тригонометричний ряд формули Ейлера-Фур’є. Ряд Фур’є.
  2. Кусково-диференційовні функції. Теорема про розвинення функцій в ряд Фур’є.
  3. Ряд Фур’є для парної та непарної функцій.
  4. Ряд Фур’є для функцій з довільним періодом.
  5. Ряд Фур’є для неперіодичної функції.
  6. Комплексна форма для ряду Фур’є.
  7. Метричні простори в шкільному курсі математики.
  8. Означення метричного простору. Приклади метричних просторів.
  9. Основні метричні простори. п-вимірний евклідовий простір. 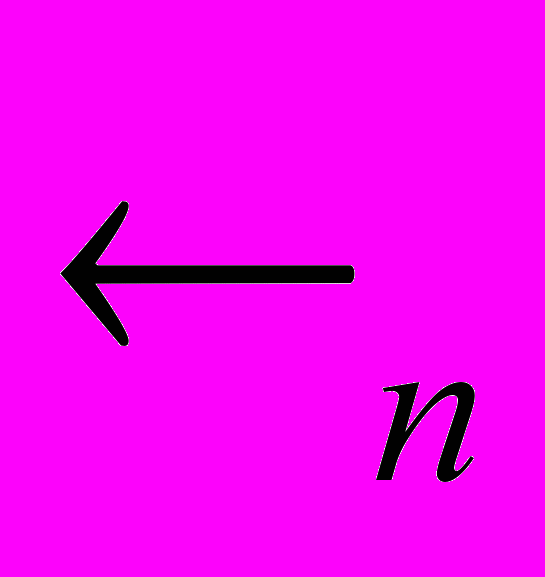. Простір .
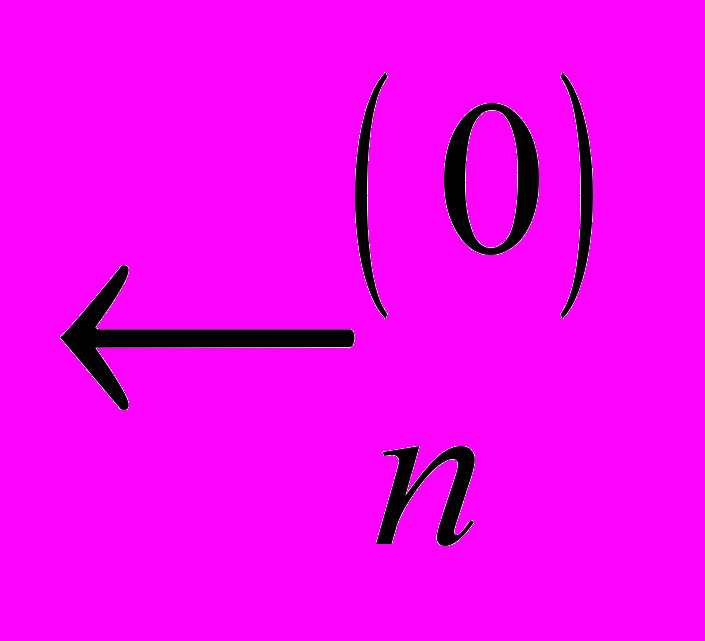  10. Простір .
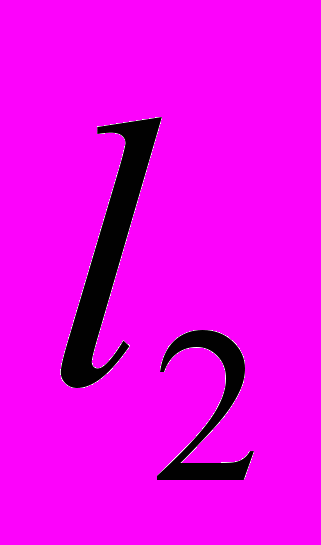  11. Простір 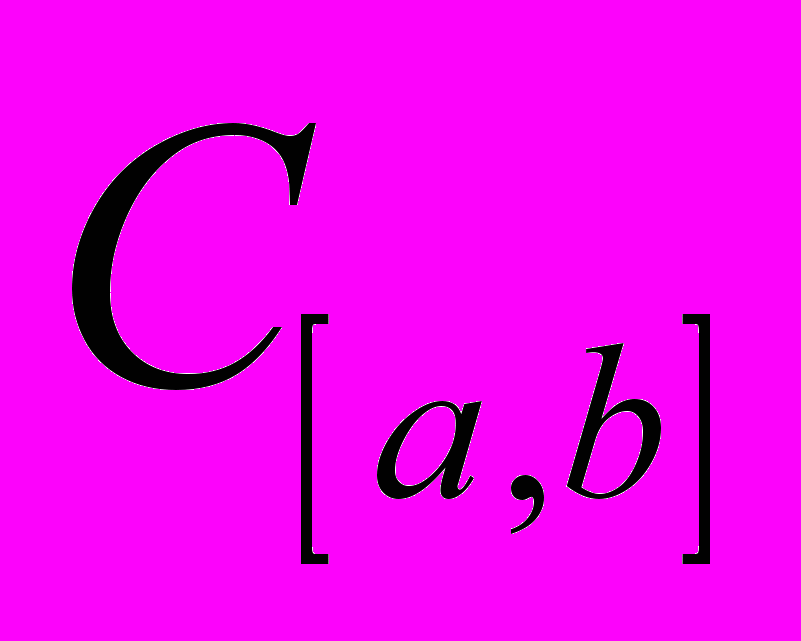. Простір .
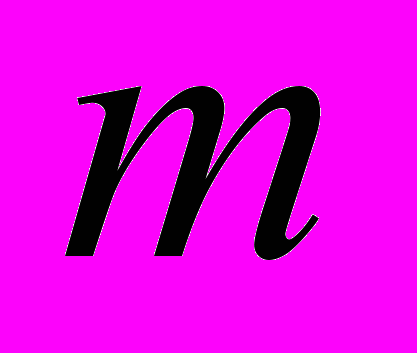  12. Збіжні послідовності та їх властивості.
  13. Поняття відкритої та замкнутої кулі, 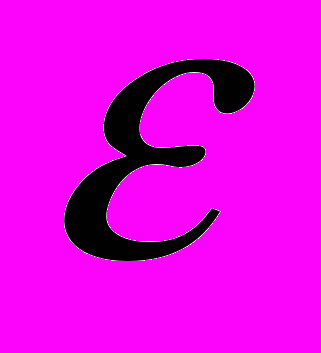-околу точки, граничної та узагальненої точки у метричному просторі.
  14. Класифікація точок множини, що лежить у метричному просторі.
  15. Необхідна і достатня умова того, щоб деяка точка множини, що належить метричному простору, була граничною.
  16. Теорема про зв’язок відкритої та замкненої множин.
  17. Критерій відкритої множини.
  18. Критерій замкненої множини.
  19. Об’єднання і переріз відкритих множин.
  20. Об’єднання і критерій замкнених множин.
  21. Повні метричні простори. Означення. Теорема: якщо послідовність має границю, то вона є фундаментальною.
  22. Теорема: для того, щоб послідовність точок евклідового простору збігалась, необхідно й достатньо, щоб вона була фундаментальною.
  23. Теорема: для того, щоб фундаментальна послідовність метричного простору була збіжною необхідно і достатньо, щоб вона мала збіжну послідовність у цьому просторі.
  24. Довести повноту евклідового метричного простору .
  25. Довести повноту простору .
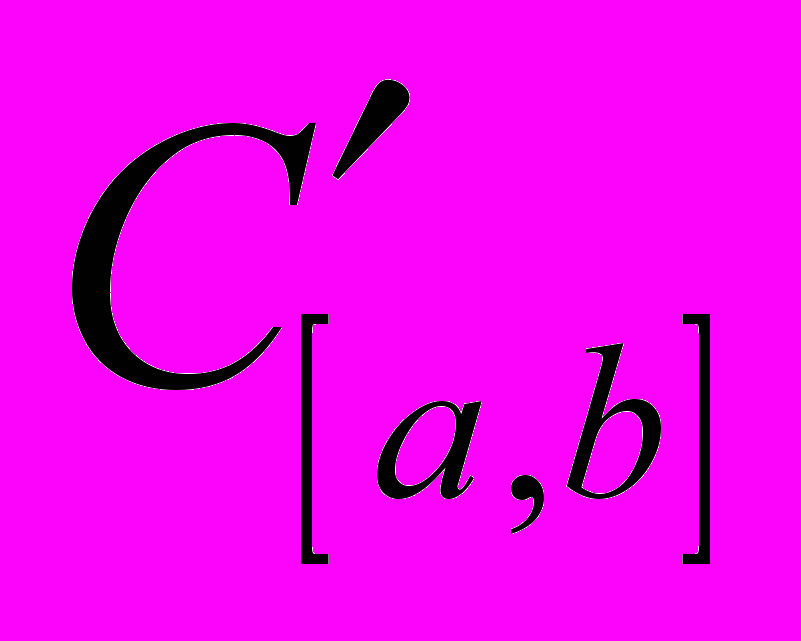  26. Компактні множини. Означення. Теорема. Непорожня множина Д метричного простору є компактною, якщо будь-яка нескінченна підмножина Д1 має принаймні одну граничну точку.
  27. Означення 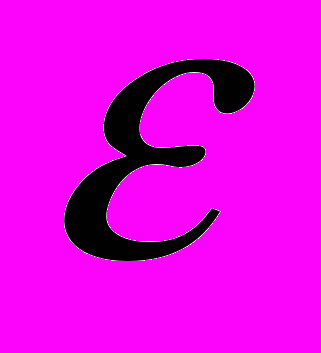-сітки. Цілком обмежена множина. Теорема Хаусдорфа, наслідки.
  28. Теорема: у евклідовому просторі множина всіх неперервних непорожніх замкнених обмежених множин утворюють компакт і тільки вони.
  29. Неперервні оператори та функціонали. Основні поняття. Означення неперервності за Коші і за Гейне.
  30. Критерій неперервності оператора в точці.
  31. Властивості неперервних операторів.
  32. Стискуючі відображення. Нерухомі точки відображення. Метод послідовних наближень.
  33. Теорема Банаха.
  34. Розв’язування системи лінійних алгебраїчних рівнянь методом стислих відображень.
  35. Функції багатьох змінних. Границя функцій багатьох змінних. Означення. Приклади.
  36. Неперервність функцій багатьох змінних. Означення, приклади.
  37. Теорема про властивості функцій багатьох змінних, неперервних на обмежених замкнених множинах.
  38. Частинні похідні функцій багатьох змінних. Геометричний зміст частинних похідних для функцій двох змінних.
  39. Диференційовність функцій багатьох змінних. Зв’язок між диференційовністю та неперервністю, між диференційовністю та частинними похідними.
  40. Повний диференціал функцій багатьох змінних. Застосування певного диференціала до наближених обчислень.
  41. Міра Жордана. Основні поняття.
  42. Зовнішня та внутрішня міри Жордана.
  43. Означення міри множини за Жорданом. Приклади.
  44. Основні теореми про вимірність за Жорданом.
  45. Критерій вимірності Жордана.
  46. Квадровані і кубовні множини.
  47. Задачі, що приводять до поняття подвійного інтеграла.
  48. Означення подвійного інтеграла. Умови інтегровності.
  49. Властивості подвійного інтеграла.
  50. Обчислення подвійного інтеграла. Випадок прямокутної області.
  51. Обчислення подвійного інтеграла. Випадок криволінійної області.
  52. Заміна змінних у подвійному інтегралі.
  53. Подвійний інтеграл у полярних координатах.
  54. Поняття про об’єм тіла. Задача про визначення маси просторового тіла.
  55. Означення потрійного інтеграла. Умови інтегровності.
  56. Властивості потрійного інтеграла.
  57. Обчислення потрійного інтеграла. Випадок прямокутного паралелепіпеда.
  58. Обчислення потрійного інтеграла. Випадок криволінійної просторової області.
  59. Заміна змінної у потрійному інтеграл. Випадок циліндричних координат.
  60. Заміна змінної у потрійному інтегралі. Випадок сферичних координат.
  61. Застосування подвійного інтеграла: обчислення площ плоских фігур; обчислення об’ємів тіла.
  62. Застосування подвійного інтеграла: обчислення площі поверхні.
  63. Застосування подвійного інтеграла у фізиці: маса плоскої пластини; статичні моменти плоскої області відносно координатних осей; координати центра маси плоскої області.
  64. Застосування подвійного інтеграла у фізиці: моменти інерції плоскої області відносно координатних осей і відносно точки.
  65. Застосування потрійного інтеграла в геометрії.
  66. Застосування потрійного інтеграла у фізиці: маса просторового тіла; статичні моменти та координати центра маси просторового тіла.
  67. Застосування потрійного інтеграла у фізиці: моменти інерції просторового тіла відносно координатних площин, координатних осей та відносно точки.
  68. Елементарні дроби. Представлення правильного раціонального дробу через елементарні дроби.
  69. Інтегрування перших трьох типів елементарних дробів.
  70. Інтегрування ІV типу елементарних дробів.
  71. Правило інтегрування раціональної функції.
  72. Інтегрування деяких видів ірраціональних виразів.
  73. Підстановки Ейлера.
  74. Інтегрування біномних диференціалів. Підстановка Чебишева.
  75. Інтегрування тригонометричних функцій.
  76. Задачі, що приводять до поняття визначеного інтеграла.
  77. Означення визначеного інтеграла.
  78. Необхідна умова існування визначеного інтеграла.
  79. Суми Дарбу та їх властивості.
  80. Критерій інтегровності функції.
  81. Класи інтегровних функцій.
  82. Властивості визначеного інтеграла.
  83. Теореми про середнє для визначеного інтеграла.
  84. Інтеграл із змінною верхньою межею, та його властивості.
  85. Формула Ньютона-Лейбніца.
  86. Заміна змінної у визначеному інтегралі.
  87. Інтегрування частинами у визначеному інтегралі.
  88. Обчислення площ плоских фігур за допомогою визначеного інтеграла.
  89. Невласні інтеграли І-го роду та їх обчислення.
  90. Ознаки порівняння для інтегралів І-го роду.
  91. Інтегральна ознака збіжності ряду.
  92. Невласні інтеграли ІІ-го роду.
  93. Інтегрування степеневих рядів.
  94. Застосування визначених інтегралів до площ обчислення.
  95. Площа криволінійного сектора у полярних координатах.
  96. Обчислення об’ємів тіл.
  97. Обчислення довжини дуги кривої.
  98. Диференціал дуги.
  99. Площа поверхні обертання.
  100. Обчислення центрів мас матеріальної кривої.
  101. Обчислення центра мас тонкої пластини.