Питання до колоквіуму І мі

Вид материала

Подобный материал:

1 2 3

ІІ МФ, МЕ

Площа криволінійної трапеції. Поняття визначеного інтеграла. Необхідна умова існування..
Поняття визначеного інтеграла і необхідна умова його існування..Котрприклад (функція Діріхле).
Поняття визначеного інтеграла. Суми Дарбу та їх властивості (довести 1-у і 2-у).
Поняття визначеного інтеграла. .Суми Дарбу та їх властивості (довести 1-у і 3-у).
Поняття визначеного інтеграла, нижнього та верхнього інтегралів Дарбу. Теорема Дарбу.
Критерій інтегровності функції за Ріманом. Довести неохідність. Коливання функції на відрізку. Наслідки.
Критерій інтегровності функції за Ріманом. Довести достатність. Коливання функції на відрізку. Наслідки.
Класи інтегровних за Ріманом функцій. Довести інтегровність неперервної функції.
Класи інтегровних за Ріманом функцій. Довести інтегровність монотонної функції.
Класи інтегровних за Ріманом функцій. Довести інтегровність неперервної функції.
Властивості визначеного інтеграла. Найпростіші властивості ( з доведенням).
Властивості визначеного інтеграла. Довести адитивну властивість.
Властивості визначеного інтеграла. Довести інтегровність добутку.
Властивості визначеного інтеграла. Довести інтегровність частки.
Властивості визначеного інтеграла. Довести теорему про середнє.
Визначений інтеграл із змінною верхньою межею інтегрування. Довести неперервність.
Визначений інтеграл із змінною верхньою межею інтегрування. Довести диференційовність.
Визначений інтеграл із змінною верхньою межею інтегрування. Довести існування первісної.
Визначений інтеграл із змінною верхньою межею інтегрування. Довести формулу Ньютона-Лейбніца.
Формула заміни змінної у визначеному інтеграліє
Формула інтегрування частинами у визначеному інтеграліє
Невласні інтеграли з нескінченним проміжком інтегрування. Достаттня ознака збіжності. Наслідок.
Невласні інтеграли з нескінченним проміжком інтегрування. Абсолютно та умовно збіжні інтеграли.
Невласні інтеграли від необмежених функцій. Достаттня ознака збіжності. Наслідок.
Невласні інтеграли .Абсолютно та умовно збіжні інтеграли.
Застосування визначеного інтеграла. Площа криволінійної трапеції та криволінійного сектора.
Застосування визначеного інтеграла. Об‘єм тіла обертання.
Застосування визначеного інтеграла. Обчислення довжини кусково-диференційовних шляхів. Поняття кривої таїї дуги. Диференціал дуги.
Застосування визначеного інтеграла. Площа поверхні обертання.
Застосування визначеного інтеграла. Центр ваги (центр мас) кривої. Перша теорема Гульдіна.
Застосування визначеного інтеграла. Центр ваги (центр мас) криволінійної трапеції. Друга теорема Гульдіна.
Застосування визначеного інтеграла. Робота сили вздовж прямої.
Поняття метричного простору. Приклади метричних просторів (,,.).
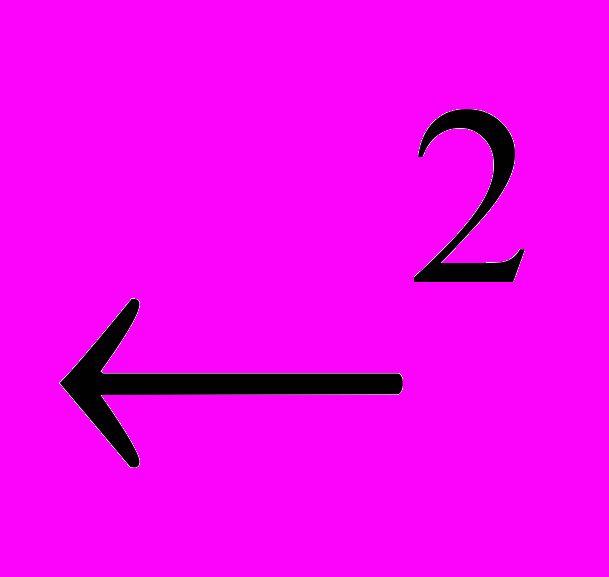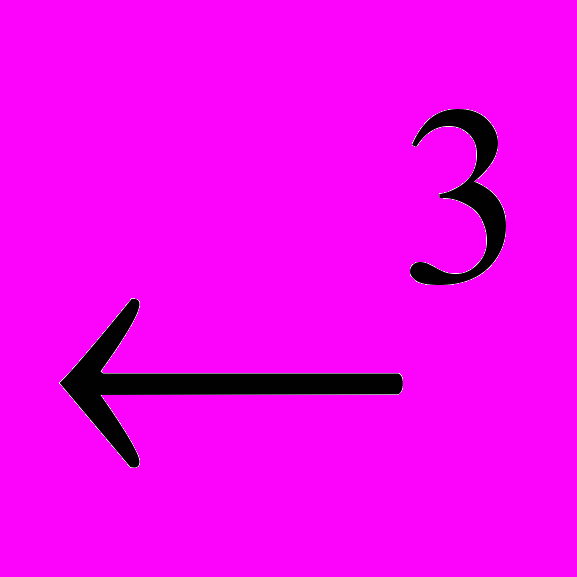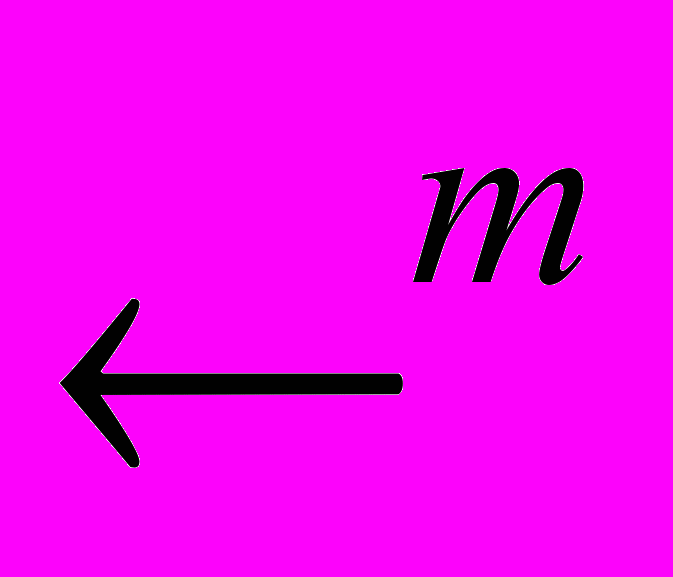Поняття метричного простору. Приклади метричних просторів. Простір ізольованих точок.
Поняття метричного простору. Приклади метричних просторів ( ).
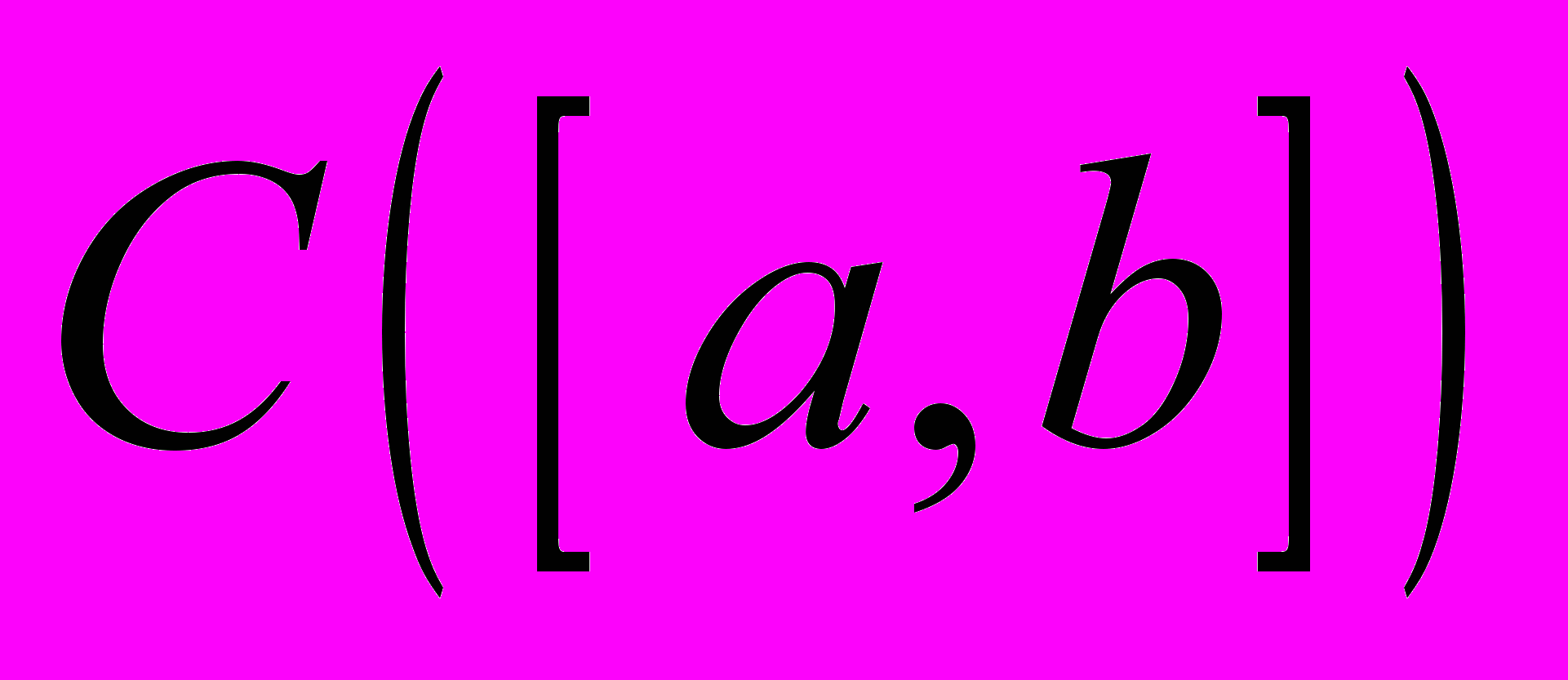Поняття метричного простору. Приклади метричних просторів ().
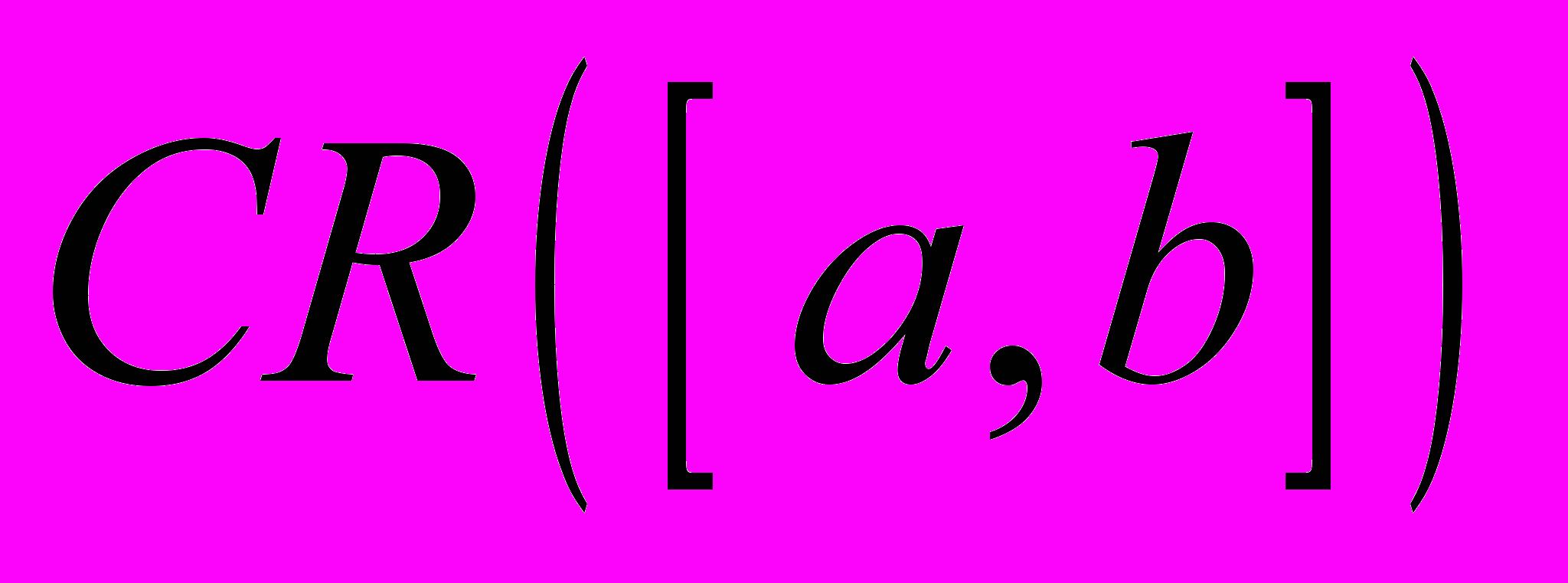Поняття метричного простору. Приклади метричних просторів (,,).
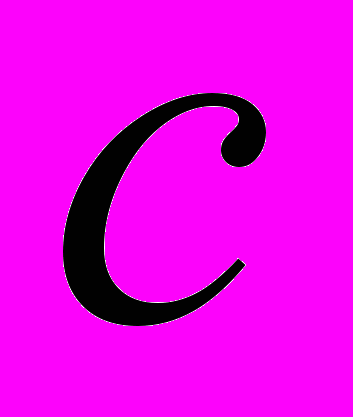Поняття метричного простору. Приклади метричних просторів ().
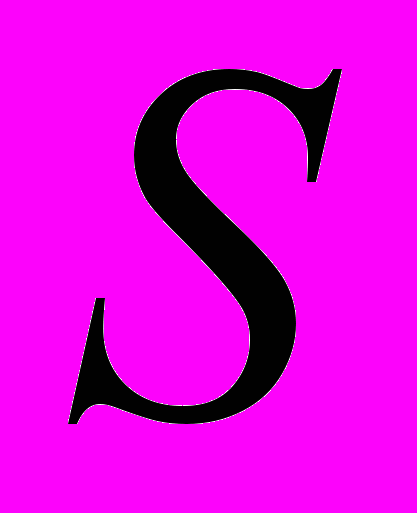Поняття метричного простору. Приклади метричних просторів ().
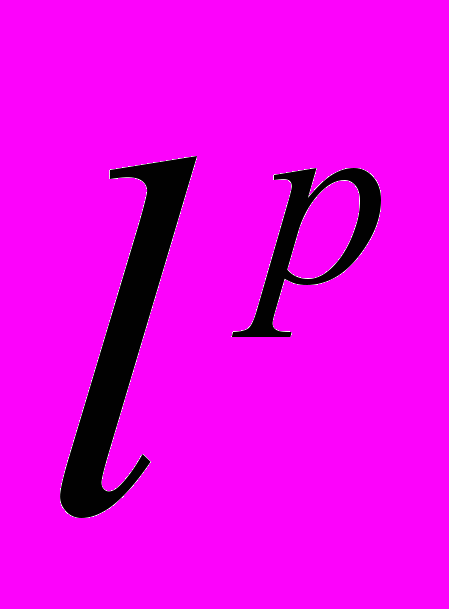Збіжні послідовності у метричних просторах. Означення границі послідовності у м.п. Критерій збіжності послідовності у просторі ізольованих точок.
Збіжні послідовності у метричних просторах. Означення границі послідовності у м.п. Критерій збіжності послідовності у просторі .
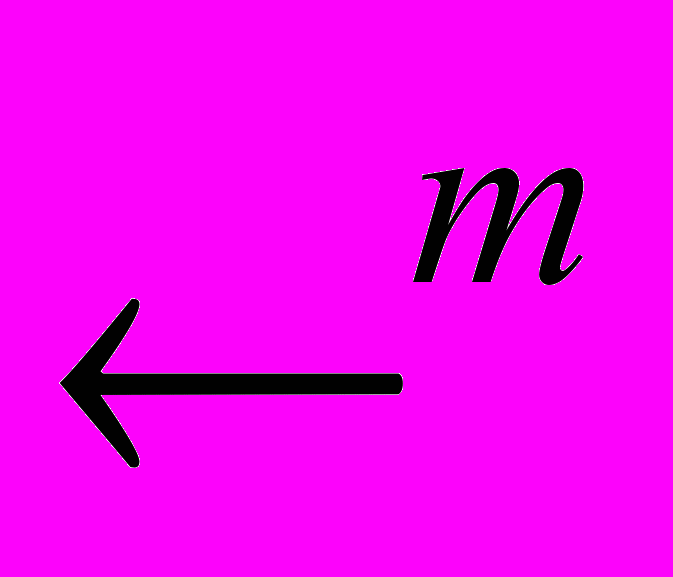Збіжні послідовності у метричних просторах. Означення границі послідовності у м.п. Збіжність послідовності у просторі .
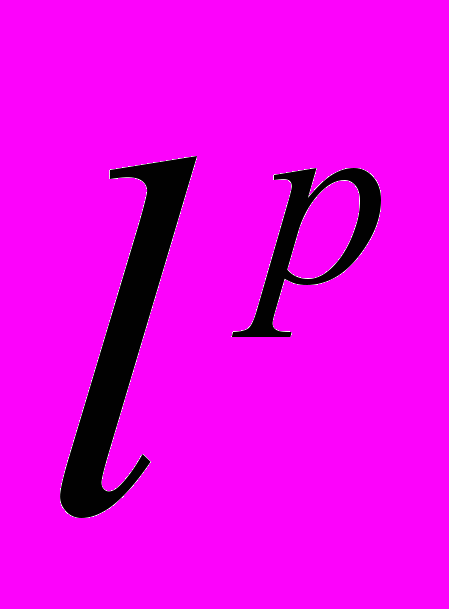Збіжні послідовності у метричних просторах. Означення границі послідовності у м.п. Критерій збіжності послідовності у просторі .
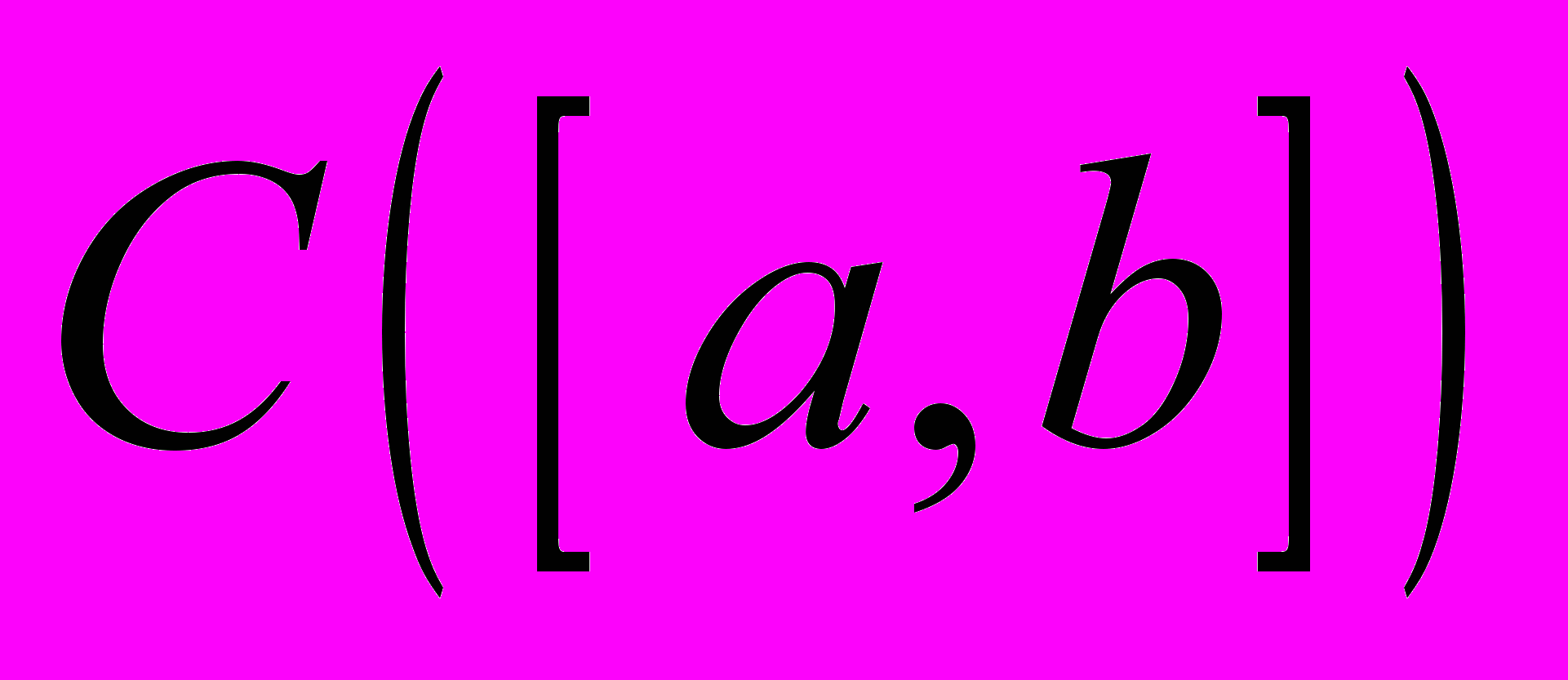Означення границі послідовності у метричному.просторі. Властивості границі послідовності. Довести властивість неперервності відстані.
Означення границі послідовності у метричному.просторі. Властивості границі послідовності. Довести обмеженість збіжної послідовності.
Теорема про заміну змінної 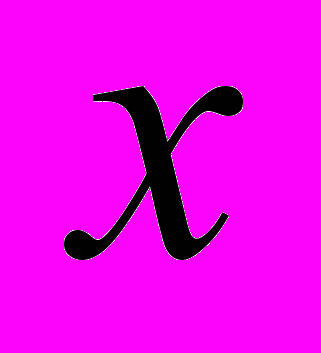у визначеному інтегралі на монотонну функцію .
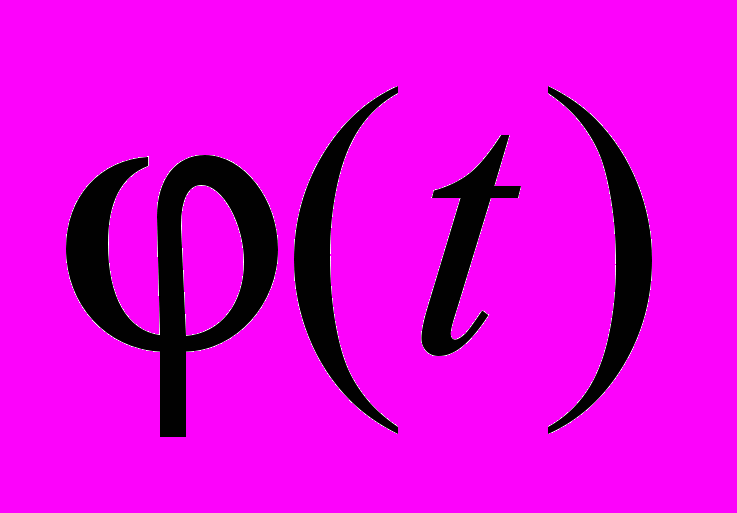Властивості про інтеграли від парної, непарної та періодичної функцій.
Означення невласного інтеграла по проміжку 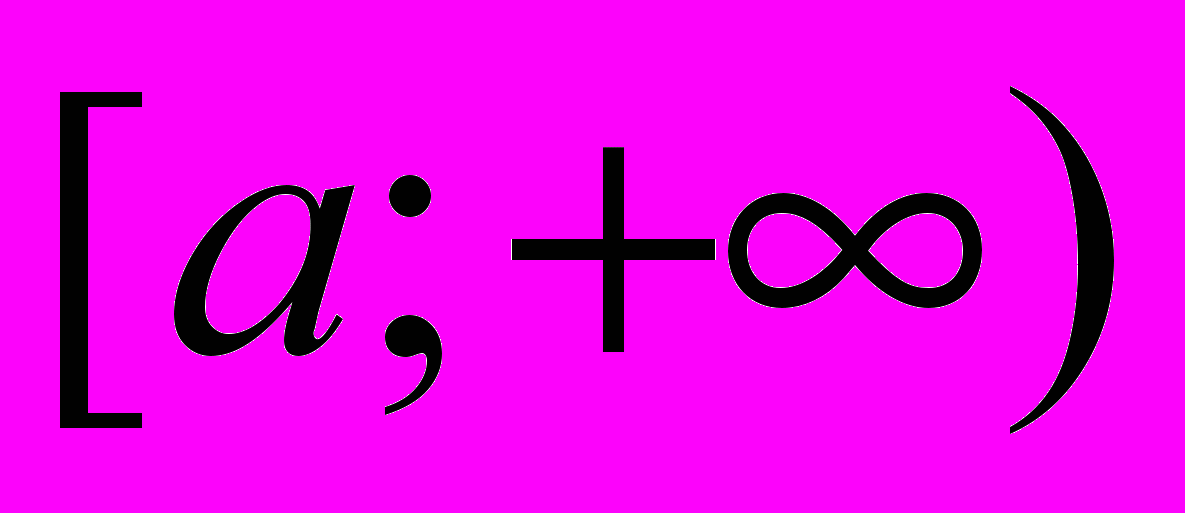. Приклади.
Формула Ньютона – Лейбніца для невласного інтеграла І-го роду. Приклади.
Лінійна властивість невласного інтеграла І-го роду.
Додатні невласні інтеграли І-го роду. Критерій збіжності, перша та друга ознаки порівняння. Приклади.
Абсолютно та умовно збіжні невласні інтеграли І-го роду. Приклади. Теорема про зв’язок між збіжністю і абсолютною збіжністю.
Невласні інтеграли по проміжках та 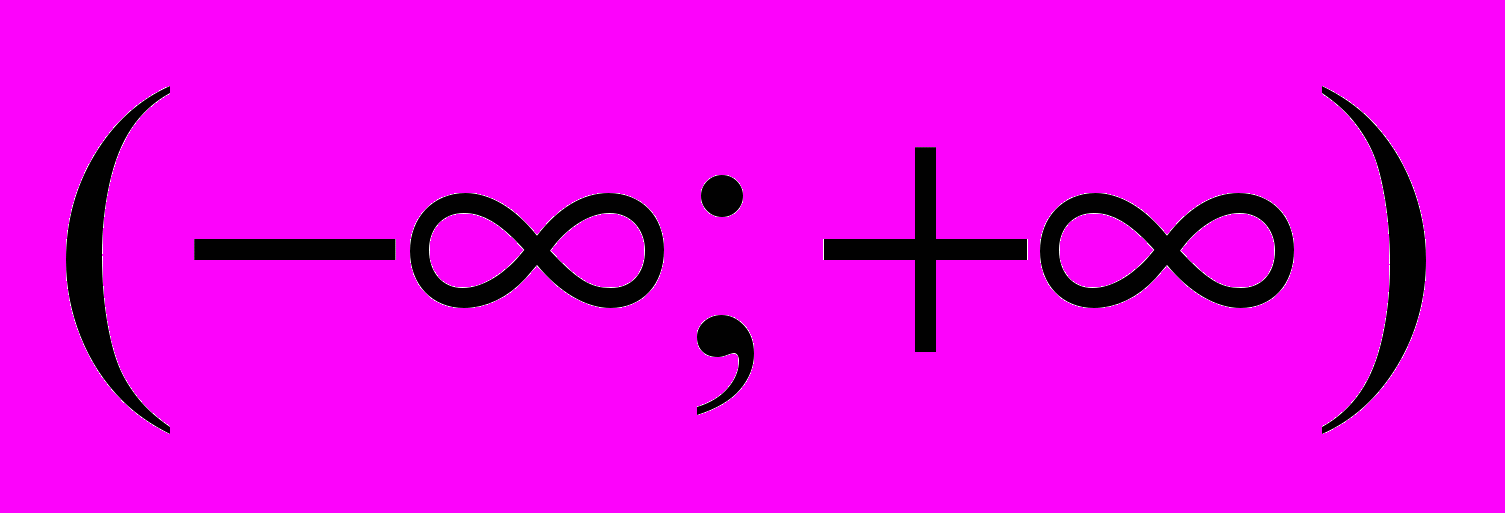. Означення, приклади, формули Ньютона – Лейбніца.
Геометричний зміст невласних інтегралів І-го роду.
Невласний інтеграл ІІ-го роду для випадку, коли особлива точка функції 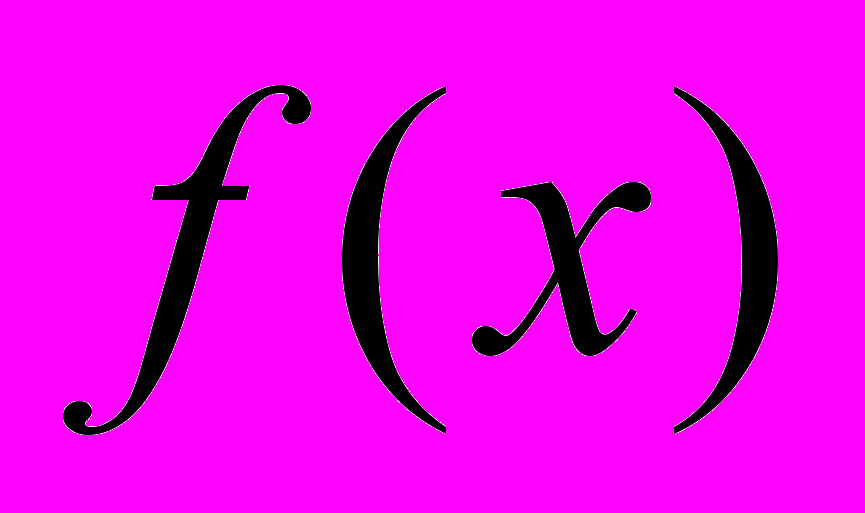збігається з кінцем відрізка 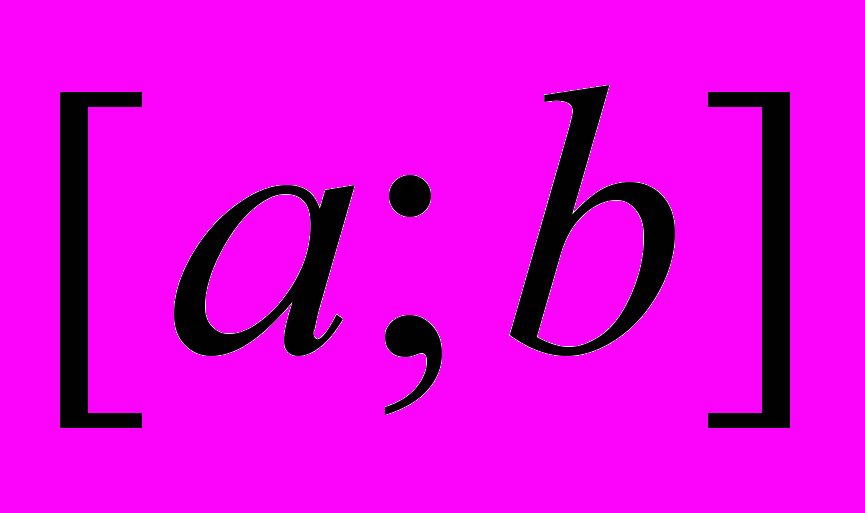. Означення, приклади, геометричний зміст.
Невласний інтеграл ІІ-го роду для випадку, коли особлива точка функції 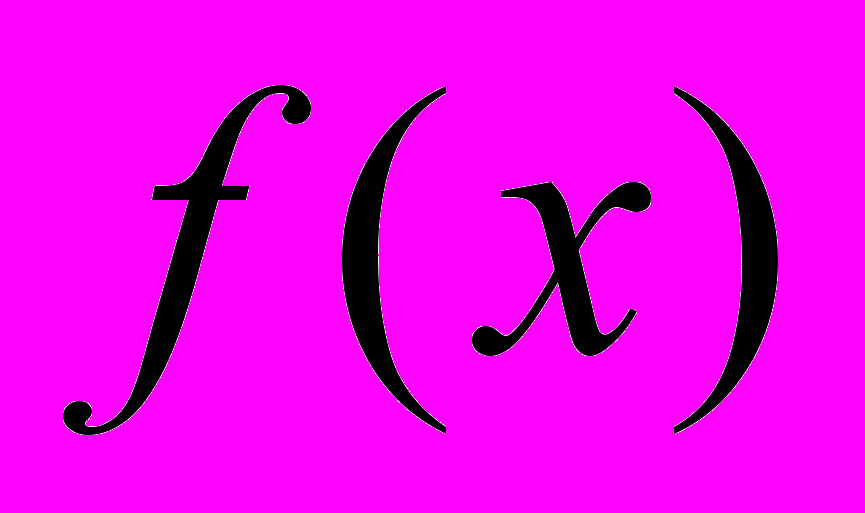лежить усередині інтервалу 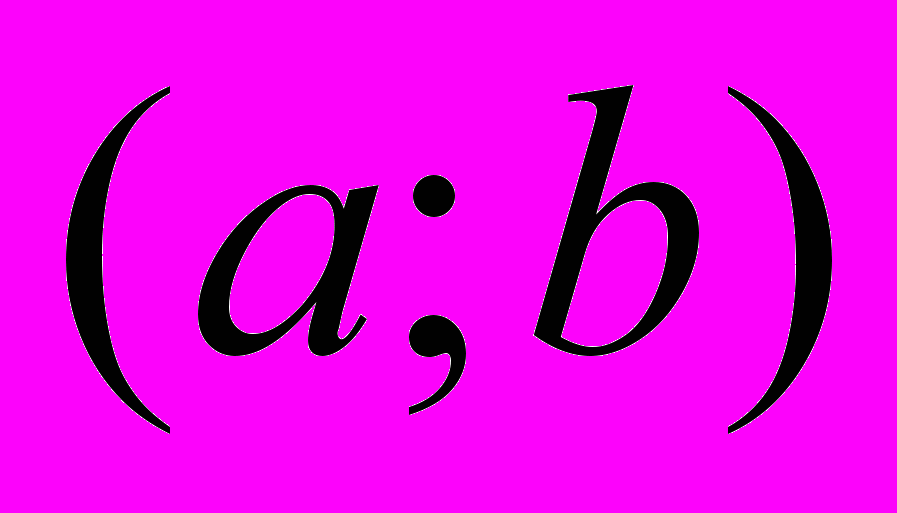. Означення, приклади, геометричний зміст.
Ознака порівняння для додатного інтеграла ІІ-го роду. Приклади.
Застосування визначеного інтеграла до обчислення площі криволінійної трапеції.
Обчислення об’єму тіла обертання.
Обчислення довжини дуги кривої, заданої параметрично.
Обчислення довжини дуги кривої, заданої явно у декартовій чи в полярній системі координат. Приклади.
Обчислення площі поверхні обертання.
Відшукання координат центра маси однорідної пластинки.
Поняття числового ряду та його суми. Геометричний і гармонічний ряди.
Зв’язок між збіжністю послідовностей і рядів.
Необхідна умова збіжності ряду. Приклади.
Критерій Коші збіжності ряду.
Властивості збіжних рядів. Довести сполучну і про розкриття дужок.
Властивості збіжних рядів. Довести властивість про розбавлення ряду.
Властивості збіжних рядів. Довести властивість про додавання членів з парними і непарними номерами.
Властивості збіжних рядів. Довести властивість про залишок ряду.
Додатні ряди. Критерій збіжності, дві ознаки порівняння.
Ознака Даламбера. Приклади.
Ознака Коші. Приклади.
Інтегральна ознака Коші.
Дослідити на збіжність ряди 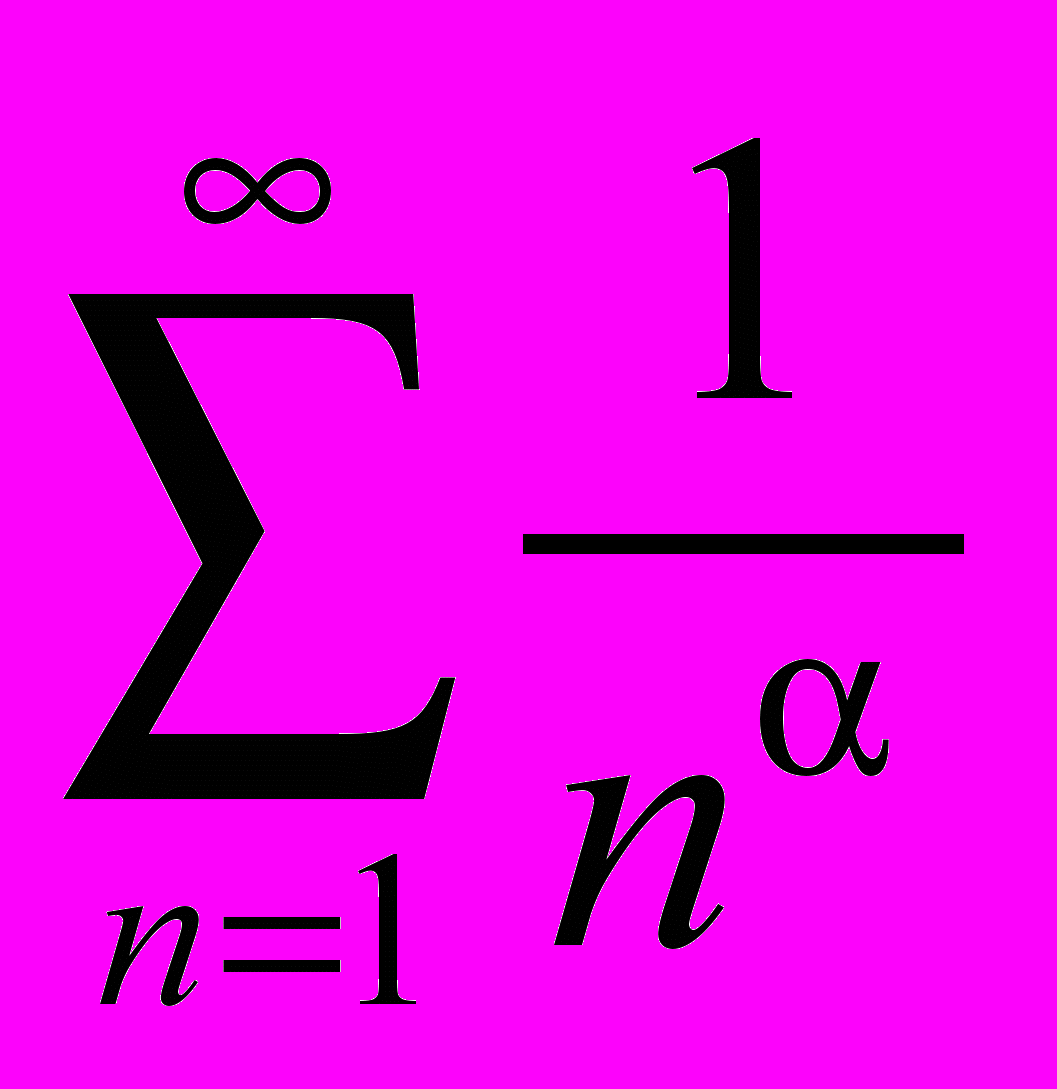і .
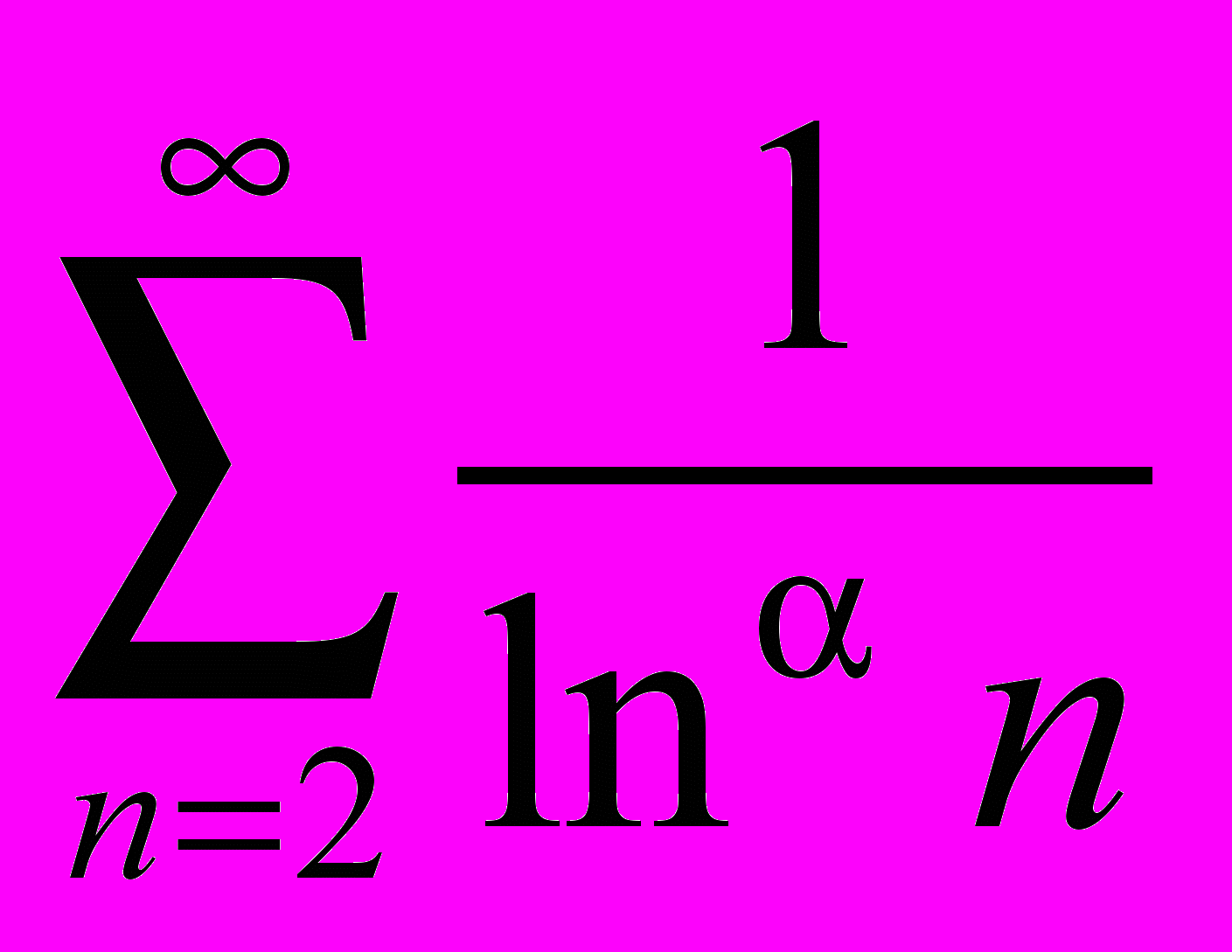Знакозмінні ряди. Ознака Лейбніца.
Абсолютно та умовно збіжні ряди. Теорема про збіжність і абсолютну збіжність.

ІІ ФІА

Ортогональна система функцій. Тригонометричний ряд. Формули Ейлера-Фур’є. Ряд Фур’є.
Кусково-диференційовна функція. Теорема про розвинення функції в ряд Фур’є.
Ряди Фур’є для парної та непарної функцій.
Ряд Фур’є для функцій з довільним періодом.
Ряд Фур’є для неперіодичної функції.
Комплексна форма ряду Фур’є.
Поняття функцій багатьох змінних. Лінії та поверхні рівня.
Метричні простори. аксіоми метричного простору. п-вимірний евклідовий простір .
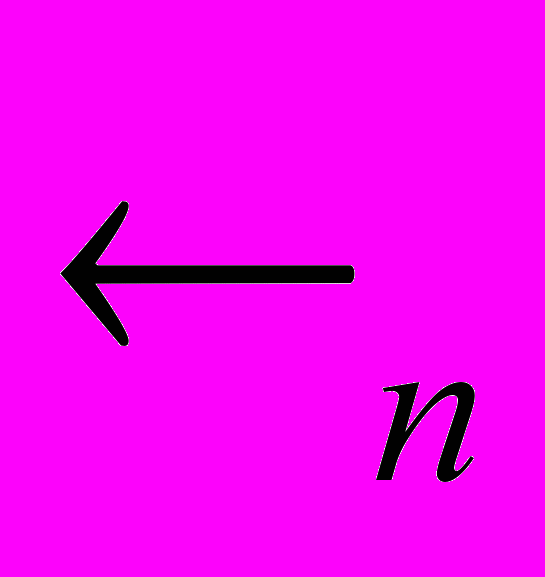Відкрита та замкнена куля, сфера. Окіл точки п-вимірного простору.
Класифікація точок множини метричного простору.
Послідовності точок метричного простору. Збіжність. Властивості збіжних послідовностей.
Границя функцій багатьох змінних. Різні означення границі.
Неперервність функції багатьох змінних.
Класифікація множин метричного простору.
Властивості функцій, заданих і неперервних на однозв’язній замкненій множині.
Частинні похідні. Означення. Геометричний зміст частинних похідних функцій двох змінних.
Повний приріс функцій. Диференційовність функцій двох змінних. Зв’язок між диференційовностю і неперервністю функцій кількох змінних.
Зв’язок між диференційовністю і частинними похідними.
Повний диференціал функції двох змінних.
Частинні похідні складеної функції двох змінних.
Інваріантність форми першого диференціала.
Застосування повного диференціала.
Похідні вищих порядків. Теорема про рівність мішаних похідних другого порядку.
Диференціали вищих порядків.
Формула Тейлора для функції двох змінних.
Диференцiальнi рiвняння першого порядку. Основнi поняття. Задача
Кошi.
Теорема Пеано (без доведення).
Теорема Кошi.
Теорема про достатню умову виконання умови Ліпшица.
Диференцiальнi рiвняння першого порядку з вiдокремлюваними змiнними.
Диференцiальнi рiвняння, які зводяться до рівнянь з вiдокремлюваними змiнними.
Однорiднi диференцiальнi рiвняння першого порядку.
Диференцiальнi рiвняння, якi зводяться до однорiдних диференцiальних рiвнянь першого порядку.
Лiнiйнi неоднорiднi диференцiальнi рiвняння першого порядку (метод Лагранжа).
Лiнiйнi неоднорiднi диференцiальнi рiвняння першого порядку (метод пiдстановки).
Лiнiйнi неоднорiднi диференцiальнi рiвняння першого порядку (метод Ейлера).
Рiвняння Бернуллi.
Диференцiальнi рiвняння в повних диференцiалах.
Критерій рівняння в повних диференціалах.
Iнтегрувальний множник.
Поле напрямків. Метод ізоклін.
Диференцiальнi рiвняння першого порядку, не розв’язанi вiдносно похiдної. Основнi поняття.
Теорема про iснування та єдинiсть розв’язку задачi Кошi для диференцiального рiвняння першого порядку, яке не розв’язане вiдносно похiдної (без доведеня).
Типи диференцiальних рiвнянь першого порядку, не розв’язаних вiдносно похiдної, якi iнтегруються в квадратурах.
Рiвняння Лагранжа.
Рiвняння Клеро.
Особливi розв’язки диференцiальних рiвнянь та їх знаходження.
Обвiдна однопараметричної сiм’ї кривих.
Задача на траєкторiї.
Диференцiальні рiвняння вищих порядкiв. Основні поняття. Задача Коші. Теорема Коші (без доведення).
Типи диференцiальних рiвнянь вищих порядкiв, якi iнтегруються в квадратурах або допускають зниження порядку.
Лiнiйнi диференцiальнi рiвняння n-го порядку. Основнi поняття.
Теорема про нульовий розв’язок лiнiйного диференцiального рiвняння n-го порядку.
Властивості лінійного диференціального оператора .
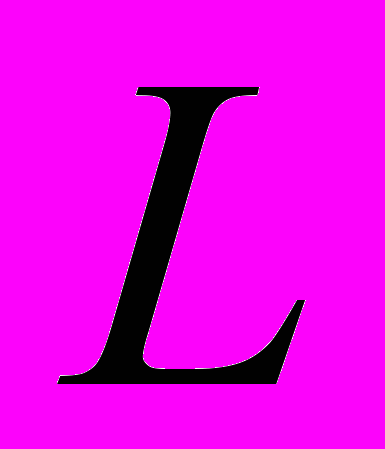Поняття про лiнiйну залежнiсть та лiнiйну незалежнiсть функцiй. Приклади.
Теорема про рiвнiсть нулю детермiнанта Вронського.
Теорема про не рiвнiсть нулю детермiнанта Вронського.
Критерiй лiнiйної незалежностi розв’язкiв лінійного диференцiального рiвняння n-го порядку.
Теорема про структуру загального розв’язку лiнiйного однорiдного диференцiального рiвняння вищого порядку.
Формула Остроградського–Ліувілля.
jЛiнiйне неоднорiдне диференцiальне рiвняння вищого порядку. Теорема про структуру загального розв’язку (без доведення).
Метод Лагранжа знаходження частинного розв’язку лiнiйного неоднорiдного диференцiального рiвняння n-го порядку.
Лiнiйнi однорiднi диференцiальнi рiвняння n-го порядку iз сталими коефiцiєнтами. Випадок:

а) простих дiйсних коренiв характеристичного рiвняння;

б) простих комплексно спряжених коренiв характеристичного рiвняння;

в) кратних коренiв.

Лiнiйнi неоднорiднi диференцiальнi рiвняння n-го порядку. Метод невизначених коефiцiєнтiв.
Математичний маятник. Закон коливання математичного маятника.
Вiльнi та вимушенi коливання.
Диференціальні рівняння. Основні поняття.
Прикладні задачі, які приводять до диференціальних рівнянь.
Диференціальні рівняння 1-го порядку з відокремлюваними змінними.
Однорідні диференціальні рівняння 1-го порядку.
Лінійні диференціальні рівняння 1-го порядку.
Рівняння Бернуллі.
Диференціальні рівняння 1-го порядку в повних диференціалах.
Інтегруючий множник.
Метод послідовних наближень розв’язування диференціальних рівнянь.
Теорема Пікара про існування та єдиність розв’язку задачі Коші для диференціальних рівнянь 1-го порядку.
Обвідна однопараметричної сім’ї кривих.
Особливі розв’язки диференціальних рівнянь 1-го порядку.
Рівняння Клеро.
Рівняння Лагранжа.
Диференціальні рівняння 1-го порядку, як поля напрямів. Ізокліни.
Ламані Ейлера.
Ізогональні та ортогональні траєкторії.
Диференціальні рівняння вищого порядку. Основні поняття.
Найпростіші типи диференціальних рівнянь вищого порядку.
Лінійні диференціальні рівняння вищого порядку. Основні поняття.

ІІІ МІ

Означення комплексних чисел.
Польові властивості множини комплексних чисел.
Модуль і аргумент комплексного числа.
Тригонометрична форма комплексного числа.
Геометричний зміст додавання і віднімання комплексних чисел.
Множення і ділення комплексних чисел.
Формула Муавра.
Корінь 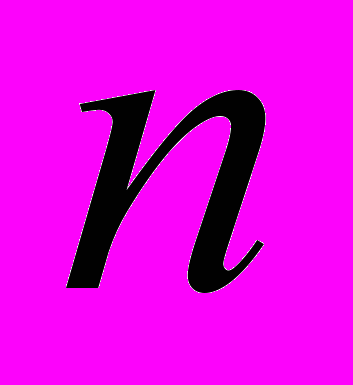-го степеня з комплексного числа.
Властивості модуля комплексного числа.
Означення комплексної послідовності.
Границя комплексної послідовності.
Нескінченна границя комплексної послідовності.
Властивості збіжних послідовностей (6 перших).
Теорема про зв’язок між збіжністю комплексної та дійсних послідовностей.
Нескінченно малі та нескінченно великі послідовності.
Означення підпослідовності.
Часткова границя послідовності.
Критерій часткової границі.
Теорема про множину часткових границь.
Теорема про існування часткової границі.
Означення ряду з комплексними членами та його суми.
Збіжні і розбіжні ряди. Необхідна умова збіжності.
Теорема про зв’язок між збіжністю комплексного ряду і дійсних рядів.
Властивості збіжних рядів (6 перших).
Означення 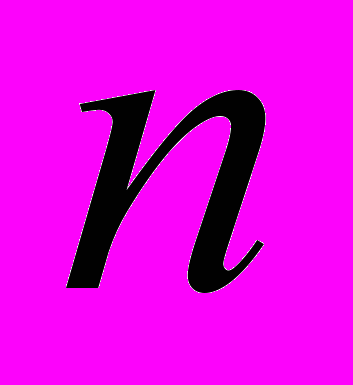-го залишку ряду і твердження про його збіжність.
Абсолютно та умовно збіжні ряди.
Критерій Коші збіжності ряду.
Теорема про зв’язок між абсолютною збіжністю комплексного ряду та дійсних рядів.
Що означає переставити місцями члени ряду?
Переставна властивість рядів.
Теорема про добуток рядів у розумінні Коші.
Який ряд називається додатним, а який – знакозмінним?
Ознаки збіжності додатних рядів: дві ознаки порівняння, Даламбера, Коші радикальна і Коші інтегральна.
Ознака Лейбніца збіжності знакозмінного ряду.
Узагальнена ознака Коші абсолютної збіжності ряду.
Поняття функції комплексної змінної, її геометричний зміст.
Поняття граничної, ізольованої, межової та внутрішньої точок множини.
Поняття відкритої, замкненої, зв’язної, компактної множин, області, однозв’язної області та замкненої області.
Поняття границі функції (три означення).
Теорема про зв’язок границі комплексної функції з границями дійсних функцій.
Властивості функцій, які мають границі.
Часткова границя функції в точці, її існування та зв’язок з границею.
Границя функції в точці у випадку, коли або границя, або точка нескінченні.
Нескінченно малі і нескінченно малі функції, зв’язок між ними.
Неперервні функції.
Теорема про зв’язок неперервності комплексної функції з неперервністю дійсних функцій.
Загальні властивості неперервних функцій.
Рівномірно неперервні функції. Критерій.
Властивості функцій, неперервних на компактних множинах.
Неперервні криві. Приклади.
Границя і неперервність складеної функції.
Неперервність оберненої функції.
Функціональна послідовність з комплексними членами, її границя.
Рівномірна збіжність функціональної послідовності.
Зв’язок між рівномірною збіжністю комплексної функціональної послідовності і дійсних послідовностей.
Критерії рівномірної збіжності функціональної послідовності.
Теорема про неперервність рівномірної границі функціональної послідовності.
Означення функціонального ряду та його суми.
Рівномірно збіжні функціональні ряди. Необхідна умова рівномірної збіжності.
Критерії рівномірної збіжності функціонального ряду.
Неперервність суми рівномірно збіжного функціонального ряду.
Ознака Вейєрштрасса рівномірної збіжності функціонального ряду. Приклади.
Степеневий ряд з комплексними членами. Його круг збіжності.
Теорема Абеля про збіжність степеневого ряду.
Теорема про формулу Коші – Адамара.
Теорема про рівномірну збіжність степеневого ряду та наслідок з неї.
Означення функцій , , .
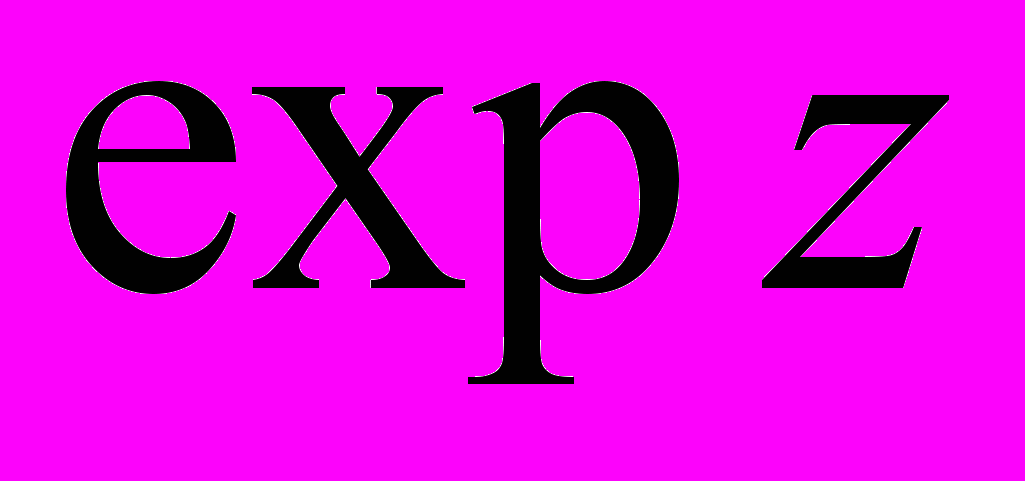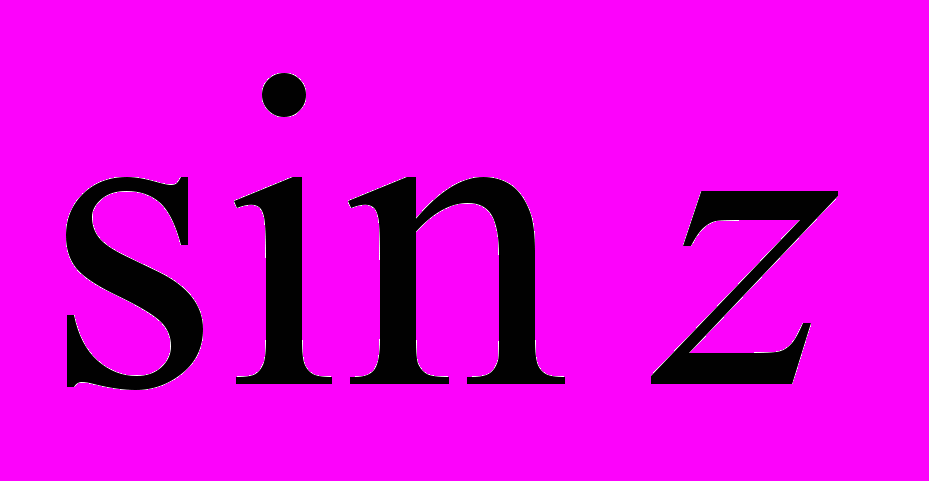Область визначення, неперервність, парність-непарність функцій , , .
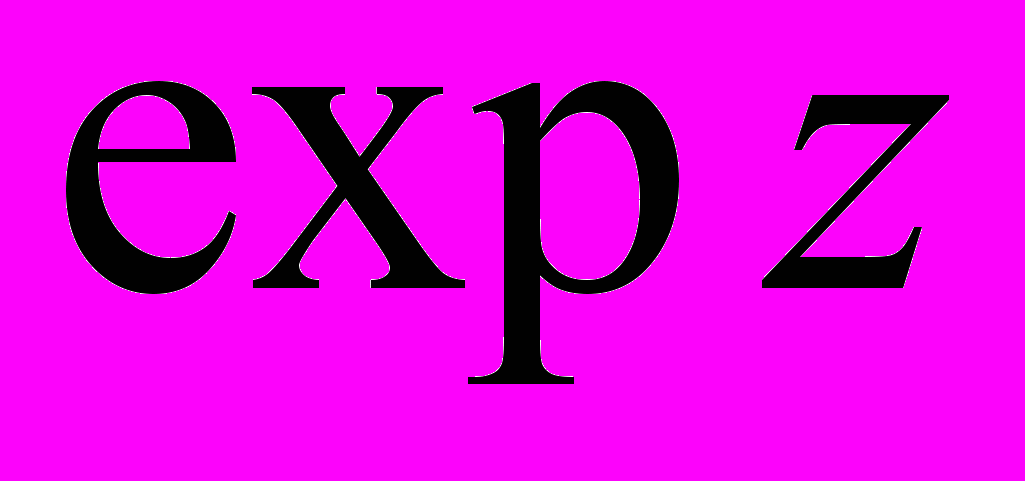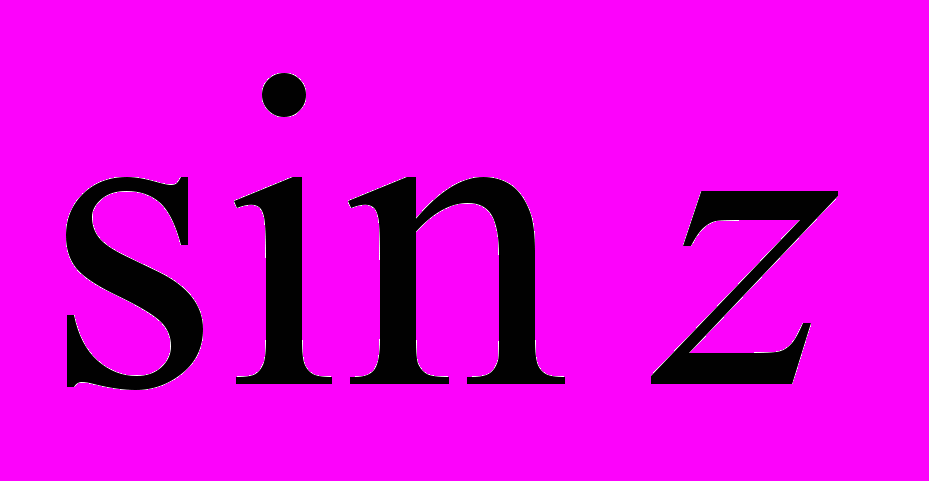Формули Ейлера про зв’язок між експоненціальною і тригонометричними функціями.
Теореми додавання і віднімання для функцій , , .
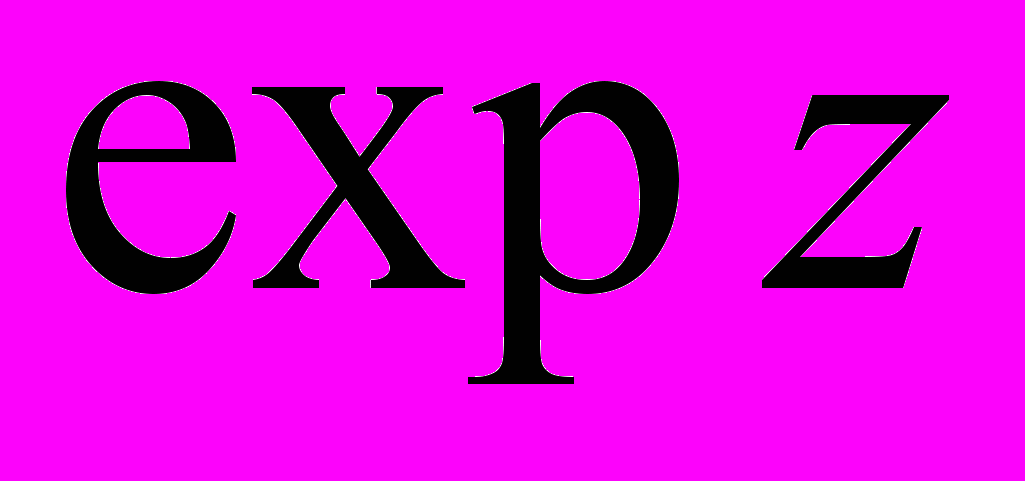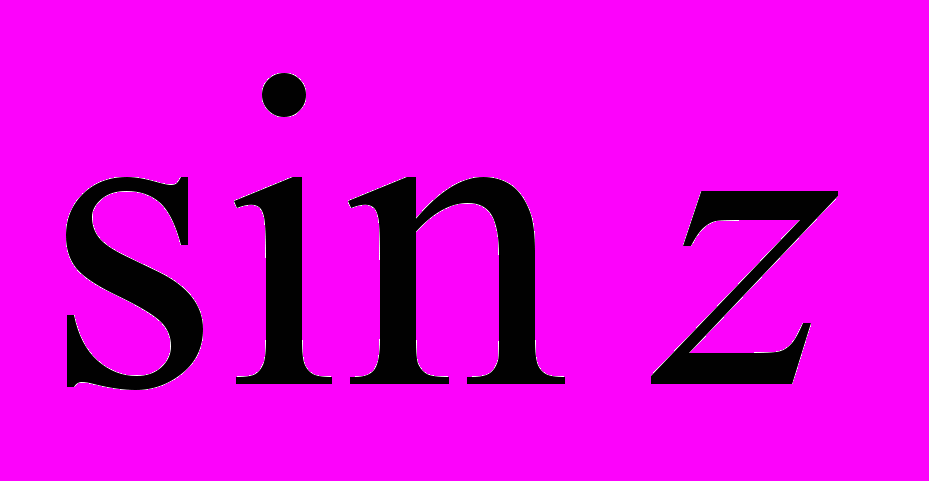Обмеженість і періодичність функцій , , .
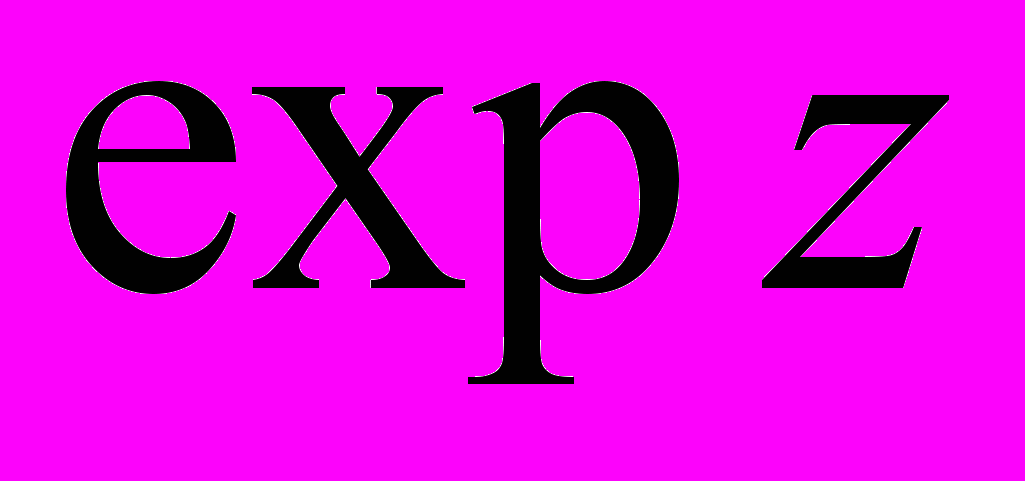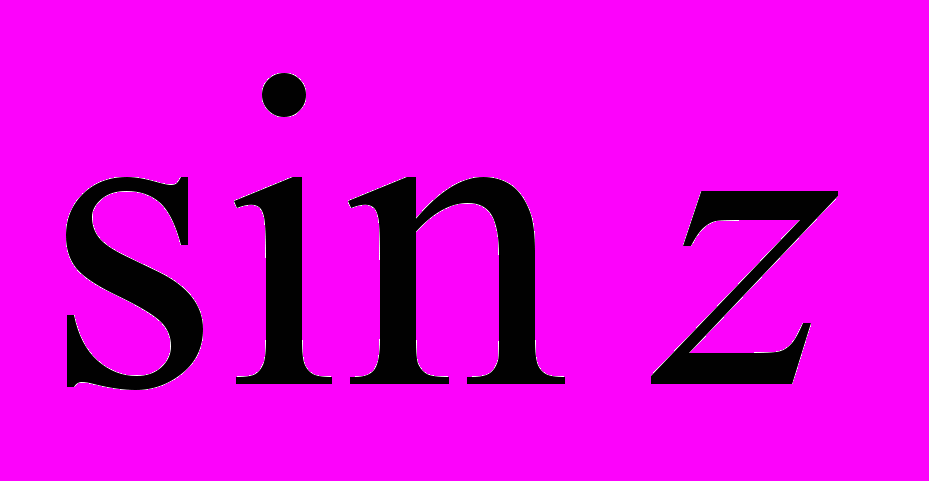Логарифм комплексного числа і логарифмічна функція.
Чи існують логарифми від’ємних чисел?
Область визначення і множина неперервності логарифмічної функції комплексної змінної.
Логарифми добутку і частки.
Поняття арксинуса комплексного числа, його існування. Формула для обчислення.
Функція .
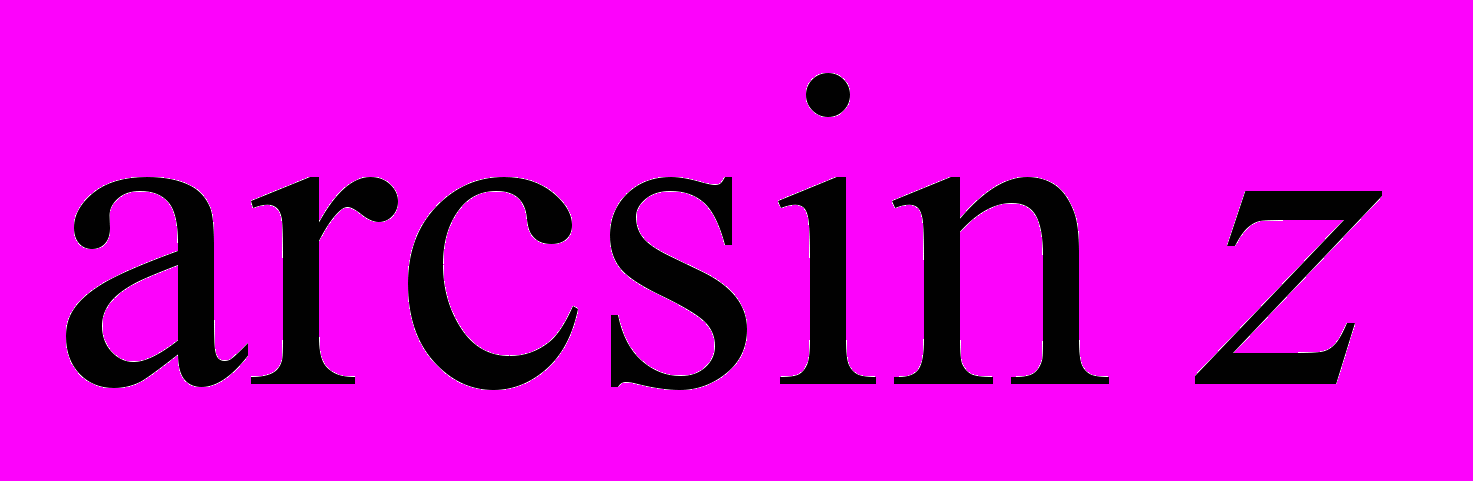Чи має розв’язки рівняння ?
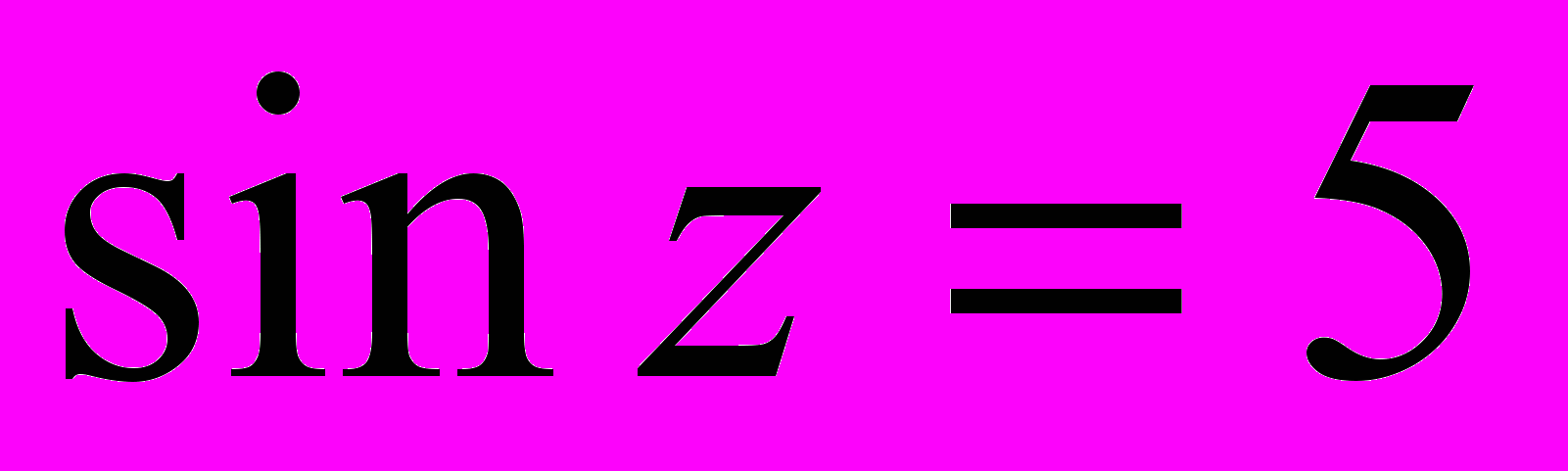Поняття арккосинуса комплексного числа, його існування. Формула для обчислення.
Функція .
Зв’язок між комплексним і дійсним арккосинусами.
Тангенс та арктангенс комплексного числа.
Гіперболічні синус і косинус та їх зв’язок з тригонометричними.
Поступове визначення поняття степеня 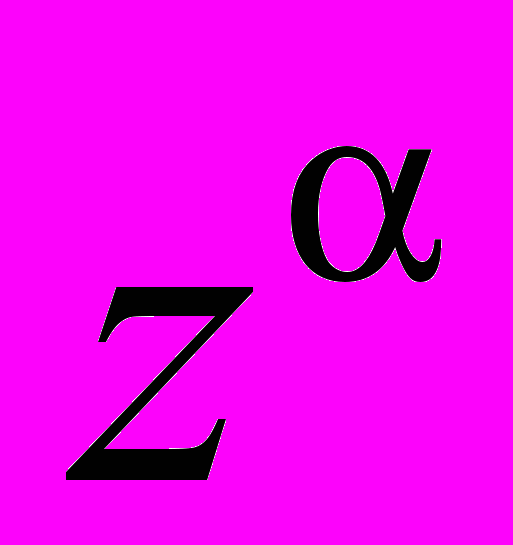у випадках , , , , (, ).
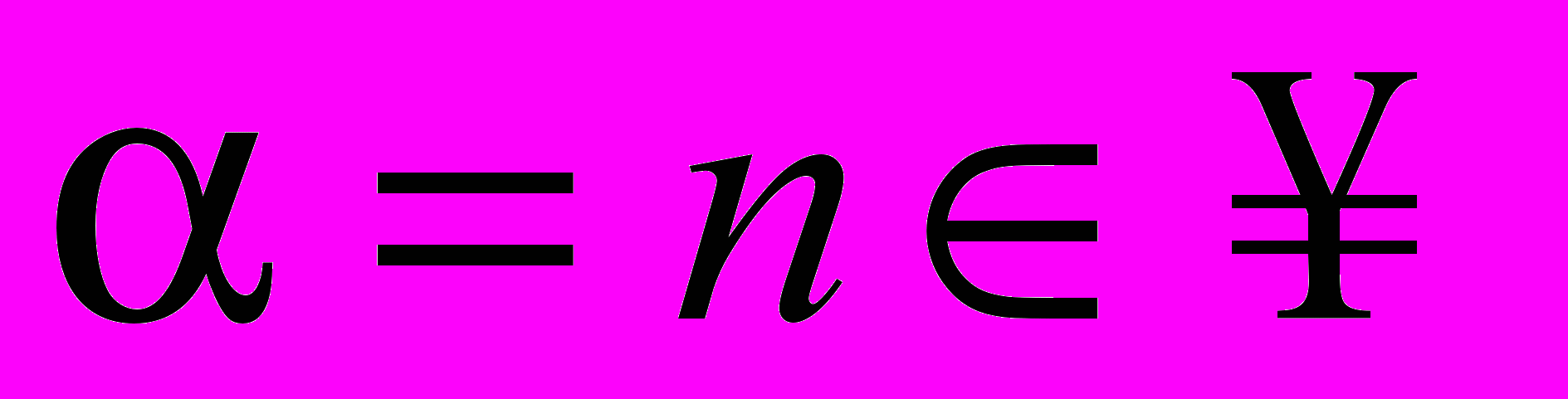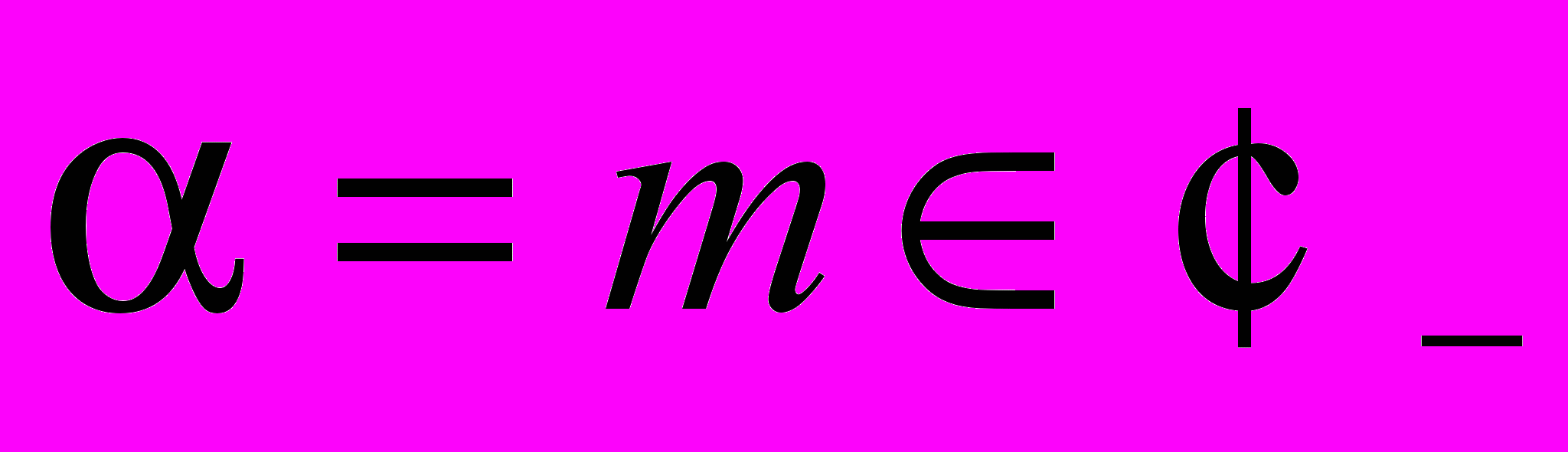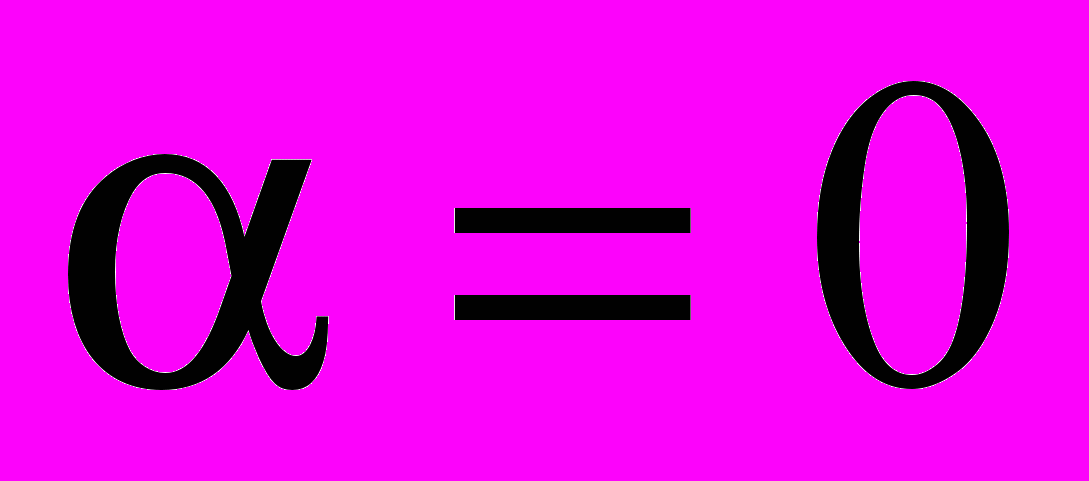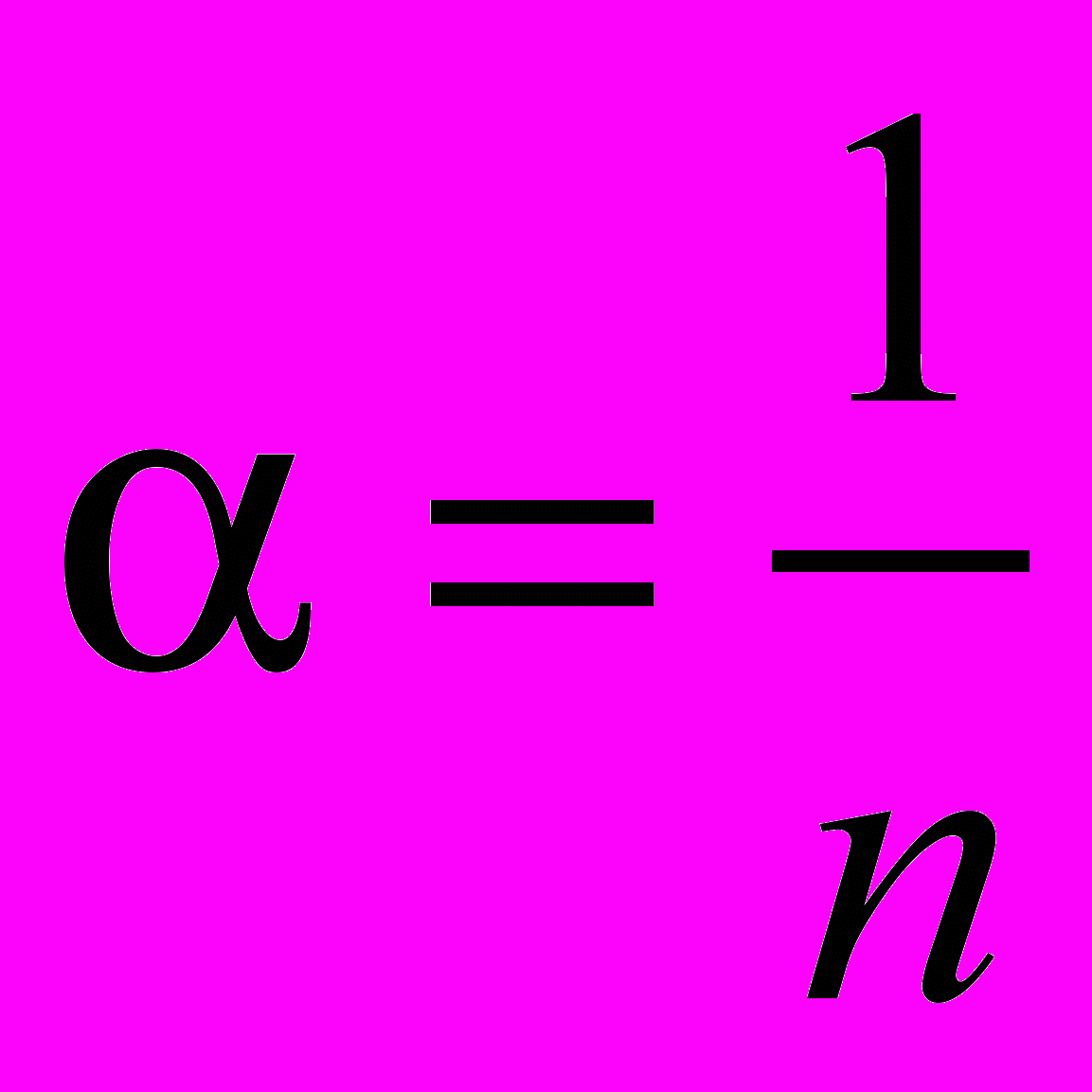
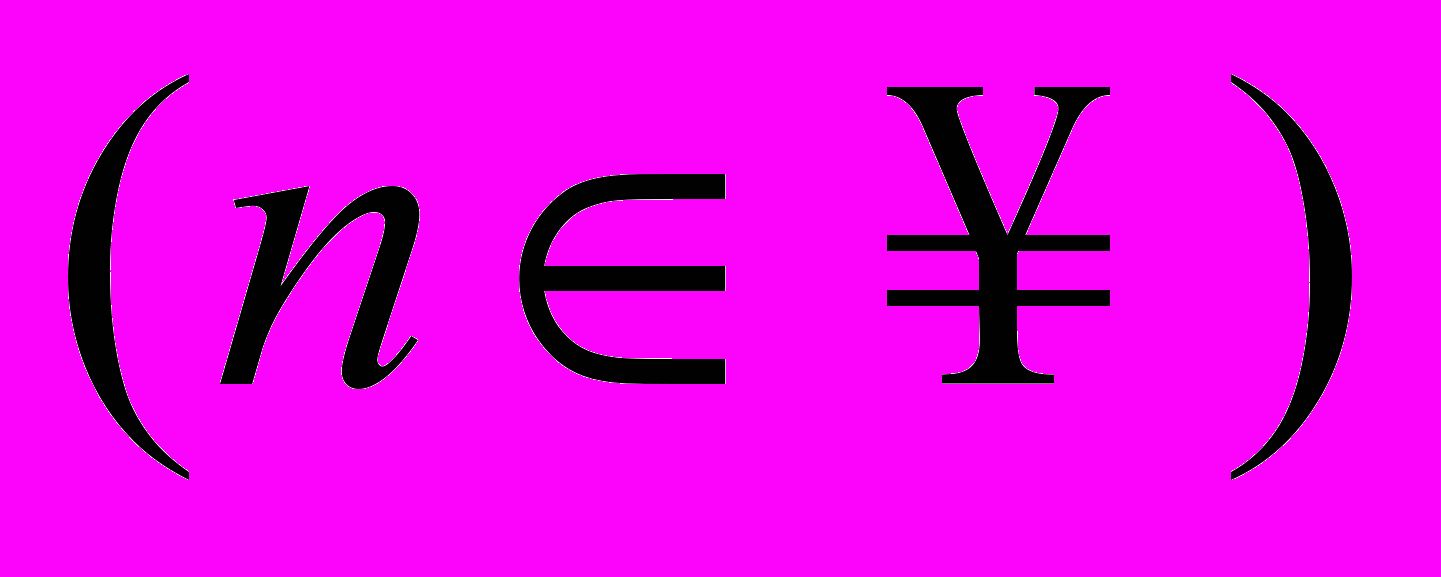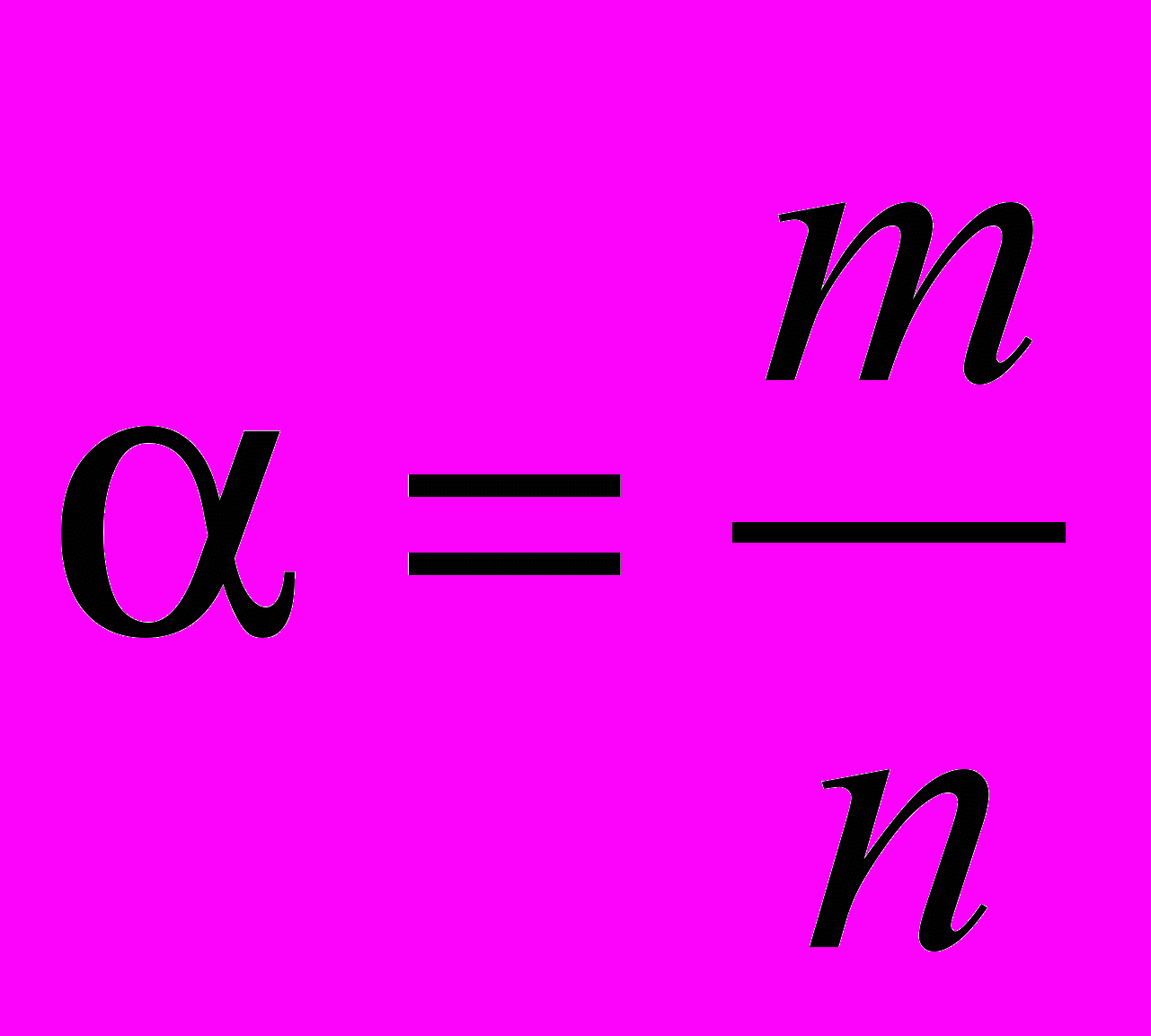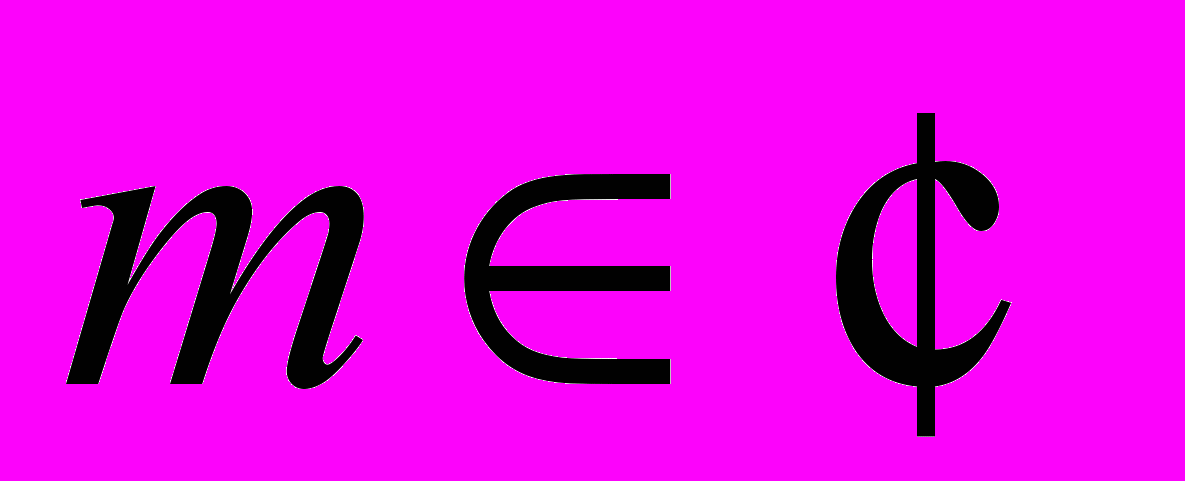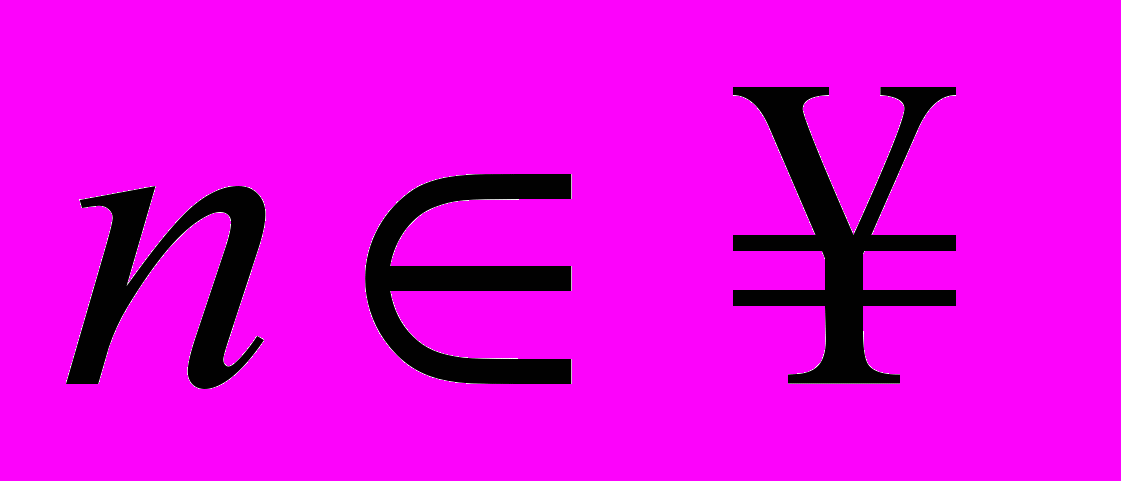Означення степеня 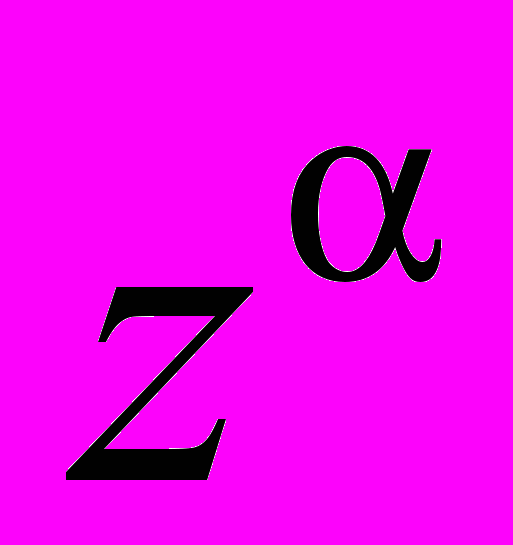у випадку 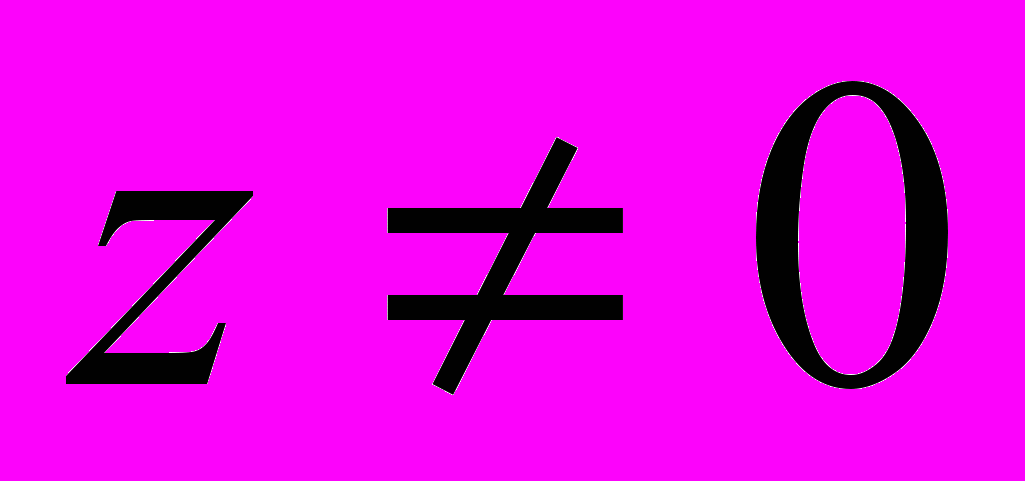, 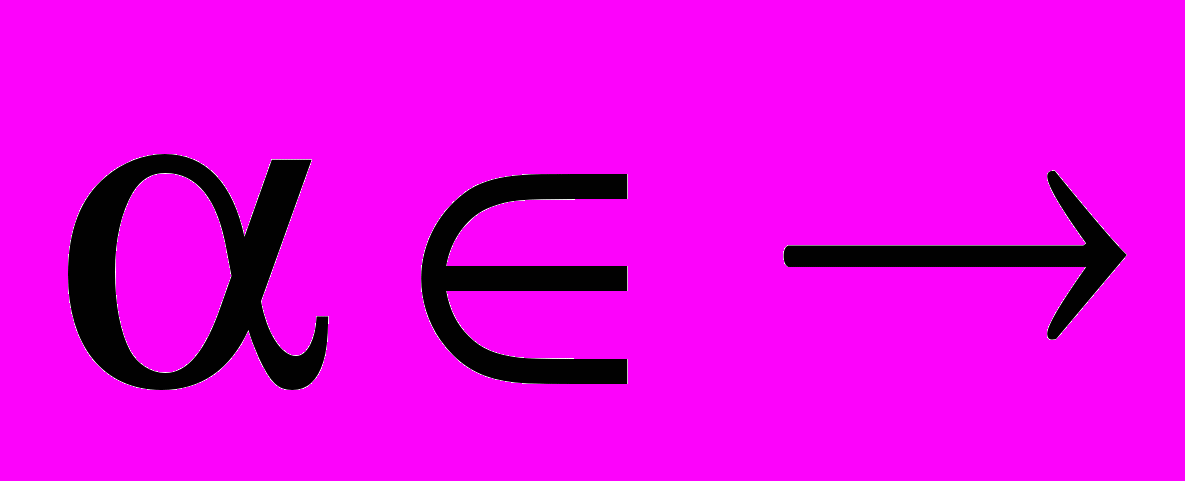. Загальна показникова і загальна степенева функції.
Основні елементарні (традиційний та мінімальний списки) та елементарні функції комплексної змінної.
Вказати однакові властивості дійсних та відповідних їм комплексних основних елементарних функцій.
Вказати відмінності між властивостями дійсних та відповідних їм комплексних основних елементарних функцій.
Загальне означення похідної функції комплексної змінної.
Що таке “чудовисько Вейєрштрасса”?
Властивості функцій, що мають похідні.
Два означення диференційовної функції комплексної змінної.
Поняття аналітичної функції у розумінні Коші.
Критерій диференційовності функції комплексної змінної. Умови Коші – Рімана.
Означення аналітичної функції у розумінні Рімана.
Геометричний зміст похідної комплекснозначної функції дійсної змінної.
Геометричний зміст похідної функції комплексної змінної.
Конформні відображення. Достатня умова конформності.
Теорема про диференціювання степеневого ряду. Наслідки.
Ряд Тейлора, його існування та єдиність.
Поняття про диференціальне рівняння I-го порядку та його розв’язки (загальний, частинний, особливий).
Приклади задач, які приводять до диференціальних рівнянь.
Диференціальне рівняння I-го порядку. Задача Коші. Теорема про існування та єдиність розв’язку задачі Коші (формулювання).
Зведення задачі Коші до інтегрального рівняння. Метод послідовних наближень відшукання розв’язку інтегрального рівняння.
Доведення теореми про існування розв’язку інтегрального рівняння (теорема Коші).
Доведення єдиності розв’язку інтегрального рівняння (задача Коші).
Продовження розв’язку задачі Коші. Означення загального розв’язку диференціального рівняння I-го порядку; означення частинного розв’язку, означення особливого розв’язку.
Поле напрямів, задане диференціальним рівнянням. Ізокліни, ламані Ейлера.
Диференціальні рівняння з відокремленими змінними: типи рівнянь, які зводяться до рівнянь з відокремленими змінними.
Однорідні диференціальні рівняння. Рівняння, які зводяться до однорідних.
Лінійні диференціальні рівняння I-го порядку. Метод варіації знаходження розв’язку лінійних неоднорідних диференціальних рівнянь першого порядку.
Рівняння Бернуллі.
Інтегрування лінійного рівняння методом підстановки. Метод Ейлера.
Рівняння в повних диференціалах. Критерій про диференціальне рівняння в повних диференціалах.
Інтегрувальний множник та його знаходження.
Диференціальні рівняння, які не розв’язані відносно похідної. Задача Коші. Теорема про існування і єдиність розв’язку задачі Коші для цього рівняння.
Типи диференціальних рівнянь, які не розв’язані відносно похідної і які інтегруються в квадратурах.
Рівняння Лагранжа і рівняння Клеро.
Знаходження особливого розв’язку для рівняння, розв’язаного відносно похідної.
Знаходження особливих розв’язків для рівняння, яке не розв’язане відносно похідної.
Обвідна сім’ї кривих. Знаходження похідної.
Обвідна сім’ї інтегральних кривих - особливий розв’язок.
Задача про ізогональні траєкторії.
Задача про ортогональні траєкторії до сім’ї кривих.

Blog

Питання до колоквіуму І мі