Курс: перший, другий Стаціонарне навчання Години на тиждень Триместр

Вид материала

Содержание

Мета дисципліни
Методи оцінювання
Методичне забезпечення
Методика іспиту
Реєстрація на іспит
Мета дисципліни
Методи оцінювання
Методичне забезпечення
Індивідуальна робота
Методика іспиту
Мета дисципліни
Методи оцінювання
Методичне забеспечення
Індивідуальна робота
Методика іспиту
Реєстрація на іспит
Факультет: АКСУ
Методи оцінювання
Метод навчання
Індивідуальна робота
...
Полное содержание

Подобный материал:

1 2 3

Цикл природничо-наукової підготовки

Дисципліна: Вища математика Факультет: АКСУ Статус дисципліни: обов’язкова Курс: перший, другий
	Стаціонарне навчання	Години на тиждень
Триместр	1/2/4/5
Лекції (год.)	70/49/56/48	5/3/4/3
Практичні заняття (год.)	56/49/28/32	4/3/2/2
КП (КР) трим	1/1/1/1
РГР	2/2/2/2
СРС (інд. заняття)	108/64/24/28	7.7/ 3,5/1,7/1,8
Всього (год./кредитів)	234/162/108/108// 612 6,5/3,5/ 3/ 3 // 16,0
Іспит (трим)	1(ОС)/2(ЗС)/4(ОС)/5(ЗС)
Залік (трим)	-
КОД:	НФД 01

Лектори: Петрук Віра Андріївна, к.п.н, доцент, член-кор. Академії ПРЕ

Кашканова Галина Григорівна, к.п.н, доцент

21021 м. Вінниця, Хмельницьке шосе, 95, Інститут Інформаційних технологій та комп’ютерної інженерії (ІнІТКІ),), кафедра вищої математики , тел. 59-84-64.

МЕТА ДИСЦИПЛІНИ:

Формування особистості студентів, розвиток їх інтелекту, аналітичного та синтетичного мислення, відповідної математичної культури, інтуїції; оволодіння математичним апаратом, необхідним для вивчення загально інженерних та спеціальних дисциплін, розвиток здібностей свідомого сприйняття математичного матеріалу, характерного для спеціальності інженера; оволодіння основними математичними методами, необхідними для аналізу і моделювання пристроїв, процесів і явищ, пошуків оптимальних рішень з метою підвищення ефективності виробництва і вибору найкращих способів реалізації цих рішень, опрацювання і аналізу результатів експериментів.

ПРОГРАМА:

Основні поняття лінійної та векторної алгебри і аналітичної геометрії: матриці та дії з ними, визначники та їх властивості, системи лінійних рівнянь, вектори і дії над ними, канонічні рівняння прямої і площини, рівняння кривих і поверхонь другого порядку; основні поняття диференціального і інтегрального числень: функції, похідної, диференціалу, невизначеного інтегралу, визначеного інтегралу, подвійного та потрійного інтегралів, криволінійних та поверхневих інтегралів; основні поняття теорії звичайних диференціальних рівнянь: диференціального рівняння, системи диференціальних рівнянь (канонічної, нормальної, автономної), розв’язку диференціального рівняння і системи, задачі Коші; основні поняття теорії рядів: суми ряду, збіжності ряду, інтервалу збіжності степеневого ряду, ряду Фур’є; основні поняття теорії функцій комплексної змінної: аналітичної функції, інтегралу функції комплексної змінної, конформного відображення, ізольованої особливої точки, лишку функції; основні поняття операційного числення: перетворення Лапласа, його властивості, інтегралу Дюамеля; основні поняття теорії імовірностей і математичної статистики: випадкової величини і випадкової події, імовірності, числові характеристики дискретних і неперервних випадкових величин; генеральної і вибіркової сукупності, вибіркової характеристики, статистичної гіпотези і статистичного критерію.

БІБЛІОГРАФІЯ:

1. Берман Г. Н. Сборник задач по курсу математического анализа. – М.: Наука, 1985.

2. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии.– М.: Наука. 1980; 1981; 1988.

3. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление.– М.: Наука. 1980; 1988.

4. Бугров Я. С., Никольский С. М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.– М.: 1981; 1985.

7. Волков Ю.І., Найко Д.А. Лінійна алгебра й аналітична геометрія з елементами програмування мовою Паскаль: Навч. посібн. – К.: УМК ВО, 1990. – 144 с.

6. Гурский Е. И. Сборник задач по теории вероятностей и математической статистике. – Минск: Вышэйш. шк., 1984.

7. Гурский Е. И. Теория вероятностей с элементами математической статистики. – М.: Высш. шк., 1971.

8. Жалдак М.И., Квитко А. Н. Теория вероятностей с элементами информатики. Практикум. – К.: Вища школа, 1989.

9. Краснов М. Л., Киселев А. И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. – М.: Наука: 1981.

10. Кудрявцев Л. Д. Краткий курс математического анализа. – М.: Наука, 1989.

11. Кузнецов Л.А. Сборник заданий по высшей математике /типовые расчеты/. – М.: Высш. шк., 1983.

12. Овчинников П. Ф., Яремчук Ф. П., Михайленко В.М. Высшая математика, – К.: Вища школа, 1987.

13. Пак В. В., Носенко Ю. Л. Вища математика. – К.: Либідь, 1996.

14. Скороход А. В. Елементи теорії імовірностей та випадкових процесів. – К.: Вища школа, 1975.

МЕТОДИ ОЦІНЮВАННЯ:

Протягом триместру студенти проходять два модульних контролі і повинні виконати 2 контрольних роботи, 1 типовий розрахунок (РГЗ) та скласти 2 колоквіуми на 7 та 14 тижні.. Оцінки знань формуються на підставі рейтингових балів, які студент отримує протягом триместру за результатами колоквіумів, аудиторних контрольних робіт, захисту домашніх робіт (РГЗ) . На основі цих оцінок студент отримує оцінку з іспиту або складає його на загальних підставах.

Іспит складається усно . Завдання містять два теоретичних та два практичних питання. Колоквіуми та аудиторні контрольні роботи розраховано на 90 хвилин.

ПЕРЕДУМОВИ:

Необхідні знання з дисциплін: “Алгебра та початок аналізу”, “геометрія”, ”фізика”, ”інформатика” (шкільний курс) .

МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ: протягом лекцій та практичних занять студентам видається методична література з розділів вищої математики:

1. Петрук В.А., Кашканова Г.Г ” Методичні вказівки до самостійної роботи з аналітичної геометрії ", Вінниця, ВПІ, 1992р.,- 42с.

2. Петрук В.А., Кашканова Г.Г. „Методичні вказівки до самостійної роботи з теми "Лінійна алгебра", Вінниця, ВПІ, 1992р.,- 30с.

3. Петрук В.А., Кашканова Г.Г. „ Методичні вказівки до самостійної роботи з теорії ймовірностей та математичної статистики ", Вінниця, ВПІ, 1992р.,- 28с.

4. Петрук В.А., Кашканова Г.Г. „Теорія функції комплексної змінної” В- во „Універсум”,1998р,- 113с.

5. Петрук В.А., Кашканова Г.Г. „Ймовірносно-статистичні моделі та статистична оцінка рішень”, В-во „Універсум”,2000р,- 140с.

6. Петрук В.А. „Дослідження найпростіших статистичних моделей”, В-во „Універсум”,2000р., - 128с.

7. Петрук В.А. „Вища математика з прикладними задачами для ігрових занять”, Вінниця, ВДТУ, 2000р., 117с.

8. Петрук В.А., Кашканова Г.Г.Хом`юк І.В. “Збірник задач з вищої математики ч. 1”, Вінниця, ВДТУ, 2001р.,-130с.

9. Петрук В.А.,Хом`юк І.В. “Збірник задач з вищої математики ч. 2”, Вінниця, ВДТУ, 2002р.,- 142с.

10. Петрук В.А., Кашканова Г.Г. “Збірник задач з вищої математики ч. 3”, Вінниця, ВДТУ, 2003р,- 127с.

11. Петрук В.А., Кашканова Г.Г. “Збірник задач з вищої математики ч.4,”, Вінниця, ВДТУ, 2004 р.,112с.

ІНДИВІДУАЛЬНА РОБОТА: індивідуальні завдання з тем: теорема про необхідні умови лінійної залежності і незалежності трьох векторів, вираження мішаного добутку векторів через їх Декартові координати, властивості визначників другого та третього порядків, метод Гаусса розв'язання систем лінійних рівнянь, відстань від точки до площини та від точки до прямої в просторі, вивести канонічні рівняння прямої в просторі, умови паралельності та перпендикулярності прямих, виведення канонічного рівняння гіперболи, її властивості, циліндричні поверхні, сфера, конуси, геометричні властивості цих поверхонь, дослідження їх форми методом перерізів, простір

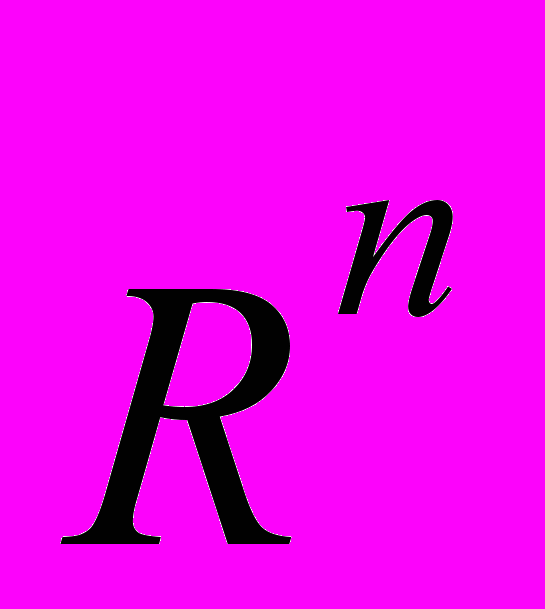, лінійні операції над векторами. Диференціал суми, добутку і частки. Інваріантність форми диференціала. Застосування диференціала в наближених обчисленнях. Похідні та диференціали вищих порядків. Диференціювання функцій заданих параметрично. Знаходження найбільшого та найменшого значень функції, диференційованої на відрізку. Дослідження випуклості функції, точки перегину. Асимптоти графіка функції. (1ОС) Інтегрування тригонометричних функцій та ірраціональностей. Застосування визначеного інтеграла. Обчислення площ в прямокутних і полярних координатах. Обчислення довжини дуги кривої, об’ємів тіл і площ поверхні обертання. Частинні похідні. Повний диференціал, його зв’язок з частинними похідними. Інваріантність форми повного диференціалу. Дотична площина та нормаль до поверхні. Геометричний зміст повного диференціалу. Частинні похідні і повні диференціали вищих порядків. Рівняння, які допускають зниження порядку. застосування до розв’язування задач про другу космічну швидкість, рух маятника, Розв’язування систем диференціальних рівнянь із сталими коефіцієнтами. Знакозмінні ряди, види збіжності, знакозмінні ряди типу Лейбніца, ознака збіжності. Застосування степеневих рядів у точних та наближених обчисленнях (2ЗС). Тригонометричні ряди Фур'є (ТРФ) для періодичних функцій з довільним періодом, для парних і непарних функцій. Комплексна форма ТРФ. Заміна змінних у подвійних інтегралах. Геометричні та фізичні застосування подвійних інтегралів. Оператори Гамільтона та Лапласа, їх застосування у векторному аналізі. Розв'язування рівняння теплопровідності (дифузії) методом сіток. Лишки, обчислення.(4ОС) Теореми подібності та запізнювання, теореми випереджання та зміщення. Теореми диференціювання та інтегрування зображення. Зображення періодичного оригіналу, застосування. Закони розподілу імовірностей дискретних випадкових величин: біноміальний, пуассонівський, геометричний, гіпергеометричний (означення, властивості, числові характеристики, приклади основних застосувань). Закони розподілу імовірностей неперервних випадкових величин: рівномірний, показниковий, нормальний або гауссовий (означення, властивості, числові характеристики, приклади основних застосувань). Імовірнісний зміст параметрів нормального закону розподілу. Теореми про імовірність попадання нормально розподіленої величини в заданий інтервал та про імовірність заданого відхилення випадкової величини від свого математичного сподівання. Правило трьох сигм та його практичне застосування Статистична гіпотеза. Нульова і конкуруюча гіпотеза. Поняття про критерії згод.и. Перевірка гіпотез про рівність часток та середніх.(5ЗС)

Методика іспиту: іспит, за призначенням.

Мова: мова викладання – українська, російська

Реєстрація на курс: дирекція Ін АЕКСУ, ауд.5308, тел.(8-0432) 59-84-58

Реєстрація на іспит: з лектором, персонально чи по телефону.

Дисципліна: Фізика Факультет: АКСУ Статус дисципліни: обов’язкова Курс: перший, другий
	Стаціонарне навчання	Години на тиждень
Триместр	2,4.5(ОС,ЗС, ВС)
Лекції (год.)	74	2
Практичні заняття (год.)	24	1
Лабораторні заняття (год.)	44	1
СРС (інд. заняття)	324	5,6
Всього (год./кредитів)	349/9.5
Іспит (трим.)	1,2,4
Залік (трим.)
КОД:	НФД 02

Лектори: Ющенко Анатолій Васильович , канд. фіз.-мат. наук, доцент.

Лисий М.В., ст. викладач.

21021 м. Вінниця, Хмельницьке шосе, 95, Інститут автоматики, електроніки та комп’ютерних систем управління (ІнАЕКСУ) тел. 59-85-15, каф. фізики, тел. 59-84-73.

МЕТА ДИСЦИПЛІНИ: Метою викладання є забезпечення фундаментальної фізико-математичної бази, без якої не можлива успішна діяльність інженера.

Вивчення курсу фізики повинно сприяти формуванню у студента наукового світогляду і сучасного фізичного мислення. Він повинен творчо використовувати набуті знання у майбутній фаховій діяльності.

ПРОГРАМА:

Частина 1.

Вступ. Предмет і моделі фізики. Методи фізичного дослідження. Розмірності фізичних величин. Основні одиниці. Фізичні основи механіки.

Елементи кінематики. Поступальний рух. Радіус-вектор, траєкторія, шлях, переміщення. Швидкість. Прискорення. Нормальне і тангенціальне прискорення. Рівномірний, рівно змінний рух. Обертальний рух. Кутова швидкість. Кутове прискорення. Зв'язок між кутовими і лінійними швидкостями і прискореннями.

Динаміка матеріальної точки. Закони Ньютона. Інерціальні системи відліку. Маса. Сила. Сили в механіці (гравітаційні, пружні, сили тертя). Імпульс. Закони збереження імпульсу. Центр мас. Робота і потужність. Енергія (кінетична, потенціальна, повна). Закон збереження енергії в механіці.

Динаміка обертального руху. Кінетична енергія обертального руху. Момент Інерції. Теорема Штейнера. Основне рівняння обертального руху. Момент сили. Момент імпульсу. Закон збереження моменту імпульсу.

Принцип відносності. Елементи релятивістської динаміки.

Механічний принцип відносності. Перетворення Галілея. Постулати Ейнштейна. Перетворення Лоренца. Відносність довжини і часу. Релятивістський закон перетворення. Елементи релятивістської динаміки.

Електростатика. Електростатичне поле. Заряд. Закон збереження заряду. Закон Кулона. Напруженість поля. Напруженість поля точкового заряду. Потік вектора електричного зміщення. Теорема Гауса. Електричне поле рівномірно зарядженої площини. Поле двох площин. Поле рівномірно зарядженої сфери, циліндра і кулі. Робота сил поля. Циркуляція вектора напруженості. Потенціал. Різниця потенціалів. Потенціал точкового заряду, системи зарядів. Зв'язок потенціалу з напруженістю поля. Речовина в електричному полі. Поляризація діелектриків. Поляризованість. Діелектрична сприйнятливість. Напруженість поля в діелектрику. Діелектрична проникність. Умови на межі двох діелектриків. П'єзоелектричний ефект. Сегнетоелектрики.

Провідник в електричному полі. Розподіл заряду. Електричне поле біля поверхні провідника. Електроємність ізольованого провідника. Конденсатори. Електроємність конденсаторів (плоского, сферичного, циліндричного). Система конденсаторів. Енергія системи зарядів, провідника, конденсатора. Енергія електричного поля. Об'ємна густина енергії.

Електричний струм. Сталий струм та його характеристики (сила струму, густина струму). Сторонні сили, е.р.с., напруга, різниця потенціалів. Закони Ома в інтегральній та диференціальній формі. Опір і його залежність від температури. Закони Джоуля-Ленца в інтегральній та диференціальній формі. Розгалужені кола. Правила Кірхгофа.

Термоелектрона емісія. Струм у вакуумі. Електровакуумні прилади. Електричний струм в газах. Несамостійні і самостійні газові розряди.

Електромагнетизм. Магнітне поле у вакуумі. Магнітне поле. Магнітна індукція. Закон Ампера. Закон Біо-Савара-Лапласа. Принцип суперпозиції. Магнітне поле прямолінійного і колового струмів. Циркуляція вектора напруженості магнітного поля. Поле тороїда і нескінченного соленоїда. Магнітний потік. Теорема Гауса. Дія магнітного поля на провідник із струмом і електричний заряд. Робота переміщення провідника і контуру із струмом в магнітному полі. Контур із струмом в магнітному полі. Магнітний момент колового струму. Сила Лоренца. Рух заряджених частинок у магнітному полі. Ефект Холла.

Явище електромагнітної індукції. Явище електромагнітної індукції. Закон Фарадея. Правило Ленца. Електронний механізм явища електромагнітної індукції. Самоіндукція. Індуктивність. Індуктивність соленоїда. Взаємоіндукція. Трансформатор.

Енергія провідника із струмом. Енергія магнітного поля. Об'ємна густина енергії. Магнітне поле в речовині. Намагніченість. Магнітна сприйнятливість. Магнітне поле в магнетику. Діамагнетизм. Парамагнетизм. Феромагнетики, їх властивості. Умови на межі двох магнетиків.

Рівняння Максвелла. Струм зміщення. Рівняння Максвелла в інтегральній формі.

Частина 2.

Коливання і хвилі. Гармонічні коливання. Загальна характеристика гармонічних коливань. Пружинний, фізичний і математичний маятник. Вільні коливання в контурі без активного опору. Зображення гармонічних коливань за допомогою векторної діаграми. Енергія гармонічних коливань. Складання коливань. Додавання однаково напрямлених коливань. Додавання взаємно перпендикулярних коливань.

Загасаючі і вимушені коливання. Механічні загасаючи коливання. Електромагнітні загасаючи коливання. Вимушені механічні коливання. Резонанс. Вимушені електромагнітні коливання. Поняття про змінний струм.

Хвилі. Пружні хвилі. Поздовжні і поперечні хвилі. Рівняння плоскої хвилі. Довжина хвилі. Хвильове рівняння. Фазова і групова швидкість хвилі. Електромагнітні хвилі та їх властивості. Вектор Пойнтінга.

Хвильова та геометрична оптика. Геометрична оптика. Світлові хвилі. Показник заломлення. Оптична довжина шляху. Закони геометричної оптики. Повне внутрішнє відбиття. Волоконна оптика.

Хвильова оптика. Інтерференція двох хвиль. Умови утворення максимумів і мінімумів. Стоячі хвилі. Інтерференція в тонких плівках. Кільця Ньютона. Інтерферометри. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракція від щілини. Дифракційна гратка. Дифракція рентгенівських променів. Формула Вульфа-Брегга. Поняття про голографію. Поляризоване світло. Закон Брюстера. Закон Малюса. Штучна анізотропія.

Квантова фізика. Корпускулярно - хвильовий дуалізм. Теплове випромінювання. Закони Кірхгофа, Віна і Стефана-Больцмана. Розподіл енергії в спектрі абсолютно чорного тіла. Гіпотеза і формула Планка. Фотоефект. Рівняння Ейнштейна. Фотони. Імпульс фотона.

Елементи квантової механіки. Гіпотеза і формула де-Бройля. Співвідношення невизначеностей. Подання стану частинки в квантовій механіці. Хвильова функція. Рівняння Шредінгера. Вільна частинка. Частинка в одномірному "потенціальному ящику. Гармонічний осцилятор. Тунельний ефект.

Частина 3.

Фізика атомів і ядер. Фізика атомів і молекул. Атом водню. Досліди Штерна і Герлаха. Спин електрона. Принцип нерозрізненості частинок. Принцип Паулі. Розподіл електронів по станам. Періодична система елементів. Рентгенівські промені. Закон Мозлі. Взаємодія атомів. Іонний та ковалентний зв'язок. Квантові генератори.

Атомне ядро. Основ ні характеристики ядра. Будова ядер. Нуклони. Енергія зв'язку, дефект маси. Ядерні сили. Радіоактивність. Закони радіоактивного розпаду. Реакції ділення та синтезу. Ядерна енергетика. Елементи радіометрії. Експозиційна доза. Поглинена доза.

Статистична фізика і термодинаміка. Фізика газів. Основні статистичні поняття. Статистичний і термодинамічний методи. Умовність. Середні значення фізичних величин. Густина атомів. Функція розподілу. Фазовий простір. Число станів в просторі імпульсів. Розподіл Фермі-Дірака, Бозе-Енштейна і Максвела-Больцмана. Критерій виродження. Розподіл Максвелпа. Середня квадратична швидкість. Розподіл Больцмана. Барометрична формула.

Кінетична теорія газів і термодинаміка. Рівняння молекулярно-кінетичної теорії для тиску. Середня кінетична енергія молекул. Рівняння стану ідеального газу. Ізопроцеси. Адіабатичний процес. Внутрішня енергія ідеального газу. Робота розширення газу. Закони термодинаміки. Перший закон термодинаміки і його застосування для ізопрцесів. Теплоємність газів. Зворотні і незворотні процеси. Теплова і холодильна машини. Цикл Карно і його к.к.д. Другий закон термодинаміки. Ентропія. Явища переносу в газах..

Фізика твердого тіла. Кристалічна гратка. Елементи зонної теорії. Будова кристалів. Дефекти в кристалах Фонони. Теплоємність кристалів та її залежність від температури. Енергетичні зони. Метали, діелектрики, напівпровідники з точки зору зонної теорії. Носії струму в кристалах. Ефективна маса. Електронні властивості металів. Розподіл електронів за енергіями в металі. Енергія Фермі.

Елементи квантової теорії електропровідності металів. Контакт двох провідників. Термоелектричні явища. Надпровідність. Електронні властивості напівпровідників. Власна провідність напівпровідників. Домішкова провідність напівпровідників. Контакти двох напівпровідників з різним типом провідності. Напівпровідникові діоди. Тунельні діоди. Подвійний р-n перехід. Транзистори. Фотоелектричні явища в напівпровідниках. Фоторезистори. Фотоелементи.

БІБЛІОГРАФІЯ:

Савельев И. В. Курс общей физики: Учеб. Пособие. В 3-х т. Т1. Механика. Молекулярная физика.- М.: Наука, 1986.- 432 с.
Савельев И. В. Курс общей физики: Учеб. Пособие. В 3-х т. Т.2.Электричество и магнетизм. Волны. Оптика.- М.: Наука, 1988.- 496 с.
Савельев И. В. Курс общей физики: Учеб. Пособие. В 3-х т. Т3. Квантовая оптика. Атомная физика. Физика атомного ядра и элементарных частиц.- М.: Наука, 1987.- 320 с.
Чертов А.Г., Воробьев А.А. Задачник по физике: Учеб. пособие.- М.: Высш. шк., 1981.- 496 с.
Зузяк П.М., Слободяник А.Д. Задачі з фізики. Програма курсу, контрольні завдання та методичні поради до розв’язування окремих задач: Навч. Посібник. - Вінниця: ВНТУ, 2003.- 172 с.
Авдєєв С.Г. Лабораторний практикум з фізики: Навч. Посібник. В 3-х частинах. - Вінниця: ВДТУ, 2000.- 172 с.

МЕТОДИ ОЦІНЮВАННЯ:

Протягом кожного триместру студенти проходять по два модульних контролі (2 письмові колоквіуми на 7 та 14 тижні). Додатково оцінюються лабораторні заняття на яких необхідно виконати 8 лабораторних робіт. Оцінки знань формуються на підставі рейтингових балів, які студент отримує протягом триместру за результатами колоквіумів, захисту лабораторних робіт. На основі цих оцінок студент отримує рейтингову оцінку, або складає іспит на загальних підставах.

Іспит складається усно. Завдання містять два теоретичних та одне практичне питання. Письмові колоквіуми та іспит розраховано на 45 хвилин роботи.

ПЕРЕДУМОВИ:

Необхідні знання з дисципліни “Загальна фізика”, “Математичний аналіз”, “Векторна алгебра”.

МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ: протягом лекцій студентам видається методична література з актуальних питань та адреса Інтернет видань.

Авдєєв С.Г. Лабораторний практикум з фізики: Навч. Посібник. В 3-х частинах. - Вінниця: ВДТУ, 2000.- 172 с.
Авдєєв С.Г. Збірник задач з фізики: Навч. Посібник. - Вінниця: ВДТУ, 1998- 128 с.
Зузяк П.М., Слободяник А.Д. Задачі з фізики. Програма курсу, контрольні завдання та методичні поради до розв’язування окремих задач: Навч. Посібник. - Вінниця: ВНТУ, 2003.- 172 с.
Т.Е.Данилюк. Методические рекомендации по решению задач с введеним элементов проблемного характера по курсу физики. - Винница: ВПИ, 1986.- 56 с.
Авдєєв С.Г., Бабюк Т.І. Лекції з фізики. Частина 1: Навч. посібник. - Вінниця: ВНТУ, 2003.- 185 с.
Авдєєв С.Г., Гель П.В., Бабюк Т.І. Резнік С.І. Фізичний практикум. Частина 3. Навч. посібник. - Вінниця: ВДТУ, 1999.- 136 с.
Бабюк Т.І., Гель П.В., Хрущак. Фізичний практикум. Частина 1. Навч. посібник. - Вінниця: ВДТУ, 2001.- с.

ІНДИВІДУАЛЬНА РОБОТА: перелік тем для самостійного опрацювання.

Динаміка матеріальної точки. Закони Ньютона. Інерціальні системи відліку. Маса. Сила. Сили в механіці (гравітаційні, пружні, сили тертя). Імпульс. Закони збереження імпульсу. Центр мас. Робота і потужність. Енергія (кінетична, потенціальна, повна). Закон збереження енергії в механіці.

Відносність довжини і часу. Релятивістський закон перетворення. Елементи релятивістської динаміки.

Речовина в електричному полі. Поляризація діелектриків. Поляризованість. Діелектрична сприйнятливість. Напруженість поля в діелектрику. Діелектрична проникність. Умови на межі двох діелектриків. П'єзоелектричний ефект. Сегнетоелектрики.

Термоелектрона емісія. Струм у вакуумі. Електровакуумні прилади. Електричний струм в газах. Несамостійні і самостійні газові розряди.

Поляризоване світло. Закон Брюстера. Закон Малюса. Штучна анізотропія.

Ядерна енергетика. Елементи радіометрії. Експозиційна доза. Поглинена доза.

Закони термодинаміки. Перший закон термодинаміки і його застосування для ізопроцесів. Теплоємність газів. Зворотні і незворотні процеси. Теплова і холодильна машини. Цикл Карно і його к.к.д. Другий закон термодинаміки. Ентропія. Явища переносу в газах.

Фотоелектричні явища в напівпровідниках. Фоторезистори. Фотоелементи.

Домашня робота – розв’язування відповідних задач до кожної теми програми з використанням вказаної літератури [3-4] (1 год. /тиждень)

Методика іспиту: іспит, за призначенням.

Реєстрація на курс: дирекція Ін АЕКСУ, ауд.5308, тел.(8-0432) 59-84-58

Реєстрація на іспит: з лектором, персонально чи по телефону.

Мова: мова викладання – українська.

Дисципліна: Інженерна графіка Факультет: Автоматики і комп’ютерних систем управління Статус дисципліни: обов’язкова Курс: перший
	Стаціонарне навчання	Години на тиждень
Триместр	1/2
Лекції (год.)	28/21	1
Практичні заняття (год.)	21/21	2/1
КП (КР) / трим
РГЗ	4/-
СРС ( інд. заняття)	15/15	1/1
Всього (год. / кредитів)	72/2 54/1,5
Іспит (трим)	1
Залік (трим)	2
КОД:	НФД 03

Лектор: Мельник Ольга Петрівна, к.т.н., доцент.

21021 м. Вінниця, вул. Воїнів Інтернаціоналістів, 7, Інститут будівництва, теплоенергетики та теплогазопостачання (ІнБТЕГП), факультет теплоенергетики та газопостачання, кафедра інженерної і комп’ютерної графіки, тел. 59-86-63, 59-8065.

Мета дисципліни: вивчення теоретичних основ побудови плоских зображень просторових об’єктів, принципів розробки та оформлення електротехнічних креслень згідно стандартів та допомогою комп’ютерних графічних систем.

ПРОГРАМА:

Прямокутні проекції елементарних геометричних фігур. Методи перетворення комплексного креслення. Криві лінії і поверхні. Визначення. Класифікація. Способи завдання. Ортогональні проекції. Алгоритми розв’язування позиційних та метричних задач. Системи та типи конструкторської документації. Основні правила оформлення креслень. Виконання креслень плоских деталей. Нанесення розмірів на кресленнях деталей. Креслення електричних схем. Електричні принципові схеми. Перелік елементів. Зображення: вигляди розрізи перерізи. Аксонометричні проекції. Друкована плата як тип електротехнічного виробу. Основні геометричні параметри. Правила оформлення робочого креслення друкованої плати. Типи з’єднань. Умовне зображення та позначення не рознімних з’єднань. Складальне креслення. Правила оформлення. Специфікація. Використання графічної системи КОМПАС для виконання графічної та текстової конструкторської документації.

БІБЛІОГРАФІЯ

Александров К.К. и др.. Электротехнические чертежи и схемы. М.:

Энергоатомиздат -1996 г.-234 с.

2. Михайленко В.Є. та інш. Нарисна геометрія. К.: Вища школа –2004 р.-265 с.

3. Чекмарев А.А. Инженерная графика. М.: Высшая школа -1993г.-250 с.

4. Потемкин А.И. Инженерная графика. КОМПАС-ГРАФИК L.T. Просто и доступно.С.-П., 2000 г.

5. Потишко А.В. Справочник по инженерной графике. К.: Будівельник -1997 г. -174 с.

МЕТОДИ ОЦІНЮВАННЯ: на протязі першого триместру студент проходять два модульних контролі які враховують виконання чотирьох розрахунково-графічних завдань, а також написання двох поточних контрольних робіт, на 5 та 10 тижнях, та два письмових колоквіуми на 7 та 14 тижнях. Протягом другого триместру студент повинен виконати дві графічні роботи, виконати письмову контрольну роботу, з двох завдань і виконати курсову роботу. Оцінки знань формуються на підставі рейтингових балів, які студент отримує протягом триместрів за результатами колоквіумів, виконання поточних контрольних робіт, виконання та захисту розрахунково-графічних та графічних робіт. На основі цих оцінок студент отримує оцінку з іспиту та диференційованого заліку, або складає останні на загальних підставах.

ПЕРЕДУМОВИ: базується на математиці та інформатиці.

МЕТОДИЧНЕ ЗАБЕСПЕЧЕННЯ: Протягом лекцій студенти забезпечені відповідним базовим „Конспектом лекцій з інженерної графіки” авт. Шевченко А.В. та інш. К.: НМКМО-1993 р.-102 с. Для виконання курсової роботи використовується навчальний посібник „Креслення електричних принципових схем та друкованих” / авт. Вітюк О.П., Кормановський С.І. та інш./ , ВДТУ: Вінниця, - 2001,- 102 с.

ІНДИВІДУАЛЬНА РОБОТА: Домашня робота складається з виконання завдань:

- РГЗ 1 „Нанесення розмірів на кресленнях плоских деталей”

( робота виконується за допомогою графічної системи КОМПАС);

РГЗ 2 „Дослідження багатогранників ”;
РГЗ 3 „Проекційне креслення”;
РГЗ 4 „Моделювання кривих поверхонь. Позиційні та метричні задачі”.

Виконання курсової роботи „Розробка та оформлення графічної конструкторської документації друкованих плат”.

МЕТОДИКА ІСПИТУ: іспит, диференційований залік , захист курсової роботи, за призначенням.

Реєстрація на курс: дирекція Ін АЕКСУ, ауд.5308, тел.(8-0432) 59-84-58

Реєстрація на іспит: у лектора, персонально чи по телефону.

Скорочення: РГЗ- розрахунково-графічні завдання.

Мова: мова викладання – українська

Предмет: Комп’ютерна графіка Факультет: АКСУ Курс 3 Статус дисципліни: обов’язкова
	Стаціонарне навчання	Години на тиждень
Триместр	9
Лекції (год.)	28	2
Практичні заняття (год.)	-
Лабораторні заняття (год.)	14	1
СРС (інд. заняття)	30	2
Всього (год. /кредитів)	72/2
Іспит (трим)	9
Залік (трим)
КОД:	НФД 1.2.4

Лектор: Коцюбинський Володимир Юрійович, к.т.н., доцент.

Інститут/Факультет: 21021, м. Вінниця, вул.;. Хмельницьке шосе, 95, корпус 5,. аудиторія А5204; тел.:8-0432-59-80-06.

МЕТА:. ознайомлення з основними способами створення та обробки графічних Web-зображень з використанням iснуючих пакетiв програм, набуття навичок роботи з найбiльш типовими з них (Corel DRAW 7, Adobe Photoshop, Paint Shop Pro, Macromedia Flash, Front Page, Photo Impact GIF Animator, Fractal Design Painter), надання інформації з основних принципів створення сучасних графічних Web - зображень та методи їх оброблення, а також технологій використання найбільш відомих програмних продуктів, якi орієнтовані роботу з графічними зображеннями; набуття уміння створювати графічні растрові та векторні Web-зображення, здійснювати їх перетворення, маштабування (Corel DRAW 7, Adobe Photoshop, Paint Shop Pro), реалізовувати анімаційну графiку (Macromedia Flash, PhotoImpact GIF Animator, Fractal Design Painter), здійснювати оптимізацію та стискання графічних зображень (GIF, JPEG SmartSaver PhotoImpact), конвертацію даних, представлених в різноманітних графічних форматах (HiJaak Pro).

ПРОГРАМА

Дисципліна "Комп'ютерна графіка" є базовою для спецiалiстiв в галузі графічних технологій, програмного забезпечення та його використання для створення графіки з застосуванням комп'ютера. Використання засобів комп'ютерної техніки в різних галузях науки, впровадження новітніх технологій, пов'язаних з роботою в глобальній мережі Internet, вимагає від фахівця знань та умінь щодо ефективного застосування засобів ЕОМ для обробки графічних даних в комп'ютерних системах передачі інформації та управління, при організації науково-дослідної діяльності та інше.

БІБЛІОГРАФІЯ

1. Графіка для Web, біблія дизайнера; пер. з англ.. – К.; діалектика,1998. –608с.

2.Загляднов И.Ю., Касаткин В.Н. Построение изображений на экране персональной ЄВМ. - К.; Техніка, 1990.-120с.

3. Алиев В.Э. Обработка графической информации на ПЭВМ. М; МФТИ, 1997.-506с.

4.Вальвачев А.Н., Графическое програмирование на языке Паскаль: Справ. пособие.- Минск; Выш. шк., 1992. –143с.

5.Дубовой В.М., Квэтный Р.Н. Основи застосування ЕОМ в інженерній діяльності. - Київ. ІСД МО України, 1994.- 285с.

МЕТОДИ ОЦІНЮВАННЯ: Протягом триместру студенти проходять по два модульних контролі відповідно до університетської модульно-рейтингової системи організації навчального процесу. На модульних контролях пропонується декілька варіантів завдань однакової складності, які охоплюють теоретичні і практичні питання відповідного курсу.

ПЕРЕДУМОВИ: базується на знанні таких дисциплін, як вища математика. Алгоритмічні мови та програмування.

Метод навчання: лекції із застосуванням плакатів, лабораторні заняття проводяться на персональних ЕОМ з відповідним програмним забезпеченням, а саме:

Операційна система Windows.Графічний редактор Adobe Photoshop 5.5.

Графічний редактор Corel DRAW 8.0Програма Paskal

Програма-оглядач Internet-ExplorerWeb- редактор Front- Page

Анімаційна програма Photoimpact GIF Animator.

Анімаційна програма Macromedia Flash.

Методичне забезпечення: Протягом лекцій конспект та методичні вказівки для виконання лабораторних робіт.

ІНДИВІДУАЛЬНА РОБОТА: спрямовується на освоєння методів стискання графічних зображень (за схемою LZW), вивчення функціональних можливостей графічних форматів EPS Tiff, - методів динамічного збереження зображень при роботі в середовищі “Pascal”, вміння розраховувати матриці перетворень при вивченні графічних перетворень у просторі, використовувати автоматизовані засоби створення Web- сторінок, будувати анімаційні зображень засобами програми “Macromedia Flesh, використовувати шаблони для створення особистих WEB – сайтів.

Методика іспиту: залікова робота складаються з двох теоретичних питань та одного практичного завдання.

Реєстрація на курс: дирекція Ін АЕКСУ, ауд.5308, тел.(8-0432) 598-458

Реєстрація на іспит: 3 лектором, персонально чи по телефону.

Мова викладання – українська. Можливе викладання російською та англійською мовами.

Предмет: “Основи дискретної математики” Факультет: АКСУ Курс: II Статус дисципліни: (за вибором) Триместр: 5 (весна)
	Стаціонарне навчання	Годин на тиждень
Лекції (год.)	32
Практичні заняття (год.)
Лабораторні заняття (год.)	24
СРС (інд. заняття)	52
Всього (год. /кредитів)	108/3
Екзамен (трим.)	5
Залік (трим.)	-
КОД:	НФД.05

Лектор:, Штовба Сергій Дмитрович к.т.н., доцент кафедри КСУ;

Інститут/Факультет: 21021, м. Вінниця. Хмельницьке шосе, 95; корпус 5; кафедра комп’ютерних систем управління, кімната 5217б; тел.: 8-0432-59-82-22; кафедра автоматики та інформаційно-вимірювальної техніки, кімната 5207; тел.: 8-0432-59-80-06

МЕТА

Дисципліна “Основи дискретної математики” надає студентам базові теоретичні знання та сприяє набуттю практичних навичок із теорії множин, теорії алгоритмів, формальних систем, графів та дискретних екстремальних задач, які необхідних для розуміння студентами місця та ролі дискретної математики в майбутній фаховій діяльності.

Знання, набуті студентами, будуть витребуванні під час професійної діяльності в галузі створення та експлуатації систем управління і автоматики.

ПРОГРАМА

Множини та операції над ними.

Нечіткі множини.

Відображення і функції.

Відношення.

Основи теорії графів.

Основи теорії алгоритмів.

Основи теорії формальних систем.

Складність алгоритмів.

Задача про розфарбування графу.

Задача про комівояжера.

Популярні екстремальні задачі дискретної оптимізації.

Мурашині алгоритми розв’язання задач дискретної оптимізації.

БІБЛІОГРАФІЯ

Бардачов Ю.М., Соколова Н.А., Ходаков В.Є. Дискретна математика. – К.: Вища школа, 2002. – 287с.
Глушков В.М. Введение в АСУ. К.: Техніка – 1974.
Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.– 480 с.
Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. – М.: Мир, 1985. – 512 с.
Biggs N. L. Discrete Mathematics. – Oxford: Oxford University Press, 2^nd eds., 2002. – 425p.
Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976. – 165 с.
Коршунов Ю.М. Математические основы кибернетики. – М.: Энергия, 1972.
Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2001.
Ротштейн А.П. Интеллектуальные технологии идентификации: нечеткая логика, генетические алгоритмы, нейронные сети. – Винница: УНІВЕРСУМ–Вінниця, 1999. – 320 с.
Орловский С.А. Проблемы принятия решений при нечеткой исходной информации. М.: Радио и связь.- 1981.- 286с.
Штовба С.Д. Муравьиные алгоритмы: теория и применение // Программирование. – 2005. – №4.– C. 1–16.
Zimmerman H.-J. Fuzzy Sets Theory and Its Applications.3^rd ed. – Kluwer Academic Publisher, 1996. – 435 p.

МЕТОДИ ОЦІНЮВАННЯ: Оцінки знань виставляються за рейтинговими балами, які отримують студенти протягом триместру за результатами контрольних заходів. За рейтинговими балами студент отримує інтегральну оцінку або дозвіл на складання іспиту. Екзаменаційний білет містить 2 теоретичних питання та 1 задачу.

ПЕРЕДУМОВИ

При вивченні дисципліни студентам знадобляться знання з “Вищої математики” та “Алгоритмічних мов та програмування”. Отримані знання використовуватимуться при вивченні дисциплін “Методи оптимізації”, “Дослідження операцій”, “Теорія автоматичного управління”, “Теорія інформації та кодування”, “Автоматизовані системи управління технологічними процесами”, “Штучний інтелект та розпізнавання образів” в дипломному проектуванні та при підготовці магістрів

Методичне забезпечення: Лекційний курс підкріплено відповідною навчальною літературою (в достатній кількості є в наявності в бібліотеці університету), виконання лабораторних робіт здійснюється у відповідності до методичних вказівок (існують у друкованому і електронному вигляді).

ІНДИВІДУАЛЬНА РОБОТА: підготовка, оформлення звітів з лабораторних робіт, підготовка до захисту лабораторних робіт, самостійне вивчення окремих розділів загального змісту. Крім того, можуть бути запропоновані реферати на теми пов’язані з проблематикою дискретної математики (дають можливість отримати додаткові бали)

Екзаменаційна методика: Письмовий іспит, за призначенням.

Реєстрація на курс: Дирекція інституту (21021, м. Вінниця, вул. Хмельницьке шосе, 95; корпус 5; кімната 5308; тел.: 8-0432-59-84-58).

Реєстрація на іспит: 3 лектором, персонально чи по телефону.

Мова: мова викладання – українська, можливо також російська та англійська.

Примітка: Ця інформація стосується студентів всіх спеціалізацій спеціальності “Системи управління і автоматики”.

Предмет: Теорія імовірностей та математична статистика Факультет: АКСУ Курс 3, (Обов’язковий )
	Стаціонарне навчання	Години на тиждень
Триместр	7
Лекції (год.)	16	1
Практичні заняття (год.)	16	1
СРС (інд. заняття)	76	5
Всього (год. /кредитів)	108/3
Іспит (трим)	-
Залік (трим)	7
КОД:	НПД 01

Лектор: Присяжнюк Василь Васильович, ст. викладач.

Інститут/Факультет: 21021, м. Вінниця, вул. Хмельницьке шосе, 95, корпус 5, Кафедра Метрології та промислової автоматики, аудиторія 5412; тел.:8-0432-59-86-72.

МЕТА: ознайомлення з основними поняттями і методами теорії імовірностей та математичної статистики, вивчення імовірнісно-статистичного матеріалу, набуття вміння розв’язувати задачі, в тому числі прикладні, яки виникають на практиці, вміння будувати математичні моделі реальних процесів.

ПРОГРАМА: Курс передбачає систематичне викладення математичних основ поняття імовірності, стохастичного експерименту, аксіоматичних основ теорії ймовірностей. Викладається теорія випадкових величин, визначення їх числових характеристик, теорія умовних математичних сподівань та умовних ймовірностей, а також розгляд основних положень розділу граничних теорем теорії ймовірностей.

Розглядаються: основні поняття і методи теорії імовірностей і математичної статистики; способи визначення чисельних характеристик випадкових величин, функцій та процесів, методи обробки статистичних даних, статистичні оцінки параметрів розподілу, критерії згод.и, основи кореляційного та регресивного аналізу, методи обробки статистичних даних на основі сучасних засобів обчислювальної техніки. Розрахунки імовірнісні характеристики випадкових величин, функцій та стохастичних процесів, визначення функцій та щільністі розподілу, виконання статистичного оцінювання параметрів розподілу, проводення статистичну перевірку гіпотези, формулювання статистичних висновків за результатами обробки даних.

Blog

Курс: перший, другий Стаціонарне навчання Години на тиждень Триместр

Содержание

Факультет: АКСУ

Мова викладання – українська. Можливе викладання російською та англійською мовами.