Программа курса лекций

Вид материала

Программа курса

Содержание Электронное строение и спектроскопия сложных молекул Метод молекулярных орбиталей в приближении Хюккеля Реакционная способность молекул Правила Вудворда – Гоффмана Строение и спектроскопия координационных соединений Электронная спектроскопия Колебательная спектроскопия Вращательная спектроскопия Квантовая механика молекул Программа семинарских занятий(4 курс, 7 сем, 34 ч, зачет)

Подобный материал:

• Программа предусматривает проведение лекций, проведение семинарских занятий, подготовку, 17.19kb.
• Программа курса лекций для студентов специальности «История», 109.25kb.
• Программа курса Конспект лекций > Тесты Задачи > Вопросы к экзамену Методические рекомендации, 1693.2kb.
• Программа курса лекций "Языки программирования Internet", 61.91kb.
• М. Н. Общая риторика программа курса лекций общая риторика программа курса, 236.54kb.
• Программа регионоведческого курса, 292.18kb.
• Программа регионоведческого курса, 292.24kb.
• Программа курса лекций, 27.96kb.
• М. В. Кричевцев Программа курса лекций Предлагаемый курс лекций, 215.31kb.
• Название курса, 106.28kb.

Квантовая механика молекул

Программа курса лекций
(4 курс, 7 сем, 32 ч, экзамен)

Профессор, д.х.н. Плюснин Виктор Федорович

Электронное строение и спектроскопия атомов

Заполнение электронных орбиталей, электронные конфигурации. Термы атомов, схемы Рассел - Саундерса и j-j-связей. Волновые функции и энергии термов. Правила Гунда. Спин-орбитальное взаимодействие, образование прямых и обращенных мультиплетов.

Двухатомные молекулы, электронные термы

Систематика термов двухатомных молекул. Правила отбора для дипольных переходов. Вариационные методы и метод молекулярных орбиталей (МО). Нахождение основного терма двухатомных молекул, молекула кислорода. Различные виды связей (s, p, d).

Электронное строение и спектроскопия сложных молекул

Теория групп, точечные группы, операции симметрии, теория представлений, характеры операций симметрии, прямое произведение представлений. Применение теории групп для нахождения МО. Электронные конфигурации и термы сложных молекул. Правила отбора для оптических дипольных переходов в сложных молекулах.

Метод молекулярных орбиталей в приближении Хюккеля

Метод МО в приближении Хюккеля (МОХ). Молекулярные p-системы. Применение метода МОХ к ароматическим системам. Заряд, порядок связи, индекс свободной валентности. Альтернантные углеводороды, расположение уровней энергии, симметрия молекулярных орбиталей, распределение спиновой плотности в нечетных альтернантных углеводородах. Циклические p-системы, энергии и вид МО. Правило 4n+2. Длинные одномерные p-системы, распространение представлений теории МО на описание твердого тела.

Учет гетероатомов в методе МОХ. Индуктивные и мезомерные заместители. Поляризуемость атом-атом. Альтернирование заряда в ароматических молекулах с заместителями. Влияние заместителей на вырожденные уровни энергии в p-системах.

Реакционная способность молекул

Метод возмущенных МО. Индексы реакционной способности, индекс локализации. Энергии конечных состояний, правило непересечения потенциальных поверхностей. Реакция двух p-радикалов, реакция молекул и радикалов. Устойчивость p-углеводородов, реакционная способность радикалов. Ориентация в реакциях нуклеофильного, радикального и электрофильного замещения в ароматическом кольце с различными типами заместителей.

Правила Вудворда – Гоффмана

Использование представлений симметрии при рассмотрении реакционной способности. Правила Вудворда - Гоффмана для синхронных реакций. Электроциклические реакции, реакции замыкания и размыкания цикла, сигматропные реакции.

Строение и спектроскопия координационных соединений

Теория кристаллического поля, потенциал кристаллического поля, использование симметрии. Расщепление d-орбиталей в октаэдрическом и тетраэдрическом полях. Диаграмма Оргела. Учет искажения симметрии комплекса. Сильное и слабое кристаллические поля, диаграммы Танабе - Сугано, спектрохимический и нефелоксетический ряды.

Теория поля лигандов (метод МО) для описания электронной структуры координационных соединений. Сравнение двух подходов. Природа оптических переходов координационных соединений. Причины появления d-d-переходов. Фотохимические реакции координационных соединений.

Электронная спектроскопия

Классификация электронных переходов. Интенсивность и положение полос поглощения. Колебательная структура электронных переходов, принцип Франка - Кондона. Связь спектров поглощения и люминесценции. Время жизни и квантовый выход люминесценции, внутренняя и интеркомбинационная конверсия. Основные законы люминесценции. Флуоресценция и фосфоресценция.

Колебательная спектроскопия

Колебания многоатомных молекул, нормальные колебания, частоты колебаний. Типы колебательных переходов, фундаментальные переходы. Классификация нормальных колебаний с помощью теории групп. Проявление колебательных переходов в спектрах инфракрасного (ИК) поглощения и комбинационного рассеяния (КР), правила отбора. Валентные и деформационные колебания, характеристические частоты, применение ИК- и КР-спектроскопии в химических исследованиях. Электронно-колебательное взаимодействие, эффект Яна - Теллера. Влияние электронно-колебательного взаимодействия на запрещенные оптические переходы.

Вращательная спектроскопия

Вращательные уровни энергии и волновые функции для различных типов молекул. Определение структуры молекул из вращательных спектров. Колебательно-вращательное взаимодействие, диаграммы Фортра. Связь ядерного спина и вращения молекул.

Квантовая механика молекул

Программа семинарских занятий
(4 курс, 7 сем, 34 ч, зачет)

Профессор, д.х.н. Плюснин Виктор Федорович

Семинар 1

1. Сложить моменты: 2 и 2; 1 и 4; 1,2 и 3; 1/2, 1/2 и 1/2.

2. Найти возможные значения орбитального момента при сложении моментов трех p-электронов.

3. Чему равно среднее значение операторов L_x, L_z, L² в состояниях p_x, p_y, p_z?

4. Найти вид операторов L_x, L_y, L_z, L₊ и L_- через функции от углов q, j и их производных.

5. Определить, как действует оператор L₊ на функцию Y_lm.

6. Определить действие операторов L_x, L_z, L² на функции d_x2, d_xz, d_yz, d_xy, d_x2-_y2.

7. Найти собственную функцию оператора L_x, если известно, что собственное значение равно нулю, а орбитальное квантовое число l = 1.

8. Чему равно L²p_xb = ?; S²p_xa = ?

9. Определить все значения полного орбитального момента для системы из трех d-электронов. Какие значения реализуются в действительности при учете принципа Паули?

Семинар 2

1. Записать операторы S_z, S², S₊, S_- для системы из двух электронов. Найти собственные спиновые функции для синглетного и триплетного состояний.

2. Спины N частиц, равные каждый s, складываются в результирующий спин S = Ns. Каков суммарный спин любых 2, 3, ... n частиц в указанном состоянии?

3. Проверить, является ли функция aa собственной функцией оператора S².

4. Найти спиновые функции для системы из двух частиц, имеющих спины: a) s₁ = 1/2, s₂ = 1; б) s₁ = 0, s₂ = 1.

5. Определить спиновые функции для системы из трех частиц, у которых спины равны 1, 1/2 и 1/2.

6. Для системы из двух одинаковых частиц со спином s определить число симметричных и антисимметричных спиновых функций по отношению к перестановкам частиц.

7. Спиновая функция из N электронов имеет вид y = a...ab...b (n штук a-функций и N-n штук b-функций). Найти среднее значение квадрата суммарного спина и вероятности различных значений полного спина S в частных случаях n = 1 и n = N - 1.

Семинар 3

1. Найти слейтеровские орбитали для Ar²⁺ (1s²2s²2p²3s²3p⁴).

2. Используя слейтеровские функции, определить каковы размеры атома и ионов Fe⁰ (1,24 A), Fe¹⁺, Fe²⁺ (0,80 A), Fe³⁺ (0,67 A), Fe⁴⁺.

3. Первый потенциал ионизации атома кислорода – 13,614 эВ, серы – 10,357 эВ, селена – 9,75 эВ. Дать качественное объяснение этому изменению. Оценить потенциал ионизации, если в приближении слейтеровских функций средняя энергия электрона, находящегося на орбитали с главным квантовым числом n,

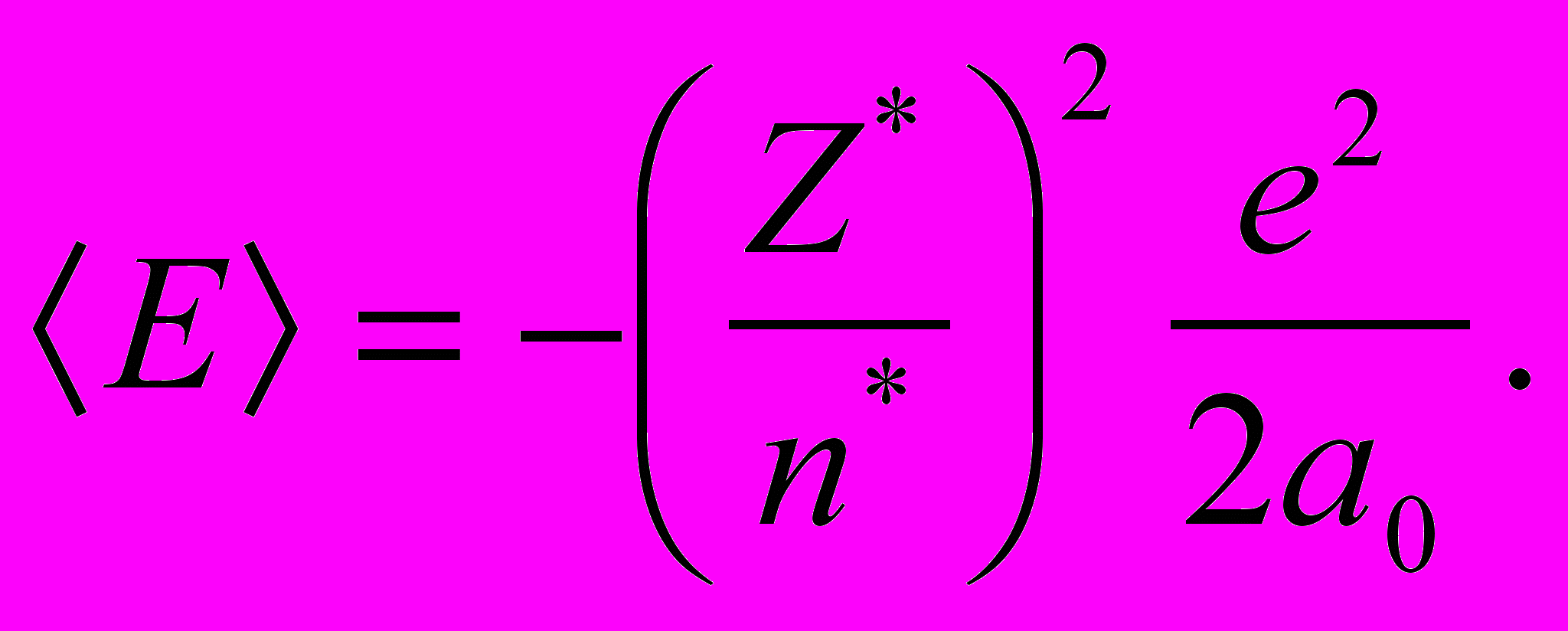
4. Определить вырождение и четность конфигураций s¹p¹d¹, s²p²d² и т. д.

5. Найти термы конфигураций p², d³, s¹p¹, s¹p¹d¹ и т. д.

6. Определить результат действия оператора V = x(l·s) на функции Y_lma, Y_lmb; оператора L_x на функции d_xy и d_z2.

7. Определить волновую функцию нижнего по энергии мультиплета конфигурации s¹p¹ в случае LS-связи.

8. С учетом спин-орбитального взаимодействия построить диаграмму уровней для конфигураций p², d², p¹d¹ и т. д.

9. Как действуют операторы L², S² и J² на функции термов ²P_1/2 и ²P_3/2 (конфигурация p¹)?

10. Выписать функции основного терма p³ электронной конфигурации.

Семинар 4

1. Найти спин-орбитальное расщепление основного терма конфигураций d⁴, d⁵, d⁶ и т. д.

2. Найти разрешенные переходы из термов ¹S, ²P, ³D и т. д.

3. Найти основной терм и его энергию для электронной конфигурации lⁿ в случае jj – связи.

4. Для терма ²P_1/2 (конфигурация p¹) определить <L_z>, <S_z> и <J_z>.

5. Найти расщепление спектральных линий в сильном магнитном поле длинноволнового перехода в атоме бора.

6. Определить поляризацию дипольных переходов в спектре атома Na, находящегося в слабом и в сильном магнитных полях.

Семинар 5

1. Определить вырождение термов: ¹S_g⁺, ³S_u^-, ³П, ⁴Ф_u и т. д.

2. Найти термы, которые могут возникнуть при сближении атомов, находящихся в основных состояниях: O + O; O + H; O + F.

3. Определить основной терм радикала OD. Какие термы могут возникнуть у линейного комплекса H-O...O-D при образовании его из радикалов в основных состояниях?

4. Найти молекулярные термы, которые могут возникнуть при сближении двух ионов золота Au³⁺, находящихся в основных состояниях, и образовании кластера Au₂⁶⁺.

5. Построить диаграмму молекулярных уровней для молекул H₂, HCl, C₂, N₂, NO.

6. Найти термы основных электронных конфигураций молекул H₂, HCl, O₂, O₂^-, O₂⁺ и т. д.

7. Найти основной терм молекулярного иона Mo²⁺–С. Электронная конфигурация иона Mo²⁺ – 4d⁴.

8. Найти разрешенные электронные переходы из термов: ¹S_g⁺, ³S_u^-, ³П, ⁴Ф_u, ²S^-, ¹S⁺, ²П, ²D_u, ³П_u.

9. Показать, что молекула He₂ неустойчива, а ион He₂⁺ устойчив.

Семинар 6

1. Как изменяется энергия связи в ряду молекул: O₂, F₂, Ne₂?

2. Оценить дипольный момент линейного радикала H-D-D.

3. Найти молекулярные орбитали аллильного радикала.

4. Рассчитать заряды, спиновую плотность, порядки связи и индексы свободной валентности для аллильного радикала, циклобутадиена.

5. Имеется орбиталь y=с₁j₁ + с₂j₂ + с₃j₃. Чему равна ее энергия?

6. Определить МО p-систем циклобутадиена и бутадиена.

7. Найти МО в приближении Хюккеля пентильного радикала.

8. Найти МО в приближении Хюккеля бензильного радикала.

9. Определить p-молекулярные орбитали триметиленметила.

10. Рассчитать энергию делокализации для аллильного радикала, бутадиена, бензола.

Семинар 7

1. Определить, какая из структур (линейная или треугольная) более устойчива для частиц H₃⁺, H₃, H₃^-.

2. Найти все операции симметрии и определить группу симметрии молекул: NH₃, H₂O, C₂H₄, C₂H₆, CH₄, CH₃, SF₆.

3. Построить таблицу умножений операций симметрии для групп C_2v, C_3v, C_4v.

4. Определить группу симметрии C_nv (найти n), в которой число двумерных представлений в 2 раза больше одномерных.

5. Определить МО p-системы циклобутадиена с помощью теории групп.

6. Найти вид МО молекулы H₂O с помощью теории групп и определить разрешенные оптические переходы.

Семинар 8

1. Все элементы группы симметрии, содержащей 16 элементов, разбиваются на 10 классов. Определить размерности неприводимых представлений данной группы.

2. Найти характеры симметричного и антисимметричного прямого произведений представлений [Е ´ Е] в C_3v-группе. По каким неприводимым представлениям они преобразуются?

3. Определить неприводимые представления, по которым преобразуются компоненты оператора импульса в группе C_3v.

4. Определить неприводимые представления, по которым преобразуются компоненты орбитального момента в группе D_3h.

5. С помощью теории групп найти МО p-систем: аллильного радикала, циклобутадиена, нафталина, бензола, бензильного радикала.

6. Определить на какие неприводимые представления распадется Т₂ представление группы Т_d при понижении симметрии от Т_d до C_3v.

7. Определить группу C_nv (определить n), в которой число двумерных представлений в 2 раза больше, чем одномерных.

8. Определить группу D_nd, в которой число двумерных неприводимых представлений в 10 раз больше одномерных НП.

9. Построить таблицу характеров для D_3d группы.

10. По каким неприводимым представлениям преобразуются прямые произведения следующих представлений: S ´ П; П ´ П; S_g⁺ ´ S_u^-; S_u^-´ П_g.



Семинар 9

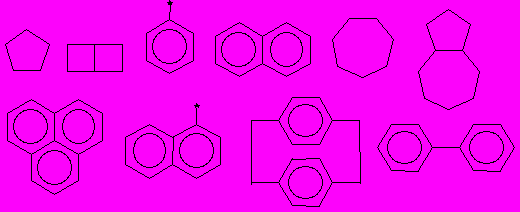
1. Проверить, являются ли альтернантными следующие радикалы и молекулы:

2. Доказать, что в нейтральных альтернан­тных углеводородах плотность p-зарядов на каждом центре равна 1.

3. В каком случае циклические углеводороды являются альтернантными?

4. Доказать, что в альтернантных углеводородах порядок связи между двумя мечеными (или немечеными) атомами равен нулю.

5. В рамках МОХ рассмотреть линейную бесконечную p-систему. Показать возникновение разрешенной энергетической зоны вместо отдельных уровней, определить ее ширину.

6. Найти МО циклического p-радикала, состоящего из трех p-центров.

7. Найти энергии и МО, пользуясь теорией циклических углеводородов, для циклобутадиена, циклопента-диенильного радикала.

8. Определить распределение спиновой плотности в радикале H₁₅, строение которого представлено на рисунке.

9. Определить распределение спиновой плотности для радикала H₅ (группа D_4h), строение которого показано на рисунке.

10. Определить изменение энергии орбитали неспаренного электрона для длинной p-системы, состоящей из N центров, при ее замыкании на концах в циклическую p-систему.

Семинар 10

1. Определить изменение спиновой плотности при введении заместителя CF₃ в разные положения пентадиенильного радикала (x = 0,3).

2. Определить относительную стабильность различных геометрических изомеров антрацена, тетрацена, пентацена (см. рисунок).

3. Линейная молекула, состоящая из N атомов водорода, замыкается на концах. Определить изменение энергии самой нижней молекулярной орбитали.

4. Чему равен выигрыш энергии при объединении ЧАУ и НАУ?

5. Определить ориентацию радикального замещения для замещенного циклобутадиена CH₃-C₄H₂-CF₃.

6. Определить направление преимущественного присоединения атома водорода к p-системе молекулы, геометрия, которой представлена на рисунке.

7. Определить распределение заряда в бензильном радикале при введении индуктивного заместителя в первое положение.

Семинар 11

1. Правила Вудворда – Гоффмана для реакции циклоприсоединения молекул. Вывести общие правила.



2. С точки зрения правил Вудворда – Гоффмана рассмотреть возможность протекания реакции Н₂ + N₂ Û N₂H₂ и Н₂ + J₂ Û 2HJ.

3. Pассмотpеть с точки зpения пpавил Вудвоpда-Гоффмана pеакцию обpазования аммиака пpи взамодействии pадикала NH с молекулой водоpода. Для атома азота учитывать только p-оpбитали. Геометpия сближения показана на pисунке. Постpоить коppеляционную диагpамму c указанием типа молекуляpных оpбиталей.

4. Рассмотреть реакцию циклозамыкания пентильного радикала (катиона или аниона этого радикала) с точки зрения правил Вудворда – Гоффмана.



5. С точки зрения правил Вудворда – Гоффмана рассмотреть реакцию.

6. Для двух одинаковых молекул H_n с точки зрения правил Вудворда – Гоффмана рассмотреть реакцию превращения, представленную на рисунке.

7. Изобразить корреляционную диаграмму для реакции бензола с молекулой этилена.

Семинар 12

1. Написать потенциал кристаллического поля для иона с электронной конфигурацией d² в поле Т_d.

2. Указать причины появления d-d-полос поглощения в оптических спектрах координационных соединений.

3. Как соотносятся величины расщеплений d-орбиталей в поле тетраэдра, октаэдра и куба?

4. Определить оператор кристаллического поля для комплекса, имеющего форму правильной тригональной бипирамиды.

5. На какие электронные состояния расщепляются термы конфигурации p² в поле правильного квадрата?

6. Предсказать характер расщепления d-орбиталей в поле тетрагональной бипирамиды.

7. Качественно изобразить поведение энергии d-орбиталей при искажении правильного тетраэдра до правильного квадрата.

8. Предсказать окраску растворов комплексов Co(H₂O)₆ и CoCl₄^2-.

9. Определить электронные состояния конфигураций e² и t₂² в поле тетраэдра.

10. Показать, что тетраэдрические комплексы с электронной конфигурацией d⁷ всегда являются высокоспиновыми.

11. Раствор комплекса Fe(H₂O)₆ бесцветен. Определить число неспаренных электронов в этом комплексе.

12. Найти расщепление (энергии) электронных состояний конфигурации p² в поле правильного треугольника.

Семинар 13

1. Определить поляризацию в спектрах оптического поглощения молекулы сим-триазин (Н₃С₃N₃).

2. Определить поляризацию электронных переходов в молекуле H₂O.

3. Определить основной терм и поляризацию переходов для p-системы аллильного радикала (C_2v).

4. Найти матрицу дипольных переходов для группы D_4h.

5. Найти отношение интенсивностей люминесценции вдоль осей Z и Y при облучении образца светом вдоль оси X и с поляризацией по оси Z.

6. Найти характер электронных переходов в ионе ванадила VO(H₂O)₅ (группа симметрии C_4v).

7. Предсказать поляризацию самой длинноволновой полосы поглощения в оптическом спектре формальдегида H₂CO.

8. Оценить интенсивность лазерного излучения, необходимую для насыщения синглетного разрешенного перехода.

9. Вывести формулу Перрена для тушения люминесценции по обменному механизму в жестких матрицах.

10. Переход (S₀ ® S₁) в пиридине поляризован вдоль оси, перпендикулярной плоскости молекулы. Определить поляризацию перехода S₀ ® T₁.

11. Вывести формулу Штерна - Фольмера для тушения люминесценции.

12. Определить отношение интенсивностей люминесценции вдоль осей Z и Y с поляризацией вдоль оси X, если образец возбуждается вдоль оси X с поляризацией под 45⁰ к оси Z.

13. В какой из молекул (бензол, нафталин, антрацен) расщепление между уровнями S₁ и T₁ больше?

14. При введении в раствор эффективного тушителя (концентрация 10^-3 М) квантовый выход люминесценции уменьшился в 1000 раз. Оценить время жизни люминесценции.

Семинар 14

1. Определить типы колебаний, проявляющихся для молекулы цикло-бутадиена в ИК-спектре.

2. Охарактеризовать КР-спектр молекулы Н₂, D₂.

3. Можно ли, анализируя экспериментальные ИК- и КР-спектры, сделать однозначный вывод о строении молекулы, состоящей из четырех одинаковых атомов?

4. Сколько валентных и деформационных колебаний имеется у молекул H₂O, NH₃, CO₂, C₆H₆, нафталина и т. д?

5. Найти неприводимые представления, по которым преобразуются деформационные колебания бензола. Сколько деформационных частот будет реализоваться в ИК- и КР-спектрах?

6. Найти колебания, разрешенные в ИК- и КР-спектрах молекул этилена, аммиака, SF₅Cl.

7. Найти разрешенные в ИК-спектре колебания для молекулы нафталина.

8. В КР-спектре иона CO проявляются три частоты. Определить строение этой частицы (плоское или объемное).

9. Для молекулы, состоящей из N атомов и принадлежащей к C_4v группе, определить число различных частот колебаний.

10. При рекомбинации двух молекул количество колебательных степеней свободы увеличилось на 4. Что можно сказать о строении реагирующих частиц и геометрии реакции?

Семинар 15

1. Определить число деформационных колебаний для молекулы С_nH_2n+1.

2. Вывести формулу для характера тензора поляризуемости для операции S_n, C_n.

3. Частота колебаний молекулы H₂ равна 4400 см^-1. Чему равна эта величина для молекулы TD?

4. Для плоской молекулы, имеющей центр инверсии, определить число четных и нечетных плоских (неплоских) колебаний.

5. Для линейной молекулы, состоящей из N атомов, определить количество различных частот колебаний.

6. Для молекулы, состоящей из N атомов и принадлежащей к C_3v-группе, определить число различных частот колебаний.

7. Для молекулы, состоящей из N атомов и принадлежащей к группе D_4h, определить число различных частот колебаний, проявляющихся в ИК спектре.

8. Можно ли однозначно решить вопрос о геометрическом строении молекулы X₄ с помощью ИК- и КР-спектроскопии?



9. Чему равно отношение числа полносимметричных деформационных колебаний к числу плоских неполно-симметричных для молекулы из N одинаковых атомов, имеющей строение, показанное на рисунке.

10. Для линейной молекулы X_n найти число четных и нечетных колебаний.

11. Определить количество различных частот плоских колебаний для молекулы из 4-х атомов, имеющей строение плоского квадрата (прямоугольника).

12. Для молекулы, состоящей из N атомов и принадлежащей к D_4h-группе, определить число различных частот колебаний, проявляющихся в ИК-спектре.

Семинар 16

1. Рассмотреть эффект Яна – Теллера на примере плоского p-анион радикала Н₆C₄, имеющего симметрию D_3h.

2. Показать, что в линейной многоатомной молекуле не будет проявления эффекта Яна – Теллера.

3. Доказать теорему Яна – Теллера для D_4h-группы.

4. Существует ли эффект Яна – Теллера для отрицательного иона бензола? Если да, то какие колебания снимают это вырождение?

5. Что можно сказать о геометрической структуре иона CH₄⁺?

6. В каком из тетраэдрических комплексов (FeСl₄^- или CuCl₄^2-) будет наблюдаться эффект Яна – Теллера?

7. Доказать теорему Яна – Теллера для группы C_6v.

8. Возможен ли эффект Яна – Теллера для молекул H₄, имещих строение сжатого тетраэдра (группа симметрии D_2d)?

9. Рассмотреть возможность проявления эффекта Яна – Теллера для p-катион-радикала (см. рисунок).

10. В каком случае (T_d или D_4h) для молекулы CuH₄⁺ будет проявляться эффект Яна – Теллера? Определить тип колебаний, снимающих вырождение. Центральный ион имеет конфигурацию 3d¹⁰.

11. Будет ли проявляться эффект Яна – Теллера для иона PuH₄³⁺ (электронная конфигурация иона плутония Pu³⁺ - 5f⁵) и какие колебания снимут вырождение, если эффект будет?

Семинар 17

1. Определить связь вращения молекулы и ядерного спина для линейного радикала H₃.

2. Связь вращения молекул с ядерным спином. Можно ли из вращательного спектра молекулы НСl определить, является ли спин ядра хлора целым или полуцелым?

3. Построить в масштабе схему вращательных уровней для плоского CH₃-радикала. Длина связи C-H равна 1,09 A.

4. Определить типы вращательных уровней для ион-радикала J₂^-.

5. Дать классификацию вращательных уровней молекулы D₂.

6. В спектре КР на чисто вращательных переходах для двухатомной гомоядерной молекулы отношение интенсивностей первой (ближайшей к линии возбуждения) линии в стоксовой области ко второй равно 1/4. Определить ядерный спин атомов молекулы.

7. Во вращательном спектре трехатомной молекулы наблюдается эквидистантный набор линий поглощения. Что можно сказать о строении такой молекулы?

8. В колебательно-вращательном спектре двухатомной молекулы существует предел сходимости линий поглощения в области меньших частот по сравнению с 0-0-переходом. В каком колебательном состоянии вращательная константа больше?

9. Построить вращательный спектр молекулы H₂.

10. Что произойдет с вращательным спектром линейной молекулы, если ее изогнуть на малый угол?

11. Установить связь вращения и ядерного спина для молекулы метана.

12. Дать классификацию вращательных уровней линейного ион-радикала (H-Be-H)^-.

13. Определить полные ядерные спины для систем протонов и дейтонов в молекуле CH₂D₂ при Т = 0 К.

14. Дать классификацию вращательных уровней молекулы Ti₂.

Задание

1. Имеется 10 одинаковых орбитальных моментов l = 2. Сколько раз встретится значение полного момента L = 1 для такой системы?

2. Найти вырождение конфигурации f², ее основной терм и его расщепление за счет спин-орбитального взаимодействия.

3. Определить термы конфигурации s¹d¹ в случае j-j-связи.

4. Под действием спин-орбитального взаимодействия терм расщепляется на 5 мультиплетов. Интервалы по энергии между соседними мультиплетами, начиная с нижнего, равны 125, 100, 75 и 50 см^-1. Кроме того, известно, что один из мультиплетов не расщепляется в магнитном поле. Каким образом из этих данных определить величины L и S для исходного терма?

5. На сколько уровней и с каким вырождением расщепляется основной терм конфигурации lⁿ в слабом магнитном поле?

6. Определить количество молекулярных термов, которые могут возникнуть при сближении двух ионов Mn²⁺ (3d⁵-конфигурация) в основных состояниях и при образовании молекулярного иона Mn²⁺-Mn²⁺.

7. Найти основной терм линейной молекулы D-Co²⁺-D.

8. Построить матрицу дипольных переходов для группы C_4v.

9. Определить число и размерность НП в группе D_kh.

10. Найти разложение симметричной части прямого произведения [E´E] в группе C_4v.

11. С помощью теории групп рассмотреть электронное строение молекулы NaH₄, имеющей квадратное строение.

12. Найти энергию, приходящуюся в среднем на один p-электрон (Е_ср=Е^p_полн/N) для бесконечно большой (N®¥) циклической p-системы.



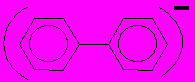
13. С помощью теории групп найти распределение спиновой плотности в p-радикале.



14. Используя теорию возмущений, определить распределение спиновой плотности в p-системе анион-радикала.

15. Используя теорию возмущений, определить, какой из двух радикалов более стабильный.



16. Определить по Вудворду - Хоффману путь для реакции циклозамыкания линейной p-системы, состоящей из N p-центров.

17. Определить разрешенность (кТ, hn) реакции метилена и молекулы водорода образованием метана. Геометрия сближения показана на рисунке. Построить корреляционную диаграмму. У атома углерода учитывать только p-орбитали.

18. Написать выражение для потенциала кристаллического поля для иона с электронной конфигурацией p¹ в поле N эквивалентных лигандов.

19. Для молекулы, состоящей из N атомов и принадлежащей к C_4v-группе определить число различных частот колебаний.

19. Определить типы колебаний (симметрию) для линейной молекулы, состоящей из N атомов и принадлежащей к группе C_¥v.

20. В плоскую молекулу (группа D_4h), состоящую из N атомов, в центр вставили атом (его там не было). Насколько увеличится количество частот плоских колебаний, проявляющихся в ИК-спектре?

22. Будет ли проявляться эффект Яна-Теллера для молекулы DH₄ (C_4v)? Найдите терм основного состояния. Считать b_H-H = 0.

23. Будет ли проявляться эффект Яна - Теллера для иона CuH₈²⁺ с симметрией D_4h (ион Cu²⁺ - конфигурация 3d⁹)?

24. Дать систематику вращательных уровней для линейного CH₂-радикала. Для молекулярной диаграммы считать орбитали 2s и 2p вырожденными.

Литература

1. 
   Ландау Л.Д., Лившиц Е.М. Квантовая механика.М.:Наука, 1974
   
2. Маррелл Дж., Кеттл С., Теддер Дж. Теория валентности. М.: Мир, 1968.
   
3. Маррелл Дж., Кеттл С., Теддер Дж. Химическая связь. М.: Мир, 1980.
   
4. Герцберг Г. Спектры и строение простых свободных радикалов. М.: Мир, 1974.
   
5. Плюснин В.Ф., Бажин Н.М. Двухатомные молекулы. Новосибирск: Изд-во НГУ, 1991.
   
6. Герцберг Г. Электронные спектры и строение многоатомных молекул. М.: Мир, 1969.
   
7. Дьюар М. Теория молекулярных орбиталей в органической химии. М.: Мир, 1972.
   
8. Дьюар М., Догерти Р. Теория возмущенных молекулярных орбиталей в органической химии. М.: Мир, 1977.
   
9. Войтюк А.А. Симметрия молекул. Новосибирск: Изд-во НГУ, 1988.
   
10. Яцимирский К.Б., Яцимирский В.К. Химическая связь. М.: Наука, 1975.
    
11. Бальхаузен К. Введение в теорию поля лигандов. М.: Мир, 1964.
    
12. Берсукер И.Б. Электронное строение и свойства координационных соединений. Л.: Химия, 1976.
    
13. Коулсон Ч. Валентность. М.: Мир, 1965.
    
14. Шусторович Е.М. Химическая связь. М.: Наука, 1973.
    
15. Вудворд Р., Гоффман Р. Сохранение орбитальной симметрии. М.: Мир, 1971.
    
16. Джаффе Г., Орчин М. Симметрия в химии. М.: Мир, 1977.
    
17. Лер Р., Марчланд А. Орбитальная симметрия в вопросах и ответах. М.: Мир, 1976.
    
18. Джилкрист Т., Сторр Р. Органические реакции и орбитальная симметрия. М.: Мир, 1976.
    
19. Пирсон Р. Правила симметрии в химических реакциях. М.: Мир, 1979.
    
20. Берсукер И.Б. Эффект Яна-Теллера и вибронные взаимодействия в современной химии. М.: Наука, 1987.
    
21. Плюснин В.Ф., Бажин Н.М. Электронная спектроскопия координационных соединений. Новосибирск: Изд-во НГУ, 1995.
    
22. Свердлова О.В. Электронные спектры в органической химии. М.: Наука, 1973.
    
23. Грибов Л.А. Введение в молекулярную спектроскопию. М.: Наука, 1976.
    
24. Наберухин Ю.И. Лекции по молекулярной спектроскопии. Новосибирск: Изд-во НГУ, 1973.
    
25. Степанов Б.И., Грибковский В.П. Введение в теорию люминесценции. М.: Наука, 1963.
    
26. Ермолаев В.Л., Бодунов Е.Н., Свешникова Е.Б., Шахвердов Т.А., Безизлучательный перенос энергии электронного возбуждения. Л.: Наука. Ленингр. отд-ние, 1977.
    
27. Уитли П. Определение молекулярной структуры. М.: Мир, 1970
    
28. Волькенштейн М.В., Грибов Л.А., Ельяшевич М.А., Степанов Б.И. Колебания молекул. М.: Наука, 1972.
    
29. Свердлов Л.М., Ковнер М.А., Крайнов Е.П. Колебательные спектры многоатомных молекул. М.: Наука, 1970.
    
30. Герцберг Г. Колебательные и вращательные спектры многоатомных молекул. М.: Мир, 1949.
    
31. Конингстайн И.А. Введение в теорию комбинационного рассеяния. М.: Мир, 1975.
    
32. Колебательная спектроскопия. Современные воззрения. /Под ред. А.Барнса и У.Орвилл-Томаса. М.: Мир, 1981.