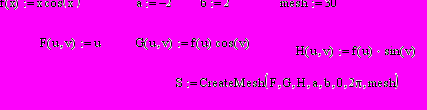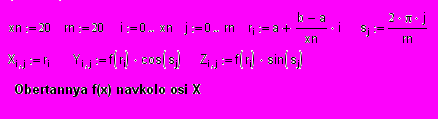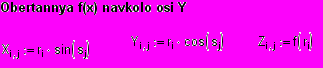Лекція № Обчислювальні й графічні можливості Mathcad

Вид материала

Лекція

Содержание Графік меню Вставка Zoom - дозволяє виділити частина графіка, Trace Побудова графіків у полярній системі координат Побудова об'ємної фігури, утвореної кривої

Подобный материал:

• MathCad Mathcad, 7.16kb.
• 1. Обчислювальні й локальні мережі та системи, 246.94kb.
• Задание в Mathcad сигналов в виде функций и векторов. В mathcad для задания различных, 94.91kb.
• «математические пакеты mathcad и mathematica в решении прикладных химических задач», 360.54kb.
• Тематический план введение, 469.57kb.
• Оптимальний розподіл однорідних ресурсів із використанням Mathcad І Excel. Мета, 61.72kb.
• Контрольная работа (типовой расчет) №2 "расчет сложной цепи периодического синусоидального, 29.02kb.
• С помощью сред Mathcad и Labview, а так же сравнительный анализ двух рассматриваемых, 89.08kb.
• Гиэфпт, г. Гатчина Ленинградской обл, 49.68kb.
• М. А. Оновлення змісту дисципліни «інформатика та обчислювальна техніка» Постановка, 64.89kb.

Лекція № 2.

Обчислювальні й графічні можливості Mathcad.


Побудова графіків функцій


Визначити функцію в Mathcad досить просто, для цього необхідно ввести ім'я функції, у дужках її параметри й оператор присвоювання. Після чого вводиться алгебраїчне вираження. Потім функція може використатися нарівні з убудованими функціями. Уведемо для приклада параболічну функцію:



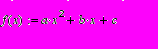
Нам довелося попередньо описати три константи a,b,c, інакше функція не може бути обчислена.

Тепер, для того щоб одержати значення функції, досить записати:



і так далі.


Для створення графіків у системі MathCAD є програмний графічний процесор. Процесор дозволяє будувати самі різні графіки в декартовой і полярній системі координат, графіки поверхонь, тривимірні фігури, графіки рівнів і т.д.

Для побудови графіків використаються шаблони. Їхній перелік представлений у підменю Графік меню Вставка або на панелі Графіки (мал. 1).



1 2 3 4 5 6 7 8 9

Рис.1

Розглянемо докладніше види побудови графіків

1. Декартов графік.
   
2. Наближення (збільшення графіка).
   
3. Спостереження графіка.
   
4. Полярний графік.
   
5. Графік поверхні.
   
6. Карта ліній рівня.
   
7. 3D столбиковая гистограмма.
   
8. 3D крапковий графік.
   
9. Векторне поле.
   

Перш ніж, викликати шаблон графіка необхідно побудувати математичну модель майбутнього графіка. Т.е. графік можна побудувати по наступному алгоритмі:

1. побудова математичної моделі;
   
2. виклик шаблона необхідного графіка.
   

Розглянемо побудову двовимірного графіка в декартовой системі координат.

Для того щоб побудувати графік, необхідно клацнути по символі декартового графіка в панелі Graph й увести в позначених позиціях біля координатних осей імена аргументу й функції f(x). Закінчується побудова клавішею Enter або щигликом миші поза графіком. Можна також явно вказати початкове й кінцеве значення по осях у маркерах початку й кінця осі, інакше вони визначаться автоматично.


Для того щоб зобразити на одному графіку кілька функцій того самого аргументу, потрібно ввести в позиції біля осі ординат ім'я першої функції, увести кому, ім'я наступної функції, кому, і т.д., розділяючи імена функцій комі. Для того щоб змінити стиль зображення - клацнути за графіком двічі й змінити параметри зображення в тимчасовому вікні, що відкрилося, настроювання зображення.

Виділивши графік подвійним щигликом миші, можна зробити його настроювання, зокрема, визначити тип, кольори й товщину лінії, а також вибрати осі.

Є ще дві цікаві кнопки графічної палітри.



Zoom - дозволяє виділити частина графіка,

Trace - відслідковує зміна координат на графіку.

Ці кнопки активні тільки при виділенні графіка.


Побудова графіка 3D-поверхні проходить аналогічним образом, як і побудова двовимірного графіка.

Побудова графіків у полярній системі координат

У полярній системі координат кожна крапка задається кутом ? і довжиною його радіуса-вектора ?(?). Графік функції звичайно будується при зміні кута ? у певних межах, найчастіше від 0 до 2?.

Від полярних координат до декартовым і навпаки можна перейти, використовуючи формули:

x=ρcos(ψ); y=ρsin(ψ );

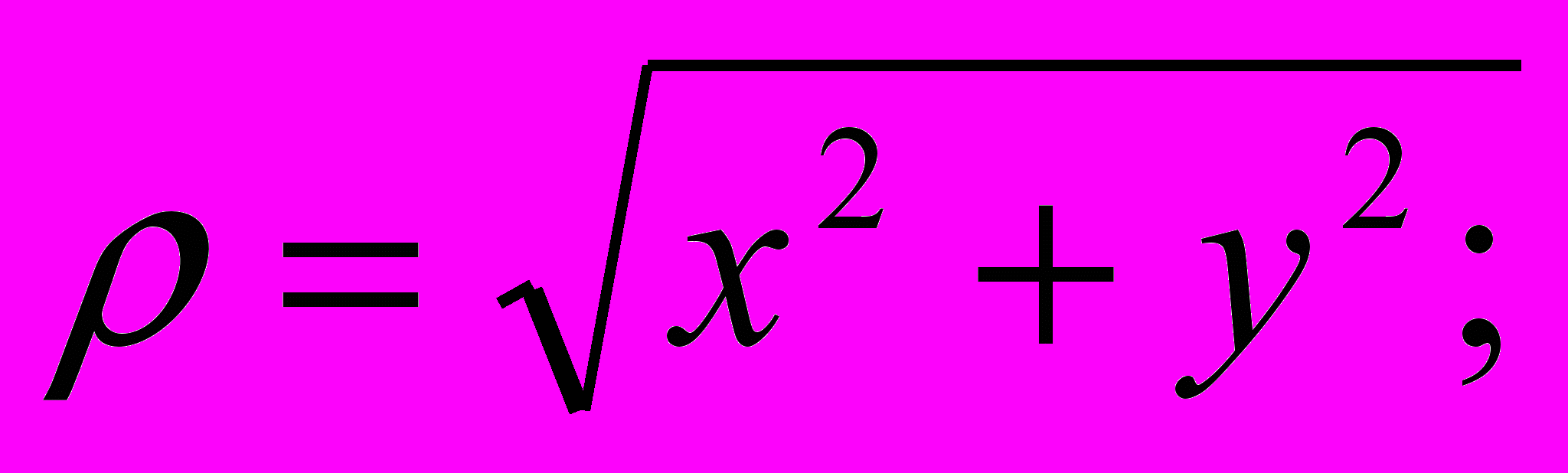
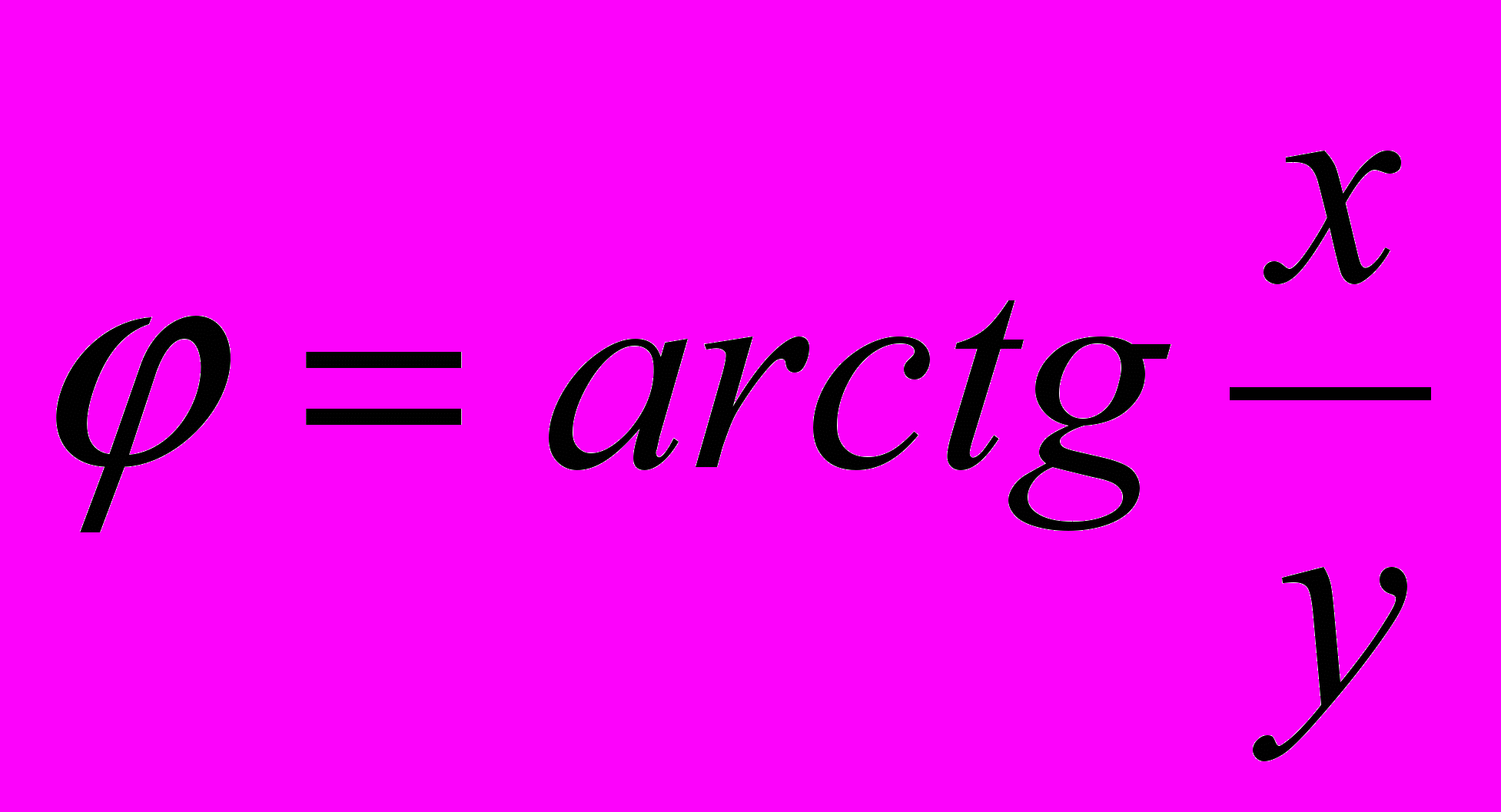
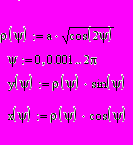
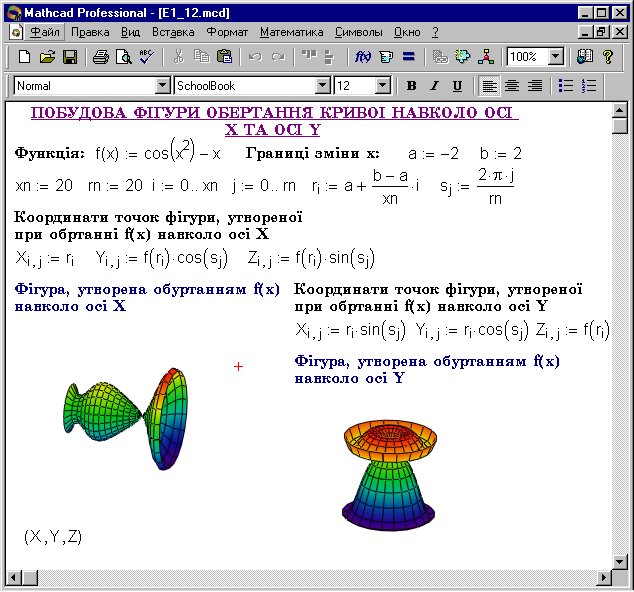
Побудова об'ємної фігури, утвореної кривої

Побудова графіка фігури обертання відбувається в такий спосіб:

1. Оголошення функції, крива якої буде обертатися. У цьому випадку краще побудувати її двовимірний графік.
   
2. Оголошення границь змін по Х графіка поверхні.
   
3. Оголошення масиву крапок по Х.
   
4. Оголошення координат крапок отриманих при обертанні навколо осі.
   

Для цих цілей використається функція CreateMesh(F,s0,s1,t0,t1,sgrid,tgrid,fmap).

Ця функція повертає масив з 3 матриць, що представляють координати x, y, z для функції F, певної у векторній параметричній формі як функція 2 параметрів sgrid, tgrid. Аргументи s0, s1, t0, t1 задають межі зміни змінних sgrid, tgrid. Аргумент fmap - трехэлементный вектор значень, що задають число ліній у сітці зображуваної функції.