Сзтм отдел главного конструктора

Математическая модель асинхронного электродвигателя

Поляк-Брагинский Н.В.

Красноярск 2003г

E-mail: polak47@mail.ru

В процессе проектирования машины обязательно должна существовать стадия определения усилий, возникающих в механизме в процессе его работы. Особенно интересен процесс запуска и разгона механизма, который характеризуется наибольшими динамическими нагрузками. Источником этих нагрузок служит двигатель, в качестве которого наиболее часто используется электродвигатель.

Одновременно с динамическими нагрузками в механизме конструктора очень интересует состояние самого электродвигателя и питающего его преобразователя, которые должны быть выбраны с условием обеспечения их работоспособности в заданном режиме работы механизма.

Все интересующие конструктора данные могут быть надежно получены при натурном моделировании механизма, которое практически исключено при проектировании тяжелых машин. Для расчета действующих усилий в механизме существует достаточное количество расчетных программ, например VisualNastran, но для обеспечения возможности расчета они должны получить в качестве исходных данных величину момента от приводного двигателя в функции времени или пути разгона.

Предлагаемая к рассмотрению математическая модель должна позволить определить текущие параметры приводного электродвигателя в процессе его работы.

В реальной практике использования электродвигателей, для применения известных теоретических зависимостей, точно описывающих все процессы, происходящие в электродвигателе, совершенно недостаточно имеющихся в справочной литературе технических параметров. Заводы-производители, по самым разным причинам, не предоставляют пользователям полного набора параметров выпускаемых ими электродвигателей.

Попытки предложить варианты расчета характеристик электродвигателей, при недостатке исходных данных, предпринимались не раз. В работах /1/ и /2/ описаны варианты, основанные на применении известной формулы Клосса. Ее использование требует знания значения критического скольжения и значений активных и реактивных составляющих сопротивлений статора и ротора, которые также входят в число неизвестных параметров и в реальных расчетах определяются приближенно. Этот метод нашел применение благодаря своей простоте и его доступности при ручном приблизительном расчете.

В /3/ предложено более сложное математическое описание, использующее схему обобщенной двухполюсной машины. Оно требует знания магнитных характеристик электродвигателя и имеет допущение о не насыщенности магнитной цепи и о том, что вся энергия магнитного поля сосредоточена только в воздушном зазоре, что заранее вносит в расчеты известные погрешности, особенно в зоне низких частот питающего напряжения.

При построении расчетной программы, которая может применяться в САПР для проверки возможности использования того или иного электродвигателя в заданном режиме работы, желательно применение достаточно просто программируемого варианта математической модели, которая не требует использования непубликуемых значений параметров.

При математической обработке результатов самых разных экспериментов применяется аппроксимация экспериментальных данных эмпирическими формулами. Такая работа, при неразвитости теории позволяет определить взаимовлияние различных факторов в процессе изучения решаемой проблемы.

В данной работе проведен обратный переход от известных, с достаточной степенью точности описывающих электродвигатель, зависимостей к подобной аппроксимации. В качестве аппроксимирующей зависимости использована зависимость момента от частоты вращения электродвигателя, которая позволяет понять физику процесса, но в чистом виде не позволяет просчитать требуемые характеристики из-за недостаточности данных.

Для более точной сходимости параметры, которые входят в эту формулу и описания ее составляющих, должны быть откорректированы для учета влияния непубликуемых параметров. В данной работе эти откорректированные параметры названы условными. Часть реальных параметров в силу того, что их значения не публикуются в официальных документах, заменяются аппроксимирующими зависимостями от частоты или скольжения. В основном это касается параметров описывающих свойства магнитопроводов.

Набор условных параметров представляет собой такой набор параметров для идеального электродвигателя, отличие значений которых от реальных значений этих параметров, на сколько это возможно, позволяет учесть все потери, искажающие реальную характеристику электродвигателя. Например, в предлагаемой системе параметров сопротивление статора представляет собой величину, такого активного сопротивления, которое может служить аналогом сопротивления статора по величине выделяемой на нем мощности. Это приводит к тому, что в системе условных параметров этот параметр несколько выше, чем его реальное значение. Разница включает в себя все потери мощности в магнитной системе.

Электромеханический момент, развиваемый на валу электродвигателя, согласно /2/ определяется, для всех его видов, по зависимости (1), которая и должна стать главной аппроксимирующей зависимостью:

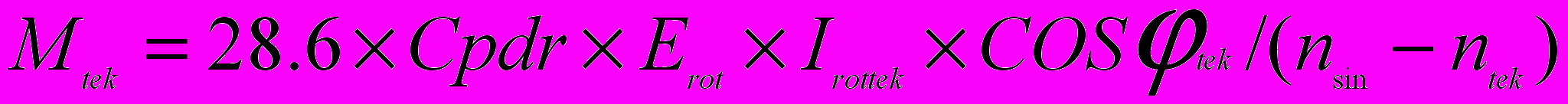(1)

Где

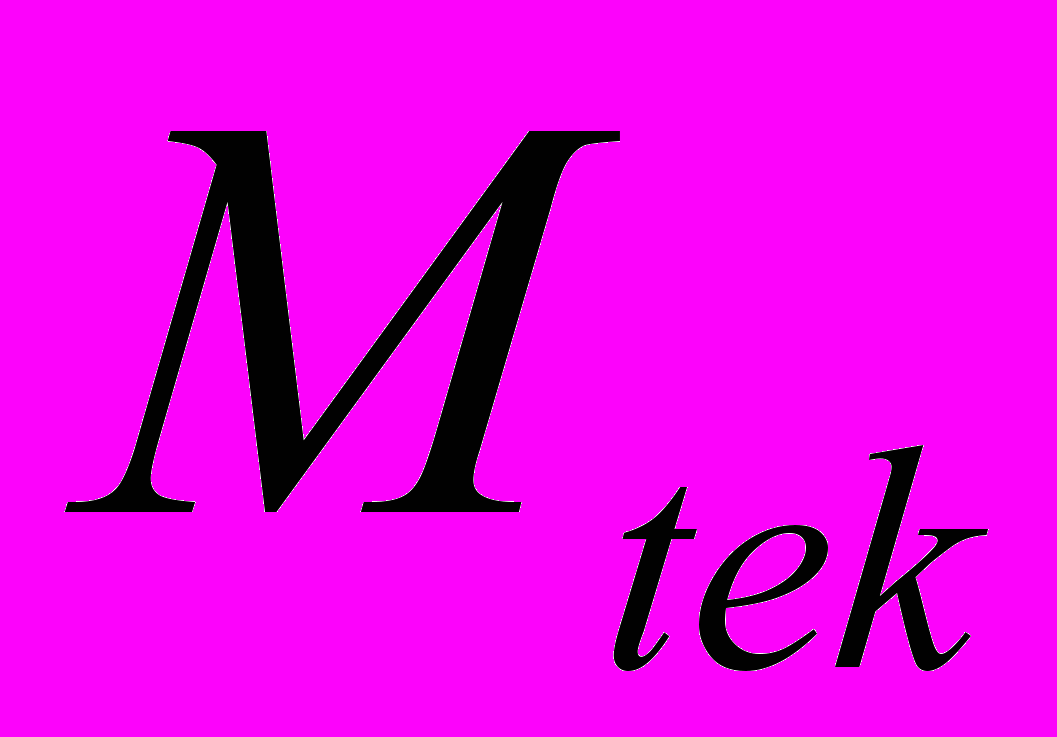- текущий момент, развиваемый электродвигателем

- напряжение на роторных обмотках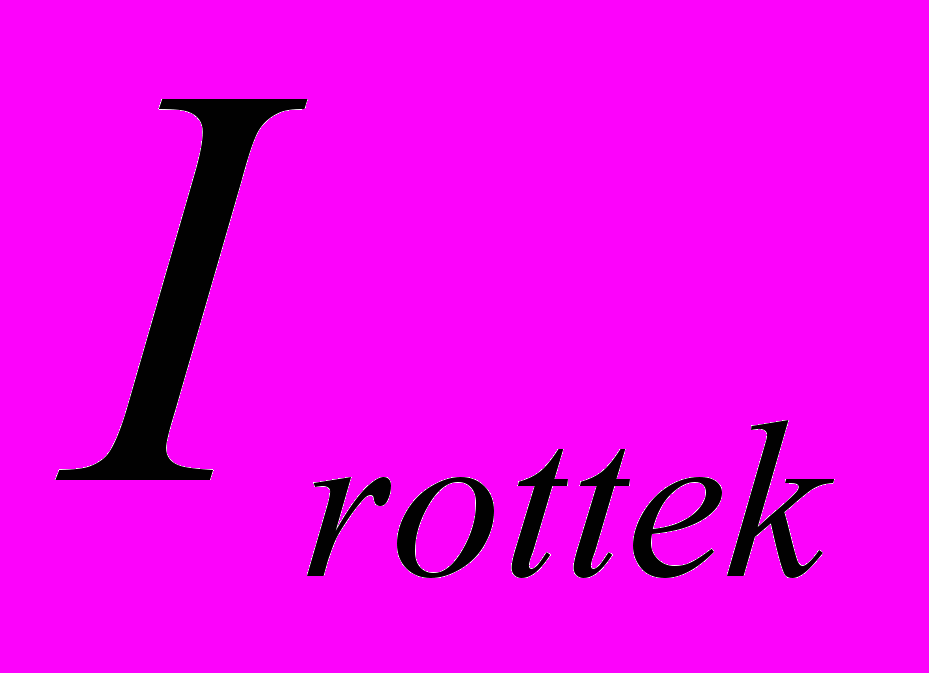

- текущее значение тока ротора

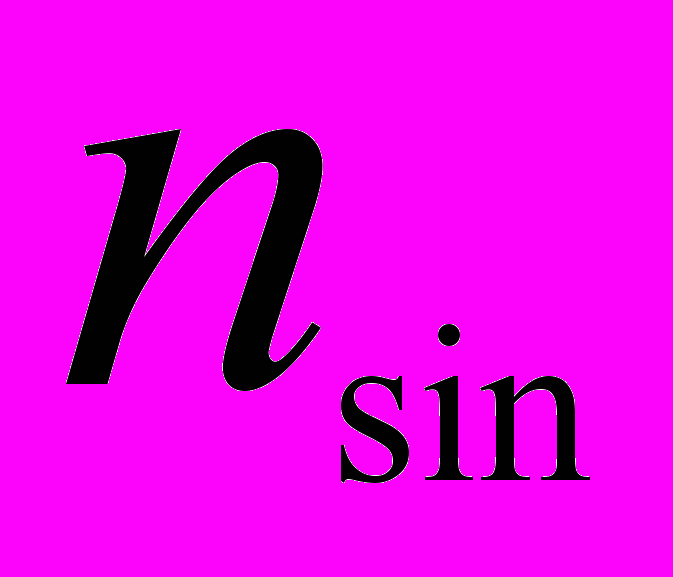- синхронная частота вращения ротора для текущей частоты

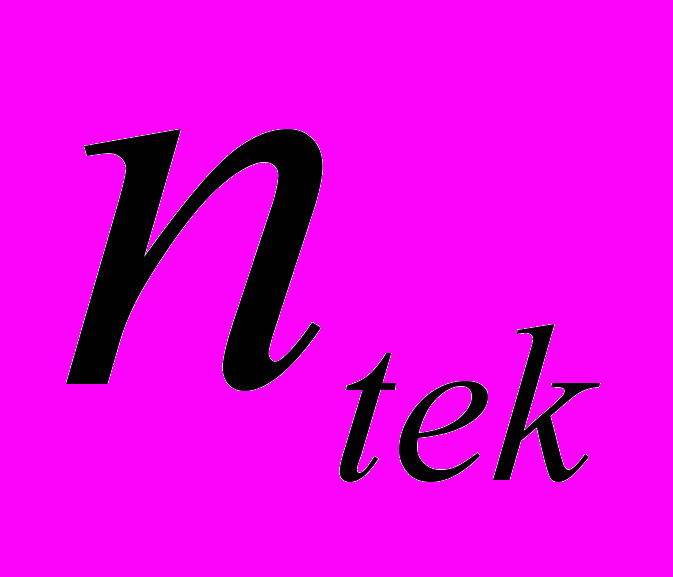- текущее значение частоты вращения ротора

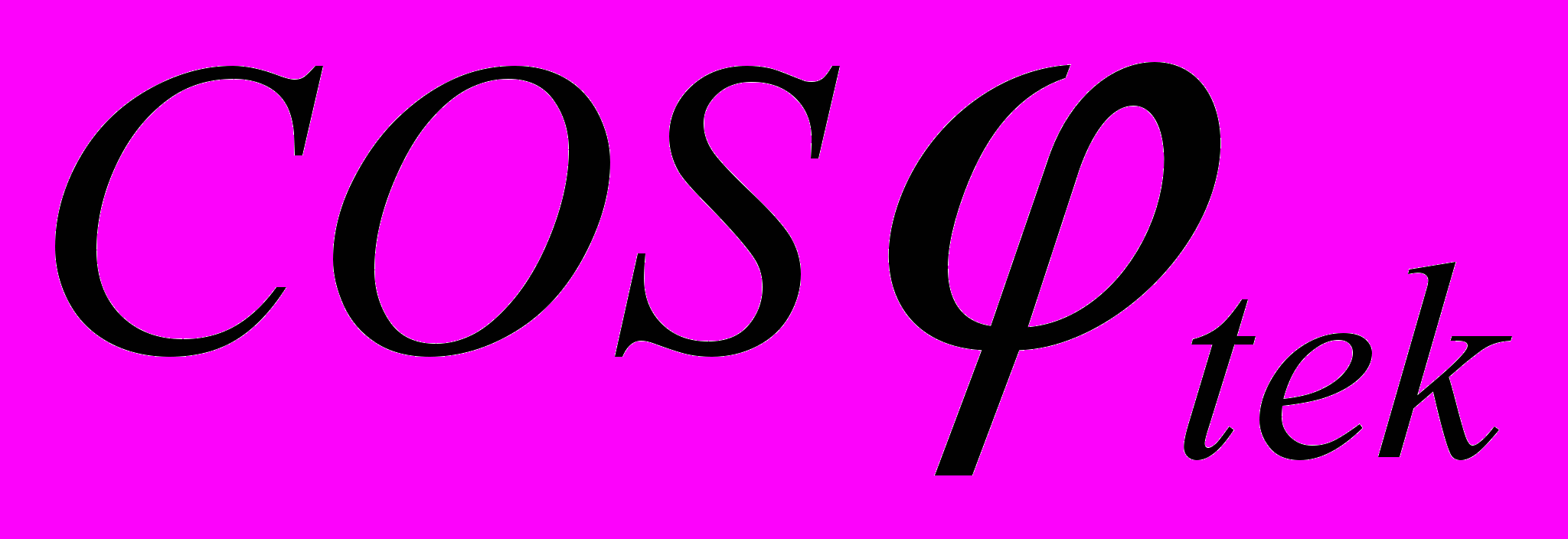- текущее значение коэффициента мощности роторной цепи

Текущее значение полного тока ротора определяется по 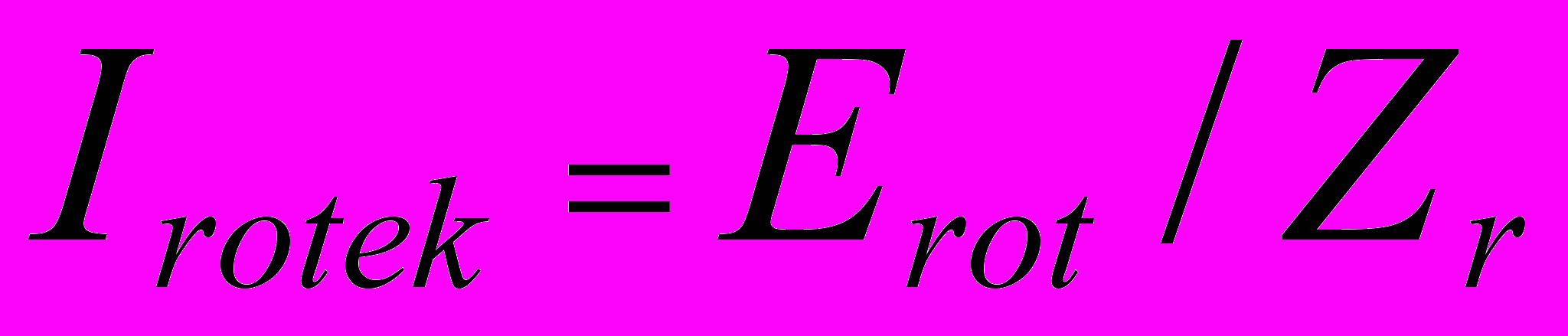(2)

(2)

Где

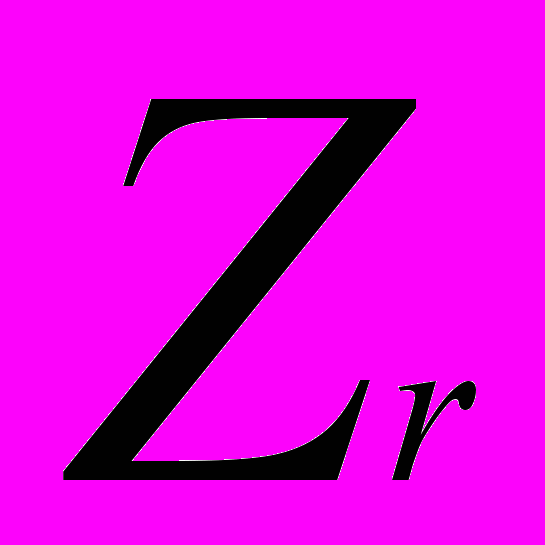- значение полного сопротивления роторной цепи

Значение полного сопротивления ротора зависит от значений его активной и реактивной составляющих. Учитывая то, что к непубликуемым параметрам электродвигателя относятся практически все параметры, характеризующие магнитные свойства электродвигателя, в качестве введенных в систему условных параметров принято соотношение между реактивной и активной составляющими полного сопротивления ротора

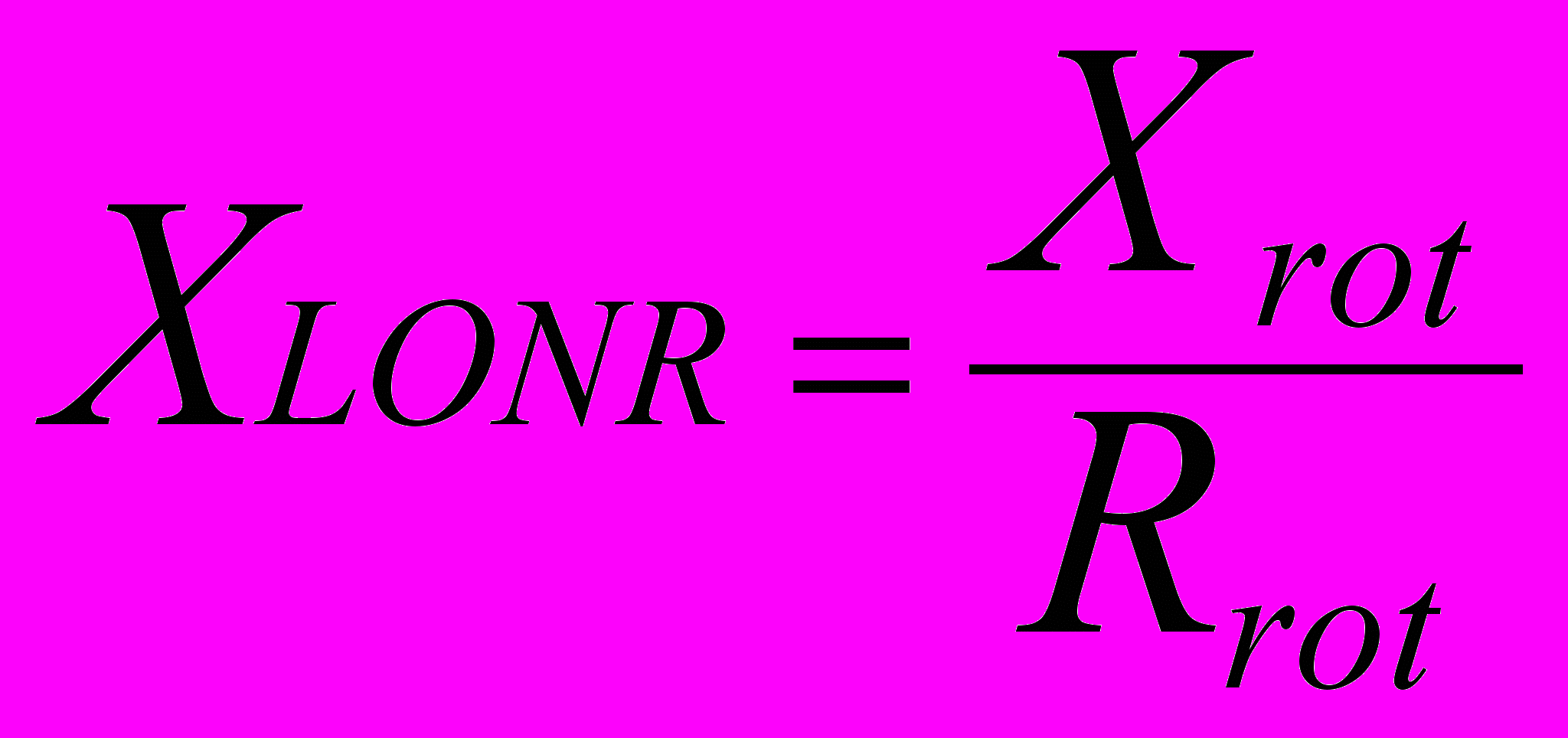(3)

Где

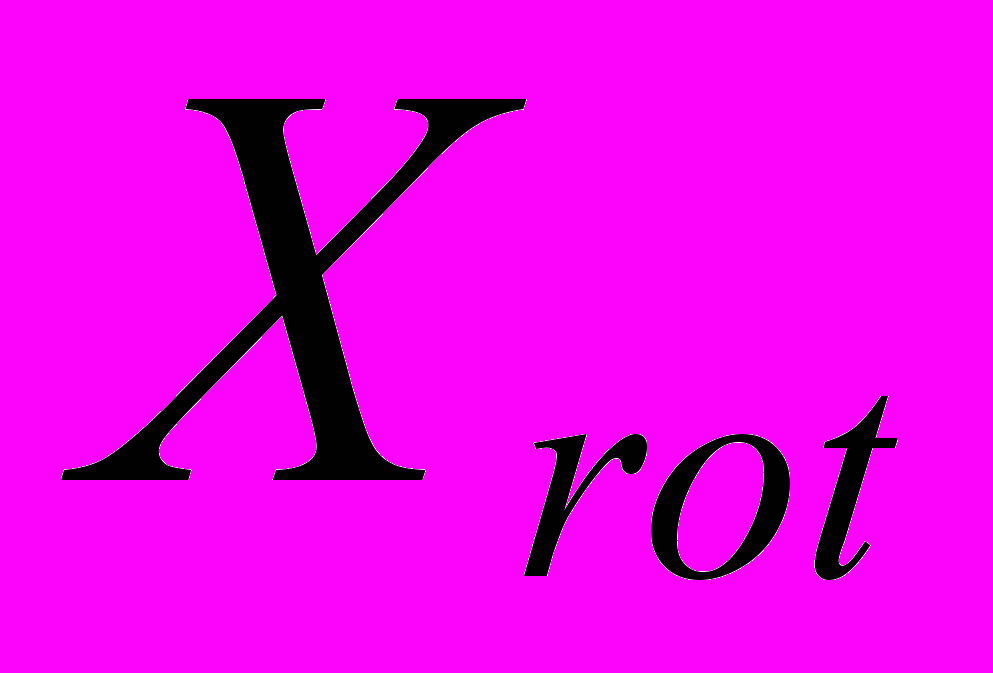- значение реактивной составляющей сопротивления роторной цепи

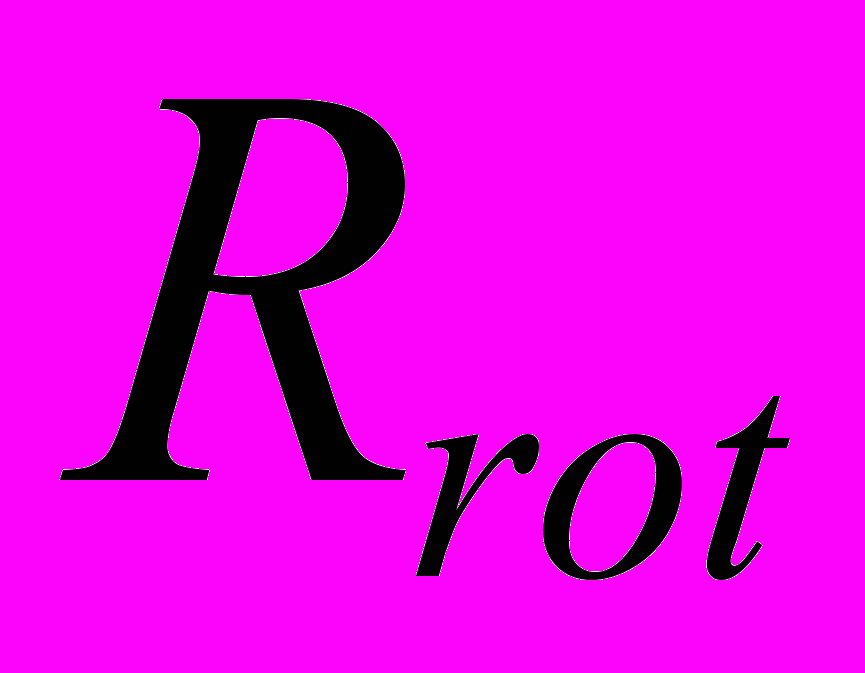- значение активной составляющей сопротивления роторной цепи

и Kpaz – коэффициент, учитывающий влияние эффекта вытеснения тока из паза. Введение этих коэффициентов позволит ввести в формулу (1) зависимость параметров электродвигателя от скольжения.

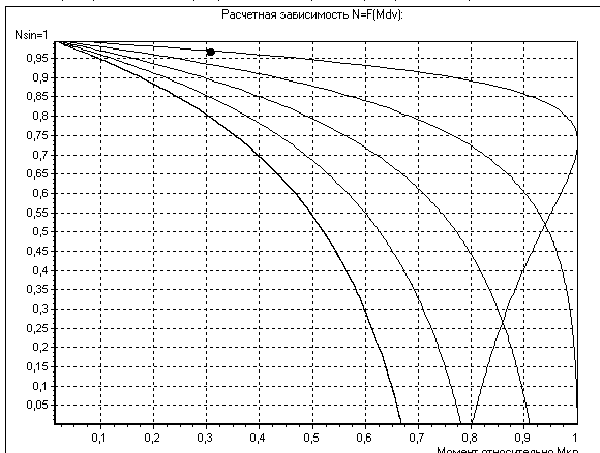
На рисунке 1 показано влияние параметра XLONR на кривизну характеристики

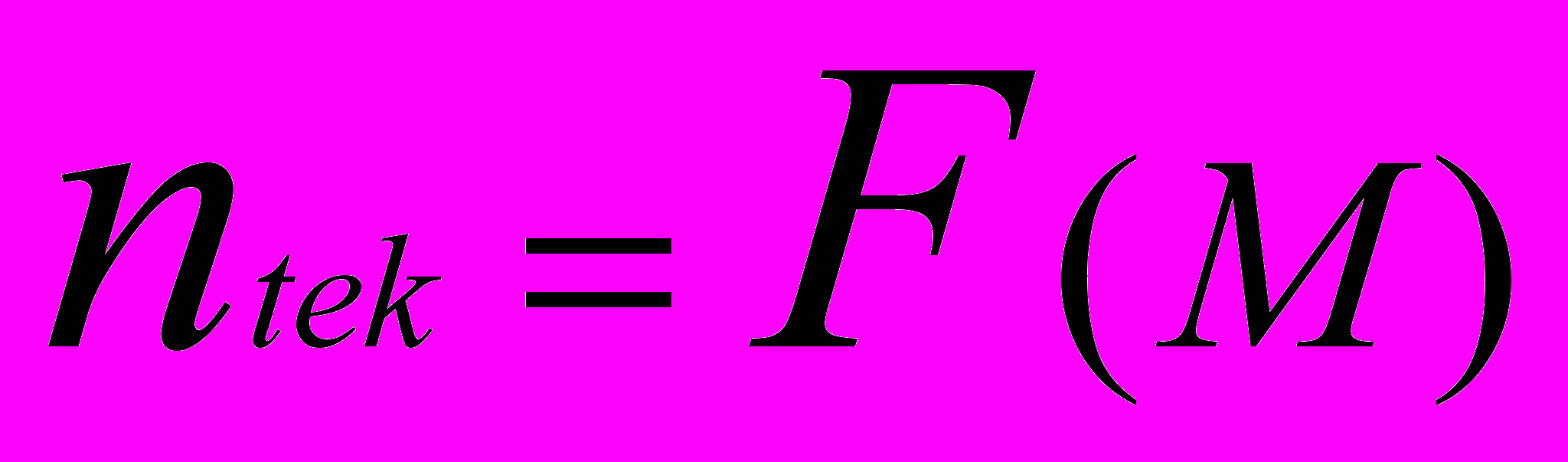. Реально изменением этого соотношения пользовались всегда, включая, на время пуска, в роторную цепь электродвигателя пусковые сопротивления. Зная из каталога параметры рабочей точки и значение критического момента, можно подобрать такое соотношение индуктивного и активного сопротивлений, которое позволяет получить нужную форму характеристики в зоне относительно больших скоростей.

На величину пускового момента оказывает большое влияние изменение активной и реактивной составляющих сопротивления ротора в связи с изменением частоты протекающего по нему тока. Это изменение наиболее заметно при большой величине скольжении, когда частота протекающего по ротору тока соизмерима с частотой питающего напряжения. В модель введен эмпирический коэффициент Kpaz, описывающий изменение активной составляющей сопротивления ротора в зависимости от частоты протекающего по нему тока. В первом приближении этот эффект подобен эффекту вытеснения тока из проводника на высоких частотах (Скин эффекту).

Рабочая точка

XLONR=0.1093

XLONR=0.05465

XLONR=0.0364

XLONR=0.02732

XLONR=0.02186

Рис.1. Влияние XLONR на кривизну характеристики электродвигателя. По оси Х отложен момент на валу электродвигателя (Мкрит=1)

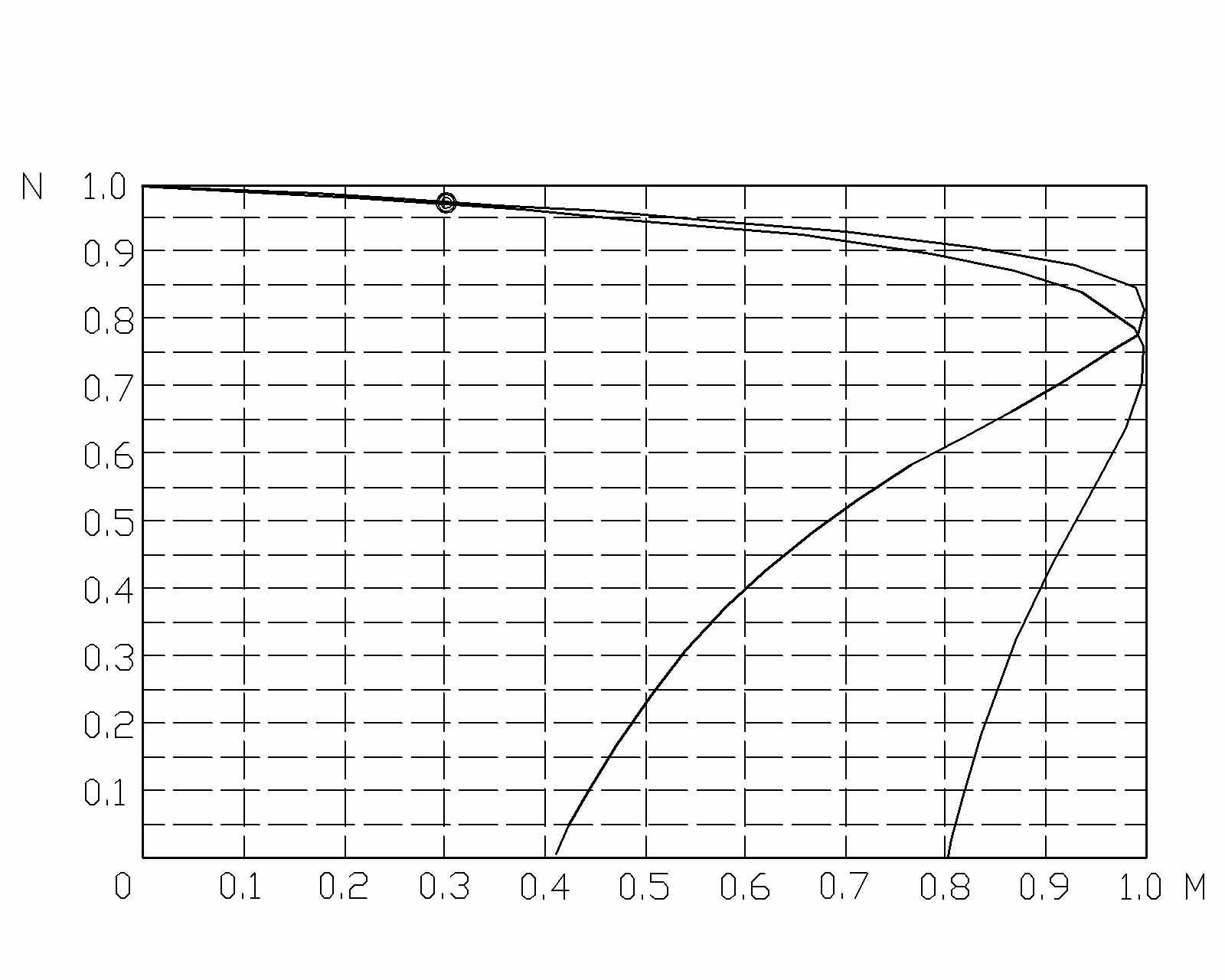
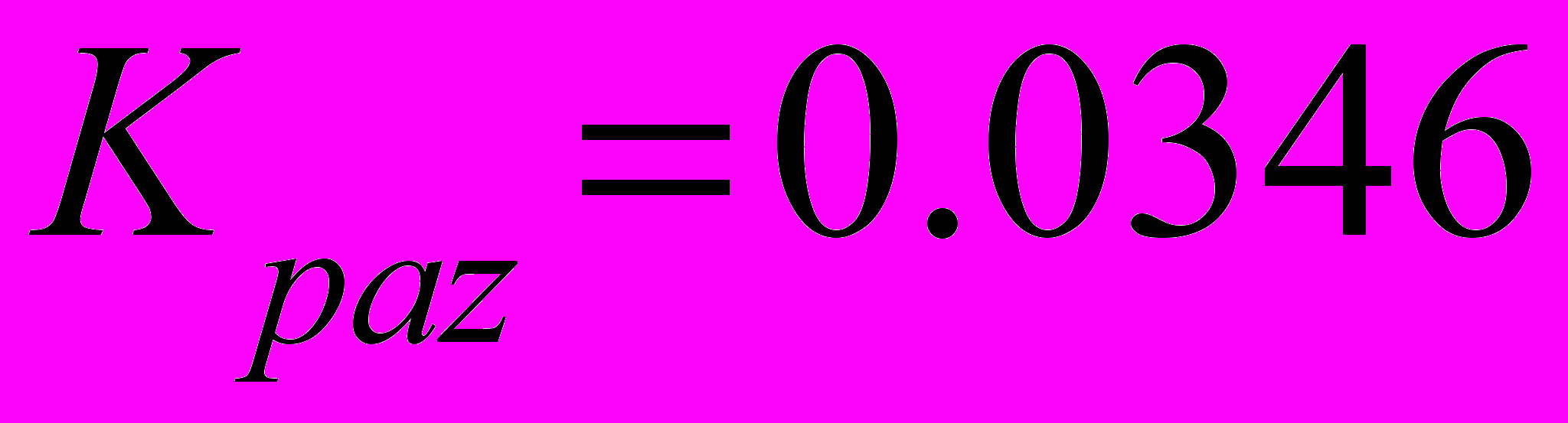
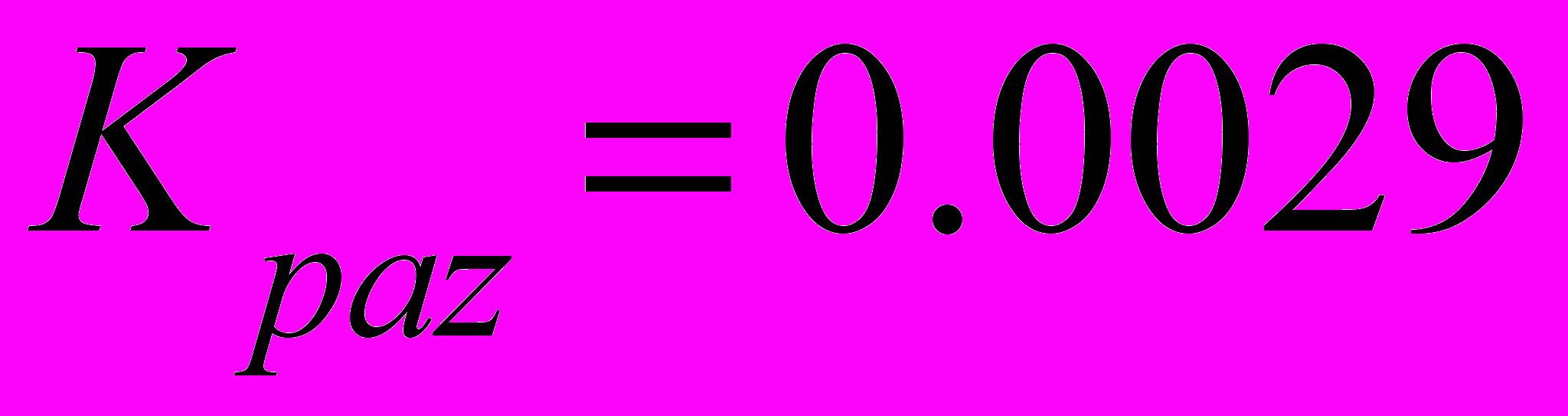
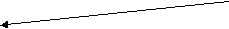
Рис.2. Влияние пазового коэффициента на величину пускового момента (XLONR=0.11)

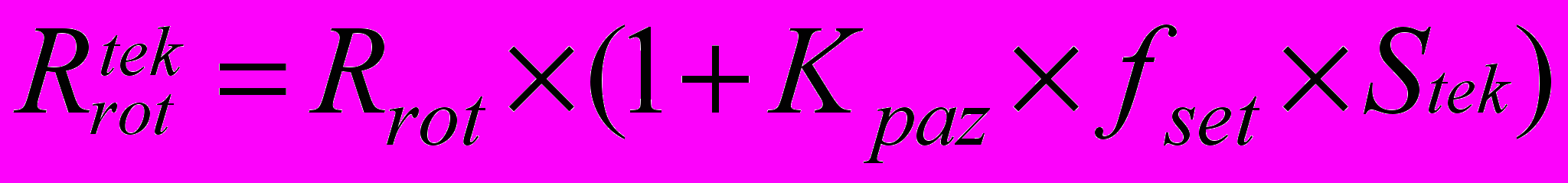(4)

Где

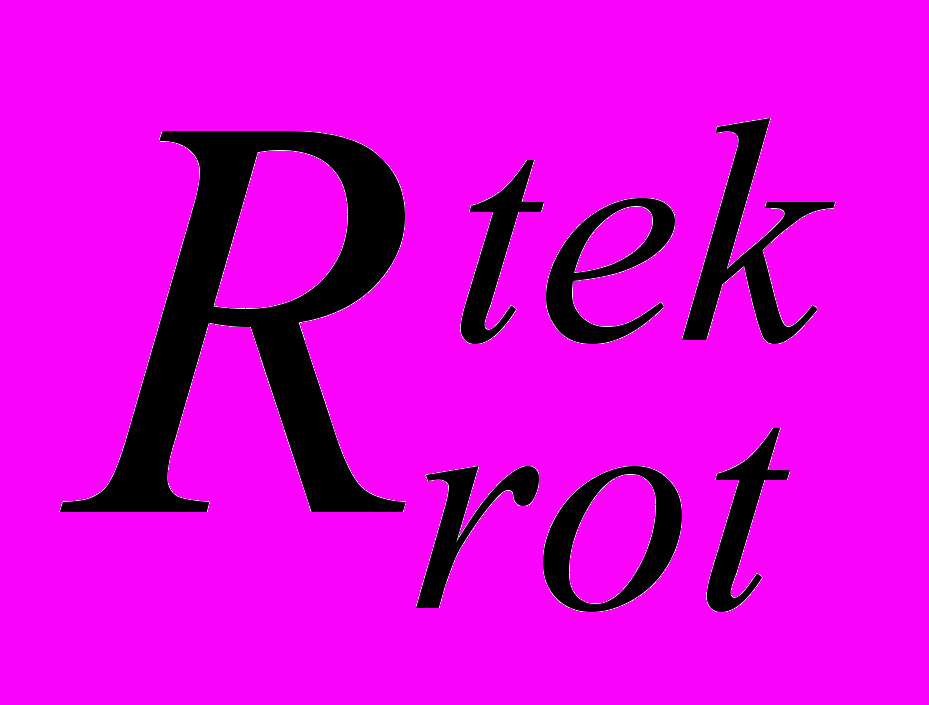- текущее значение активной составляющей сопротивления роторной цепи

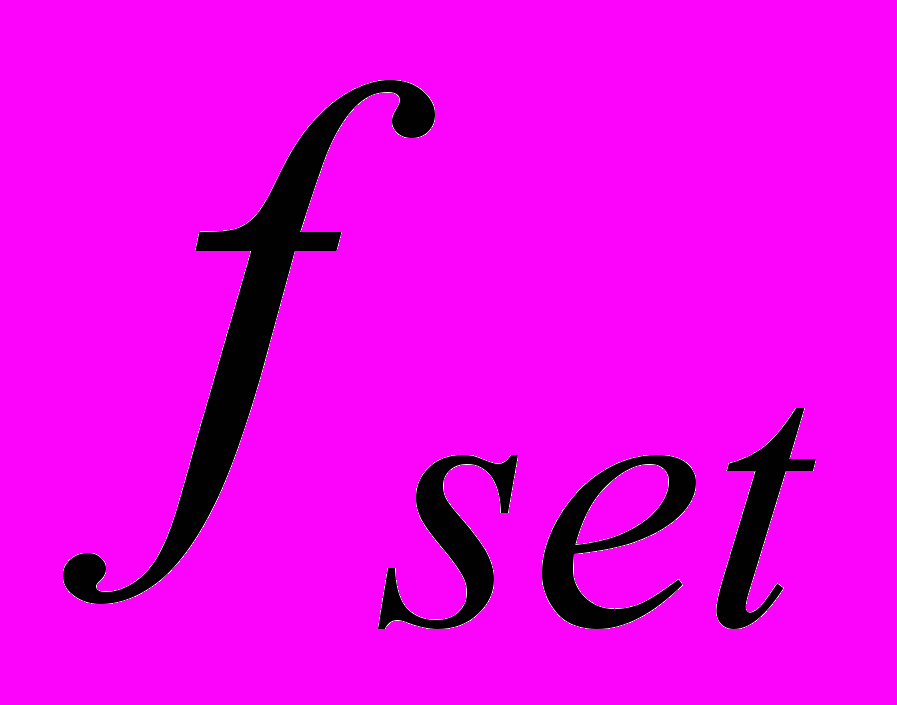- частота питающей сети

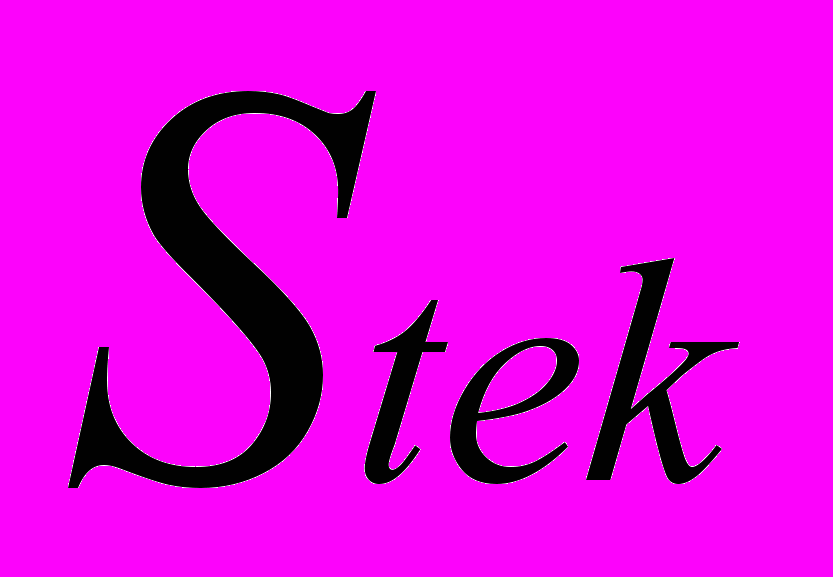- текущее значение скольжения

В каталогах электродвигателей, в большинстве случаев, указано значение пускового момента. Знание этой точки дает возможность подобрать такое значение Kpaz, которое, наряду с правильно подобранным значением XLONR, позволяет получить форму характеристики электродвигателя адекватную реальной.

При отсутствии данных о пусковом моменте подбор Kpaz возможен, если известны значения для нескольких рабочих точек. В каталогах кранового оборудования принято давать значения параметров для 4-х или 5-ти режимов работы электродвигателя.

Проверка характеристики показала, что полученная методика очень хорошо согласуется с практикой в зоне стандартной частоты, но дает отклонения в сторону завышения момента в зоне низких частот. Это объясняется тем, что модель не учитывает реальные магнитные параметры, а в зоне низких частот их влияние на форму характеристики усиливается. Для компенсации отмеченного, в формулу момента модели введен понижающий эмпирический коэффициент:

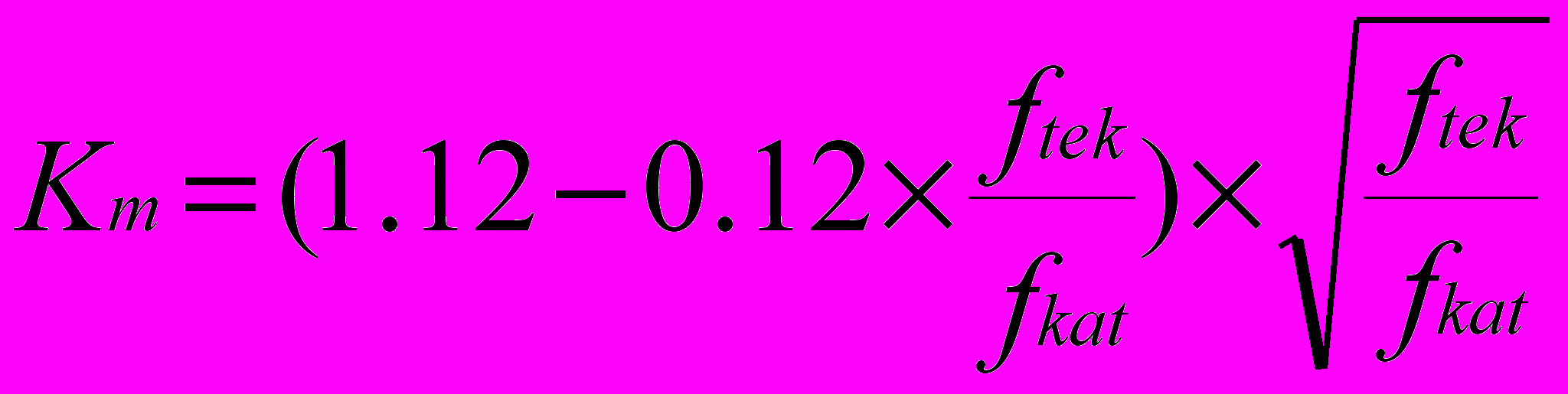(5)

Где

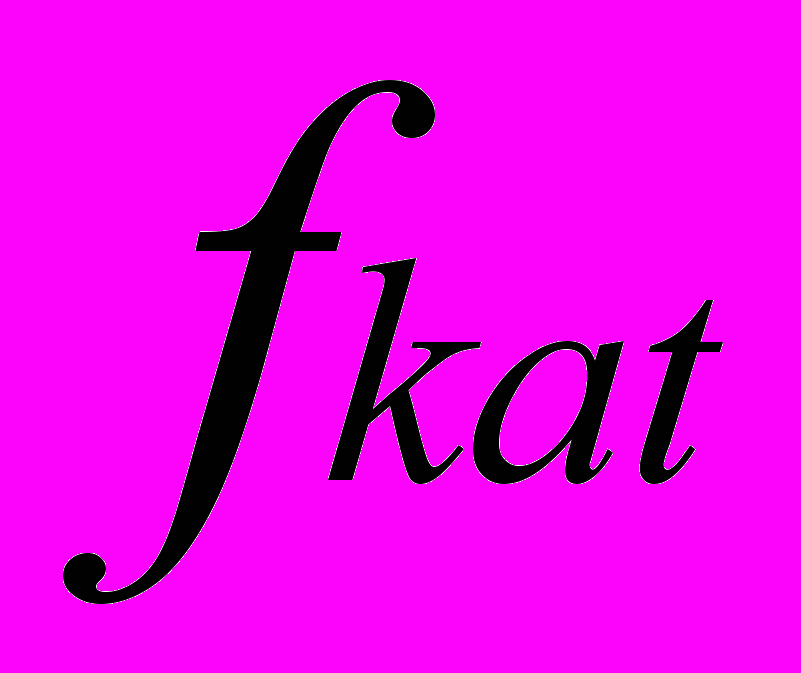- каталожное значение частоты питающей сети

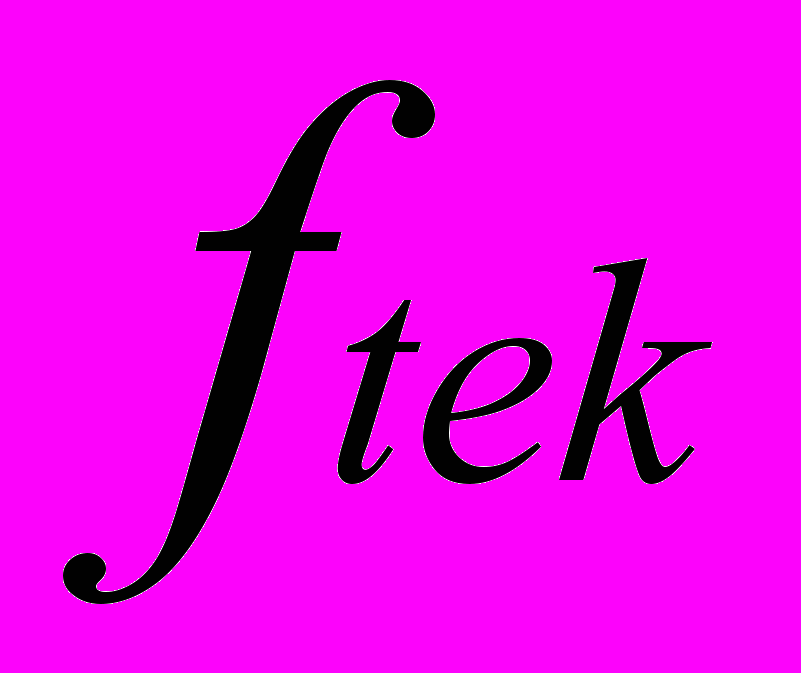- текущее значение частоты питающей сети

Получив правильное описание характеристики электродвигателя, мы получаем гарантию того, что потери, рассчитанные в конкретном режиме, будут достаточно точно соответствовать реальности.

Для выделения мощности потерь введен параметр «коэффициент полезного действия ротора», который определяется по (6), как отношение значений моментов, рассчитанных по значениям механических и электрических параметров, по формуле (1) и по известной зависимости (7) из каталожных значений скорости и мощности.

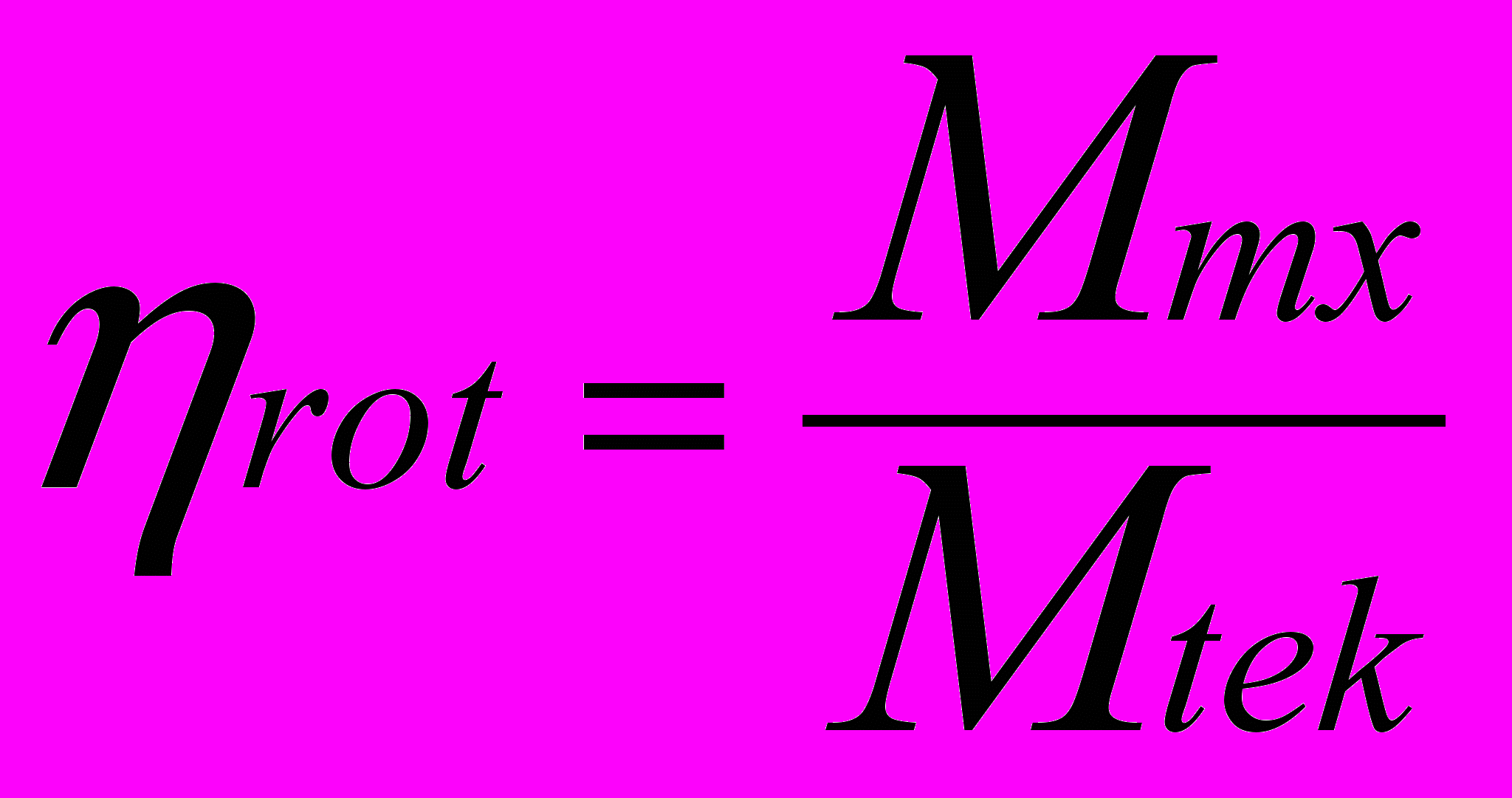(6)

Где

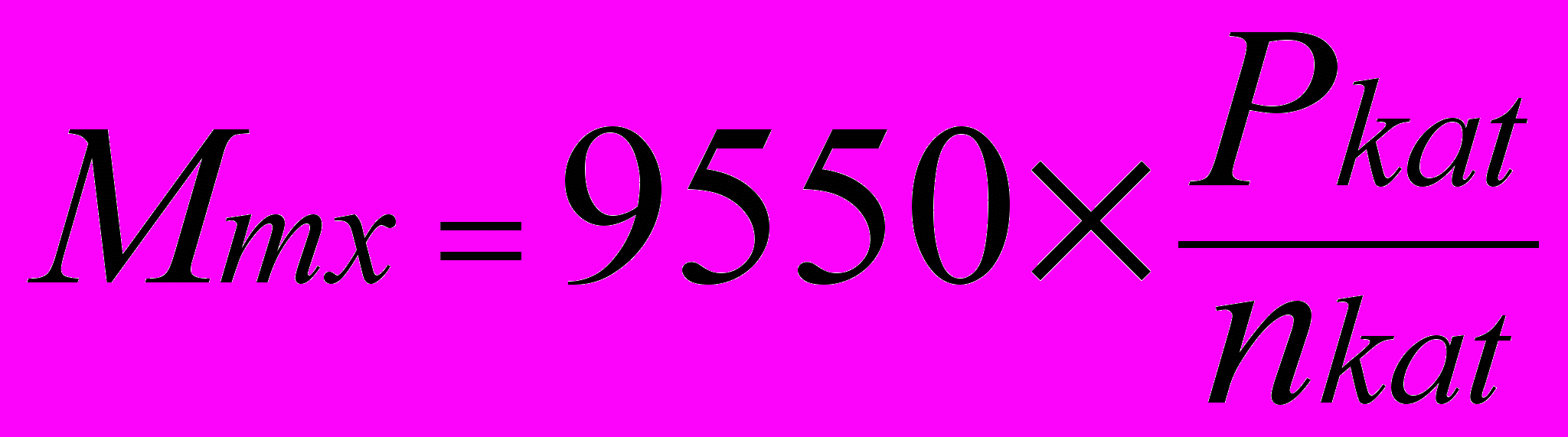(7)

В процессе расчета текущей рабочей точки, знание этого коэффициента позволяет выделить полезную (механическую) составляющую мощности и, соответственно, мощность потерь.

Для учета влияния скорости вращения ротора на теплообмен применена зависимость (8). Она выведена из условия применения модели тепломассобмена при обтекании плоской пластины турбулентным потоком. Использовалось допущение, что скорость и количество охлаждающего воздуха находятся в прямой зависимости от скорости вращения ротора электродвигателя /4/.

( 8 )

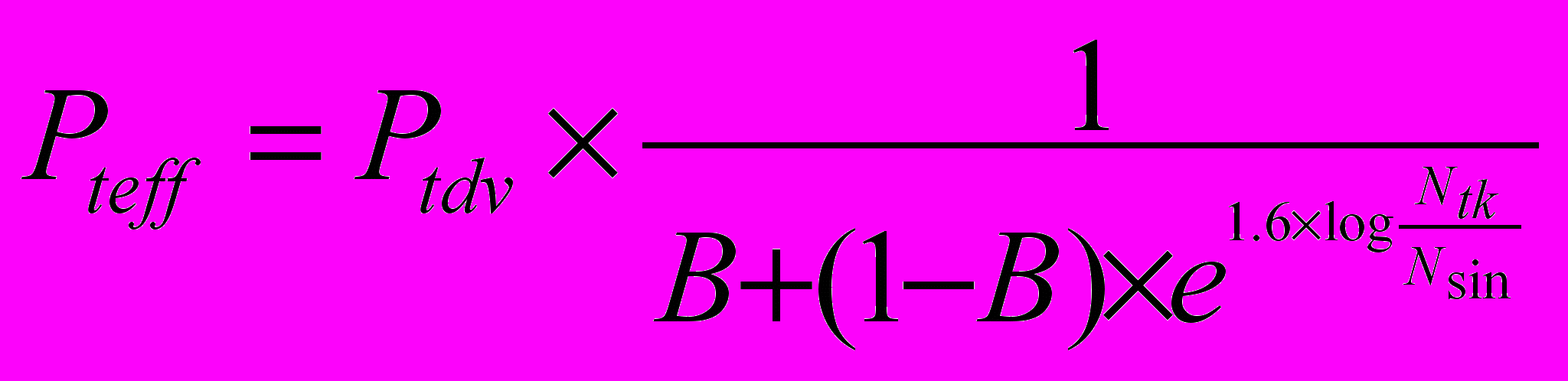
Где

Pteff - эффективное тепловыделение электродвигателя при данном режиме,

Ptdv - расчетное значение мощности тепловыделения, равное разности значений механической и электрической мощностей, рассчитанных при данном режиме работы электродвигателя,

В - доля теплосъема, которая не зависит от скорости вращения ротора.

ntk - текущая частота вращения ротора

nsin - каталожное значение синхронной скорости вращения ротора.

Значения, рассчитанные с учетом зависимости (8), хорошо согласуются с данными многих производителей электроприводов и теорией. Значение В, для большинства крановых электродвигателей переменного тока, согласно /3/ таблица 14-2, составляет 0.45.

Программа для расчета условных параметров XLONR и Kpaz

и получения нестандартных характеристик электродвигателя.

На рисунке 3 представлен алгоритм расчета условных параметров XLONR и Kpaz. Предварительно обрабатываются данные рабочего режима, представленного в каталоге или на табличке электродвигателя. В основной части программы, численным методом, ведется подбор параметров XLONR и Kpaz.

В схеме алгоритма приняты следующие обозначения:

OMMO – текущее значение соотношения между пусковым и критическим значениями момента (используется для сравнения с заданным значением)

OMMOZ – заданное значение соотношения между пусковым и критическим значениями момента (задано из каталога)

dn – приращение скорости при расчете характеристики электродвигателя.

ns – значение синхронной скорости (задано числом полюсов и частотой питающей сети)

nt – текущее значение скорости

Ax – переменная для сохранения значения XLONR прошлого цикла

Ao – переменная для сохранения значения OMMO прошлого цикла

TM – значение точности до которого ведется подгонка параметра

Mt – текущее значение момента

Mmax – максимальное значение момента (используется для сравнения со значением критического момента)

Mkr – значение критического момента (задано из каталога)

SMI (Mt, nt) – процедура расчета текущих значений момента, скорости и прочих параметров построенная на предлагаемой модели.

Подгонка искомых параметров производится численным методом. Начальные значения искомых параметров вводятся в начале алгоритма. Для каждой пары искомых параметров просчитывается характеристика электродвигателя, после сравнения полученного значения максимального момента с заданным значением критического момента исправляется значение XLONR, и характеристика строится заново. После достижения заданной точности определяется отношение пускового и критического моментов, по которому вводятся коррективы в значение Kpaz, его подгонка также ведется до достижения заданной точности отношения OMMO.

После получения значений искомых параметров на экран выводится характеристика электродвигателя. Полученный набор параметров электродвигателя может быть записан в базу данных для его использования при расчете нестандартных характеристик. В частности, для проверки возможности запуска электродвигателя от частотного преобразователя имеется возможность ввода внешних параметров и получения на экране семейства характеристик для различных частот, напряжений и внешних сопротивлений.

После расчета выводятся значения максимальных значений токов статора и пусковых моментов для проверки возможности использования конкретного частотного преобразователя и возможности преодоления механизмом стартового момента сопротивления.

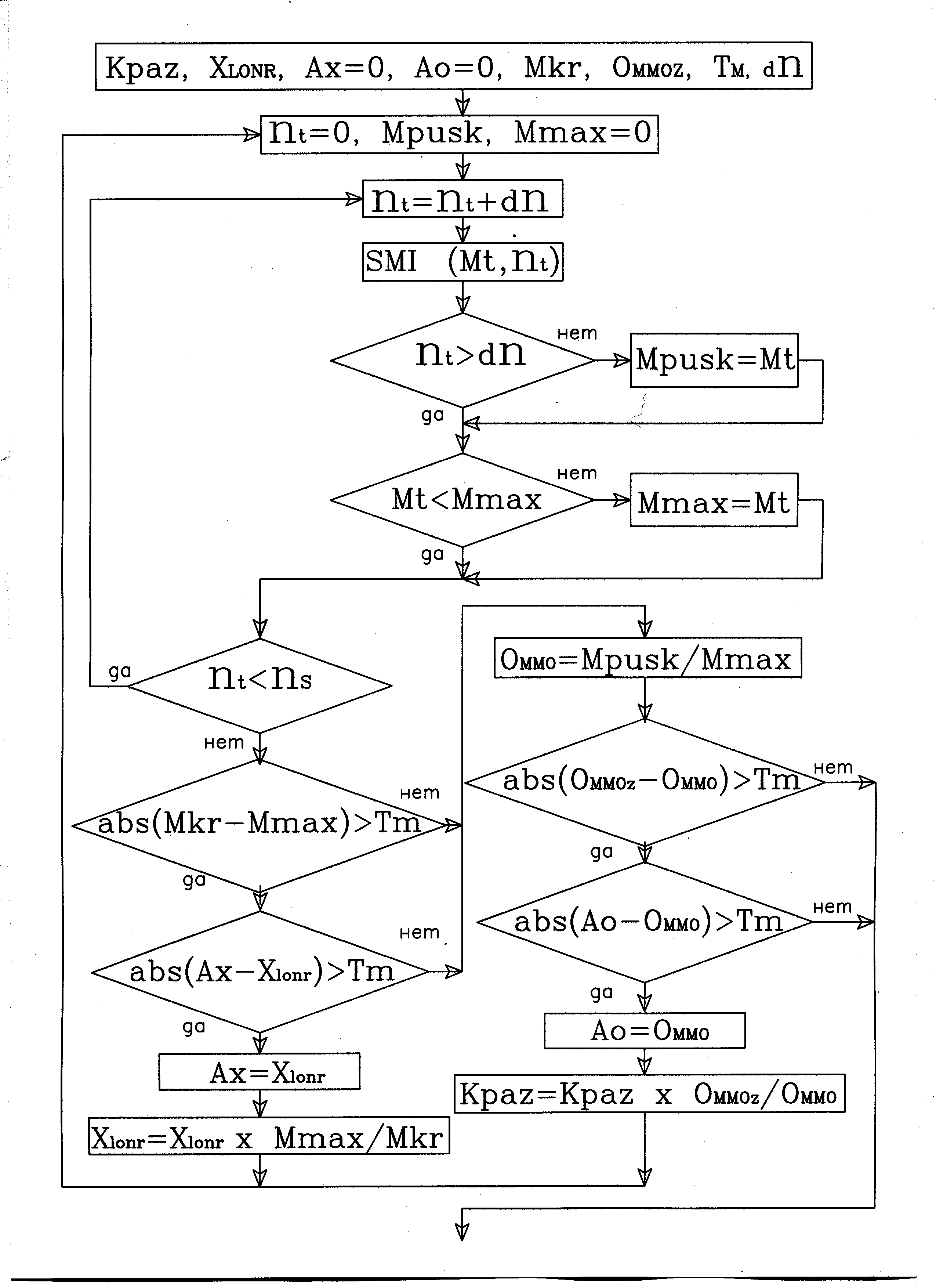
Рис.3. Алгоритм расчета условных параметров XLONR и Kpaz.

Анализ точности получаемых результатов

С целью проверки полученной модели было проведено сравнение каталожных данных на серию крановых электродвигателей /5/ с данными, полученными с применением предлагаемой модели. Для каждого двигателя строилась его характеристика, и определялось среднеквадратичное отклонение каталожных данных от нее. Результаты сравнения представлены в таблице 1

Анализ полученных погрешностей показал их хорошее подчинение нормальному распределению, что видно на рис.4.

Наибольшая ошибка совпадения была получена при обработке данных электродвигателя MTH312-6. На рисунке 5 показано взаимное положение каталожных значений (треугольники) и кривой, рассчитанной по предлагаемой модели в предположении, что частота сети равна строго 50Гц (гладкая кривая). Разброс точек составил +0,5%  -0,58% по скорости, что соответствует /6/, но выглядит разброс, как регулярное отклонение.

Таблица 1.

N	Двигатель	Ошибка	N	Двигатель	Ошибка	N	Двигатель	Ошибка
1	MTF011-6	0,033	15	MTKF012-6	0,056	29	MTH211-6	0,024
2	MTF012-6	0,098	16	MTKF111-6	0,065	30	MTH311-6	0,086
3	MTF111-6	0,077	17	MTKF112-6	0,088	31	MTH312-6	0,126
4	MTF112-6	0,064	18	MTKF211-6	0,062	32	MTH411-6	0,043
5	MTF211-6	0,046	19	MTKF311-6	0,049	33	MTH412-6	0,071
6	MTF311-6	0,041	20	MTKF312-6	0,029	34	MTH311-8	0,048
7	MTF312-6	0,095	21	MTKF411-6	0,032	35	MTH312-8	0,109
8	MTF411-6	0,077	22	MTKF412-6	0,024	36	MTH411-8	0,054
9	MTF412-6	0,025	23	MTKF311-8	0,056	37	MTH512-6	0,049
10	MTF311-8	0,021	24	MTKF312-8	0,045	38	MTH512-8	0,071
11	MTF312-8	0,080	25	MTKF411-8	0,059	39	MTH612-6	0,089
12	MTF411-8	0,075	26	MTKF412-8	0,047	40	MTH613-6	0,098
13	MTF412-8	0,080	27	MTH111-6	0,062	41	MTH612-10	0,041
14	MTKF011-6	0,065	28	MTH112-6	0,046	42	MTH711-10	0,054
	Среднее относительное отклонение по всей серии двигателей							0,061

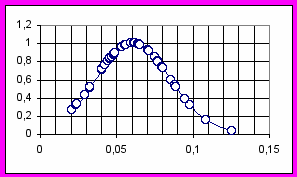
Рис.4. Плотность вероятности величины ошибки.

Согласно /8/, в некоторых случаях допустимо уменьшение частоты питающей сети на 1Гц. Был проведен расчет модельных характеристик рассматриваемого электродвигателя в предположении, что частота сети в момент проведения испытаний составляла 49Гц. На графике это линия с маркерами. Среднеквадратичное отклонение каталожных данных от линии соответствующей 49Гц составило 0,022.

Согласно /7/ скольжение определяется стробоскопом с питанием его лампы от общей, со статором двигателя, сети. Допустимо измерение величины скольжения проводить либо с помощью индуктивной катушки, размещенной около торца электродвигателя, либо прямым измерением частоты в цепи ротора (при испытании электродвигателя с фазным ротором).

Согласно /6/ точность измерения величины скольжения должна быть не хуже 20% (до величины скольжения 0,06). Допустимо измерение скольжения через измерение величины частоты вращения ротора, которая должна измеряться с точностью не хуже 0,5%, что дает те же 20% погрешности при определении величины скольжения.

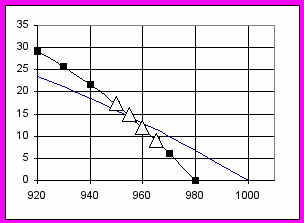
Рис.5. Расчетные кривые и данные каталога для электродвигателя MTH312-6.

(По оси Х – частота вращения об/мин, по оси Y - мощность квт)

Влияние остальных ошибок, определенных /6/, на точность получаемых результатов не велико. Допустимая ошибка измерения момента, при использовании динамометра, и мощности составляет 1%.Согласно /7/ при невозможности использования динамометра значение момента определяется через измерение подводимой мощности и мощностей потерь в контурах ротора, в стали и механических. Из полученных значений, пересчетом, получают значение полезной мощности. А из него и измеренного значения частоты вращения ротора получают значение момента, что уже дает примерно3% ошибки. В /5/ указано, что ряд параметров реальных двигателей могут отличаться от каталожных значений на 5%.

Из приведенного анализа можно сделать вывод, что главная составляющая получаемой ошибки заключается в неточностях при экспериментальном определении величины скольжения. Эту неточность можно было бы уменьшить при условии, что для всех электродвигателей опубликованы значения нескольких рабочих точек.

В противном случае имеет смысл признать, что с доверительной вероятностью 0,9 ошибка метода составляет 1,282 * 6,1% = 7,82% где 1,282 – квантиль нормированного нормального распределения для уровня доверительной вероятности 0,9.

При отработке представленной модели, подготовлена программа для расчета набора условных параметров электродвигателя по данным стандартных каталогов, которая, в настоящее время, позволяет рассчитать параметры реального электродвигателя при его работе с частотным преобразователем в пусковом, самом сложном для расчета режиме. Интерфейс этой программы представлен на рисунке 6.

Эта программа уже использовалась на практике. При запуске в работу штыревого крана, использующего для управления механизмом передвижения крана частотный электропривод на базе преобразователя фирмы SIEMENS и крановые электродвигатели, выявилась невозможность правильно рассчитать необходимую мощность электродвигателей для частотного привода с помощью общепринятых методик. Согласно стандартному расчету, на механизм передвижения крана достаточно установить электродвигатели суммарной мощностью 15 квт, расчетная загрузка такого комплекта составляла 0,8. При опробовании крана выявилось, что такой набор двигателей с большим трудом обеспечивал пуск крана только на ровном рельсе, любое увеличение местного сопротивления передвижению не давало механизму тронуться. Дело в том, что стандартные методики расчета крановых механизмов не учитывают то, что при пуске электродвигателя от магнитного контроллера пусковой момент достигает 2,5 крат от номинального момента, а при частотном пуске такое увеличение пускового момента вызывает недопустимо большую токовую перегрузку и двигателя и преобразователя. Причем, электродвигатели крановых серий (4МТ…) позволяют большее увеличение пускового момента в зоне малых частот, чем общепромышленные (АИР…). Это было проверено на практике и хорошо было видно при расчете пускового режима с помощью предлагаемой модели.

Расчет показал, что, находясь на рельсовом стыке, кран стронется с места при токе преобразователя 144А. Реально пусковой ток оказался равным 112 – 136А. Разница может быть объяснена как неточностями модели, так и неточностями расчета момента сопротивления и отличием реальной формы рельсового стыка от теоретической, принятой в расчете.

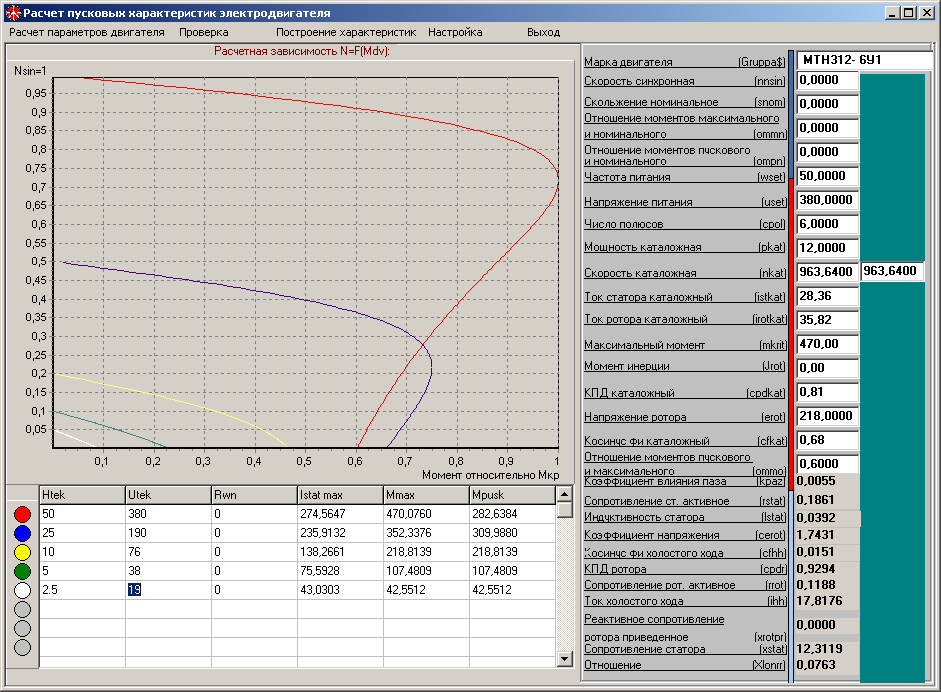
Рис.6 Интерфейс программы расчета условных параметров.

Заключение

Полученная математическая модель может быть использована при расчетах режимов электродвигателей с помощью ЭВМ. Процедура, основанная на этой модели, использована в разрабатываемой программе для определения загрузки электродвигателя в реальном рабочем цикле. Эта программа, будучи включенной в математическую модель проектируемого механизма, кроме загрузки, позволит получить силовые воздействия на механизм от приводного электродвигателя в каждый текущий момент времени еще на стадии его проектирования.

Применение описанной модели позволит более точно, чем при традиционных методах расчета, еще на стадии проектирования, определять необходимые прочностные и динамические параметры механизма и возможность выполнения им заданных функций, в заданном режиме работы, без его натурного моделирования.

Литература

[1] Вешеневский С.Н. Характеристики двигателей в электроприводе. Изд. 6-е, исправленное. М., Энергия, 1977. 432с. с илл.

[2] Хализев Г.П. Электрический привод. Учебник для техникумов. М.» Высшая школа», 1977. 256с., с илл.

[3] Чиликин М.Г., Ключев М.И., Сандлер А.С. Теория автоматизированного электропривода: учеб. Пособие для вузов. М.Энергия 1979. 616с., с илл.

[4]. А.В. Лыков «Тепломассообмен» (справочник) М. Энергия 1971 560с. с илл.

[5] Двигатели асинхронные трехфазного тока крановые и металлургические. Каталог 01.30.01.-82 (17-78). Информэлектро 1982

[6] ГОСТ 11828-86 [СТ СЭВ 1347-78] Машины электрические вращающиеся. Общие методы испытаний.

[7] ГОСТ 7217-87 [СТ СЭВ 168-85] Машины электрические вращающиеся. Двигатели асинхронные. Методы испытаний.

[8] ГОСТ13109-87 Электрическая энергия. Требования к качеству электрической энергии в электрических сетях общего назначения.

Blog

Сзтм отдел главного конструктора

Содержание