Ительной мере ограничивается недостатками современных методик математического моделирования реальных объектов в условиях фрикционного контактного взаимодействия

Вид материала

Документы

Подобный материал:

• Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
• Аннотация дисциплины «основы математического моделирования», 29.01kb.
• Курс «Основы математического моделирования» реализуется в рамках специальностей 0647, 117.15kb.
• Задачи : 1 дать понятие математической модели, раскрыть суть метода математического, 187.03kb.
• Анализ методик использования моделирования в процессе обучения дошкольников математике, 472.24kb.
• Экзаменационные вопросы по дисциплине «Моделирование социально-экономических процессов», 24.82kb.
• Рабочая программа дисциплины методы построения и анализа сложных математических моделей, 104.9kb.
• Математические модели в иммунологии и вирусологии, 23.06kb.
• Учение студентов основам математического моделирования, необходимых при проектировании,, 28.67kb.
• Рабочая программа учебной дисциплины методы математического моделирования Наименование, 122.11kb.

Использование математического моделирования для определения оптимальных параметров структуры функционально-градиентных металлических систем в условиях трения

Н.О. Кузин

Информационно-вычислительный центр Львовской железной дороги, Львов, Украина

Проектирование новых и широкое внедрение существующих функционально-градиентных материалов для работы в узлах трения в значительной мере ограничивается недостатками современных методик математического моделирования реальных объектов в условиях фрикционного контактного взаимодействия.

Для прикладной трибологии характерно использование постановок контактных задач механики, при котором одно из тел является абсолютно жестким, либо рассмотрение контакта двух однородных и изотропных упругих объектов, что явно не отвечает современным потребностям инженерной практики.

Поэтому разработка методик определения необходимых параметров механических характеристик поверхностных слоев деталей узлов трения, а также условий их сопряжения для обеспечения заданных эксплуатационных свойств всего узла трения является актуальной научной проблемой.

С позиций математического и компьютерного моделирования такой класс задач относится к обратным задачам механики деформируемого твердого тела, которые в общем случае могут быть некорректными, нелинейными и не иметь единственного решения.

В случае учета только силовой составляющей фрикционного взаимодействия в области упругого нагружения задачу оптимального проектирования трибологической системы в работе сформулировали в следующем виде. Рассматривали контактное взаимодействие координатно-неоднородных упругих тел с учетом возможности появления в них релаксационных процессов [1], которые описываются следующим набором механических характеристик {E_i, μ_i, Α_i, Β_i, C_i, Τ_i}, где E_i, μ_i - упругие характеристики, Α_i, Β_i, C_i - характеристики релаксационных процессов, Τ_i - прочностные характеристики тел, i=1,2. Отметим, что учет релаксационных процессов при упругом нагружении особенно актуален при напряжениях, уровень которых находится выше предела пропорциональности.

Примем, что в результате силовой нагрузки в обоих телах проходят процессы разупрочнения материала, которые описываются уравнением:

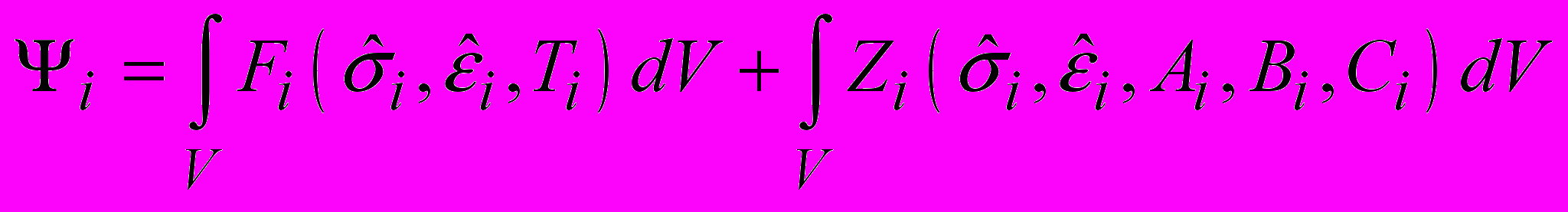. (1)

Первая составляющая выражения (1) соответствует классическим теориям прочности твердых тел (в зависимости от конкретизации функции F_i это может быть 1-4 теория прочности); второе слагаемое учитывает тот факт, что даже во время упругих нагрузок часть энергии, которая передается телу, расходуется на процессы разупрочнения, которые можно трактовать как образование повреждаемости. При этом общая величина накопления деградационных характеристик в обоих телах равна:

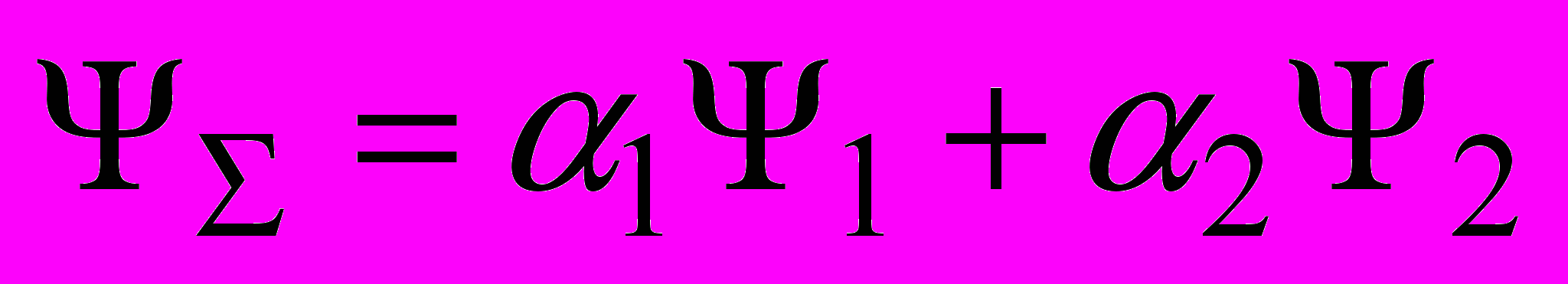, (2)

где α_i – коэффициент учета «важности» тел в паре трения.

Вариационную постановку задачи нахождения оптимальных параметров строение металлических систем представим в следующем виде: необходимо определить такие функции, характеризующие механические свойства тел, которые минимизируют функционал (2), при заданной силовой нагрузке.

Рассмотренные в работе подходы позволили предложить пути увеличения долговечности узлов трения рациональным выбором параметров структуры тел сопряжения, который обеспечивает не только повышение контактной прочности поверхностных слоев, но и их долговечности за счет реализации целенаправленных диффузионных потоков, при залечивании зон повреждений [2].


1. Бурак Я., Кузін М. Побудова математичної моделі механіки металічних пружних систем з врахуванням дисипативних процесів // Машинознавство. – 2008. – № 10. – c. 8-11.

2. Кузін М.О. Використання підходів термодинаміки для континуального опису зміни довговічності металічних систем в умовах зовнішніх навантажень //Поліграфія та видавнича справа. – 2010. - № 2 (52). – с. 123 – 130.