Методы и программные средства повышения эффективности распознавания групп звезд в автономной астронавигации

Вид материала

Автореферат

Содержание Общая характеристика работы Объектом исследования Целью диссертационной работы Методы исследования На защиту выносятся Достоверность научных результатов Научная новизна Практическая значимость Реализация результатов Апробация работы Структура и объем работы Содержание работы Примечание – Цифрами помечено: 1 – участок звездного неба, 2 – оптическая система, 3-фоточувствительная матрица, 4 – вычислитель Во второй главе Метод, основанный на критерии постоянства взаимных угловых расстояний. Непараметрический алгоритм предварительной селекции. Параметрический алгоритм предварительной селекции. Алгоритм, основанный на близости скоростей движения проекций. Основные результаты диссертационной работы Список работ, опубликованных по теме диссертации ... Полное содержание

Подобный материал:

• Генераторы стратегий управления (гсу) программные средства, предназначенные для повышения, 7.48kb.
• В. В. Климов национальный исследовательский ядерный университет «мифи» модели, методы, 10.26kb.
• Автономной Республике Крым в 2011 году республиканский конкурс, 86.13kb.
• «интеллектуальные, самообучающиеся, эволюционирующие организации: методы, модели, программные, 43.37kb.
• Методы и программные средства поддержки принятия решений на основе нечётких ситуационных, 283.62kb.
• Государственное общеобразовательное учреждение, 147.4kb.
• Методы и средства анализа безопасности программного обеспечения, 749.47kb.
• Комплекс программ адаптивного управления электрическими сетями дорофеев В. В., Моржин, 100.37kb.
• Рабочая программа аннотация Наименование дисциплины Программные средства обработки, 76.7kb.
• Методы и программные средства поиска решения на основе аналогий в интеллектуальных, 324.29kb.

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)


На правах рукописи


Кружилов Иван Сергеевич


МЕТОДЫ И ПРОГРАММНЫЕ СРЕДСТВА ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ РАСПОЗНАВАНИЯ ГРУПП ЗВЕЗД В АВТОНОМНОЙ АСТРОНАВИГАЦИИ


Специальность 05.13.11 – Математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук


Москва – 2010


Работа выполнена в ГОУ ВПО «Московском энергетическом институте (техническом университете)» на кафедре Прикладной математики.

Научный руководитель:	кандидат технических наук, доцент Шамаева Ольга Юрьевна
Официальные оппоненты:	доктор технических наук, профессор Климанов Вячеслав Петрович; доктор физико-математических наук, доцент Попов Виктор Юрьевич
Ведущая организация:	Ижевский государственный технический университет

Защита диссертации состоится 18 июня 2010 г. в 16 час. 00 мин. на заседании диссертационного совета Д 212.157.01 при Московском энергетическом институте (техническом университете) по адресу: 111250, Москва, ул. Красноказарменная д.13, аудитория М-704.


С диссертацией можно ознакомиться в библиотеке Московского энергетического института (технического университета)


Отзывы в двух экземплярах, заверенные печатью организации, просьба отправлять по адресу: 111250, Москва, Красноказарменная ул., д.14, Ученый совет МЭИ (ТУ).


Автореферат разослан «___» мая 2010 г.


Ученый секретарь

диссертационного совета Д 212.157.01

кандидат технических наук, доцент Фомина М.В.


ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность темы исследований. Разработка эффективных методов и программных средств автономной ориентации космических аппаратов (КА) позволяет повысить точность ориентации КА, которая существенно влияет на работу систем связи, телевещания, определение координат объектов на поверхности Земли. Автономная ориентация космического аппарата в пространстве осуществляется с помощью гироскопов или специальных оптоэлектронных приборов, которые определяют ориентацию по различным небесным объектам – Солнцу, Земле (в инфракрасном диапазоне), звездам. Среди перечисленных способов определения ориентации наибольшей точностью обладает ориентация по звездам.

Приборы определения звездной ориентации относятся к классу систем реального времени, поскольку существуют ограничения на время ориентации, составляющее для современных приборов 1 – 4 с. Необходимо также учитывать ограничения на мощность процессора, используемого в приборе, что связано со сложностью электроснабжения автономных систем в космосе и проблемой терморегуляции бортового вычислительного блока. Частота процессоров, используемых для автономной звездной ориентации составляет порядка 100 200 МГц, а объем используемого ОЗУ и ПЗУ не превышает нескольких Мб.

Процедура автономной ориентации по звездам существенно затруднена наличием оптических искажений (дисторсия, хроматическая аберрация и т.д.), собственными шумами фоточувствительной матрицы и прибора, засветкой от Солнца, Луны и газопылевого облака КА, наличием «ложных» звезд, в том числе помехами типа «светящаяся частица». Требуемая точность в ориентации КА для современных приборов составляет порядка десятка угловых секунд, в то время как разрешающая способность матриц составляет порядка угловой минуты. Благодаря разработке эффективных методов и программного обеспечения, учитывающих, с одной стороны, доступные характеристики бортового вычислителя, с другой стороны наличие оптических искажений, помех аппаратуры и «ложных» звезд, возможно значительно повысить точность ориентации.

Актуальность диссертации обусловлена необходимостью разработки математического и программного обеспечения, направленных на повышение эффективности и точности процедур распознавания групп звезд на основе введения и исследования дополнительных критериев селекции помех типа «светящаяся частица» и разработки эвристических алгоритмов и строгих статистических правил, базирующихся на этих критериях.

Выполненные исследования опираются на результаты работ в области распознавания образов и обработки графической информации в системах реального времени как отечественных, так и зарубежных ученых: В.И. Федосеева, О.М. Ежова, В.М. Абакумова, С.В. Воронкова, А.А. Форша, Г.А. Аванесова, И.А. Чусляевой, D. Mortari, A. Saaman, M. Kolomenkin, C. Padgett, J. Junkins, C. Liebe R. Bezooijen, D. Baldini, E. Ketchum, B.M. Quine, J. Hong, K. Mighell, A. Secroun, H. Canabal, C. Rao, M. Na, B. Spratling, C. Li, G. Rousseau, A. Wald, J. NeymanБ, E. Pearson и др.

Объектом исследования являются методы, алгоритмы и программные средства распознавания звезд для задачи определения автономной ориентации космического аппарата в пространстве. Предмет исследования составляют методы и алгоритмы повышения эффективности процедуры распознавания групп звезд и их вероятностные и вычислительные характеристики.

Целью диссертационной работы является разработка методов и программных средств для повышения эффективности и точности процедуры распознавания групп звезд астроприборами при наличии помех различного типа и оценке качества работы предложенных методов. Для достижения указанной цели ставились и решались следующие задачи:

1. анализ вычислительной сложности и устойчивости современных методов распознавания групп звезд к наличию «ложных звезд»;
   
2. исследование и создание программной модели отображения проекций светящихся точек на фоточувствительной матрице при движении космического аппарата по орбите, оценка нелинейности движения траекторий и максимальной разности скоростей движения проекций звезд при заданной угловой скорости вращения спутника;
   
3. исследование характеристик алгоритмов, определяющих координаты точечных источников света на фоточувствительной матрице для гауссовской формы сигнала и пуассоновском характере помех; создание программного обеспечения для моделирования алгоритмов и визуализации их работы;
   
4. разработка и исследование эвристических методов селекции помех типа «светящаяся частица», позволяющих уменьшить асимптотическую сложность выполнения селекции звезд и «светящихся частиц» по сравнению с переборными алгоритмами, программная реализация методов и создание программного обеспечения для визуализации их работы.
   
5. разработка и исследование статистических процедур для селекции звезд и помех типа «светящаяся частица» и их программная реализация.
   

Методы исследования. Поставленные задачи решаются с использованием статистического анализа, методов проверки многокритериальных гипотез, метода максимального правдоподобия, теории графов, численных методов, методов анализа вычислительной сложности алгоритмов и программного моделирования.

На защиту выносятся:

1. классификация методов распознавания групп звезд с оценкой их вычислительной сложности и устойчивости по отношению к наличию помех типа «светящаяся частица»;
   
2. модель движения проекций светящихся частиц по плоскости фоточувствительной матрицы;
   
3. метод селекции звезд, основанный на критерии постоянства скоростей проекций, и анализ его характеристик;
   
4. метод селекции звезд, основанный на критерии постоянства взаимных угловых расстояний, и анализ его характеристик;
   
5. результаты имитационного моделирования по определению координат центра проекции точечного источника света на фоточувствительной матрице методом максимального правдоподобия.
   

Достоверность научных результатов подтверждена теоретическими выводами, результатами программного моделирования, а также сравнением полученных результатов с результатами, приведенными в научной литературе.

Научная новизна исследования состоит в следующем:

1. предложена классификация алгоритмов распознавания групп звезд, дана оценка их вычислительной сложности и устойчивости по отношению к наличию «ложных» звезд;
   

6. исследованы траектории движения проекций звезд на фоточувствительной матрице при вращении космического аппарата по орбите, произведена оценка нелинейности движения траекторий и максимальной разности скоростей движения проекций звезд при заданной угловой скорости вращения спутника;
   

2. получены характеристики алгоритма определения координат положения точечного источника света методом максимального правдоподобия для гауссовской формы сигнала и пуассоновского характера помех, сделаны выводы об оптимальном отношении радиуса рассеяния проекции к размерам элементарного фотоприемника с точки зрения минимизации погрешности определения координат;
   
3. разработаны эвристические алгоритмы предварительной селекции звезд, основанные на критериях отбора по постоянству взаимных угловых расстояний и постоянству скоростей проекций звезд, позволяющие с высокой вероятностью осуществлять селекцию помех типа «светящаяся частица» и требующие меньше времени выполнения по сравнению с переборными алгоритмами;
   
4. разработана последовательная (вальдовская) статистическая процедура для селекции звезд с заданной вероятностью ошибок пропуска и ложного обнаружения.
   

Практическая значимость работы заключается в разработке методов и программных средств, которые повышают вероятность правильного распознавания групп звезд при автономной ориентации космического аппарата. Реализованные программные средства обладают по сравнению с существующими большим быстродействием и требуют меньший объем памяти. Разработанные методы и программные средства учитывают особенности современной вычислительной техники, оптики и фоточувствительных датчиков. Для тестирования и анализа алгоритмов распознавания звезд созданы программные средства визуализации процесса распознавания.

Реализация результатов. Предложенные в работе методы и алгоритмы и созданные на их основе программные средства, использованы при разработке современных приборов звездной ориентации в ОАО «НПО «Геофизика-Космос», которые применяются в отечественных космических аппаратах специального назначения. Благодаря применению результатов диссертационного исследования уменьшено время и увеличена точность ориентации космического аппарата. Акт о внедрении и использовании результатов работы прилагается.

Результаты работы использованы в НИР, выполненной в рамках Аналитической ведомственной целевой программы Рособразования «Развитие научного потенциала высшей школы» (направление №2.2.2.3 «Развитие научной и академической мобильности в рамках международного сотрудничества») по теме № 8093 «Разработка и исследование алгоритмов для задачи астронавигации космических аппаратов» (рук. и отв. исп.: Кружилов И.С.).

Апробация работы. Основные положения и результаты диссертации докладывались и обсуждались на Международных научно-технических конференциях: «Радиотехника, электроника и энергетика» (г. Москва, 2005 г., 2007 – 2009 гг.), «Радиолокация, навигация, связь» (г. Воронеж, 2009 г.), «Информационные средства и технологии» (г. Москва, 2005 г., 2008 г., 2009 г.), Digital Signal Processing and its Applications (г. Москва, 2010 г.). В рамках программ Германской академической службы обменов (DAAD) «Ostpartnerschaft» и «Michail Lomonosow II» были проведены две научные стажировки в Техническом Университете Ильменау (Германия). Результаты исследований, полученных во время стажировок, были доложены и обсуждены на семинарах в г. Бонне (ноябрь 2009 г.) и г. Москве (апрель 2010 г.).

Публикации. Основные результаты диссертационной работы опубликованы в 13 печатных работах, включая 4 работы в изданиях, рекомендуемых ВАК.

Структура и объем работы: Диссертация содержит 117 стр. машинописного текста, состоит из введения, четырех глав, заключения, списка используемой литературы (102 наименования) и 4-х приложений.


СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность темы диссертации, ее научная новизна и практическая значимость, сформулированы цели работы и задачи, приведено краткое содержание диссертации по главам.

Приборы звездной ориентации осуществляют определение положения КА по последовательности кадров участков звездного неба. Схема функционирования прибора представлена на рисунке 1. Свет от звезд, проходя через оптическую систему, проецируется на фоточувствительную матрицу. Данные с матрицы проходят аналого-цифровое преобразование и поступают для обработки в вычислительный блок прибора. Задача программной составляющей прибора состоит в анализе последовательности кадров звездного неба для выделения на фоне помех звезд и их поиске в бортовом каталоге. После нахождения звезд в бортовом каталоге система выдает положение КА в геоцентрической системе координат.



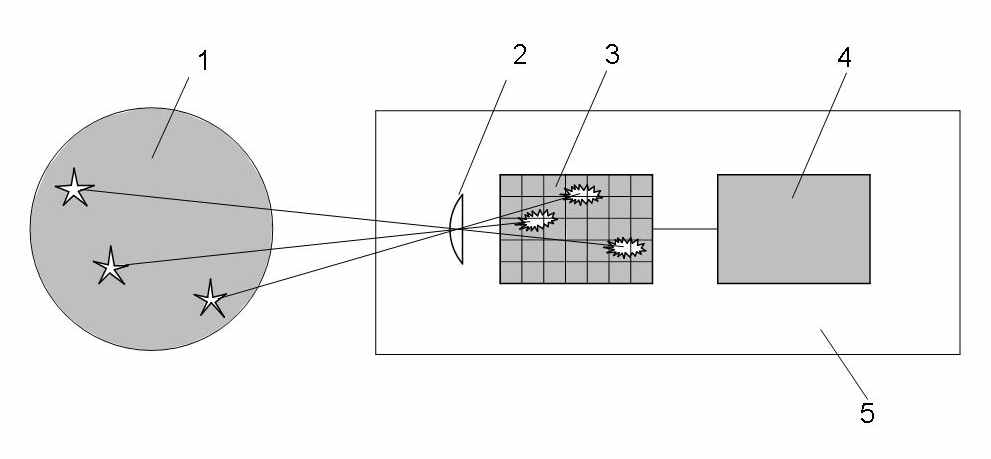
Рисунок 1 – Схема функционирования прибора звездной ориентации

Примечание – Цифрами помечено: 1 – участок звездного неба, 2 – оптическая система, 3-фоточувствительная матрица, 4 – вычислительный блок, 5-опто-элетронный прибор.

В первой главе приводится обзор существующих методов и программных средств распознавания групп звезд (star identification algorithms) для задачи автономной ориентации КА (lost-in-space).

В диссертационной работе предложена классификация алгоритмов распознавания групп звезд в бортовом каталоге. Выделены следующие классы алгоритмов: геометрические алгоритмы (polygon algorithm), графовые алгоритмы, сеточные алгоритмы (grid algorithm), алгоритмы, основанные на нейронных сетях. Идея геометрических алгоритмов заключается в том, что группы звезд характеризуются различными свойствами (площадь, периметр и т.д.) составленными из них сферических многоугольников. Поиск в каталоге групп звезд, зафиксированных в поле зрения прибора, осуществляется, согласно этим характеристикам.

Суть графовых алгоритмов заключается в поиске изоморфного подграфа в графе, при наличии погрешности в весах ребер подграфа. Характерной особенностью графовых алгоритмов является то, что в бортовом каталоге хранятся все взаимные угловые расстояния рабочих звезд, попадающих одновременно в поле зрения прибора. Среди графовых алгоритмов выделяют три основных типа: переборные алгоритмы, выборная схема (voiting scheme) и алгоритмы сопоставления групп (match group algorithms). Одной из последних модификаций графовых алгоритмов является выборная схема Коломенкина, основанная на построении таблицы соответствия между звездами в поле зрения прибора и звездами в каталоге. Для алгоритмов сопоставления групп одна звезда (чаще всего наиболее яркая) принимается за ведущую, и угловые расстояния вычисляют только между ней и остальными рабочими звездами. В каталоге ищутся пары звезд, имеющие заданные угловые расстояния и одну общую звезду. Таким образом, получаются группы соответствия звезд из поля зрения прибора и звезд из каталога. Группа (группы), имеющая больше всего соответствий, считается истинной, а остальные группы отбрасываются как ложные.

В сеточных алгоритмах группа звезд опознается как дискретизированный образ на декартовой системе координат. Среди всех звезд выбирается опорная звезда (pivot star) и ближайшая к ней. Система координат плоскости анализа преобразуется таким образом, что опорная и ближайшая к ней звезды лежат на одной оси координат. В дальнейшем анализируются только звезды, находящиеся в пределах заданного радиуса от опорной звезды. Плоскость анализа делится на квадратные сегменты. Если на площадь сегмента попадает проекция светящейся точки, то соответствующее сегменту значение принимается равным 1, и 0 - в противном случае. Дальнейший анализ состоит в побитовом сравнении полученного образа с образами, хранящимися в базе данных.

Алгоритмы поиска звезд в бортовом каталоге характеризуются размерами базы данных, временем поиска в базе данных и временем вычисления базовых характеристик, которые зависят от: f – количества звезд в поле зрения прибора, b – количества звезд в распознаваемом образе, n – количества звезд в каталоге, k - количества «ложных» звезд. В работе произведен сравнительный анализ сложности и устойчивости к наличию «ложных звезд» алгоритмов распознавания групп звезд, результаты которого представлены в таблице 1.

Таблица 1 – Сравнительные характеристики алгоритмов распознавания групп звезд

№	Название	Размер БД	Суммарное время обращения к БД	Время вычисления базовых характеристик	Устойчивость к наличию ложных звезд	Относительное увеличение времени поиска в зависимости от кол-ва «ложных» звезд
1	Переборные Алгоритм	O(n·f)	O(fb) b = 3 или 4	O(f2)	устойчив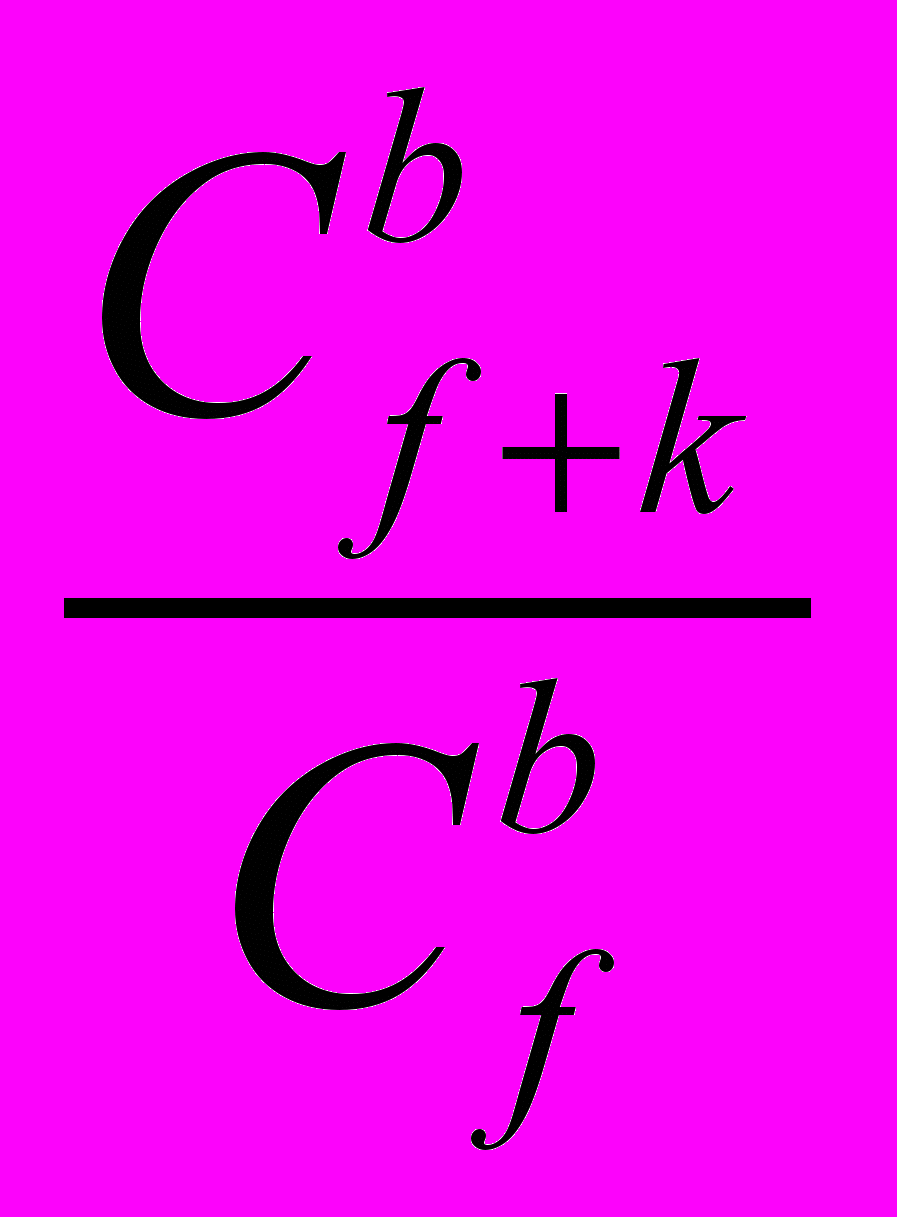
2	Геометрические Алгоритмы	O(n)	O(ln(n)f)	O(f)	неустойчив	k/f
3	Сеточные алгоритмы	O(n)	O(ln(n))	O(f)	неустойчив	k/f
4	Выборная схема Коломенкина	O(n·f)	O(f2)	O(f2)	устойчив	k2/f2
5	Алгоритмы сопоставления групп	O(n·f)	O(f2); O(f)	O(f2); O(f)	устойчив	k/f

Наличие «ложных» звезд в поле зрения прибора приводит к заметному увеличению времени идентификации групп звезд и вероятности ложного распознавания. «Ложными» звездами являются как, собственно, звезды, не вошедшие в базу данных прибора («нерабочие» звезды), так и помехи типа «светящаяся частица». Помехи последнего вида возможно выделить еще до этапа поиска звезд в базе данных прибора. Наиболее устойчивыми к наличию ложных звезд являются графовые алгоритмы, но они обладают тем недостатком, что производят селекцию ложных звезд и поиск звезд в каталоге одновременно. При этом не используется информация, которая могла бы повысить вероятность селекции помех типа «светящаяся частица». На основании проведенного в главе анализа высказано предположение о необходимости разработки методов и программных средств, осуществляющих предварительную селекцию помех типа «светящаяся частица» до этапа поиска группы звезд в базе данных прибора. Разработка таких методов и программных средств и исследование их эффективности обусловлены необходимостью повышения вероятности правильного распознавания звезд. Для анализа характеристик групп звезд, хранящихся в базе данных прибора, было реализовано программное обеспечение, визуализирующее вращение небесной сферы и ее отображение через оптическую систему.

Предварительная селекция помех типа «светящаяся частица» на 2010 г. осуществляется по дальности, уровню сигнала, оптическому спектру и скорости движения. Среди этих критериев высокую вероятность правильной селекции может обеспечить только селекция по скорости. Однако, разработанные на текущий момент алгоритмы, основанные на селекции по скоростям, используют только абсолютное значение скорости, и поэтому малоэффективны. Задачей исследования является совершенствование существующих, и разработка новых методов и эффективных программных средств для предварительной селекции помех типа «светящаяся частица».

Во второй главе предложены и исследованы методы и программное обеспечение для предварительной селекции помех типа «светящаяся частица» на основе введения критериев постоянства скоростей и постоянства взаимных угловых расстояний. На основании теоретических оценок и имитационного моделирования произведено исследование траекторий движения проекций звезд по фоточувствительной матрице, вызванного вращением спутника по орбите.

Пусть x(t), y(t) – координаты траекторий движения светящейся точки по плоскости анализа (так будет далее называться фоточувствительная матрица с введенной на ней системой координат). В дискретные моменты времени t_m производятся измерения координат светящихся точек (ξ_m,η_m), где



и ε_xm ,ε_ym – погрешности измерений, вызванные оптическими искажениями и собственными шумами светочувствительной матрицы. Предполагается, что погрешности распределены нормально 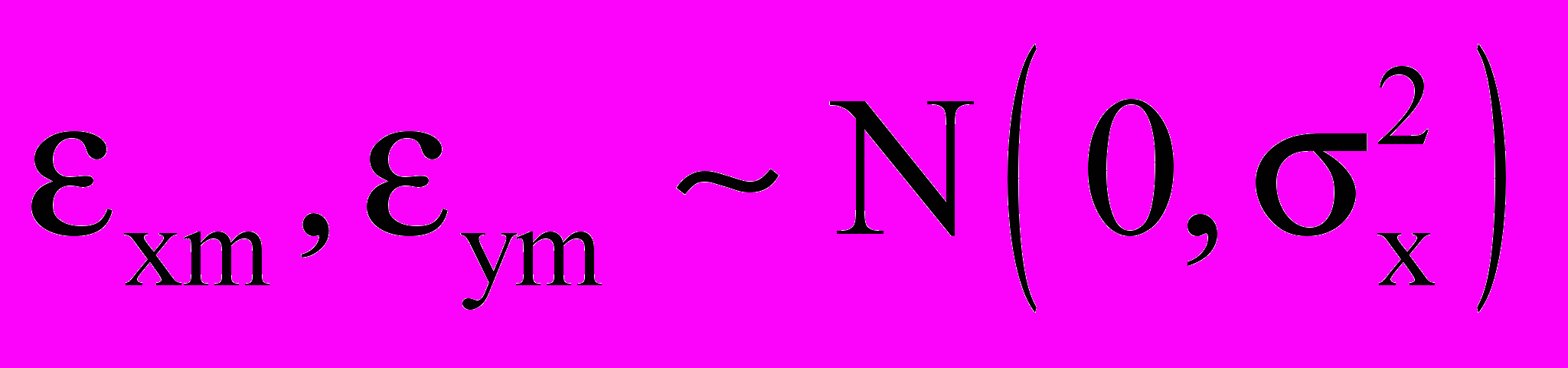. Совокупность всех измерений 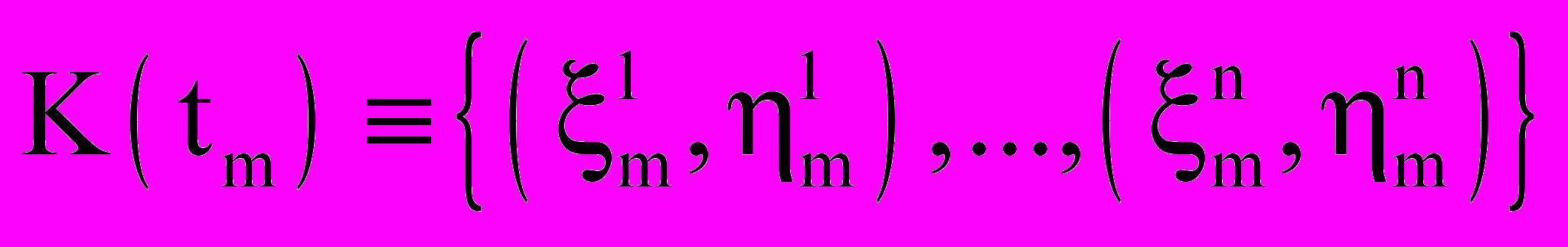в m-тый момент времени называется m-ным кадром. В этой совокупности есть отметки от незвездных траекторий x(t), y(t), подчиняющихся неизвестному случайному закону движения. По последовательности кадров K(t₁),..., K(t_n) требуется построить алгоритм, который обнаруживает траектории звезд, производит сопровождение траекторий, после n кадров выдает решение о 4-х звездах и их взаимные угловые расстояния, по которым далее определяется ориентация.

В работе было предложено два метода селекции помех типа «светящаяся частица» – метод, основанный на критерии постоянства скорости изменения взаимных угловых расстояний, и метод, основанный на критерии постоянства скоростей движения проекций звезд. Разработано программное обеспечение для визуализации, тестирования и отладки предложенных методов.

Метод, основанный на критерии постоянства взаимных угловых расстояний. Основным отличием звезд от помех «светящаяся частица» является то, что угловые расстояния между звездами неизменны, тогда как расстояния между звездами и частицами меняются со временем. Поскольку угловые расстояния на каждом кадре измеряются с погрешностью, то использование в качестве меры изменения взаимных расстояний разницы между начальным и конечным значением неэффективно, так как не используется информация всех остальных кадров, позволяющая уменьшить погрешности измерений. Как было показано в диссертации, для анализа изменения взаимных угловых расстояний между светящимися объектами достаточно ограничиться лишь их линейной составляющей. Оценка линейной составляющей движения производится методом наименьших квадратов или с помощью фильтра Калмана.

Таким образом, выделение группы звезд среди f светящихся точек сводится к анализу вещественной симметричной матрицы М размерности f×f. Каждый элемент матрицы m_i,j – линейная составляющая (скорость) изменения взаимных угловых расстояний между точками i и j. Если i и j являются звездами, то m_i,j распределено нормально с нулевым математическим ожиданием m_i,j~N(0, 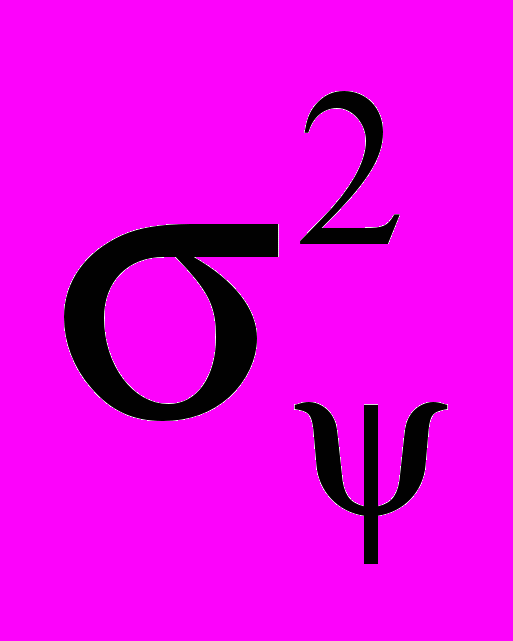). Если в паре есть хотя бы одна «не звезда», то m_i,j подчиняется распределению с математическим ожиданием отличным от нуля.

На этапе предварительного отбора с помощью одного из эмпирических алгоритмов, имеющих сложность O(f²·ln(f)), выделяются 5 - 6 светящихся точек, таких, что среди них с большой вероятностью содержатся 4 звезды. Благодаря этому анализ матрицы размером f×f сводится к анализу матрицы 5×5, что уменьшает сложность алгоритма селекции. Процедура окончательного отбора заключается в полном переборе всех сочетаний по 4 из числа предварительно отобранных светящихся точек. Окончательное решение о том, что точки являются звездами, принимается на основании статистического критерия Неймана-Пирсона. В работе предложены две модификации алгоритма предварительной селекции звезд – параметрический и непараметрический алгоритмы.

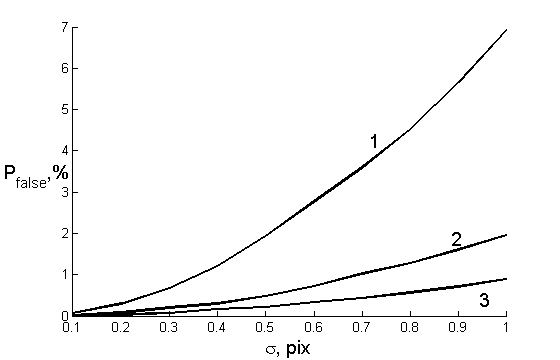
Непараметрический алгоритм предварительной селекции. Идея непараметрического алгоритма основана на том факте, что каждой светящейся точке соответствует ряд (строка матрицы) скоростей изменения парных с ней точек. Если каждую строку матрицы М упорядочить по возрастанию, звездам (если они существуют) будут соответствовать первые элементы отсортированного ряда. Зависимости вероятности ложного распознавания групп звезд от среднеквадратичного отклонения (СКО) погрешности определения координат проекций звезд, полученные в результате модельного эксперимента, представлены на рисунке 2. Основные этапы алгоритма:

1. Для строк i=1..n матрицы M скоростей изменения межзвездных расстояний упорядочить по возрастания элементы каждой i-той строки матрицы m_i,1,…,m_i,n и сформировать вектор перестановок J_i = <j_i,1, …, j_i,n> содержащий номера элементов исходной матрицы.
   
2. Для первых 4 элементов каждой упорядоченной i-той строки m_i,j1,…,m_i,jn вычислить их евклидову норма и сформировать массив норм bn.
   
3. Упорядочить по возрастанию массив bn и сформируется вектор перестановок строк I= <i₁, …, i_n>.
   
4. Для последующего анализа выбирать первые 5 строк i₁,…,i₅, соответствующих 5 наименьшим значениям массива bn.
   
5. Проанализировать целочисленную матрицу, M1=||J_ik,p||, k=1..5, p=1..n и выбрать 6 наиболее часто встречающихся номеров светящихся точек.
   
6. Д
   ля выбранных 6 точек построить всевозможные сочетания из 6 по 5. В качестве решения берется то сочетание, у которого сумма квадратов элементов будет наименьшей.
   

Рисунок 2 – Зависимость вероятности ложного распознавания группы звезд непараметрическим алгоритмом от СКО погрешности определения координат энергетических центров проекций звезд.

Примечание – по оси Х – СКО погрешности определения координат в долях от размера пикселя, по оси Y – вероятность ложного обнаружения в %. Количество звезд в кадре – 4, «светящихся частиц»­ – 5, Цифрами обозначено: скорость движения «светящихся точек» 1 – V=1'/кадр, 2 – V=2'/кадр, 3– V=3'/кадр.

Параметрический алгоритм предварительной селекции. Идея параметрического алгоритма основывается на том, что если светящаяся точка является звездой, то существует как минимум еще 3 светящихся точки, скорость изменения угловых расстояний между которыми будет меньше некого порога Δ (параметра алгоритма). Основные этапы алгоритма:

1. Определить элементы матрицы m_i,j для которых выполняется условие m_i,j < Δ.
   
2. Выделить строки, для которых количество элементов, удовлетворяющих условию m_i,j < Δ, будет больше или равно 3. Сформировать из этих строк новую матрицу М.
   
3. Если размер сформированной в п. 2 матрицы равен 5 или 4, то взять в качестве решения номера строк, полученные в п. 2 .
   
4. Если размер сформированной в п. 2 матрицы меньше 4, то селекция светящихся частиц невозможна.
   
5. Для каждой строки k матрицы М вычислить величину ошибки 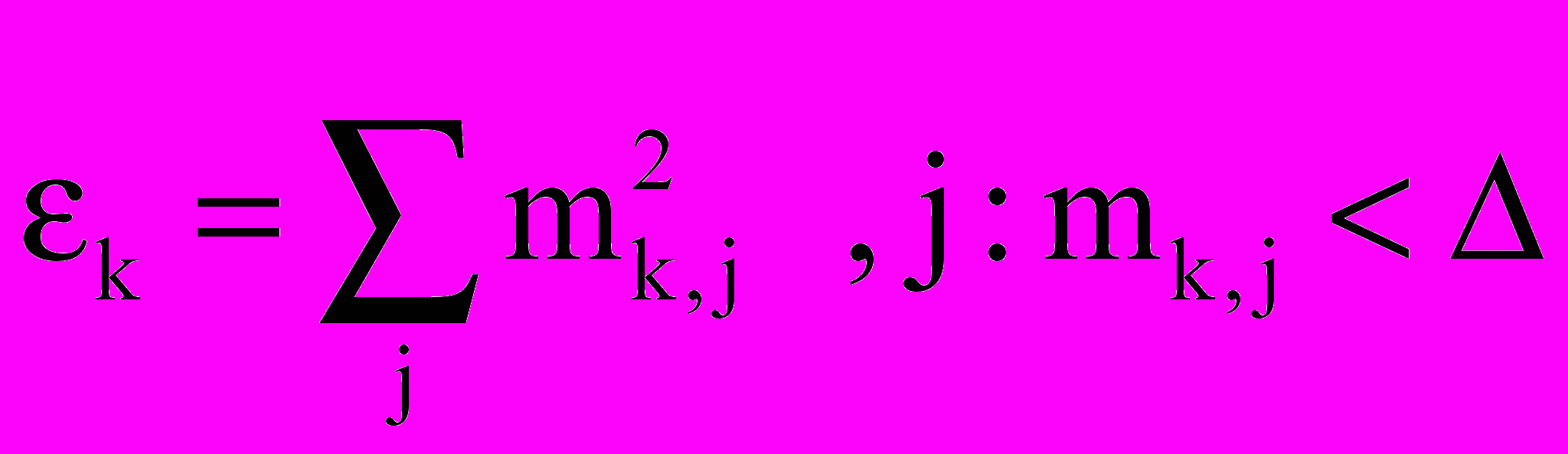. Упорядочить строки по этой величине.
   
6. Начиная со столбца, имеющего наибольшую величину ошибки, удалить столбцы, так, чтобы осталось только 5 столбцов, имеющих наименьшую погрешность (номера с 6 по n-й). Оставшиеся номера и будут искомым решением.
   

Если в качестве критерия селекции использовать не постоянство угловых расстояний, а равенство скоростей движения проекций, то можно достичь существенного сокращения времени работы алгоритма за счет обработки массива скоростей (размерность 1×f) вместо матрицы изменения взаимных угловых расстояний (размерность f×f), а также отсутствия необходимости вычислять взаимные угловые расстояния между звездами. Для того чтобы определить, при каких условиях возможно использование критерия селекции по равенству скоростей, необходимо определить, по каким траекториям движутся проекции звезд по фоточувствительной матрице.

В работе показано, что в случае орбитального движения КА, проекции звезд на матрице движутся по кривым 2-го порядка. Вид траектории зависит от соотношения углов между оптической осью и осью вращения КА - угол β и осью вращения и направляющим вектором на звезды - угол φ. Характер кривой будет определяться следующим правилом:

• если угол β > φ, то траектория проекции будет описывать эллипс;
  
• если угол β = φ, то траектория проекции будет описывать параболу;
  
• если угол φ>β, то траектория проекции будет описывать гиперболу.
  

Проекции звезд движутся по матрице по нелинейным траекториям с неравномерной скоростью, что затрудняет использование критерия отбора по равенству скоростей во всех случаях. В процессе исследования было разработано программное обеспечение, моделирующее вращение спутника. На основе результатов моделирования, сделан вывод, что для случая орбитального вращения спутника со скоростью порядка ω=0.1°/с, в качестве критерия селекции может быть использован признак равенства скоростей проекций звезд.

Алгоритм, основанный на близости скоростей движения проекций. Алгоритм выделения звезд из множества светящихся точек состоит из трех основных частей - первичного, вторичного и третичного анализа. Задачей первичного анализа информации является определение скорости проекций звезд и направлений их движения. Входными аргументами алгоритма первичного анализа являются последовательно поступающие в вычислительный блок прибора координаты светящихся точек на фоточувствительной матрице. В результате первичного анализа оцениваются покоординатные составляющие скоростей движения светящихся точек по плоскости анализа.

Оценка скорости движения проекций точечных источников света (ТИС) по плоскости анализа производится методом наименьших квадратов (МНК). Поскольку оцениваемая скорость является двухмерной величиной, то скорость движения i-той точки 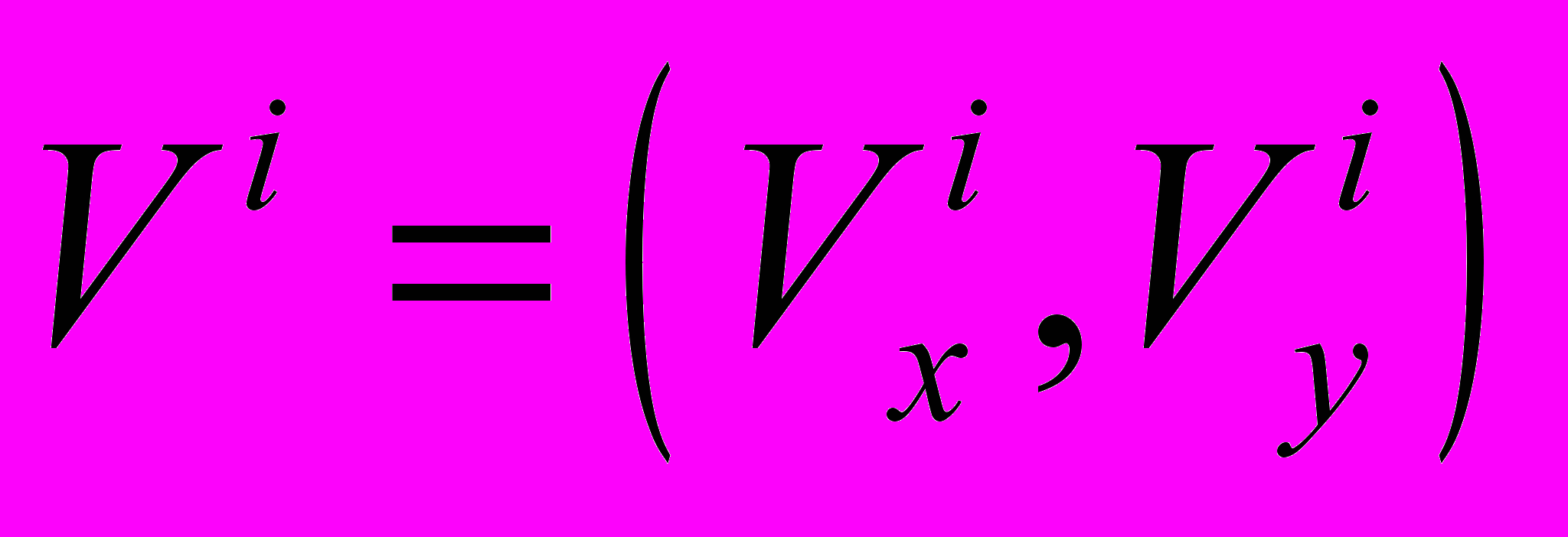можно интерпретировать как точку на плоскости, имеющую координату 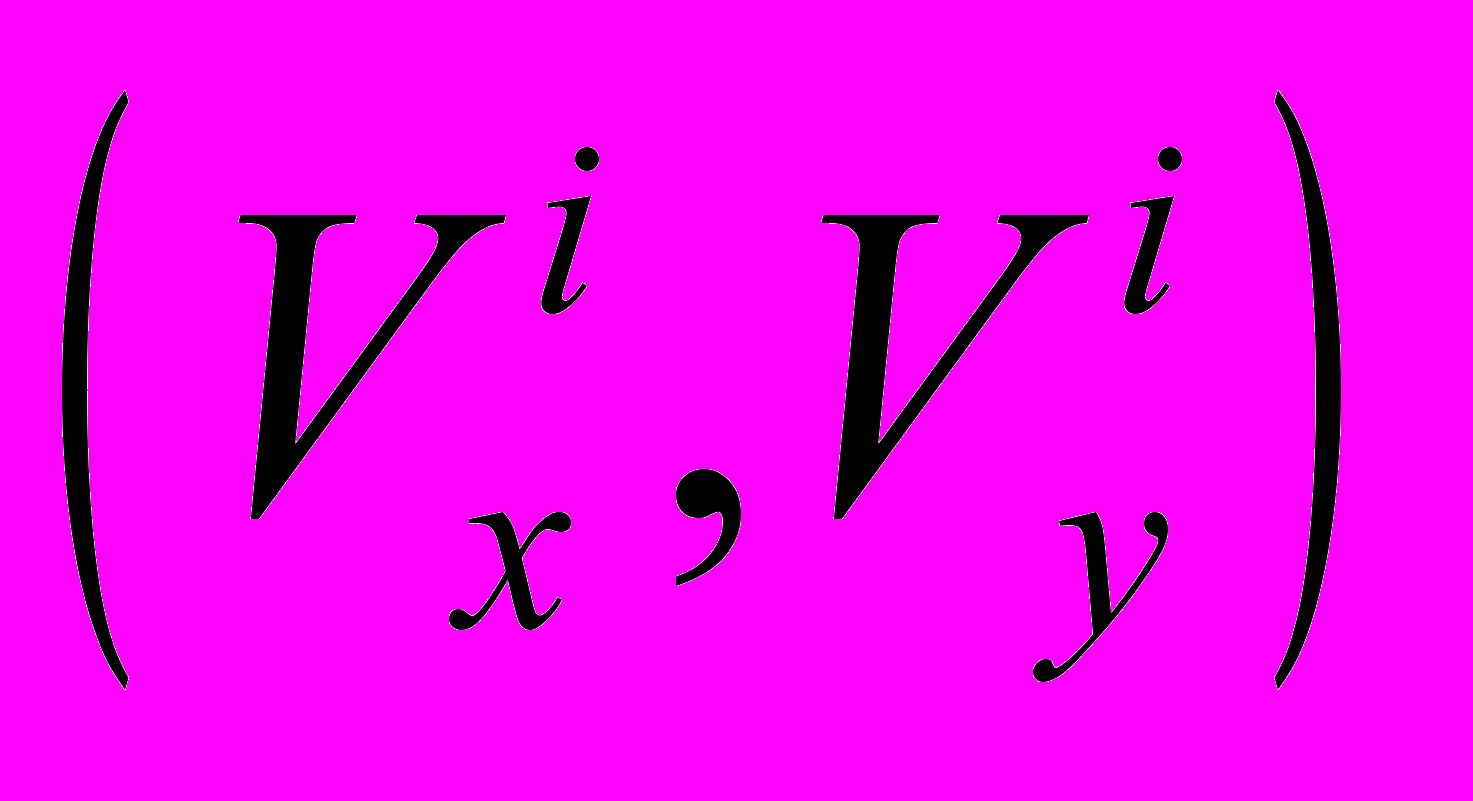. Это позволит дать наглядную геометрическую интерпретацию предложенному алгоритму селекции. Если же скорость 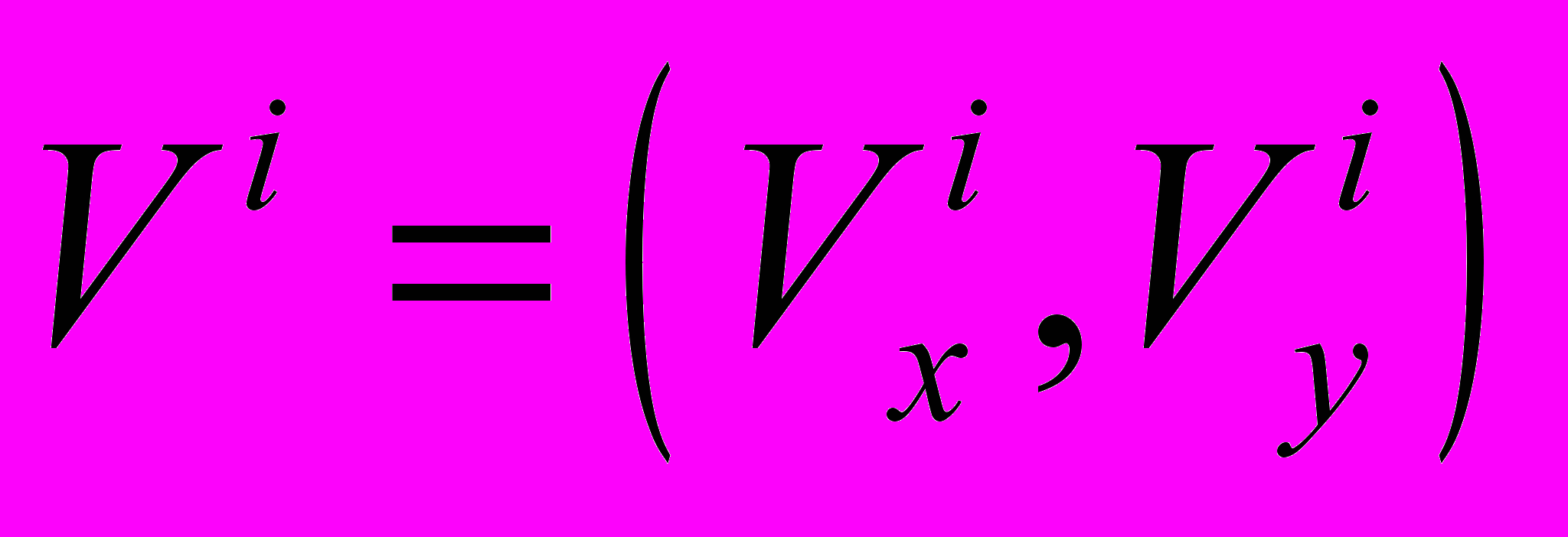отождествлять с объектом единичной массы на плоскости с координатой 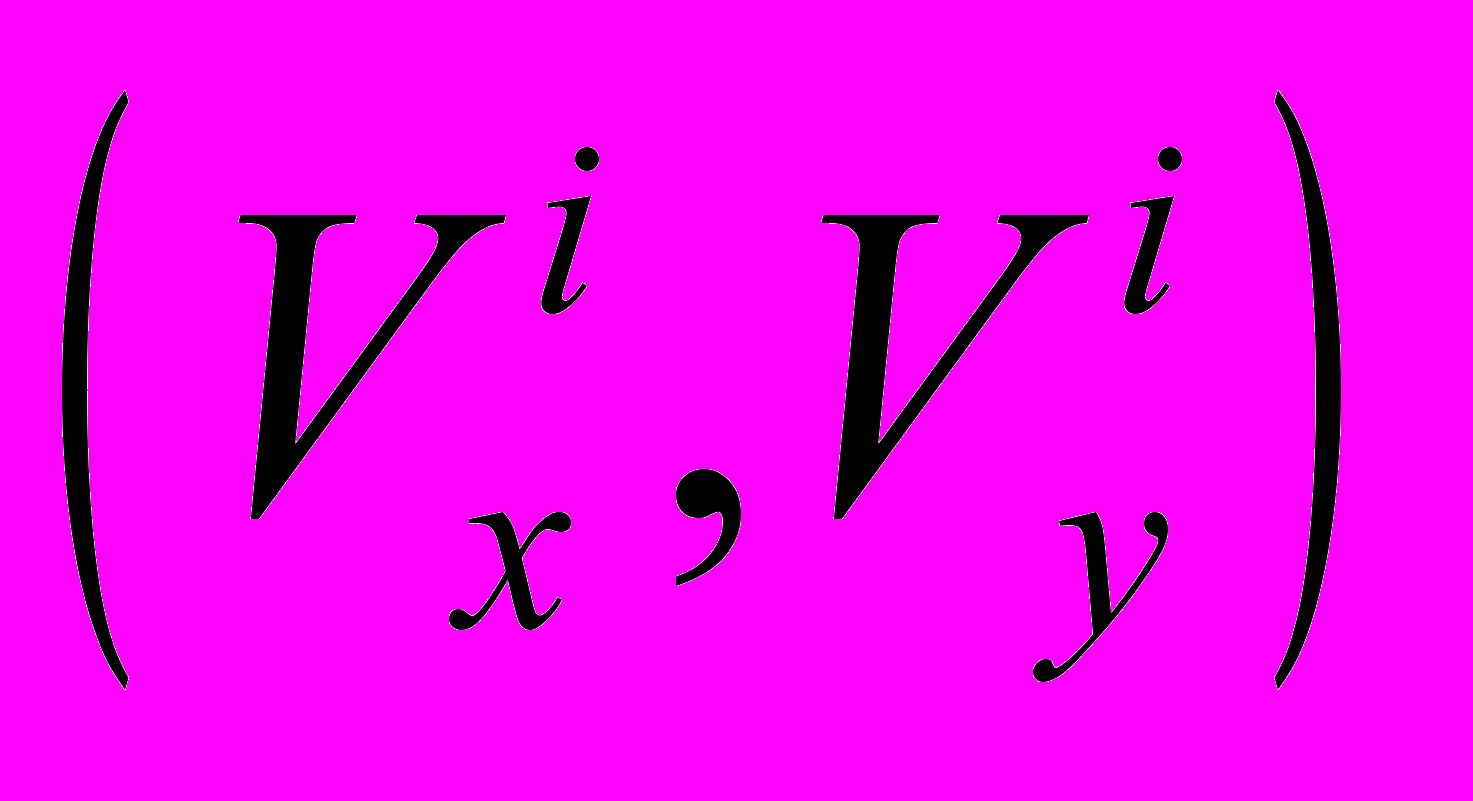, то при работе с алгоритмом анализа скоростей нескольких объектов это позволит использовать такие понятия как «центр тяжести» и «момент инерции», как меру близости объектов по скоростям. Отображение скоростей движения точек на плоскости представлено на рисунке 3.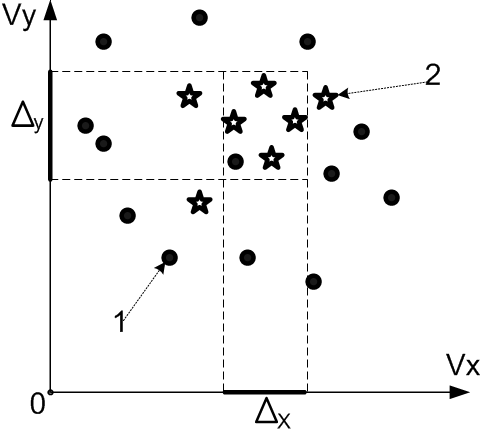



Рисунок 3 – Иллюстративная плоскость отображения скоростей светящихся точек.

Примечание – Цифрами обозначены: 1 – кружки соответствуют скоростям проекций частиц газово-пылевого облака КА на плоскости анализа, 2 - звездочки соответствуют скорости проекций звезд на плоскости анализа

Выбор звезд для распознавания на основе полученной в результате первичного анализа информации может быть осуществлен путем полного перебора всех сочетаний по 4 из множества анализируемых объектов. В этом случае сложность алгоритма будет пропорциональна и составит порядка O(f⁴). Такая сложность алгоритма неприемлема при тех ограничений, которые накладываются на время решения задачи. Для уменьшения асимптотического времени выполнения алгоритма в работе предложено использовать эвристическую процедуру отбора – вторичный анализ. На этапе вторичного анализа среди всех анализируемых объектов, чьи скорости движения были оценены алгоритмом первичного анализа, предварительно выделяется 5-6 ТИС с близкими скоростями для последующего окончательного отбора, осуществляемого на этапе третичного анализа. В изложенном ниже алгоритме вторичного анализа наиболее трудоемкой операцией является сортировка по скоростям, поэтому алгоритмическая сложность вторичного анализа составляет O(f·ln(f)).

Алгоритм вторичного анализа заключается в следующем. Упорядочиваем Х-составляющую скорости в порядке возрастания 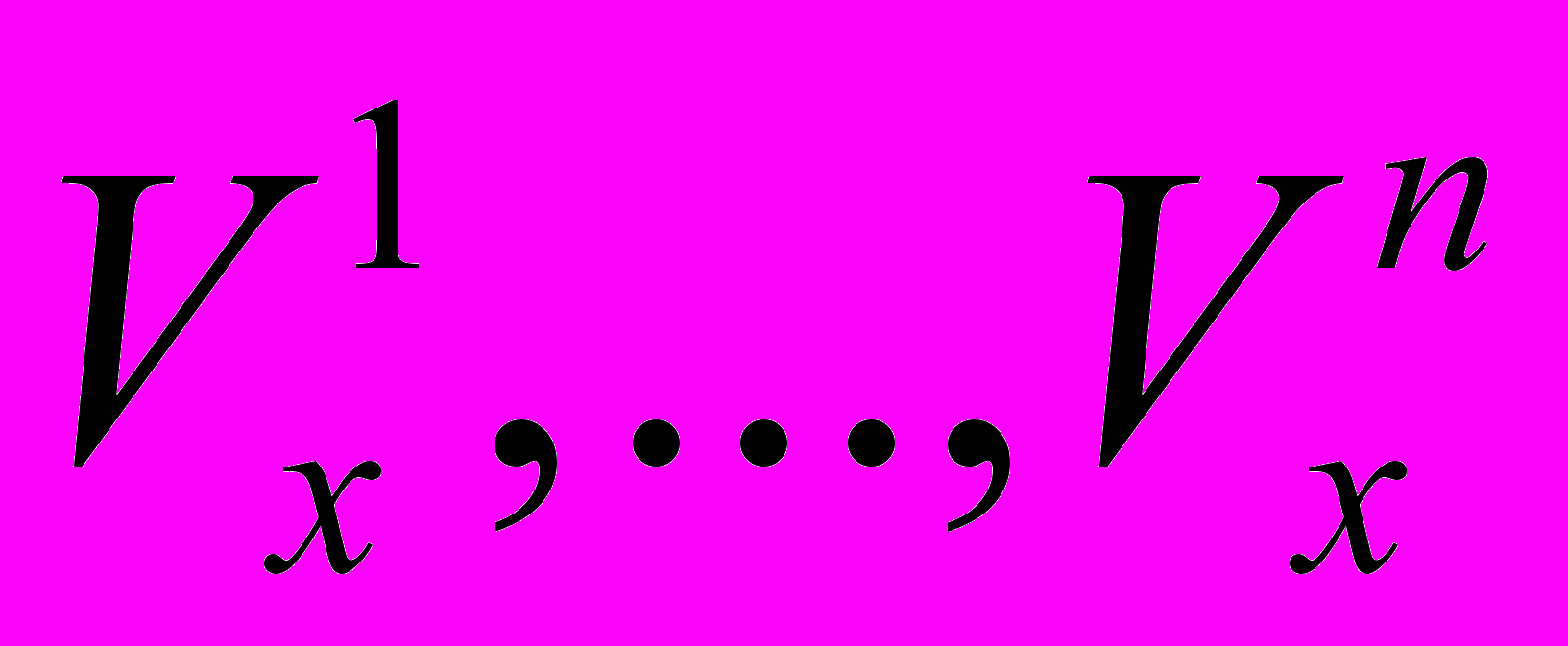. Каждому компоненту 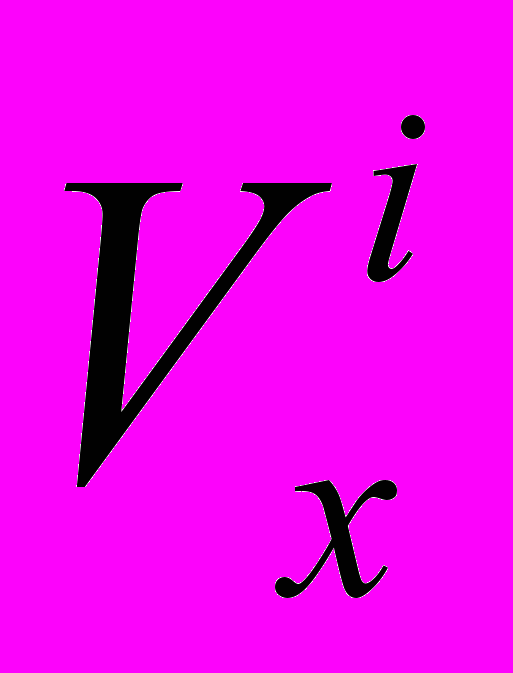ставим в соответствие компоненту 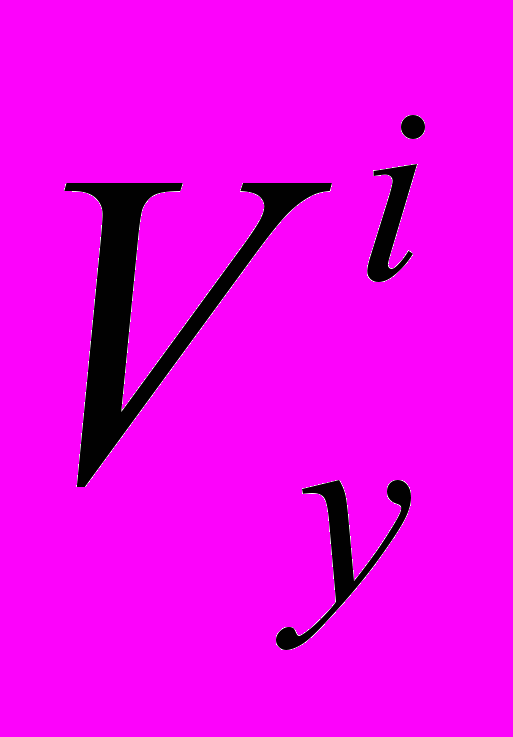. Далее сравниваются все элементы, удаленные друг от друга в вариационном ряду на K=5 позиций и вычисляется разность ∆_x между максимальной и минимальной скоростью в группе: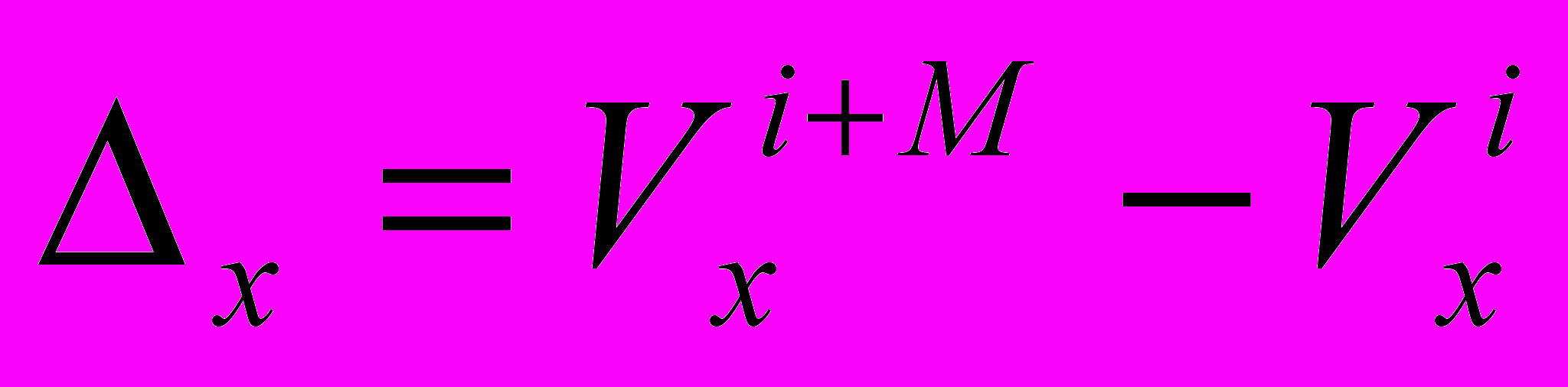 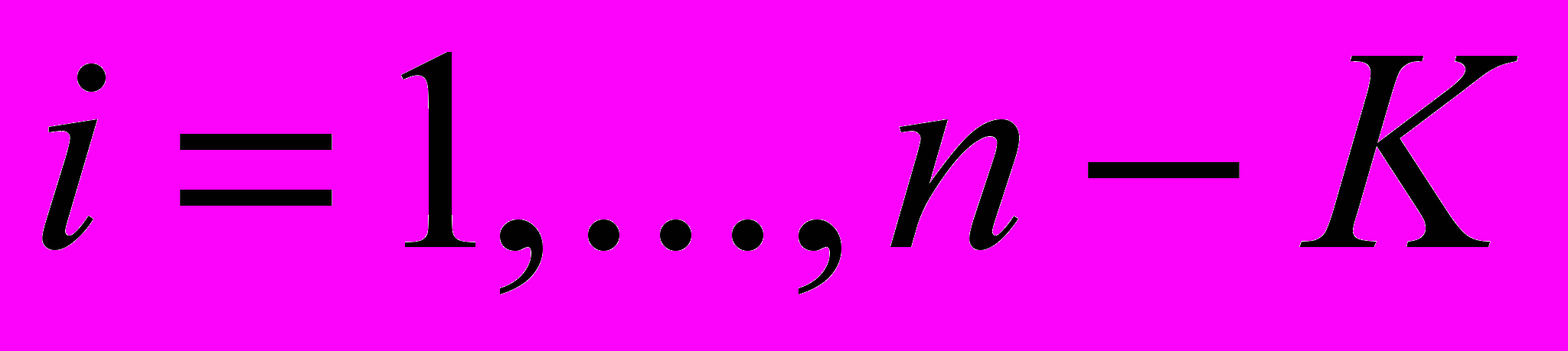. Если 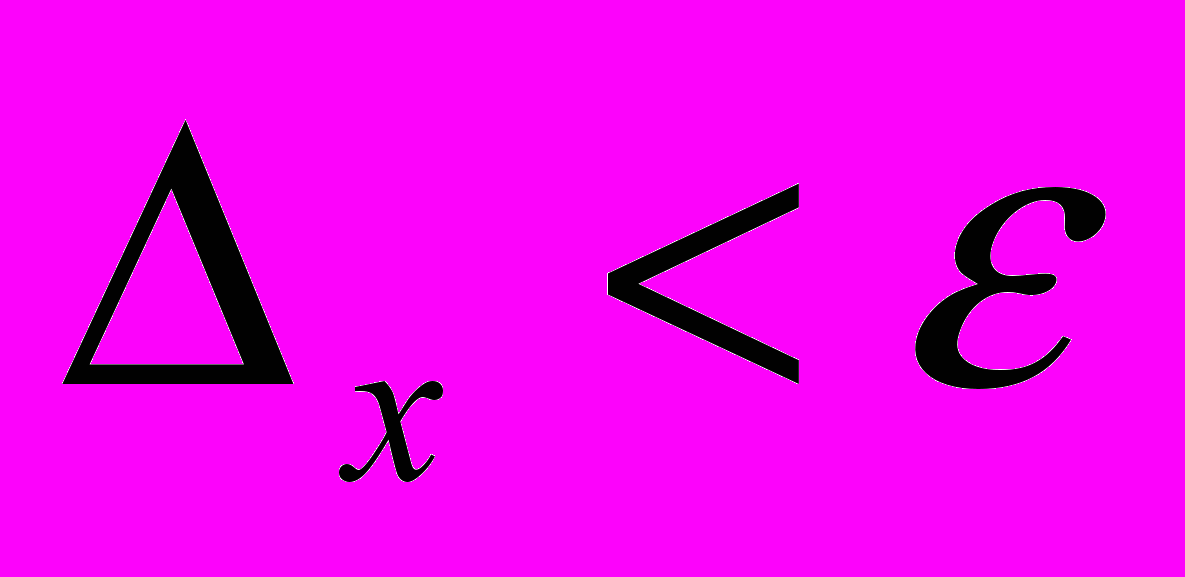, где ε - заранее заданная величина, характеризующая требуемую меру скученности объектов, то данные точки удовлетворяют условию по масштабу разброса по оси ОХ, поскольку все они умещаются в отрезке заданной длины. Далее, группы точек по оси ОХ, удовлетворяющие условию отбора, проверяются на аналогичное условие по оси ОY. Выполнение условия отбора в геометрической интерпретации метода означает, что скорости выделенных K точек близки и располагаются в квадрате со стороной ε. В итоге выделяются несколько групп из K точек близких по скоростям.

Окончательный отбор группы из K точек может быть осуществлен в соответствии с критериями минимизации «момента инерции» или «размера строба» группы K точек. Согласно критерию минимизации «момента инерции» выбирается те K объектов, момент инерции скоростей которых наименьший. При использовании критерия минимизации «размера строба» отбирается та группа точек, которая умещается в круге наименьшего радиуса. Результатом вторичного анализа является группа из K точек с минимальным разбросом по скоростям.

В процессе третичного анализа среди группы светящихся точек, выделенных на этапе вторичного анализа, выбираются 4 точки, принимаемые за звезды. На каждом кадре имеется K векторов скоростей светящихся точек: 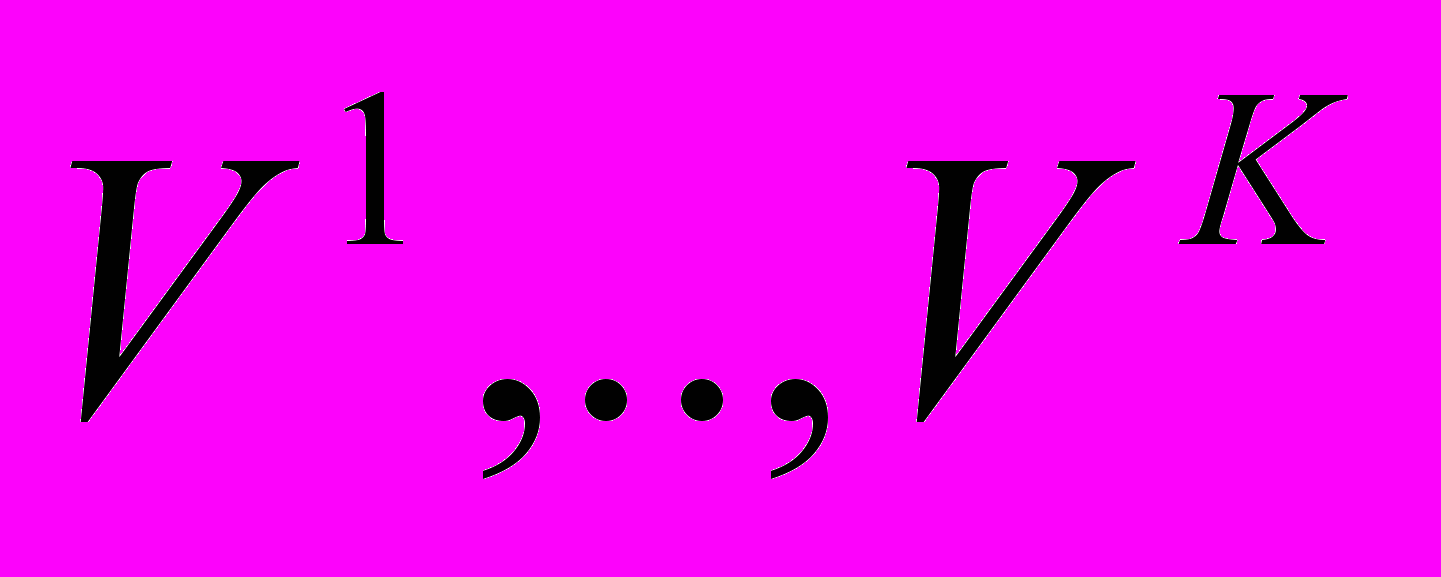. Обозначим математическое ожидание скоростей движения проекций светящихся точек как: 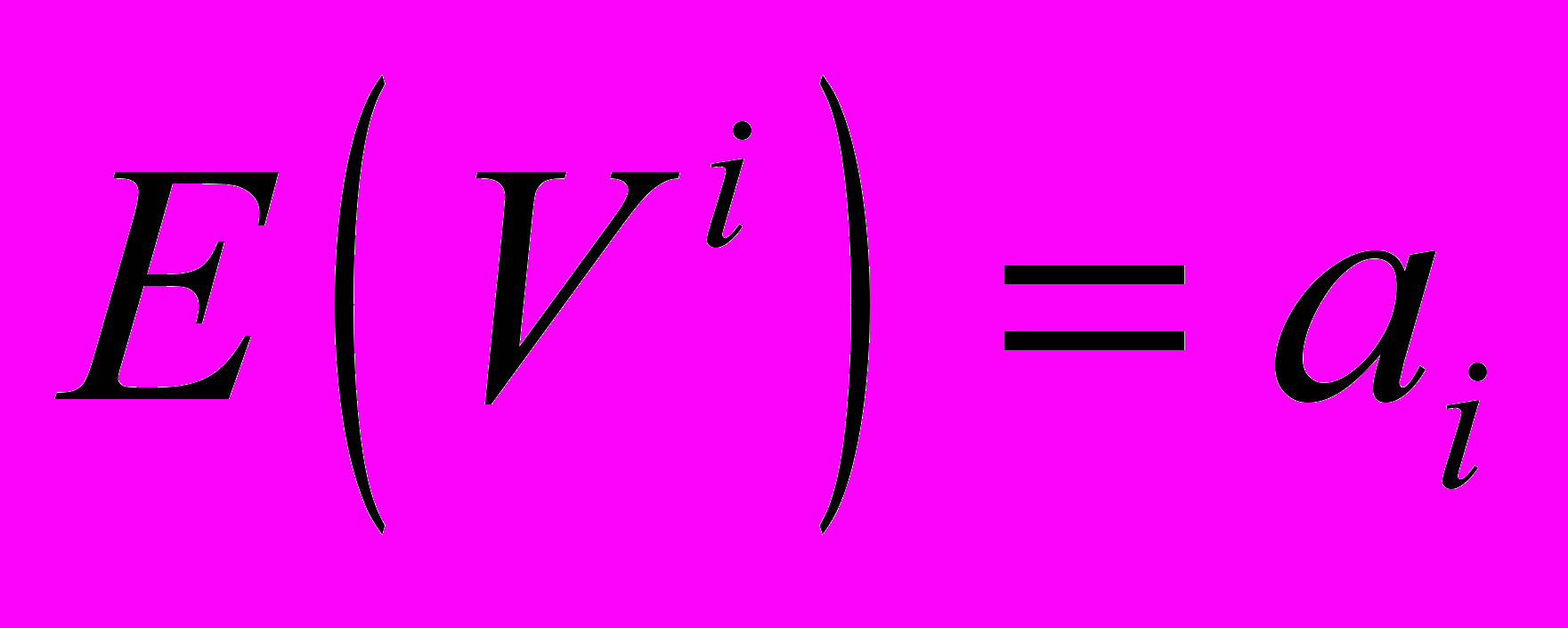. Предполагается, что в группе выделенной после вторичного анализа среди K светящихся точек нужно отбросить одну «не звезду». Таким образом, существует K+1=6 конкурирующих гипотез:

• H 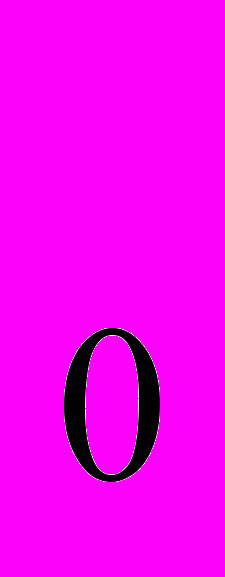(все звезды):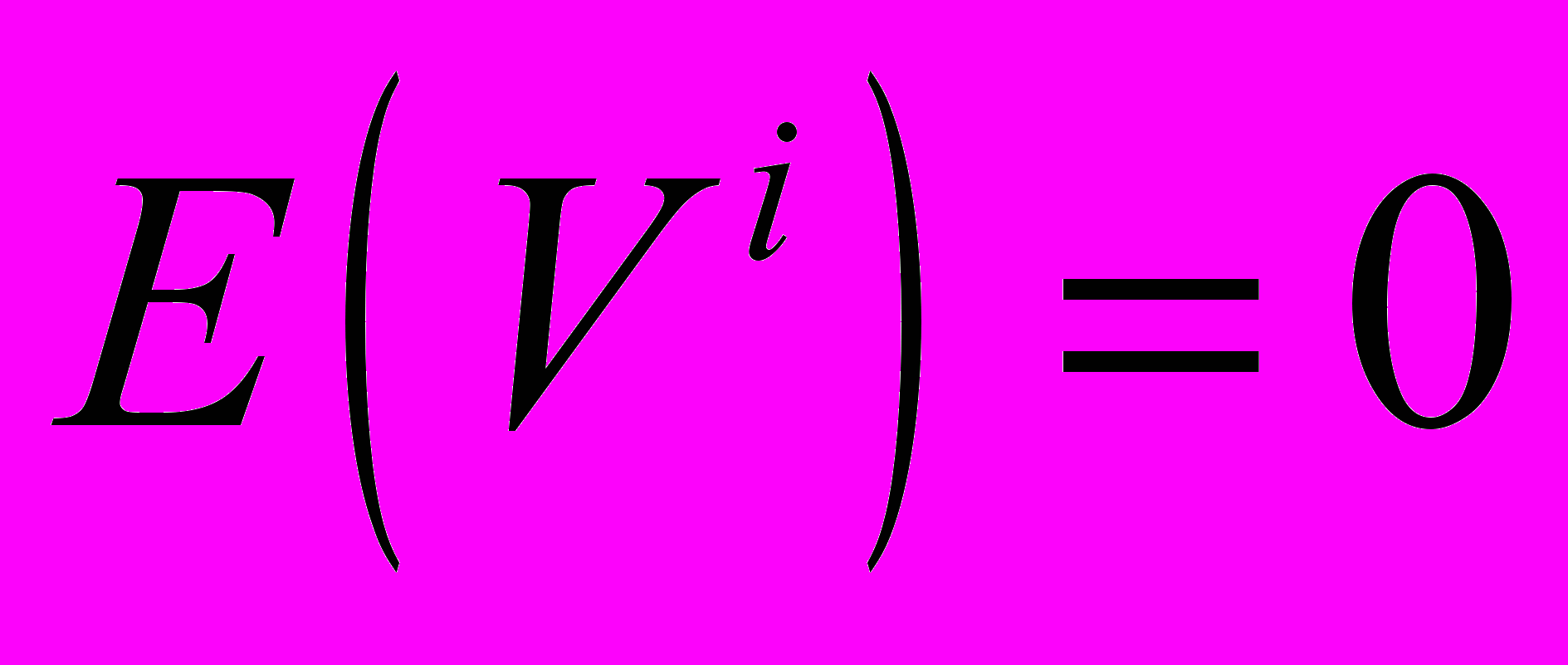
  
• H 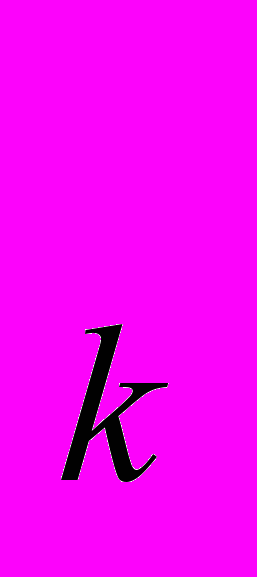(k-тая точка не звезда, k=1,..,K): 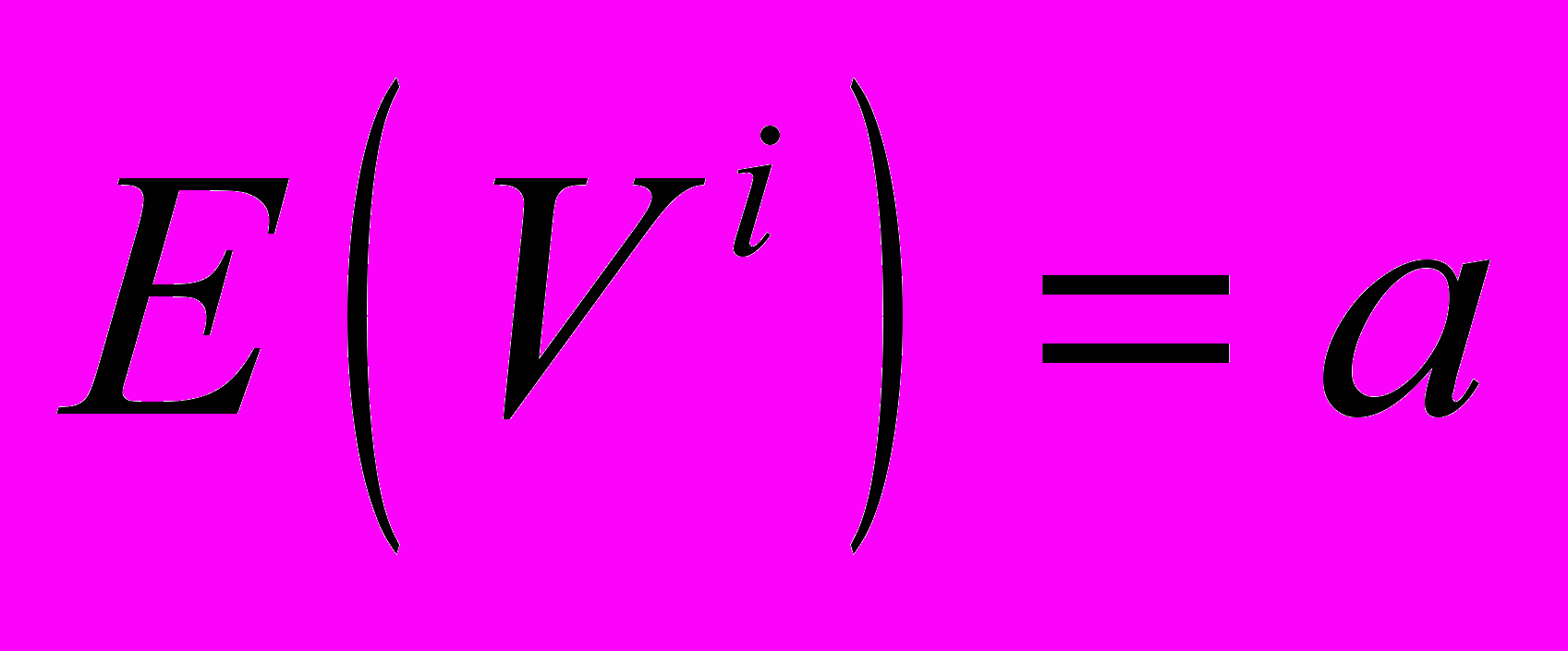,,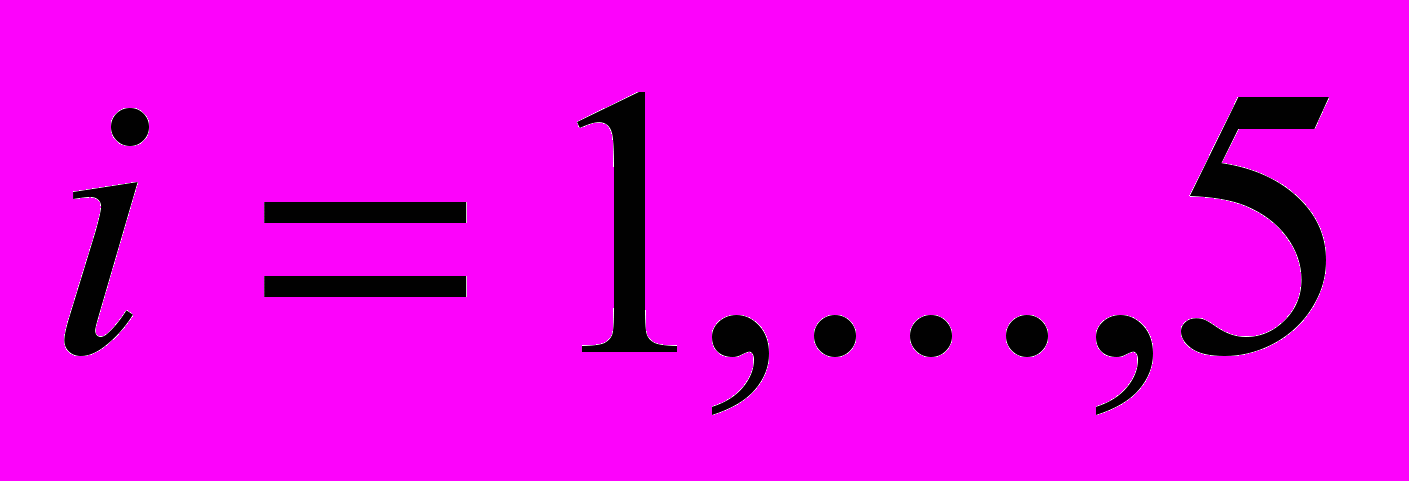i≠k и ,,
  
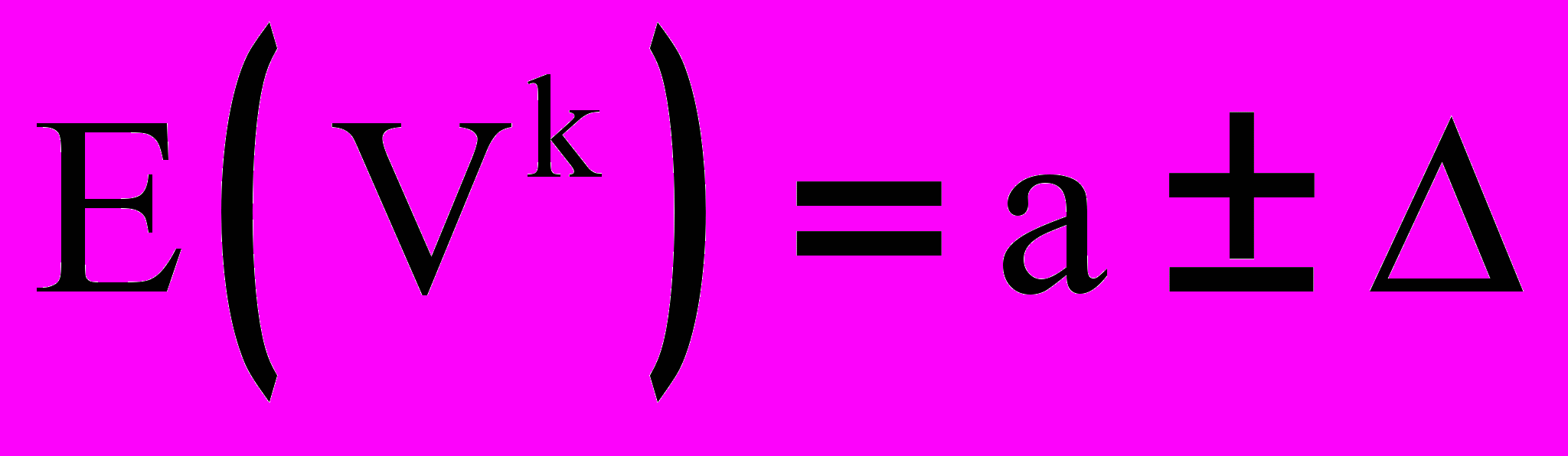  где < ε - величина отклонения по скорости, которую алгоритм должен надежно различать. Последовательное решающее правило на n-ном шаге выглядит следующим образом. Вычисляются разности скоростей при H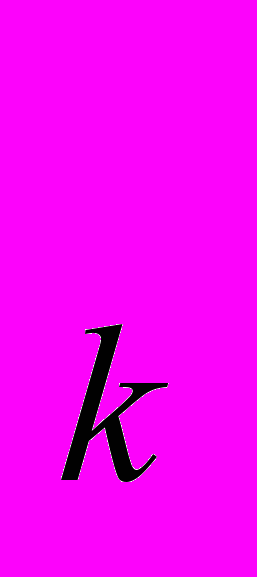 , 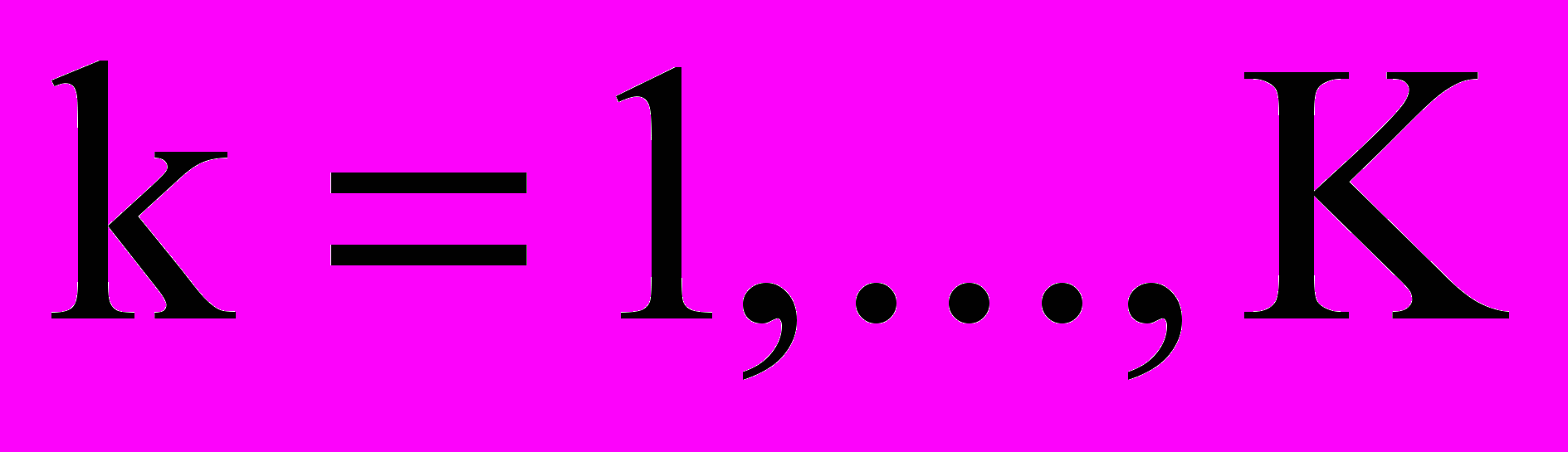: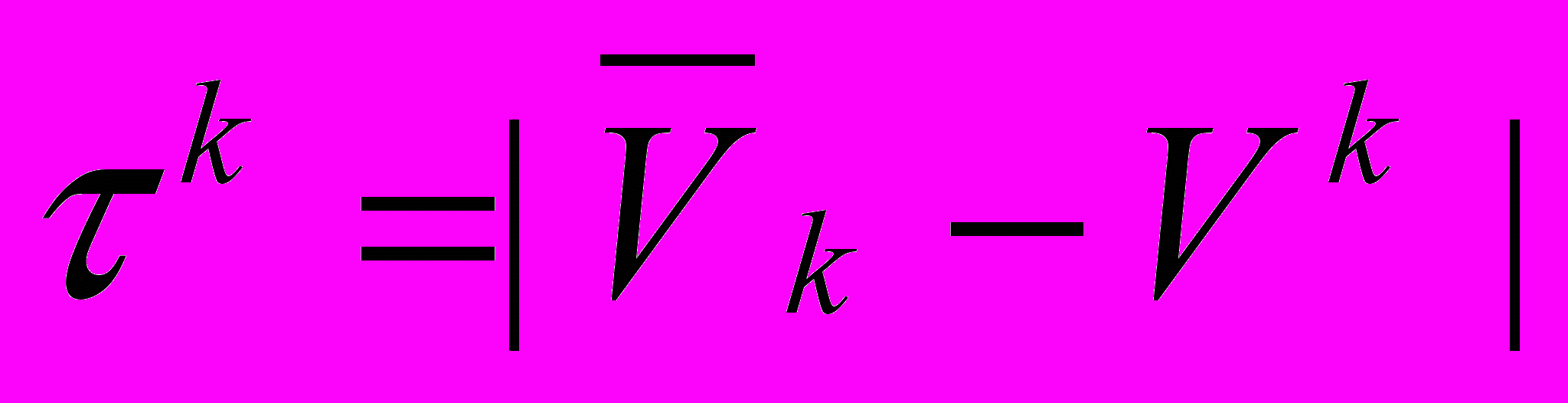, где .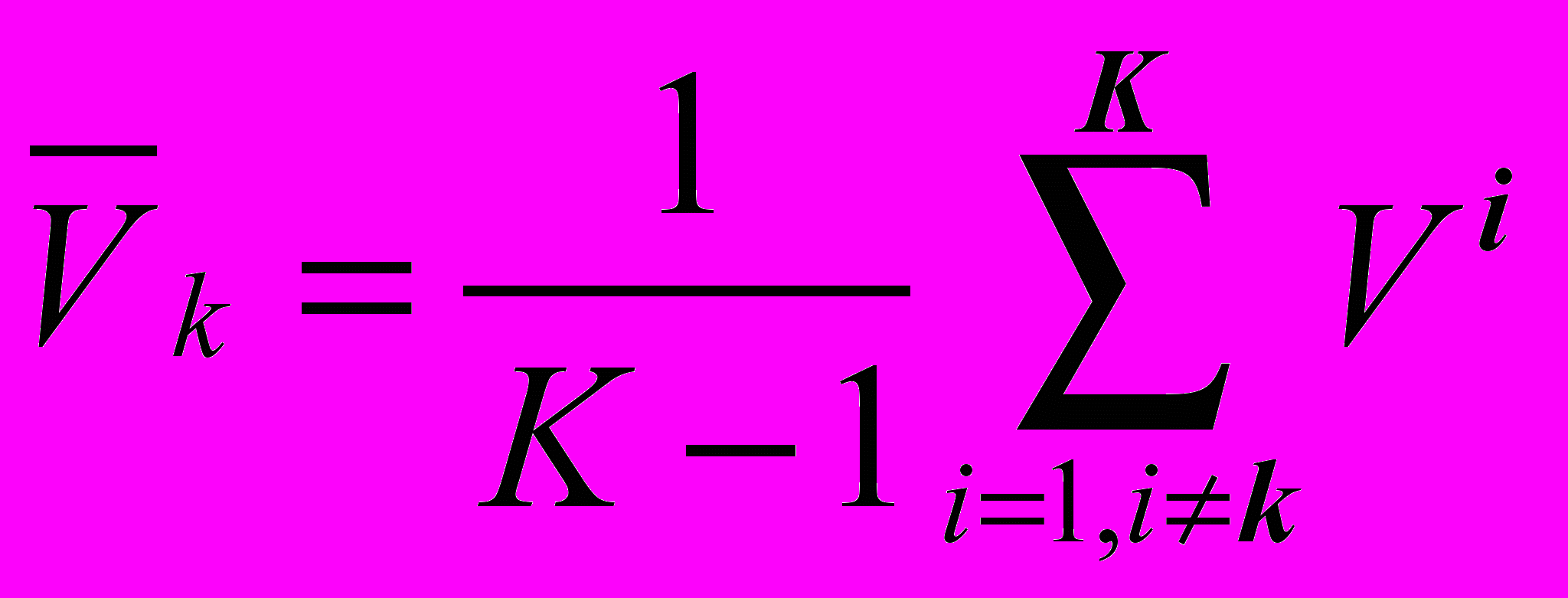
  

Рассмотрим неравенство, полученное в работе:

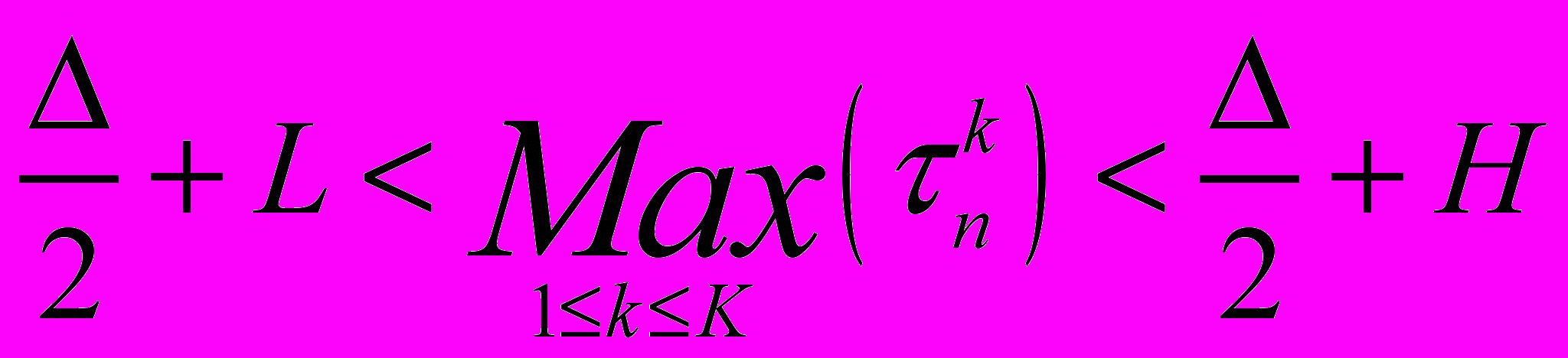, где 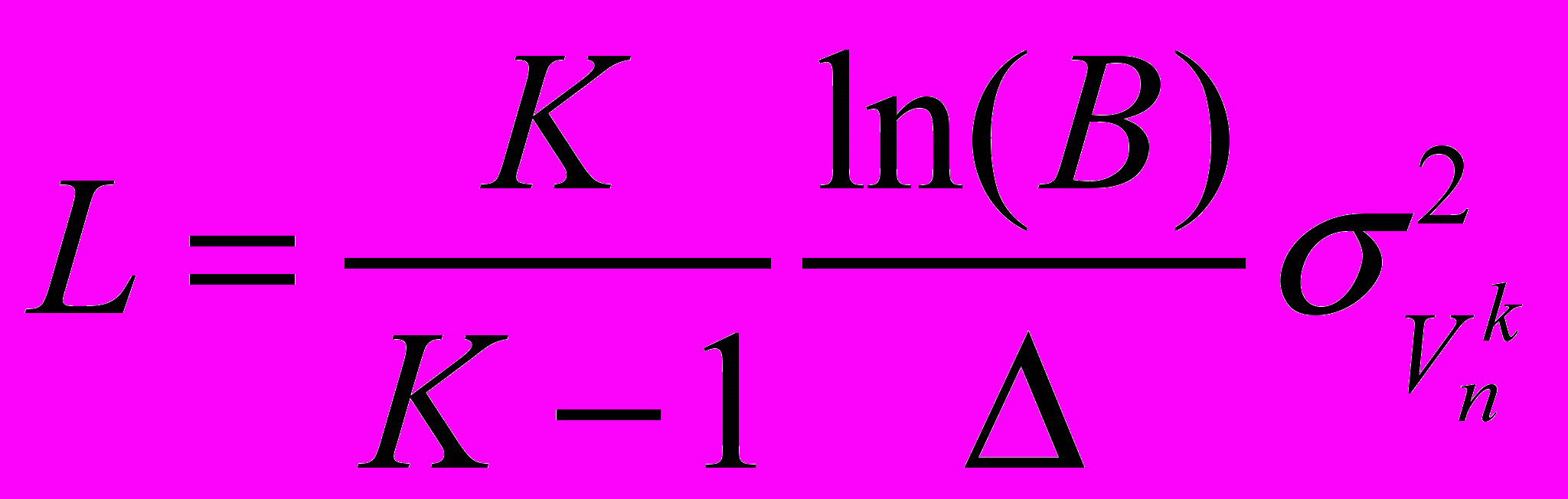, , 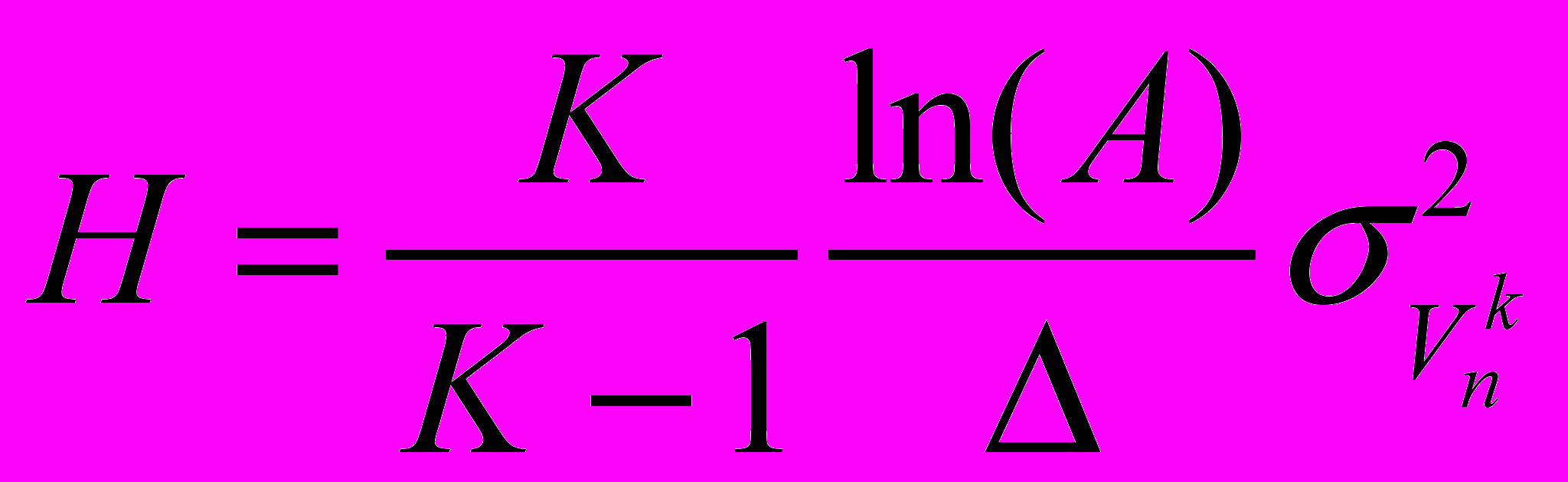, 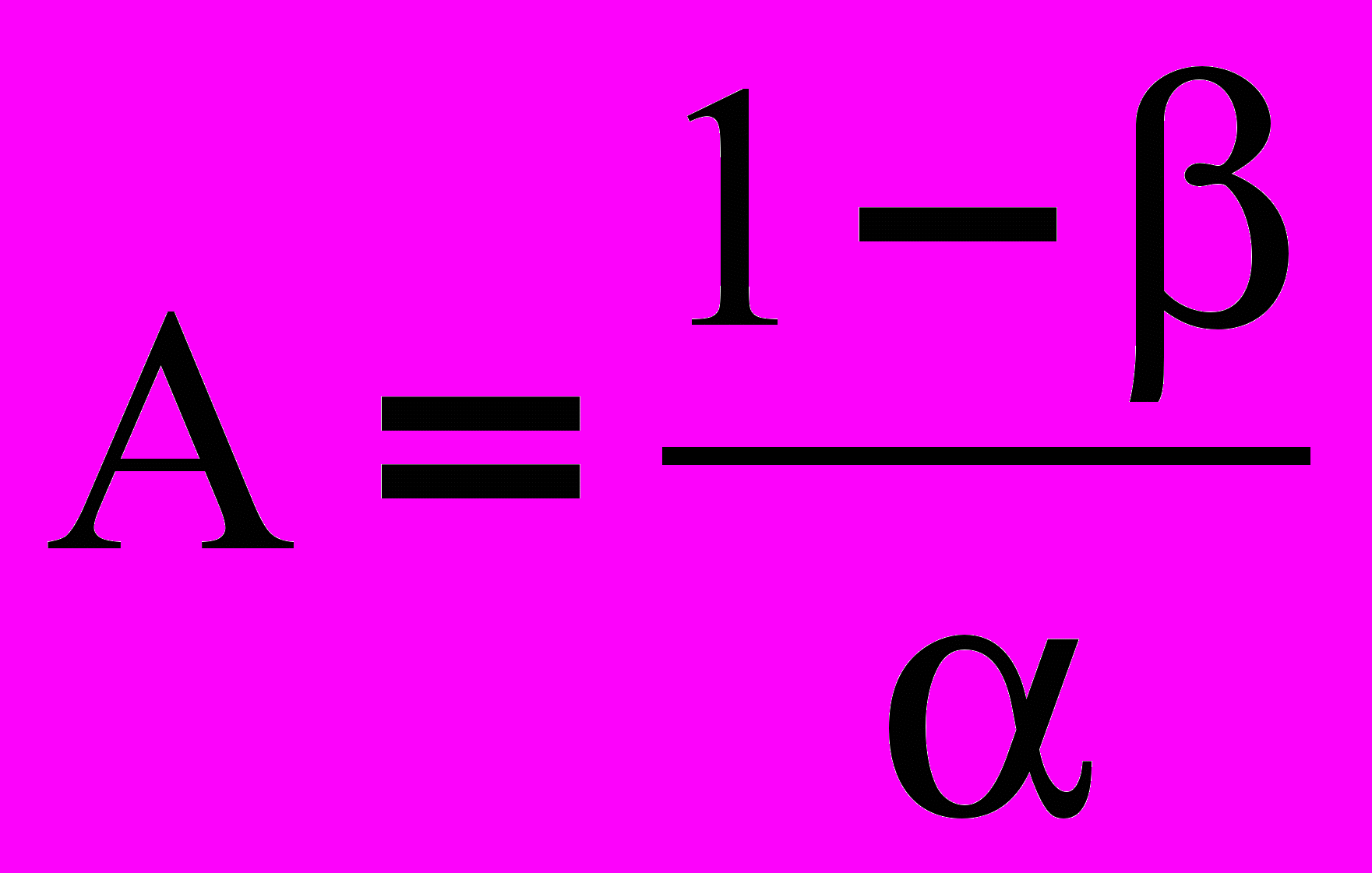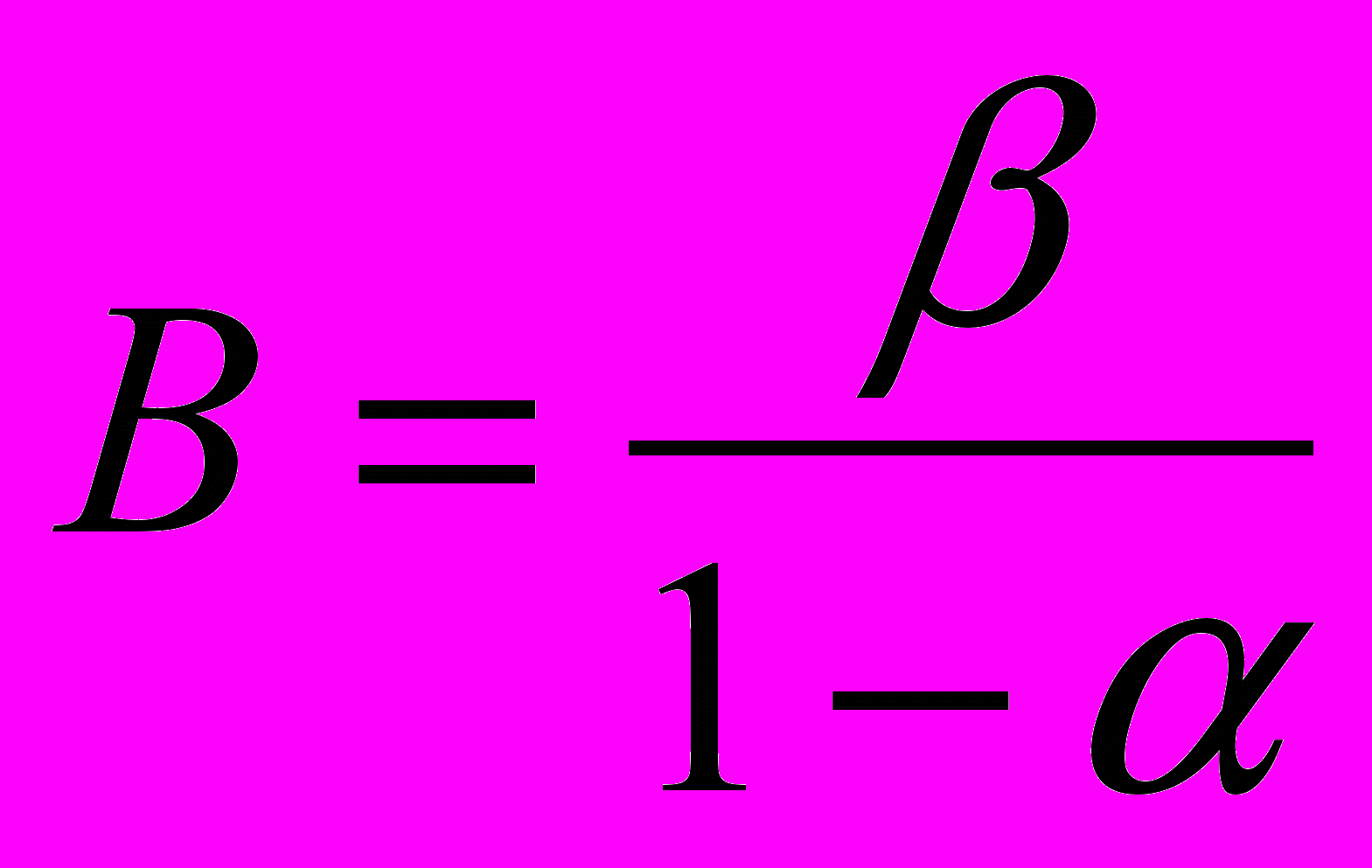- пороги последовательного правила Вальда, α и β – вероятности пропуска и ложного обнаружения соответственно, 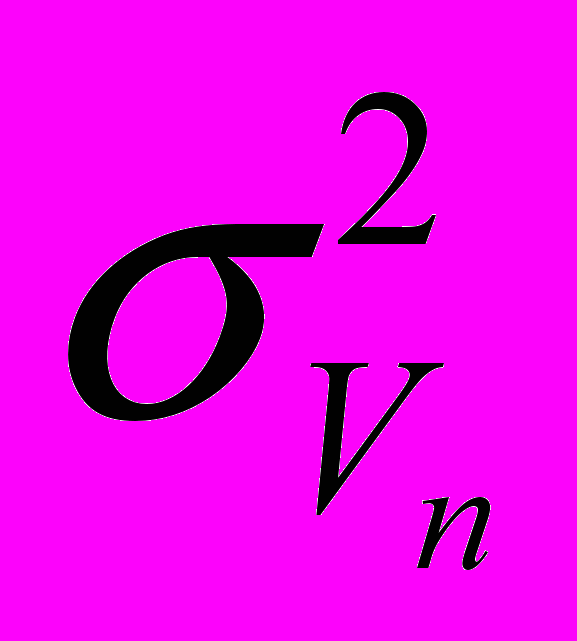- дисперсия скорости на n–ом шаге. Если неравенство выполняется, то наблюдения продолжаются, в противном случае принимается окончательное решение о распознавании. В случае остановки процедуры решение определяется следующим правилом:

если 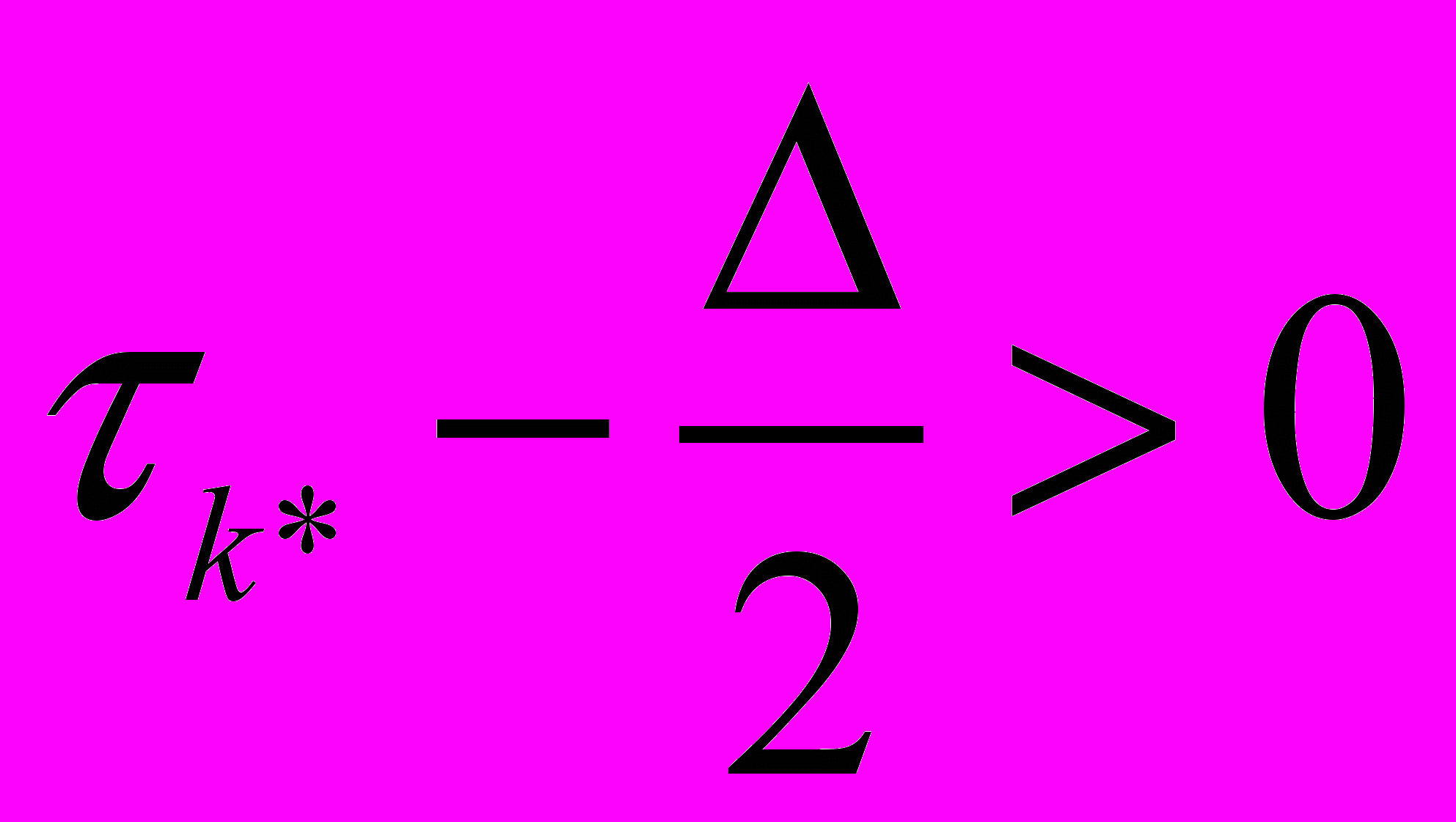, то принимается гипотеза H_k*. ,где 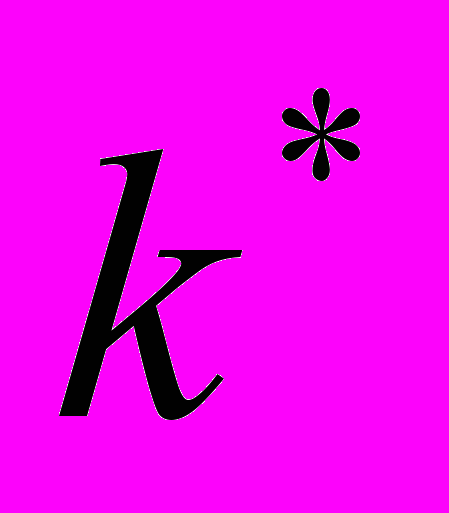- номер светящейся точки, на котором достигается ;

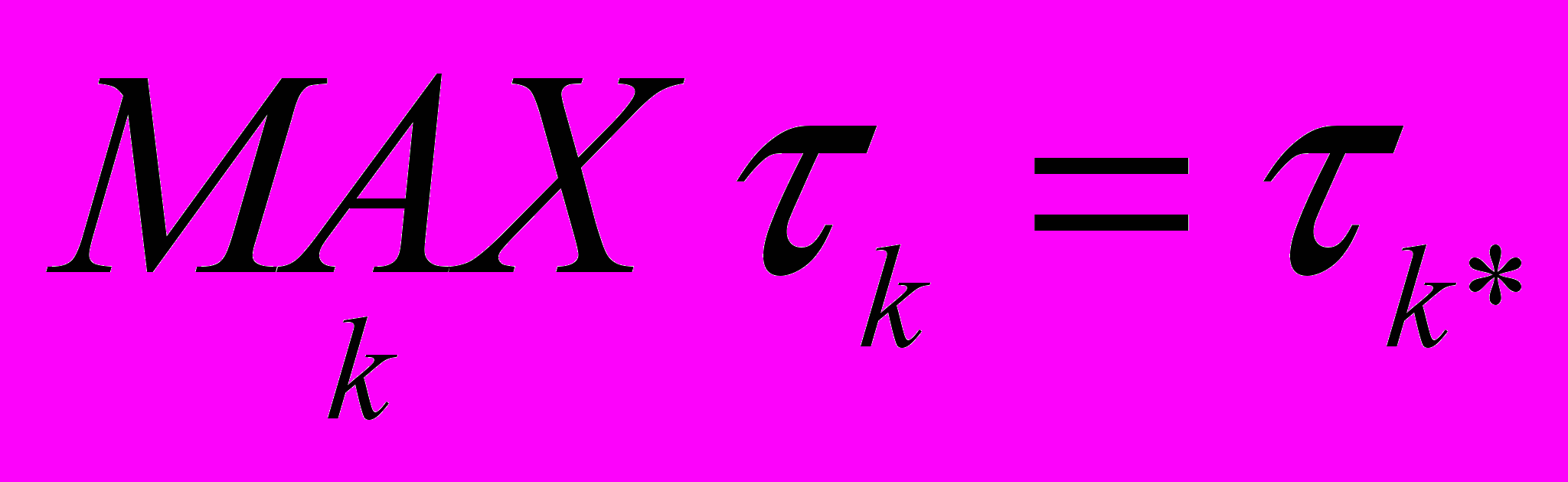если 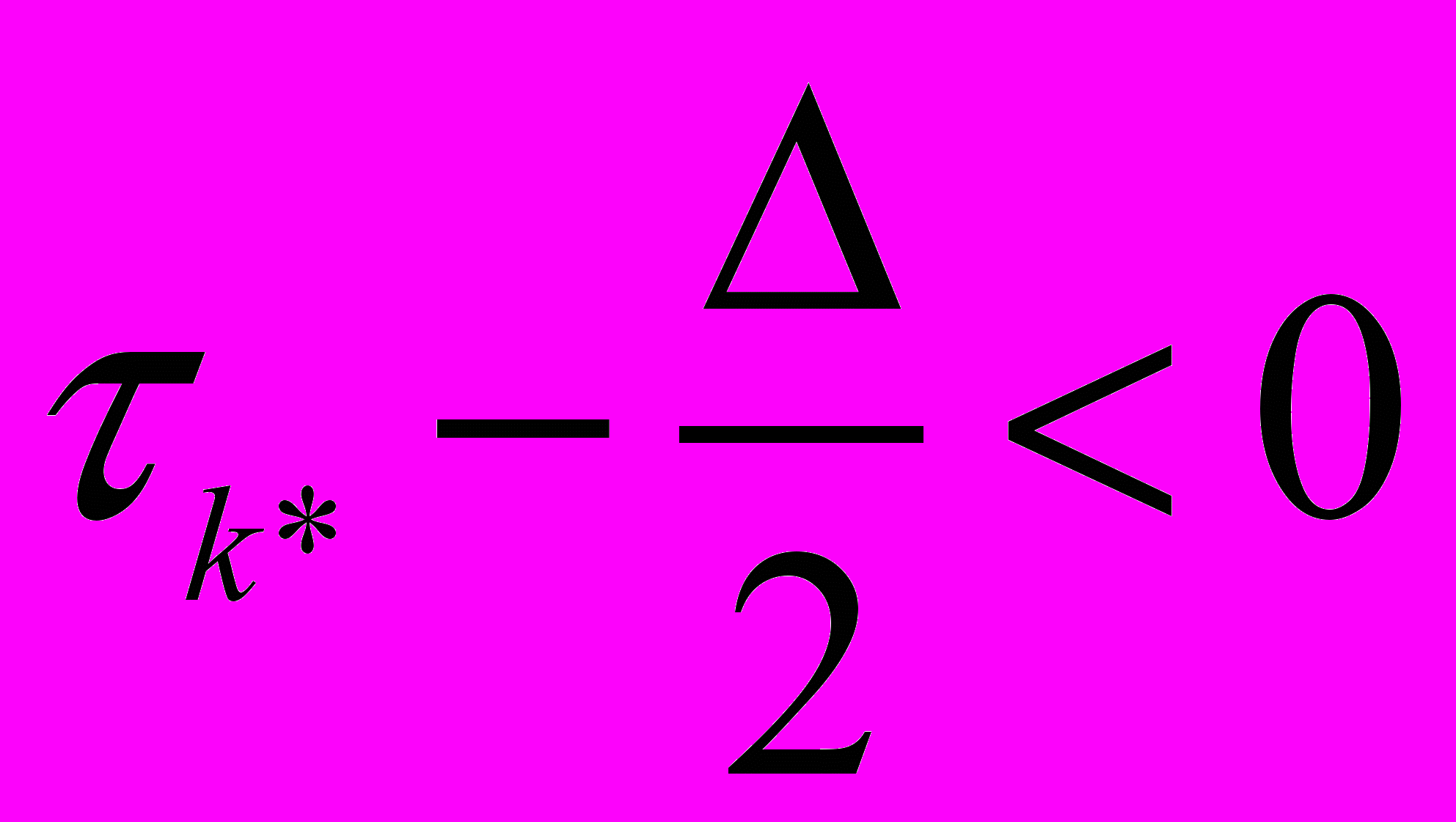, то принимается гипотеза H₀.

Сравнительные характеристики алгоритмов селекции помех типа «светящаяся частица», предложенных и реализованных в работе, представлены в таблице 2.

Таблица 2 – Сравнительная характеристика алгоритмов селекции звезд

Алгоритм	Селекция по критерию постоянства скоростей проекций	Селекция по критерию постоянства взаимных угловых расстояний
		Параметрический метод предварительного отбора	Не параметрический метод предварительного отбора
Требуемое количество кадров для селекции	≈20	≈30
Ограничения на количество наблюдений	Произвольное количество наблюдений (последовательный анализ Вальда)	Фиксированное количество наблюдений (критерий Неймана-Пирсона)
Вычислительная сложность	O(f·ln(f))	O(f2ln(f))
Сложность реализации	Прост в реализации	Трудоемок в реализации, но проще параметрического метода	Трудоемок в реализации и отладке. Требует построения дополнительных таблиц
Ограничения	Малоэффективен для случая, если угол между оптической осью и осью вращения прибора β<10º	Требует априорной информации о погрешности определения координат	Отсутствуют
Объем используемой памяти	O(f)	O(f2)
Нижний предел распознаваемой скорости, для которой даны характеристики	6 угл. мин/с
Достижимые вероятностные характеристики для орбитального вращения	Pправ. обн=0.95	Pправ. обн=0.98	Pправ. обн=0.97
	Рпроп=0.02 – параметр эксперимента

В третьей главе Произведен обзор и сравнение алгоритмов определения положения точечных источников света, спроецированных на фоточувствительную матрицу.

Для увеличения надежности распознавания необходимо уменьшить минимальное значение скорости движения помех типа «светящаяся частица», которую можно распознавать с заданной вероятностью. Для этого необходимо знать погрешность определения линейной скорости изменения взаимных угловых расстояний между звездами. В работе показано, что угол между двумя светящимися точками определяется с погрешностью, подчиненной нормальному закону. В диссертационной работе приведена оценка СКО линейной составляющей изменения межзвездного угла σ_V после n-го кадра: 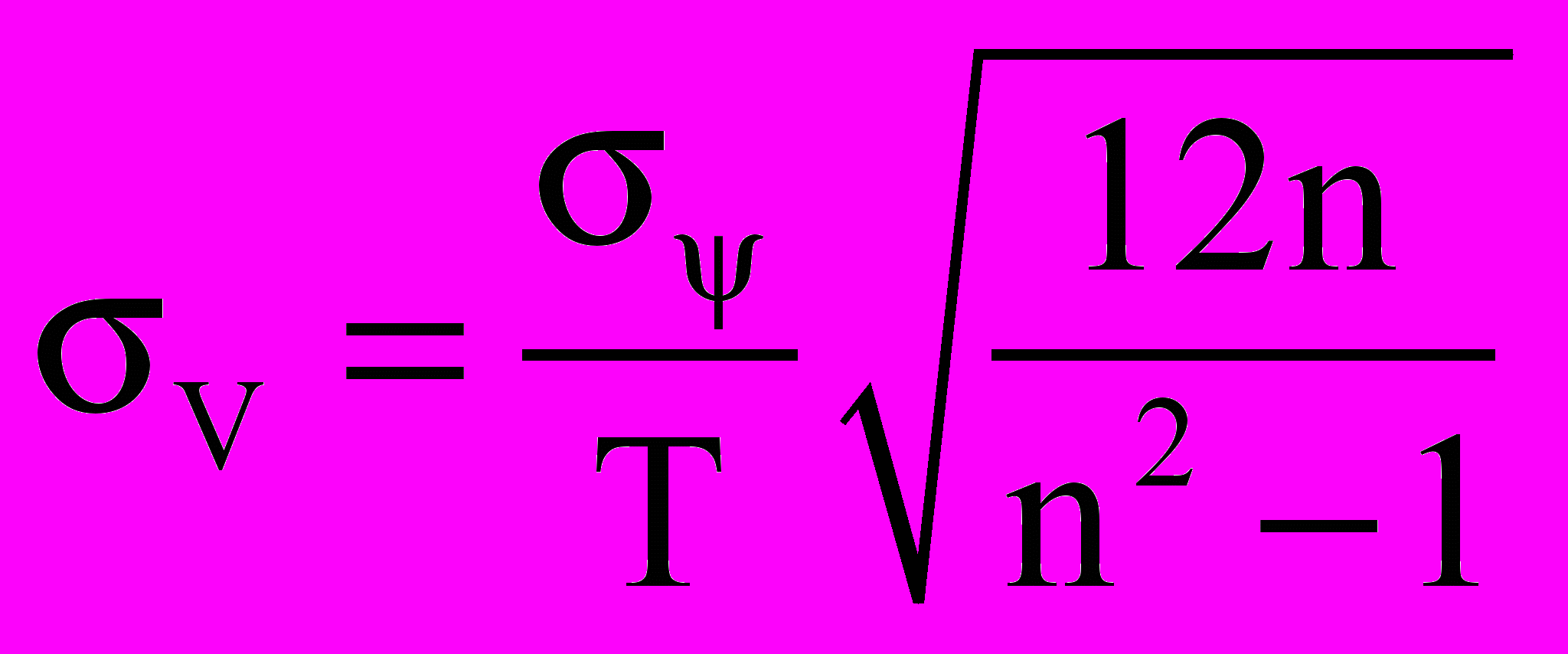, где σ_Ψ – СКО погрешности определения угла между двумя светящимися частицами, Т - общее время обнаружения. Из полученной оценки следует, что увеличение количества кадров при сохранении общего времени распознавания, не дает существенного улучшения результата. Поскольку точность определения координат уменьшается при сокращении времени накопления сигнала и 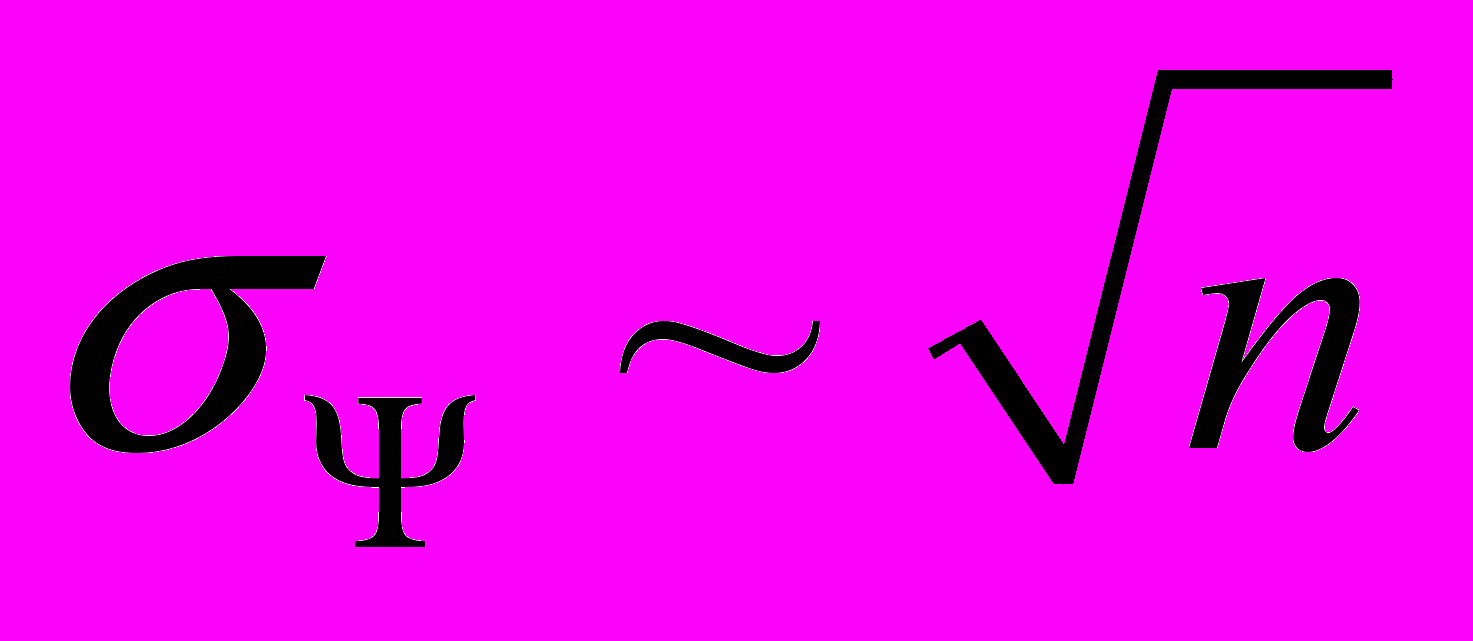. Таким образом, единственным эффективным путем уменьшения порога скорости движения помех типа «светящаяся частица» является уменьшение погрешности определения координат центра проекции звезды.

Свет ТИС после прохождения через оптическую систему проецируется на матрицу размытым пятном. Ошибка в определении координат светового источника зависит от характеристик матрицы, параметров проецируемого изображения и от используемого алгоритма определения координат. В работе предложено разделить методы определения координат ТИС на 2 класса – требующие априорной информации об анализируемых сигналах и шумах, и не требующие никакой предварительной информации. В работе проанализирована сложность создания и отладки программных средств для определения координат центра ТИС. Сделан вывод, что метод «центр тяжести» наиболее подходит для использования в приборах звездной ориентации с маломощным процессором.

В Главе 4 рассмотрены особенности вычислительного блока приборов звездной ориентации, описаны методики моделирования алгоритмов определения координат ТИС и алгоритм пересчета звездного бортового каталога, представлены особенности программной реализации предложенных в работе алгоритмов и степень их внедрения при разработке и производстве звездных приборов.

Для увеличения вероятности правильной селекции звезд, в диссертационной работе определено оптимальное соотношение размера проекции к размеру элементарного фотоприемника, при котором погрешность определения координат будет минимальной. С помощью интерпретатора MATLAB проведено имитационное моделирование для двух методов определения координат – «центра тяжести» и метода максимального правдоподобия.

Реализованная в работе модель основана на предположении, что фоточувствительная матрица представляет собой совокупность прилегающих друг к другу пикселей без зазоров между ними. Геометрически плоскости матрицы соответствует область проекции изображения G, изображенная на рисунке 4. Область G разбита на прилагающие друг к другу непересекающиеся подобласти g_ij прямоугольной формы, соответствующие пикселям матрицы. Модель построена исходя из предположения, что количество фотонов, попавших на каждый элементарный фотоприемника, есть случайная величина, распределенная по закону Пуассона. Результаты моделирования, представленные на рисунке 5, для положения центра проекции, соответствующего точке «5» на рисунке 4, показывают, что оптимальное отношение радиуса рассеяния к размеру элементарного фотоприемника, при котором достигается наименьшая погрешность определения координат, для используемых в моделирование параметров составляет около 0.3 – 0.4.

Знание характеристик алгоритмов определения координат энергетических центров дает возможность оптимальным образом подобрать алгоритм и настройки оптической системы для каждого конкретного типа приборов звездной ориентации. Такой оптимальный подбор алгоритмов и параметров системы уменьшает погрешность определения координат на 15-20%. В свою очередь это обеспечивает увеличение точности ориентации КА и уменьшает общее время, требуемое для определения положения КА в космическом пространстве. Задача определения координат точечных источников света возникает не только при ориентации КА по звездам, но и в других отраслях как робототехника и геодезия, поэтому полученные результаты моделирования имеют важное прикладное значение.



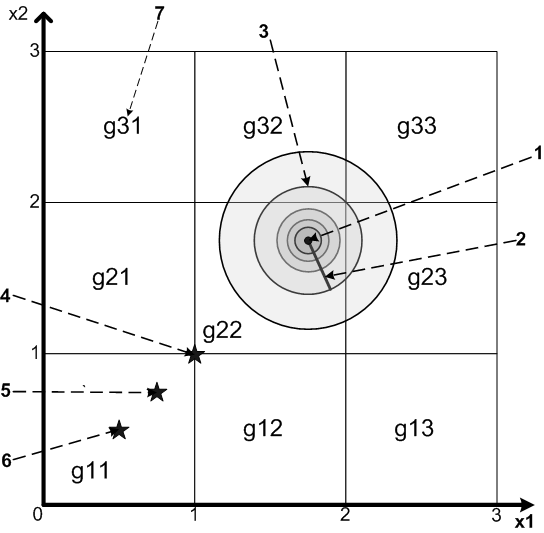
Рисунок 4 – Область проекции изображения G.

Примечание – Цифрами обозначено: 1 – центр проекции ТИС х0, 2 – радиус рассеяния r, 3 – линии уровня мощности сигнала, 4, 5, 6 – положения центра проекции относительно приемной структуры, использовавшиеся при моделирование, 7 – подобласть g области G, соответствующая элементарному фотоприемнику.

В главе был произведен обзор характеристик современных цифровых сигнальных процессоров, чья частота на текущий момент (2010 г.) составляет от 100 до 1000 мГц. Для приборов звездной ориентации чаще используются процессоры частотой 100-200 мГц. Ограничения на объем ОЗУ и ПЗУ, используемого в астроприборах, составляют порядка нескольких Мб, что вызвано требованиями к радиационной стойкости прибора. Указанные ограничения на объем памяти требуют экономичного представления и хранения данных.

В рамках диссертационного исследования было создано программное обеспечение, реализующее предложенные алгоритмы и методы. Алгоритмы, предназначенные для использования непосредственно в вычислительном блоке прибора, были реализованы на языке низкого уровня – ассемблера для процессора NM6403. разработанного ЗАО НТЦ «Модуль» (г. Москва). Средства визуализации работы предложенных методов и алгоритмов реализованы на высокоуровневых языках объектно-ориентированного программирования C++ Bilder и Delphi. Алгоритмы, требующие сложной матричной арифметики, реализованы в среде интерпретатора MATLAB и могут быть использованы на любой платформе, на которой имеется соответствующий интерпретатор. Созданное программное обеспечение используется в ОАО «НПО «Геофизика-Космос» для астроприборов.



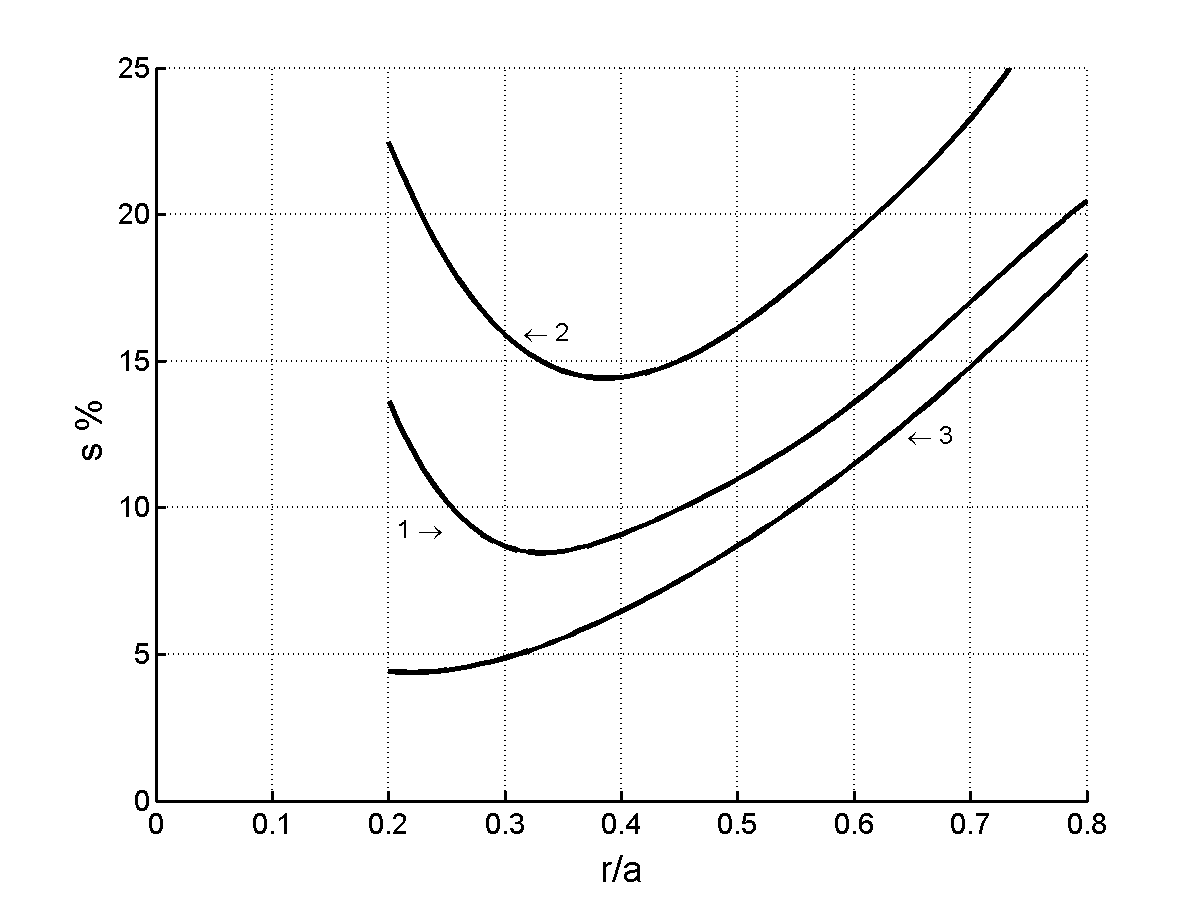
Рисунок 5 – Зависимость СКО определения координат от величины радиуса рассеяния.

Примечание – Цифрами обозначено: 1 – СКО координат полученных ММП, 2 – СКО координат полученных методом ЦТ, 3 – оценка СКО координат, основанная на неравенстве Рао-Крамера.

В Заключение приведены основные результаты работы и указаны направления дальнейших исследований. В Приложениях приведены акт о внедрении результатов диссертационной работы, характеристики современных сигнальных процессоров и детальное описание компонент созданного программного обеспечения.


ОСНОВНЫЕ РЕЗУЛЬТАТЫ ДИССЕРТАЦИОННОЙ РАБОТЫ

1. Проведено исследование методов распознавания групп звезд из поля зрения прибора на основании информации базы данных прибора. Предложена классификация методов и приведены данные по их трудоемкости и устойчивости к наличию «ложных» звезд. Сделан вывод, что наибольшей устойчивостью по отношению к наличию «ложных» звезд обладает выборная схема Коломенкина.
   
2. Построена математическая и программная модель движения проекций светящихся частиц по плоскости фоточувствительной матрицы, на основе которой исследован тип траекторий движения проекции при равномерном вращение спутника по орбите и установлен вид поля скоростей движения проекций, даны оценки нелинейности траекторий. Показано, что при равномерном вращение КА проекции звезд движутся по кривым второго порядка.
   
3. Разработан эвристический метод предварительный селекции помех типа «светящаяся частица» использующий критерий постоянства скоростей проекций. Метод селекции и программное обеспечения для визуализации его работы реализованы на языке Delphi. Предложенный алгоритм позволяет распознавать частицы, движущиеся со скоростью 6 угл. мин/с с вероятностью 0.95.
   
4. Разработана и реализована процедура окончательного отбора, основанная на последовательном правиле Вальда, осуществляющая селекцию звезд с заданными вероятностями пропуска и ложного обнаружения.
   
5. Разработан эвристический метод предварительный селекции помех типа «светящаяся частица», анализирующий матрицу скорости изменения взаимных угловых расстояний. Метод селекции и программное обеспечения для визуализации его работы реализованы на языке C++. Предложенный алгоритм позволяет распознавать частицы, движущиеся со скоростью 6 угл. мин/с с вероятностью 0.98.
   
6. Разработанные и реализованные в работе алгоритмы предварительной селекции помех типа «светящаяся частица» увеличивают вероятность правильного распознавания групп звезд и уменьшают время, требуемое для распознавания. Так, если в поле зрения прибора попадает столько же «светящихся частиц», сколько и звезд, то использование процедуры предварительной селекции уменьшает время работы алгоритма распознавания в 4 раза.
   
7. Проведено имитационное моделирования для определения координат центра проекции точечного источника света на плоскости фоточувствительной матрицы методом максимального правдоподобия. Программное обеспечение для проведения моделирования реализовано в среде интерпретатора MATLAB. Результаты моделирования показали, что метод максимального правдоподобия обладает точностью на 25% большей по сравнению с методом «центр тяжести», но на 10% меньшей по сравнению с оценкой Рао-Крамера. При этом метод «центр тяжести» менее трудоемок и проще в реализации и отладке.
   
8. На основании моделирования определено оптимальное отношение радиуса рассеяния проекции точечного источника света к размеру элементарного фотоприемника матрицы с точки зрения минимизации погрешности оценки координат центра проекции. Такое отношение составляет 0,3 – 0,4. Правильный выбор отношения радиуса рассеянья к размеру пикселя позволяет увеличить точность ориентации по сравнению с существующей на 15 – 20%.
   
9. Для тестирования и анализа алгоритмов распознавания звезд созданы программные средства визуализации процесса распознавания, реализованные в средах разработки Delphi, C++ Bilder, MATLAB. Программные средства, предназначенные для эксплуатации на орбите, реализованы на языке низкого уровня для процессора NM6043.
   

СПИСОК РАБОТ, ОПУБЛИКОВАННЫХ ПО ТЕМЕ ДИССЕРТАЦИИ

1. Кружилов И.С. О влиянии относительного размера изображения на погрешность определения координат // Компьютерная оптика. -2009. –Т. 32. № 3. –С. 210-215. – ISSN 0134-2452.
   
2. Кружилов И.С. Селекция звезд по скоростям в алгоритме астронавигации // Системы Управления и Информационные Технологии. –2009. –№ 3. –С. 55-58. –ISSN 1729-5068.
   
3. Кружилов И.С., Шамаева О.Ю. Алгоритм селекции звезд по постоянству угловых расстояний // Программные продукты и системы. –2009. –№ 3. –С. 82-84. –ISSN 0236-235X.
   
4. Кружилов И.С. Селекция звезд в задаче астронавигации по признаку постоянства угловых расстояний // Вестник МЭИ. -2009. –№ 6. –С 199-205. –ISSN 1993-6982.
   
5. Kruzhilov I. Estimation of stars coordinates for stars trackers // 12^th International Conference and exhibition on DIGITAL SIGNAL PROCESSING AND ITS APPLICATIONS. Moscow. 2010. -P. 218. –ISBN 978-5-904602-07-9.
   
6. Кружилов И.С. Выбор размера проекции для алгоритмов определения координат точечных источников света // XV международная научно-техническая конференция РАДИОЛОКАЦИЯ, НАВИГАЦИЯ, СВЯЗЬ : в 3 т. –Воронеж: НПФ «САКВОЕЕ» ООО. 2009. –Т. 1. –С. 321-329. –ISBN 978-5-904259-01-3.
   
7. Кружилов И.С. Метод отбора звезд в алгоритме астронавигации // Математика, компьютер, образование. Сборник научных тезисов. Выпуск 14. –Ижевск: НИЦ «Регулярная и хаотическая динамика». 2007. -С. 72. –ISBN 5-93972-582-1.
   
8. Кружилов И.С. Особенности разработки алгоритмов фильтрации светящихся источников в астроприборах. Труды XVI международной научно-технической конференции «Информационные средства и технологии» : в 3 т. –М.: Издательский дом МЭИ. 2008. –Т. 3 –С. 50-57. –ISBN 978-5-383-00317-6.
   
9. Кружилов И.С. Алгоритм распознавания звезд в задаче астронавигации // Труды международной научно-технической конференции «Информационные средства и технологии»: в 2 т. –М.: Янус-К. 2005. -Т. 2. -С. 28-30. –ISBN 5-8037-0287-0.
   
10. Кружилов И.С. Распознавание образов для алгоритма астронавигации // РАДИОЭЛЕКТРОНИКА, ЭЛЕКТРОТЕХНИКА И ЭНЕРГЕТИКА тринадцатая международная научно-техн. конф. студентов и аспирантов: Тезисы докладов: в 3 т. –М.: МЭИ, 2007 г. -Т. 1. С. 369-370. –ISBN 978-5-903072-97-2.
    
11. Кружилов И.С., Шамаева О.Ю. Выбор размера проекции для алгоритмов определения координат точечных источников света // Моделирование и анализ данных: Труды факультета информационных технологий МГППУ (Вып. 4). -М.: РУСАВИА. 2009 –C. 46-54 –ISBN 978-5-900078-63-2.
    
12. Kruzhilov I. Evaluation of maximal error of star selection criterion for the problem of astronavigation // Mathematic, Computer, Education 15. Dubna. 2008. –P. 452.
    
13. Kruzhilov I. S. Movement of stellar projection on plane of analysis in astronavigation problem. // 13-th Annual Conference of under-graduate and post-graduate students "RADIO-ELECTRONICS, ELECTRICAL and POWER ENGINEERING". Moscow. 2008. –P. 289.