Лекция 8 Системное программирование. Системное проектирование взаимодействия процессов. Сети Петри. Флаговые и пусковые функции. Асинхронные протоколы
| Вид материала | Лекция |
- Рабочая программа учебной дисциплины (модуля) Системное программирование, 108.12kb.
- Техническое задание на выполнение курсовой работы по дисциплине "Системное программирование, 120.51kb.
- Асинхронные программы. Возможные некорректности в их работе. Сети Петри. Разметка сети, 70.35kb.
- Стэнли Янг системное управление организациейянг С. Системное управление организацией, 6260.5kb.
- Программа вступительного экзамена по специальности 05. 13. 18 Математическое моделирование,, 115.33kb.
- Общая характеристика и классификация программного обеспечения и базовых технологий, 132.64kb.
- М. В. Ломоносова Факультет вычислительной математики и кибернетики Н. В. Вдовикина,, 2124.49kb.
- Ые системы", "Операционные системы, среды и оболочки" и "Операционные системы и системное, 1294.27kb.
- Программа вступительного экзамена, 67.56kb.
- Лекция: Сети и сетевые операционные системы, 585.67kb.
Лекция 8
Системное программирование. Системное проектирование взаимодействия процессов. Сети Петри. Флаговые и пусковые функции. Асинхронные протоколы.
Под системой в этом случае понимают вычислительную систему (ВС), состоящую из процессоров (обычно разнородных) и запоминающих устройств. Например, процессоры: арифметическое устройство, устройство – шина, устройство управления памятью, устройство управления диском, устройство печати, устройство управления каналом и т.д.. Все эти устройства взаимодействуют между собой. Проектирование (программирование) такой ВС по сути дела имеет целью взаимоувязку процессов, происходящих в отдельных элементах системы, при выполнении конкретной нужной пользователю задачи. Для целей взаимоувязки (согласования) процессов в ВС служит специальный инструмент – операционная система, которая «прячет» от пользователя очень сложную логику взаимодействия процессов, оставляя ему только манипуляцию инструкциями, управляющими ОС. Иногда для объединения различных устройств в ВС нельзя воспользоваться штатной ОС, приходится создавать свою специализированную ОС. Пользователь, а тем более системный программист, должен понимать логику описания взаимодействия процессов в ВС. Одним из способов формализации такой логики могут служить сети Петри (PN).
Взаимодействие в PN моделируется событиями, которые запускают те или иные процессы. Содержательно, в большинстве случаев, события связаны с освобождением (или захватом) различных вычислительных ресурсов (памяти, каналов, устройств) или с сигналами о выполнении той или иной работы (процесса) в устройстве (или группе устройств), которые поступают на объекты управления в виде сообщений.
Другим способом описания логики взаимодействия процессов может служить формальная система – асинхронный автомат, предложенная в 1967 г. Котовым – Нариньяни, которая в интерпретации к системному программированию носит название – «Метод пусковых и флаговых функций». По сути дела пусковые и флаговые функции специфицируют основные элементы сетей Петри. Таким образом, моделью взаимодействия общего вида служит сеть Петри, поведение которой управляется событиями.
I. Сети Петри. Асинхронно взаимодействующие процесы
- Парадигмы последовательно-параллельных
процессов
Процесс в некоторой системе может наблюдаться только через последовательность событий, а каждое событие связано только с изменением сущностей (характеристик), определяющих (выделяющих из множества объектов) систему.
а) Парадигма Клини.
Вводится множество цепочек (последовательностей) событий. Цепочки событий альтернативны, то есть не могут выполняться одновременно. Для структурного описания множества цепочек служат регулярные выражения (формулы), либо графы машины состояний, которые представляют собой сети Клини (CN).
б) Парадигма Ван-Хао (Вонга).
В сетях Ван-Хао (WN) события от вершины – инициатора распространяются «фронтально» (параллельно, независимо друг от друга). Для описания фронтального процесса WN представляется специальной ярусно-параллельной формой (ЯПФ), по которой строятся различные деревья (сценарии) фронтального распространения событий.
CN и WN отражают различные, по сути дела взаимоисключающие, модели событийных процессов, и не могут претендовать на универсальное описание.
в) Парадигма Петри.(PN)
Основное свойство процессов, как последовательностей событий, заключается в их взаимодействии. При этом взаимодействие предполагает «запуск» некоторого процесса, может быть, несколькими событиями, которые произошли в других процессах. В связи с тем, что события происходят «одномоментно» (не имеют длительности), для фиксирования совпадения необходимо их «помнить». Для моделирования событийного взаимодействия процессов немецкий ученый Петри в 1963 г. предложил специальную сеть (PN), которая имеет свойства CN и WN и, кроме того, она содержит элементы памяти о произошедших ранее событиях, а также содержит элементы, генерирующие события.
- Формальная система для сетей Петри.
Формальная система
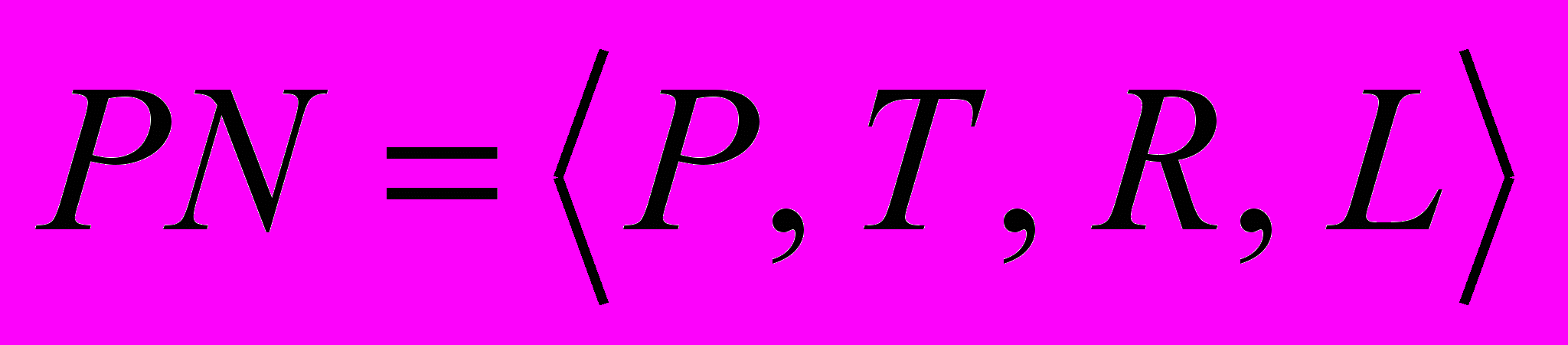 определяет сеть Петри, где
определяет сеть Петри, где 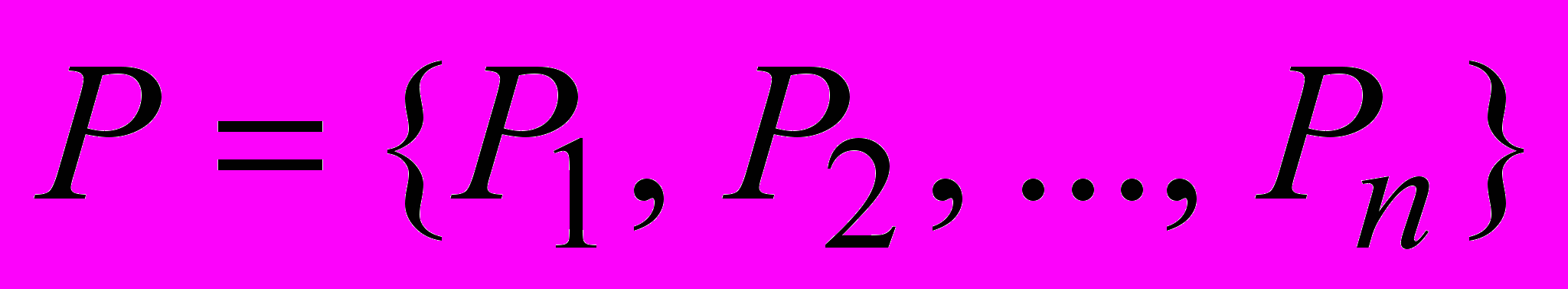 – множество позиций,
– множество позиций, 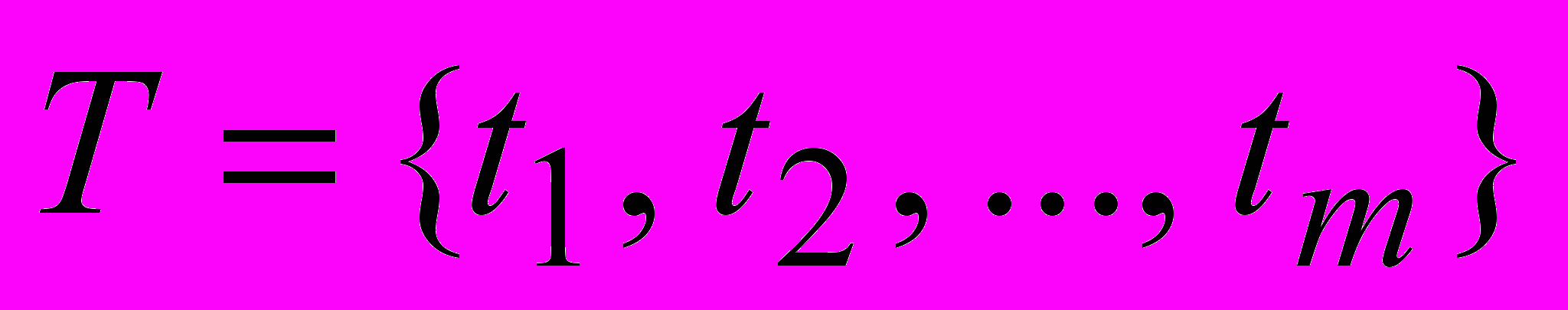 – множество переходов; R – отношение, связывающее Р и Т в правильно построенные формулы (ППФ), L – разметка сети PN.
– множество переходов; R – отношение, связывающее Р и Т в правильно построенные формулы (ППФ), L – разметка сети PN.ППФ для PN суть картинка и задаётся направленным графом с двумя типами вершин Р и Т, при этом картинка PN понимается как некоторая формула, построенная по формальным правилам и называется ППФ(PN).
Процесс построения ППФ(PN) определяется индуктивно.
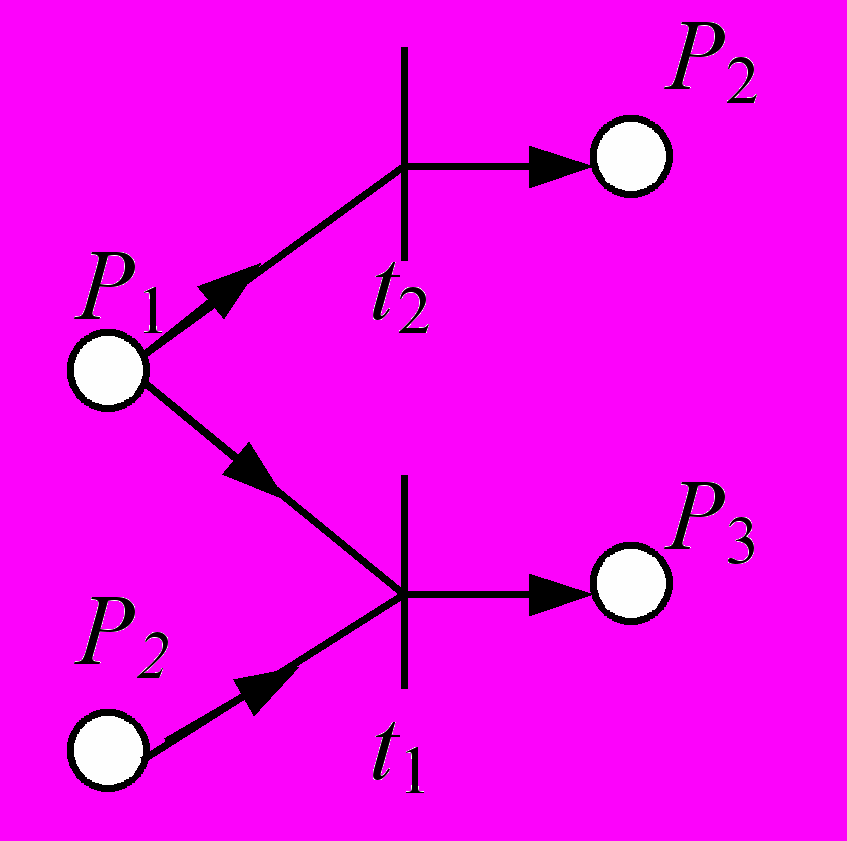
1) Элементарные ППФ(PN) – суть картинки следующего вида
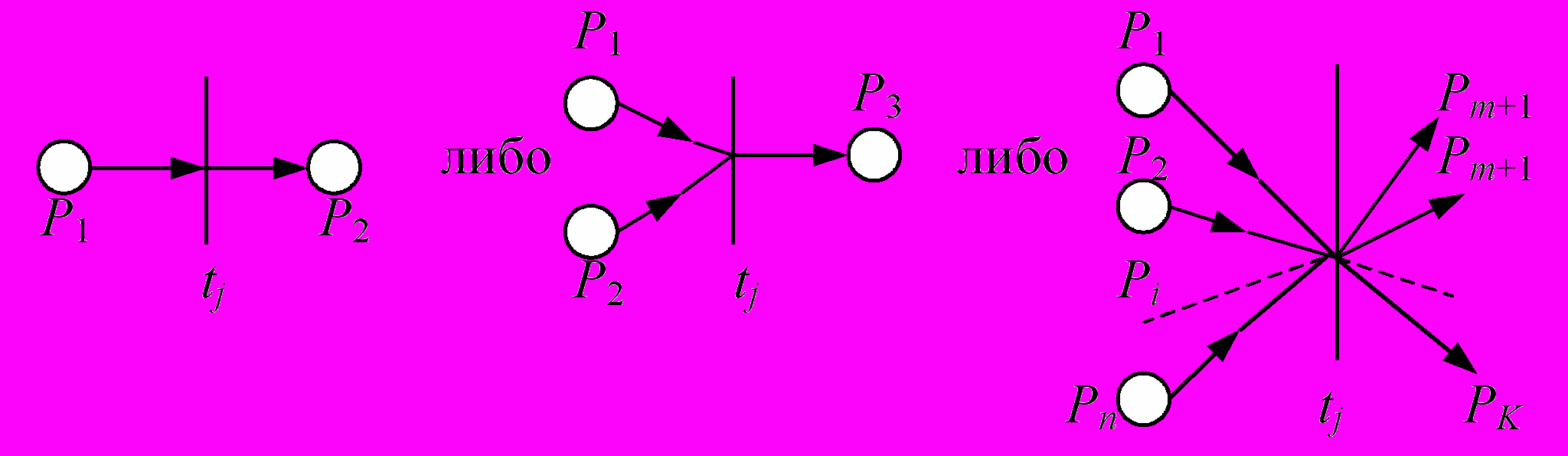
где все Pi в бинарном отношении (Pi tj) называются входными позициями для перехода tj, а Pk в бинарном отношении (tj Pk) называются выходными позициями для перехода tj. Элементарная ППФ содержит ровно одну вершину типа t.
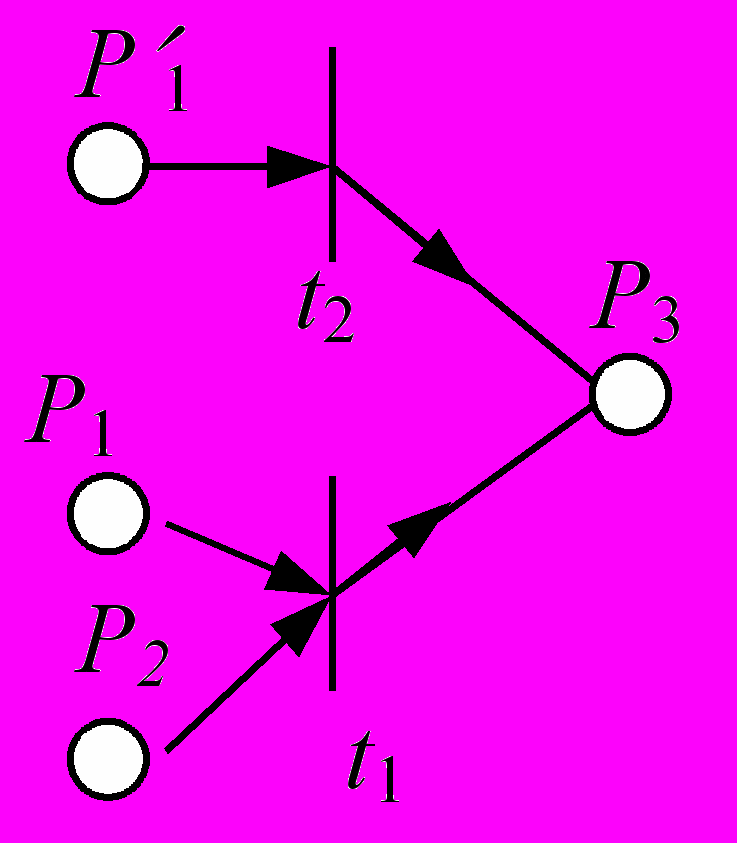
2) Операция композиции (конструирования) – отождествление вершин P в нескольких ППФ, дает снова ППФ. Пусть заданы две сети Петри PN1 и PN2. Из них можно сконструировать сложные сети Петри, показанные на примерах а), б), в).
а) отождествление (Р3 Р1 = Р3) и отождествление (Р1 Р2 = Р1)

б) отождествление (Р1 Р1 = Р1) в) отождествление (Р3 Р2 = Р3)
Определение разметки PN. Каждая позиция P PN может быть пустой, либо содержать отметку (фишку), в этом случае говорят, что P PN «занята». Для некоторых типов сетей позиция может содержать несколько фишек (может быть бесконечное число фишек). В настоящем рассмотрении позиция может быть в двух состояниях: «занята» / «не занята». В этом случае PN называется простой сетью Петри.
1.3 Интерпретация PN задает правила «срабатывания» переходов в PN и изменение разметок позиций, и тем самым определяет возникновение событий в PN, связанных с совершением переходов.
1) Правила срабатывания PN.
а) Переход называется подготовленным к срабатыванию, если во всех входных позициях «стоят» фишки, а все выходные позиции «пустые»
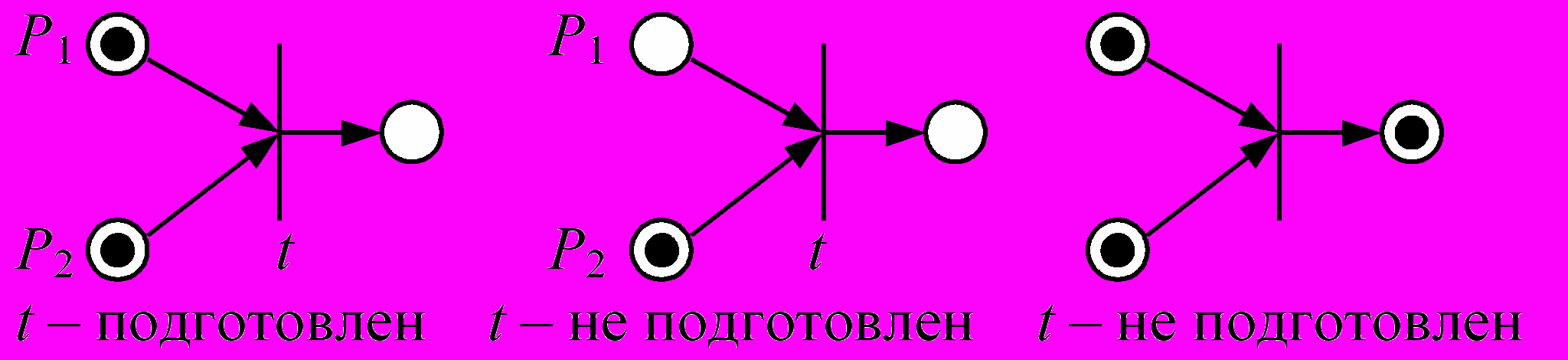
2) Правило изменения разметки при срабатывании перехода. Если переход подготовлен, то он может сработать и при этом все входные позиции освобождаются (становятся пустыми), а все выходные позиции занимаются фишками.
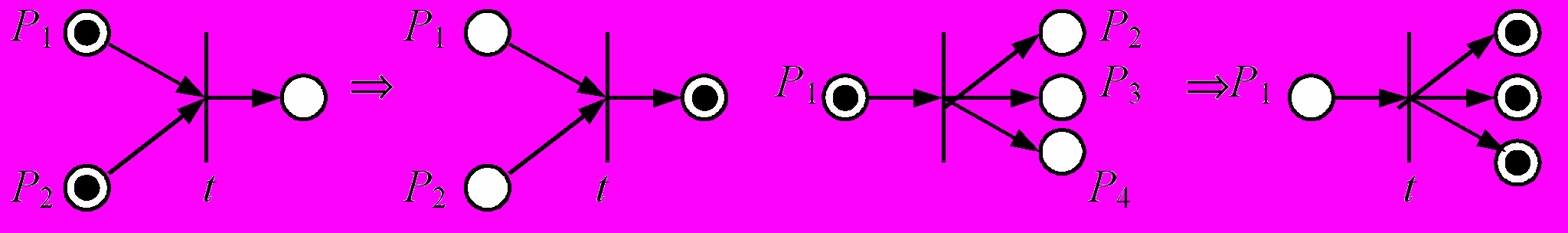
3) Правило единственного срабатывания определяется следующими картинками (формулами).
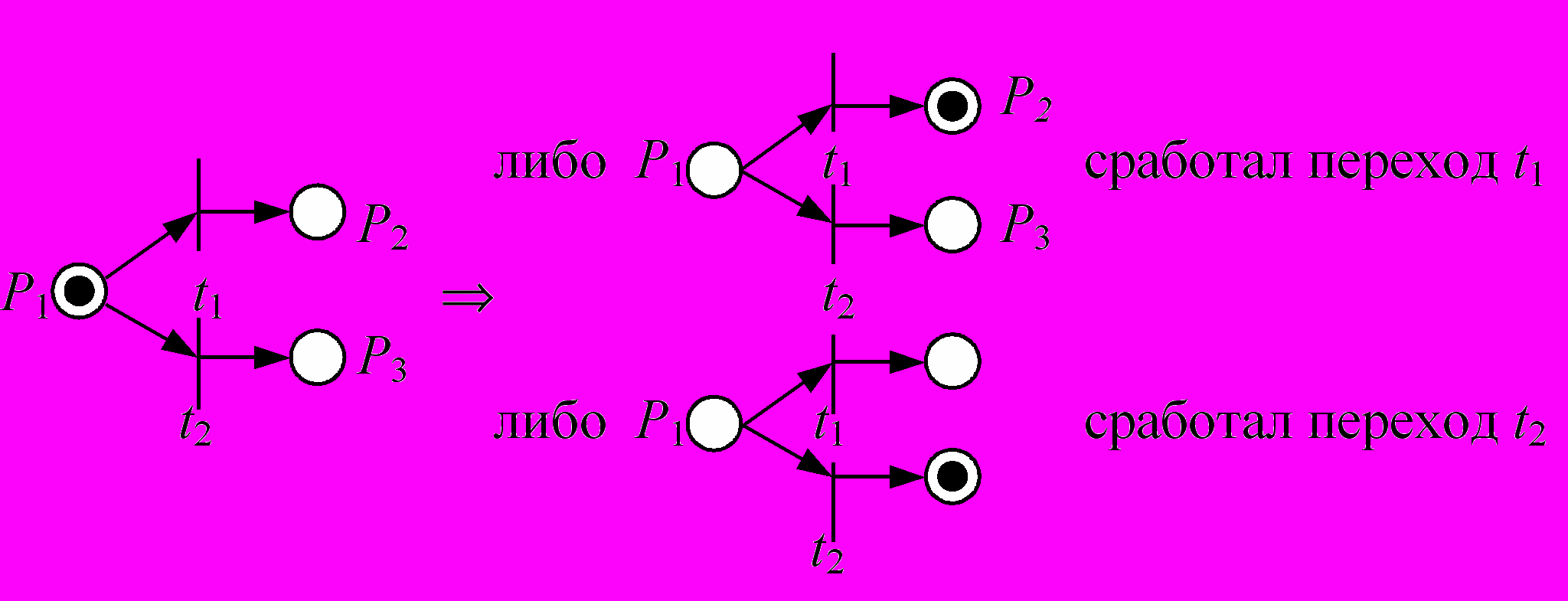
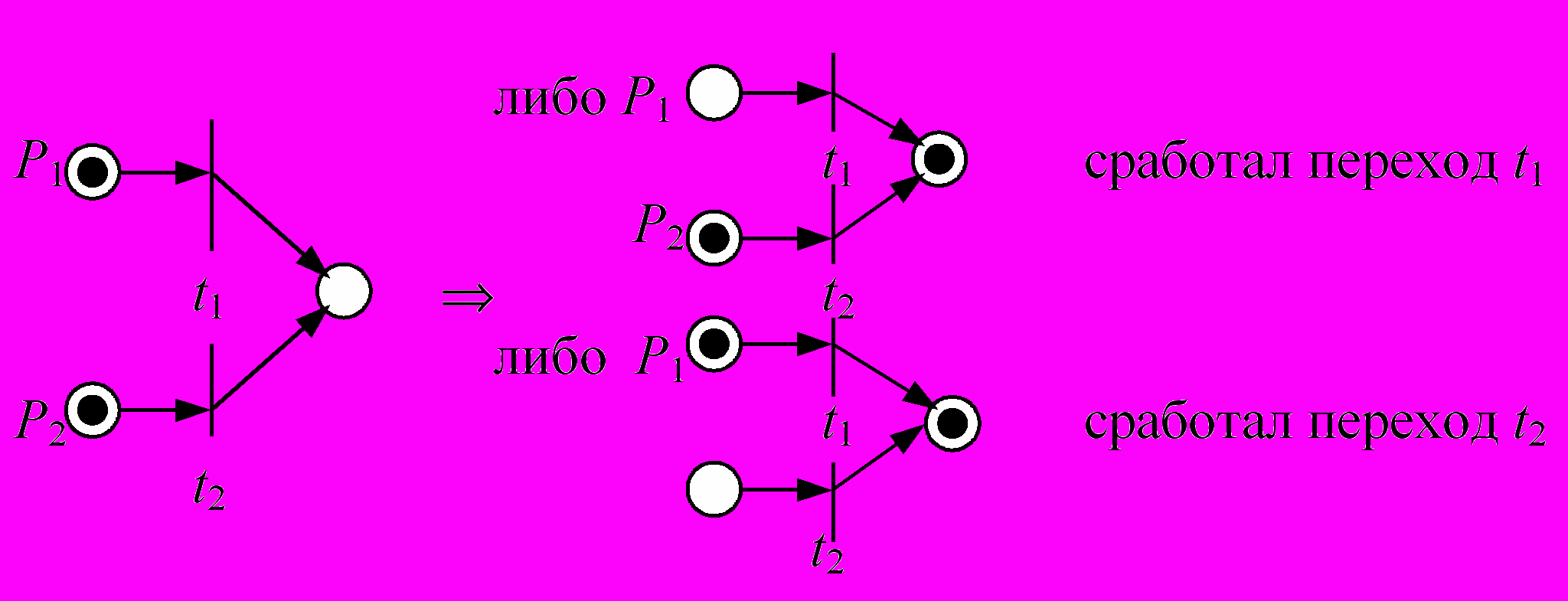
1.4. Семантика PN задает различные сценарии развития событий, то есть различные цепочки событий или в общем случае деревья событий (распространение фронта событий), которые порождают процессы, происходящие в системе.
- Семантика перехода t. С переходом t всегда связан некоторый процесс, который «включается» входными событиями, в результате процесса изменяется сущность (некоторая характеристика процесса), которая отмечается соответствующим выходным событием. С каждым переходом t (и, соответственно, с процессом) связан свой собственный процессор, который производит изменения сущности. Поэтому, когда срабатывает выходное событие, контролирующее изменение сущности, вообще говоря, процесс может продолжаться и дальше.
Таким образом семантика перехода St определяется
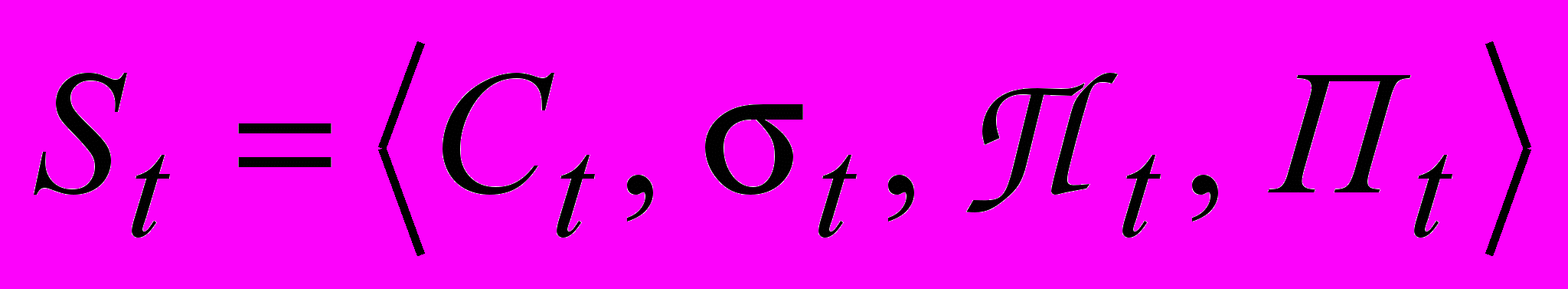 , где Ct – концепт (сущность) изменение которого должно контролироваться некоторым событием t, Пt – процесс (программа), приводящий к изменению Ct, Пt – процессор, который реализует процесс.
, где Ct – концепт (сущность) изменение которого должно контролироваться некоторым событием t, Пt – процесс (программа), приводящий к изменению Ct, Пt – процессор, который реализует процесс.- Семантика позиции. Позиция в сетях Петри исполняет роль памяти для выходного события, связанного с выполнением перехода, то есть изменением сущности. Если процесс Пt является программой, то событие заключается в наступлении значения «истинности» некоторого предиката, которое нужно для управления другим процессом (программой). Выходная позиция (память) освобождается сразу же после использования сообщения о событии для запуска другого перехода (процесса). Такое «пропадание памяти» о выходном событии не страшно, так как выходное событие «клонируется» в других входных позициях, «действующих» на множество других процессов.
- Семантика события. Входное событие наступает и запускает соответствующий переход, когда выполнено условие срабатывания перехода. Выходное событие наступает, когда процесс П выполнил некоторое условие.
Содержательно событие может быть связано с наличием, отсутствием или возвратом некоторого ресурса, необходимого для выполнения процесса. В системном программировании события ассоциируются с приказом (исполнением или его отменой), с угрозой (парированием угрозы) некоторому процессу, с окончанием некоторого процесса либо с неправильным его завершением.
При моделировании явлений живой природы и социальных явлений события связываются с интервальными или пороговыми значениями переменных, либо с конечным набором значений признаков, которые описывают сущности явления.
- Семантика сценариев описывается через множество альтернативных цепочек переходов и связанных с ними событий. Приведём несколько примеров.
Пример 1.
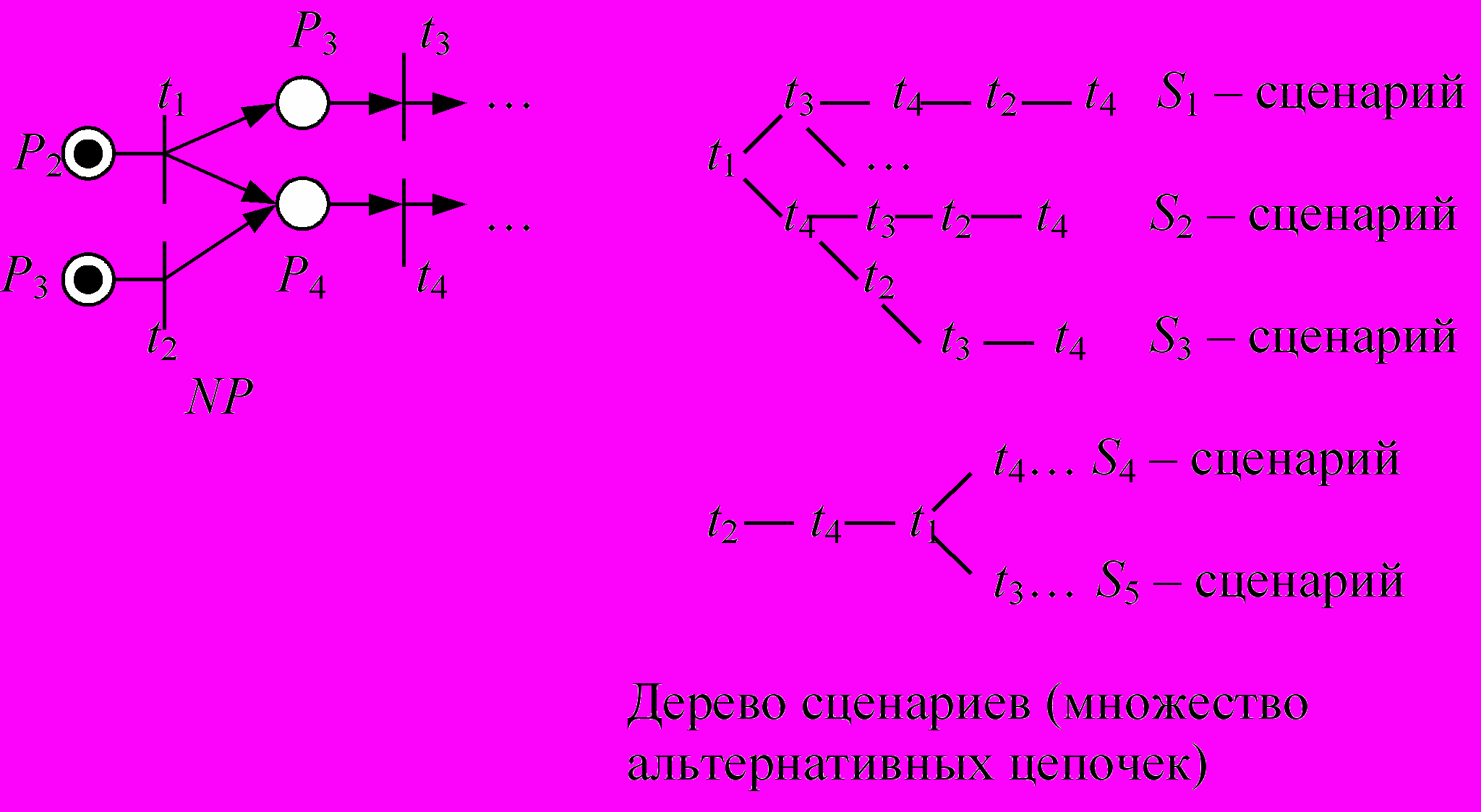
Если бы в момент окончания каждого перехода зажигалась лампочка характерного цвета, то последовательность вспыхивания лампочек происходила бы по одному из пяти сценариев.
П
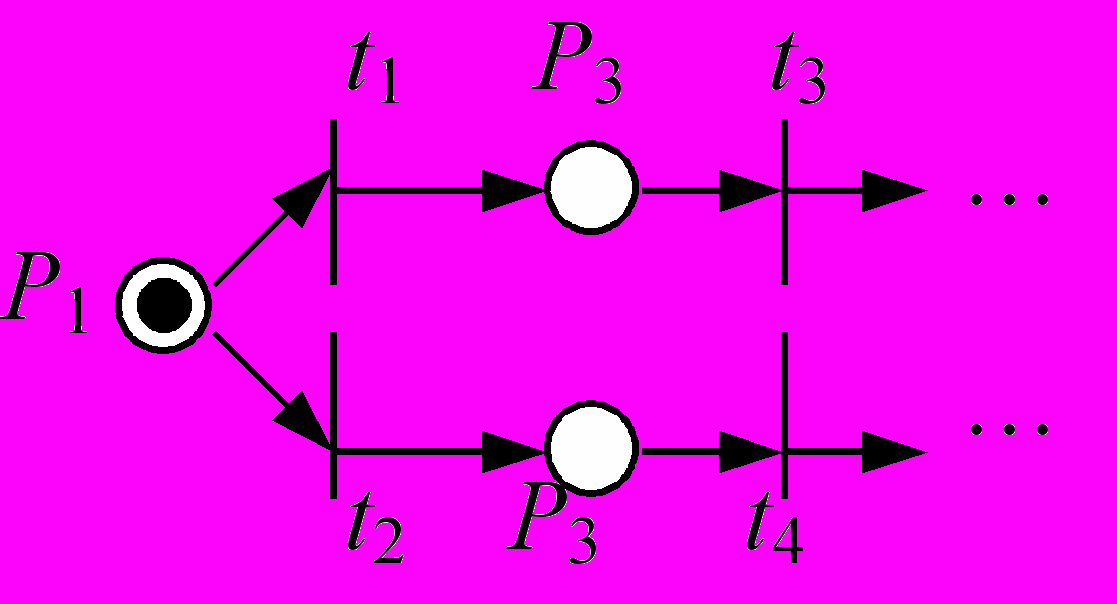 ример 2. PN аналог ЯПФ – две параллельные цепочки событий, два параллельных (независимых процесса), четыре сценария.
ример 2. PN аналог ЯПФ – две параллельные цепочки событий, два параллельных (независимых процесса), четыре сценария.S1 – t1 t2 t3 t4; S2 – t2 t1 t3 t4; S3 – t1 t2 t4 t3;; S1 – t2 t2 t4 t3.
РN является формулой в формальной системе. Если ввести интерпретацию переходов t в сети в виде количества квантов времени исполнения перехода , то множество конкретных сценариев при всех возможных значениях всех переходов не превысит множества цепочек событий в сети Петри. Таким образом формула (картинка) PN задает только логику взаимосвязи процессов. Конкретная реализация протекания процессов (сценарий) возникает при конкретных значениях времен переходов. (см. примеры 4, 5).
Пример 3. Четыре обедающих философа. Одновременно (независимо, параллельно) могут существовать в системе четыре процесса (4 процессора – 4 философа), каждый философ либо ест, либо беседует. Одновременно могут есть только два философа, используя разделяемые ресурсы (2 ножа, 2 вилки).
а
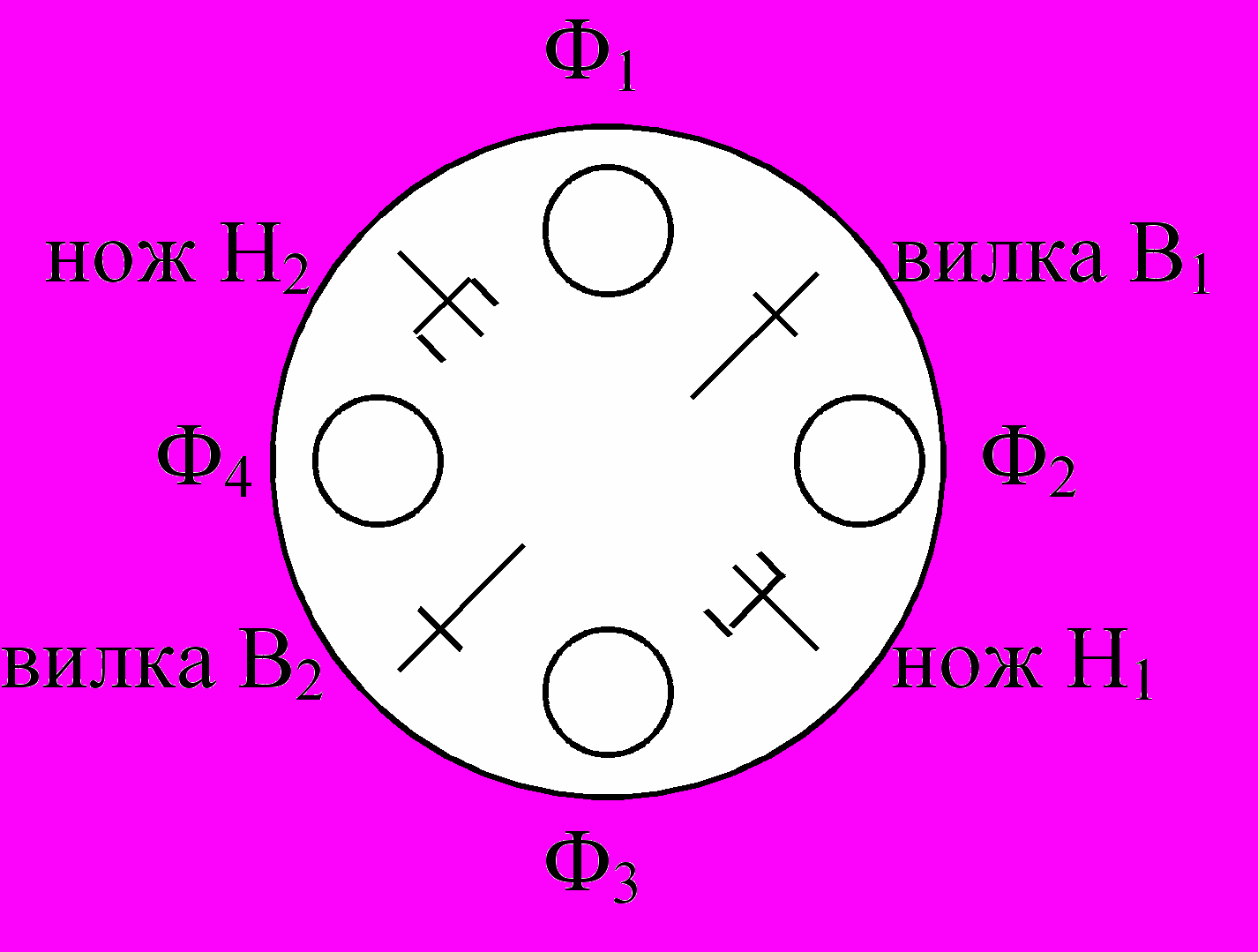 ) Содержательная модель
) Содержательная модель б) Сеть Петри
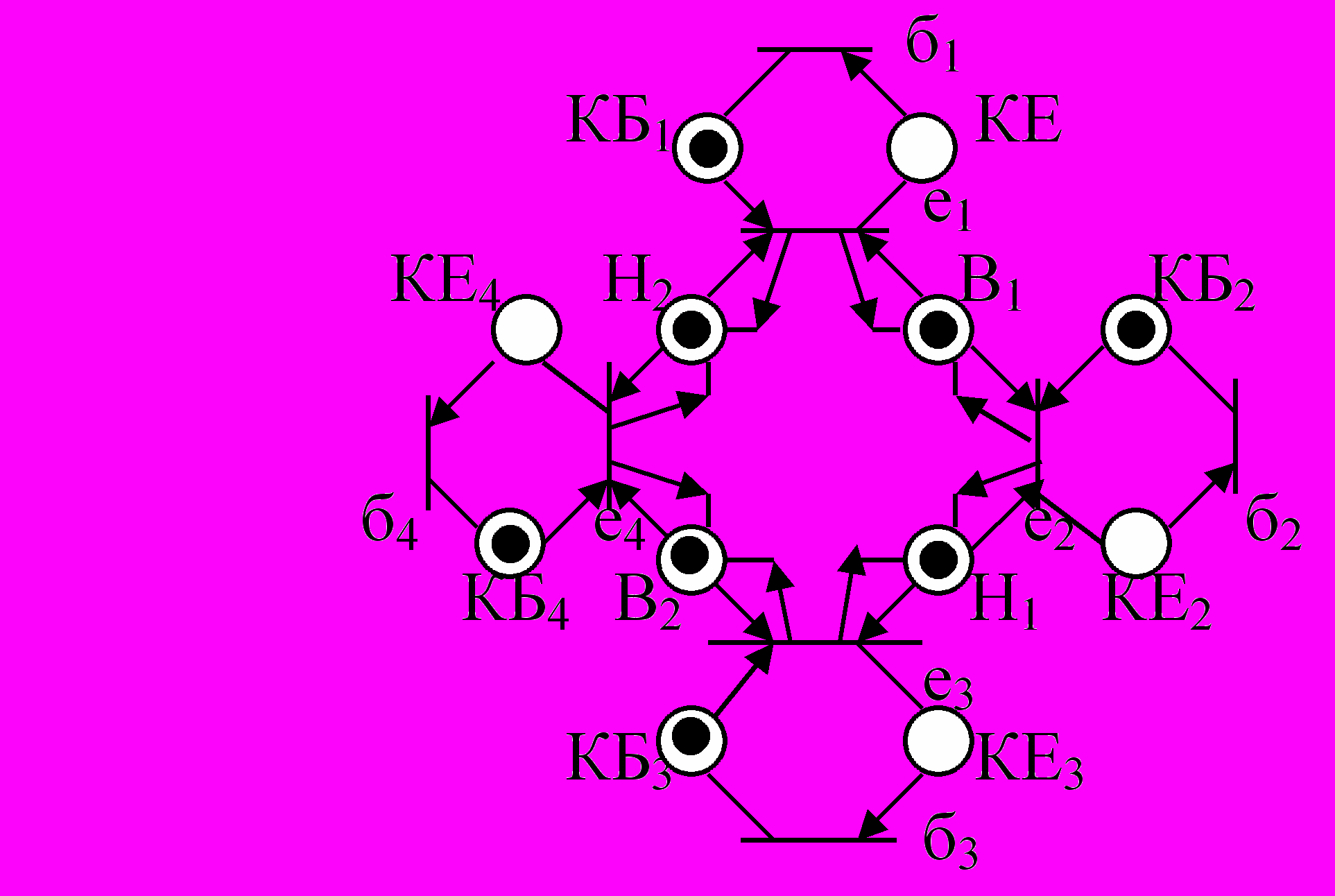
Процессы События
б1–Ф1 беседует
б2–Ф2 беседует
б3–Ф3 беседует
б4–Ф4 беседует е1–Ф1 ест
е2–Ф2 ест
е3–Ф3 ест
е4–Ф4 ест
КБ1–Ф1 закончил беседу
КБ2–Ф2 закончил беседу
КБ3–Ф3 закончил беседу
КБ4–Ф4 закончил беседу
КЕ1–Ф1 закончил есть
КЕ2–Ф2 закончил есть
КЕ3–Ф3 закончил есть
КЕ4–Ф4 закончил есть
В1, В2 – вилки свободны
Н1, Н2 – ножи свободны
Событийные взаимодействия процессов могут быть показаны графом в виде ярусно-параллельной формы, введенной ранее для информационных взаимосвязей между процессами в ИСА.
Для примера 3 ЯПФ независимых (параллельных) процессов системы «четыре обедающих философа» имеет вид:
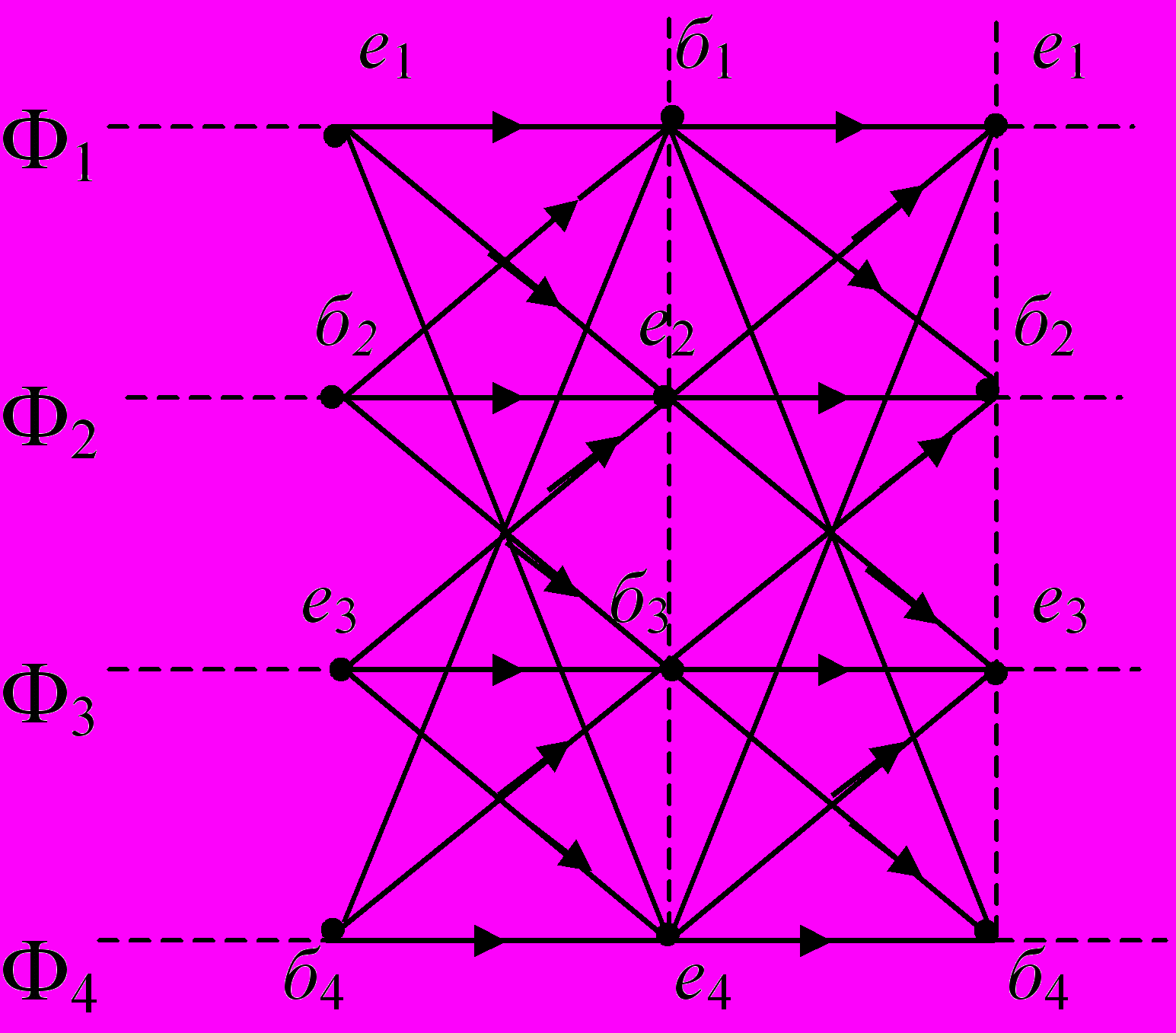
Все возможные сценарии, происходящие в системе четырёх обедающих философов, могут быть показаны на ЯПФ.
Процессы в ЯПФ связаны бинарным отношением «следует за», время работы каждого процесса может быть любым (в семантической модели каждый философ может тратить на еду и на беседу произвольное время). Если, в некотором смысле, «натянуть» граф ЯПФ на сетку физического времени, то процессы в процессорах Ф1, Ф2, Ф3, Ф4 – могут «скользить по процессорным стержням», а дуги «следуют за» должны быть «резиновыми». Процессы в каждом процессоре могут быть такими, что философы могут обгонять друг друга, приостанавливаться так, чтобы не рвать связи «следует за». Наделяя каждый элементарный процесс временем его «работы» можно моделировать поведение («гонки») в системе.
1.5 Сети Петри для конвейерных (pipe-line) систем.
Пример 4 Идеально сбалансированный синхронный конвейер. Модель RISC процессора. RISC-PN:
 RISC (Reduced Instruction Set Computer) – буквально: вычислительная машина с сокращенным набором команд. Каждая команда раскладывается на элементарные операции, которые выполняются последовательно на станциях конвейера. Каждая конвейерная операция выполняется ровно за квантов времени (такт конвейера). Входные данные поступают в каждом такте, выходные данные получаются через 4 такта. В RISC-конвейере обрабатываются одновременно данные поступившие за 4 последовательных такта.
RISC (Reduced Instruction Set Computer) – буквально: вычислительная машина с сокращенным набором команд. Каждая команда раскладывается на элементарные операции, которые выполняются последовательно на станциях конвейера. Каждая конвейерная операция выполняется ровно за квантов времени (такт конвейера). Входные данные поступают в каждом такте, выходные данные получаются через 4 такта. В RISC-конвейере обрабатываются одновременно данные поступившие за 4 последовательных такта.П
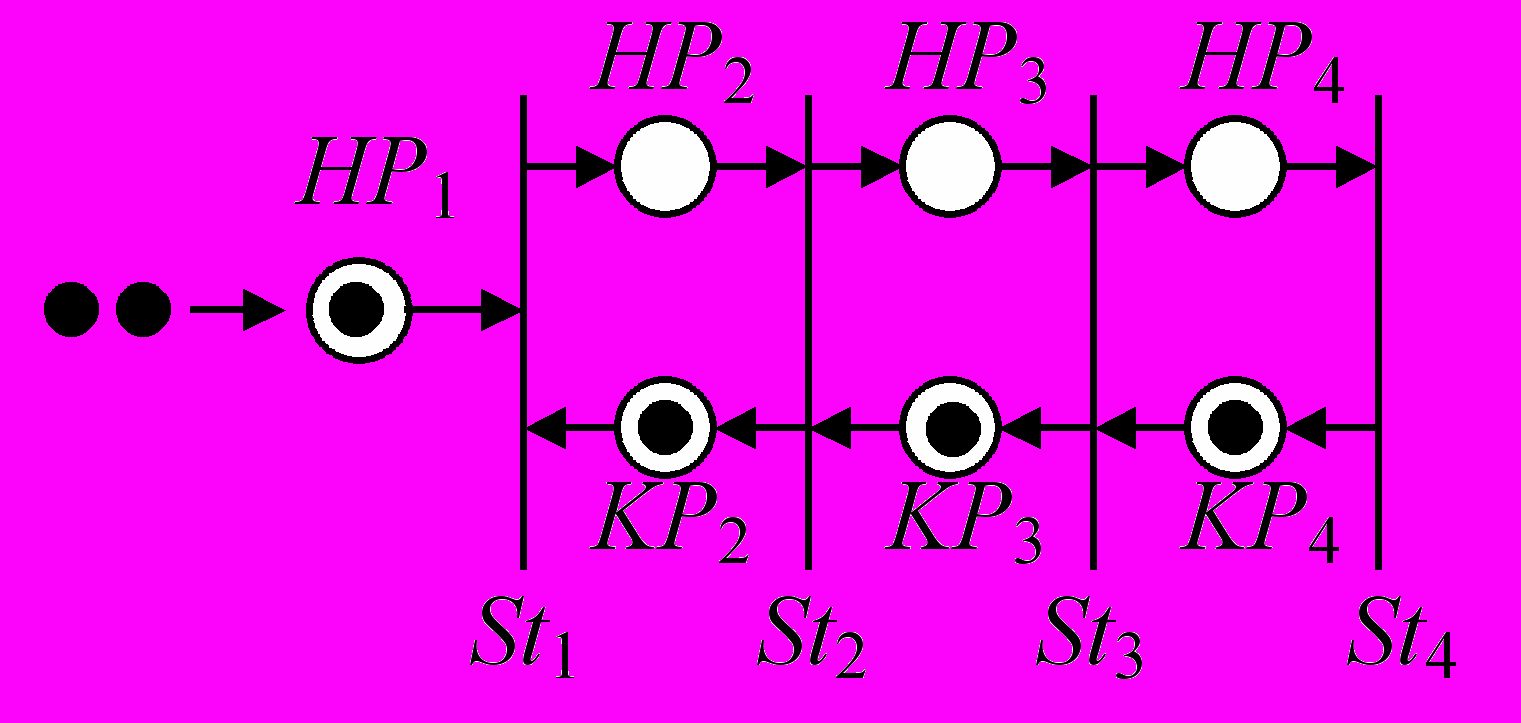 ример 5 Асинхронный конвейер. Информационный шлюз в Internet.
ример 5 Асинхронный конвейер. Информационный шлюз в Internet.События в шлюзе:
HPi – информация на входе станции есть; KPi – станция свободна и готова к работе
Процессы на станциях обра-
ботки имеют времена:
1 = 1 такт; 2 = 3 т.; 3 = 2 т.;
4 = 4 т.

Диаграмма работы информационного шлюза.
1.6. CASH – конвейер. CFN (cash flow net).
Позиция в PN может быть «занята» более чем одной фишкой и таким образом может быть накопителем фишек (cash – позиция). В случае, когда cash –позиция является выходной для некоторого перехода t, правило срабатывания для t не требуют свободной позиции, после срабатывания перехода t фишка прибавляется к содержимому накопителя. PN с cash – позициями иногда называются cash flow net. (CFN) применяются для моделирования асинхронных взаимодействующих процессов, где идёт накопление вещества, энергии, информации. Процессы запускаются, если соответствующие накопители не пусты. На рисунке приводится пример банковского CFN – конвейера.
Пример 6: CFN – банковский конвейер «инвестирование бизнес – проектов».
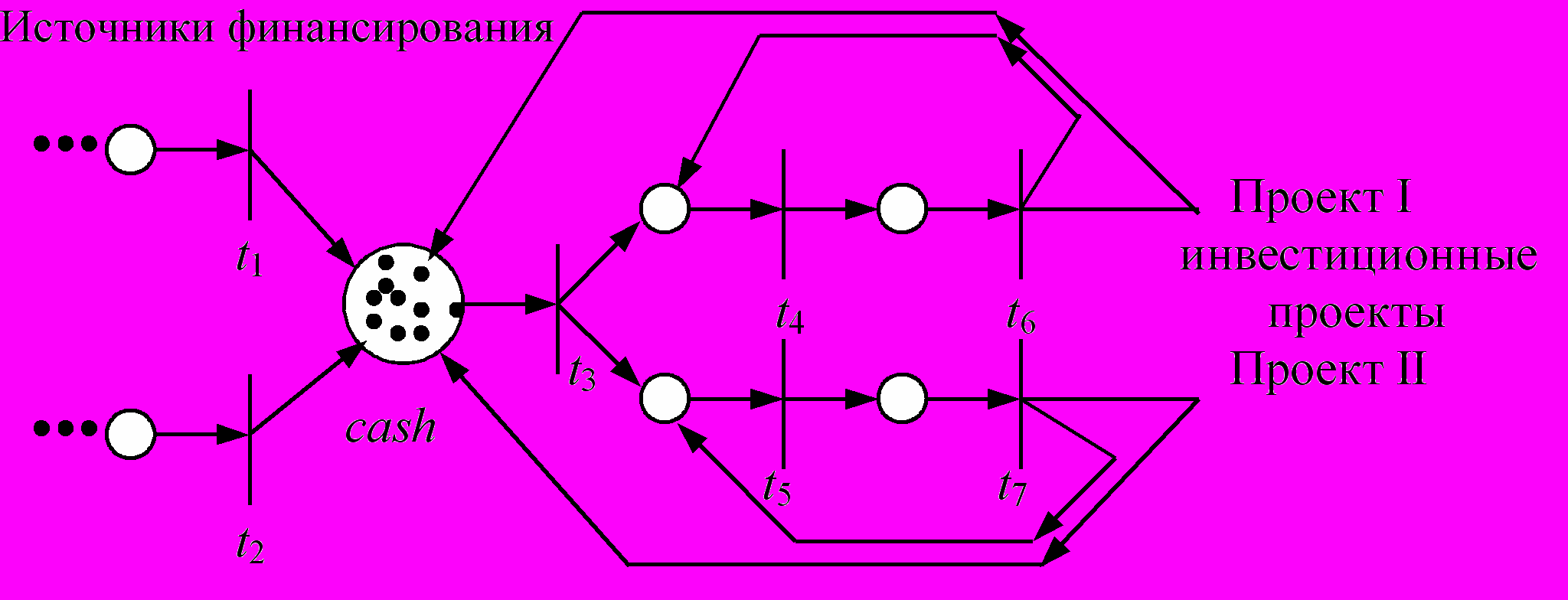 t4, t5 – начальные стадии проектов (не дающие денежной отдачи),
t4, t5 – начальные стадии проектов (не дающие денежной отдачи),t6, t7 – стадии самофинансирования и возврата долга в cash.
Имитационное моделирование CFN. Задаются времена процессов t1, t2, t3, t4, t5, t6, t7. Задача моделирования – выделить кризисные ситуации, т.е. выделить такие комбинации времён процессов, которые приводят к заданному классу сценариев, например, тупиковых, когда cash не успевает наполняться и все процессы останавливаются, либо когда процессы возврата денег недопустимо затягиваются.
В имитационную модель CFN можно вводить неопределённость в виде предсказуемости/непредсказуемости поведения элементов системы.
II.Метод пусковых и флаговых функций. Асинхронные
протоколы.
Рассмотрим элементарную сеть Петри.
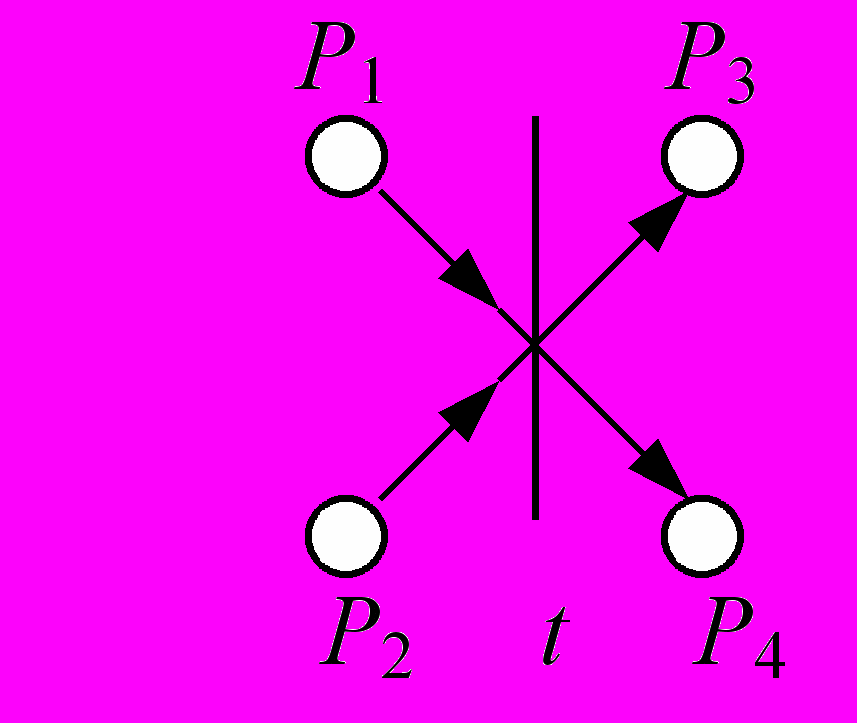
Сопоставим входным позициям флаговые функции (иногда говорят «флаги»)
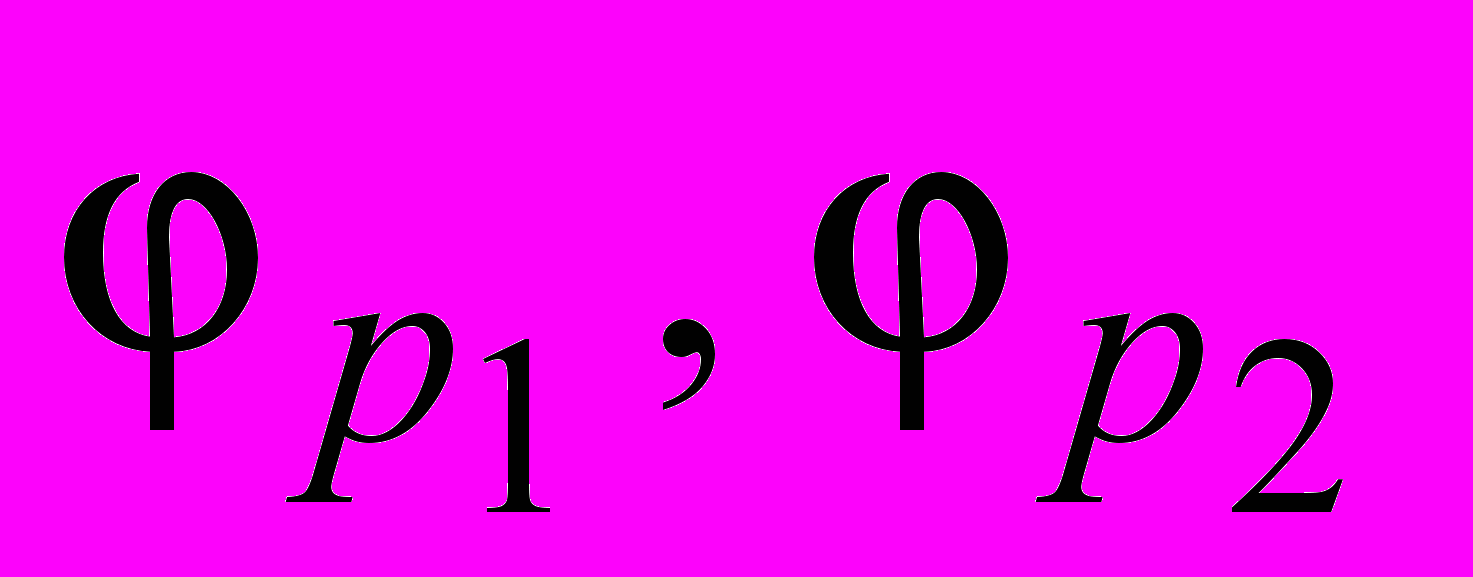 , аналогично и выходным позициям флаги –
, аналогично и выходным позициям флаги – 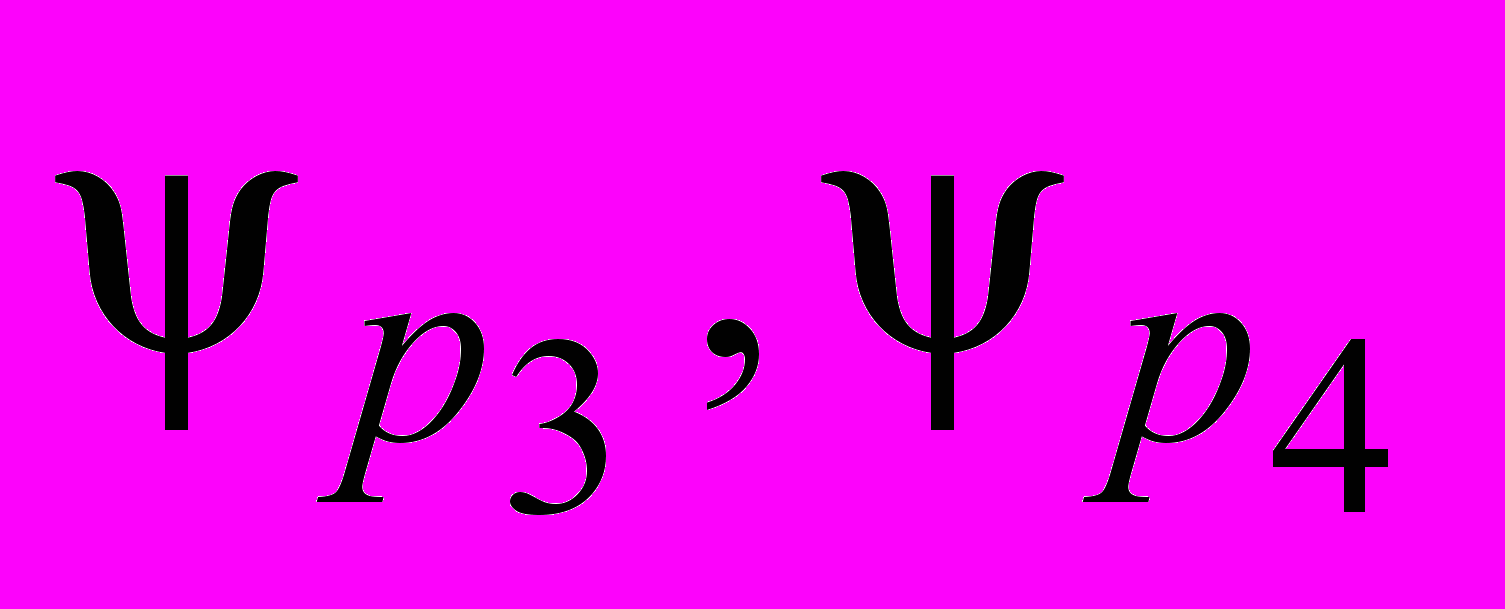 . Введём интерпретацию –
. Введём интерпретацию – 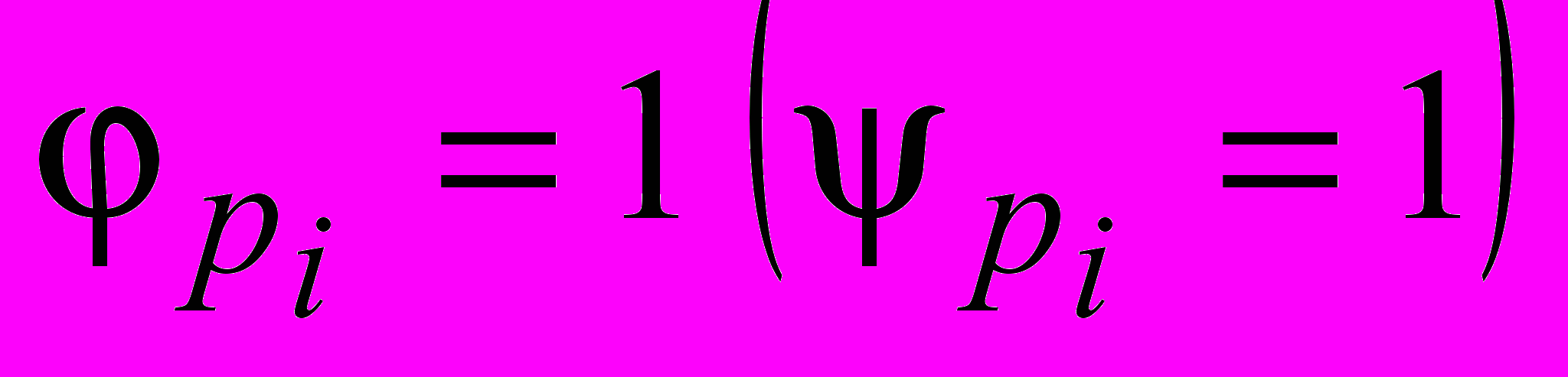 – флаг поднят;
– флаг поднят; 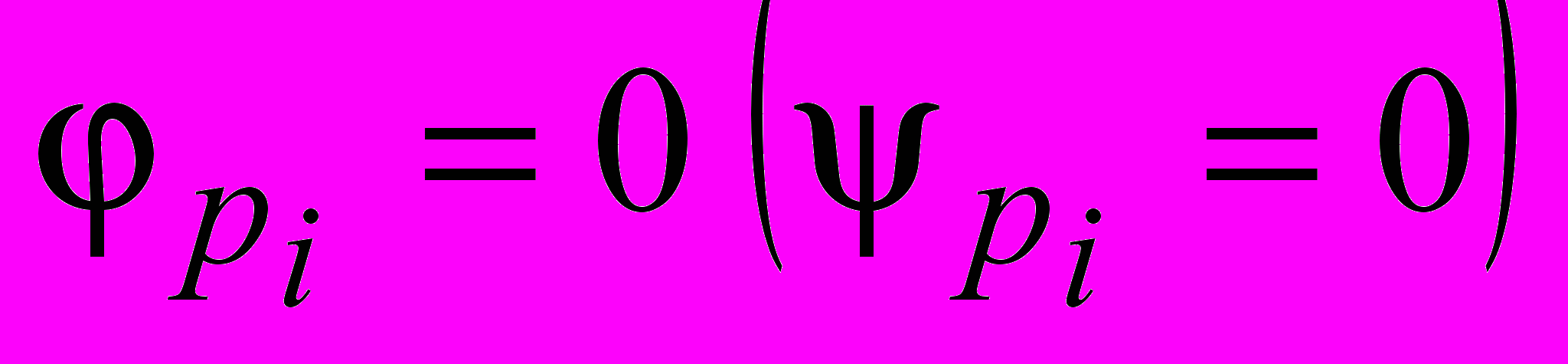 – флаг опущен (снят). Поднятые (опущенные) флаги соответствуют занятости (освобождению) позиции фишкой и таким образом определяют память о событиях, произошедших при срабатывании перехода. Каждому переходу t соответствует пусковая функция
– флаг опущен (снят). Поднятые (опущенные) флаги соответствуют занятости (освобождению) позиции фишкой и таким образом определяют память о событиях, произошедших при срабатывании перехода. Каждому переходу t соответствует пусковая функция 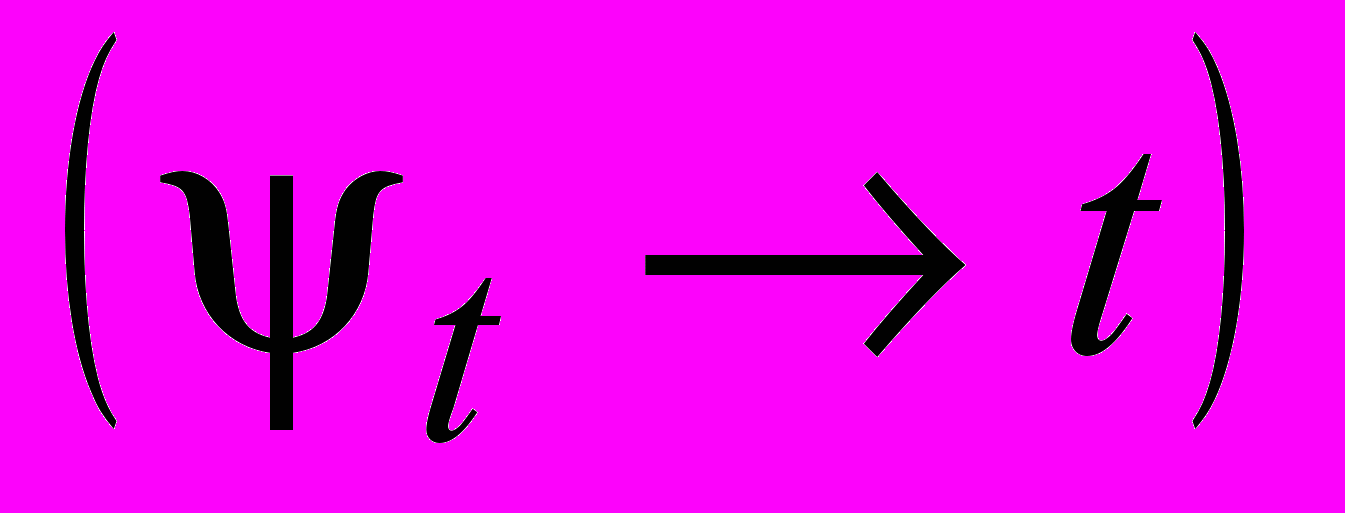 инициирующая процесс Пt, когда флаги всех входных позиций подняты, а выходных позиций опущены.
инициирующая процесс Пt, когда флаги всех входных позиций подняты, а выходных позиций опущены.Асинхронный протокол для элементарной PN определяет запуск (начало) и окончание процесса Пt и задаётся правилами вида:
а) Начало Пt, если
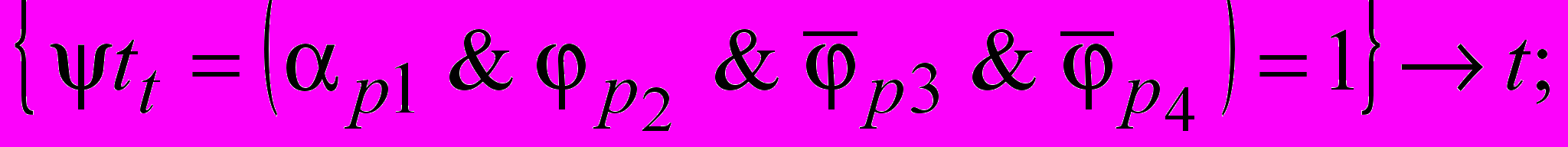 .
.б) Окончание Пt -

Если пусковая функция
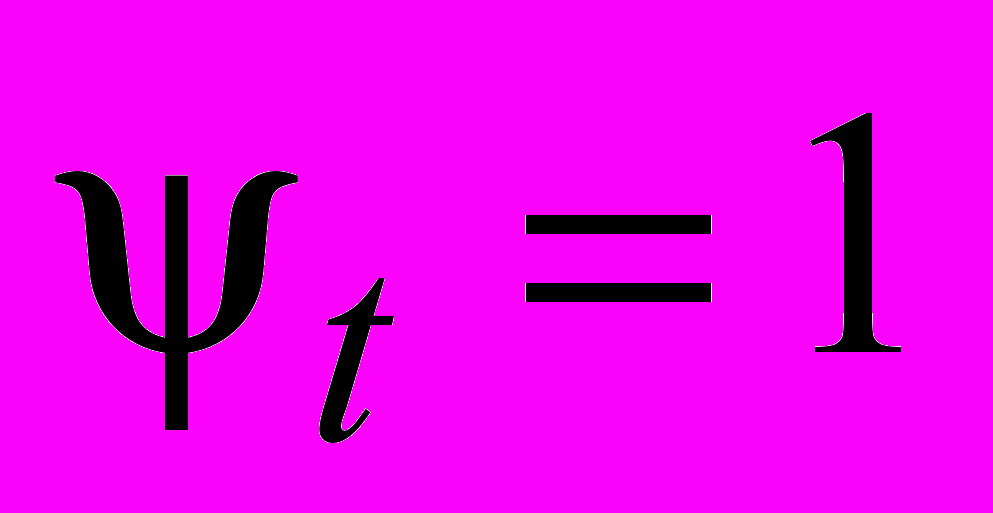 , то она инициирует процесс Пt и присваивает новые значения флагам. Память для хранения совокупности флагов, управляющих процессом, называется флаговым регистром.
, то она инициирует процесс Пt и присваивает новые значения флагам. Память для хранения совокупности флагов, управляющих процессом, называется флаговым регистром.Часто процессом называется процесс решения прикладной задачи пользователя. В этом случае несколько процессов такого рода требует для своей реализации одних и тех же ресурсов процессоров, памяти, каналов и т.д. С точки зрения операционной системы в ВС идут несколько прикладных задач (приложений) с разделяемыми ресурсами. При этом процесс Пt, погруженный в ОС, должен снабжаться дополнительными программными процедурами, работающими с флаговым регистром. Программа
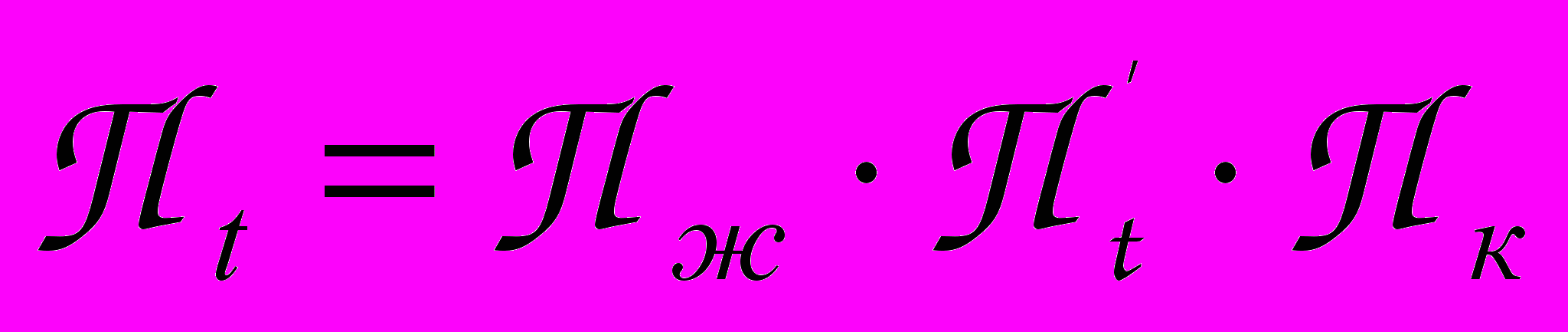 , где
, где  ж – ожидание поднятия входных флагов (циклический опрос флагового регистра),
ж – ожидание поднятия входных флагов (циклический опрос флагового регистра),  к – окончание процесса, опускание входных флагов и поднятие выходных флагов, обозначающих освобождение ресурсов, П
к – окончание процесса, опускание входных флагов и поднятие выходных флагов, обозначающих освобождение ресурсов, П – собственный вычислительный процесс. Если два процесса разделяют один и тот же ресурс R,
– собственный вычислительный процесс. Если два процесса разделяют один и тот же ресурс R, 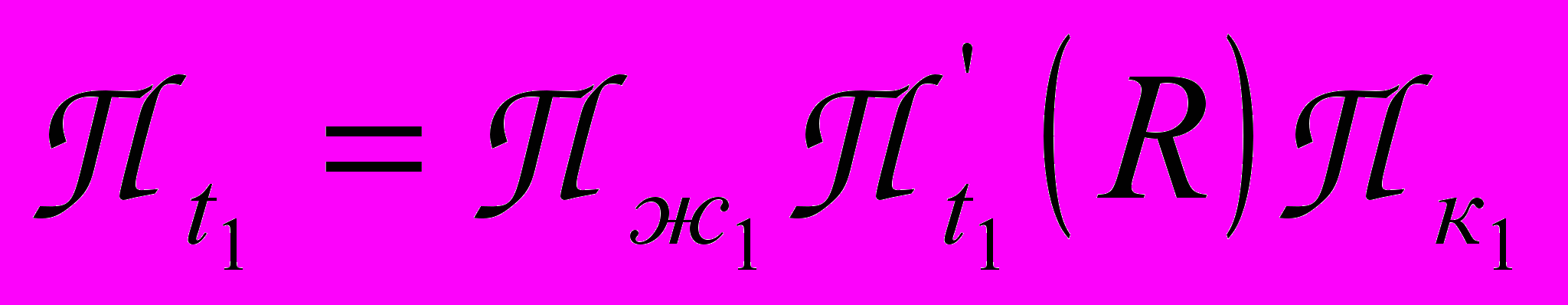 и
и 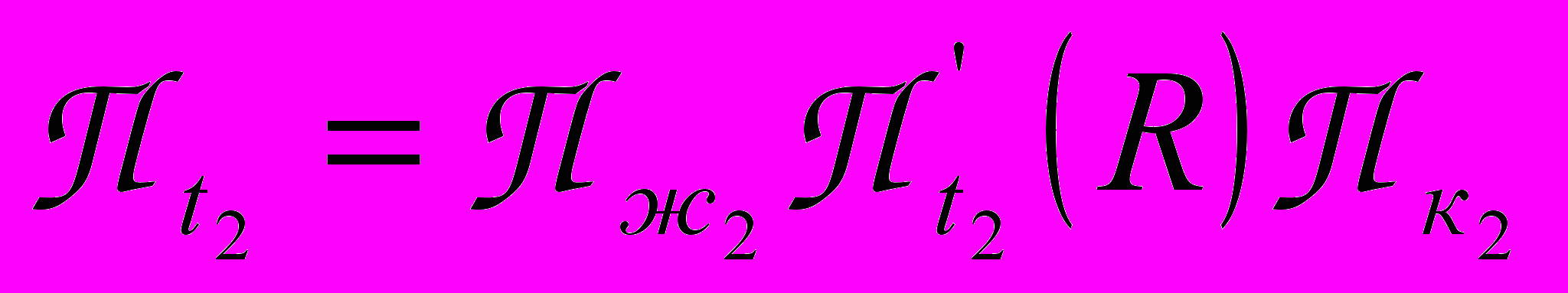 , то
, то 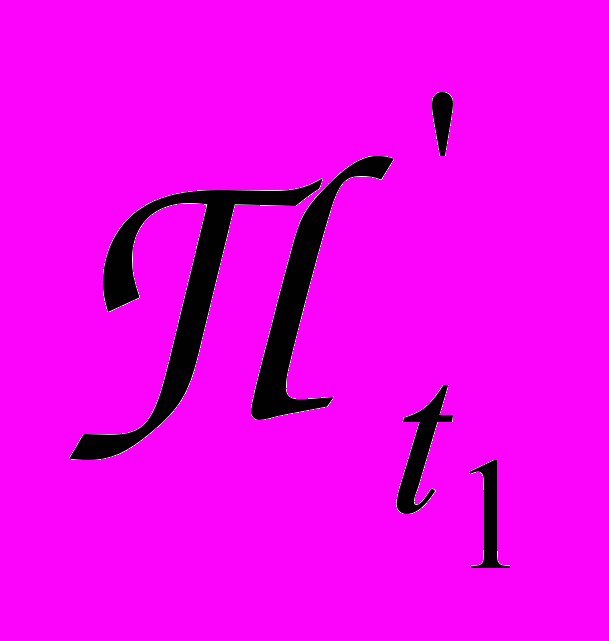 и
и 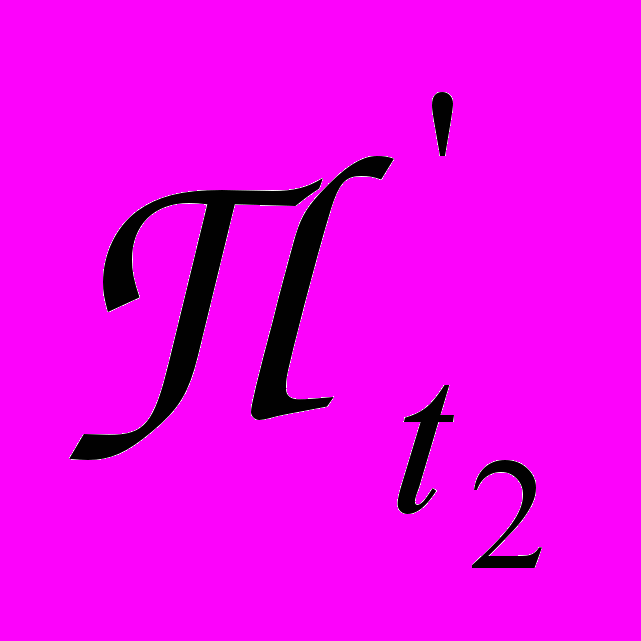 – называются критическими участками соответствующих программ и не могут выполняться одновременно.
– называются критическими участками соответствующих программ и не могут выполняться одновременно.- Асинхронное взаимодействие в мониторе (поставщик – потребитель) с одним общим разделяемым ресурсом.
Пример 7.. Система «поставщик – потребитель».
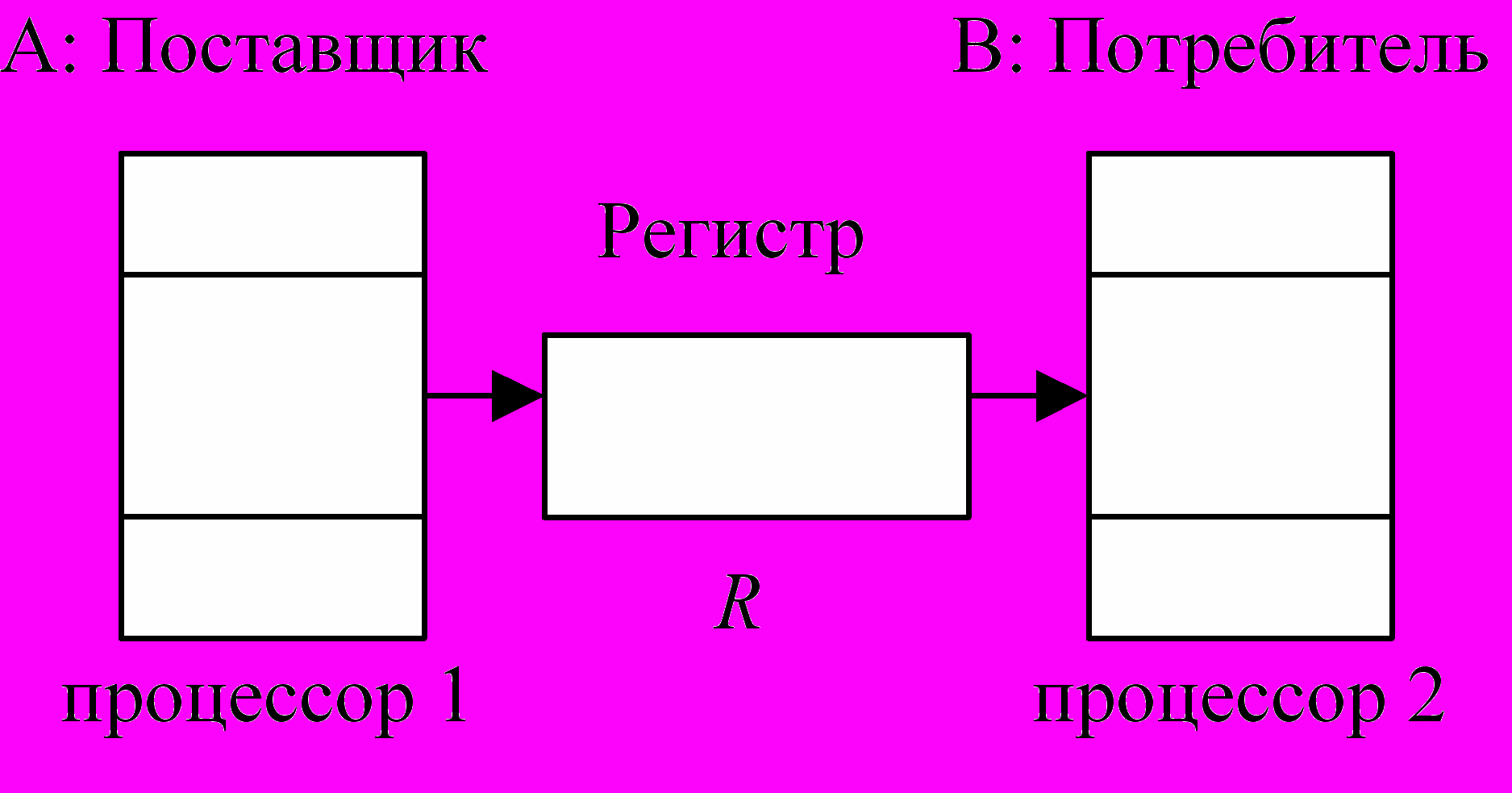
Поставщик генерирует сообщения и помещает их в регистр R. Потребитель считывает и обрабатывает сообщения, беря их из регистра R.
Процессы: П1п – программа на процессоре П1 использует печать; П1Д – программа на процессоре П1 использует диск; П2Д – программа на процессоре П2 использует диск; П2п – программа использует печать. PN для системы «поставщик – потребитель» приведена ниже.
Пример 8. Сеть Петри системы (поставщик – потребитель).
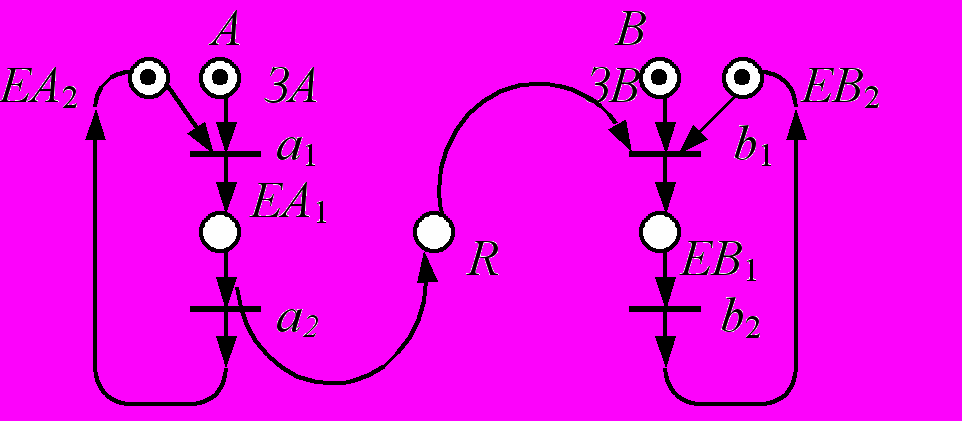
Процессы События
а1 – подготовка сообщений 3 А – запрос на посылку
а2 – запись сообщений в R сообщений.
b1 – считывание сообщений ЕА2 – разрешение на сообще-
из R ние.
b2 – обработка сообщений ЕА1 – сообщения подготовле-
ны.
R – регистр свободен (занят).
ЗВ – запрос на приём сообще-
ний.
ЕВ2 – разрешение на прём
сообщений.
ЕВ1 – сообщения считаны из R.
Асинхронный протокол системы «поставщик – потребитель».
Флаговые функции:
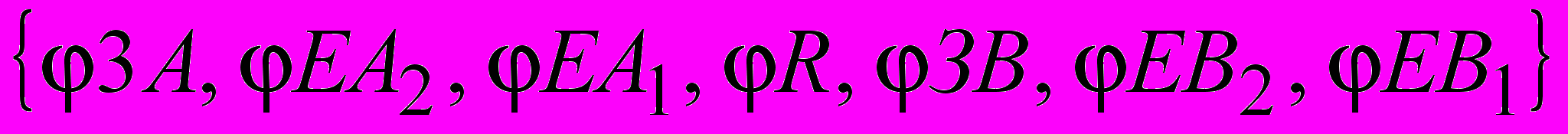 флаговая функция принимает значение = 1 (флаг поднят, если произошло событие), иначе =0 (флаг опущен)
флаговая функция принимает значение = 1 (флаг поднят, если произошло событие), иначе =0 (флаг опущен)Пусковые функции:
 .
.Правила протокола:
1)
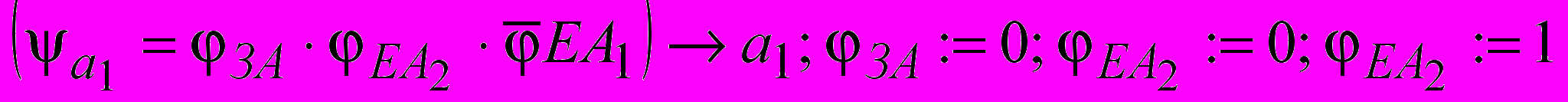
2)
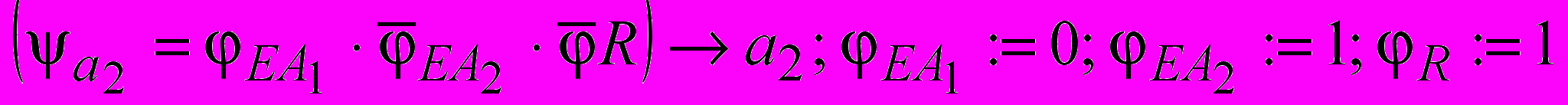
3)
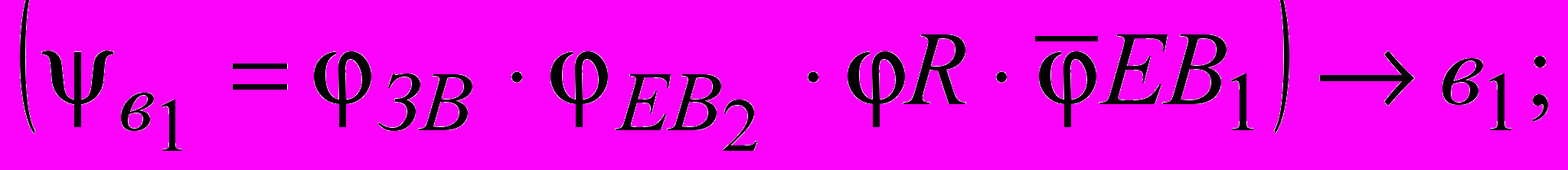
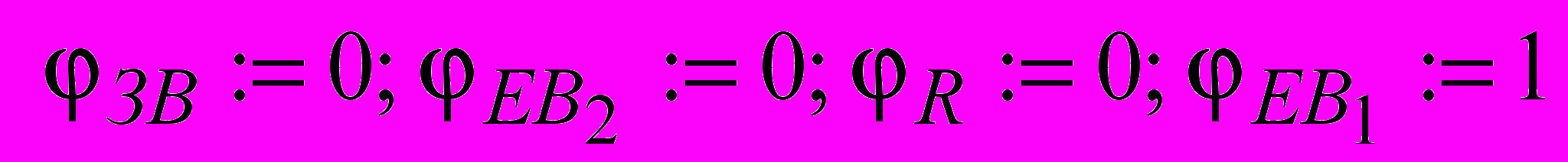
4)
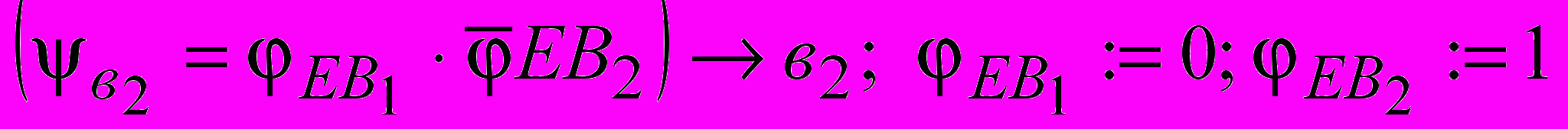
2.2 Модели тупиковых ситуаций. (Тупики).
Тупиковой ситуацией в системе процессов с разделяемыми ресурсами называется такая, когда процессы «захватили» ресурсы так, что любой из них не может продолжать движение.
Следующий пример описывает логику взаимосвязи двух процессов, которая может привести к тупику.
Пример 9. Два процесса П1и П2 имеют два разделяемых ресурса – «печать» и «диск», которые используют так, как показано в соответствующей PN.
 – программы, требующие печать,
– программы, требующие печать, 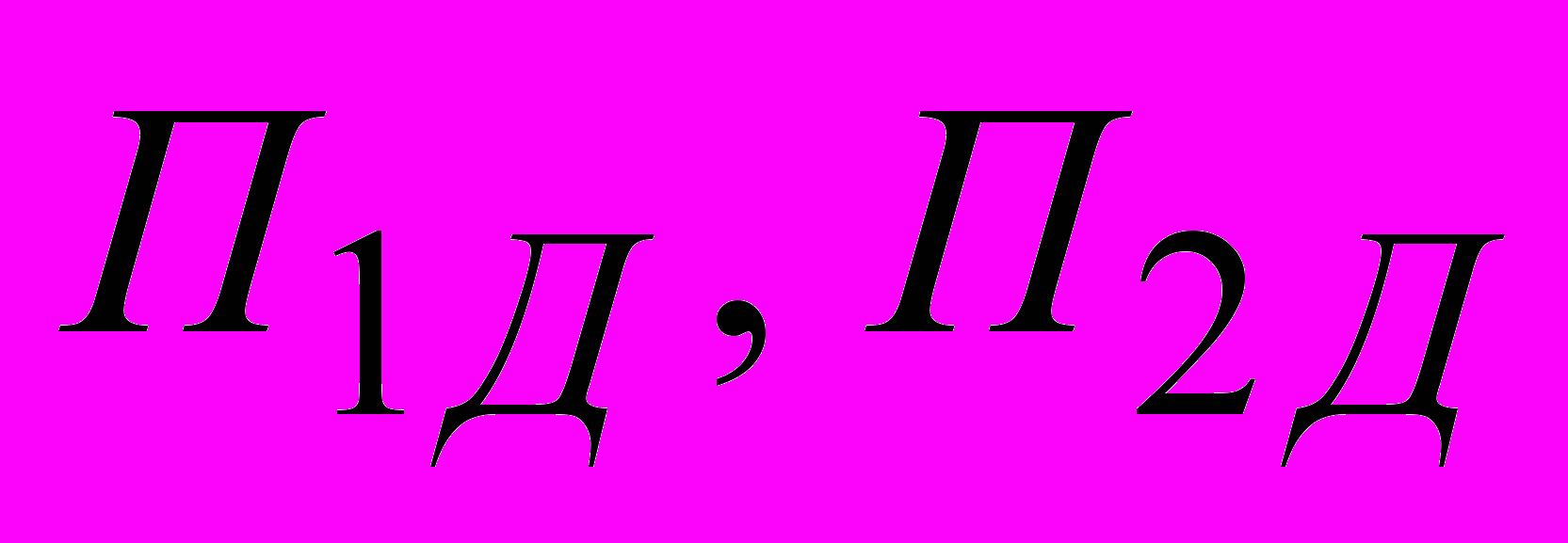 – программы, требующие диск.
– программы, требующие диск.а) Начальная ситуация б) Тупиковая ситуация
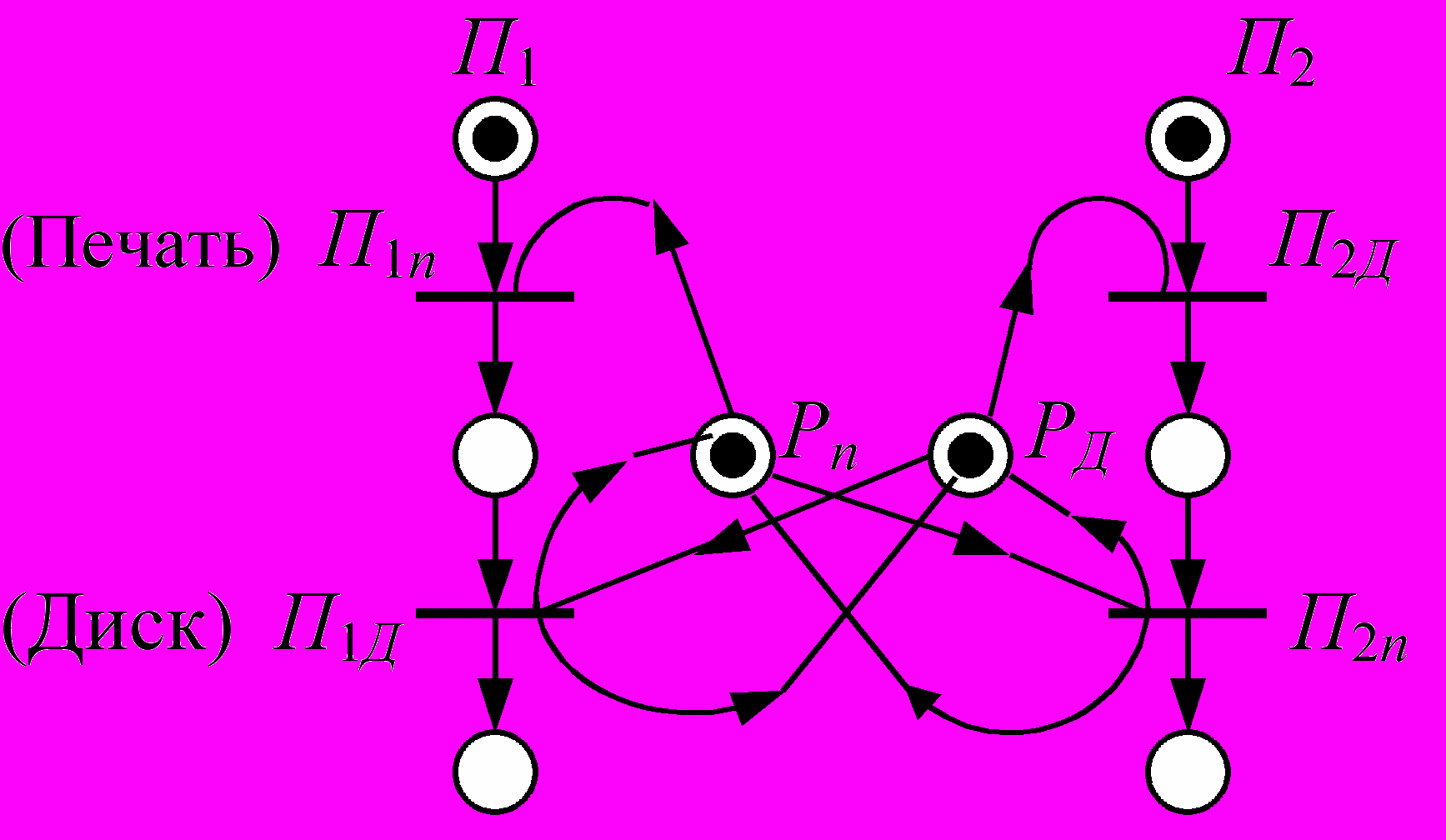

События: П1 – захват диска, П2 – захват печати, Рп – освобождение печати, РД – освобождение диска.
Программа П1, – «захватила» печать, а П2 – «захватила» диск, далее система перешла в тупиковую ситуацию. До сих пор проблема тупиков («смертельных объятий») не имеет универсального решения. В каждом конкретном случае для разрешения проблемы тупиков применяются эвристики. Но всегда существует самый плохой выход избежать тупиковой ситуации. Это способ создания безтупиковой системы с правилом использования ресурсов – «всё или ничего». Процессы в системе «закрываются» флагами в соответствии с PN2, приведенной на рисунке.

Либо П1 либо П2 захватит все ресурсы. Программы П1; П2 могут работать только последовательно, но не параллельно. Проблема тупиков заключается в решении следующих задач: 1) распознавание тупиковых ситуаций и 2) введение защиты от тупиков. И распознавание и защита от тупиков (расстановка флаговых и пусковых функций) решаются эвристическими методами (набором правил, полученным от экспертов и имитационным моделированием).
2.3 Семафоры Дейкстры для синхронизации потоковых процессов
В системных программах очень часто встречаются ситуации, когда используются буферы (накопители) информации, при этом один процесс наполняет буфер данными, а другой процесс забирает данные из буфера. Очевидно, что такая логика взаимодействия может быть промоделирована PN с позицией типа cash. В этом случае принимается, что cash имеет неограниченный объем (может хранить бесконечно большое количество фишек). На самом деле в реальности объем cash всегда ограничен. Дейкстра предложил ввести в процессы, «наливающие» в cash данные, и «выкачивающие» данные из cash, специальные контролирующие процедуры (семафоры). Далее на рисунке показана модель такого «cаsh» и приведены программы и процедуры, которые носят название «семафоров Дейкстры».
Семафоры и семафорные функции Дейкстры.
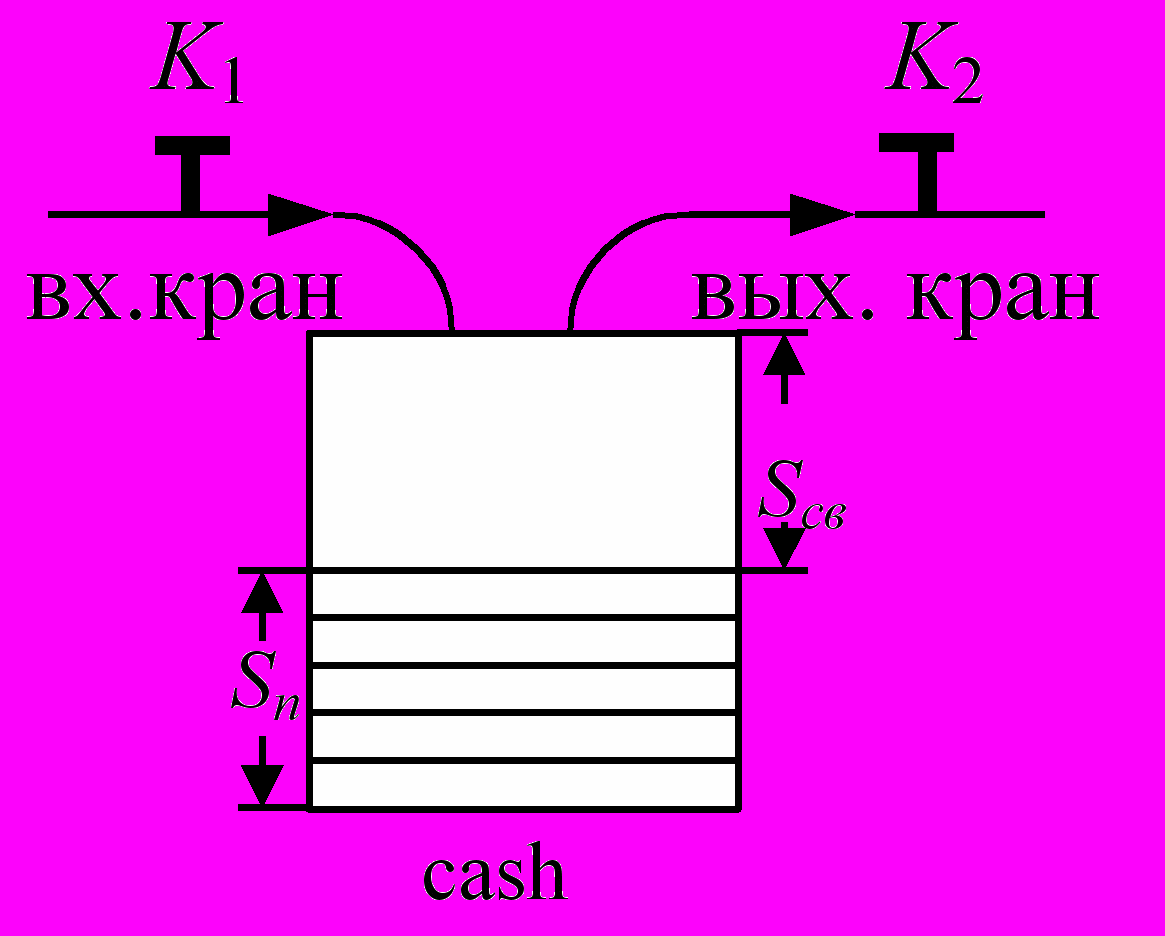
Входной кран K1 закрывается,
когда Sсв = 0;
выходной кран K2 закрывается,
когда Sn = 0.
Процедура для процесса Процедура для процесса
«наливающего» cash «выкачивающего» cash
begin begin
while Sсв > 0 DO while Sп > 0 DO
begin begin
P: Sсв: = Sсв – 1 P: Sn: = Sn – 1
V: Sn: = Sn+ 1 V: Sсв: = Sсв + 1
end end
end end
Закрой кран K1 Закрой кран K2
Переменные Sсв, Sn – называются семафорами, а P, V – семафорными функциями Дейкстры.
Пример 10. Монитор Хоара для почтового ящика сообщений между двумя процессами.
- Содержательная задача.
Два процесса: А – готовит и посылает сообщения в почтовый ящик (ПЯ), В – вынимает сообщения из ПЯ и их обрабатывает. Общий ресурс – ПЯ, доступ к которому имеют либо А либо В, но не оба вместе. «А» складывает сообщения в ПЯ, пока он не переполнится. «В» выбирает сообщения, пока ПЯ не будет пустым.
- Математическая модель.
Сеть Петри, совмещенная с семафорами Дейкстры.
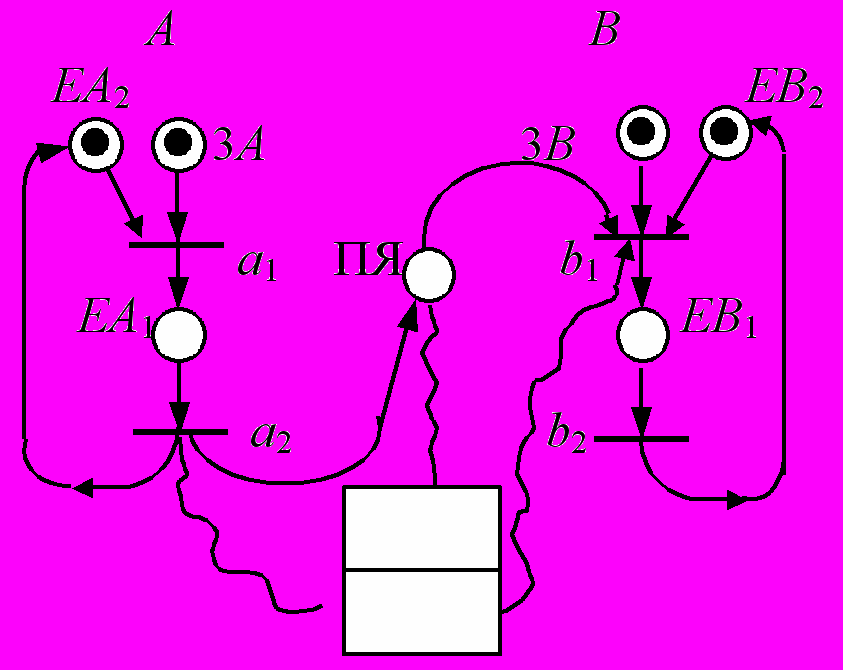
Семафоры
Sсв – число свободных ячеек ПЯ
Sn – число ячеек ПЯ, занятых
сообщениями
SПЯ – ёмкость ПЯ, (число ячеек
ПЯ)
Sсв = SПЯ – Sn
 Процессы События
Процессы События- а
 1 – подготовка сообщений 3А – запрос на засылку
1 – подготовка сообщений 3А – запрос на засылку
- а2 – запись сообщений в ПЯ сообщений в ПЯ
- b1 – считывание сообщений ЕА2 – разрешение на
из ПЯ сообщение
- b2 – обработка сообщений ЕА1 – сообщения
подготовлены
ПЯ – ПЯ свободен (занят)
ЗВ – запрос на прием
сообщений
ЕВ2 – разрешение на
прием сообщений
ЕВ1 – сообщения считаны
из ПЯ
Семафорные процедуры
Procedure посылка Procedure выемка
begin begin
while Sсв >0 do while Sn >0 do
begin begin
процесс а2; процесс b1;
P: Scв: = Sсв – 1; P: Sn: = Sn – 1;
V: Sn = Sn + 1; V: Sсв = Sсв+ 1;`
end end
end end
- Асинхронный протокол монитора Хоара.
Флаговые функции: (3А, ЕА2, ПЯ, 3В, ЕВ2, ЕВ1) = 1 (флаг поднят, если произошло событие ), иначе = 0 (флаг опущен).
Пусковые функции: а1 а1; а2 procedure посылка; b1 – procedure выемка; b2 b2.
Правила протокола:
- (а1 = 3АЕА2ЕА1) а1; 3А: = 0; ЕА2: = 0; ЕА2: = 1.
- (а2 = ЕА1ЕА2) procedure посылка; ЕА1:=0; ЕА2:=1; ПЯ:=1.
- (b1 = 3BEB2ПЯEB1) procedure выемка; 3В: = 0; ЕВ2: = 0; ЕВ1: = 1.
- (b2 = ЕB1ЕВ2) b2; ЕВ1: = 0; ЕВ2: = 1.
