«Двумерная визуализация таблиц на примере гип-105а»

Вид материала

Пояснительная записка

Содержание Обзор современных методов визуализации лексикографической информации Рисунок 1 – Визуальный словарь Модель оптимального представления координат понятий в пространстве Рис. 2 -Оптимальное расположение городов на плоскости, согласно матрице расстояний Схема работы метода наискорейшего спуска Пример визуализации студентов ГИП-105а в Excel Рисунок 2 – Исходные данные Рисунок 3 – Матрица расстояний между студентами Программная реализация Рисунок 5 – Оптимальное представление студентов ГИП-105 в двумерном пространстве

Подобный материал:

• Программно-технический комплекс 14 Задачи гис 14 гип как проблемно-ориентированные, 1019.49kb.
• Настоящей дипломной работы «Управление дебиторской задолженностью на предприятии (на, 273.43kb.
• Интерактивное объемно-ориентированное геометрическое моделирование и визуализация функционально-заданных, 60.11kb.
• Задача№1. Тема «Составление таблиц и графических изображений», 1841.95kb.
• «Построение таблиц истинности логических выражений с использованием электронных таблиц», 487.41kb.
• Методические указания к лабораторным работам для студентов по направлению подготовки, 631.96kb.
• Методическая разработка по дисциплине «Информатика» Тема: «Организация данных в виде, 447.07kb.
• Аннотация диплом, 456.71kb.
• Лабораторная работа по теме «Построение таблиц истинности с помощью электронных таблиц, 32.44kb.
• Дипломной работы сформулирована как «Пути и средства повышения эффективности управления, 383.74kb.

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ


ГОУВПО «Самарский государственный архитектурно-строительный университет»


Факультет информационных систем и технологий


Кафедра прикладной математики и вычислительной техники


ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОЙ РАБОТЕ


по дисциплине

МЕТОДОЛОГИЯ

НАУЧНЫХ ИССЛЕДОВАНИЙ


На тему


«Двумерная визуализация таблиц на примере ГИП-105а»


6 СЕМЕСТР 3 КУРС


Научный руководитель: Пиявский С.А.

Проверили:	Выполнил студент ГИП-105а Бойцев А.В.
Пиявский С.А. _________________	_______________________

Общая оценка __________


Методический руководитель _______________________


2008 г.

Содержание

Введение

Начнём с понятия визуализации. Итак, визуализация информации – это представление информации в виде графиков, диаграмм, структурных схем, таблиц, карт и т.д.

Современные компьютерные технологии используют широкий спектр методов визуализации информации. Мощным средством анализа информации являются интерактивные средства модификации графических представлений. Особенно широко графические методы используются в разведочном анализе данных, позволяя выявлять закономерности в многомерных массивах информации.

Благодаря компьютеризации визуализация информации играет все большую роль в повышении эффективности коммуникаций. Использование слайд-фильмов и современных средств вывода информации на большой экран позволяет существенно повысить эффективность лекций, докладов и презентаций.

Также, визуализация информации позволяет повысить эффективность коммуникаций и без помощи компьютерных технологий. Пример тому - образные схемы. В этих схемах участники проблемных ситуаций выражают свои представления в произвольной форме с помощью примитивных рисунков, графиков, текстовых подписей. Оказалось, что отсутствие стандартизации элементов рисунка не создает коммуникативных затруднений для участников обсуждений. Наоборот, использование невербальных форм представления информации позволяет легко концентрировать внимание на узловых точках проблемы.

Результаты междисциплинарных исследований позволяют утверждать, что визуализация является одним из наиболее перспективных направлений повышения эффективности методов анализа и представления информации.

Обзор современных методов визуализации лексикографической информации

Лексикогра́фия — раздел языкознания, занимающийся вопросами составления словарей и их изучения. Наука, изучающая семантическую структуру слова, особенности слов, их толкование.

Лексикография представляет слово в совокупности всех его свойств, поэтому словарь оказывается не только уникальным и незаменимым пособием по языку, но и важнейшим инструментом научных исследований – статья из ссылка скрыта – свободной энциклопедии.

Собственно, методов визуализации именно лексикографической информации мною было найдено немного, а именно - один – ссылка скрыта и его различные дополнения, созданные авторами самого словаря. Идея визуального словаря состоит в следующем - для каждого слова строится его понятийное окружение, позволяющее с первого взгляда понять смысл этого слова через определяющие термины, и быстро перейти на определяющее слово, смысл которого требуется узнать. Перемещаясь по семантическому окружению слова, с помощью визуального интерфейса, можно быстро ознакомиться с интересующей вас предметной областью.

Для быстрого поиска слова на сайте визуального словаря имеется поисковый сервис, который ищет слово по всем имеющимся в системе разделам.

Надо сказать, что визуальный словарь – это реализация так называемой теории «смысл ↔ текст», которая была создана И. А. Мельчуком в середине 1960-х годов в Москве при активном участии ряда других московских лингвистов. Эта теория представляет собой описание естественного языка, понимаемого как устройство, обеспечивающее человеку переход от смысла к тексту и наоборот. Теория постулирует многоуровневую модель языка, то есть такую, в которой построение текста на основе заданного смысла происходит не непосредственно, а с помощью серии переходов от одного уровня представления к другому. Помимо двух «крайних» уровней — фонологического (уровня текста) и семантического (уровня смысла), выделяются поверхностно-морфологический, глубинно-морфологический, поверхностно-синтаксический и глубинно-синтаксический уровни. Каждый уровень характеризуется набором собственных единиц и правил представления, а также набором правил перехода от данного уровня представления к соседним. На каждом уровне мы имеем дело, таким образом, с особыми представлениями текста.

Семантическое представление является неупорядоченным графом («сетью»), который мы и можем увидеть, найдя интересующее нас слово в визуальном словаре (в качестве примера был взят термин «компьютерный вирус»):



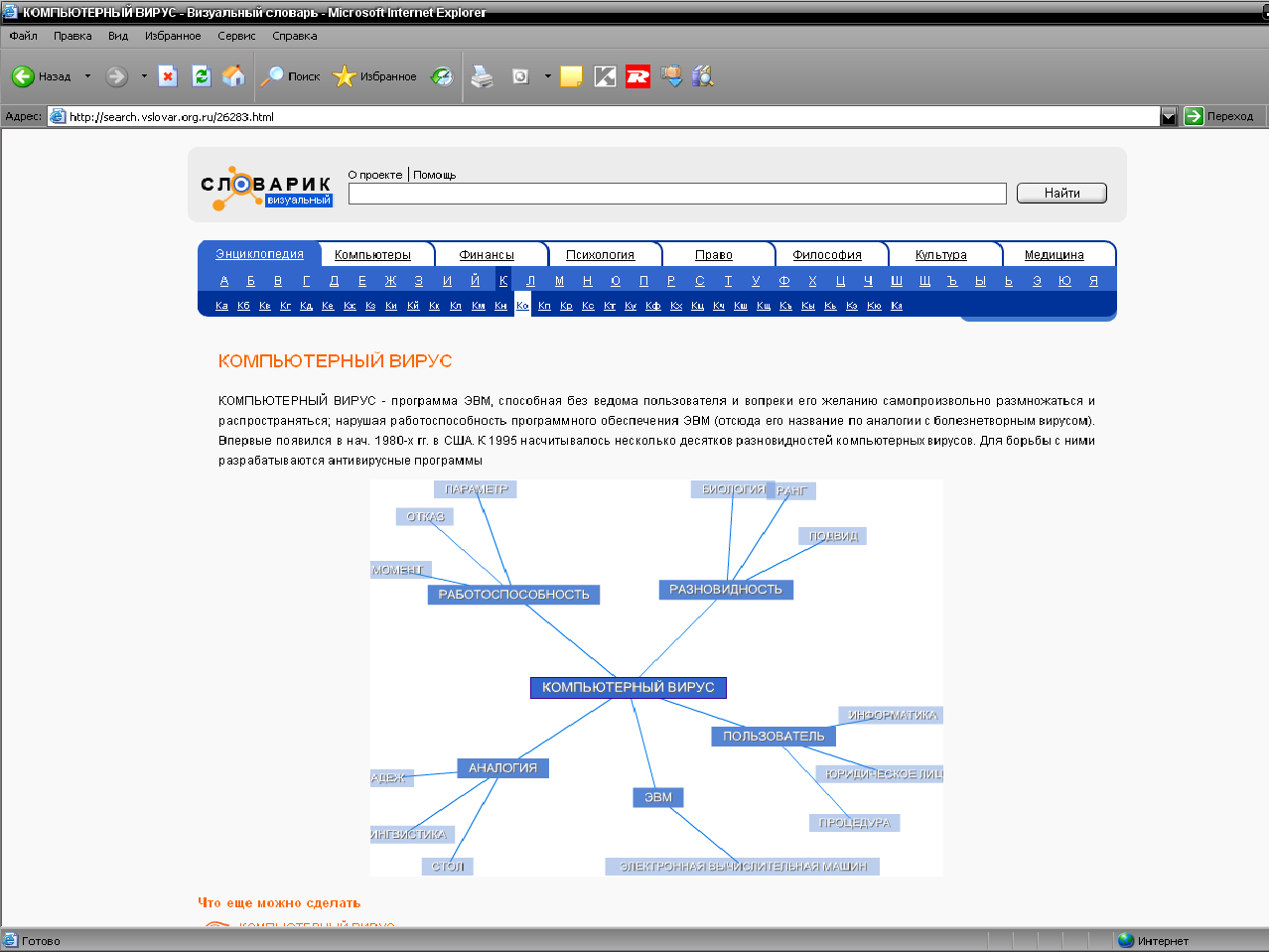
Рисунок 1 – Визуальный словарь


Система позволяет осуществлять быстрый переход между статьями и категориями (категории - работоспособность, ЭВМ и т.п., статьи – отказ, процедура, подвид и т.п.).

Модель оптимального представления координат понятий в пространстве

Разберем задачу оптимальной визуализации на примере задачи «правильного» расположения на плоскости городов при известных расстояниях между ними. Имеется следующая матрица расстояний (Табл. 1) между городами в условных единицах (измерения расстояний производились по карте России).

Таблица 1. Матрица расстояний между российскими городами

	М о с к в а	С а м а р а	В л а д и в	Е к а т е р	Т а м б о в	И р к у т с	Я к у т с к
Москва	0	11	82	19	4	53	62
Самара	11	0	70	10	8	44	58
Владивосток	82	70	0	65	83	29	27
Екатеринбург	19	10	65	0	17	35	48
Тамбов	4	8	83	17	0	52	63
Иркутск	53	44	29	35	52	0	23
Якутск	62	58	27	48	63	23	0

Необходимо расположить города на плоскости так, чтобы новое построение наиболее полно соответствовало исходной матрице расстояний. В качестве базовой схемы оптимизации была выбрана схема сети – иерархическая модель целочисленного линейного программирования и нелинейной оптимизации функции многих переменных. Метод, с помощью которого была решена задача нахождения координат объектов – градиентный метод оптимизации функции нескольких переменных. Остановимся подробнее лишь на результате оптимизации. Схематически его можно представить в следующем виде:


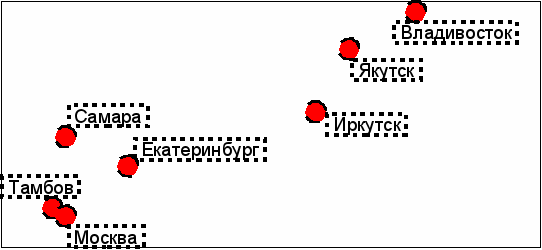
Рис. 2 -Оптимальное расположение городов на плоскости, согласно матрице расстояний



По схеме можно судить о том, что города расположились на плоскости в соответствии с начальной матрицей расстояний и фактически повторяют расположение на карте России, зеркально отраженное относительно оси абсцисс. Данный пример раскрывает основную идею кластеризации объектов – то есть выделения групп объектов по признаку близости данных объектов. Однако расположение большого числа объектов в трехмерном пространстве гораздо более сложная задача.

Цель – разместить объекты в пространстве так, чтобы геометрическая близость между ними в наибольшей степени соответствовала матрице расстояний. Как уже было сказано выше, имеется матрица расстояний между понятиями, для которых мы хотим добиться оптимальной визуализации в пространстве. Введем критерий оптимизации F для задачи оптимальной визуализации набора из n понятий:

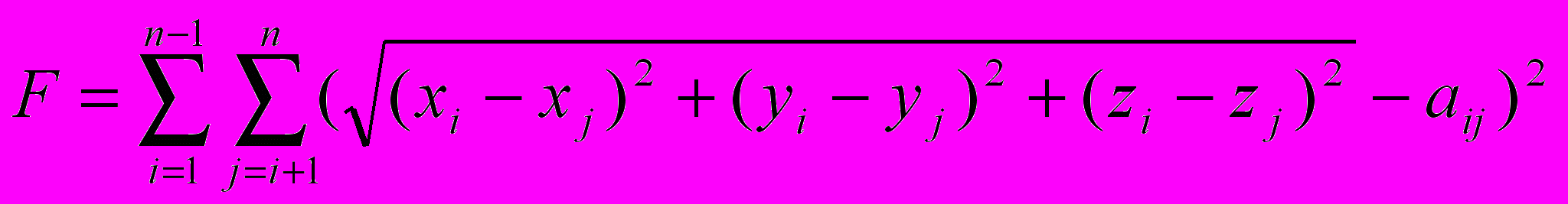, (7)

где x_i и x_j, y_i и y_j, z_i и zj – координаты по осям x, y и z понятий i и j соответственно. Необходимое направление оптимизации функции F на минимум, т.е.

F→min (8)

Для решения поставленной задачи оптимизации хорошо подошла модификация градиентного метода оптимизации функции нескольких переменных – метод наискорейшего спуска. От реализации «чистого» градиентного метода пришлось отказаться по причине крайне медленной работы алгоритма на больших массивах данных. Принцип работы градиентного метода оптимизации [5], а также его модификации – метода наискорейшего спуска описан ниже:

Выбираем любую точку 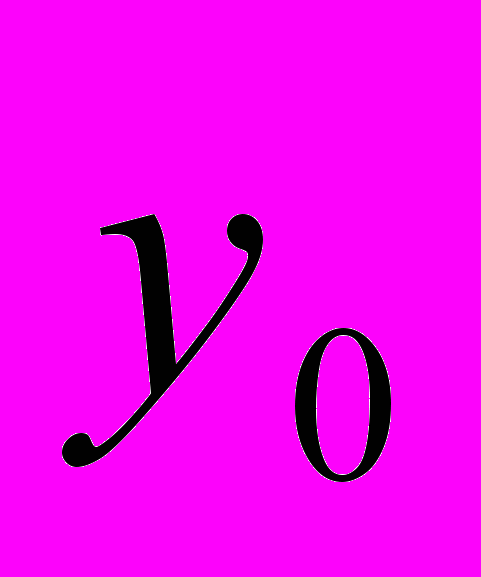– так называемое начальное приближение и вычисляем 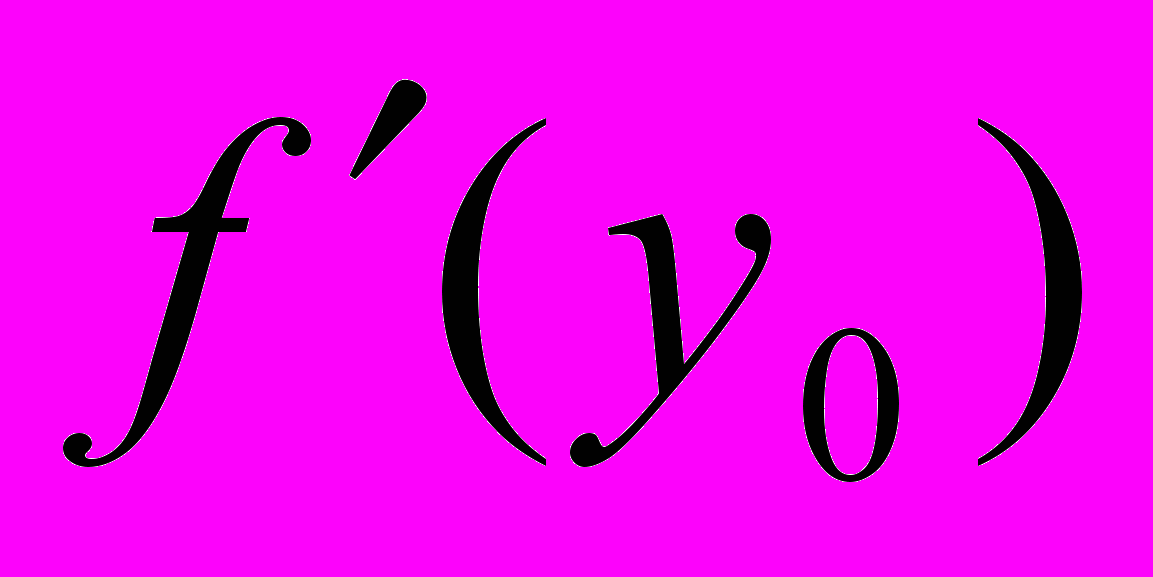– градиент функции в этой точке. Для этого можно вычислить значение функции 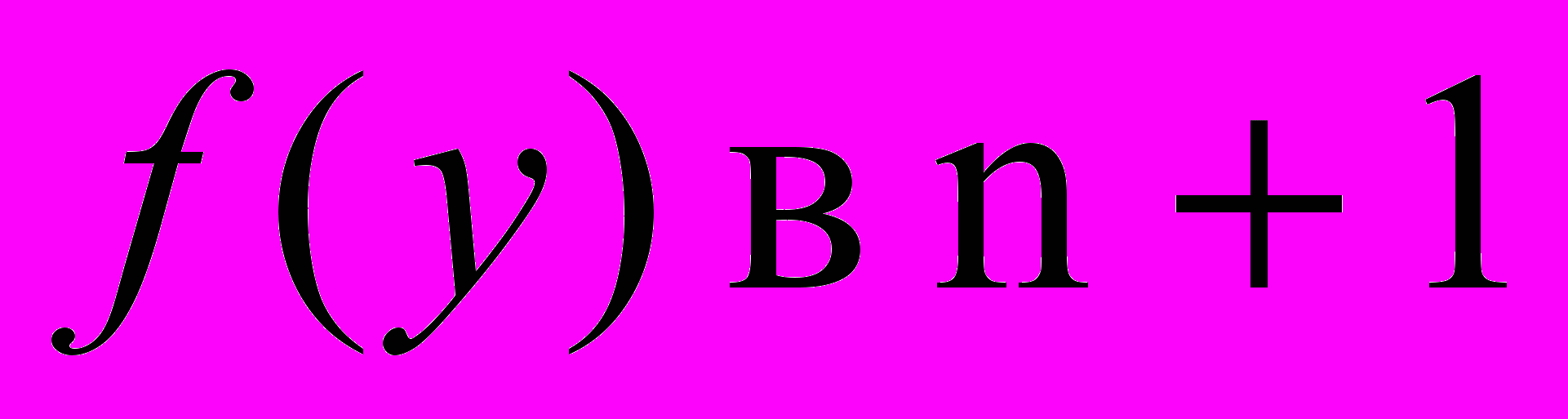точках: точке 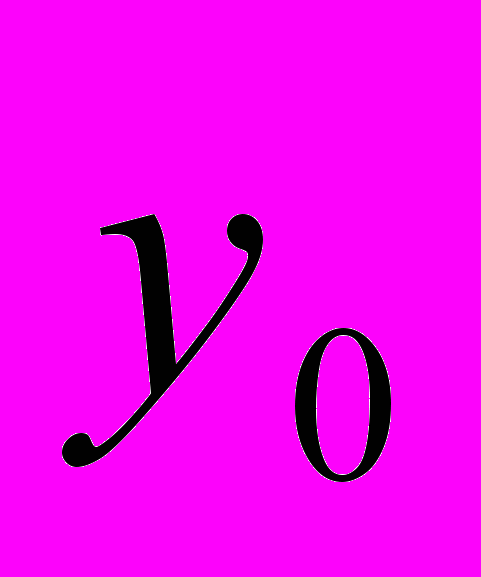и в n точках, сдвинутых относительно нее на малый шаг h в направлении каждой из координатных осей пространства векторов y. Тогда приближенно

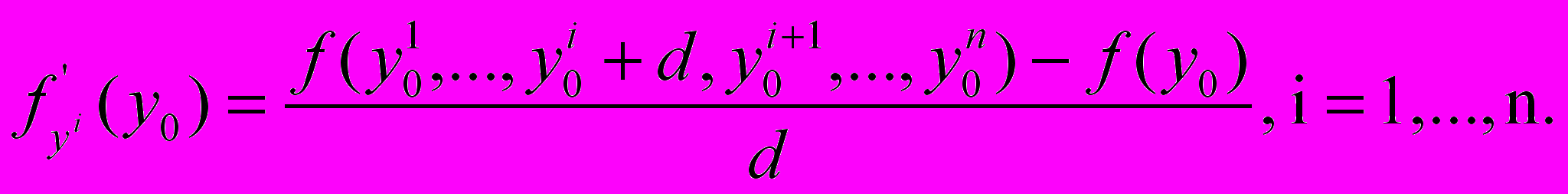(9)

Напомним, что градиент задает в пространстве векторов y направление наибольшего возрастания функции, соответственно противоположное направление 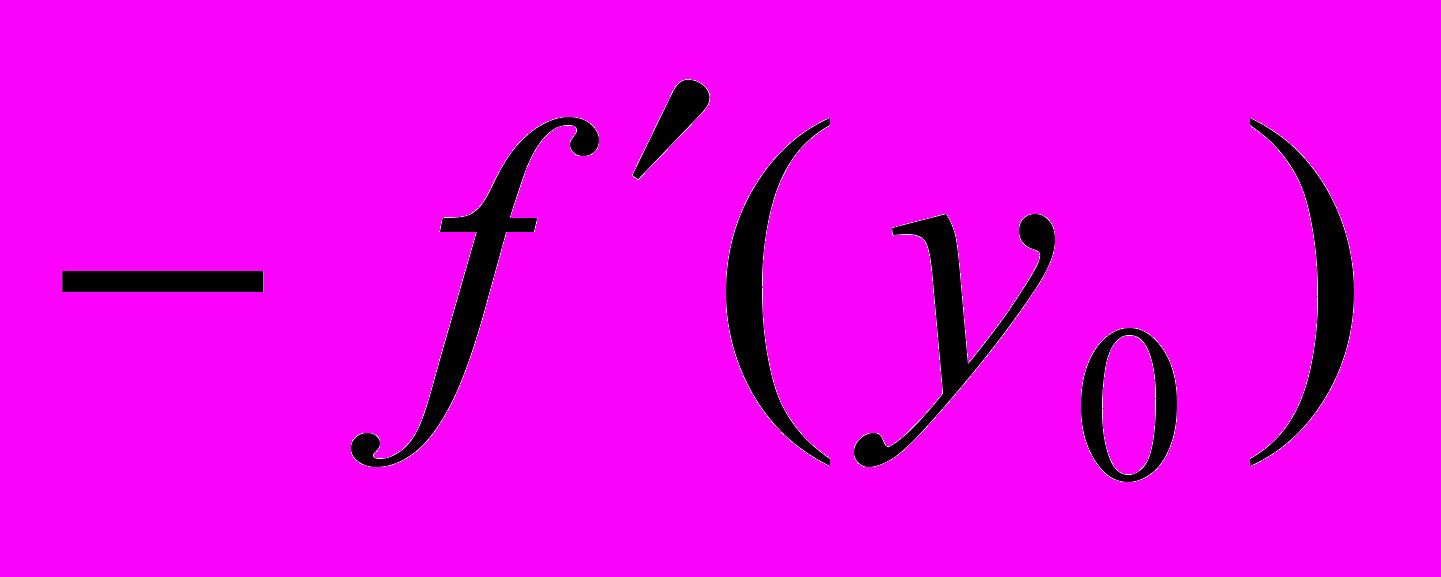будет направлением наибольшего ее убывания. Продвинемся в этом направлении, приближающем нас к точке минимума, на шаг h . Мы придем к точке

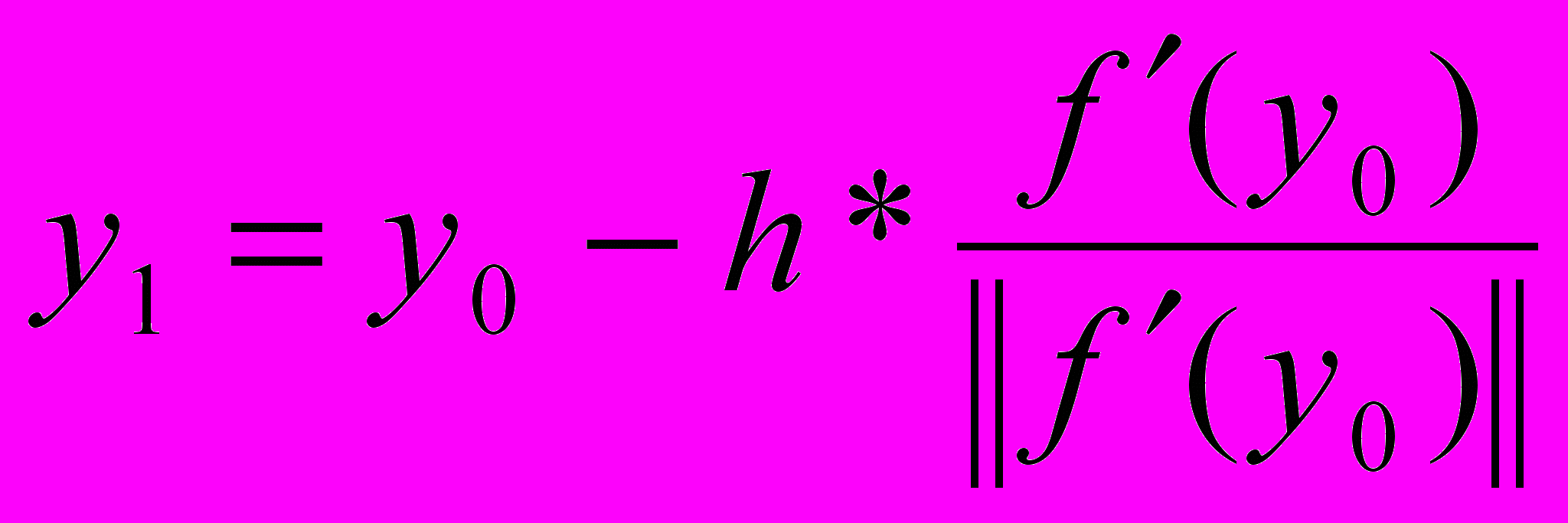, (10)

где

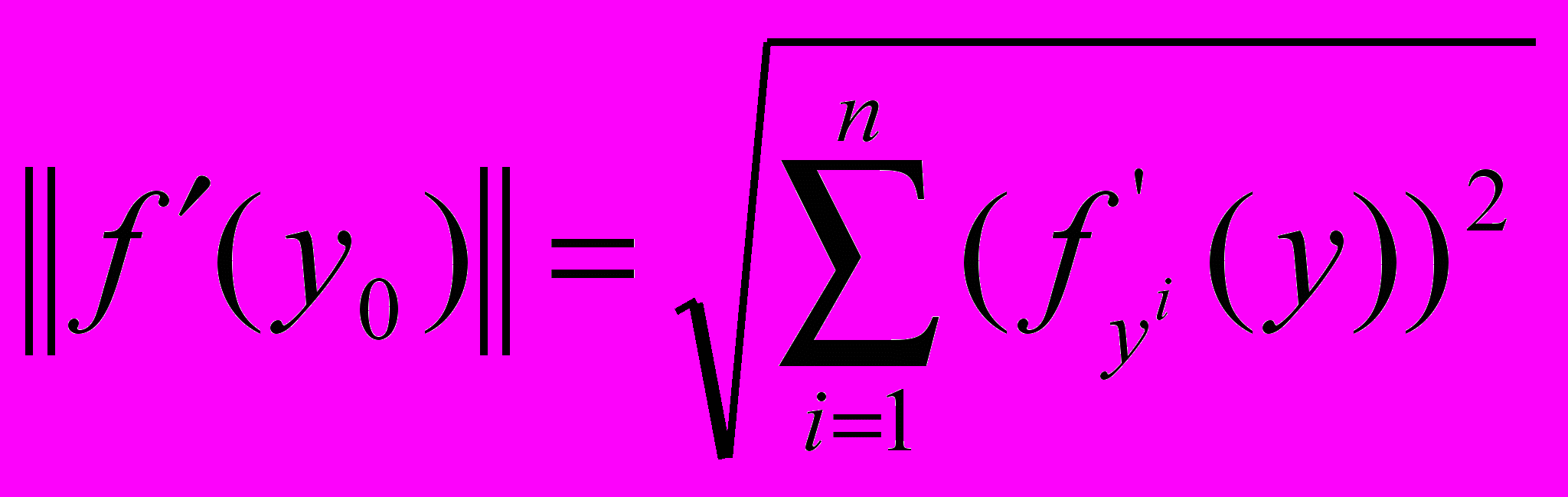(11).

В этой точке вновь вычислим градиент 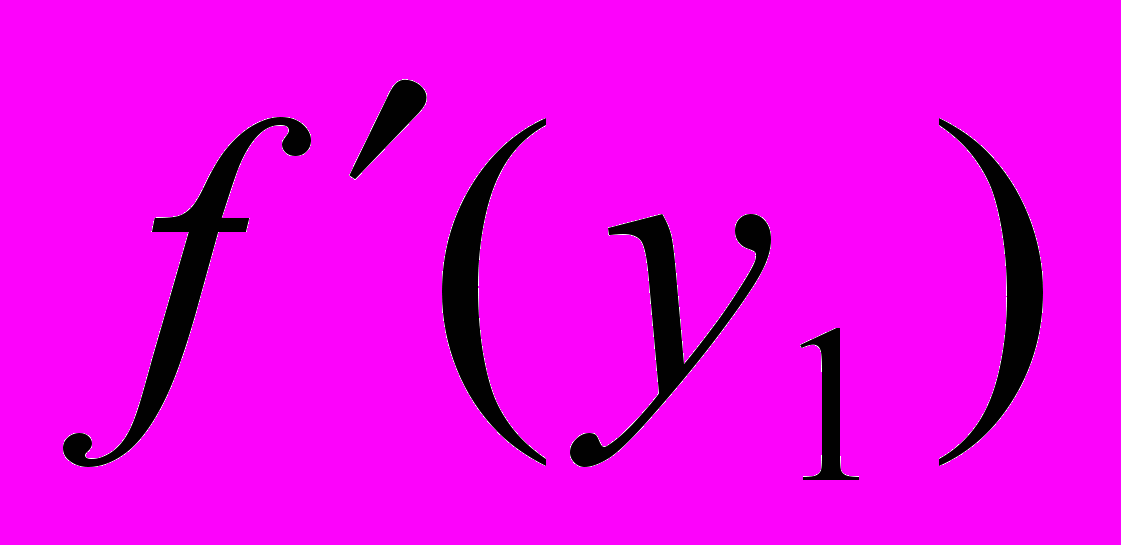и продвинемся на тот же шаг h в направлении антиградиента в точку 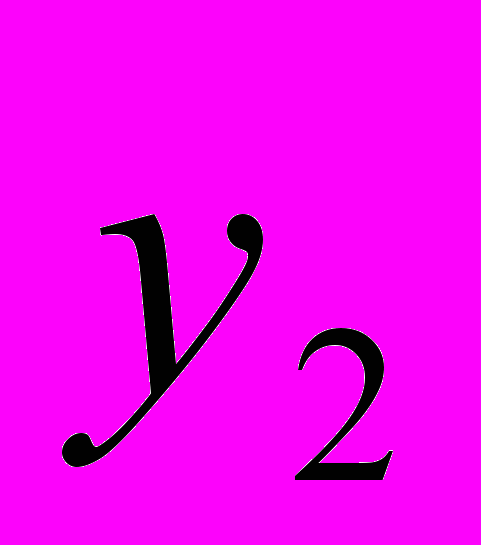и так далее. Вообще,


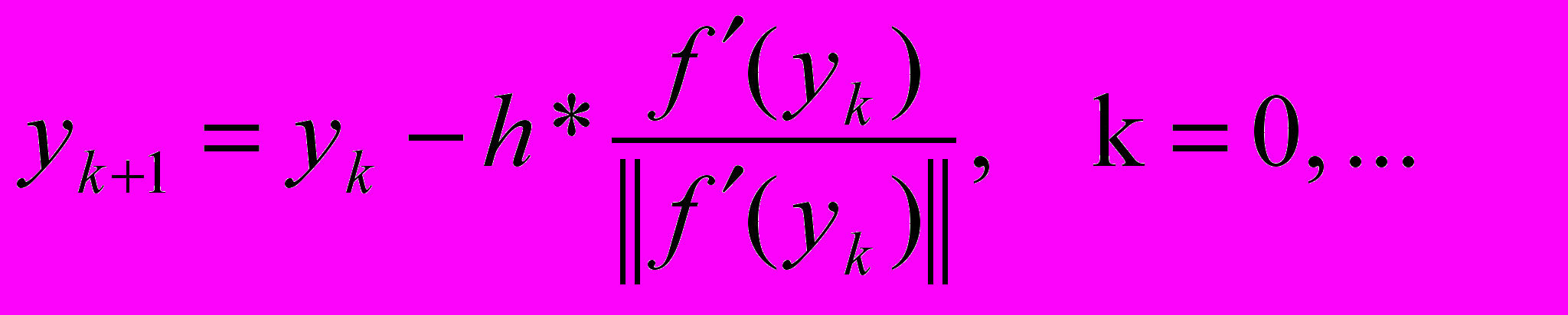. (12)


Доказано, что, двигаясь с бесконечно малым шагом h , мы придем в точку . При этом траектория движения в каждой точке будет, очевидно, перпендикулярна проходящей через эту точку линии уровня f(y). Можно записать и уравнение этой траектории, перейдя в (12) к пределу ,

(13)

или

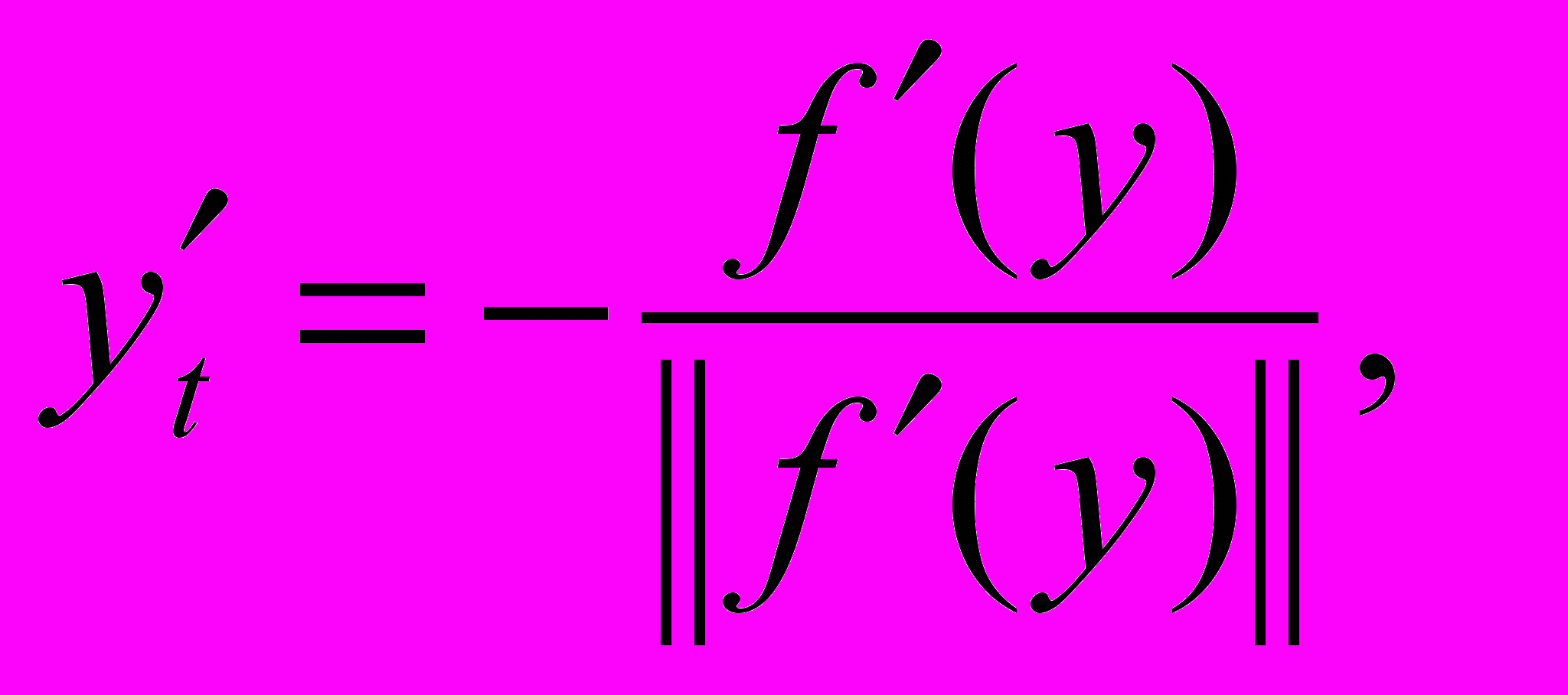(14)

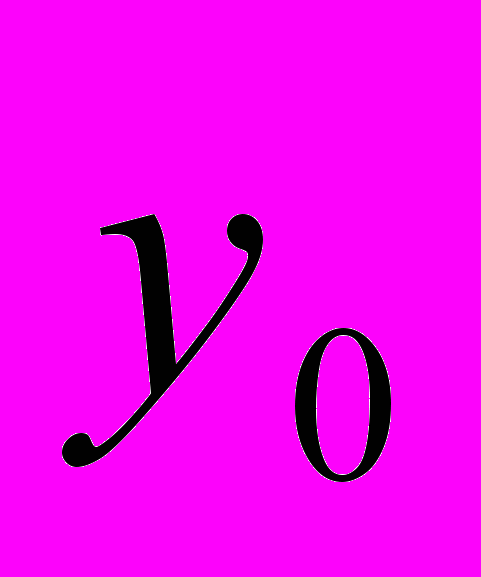
где t – длина пройденного по траектории пути от точки 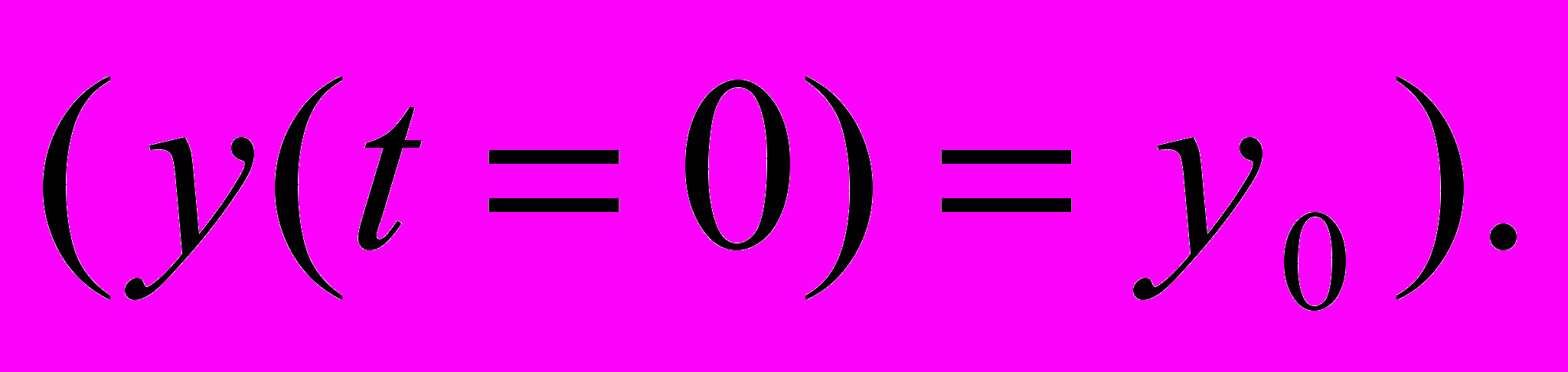Тогда переход от точки 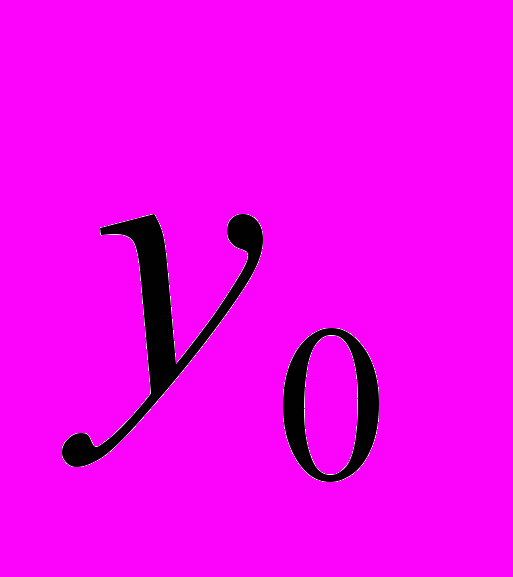к можно осуществить, решая задачу Коши для системы обыкновенных дифференциальных уравнений.

При реализации градиентного метода на ЭВМ вместо бесконечно малого шага h приходится брать малую, но конечную величину. При данном условии сходимость метода нарушается и точка оптимума может не быть достигнута. Простейший пример – зацикливание, когда из точки 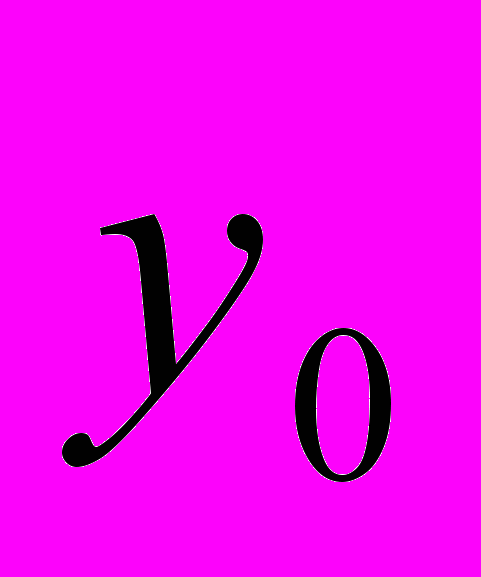попадаем в 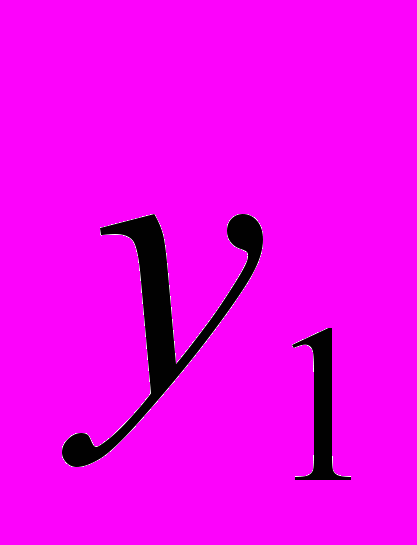, а оттуда снова в 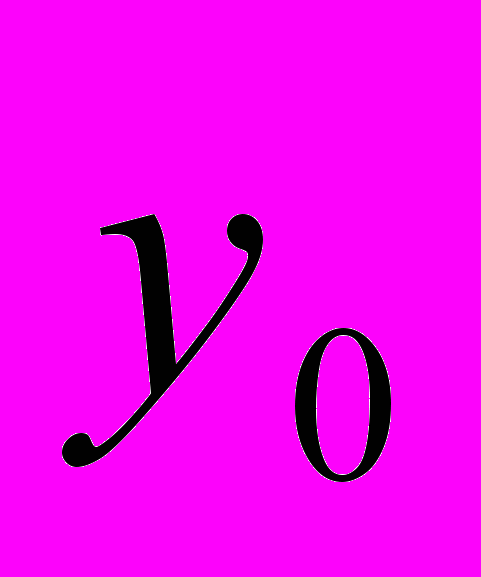и т.д. При малых значениях шага h движение к оптимуму будет довольно длительным. Этого можно избежать, если не вычислять значения градиентов в каждой новой точке (при большом количестве объектов именно этот момент является узким местом алгоритма), а двигаться в выбранном направлении антиградиента до тех пор, пока уменьшается (при минимизации) значение оптимизируемой функции.

Схема работы метода наискорейшего спуска

xo


xc = xo

grad f(xc)



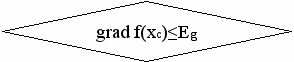
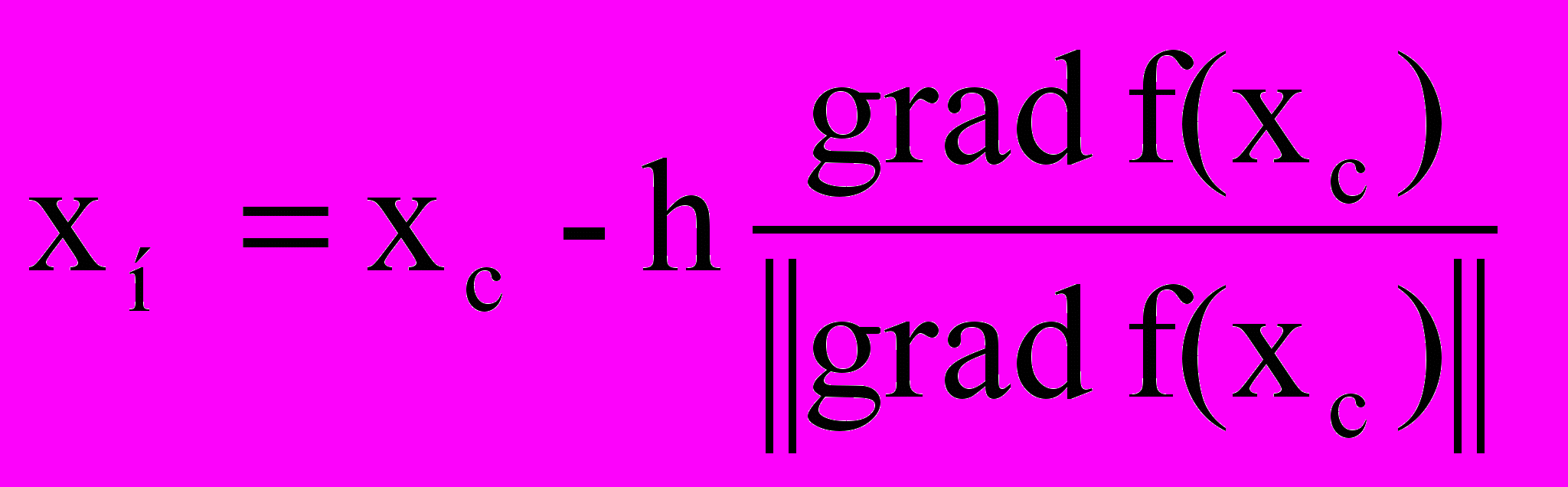
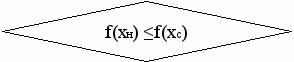
xc = xн

да

да

да

нет

нет

нет

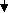
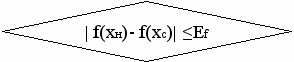
Пример визуализации студентов ГИП-105а в Excel

Возьмём список группы ГИП-105а и для каждого студента укажем его рейтинг контрольных точек, рейтинг посещаемости, и личные достижения в общественной деятельности, науке, культуре и спорте (сведения о личных достижениях, как и рейтинг, взяты с сайта факультета – sciyouth.ru)



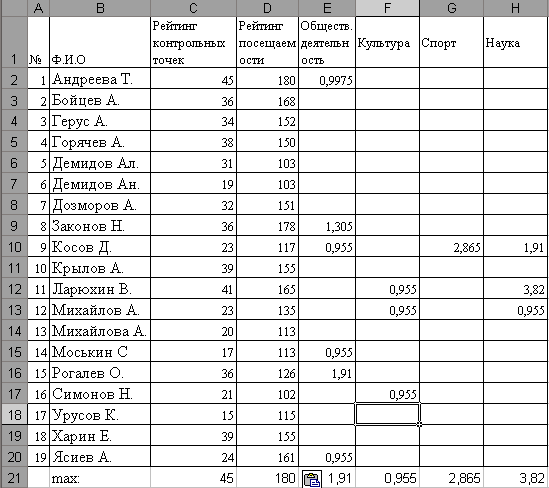
Рисунок 2 – Исходные данные


Найдём расстояние между каждым студентом, составив матрицу расстояний.



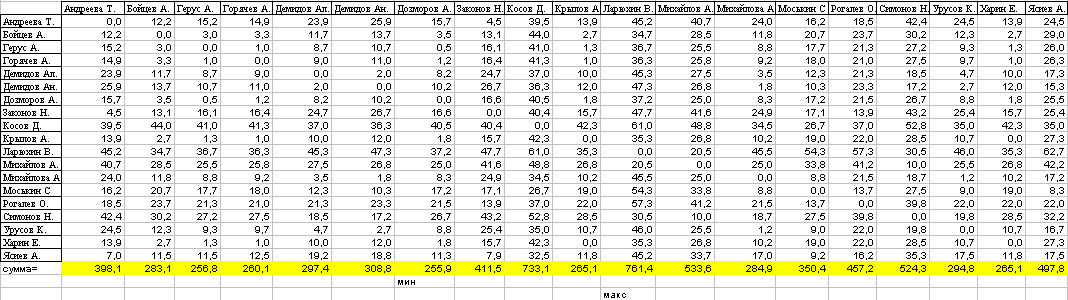
Рисунок 3 – Матрица расстояний между студентами




Рисунок 4 – Визуальное отображение студентов ГИП-105а на плоскости, согласно матрице расстояний

Программная реализация

Модель оптимального представления координат в двумерном пространстве была реализована в Excel.

Результаты оптимизации представлены в графическом виде на рисунке 5.


Так же, планировалось реализовать двумерную и трехмерную модель в C#, используя линейное программирование, а именно – бесплатную библиотеку solver55.dll, но, к сожалению, на её реализацию не хватило времени.




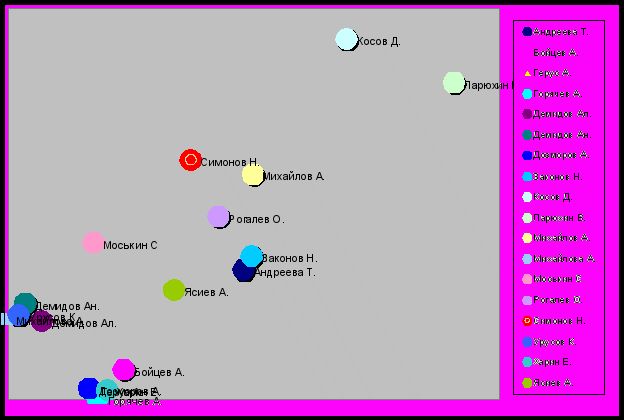
Рисунок 5 – Оптимальное представление студентов ГИП-105 в двумерном пространстве


Как видно из рисунка, были выделены 3 кластера, центрами которых являются студенты Законов Н., Горячев А. и Урусов К., но остались студенты, которые, вероятно, в силу своей исключительности, находятся в отдалении от всех остальных студентов – Косов Д. и Ларюхин В.. Впрочем, это совсем не значит, что они не контактируют с остальными или не могут с ними дружить.


Список использованной литературы

1. Википедия – свободная энциклопедия (ссылка скрыта )
   
2. Визуальный словарь - ссылка скрыта
   
3. Методические указания к выполнению лабораторных работ по дисциплине «Методы оптимизации и принятия решений» / С.А.Пиявский; Самарск. гос. арх.-строит. ун-т./ Самара, 2007.