Geum.ru

1. Модели индивидуального риска

Вид материалаДокументы
Подобный материал:
Глава 1. Риски страхования

1. Модели индивидуального риска

Данная модель используется для определения страховых тарифов, резервов страхования и перестрахования. Пусть S- случайные финансовые потери страховой компании в течение некоторого фиксированного интервала времени исполнения страховых контрактов. Тогда S - это СВ, распределение которой необходимо знать для определения рационального ведения дел страховых компаний.

Модель индивидуального риска принимается:



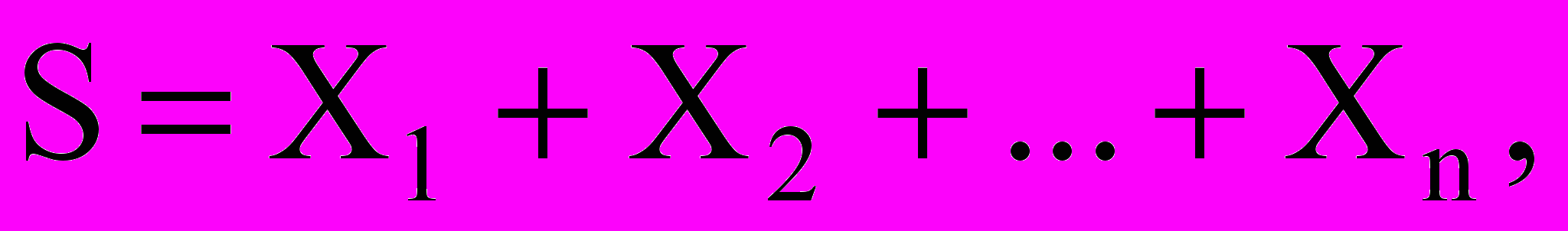
где 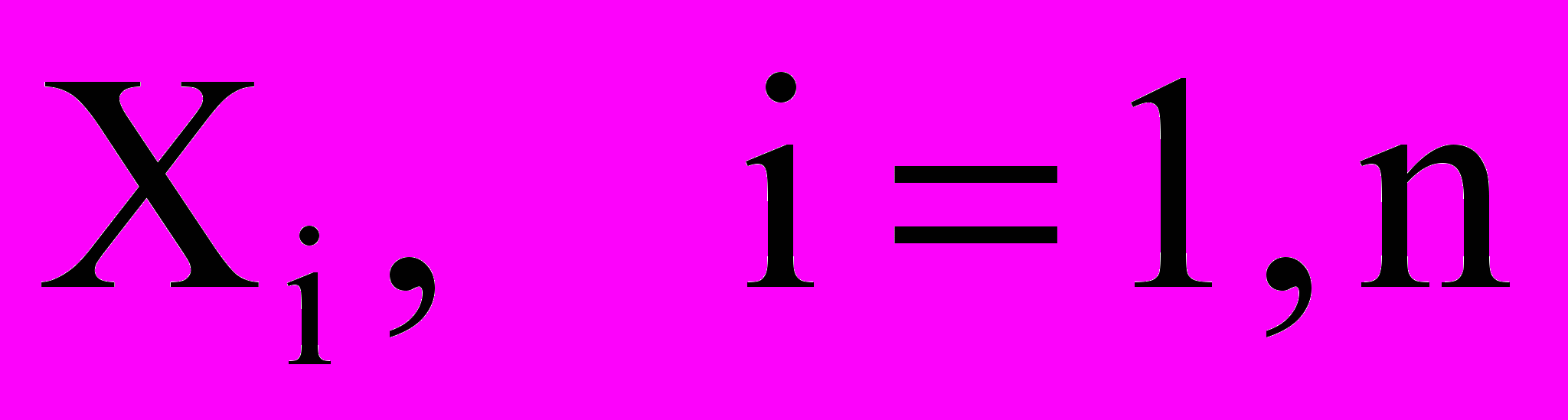-- потери, приходящиеся на i-ый страховой контракт, n-число исполняемых страховых контрактов.

Потери 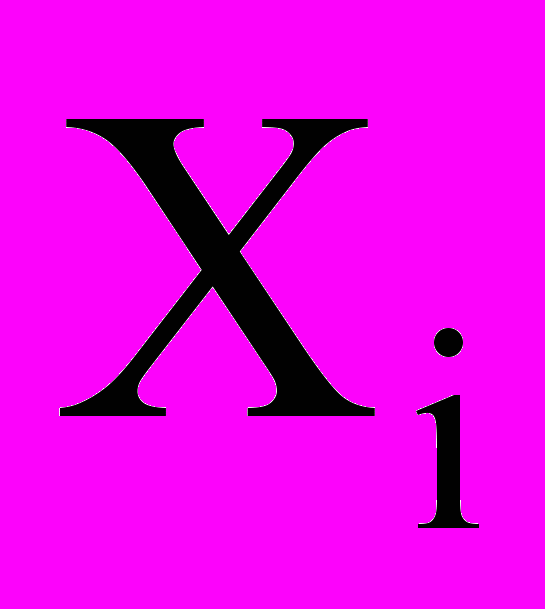, наз. суммами индивидуальных исков, S наз. совокупным иском. Положим, что 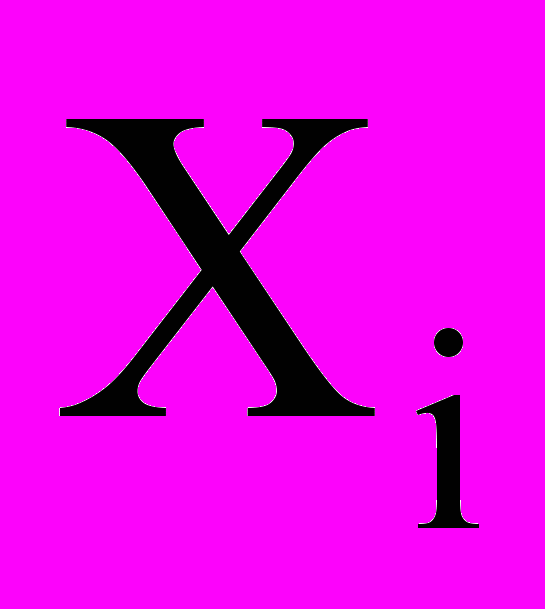-- независимые СВ. Кроме того, рассматриваемая модель не учитывает изменения стоимости денег во времени.

Пусть n - известно и фиксировано к началу рассматриваемого периода времени, n – число застрахованных.

В качестве примера рассмотрим модель страхования жизни. При страховании жизни на один год, страховая компания соглашается заплатить сумму кратную b рублей, если застраховавшийся умирает в течение срока исполнения контракта, и ничего не платит, если застраховавшийся проживет этот год.

Пусть q -- вероятность выплаты в течение года. СВ иска X может быть описана с помощью своего распределения, которое определяется распределением вероятности или функцией распределения.

Распределение вероятности имеет вид:



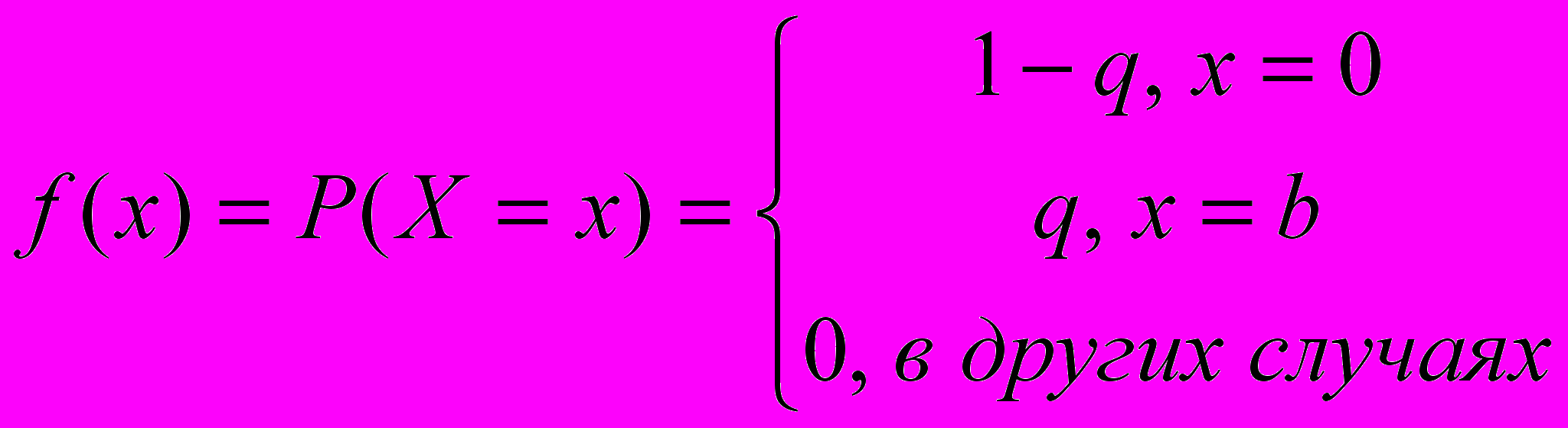
и соответственно функция распределения имеет вид:



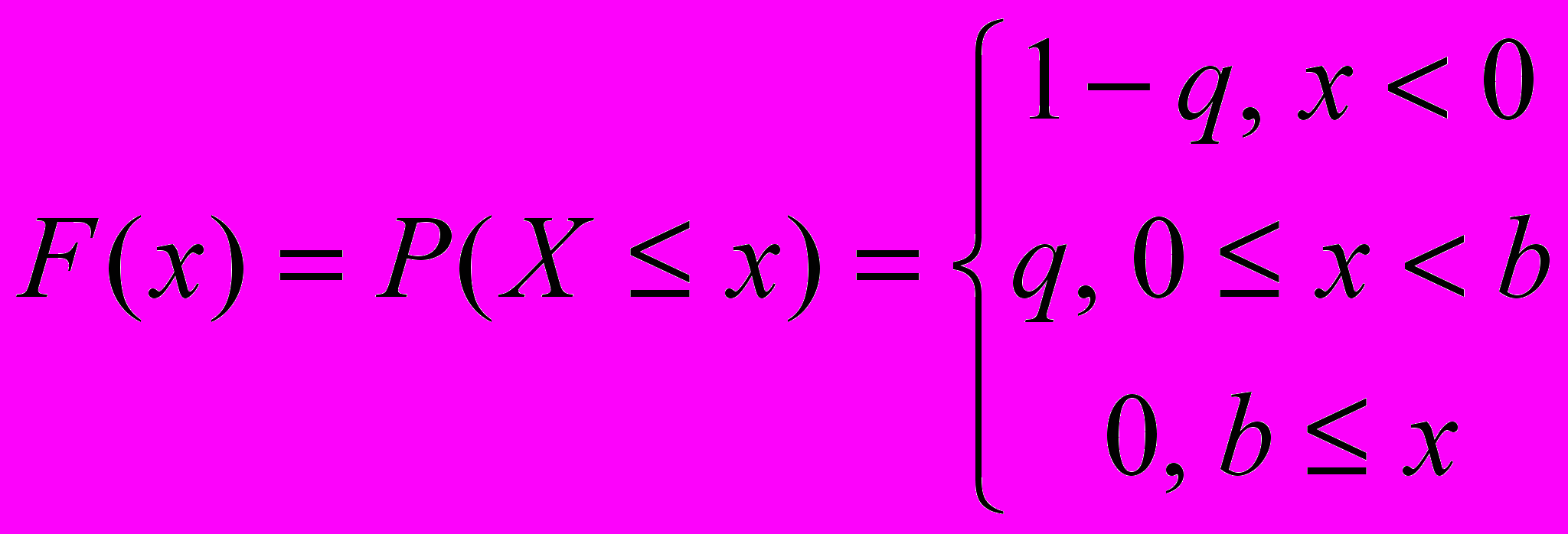
Сумма индивидуального иска X может быть представлена в виде:

, (*)

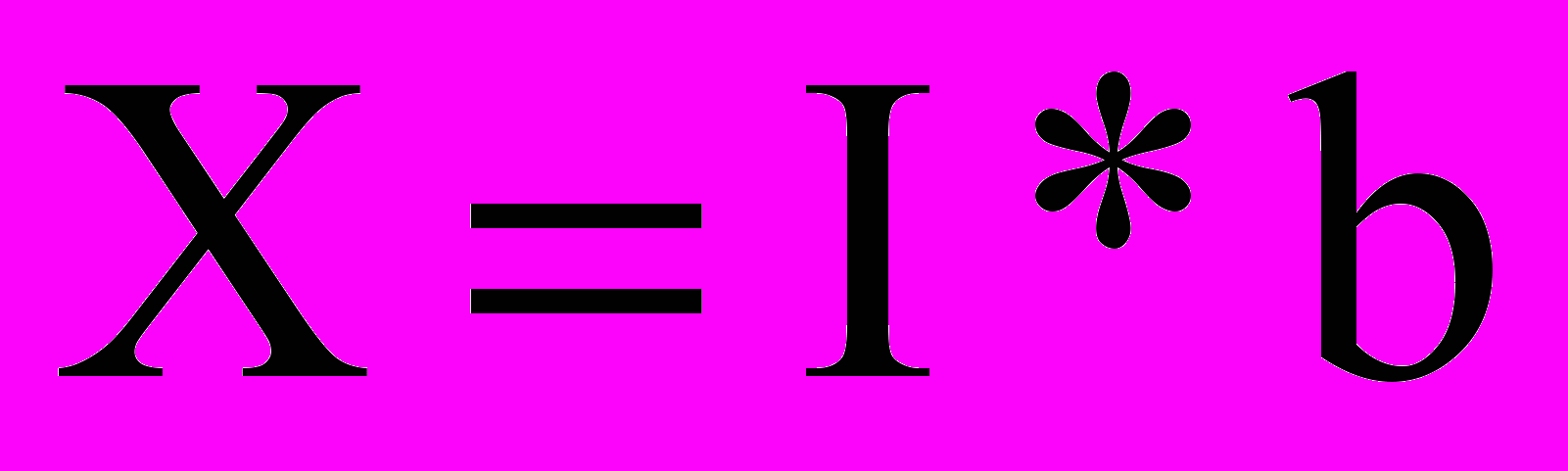где b – сумма, выплачиваемая в результате смерти,

I – индикатор события,



Вероятно, что

,

.

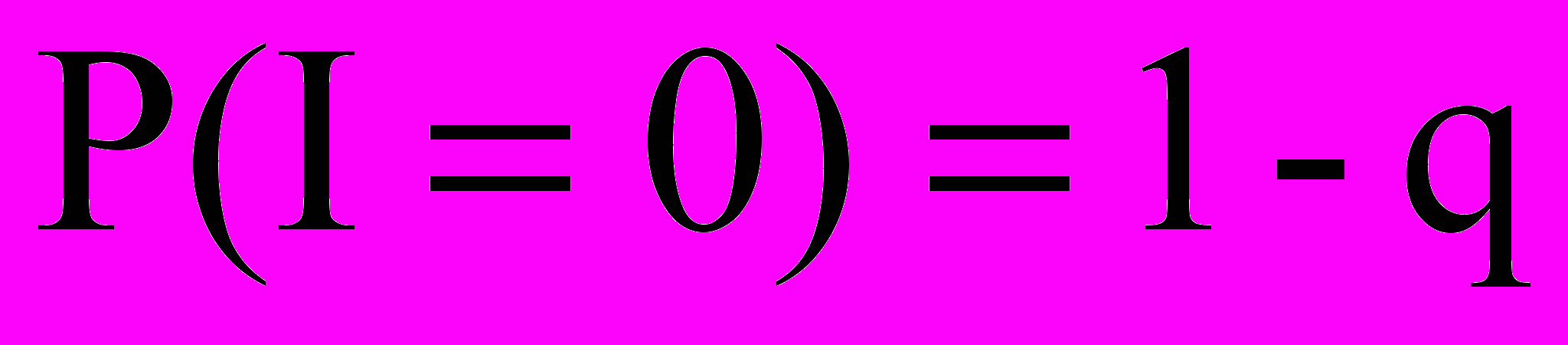Найдем характеристики этой СВ:

,

,

,

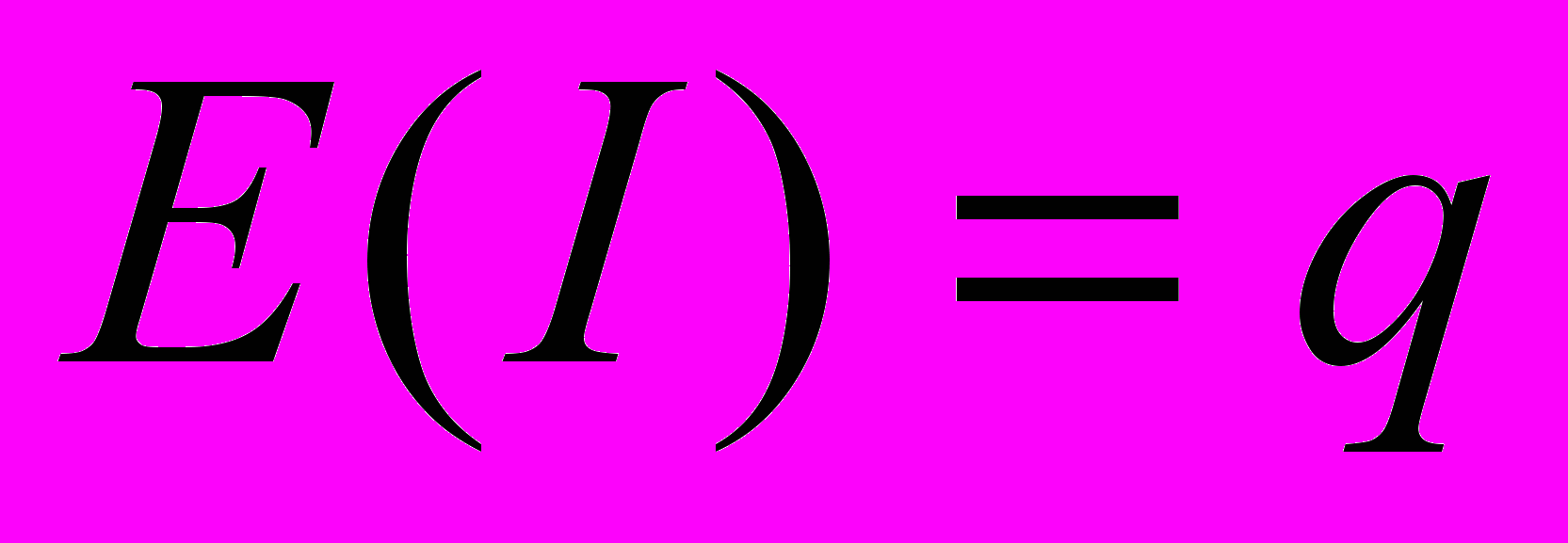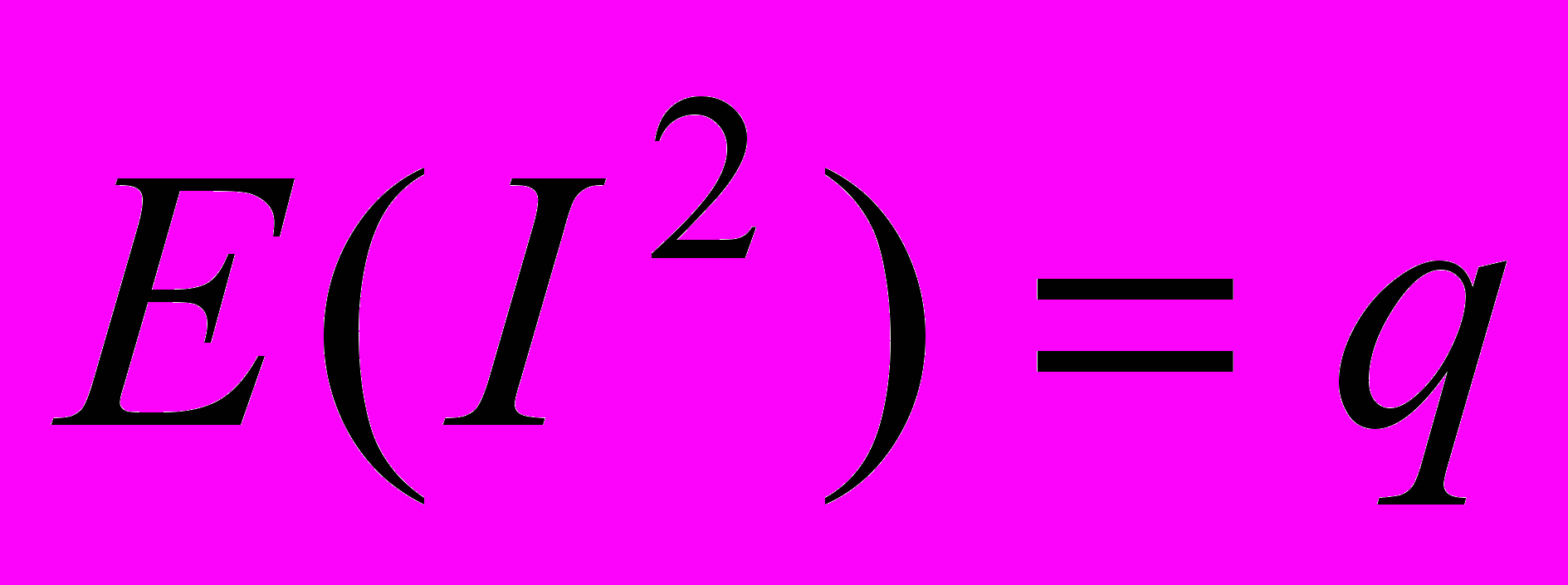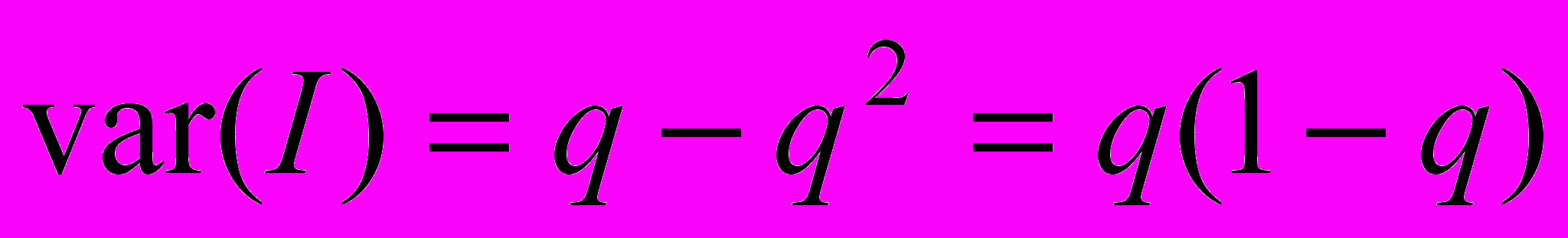тогда





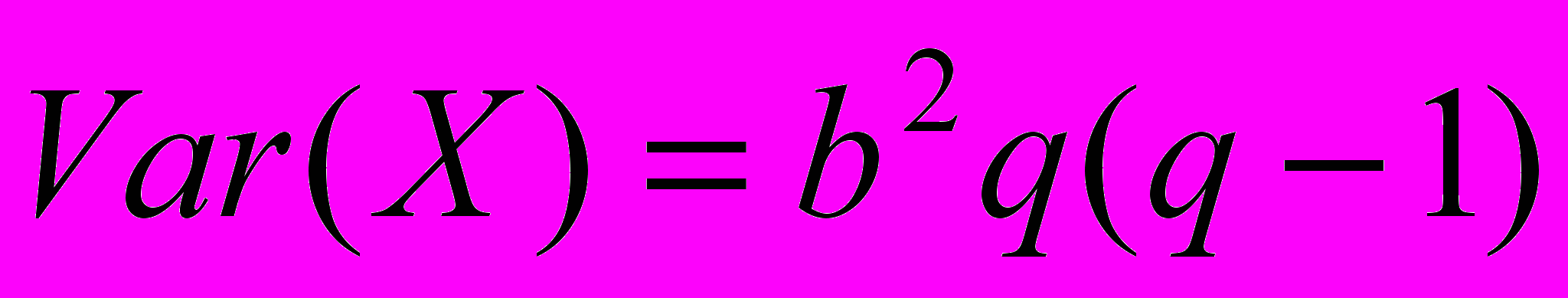
Построим более общую модель, в которой сумма выплаты по контракту является также СВ и в течение контрактного срока может произойти несколько выплат по одному контракту. Речь идет о контрактах, связанных со страхование здоровья, автомобиля и др. собственности. Общую формулу (*) тогда можно переписать в виде:

,

где X – СВ выплат за рассматриваемый период,

B – полная сумма выплат по контракту в течении этого срока,

I – индикатор события, что хотя бы одна выплата произойдет.





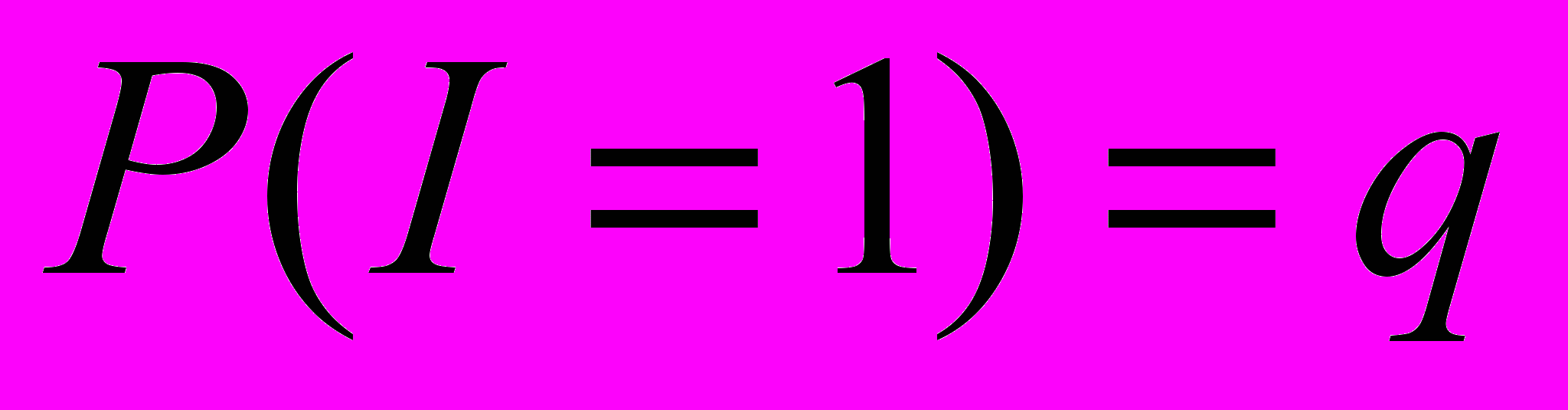
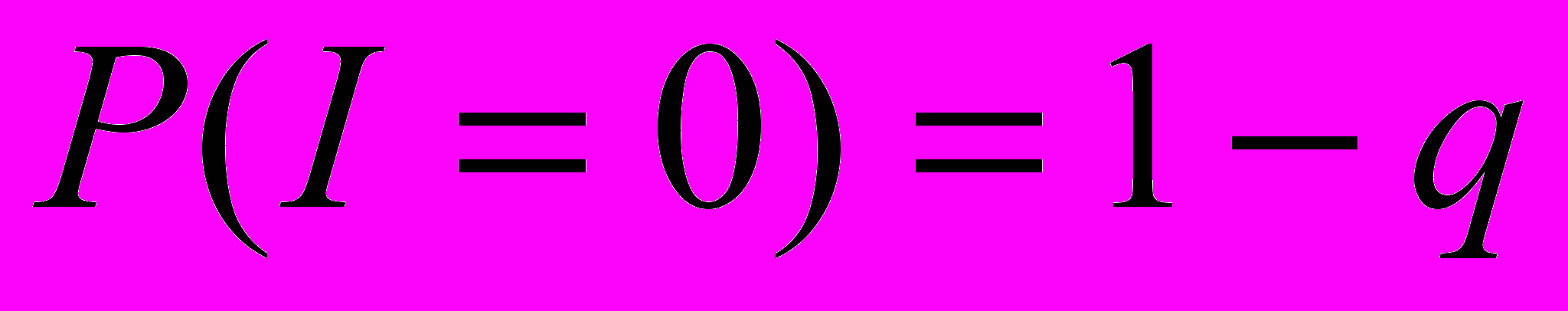
Распределения I и B находятся в зависимости от рассматриваемой ситуации.

Рассмотрим пример: рассмотрим одногодичный срок страховой жизни, оплачивающего увеличенное пособие в случае непредвиденной смерти. Если смерть непредвиденная, то пособие равно 50 000, во всех остальных случаях смерти пособие равно 25 000. пусть для конкретной личности, учитывая ее возраст, профессию и здоровье, вероятность непредвиденной смерти рана 0,0005, а вероятность смерти в других случаях равна 0,002. исходя из этого:



,

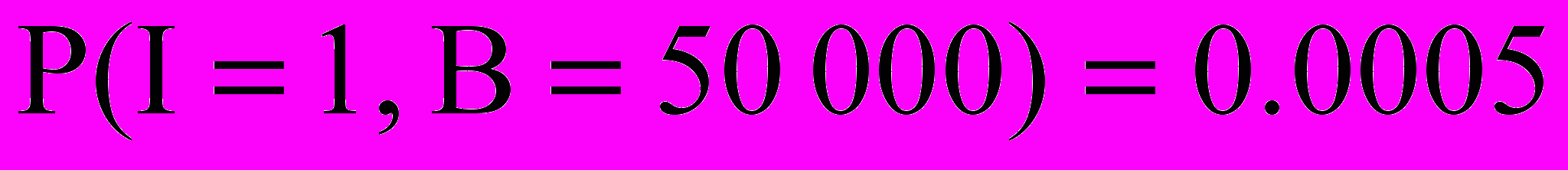
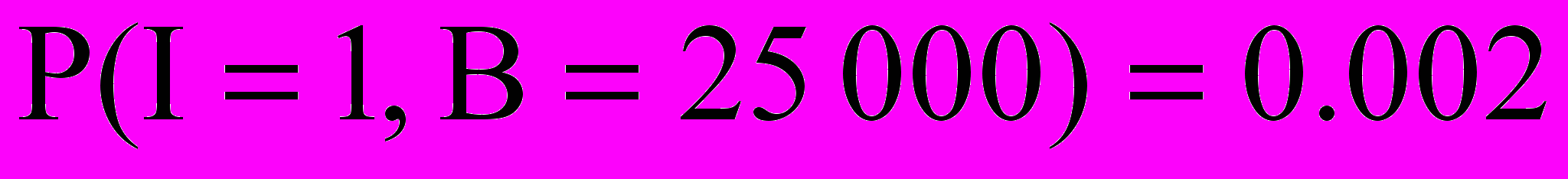тогда





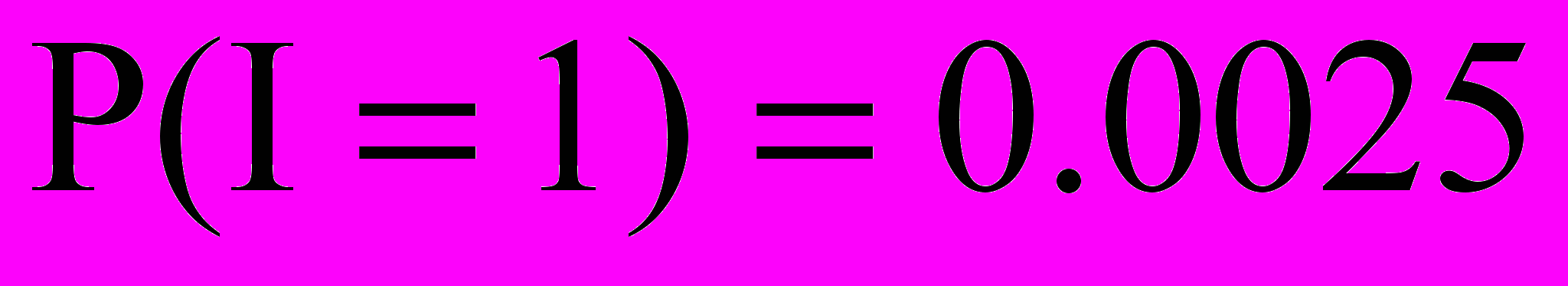
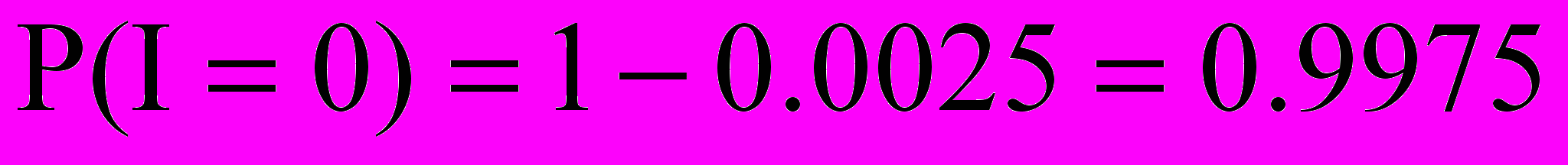
пользуясь формулами для условных вероятностей:





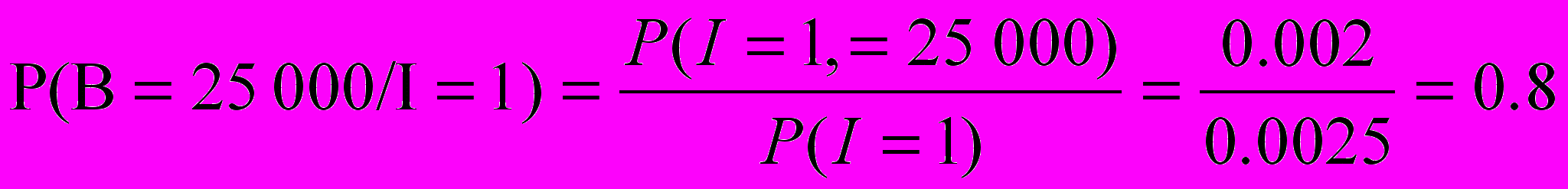
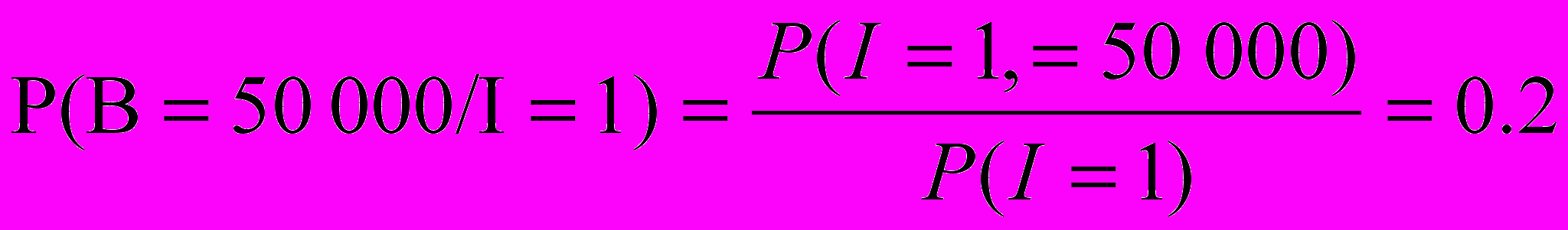
Модели индивидуального риска, иски страховых организаций представляются как сумма исков множества отдельных страхователей. Естественной задачей является определение распределения суммы исков.

Существует два метода определения этой суммы, основанные на распределении суммы независимой СВ.

Первый метод носит название «МЕТОД СВЕРТОК»:

,

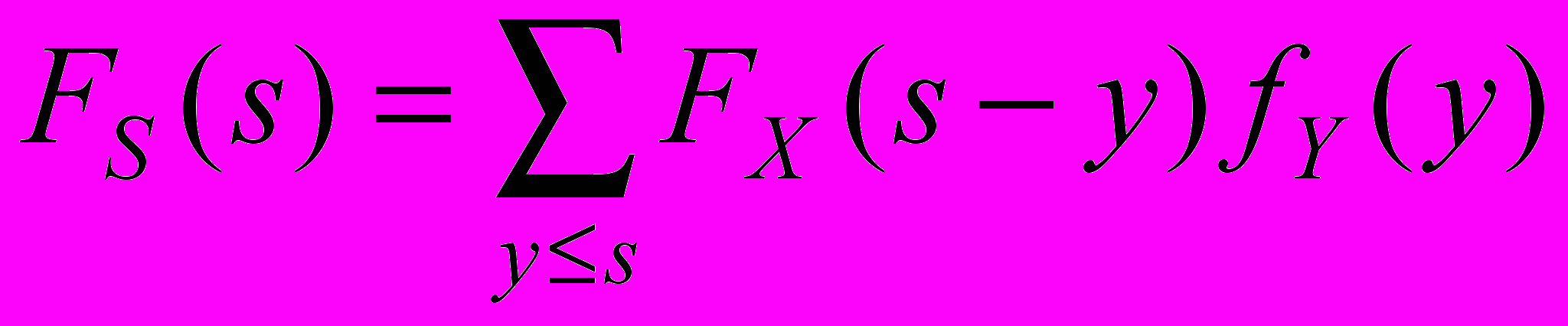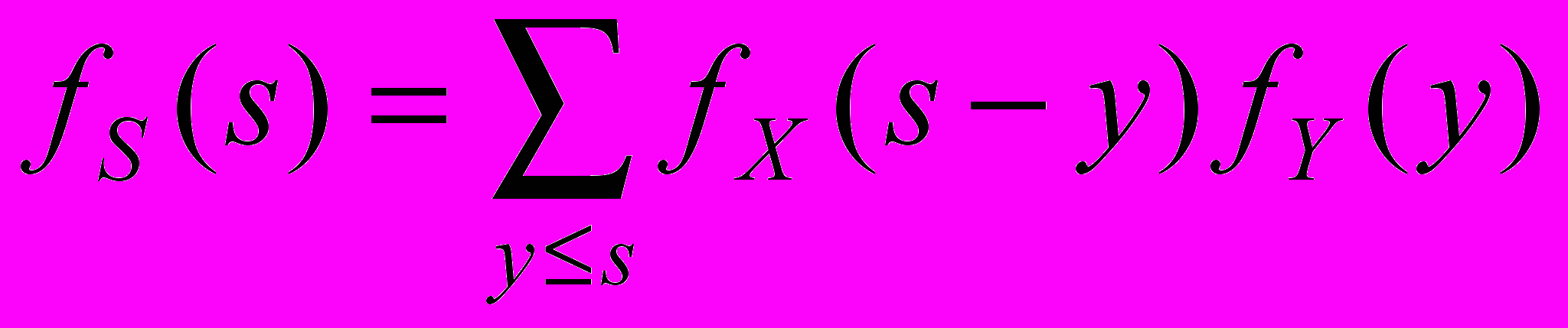- для дискретных СВ.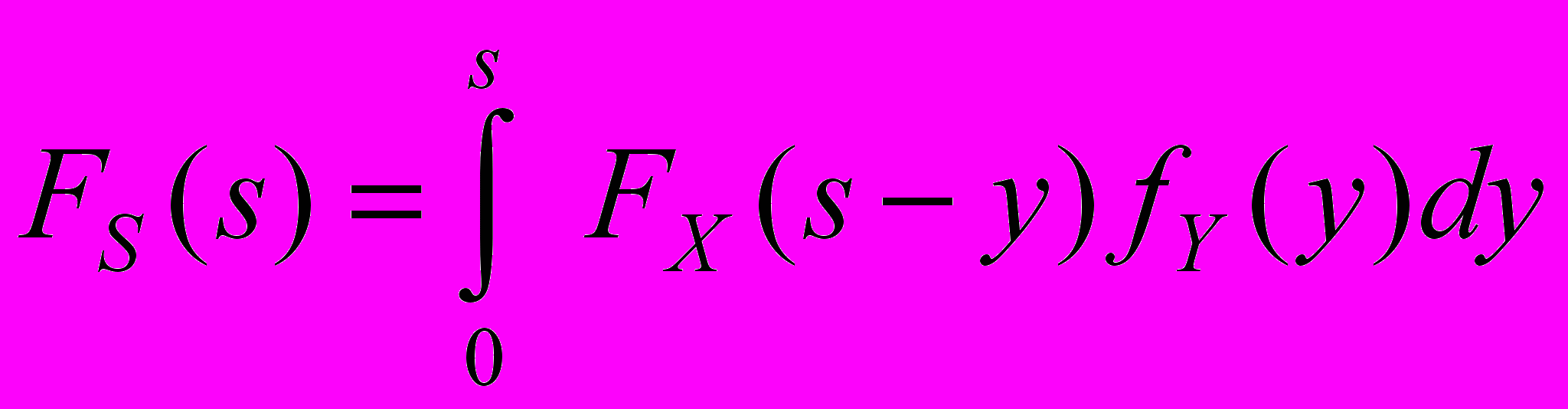



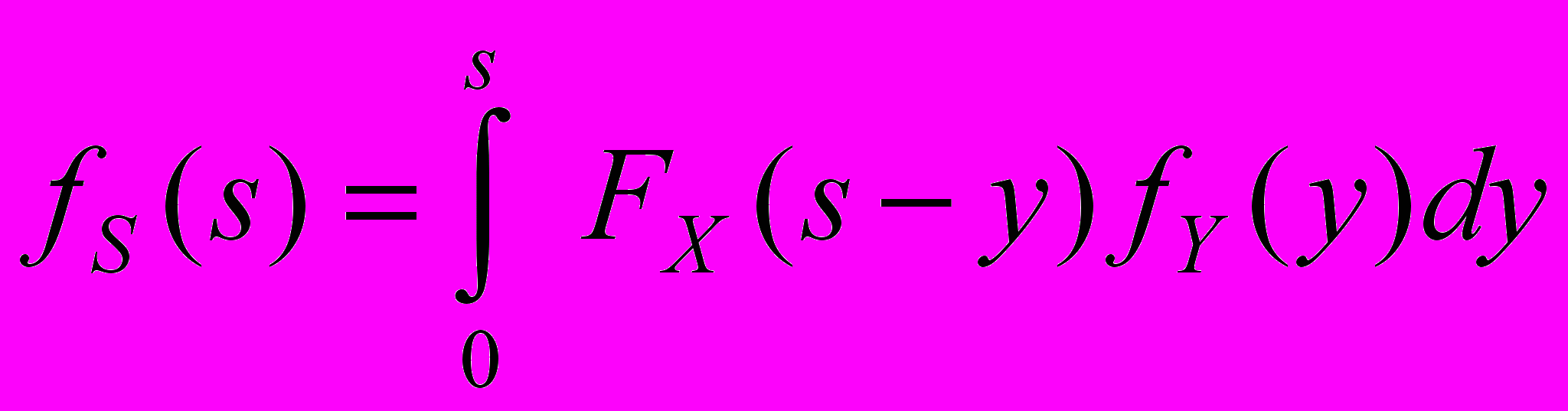- для непрерывных СВ.

Операция, описанная данными формулами, называется сверткой пары функций распределения .

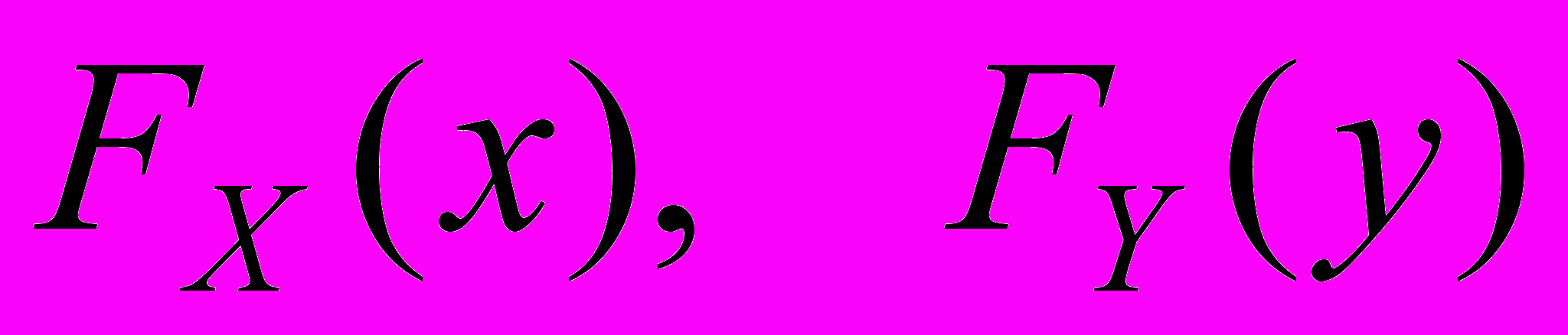Операция свертки может быть очень громоздкой при вычислении.

Второй метод вычисления распределения суммы независимой СВ основан на единственности производящей функции моментов:

,

,

(**)

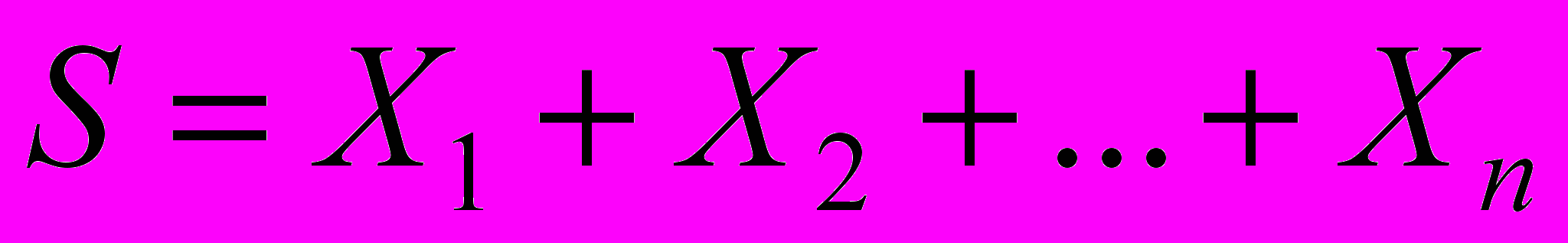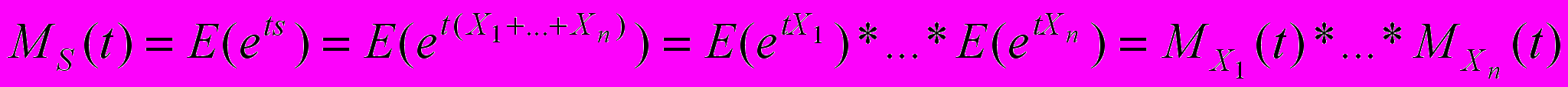Единственность распределения (**) позволяет вычислить распределение S.