В. И. Моисеев Вэтой работе я хотел бы обратить внимание читателей на возможность сближения двух позиций в философской логике позиции польского логика Станислава Лесьневского, представленной его логической системо

Вид материала

Документы

Содержание 6. Законы экстенсиональности в Онтологии 7. Проблема согласования онтологических определений Теорема модального нуля 8. Заключительные замечания

Подобный материал:

• В. И. Моисеев Вэтой работе я хотел бы выдвинуть одну гипотезу и попытаться обосновать, 265.19kb.
• Перед началом работы я ставил перед собой довольно расплывчатую цель, «поискать что-то, 906.15kb.
• Г. В. Диалектика как деятельная способность, 479.69kb.
• Вэтой курсовой работе будет рассмотрена оперативная память как с логической, так, 256.78kb.
• Поппер К. Логика социальных наук, 468.03kb.
• Доклад о социально экономическом развитии, 247.06kb.
• Буддизм в Китае и на Дальнем Востоке, 636.3kb.
• Ж. В. Котов Кпроблеме свободы печати у молодого Маркса. Приднепровская государственная, 162.48kb.
• Программа учебной дисциплины "Логика" Санкт-Петербург 2007, 191.2kb.
• Уважаемые читатели!, 1853.2kb.

5. Проблема онтологических определений


Как я уже отмечал выше, Лесьневский использует, кроме прототетических, еще и так называемые «онтологические» определения в L-Онтологии в следующей форме:

а(а _L С  a _L a  (a)),

где С – вновь вводимое имя, (a) – пропозициональное выражение, содержащее только переменную а в качестве свободной переменной.

Роль функтора Лесьневского в моей версии Онтологии играет предикат Moda. Я введу ряд определений, которые позволят приблизить мои обозначения к обозначениям Лесьневского:

-Определения


D. a  b  Moda(b,a), где “a  b” читается как “a есть b”

DP. a ₁ b  PModa(b,a), где “a ₁ b” читается как “a положительно есть b”

D*. a * b  Model(b,a), где “a * b” читается как “b есть модель для модуса a”


В моей версии Онтологии можно было бы также принять схему онтологических определений, подобных определениям Лесьневского:

(*) а(а  С  a  a  (a)),

где С – вновь вводимое имя, (a) – пропозициональное выражение (типа «S»), содержащее только переменную а в качестве свободной переменной. Поскольку а  а равносильно Modus(a), то (*) можно записать также в следующем виде:

(*’) а(а  С  Modus(a)  (a)).

В этом определении С вводится как мода некоторого класса модусов.

В общем случае можно использовать различные виды онтологических определений.

Под модусно-модальным онтологическим определением я буду понимать следующий вид определения:

(**) а(С  а  а  а  (a)),

где С – вновь вводимое имя, (a) – пропозициональное выражение (типа «S»), содержащее только переменную а в качестве свободной переменной. Поскольку а  а равносильно Modа(a), то (**) можно записать также в следующем виде:

(**’) а(С  а  Modа(a)  (a)).

В этом виде определений переменная а фигурирует как мода определяемого термина С, т.е. С вводится как модус всех мод некоторого класса.

Еще один вид онтологических определений – модусно-модельные онтологические определения. Они имеют следующую форму:

(***) а(С * а  Model(а)  (a)),

где С – вновь вводимое имя, (a) – пропозициональное выражение (типа «S»), содержащее только переменную а в качестве свободной переменной. Определяемый термин С вводится здесь как модус некоторого класса моделей.

Перепишем теперь приведенные выше определения в полном виде, через предикат Mod. Получим:

а(Mod¹²(С,a)  Modus(a)  (a)) – для модально-модусных определений

а(Mod¹²(a,C)  Moda(a)  (a)) – для модусно-модальных определений

а(Mod²³(С,a)  Model(a)  (a)) – для модусно-модельных определений

При таком представлении возникает возможность расширить эти три вида определений на общий случай онтологического определения, в дефиниендуме которого фигурирует предикат Mod^k1…km, содержащий на том или ином месте определяемый термин. В частности, должны будут возникнуть и проекторные определения, когда определяемый термин f_C типа (N,N)/N будет стоять на 4-м месте в предикате Mod.

Результатом такого обобщения является следующий общий вид онтологических определений.


Dⁱ_k1,…,km. x_k1…x_km(y_p1...y_pnMod(x_k,C,y_p)  Mod^k1…km(x_k1,…,x_km)  (x_k1,…,x_km)),


где переменные x_k1,…,x_km стоят на k_1,…, k_m-х местах соотв., переменные y_p1,..., y_pn стоят на p_1,..., p_n-х местах соотв. в предикате Mod из дефиниендума. Далее m+n = 3, все i, k_j и p_s, где j=1,.., m, s=1,.., n, не равны между собой. Определяемый термин C стоит на месте под номером i в предикате Mod из дефиниендума. Все эти условия обозначены символом Mod(x_k,C,y_p). Переменные или константы с индексом 4 (т.е. стоящие на 4-м месте в предикате Mod) имеют тип (N,N)/N. Другие переменные имеют тип N.

Например:


D²₁. a(C  a  Moda(a)  P(a)) – случай модусно-модального определения.


D¹₂. a(a  C  Modus(a)  Q(a)) – случай модально-модусного определения.


D²₃.a(C * a  Model(a)  Q(a)) – случай модусно-модельного определения.


D²₁₃. ab(Mod(a,C,b)  Mod¹³(a,b)  P(a,b) – случай модусно-модально-модельного определения.


В общем случае, по аналогии с числом слабых включений, может быть введено 28 видов онтологических определений с нотацией Dⁱ_k1,…,km.

Как и у Лесьневского, использование тех или иных онтологических определений может приводить к неконсервативным расширениям первоначальной версии онтологии. В этом случае в Проективно-модальной Онтологии может быть поставлена задача поиска некоторых общих критериев консервативности (некреативности) онтологических определений.


6. Законы экстенсиональности в Онтологии


В общем случае Слупецкий пишет следующее о правиле экстенсиональности в Онтологии Лесьневского: “Согласно этому правилу, в систему могут добавляться выражения некоторой специальной формы, независимо от того, какие теоремы были присоединены к системе ранее. Таким образом, правило экстенсиональности представляет из себя некоторое аксиоматическое правило. Я буду обозначать выражения, присоединенные к системе на основании правила экстенсиональности, как «законы экстенсиональности»… Пусть переменная  представляет предложениеобразующие функторы одного аргумента и пусть неэквиформные переменные  и  являются аргументами таких функторов⁸ ”. Затем Слупецкий пишет о том, что законы экстенсиональности представляют из себя импликации, консеквент которых имеет следующую вид:

 {()  ()}

Что же касается вида антецедента импликации, то он зависит от семантической категории переменных  и . Например, если эти переменные являются именными переменными (имеют категорию «N»), не эквиформными переменной x, тогда антецедент в соответствующем законе экстенсиональности будет иметь следующий вид:

x(x _L   x _L )

Таким образом, в целом получим следующий закон экстенсиональности для этого случая:

x(x _L   x _L )  {()  ()}

В такой форме закон экстенсиональности позволяет выражать эквивалентность переменных по L-функтору _L в языке L-Онтологии, через равносильность выражений () и (). В частности, из закона экстенсиональности можно вывести следующее правило подстановки:

( =_L   ())  (),

позволяющее заменять вхождения терма  на вхождения терма  в формуле .

Каждый из введенных выше видов эквивалентности может быть обеспечен соответствующим законом экстенсиональности (LE – Law of Extensionality) и в Проективно-модальной Онтологии. Например:


(LE¹₂)  ¹₂   {()  ()}


Закон экстенсиональности (LE¹₂) согласован с равенством мод «a ¹₂ b» (здесь  представляет собой предложениеобразующие функтор одного аргумента, а неэквиформные переменные  и  являются аргументами таких функторов и имеют тип N).

Поскольку Теорема верхней и нижней эквивалентности утверждает равносильность равенств «a ¹₂ b» и «a ²₁ b», то из (LE¹₂) может быть как теорема выведен закон экстенсиональности (LE²₁):


(LE²₁)  ²₁   {()  ()}


В общем случае могут приниматься законы экстенсиональности (LE ⁱ_k1…km):


(LE ⁱ_k1…km)  ⁱ_k1…km   {()  ()},


где (a ⁱ_k1…km b) - ⁱ_k1…km-равенство между a и b.

Я принимаю версию Онтологии с законами экстенсиональности LE²₁, LE³₁₂₄, LE⁴₁₂₃.

Принятие тех или иных законов экстенсиональности будет обеспечивать разные типы и степени «разрешающей способности» Онтологии, т.е. способности или неспособности отождествлять формулы () и (), фигурирующие в консеквентах законов экстенсиональности. В версии Онтологии с законами экстенсиональности LE²₁, LE³₁₂₄, LE⁴₁₂₃ логическая система строится как обладающая «умеренной степенью близорукости», т.е. не различающая моды и модусы на основании только множеств их мод и модусов и не принимающая во внимание множества моделей и проекторов этих мод-модусов. Этот выбор в определенной степени был также данью стратегии максимальной близости Онтологии к L-Онтологии. В общем случае можно пытаться строить иные версии Онтологии, принимающие те или иные версии законов экстенсиональности.


7. Проблема согласования онтологических определений


Еще одна интересная проблема онтологических определений – проблема согласованности модальных и модусных определений одной константы. Имеется в виду, что одна и та же константа может быть введена и через модусное и через модальное определение. В связи с этим возникает вопрос, согласованы ли эти опредления, т.е. не возникнет ли противоречий в связи с такими двойными определениями, и если нет, то каковы критерии такой согласованности ? В модусных определениях константа определяется «сверху» - через свойство всех модусов, содержащих данную константу как свою моду. В модальных определениях, наоборот, константа определяется «снизу» через свойство всех мод, содержащихся в данной константе как модусе.

Пусть в общем случае даны два онтологических определения – модально-модусное и модусно-модальное – некоторой константы С:

(1) х(х  С  х  х  (х)) – модально-модусное определение константы С

(2) х(С  х  х  х  (х)) – модусно-модальное определение константы С

Возникает вопрос, согласованы ли между собой свойства  и , т.е. на самом ли деле они, хотя и по-разному, но определяют один и тот же объект С ? Эту же проблему можно сформулировать и несколько иначе: пусть дано одно из определений, например (1), использующее модусное свойство ; как в этом случае правильно сформулировать свойство  в определении (2), чтобы было согласование со свойством , т.е. чтобы оба определения определяли один объект С ?

Для обозначения возможного решения этой задачи, я предположу, что даны два онтологических определения

(3) х(х  С  х  х  ⁺(х)) – модально-модусное определение константы С

(4) х(С  х  х  х  ^-(х)) – модусно-модальное определение константы С

со свойствами ⁺ и ^-, для которых как бы уже выполнено условие согласования, т.е. оба определения определяют один объект С. Исследуем отношения этих свойств при подобном идеализирующем предположении.

Прежде всего замечу, что при верности определений (3) и (4), мы можем заключить:

(5) х(х  х  (х  С  ⁺(х)))

(6) х(х  х  (С  х  ^-(х)))

Таким образом, если х есть модус или мода, то выполнение свойства ⁺ на х равносильно тому, что х есть модус для С, х  С (или, выполнение свойства ^- на х равносильно тому, что х есть мода С, С  х). Однако предикат  ведет себя как отношение нестрогого порядка (см. D и Теорему модусного порядка), в связи с чем свойства ⁺ и ^- также ведут себя как предикаты нестрого порядка переменной х относительно константы С. Свойство ⁺ ведет себя как одноместный предикат «С меньше или равно х», свойство ^- - как одноместный предикат «х меньше или равно С». Такие нестрогие порядки я буду называть дополнительными нестрогими С-порядками. Теперь мы можем пытаться решать поставленную выше задачу, исследуя, как в общем случае ведут себя два дополнительных нестрогих С-порядка.

В общем случае С-порядок х  С или С  х есть результат ограничения двуместного отношения нестрогого порядка х  у, в котором на место одной из переменных подставлена константа С (предполагается рассмотрение некоторого множества элементов, на котором заданы дополнительные нестрогие порядки  и , и С – некоторый элемент этого множества). Свойства нестрогого порядка, как известно, вполне описываются тремя основными условиями: рефлексивности х(х  х), антисимметричности ху(х  у  у  х  х=у) и транзитивности хуz(x  y  y  z  x  z). Следовательно, свойства С-порядка вполне будут описываться также этими тремя свойствами, с учетом тех ограничений, которыми образован С-порядок. Рассмотрим их с этой точки зрения для дополнительных С-порядков х  С и С  х.

1. Рефлексивность: х(х  х). Так как здесь на первом и втором местах двуместного предиката  фигурирует один и тот же элемент, то для С-порядка, как результата подстановки в нестрогий порядок константы С, возможен в этом случае только один вариант С  С. В нашем случае, при ограничении вводимых констант модусами-модами, это должно будет выразиться в формуле С  С  (^-(С)⁺(С)).

2. Антисимметричность: ху(х  у  у  х  х=у). Переходя к С-порядку, мы можем подставить С либо на место х, либо на место у в формулах х  у и у  х. В любом случае мы получим свойство ху(х  С  С  х  х=С), что можно будет выразить в утверждении х([х  х  ^-(х)  ⁺(х)]  х = С)).

3. Транзитивность: хуz(x  y  y  z  x  z). Здесь мы можем подставить константу С на место х, у или z. Но такие подстановки должны приводить по крайней мере к превращению первых двух отношений, x  y и y  z, в случаи С-порядка. При таком ограничении возможна подстановка С только на место у. Тогда получим: хz(x  С  С  z  x  z), что для нашего модального случая даст формулу: хz([х  х  z  z  ^-(x)  ⁺(z)]  z  x).

Итак, мы получаем следующие аналоги указанных требований к порядку для свойств ^- и ⁺:


(i) С  С  ^-(С)⁺(С)

(ii) х([х  х  ^-(х)  ⁺(х)]  х = С))

(iii) ху([х  х  у  у  ^-(x)  ⁺(у)]  у  x)


Эти условия и можно рассматривать как требования согласованности свойств ^- и ⁺ в случае модально-модусных и модусно-модальных онтологических определений (5) и (6), определяющих одну константу С. Условия (i)–(iii) требуют, чтобы свойства ^- и ⁺ вели себя как дополнительные нестрогие С-порядки.

В свойствх (i) и (ii) фигурирует константа С. Может возникнуть вопрос, какой смысл имеет формулировка таких свойств, когда мы еще не можем использовать определения (5) и (6) и только проверяем возможность их принятия ? Ведь в этом случае мы не знаем, что такое С ? Здесь я должен заметить следующее. Хотя мы не можем пока принять оба онтологических определения (5) и (6), но мы всегда можем работать пока только с одним из них, проверяя согласованность с ним второго определения. В этом случае мы можем использовать константу С, доказывать теоремы о ее свойствах, используя пока только одно онтологическое определение. В этом смысле мы уже можем кое-что знать о С и использовать эти знания при доказательстве (i) и (ii). Приведу пример.

Допустим, нам нужно проверить согласованность определений

(7) а(а 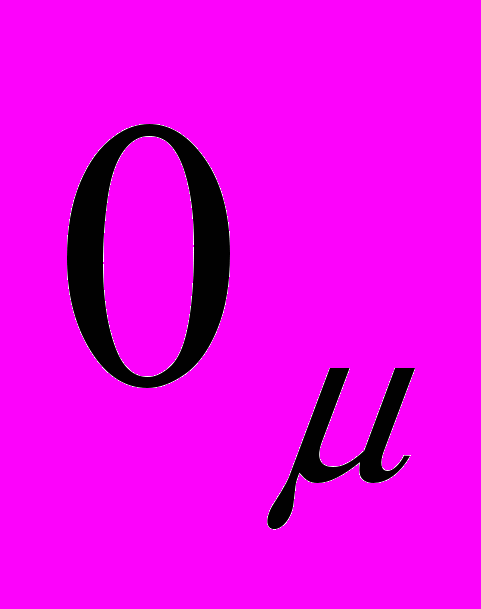  а  а  Moda(a))

(8) а( 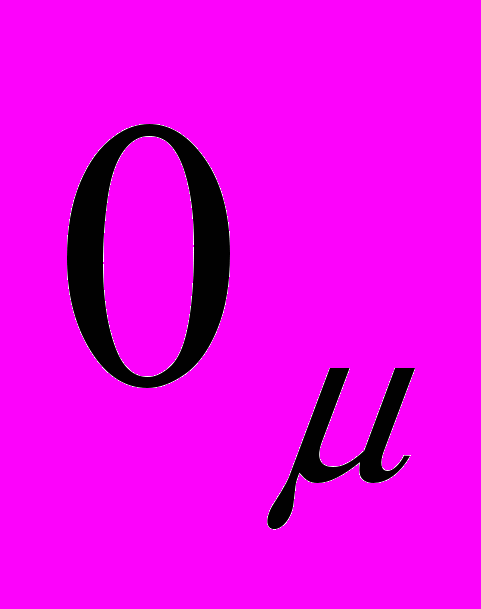 а  а  а  NModa(a))

т.е. модально-модусного и модусно-модального определения константы нулевой моды 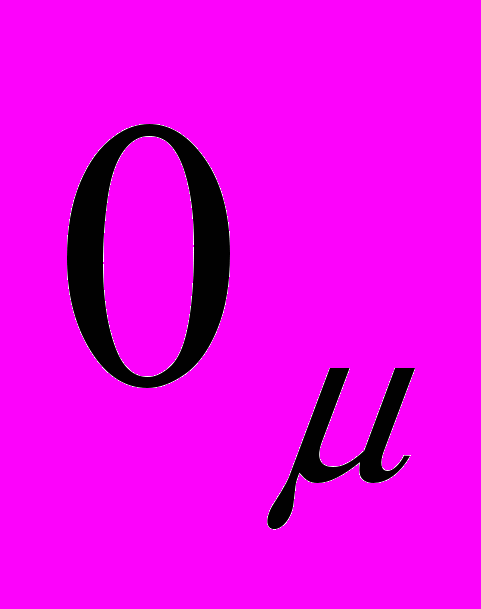. Я буду в качестве первичного использовать модусно-модальное определение (8). На этой основе можно доказать следующую теорему.

Теорема модального нуля. a = 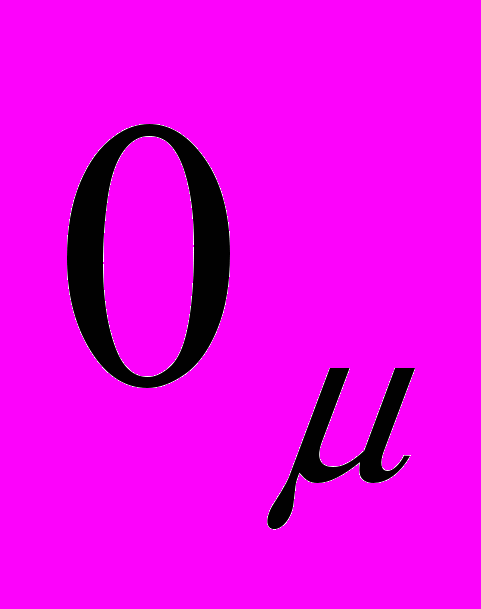 NModa(a)

Используя этот результат, покажем теперь выполнение свойств (i)–(iii) для Moda (как ⁺) и NModa (как ^-):

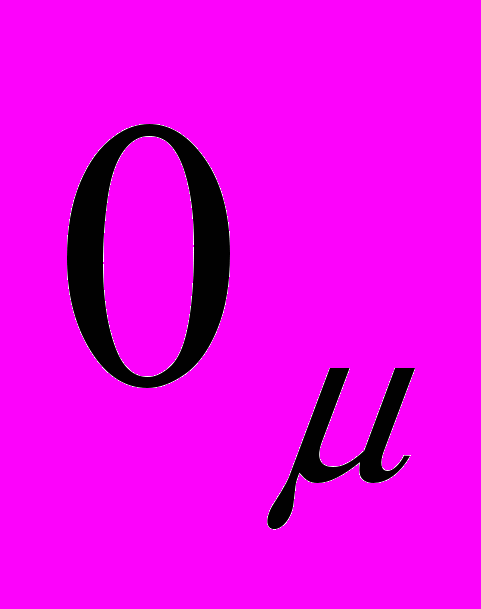
(i) 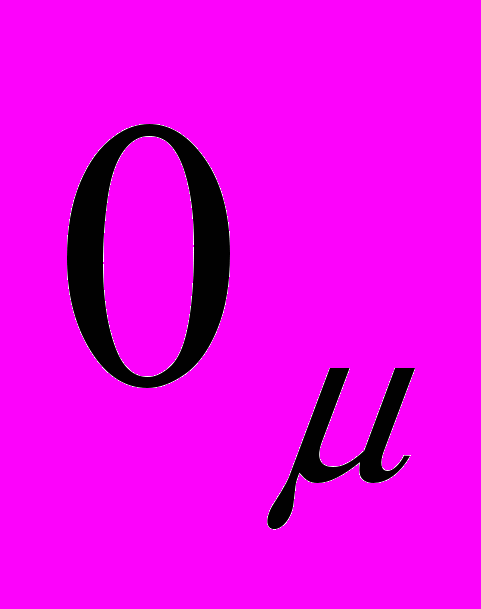  NModa(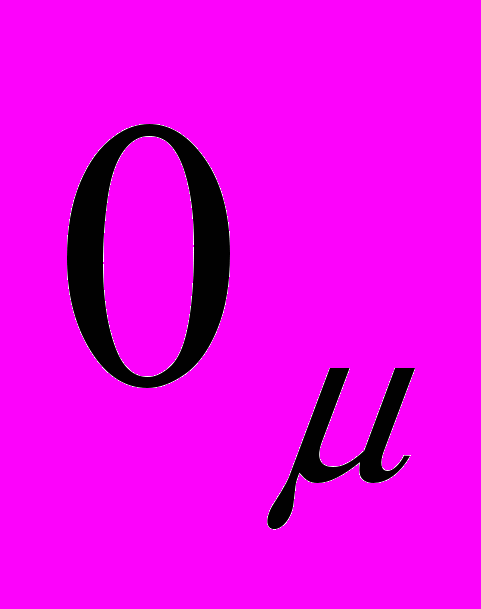)  Moda(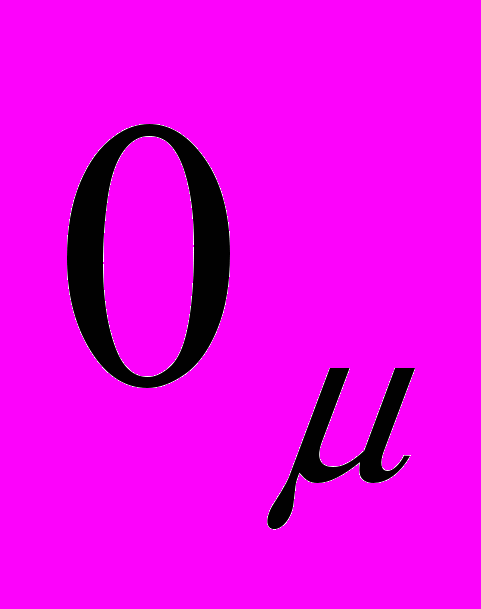). Если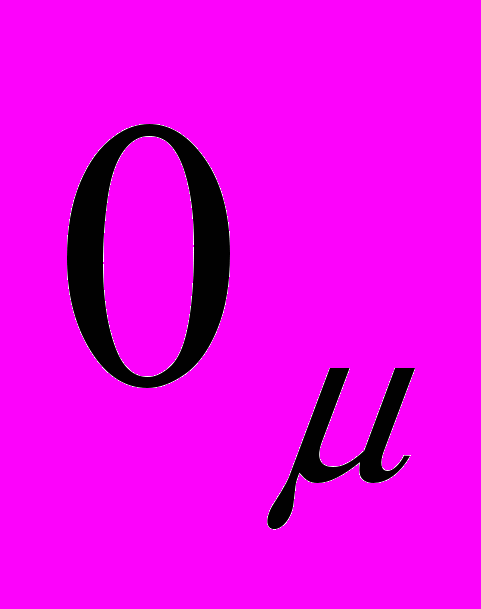 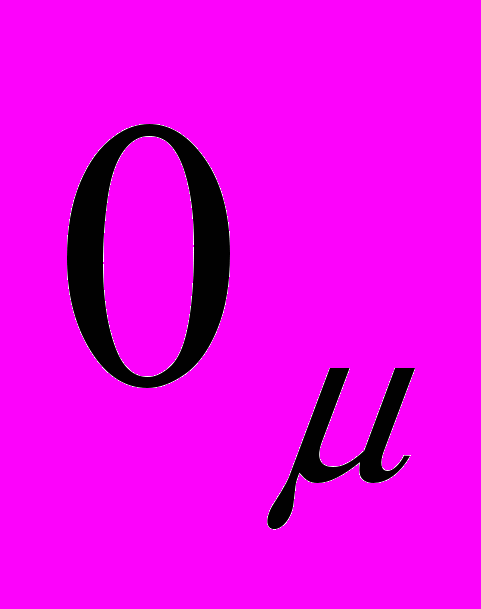 , то 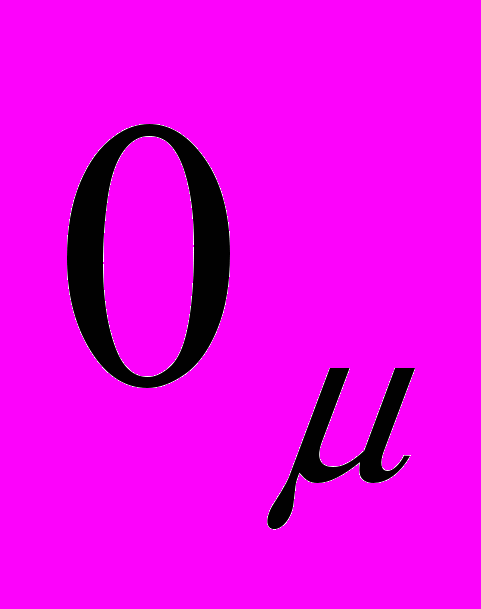= 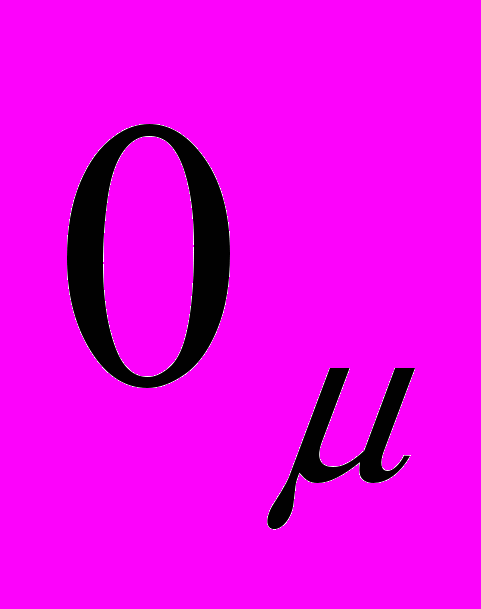, т.е. NModa(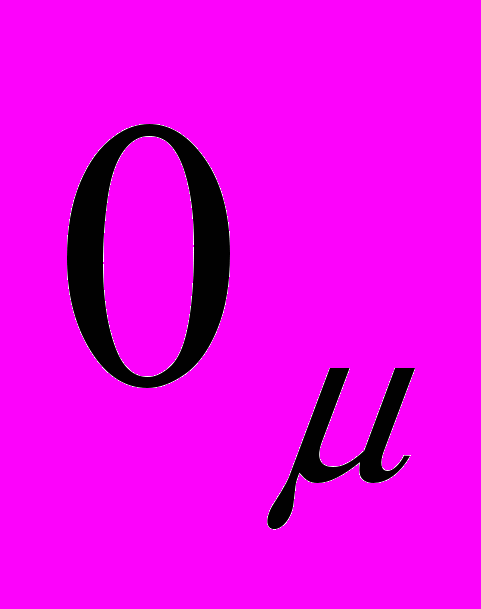), согласно Теореме модального нуля. Если же NModa(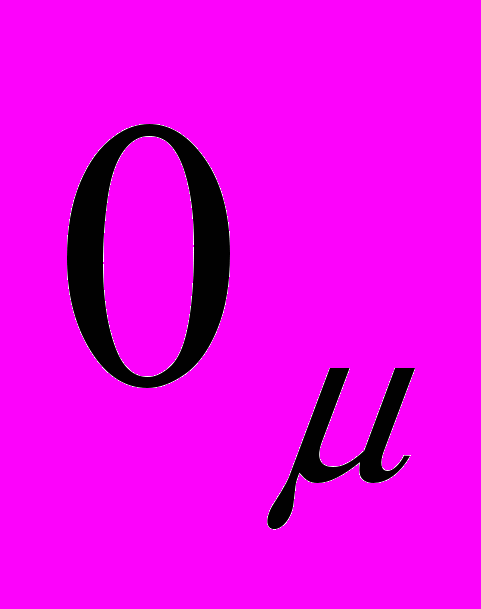), то Moda(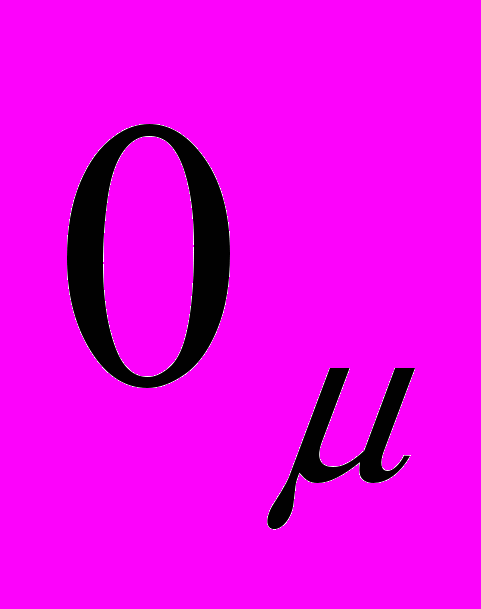), согласно определению нулевой моды.

(ii) х([х  х  NModa(х)Moda(х)]  х = 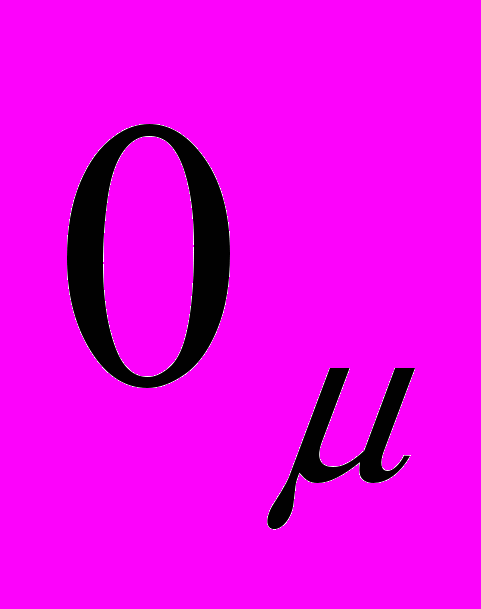)) – здесь имеем импликацию NModa(х)  х = 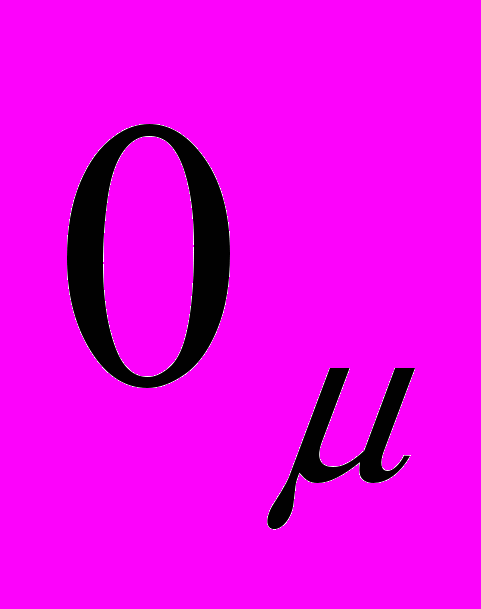, согласно Теореме модального нуля, откуда получаем (ii).

(iii) ху([х  х  у  у  NModa(x)  Moda(у)]  у  x) – см. Теорему универсальности нулевой моды.

Таким образом, все три свойства дополнительных нестрогих 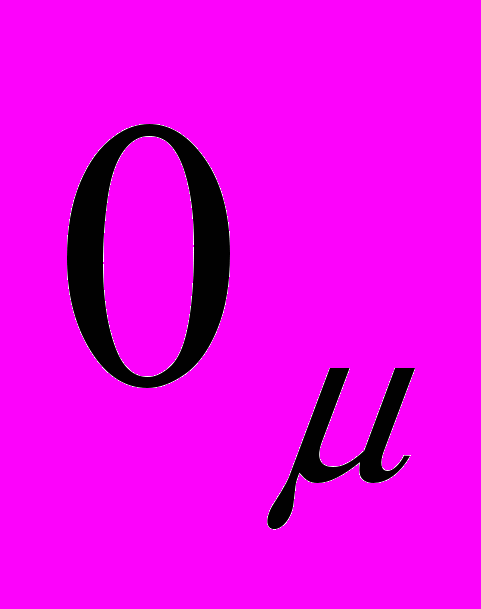-порядков выполнены, т.е. свойства NModa и Moda ведут себя как именно такие порядки, что доказывает согласованность определений (7) и (8).


8. Заключительные замечания


Продолжая в том же духе, можно развить некоторую аксиоматическую систему, которая хотя и опирается во многом на формализм логических систем Лесьневского, но далеко выходит за границы номинализма L-Онтологии и гораздо более существенно выражает глубинные интуиции Lingua Philosophica. Хотелось бы подчеркнуть, что развиваемая в Проективно-модальной Онтологии центральная конструкция модуса не может быть в общем случае сведена только к множеству мод этого модуса. Модус – это уже любой источник своих предикаций-мод, нечто, гораздо более близкое интуиции «единого» в Lingua Philosophica. Такого рода концепт может быть положен в основание нового образа рациональности, рождающегося сегодня в современной науке и культуре. В частности, на его основе можно пытаться построить более «холистический» образ математического знания, преодолевающего диктат теоретико-множественного номинализма. На этой основе можно надеяться на существенное сближение ресурсов строгости и универсальности философской мысли, олицетворяющего себя в сближении казалось бы столь полярных подходов Лесьневского и Соловьева.