В. И. Моисеев Вэтой работе я хотел бы обратить внимание читателей на возможность сближения двух позиций в философской логике позиции польского логика Станислава Лесьневского, представленной его логической системо

Вид материала

Документы

Содержание 3. Онтология как синтез L-Онтологии и логики всеединства 4. Аксиомы и первичные определения Онтологии Определение положительной эквивалентности Первая теорема собственных моделей Вторая теорема собственных моделей Третья теорема собственных моделей Теорема модальности модуса Теорема модусности моды Теорема эквивалентности моды и модуса Теорема тождественной моды Теорема антитранзитивности Теорема положительной эквивалентности Теорема положительной эквивалентности Теорема эквивалентности положительных модуса и тождественной моды Теорема эквивалентности положительных моды и модуса Первая теорема нулевой моды Вторая теорема нулевой моды Вторая теорема нулевой моды Теорема минимальности нулевого модуса Теорема универсальности нулевой моды ... Полное содержание

Подобный материал:

• В. И. Моисеев Вэтой работе я хотел бы выдвинуть одну гипотезу и попытаться обосновать, 265.19kb.
• Перед началом работы я ставил перед собой довольно расплывчатую цель, «поискать что-то, 906.15kb.
• Г. В. Диалектика как деятельная способность, 479.69kb.
• Вэтой курсовой работе будет рассмотрена оперативная память как с логической, так, 256.78kb.
• Поппер К. Логика социальных наук, 468.03kb.
• Доклад о социально экономическом развитии, 247.06kb.
• Буддизм в Китае и на Дальнем Востоке, 636.3kb.
• Ж. В. Котов Кпроблеме свободы печати у молодого Маркса. Приднепровская государственная, 162.48kb.
• Программа учебной дисциплины "Логика" Санкт-Петербург 2007, 191.2kb.
• Уважаемые читатели!, 1853.2kb.

3. Онтология как синтез L-Онтологии и логики всеединства


Теперь остается соединить методы L-Онтологии, которые Лесьневский использовал для своей номиналистической версии, с логикой всеединства. Для этого нужно суметь различить, что в L-Онтологии является общим для любой возможной онтологии, а что связано с частными смыслами именно L-Онтологии. Конечно, в первую очередь таким специфическим моментом L-Онтологии является номинализм Лесьневского. Он выражается в наложении ограничений на субъекты предикации в формулах a  b. Как я уже говорил, в формуле a  b Лесьневский использовал субъект-предикатную структуру, которую теперь можно увидеть как частный случай отношения модуса и моды. В формуле a  b в качестве субъекта (модуса) выступает а, в качестве его предиката (моды) – b. Отсюда мы получаем первый ключ к переинтерпретации L-Онтологии: мы можем прочесть формулу a  b как некоторый специфицированный случай модального отношения «b есть мода модуса a». Номинализм здесь выразится в том, что модус a у Лесьневского оказывается максимальным модусом, т.е. нельзя найти, отличный от a, модус, для которого a был бы модой. Имена, стоящие слева от -функтора у Лесьневского, выражают собой материальные объекты как вершины модальной иерархии. В номинализме нет ничего выше отдельных вещей. Все остальное – предикаты (моды) этих вещей. Вот это конечно нечто неуниверсальное, что принимается не любой версией онтологии, но только номиналистическими вариантами. И от этого ограничения Лесьневского нужно суметь отойти. Хотелось бы построить наиболее универсальную версию философской Онтологии, в рамках которой затем можно было бы выражать любые частные онтологии – номиналистические, реалистические, какие-угодно. С другой стороны, очень заманчиво использовать мощные логические средства L-Онтологии, включающие в себя бесконечную иерархию функторов и кванторов по ним, огромные выразительные возможности этой системы. Так постепенно у меня оформилась идея строить некоторую версию Онтологии, используя языковые средства L-Онтологии, насколько это возможно без -функтора (как он понимался Лесьневским. Функтор  у Лесьневского я буду далее обозначать как _L). Сначала я хотел обойтись некоторым трехместным предикатом Mod(a,b,c) – «a есть мода модуса b в модели c». Затем я осознал необходимость явного указания и участвующего в этом отношении проектора и начал использовать четырехместный предикат Mod(a,b,c,f) – «a есть мода модуса b в модели c с проектором f». Так я вплотную подошел к средствам некоторой аксиоматической системы, которая: 1) должна содержать некоторый первичный предикат Mod(a,b,c,f), выражающий онтологическую тетраду, 2) должна быть максимально близкой к L-Онтологии, насколько это возможно при смене первичного предиката, 3) должна опираться на L-Онтологию как на некоторый источник возможных аналогий, которые можно пытаться воспроизводить в новой версии Онтологии. Так L-Онтология и работа, проведенная Лесьневским, должна была стать некоторой «нитью Ариадны» при построении новой системы, но только в меру универсального заряда L-Онтологии, выходящего за рамки только номинализма. Для этого приходилось постоянно отслеживать меру универсальности тех или иных конструкций L-Онтологии. Не могу сказать, что мне все здесь кажется адекватным и до конца понятным. Скорее массив нового логоса еще только в некоторой мере оказался проявленным для меня и очень многое еще в ментальном тумане. Но уже и эта проявленная часть очень интересна.

Ближайшая цель теперь состоит в следующем. Представим, что мы начали лепить Онтологию заново, размягчив глину Лесьневского. Мы можем что-угодно принять, что-угодно отбросить из этой вселенной. Я предпочитал двигаться осторожно, минимально изменяя логическую вселенную польского мыслителя. Мы отбрасываем его -функтор, но нам понадобится своя версия этого функтора, способная выражать модальное отношение теперь уже в общем, а не только номиналистическом, смысле. Нужно, кроме того, выразить все основные понятия логики всеединства, сформулированные в пунктах 1-7. Наконец, нужно будет подумать над аксиомами новой системы, соотнося их с Аксиомой L-Онтологии. Вот первая задача.


4. Аксиомы и первичные определения Онтологии


Думая над определениями, я постепенно и пришел к идее четырехместного предиката Mod(a,b,c,f), поскольку на его основе можно единообразным способом породить множество нужных производных предикатов. Хочу заметить, что Лесьневский использует два вида первичных переменных – пропозициональные переменные (этот класс выражений обозначается как «тип S») и именные переменные («тип N»). На основе этих первичных выражений языка могут образовываться более сложные выражения. Например, конъюнкция p  q может быть выражена как функтор (p,q), что соответствует типу (S,S)/S (порядок чтения – слева направо) - двуместному функтору на выражениях типа S, образующему в результате так же тип S. В общем случае, если даны типы Т₁, Т₂, …, Т_n, то на их основе могут быть построены два вида n-местных функторов: имяобразующий функтор типа (Т₁, Т₂, …, Т_n)/N и предложениеобразующий функтор типа (Т₁, Т₂, …, Т_n)/S. Так продолжая и далее, можно строить бесконечную иерархию типов выражений L-Онтологии.

Я предположил, что, коль скоро функтор f в предикате Mod(a,b,c,f) несет смысл проектора, определенного на модусах и моделях, т.е. f(b,c) дает моду а, то функтор f, во-первых, должен иметь тип (N,N)/N, поскольку имена a, b, c для обозначений мод, модусов и моделей имеют тип N, т.е. это либо имена-константы, либо именные переменные. Следовательно, весь предикат Mod имеет тип: (N,N,N, (N,N)/N)/S. В соответствии с порядком мест 4-местного предиката Mod, я буду также называть моды 1-объектами (им отводится 1-место в предикате Mod), модусы – 2-объектами, модели – 3-объектами, проекторы – 4-объектами. С этими номерами будут связаны формы различных нотаций в Проективно-модальной онтологии.

Далее встал вопрос о производных предикатах, которые можно образовать на основе предиката Mod. Допустим, нам нужно ввести трехместный предикат Mod(a,b,c), утверждающий, что «а является модой модуса b в модели с». Здесь оказывается не важен конкретный проектор f, при котором образуется эта мода. Поэтому естественно определить предикат Mod(a,b,c) через Mod(a,b,c,f), связав в последнем квантором существования переменную f. Получим: Mod(a,b,c)  fMod(a,b,c,f). Так можно действовать и дальше, связывая кванторами существования те или иные переменные в Mod(a,b,c,f).

Под первичными определениями Онтологии я буду в первую очередь понимать прототетические определения вида


Dk₁…k_m. (x_k1,…,x_km)  х_p1...х_pnMod(x_k,x_p),


где (x_k1,…,x_km) – определяемое выражение типа S. Выражение (x_k1,…,x_km) содержит в качестве свободных переменных только переменные x_k1,…,x_km типа , где 1≤k_j≤4 при j=1,..,m, тип  - это либо тип N при k_j < 4, либо (N,N)/N при k_j = 4. Под обозначением х_p1...х_pnMod(x_k,х_p) имеется в виду выражение, образованное навешиванием кванторов существования х_p1...х_pn на предикат Mod по переменным х_p1,...,х_pn типа , где 1≤p_s≤4 при s=1,..,n, и тип  - это либо тип N при p_s < 4, либо (N,N)/N при p_s = 4. В предикат Mod входят только переменные x_k1,…,x_km и х_p1,...,х_pn, так что переменная k_j стоит на k_j-ом месте в предикате Mod, перменная p_s – на p_s-ом месте, и m+n = 4.

При m свободных переменных x_k1,…,x_km в предикате Mod возможно всего = первичных определений. Так как m  1, n  1 и m+n = 4, то m может принимать три значения 1, 2 и 3. Отсюда общее количество первичных определений равно 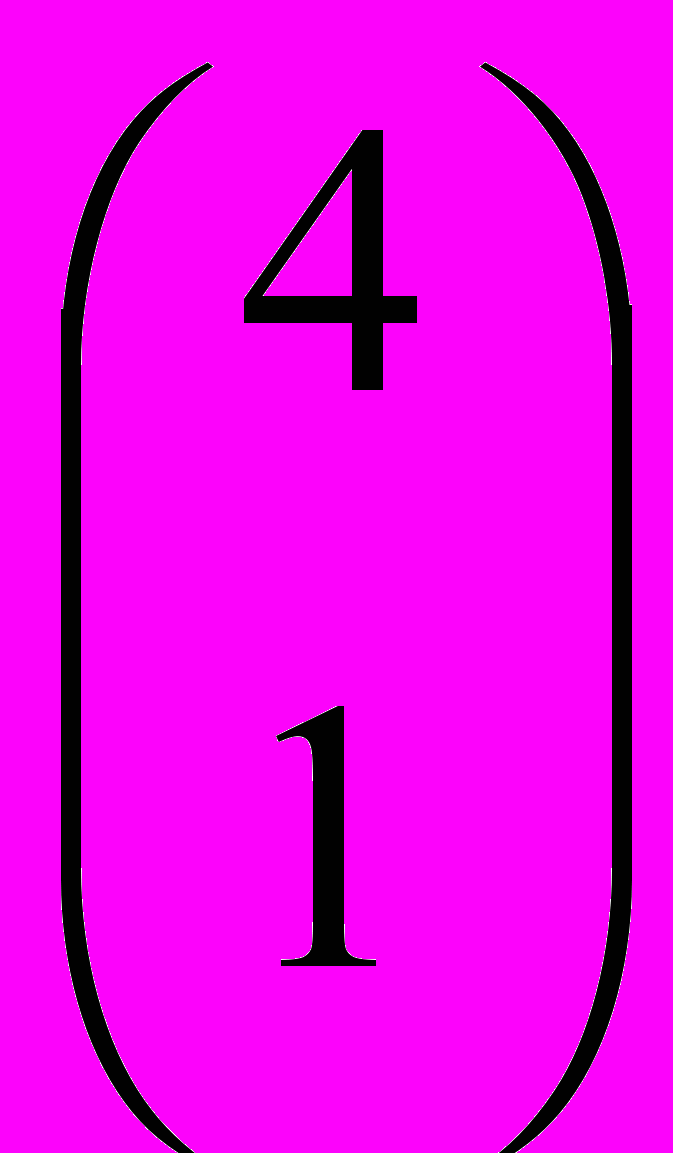++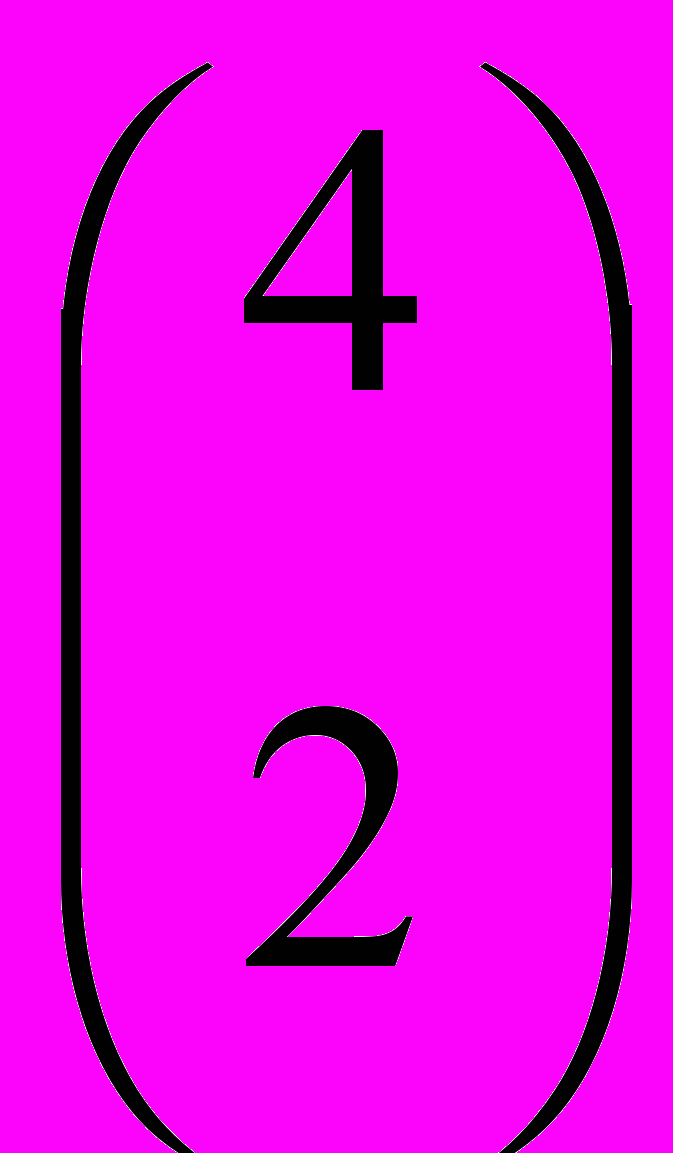 = 4 + 6 + 4 = 14. Я буду обозначать выражения типа (x_k1,…,x_km) также символом Mod^k1…km(a₁,…,a_m), где выражения a₁,…,a_m подставлены в предикат Mod на места вхождения переменных x_k1,…,x_km соотв., согласуясь с ними по типам. Специально можно выделить следующие случаи (после двоеточия приведены уникальные обозначения выражения Mod^k1…km(a₁,…,a_m)):


D123. Mod¹²³(a,b,c) : Mod(a,b,c)  fMod(a,b,c,f),


где “Mod(a,b,c)” читается как “а есть мода модуса b в модели с” (т.е. универсальное обозначение Mod¹²³(a,b,c) передано здесь как уникальное обозначение Mod(a,b,c). Индексы «1», «2» и «3» указывают номера мест в предикате Mod, переменные на которых не связаны квантором существования. Таким образом, здесь свободны 1-, 2- и 3-объекты, а 4-объекты связаны). Аналогично и ниже:


D12. Mod¹²(a,b) : Moda(a,b)  cfMod(a,b,c,f),

где “Moda(a,b)” читается как “a есть мода модуса b”


D23. Mod²³(b,с) : Model(c,b)  afMod(a,b,c,f),

где “Model(c,b)” читается как “c есть модель для модуса b”


D1. Mod¹(а) : Moda(a)  bcf Mod(a,b,c,f),

где “Moda(a)” читается как “a есть мода”


D2. Mod²(b) : Modus(b)  acf Mod(a,b,c,f),

где “Modus(b)” читается как “b есть модус”


D3. Mod³(с) : Model(c)  abf Mod(a,b,c,f),

где “Model(c)” читается как “c есть модель”


D4. Mod⁴(f) : Projector(f)  abcMod(a,b,c,f),

где “Projector(f)” читается как “f есть проектор”.


Во-вторых, под первичными определениями я буду понимать прототетические определения вида


DI ⁱ_k1…km. a ⁱ_k1…km b  x_k1…x_km(y_p1...y_pnMod(...a...)  y_p1...y_pnMod(...b...)).

DE ⁱ_k1…km. a ⁱ_k1…km b  x_k1…x_km(y_p1...y_pnMod(...a...)  y_p1...y_pnMod(...b...)).


Эти записи означают, что переменные x_k1,…,x_km стоят соотв. на k_1,…, k_m-ных местах, переменные y_p1,..., y_pn – на p_1,..., p_n-ных местах соотв. в предикатах Mod. Здесь m+n = 3, все i, k_j и p_s где j=1,.., m, s=1,.., n, не равны между собой. Термы а и b стоят на i-том месте в предикатах Mod. Переменные с индексом 4 (или стоящие на 4-м месте в предикатах Mod) – это переменные типа (N,N)/N. Все остальные переменные имеют тип N.

Из этих определений видно, что a ⁱ_k1…km b  (a ⁱ_k1…km b)  (b ⁱ_k1…km a).

Выражение a ⁱ_k1…km b я буду называть «слабым ⁱ_k1…km-включением а в b», выражение a ⁱ_k1…km b - «слабым ⁱ_k1…km-равенством а и b».

Каждому «слабому равенству» «a ⁱ_k1…km b» соответствует свое «сильное равенство»:


DSE ⁱ_k1…km. a =ⁱ_k1…km b  a ⁱ_k1…km b  Mod(…a…)  Mod(…b…),


где под обозначением Mod(…a…) здесь имеется в виду предикат Mod, в котором связаны кванторами существования все переменные, кроме переменной а, стоящей на i-том месте. В выражениях с индексной формой ⁱ_k1…km индекс i может пробегать значения от 1 до 4, и при каждом фиксированном i m может принимать значения от 1 до 3. Таким образом, при каждом i получим ++= 3+3+1 = 7 вариантов определений, следовательно, всего 47 = 28 вариантов. Отношение с индексной формой ⁱ_k1…km выражает равенство или включение i-объектов по k₁-, k₂-,…,k_m-объектам.

Например, модусы могут быть равны между собой по следующим семи основаниям:


a ²₁ b  x₁(y₃y₄Mod(x₁,a,y₃,y₄)  y₃y₄Mod(x₁,b,y₃,y₄)) – равенство по модам


a ²₃ b  x₃(y₁y₄Mod(y₁,a,x₃,y₄)  y₁y₄Mod(y₁,b,x₃,y₄)) – равенство по моделям


a ²₄ b  x₄(y₁y₃Mod(y₁,a,y₃,x₄)  y₁y₃Mod(y₁,b,y₃,x₄)) – равенство по проекторам


a ²_1,3 b  x₁x₃(y₄Mod(x₁,a,x₃,y₄)  y₄Mod(x₁,b,x₃,y₄)) – по модам и моделям


a ²_1,4 b  x₁x₄(y₃Mod(x₁,a,y₃,x₄)  y₃Mod(x₁,b,y₃,x₄)) – по модам и проекторам


a ²_3,4 b  x₃x₄(y₁Mod(y₁,a,x₃,x₄)  y₁Mod(y₁,b,x₃,x₄)) – по моделям и проекторам


a ²_1,3,4 b  x₁x₃x₄(Mod(x₁,a,x₃,x₄)  Mod(x₁,b,x₃,x₄)) – по модам, моделям и проекторам


Отдельно можно выделить следующие равенства и включения:


DE²₁. a ²₁ b : a  b  c(Moda(c,a)  Moda(c,b)),

где “a  b” читается как “a слабо равно b”


DSE²₁. a =²₁ b : a = b  a  b  Modus(a)  Modus(b),

где “a = b” читается как “a равно b”


DI²₁. a ²₁ b : a  b  c(Moda(c,a)  Moda(c,b)),

где “a  b” читается как “a слабо включено в b”


DE²₃. a ²₃ b : a * b  x(Model(x,a)  Model(x,b)),

где “a * b” читается как “a модельно равно b”


В-третьих, под первичными определениями я буду понимать т.н. валентные определения, среди которых, по крайней мере, содержатся следующие:


DPModa1. PModa(a)  b(Moda(b,a)  Moda(a,b))  Moda(a),

где “PModa(a)” читается как “a есть положительная (ненулевая) мода”

Здесь положительная мода определяется как такая мода, которая имеет не равную себе моду.


DNModa. NModa(a)  b(Moda(b)  Moda(a,b))  Moda(a),

где “NModa(a)” читается как “a есть нулевая мода”

Таким образом, нулевая мода определяется как мода всех мод.


DPModa2. PModa(a,b)  Moda(a,b)  PModa(a),

где “PModa(a,b)” читается как “a есть положительная мода модуса b”

Здесь вводится двуместный предикат, утверждающий, что а является не просто модой модуса b, но его положительной модой.


DPModus. PModus(a)  bPModa(b,a),

где “PModus(a)” читается как “a есть положительный модус”

Положительный модус определяется как модус, у которого найдется положительная мода.


DIModa. IModa(a)  Modus(a)  b(Modus(b)  Moda(b,a)),

где “IModa(a)” читается как “a есть бесконечный модус”

Бесконечный модус – модус всех модусов, т.е. все модусы являются его модами.


DAt. At(a)  PModus(a)  b(PModa(b,a)  (b =²₁₃₄ a)), здесь “At(a)” читается как “a есть атом”. В этом смысле атом – это такой положительный модус, который не имеет отличных от себя положительных мод.


На основе отношения «быть положительной модой» также можно определить эквивалентность, когда два модуса a и b являются положительными модами друг друга. Эта эквивалентность (ниже будет показано, что это в самом деле эквивалентность) отличается от просто равенства двух модусов, представляя из себя более сильный – позитивный – вариант такого равенства.


Определение положительной эквивалентности


DPE. a  b  PModa(a,b)  PModa(b,a),

где “a  b” читается как “a положительно эквивалентно (равно) b”


Теперь после этих первичных определений я введу аксиомы Онтологии.


(AO1) Moda(a,b)  Modus(a)  d(Moda(b,d)  Moda(a,d))  Moda(b,b)


В этой первой аксиоме определяются свойства отношения «быть модой модуса» (Moda). Требуется, чтобы это отношение было транзитивным и рефлексивным, чтобы всякая мода одновременно была и модусом.


(AO2) Mod(a,b,c,f)  (a =¹₂₃₄ f(b,c))  aMod(a,b,c,f)


В этой аксиоме выражается связь функтора f с предикатом Mod: 1) если функтор f используется в предикате Mod(a,b,c,f), то это означает, что мода а есть результат действия f на модус b и модель с, 2) с другой стороны, если окажется, что для некоторого функтора f типа (N,N)/N имеет место равенство a =¹₂₃₄ f(b,c) и, кроме того, f есть проектор для модуса b и модели с, то отсюда мы можем заключить, что а есть мода модуса b в модели с и с проектором f. Следовательно, никаких специальных свойств, кроме того, что это должно быть отображение из модусов и моделей в моды, я не требую от проектора (точнее говоря, я не требую ничего большего, кроме того, что следует из аксиомы АО2).

Теперь можно начинать доказывать различные теоремы. Для примера я приведу доказательство следующей простой теоремы.


Первая теорема собственных моделей. Moda(a,b)  c(Model(c,b)  Mod(a,b,c)), т.e., если а есть мода модуса b, то найдется модель c такая, что c есть (собственная) модель модуса b и a есть мода модуса b в модели c.

Доказательство.(1) Moda(a,b) посылка

(2) Moda(a,b)  cf Mod(a,b,c,f) D12.

(3) cf Mod(a,b,c,f) MP (1), (2)

(4) f Mod(a,b,c₀,f) c-снятие (3)

(5) af Mod(a,b,c₀,f) a-введение (4)

(6) af Mod(a,b,c₀,f)  Model(c₀,b) D14.

(7) Model(c₀,b) MP (5), (6)

(8) f Mod(a,b,c₀,f)  Mod(a,b,c₀) D123.

(9) Mod(a,b,c₀) MP (4), (8)

(10) Model(c₀,b)  Mod(a,b,c₀) -введение (7), (9)

(11) c(Model(c,b)  Mod(a,b,c)) c-введение (8)


Я использовал здесь следующие правила вывода ():

1. A  B  A  B – переход от эквивалентности к импликации. Это правило может быть рассмотрено как частный случай снятия конъюнкции (-снятия) – см. ниже. Особенно часто это правило может применяться в тех случаях, когда эквивалентность A  B представляет из себя какое-либо определение. В этих случаях можно приводить ссылку на название определения справа от импликации A  B (см. строчки (2), (6) и (8)).
   
2. AB, A  B, правило модус поненс (modus ponens, MP). Если формула B выводится из формул (i)AB и (j)B в доказательстве, тогда можно писать “MP (i), (j)” или “MP (j), (i)” справа от формулы B (см. строчки (3), (7) и (9)).
   
3. aA(a)  A(a_i), правило снятия квантора существования (a-снятие). Как и в L-Онтологии, на место переменной а в формуле А подставляется индексированная переменная a_i, которая не должна быть эквиформной (равной по форме) никакой ранее появившейся в доказательстве переменной. Подстановки на место индексированной переменной запрещены. Если A(a_i) выводится из (i)aA(a), тогда можно писать “a-снятие (i)” справа от формулы A(a_i) (см. строчку (4)).
   
4. {A(a)}_a[b]  aA(a) – правило введения квантора существования (a-введение), где {A(a)}_a[b] есть результат правильной подстановки терма b на место терма a в формуле A(a). Для этого правила нет никаких ограничений. Если aA(a) выведена из (i) {A(a)}_a[b], то можно писать “a-введение (i)” справа от aA(a) (см. строчки (5) и (11)).
   
5. A, B  AB - правило “-введения”. Если AB выведена из строки (i)A и строки (j)B в доказательстве, тогда можно писать “-введение (i), (j)” справа от AB (см. строку (10)).
   

Доказательство Первой теоремы собственных моделей использует теорему дедукции: если формула А влечет формулу В, то формула АВ является теоремой. В этом случае формула А обозначается как посылка доказательства (см. строку (1)). Если А представляет из себя конъюнкцию нескольких формул, то каждая из этих формул используется как посылка (под своим номером) в доказательстве. В этом случае правило -введения A(a)  aA(a) ограничивается тем условием, что переменная a не должна появляться в посылках доказательства, а также переменная a не должна появляться в предшествующих выражениях доказательства, содержащих, кроме a, индексированную переменную. Также следует заметить, что в доказательствах, использующих посылки, нельзя применять подстановки на места свободных переменных, фигурирующих в посылках.

Ниже я буду также предполагать использование других правил вывода и теорем Исчисления предикатов, поскольку последнее может быть выведено как частный случай в L-Онтологии. Для такого погружения достаточно уже средств Прототетики и общей логики именных выражений L-Онтологии (более подробно о правилах вывода в L-Онтологии см.⁷). Все эти средства сохраняются и в моей версии Онтологии. Что касается Онтологических определений и Правила экстенсиональности, лежащего в основании неэлементарной Онтологии, то об этом будет сказано ниже. Я буду также предполагать использование правила подстановки в той же форме, как оно используется в L-Онтологии. Однако, чтобы не загромождать изложение излишними техническими деталями, во многих случаях я буду давать только формулировки теорем или краткие комментарии к их доказательству.

Используя те же логические средства, могут быть доказаны, например, следующие теоремы.

Вторая теорема собственных моделей. Model(a,b)  c(Moda(c,b)  Mod(c,b,a)), т.e., если a есть (собственная) модель модуса b, тогда найдется мода c модуса b такая, что c есть мода модуса b в модели a.

Третья теорема собственных моделей. Model(a)  bModel(a,b), т.e., если a есть модель, то найдется модус b, для которого а есть (собственная) модель.

Теорема модельной данности. Modus(a)  bModel(b,a), т.e., если a есть модус, то для а найдется (собственная) модель b.


Во всех трех теоремах собственных моделей и в Теореме модельной данности фигурирует предикат Model(a,b) – «а есть (собственная) модель модуса b». В общем случае, если верны предикаты Model(a) и Modus(b), т.е. а есть модель, b есть модус, то, вообще говоря, не обязательно верно, что Model(a,b), т.е. не всякая модель может быть моделью модуса. Тем не менее, если а есть (собственная) модель модуса b, то верны приведенные выше три теоремы собственных моделей. Первая из них утверждает, что за всякой модой модуса найдется соответствующая модель этого модуса, в которой модус и образует данную моду. Вторая теорема, наоборот, утверждает, что для всякой модели модуса найдется соответствующая мода модуса, которая образуется в этой модели. Третья теорема утверждает, что нет «пустых» моделей, в которых ни один модус не образовывал бы своей моды. Наконец, Теорема модельной данности говорит о том, что всякий модус обладает своей моделью, т.е. нет «модельно пустых» модусов, не обладающих своими моделями. Все эти свойства являются следствием принятия в качестве первичного предиката предиката Mod(a,b,c,f), тесно связывающего воедино понятия «мода», «модус», «модель» и «проектор».

Природа Определений согласования такова, что легко могут быть доказаны следующие Леммы согласования, часто использующиеся в различных доказательствах:


Лемма 1 (Первая лемма согласования). Mod(a,b,c,f)  Moda(a)  Modus(b)  Model(c)  Projector(f)

Лемма 2 (Вторая лемма согласования). Mod(a,b,c)  Moda(a,b) Moda(a,c)Model(c,b)

Лемма 3 (Третья лемма согласования). Moda(a,b)  Moda(a)  Modus(b)

Лемма 4 (Четвертая лемма согласования). Moda(a,b)  Moda(a)  Model(b)

Лемма 5 (Пятая лемма согласования). Model(a,b)  Model(a)  Modus(b)


Например, Первая лемма согласования может быть доказана следующим образом.


Лемма 1 (Первая лемма согласования). Mod(a,b,c,f)  Moda(a)  Modus(b)  Model(c)  Projector(f)

Доказательство. (1) Mod(a,b,c,f) посылка

(2) bcfMod(a,b,c) bcf-введение (1)

(3) bcfMod(a,b,c)  Moda(a) D1.6.

(4) Moda(a) MP (2), (3)

(5) acf Mod(a,b,c,f) acf -введение (1)

(6) acf Mod(a,b,c,f)  Modus(b) D1.5.

(7) Modus(b) MP (5), (6)

(8) abf Mod(a,b,c,f) ab-введение (1)

(9) abf Mod(a,b,c,f)  Model(c) D1.7.

(10) Model(c) MP (8), (9)

(11) abc Mod(a,b,c,f) abc-введение (1)

(12) abc Mod(a,b,c,f)  Projector(f) D1.9.

(13) Projector(f) MP (11), (12)

(11) Moda(a)  Modus(b)  Model(c)

 Projector(f) -введение (4), (7), (10), (13)


Теорема тождественной моды. Modus(a)  Moda(a,a), т.e., если a есть модус, то а есть мода самого себя.

Эта теорема утверждает, что всякий модус является одновременно и своей собственной модой, доказательство чего следует из первой Аксиомы Онтологии (АО1), утверждающей, в частности, рефлексивность предиката «быть модой модуса».

Теорема модальности модуса. Modus(a)  Moda(a), т.e., если a есть модус, то а есть мода.

Следовательно, всякий модус – одновременно мода, что и понятно из предыдущей теоремы, где утверждается, что модус – мода самого себя, и, в частности, - просто мода.

Теорема модусности моды. Moda(a)  Modus(a), т.e., если a есть мода, то а есть модус.

Эта теорема, наоборот, утверждает, что всякая мода является модусом. В доказательстве этой теоремы используется Первая Аксиома Онтологии (АО1), позволяющая заключить от модальной природы а к модусности а.

Соединяя вместе последние две теоремы, получим:

Теорема эквивалентности моды и модуса. Moda(a)  Modus(a), т.e., a есть мода если и только если (е.т.е.) a есть модус.

Следовательно, понятия «мода» и «модус» имеют лишь относительный смысл. В общем случае любая мода – модус, а любой модус – мода.

Используя модус-модальную эквивалентность, можно теперь все теоремы, относящиеся к модусам, формулировать как теоремы для мод, и обратно. Например:

Теорема тождественной моды*. Moda(a)  Moda(a,a), т.e., если a есть мода, то a есть модус и а есть мода модуса a.

Теорема эквивалентности модуса и тождественной моды. Modus(a)  Moda(a,a), т.e., a есть модус е.т.е. a есть своя собственная мода.

Доказательство 1. Для доказательства Modus(a)  Moda(a,a) см. Теорему тождественной моды.

2. Для доказательства Moda(a,a)  Modus(a) см. Лемму 3.


Теорема транзитивности. Moda(a,b)Moda(b,c)  Moda(a,c), т.e., если a есть мода модуса b и b есть мода модуса c, то a есть мода модуса c.

Это свойство практически заложено в формулировке Первой аксиомы АО1.


Теорема модусной эквивалентности.

1. Modus(a)  a = a
   
2. a = b  b = a
   
3. a = b  b = c  a = c
   

Согласно этой теореме, отношение = есть отношение эквивалентности на модусах. В самом деле, эта теорема может быть сформулирована в следующем виде:

Теорема модусной эквивалентности*.

1. Modus(a)  a = a
   
2. Modus(a) Modus(b)  (a = b  b = a)
   
3. Modus(a) Modus(b) Modus(c)  (a = b  b = c  a = c)
   

Принимая во внимание теорему эквивалентности моды и модуса, последняя теорема может быть переписана также в следующей форме:

Теорема модусной эквивалентности**.

1. Moda(a)  a = a
   
2. Moda(a) Moda(b)  (a = b  b = a)
   
3. Moda(a) Moda(b) Moda(c)  (a = b  b = c  a = c)
   

В связи с этим, равенство = может быть теперь представлено и как эквивалентность на модах.

Теорема модусного порядка.

1. Modus(a)  Moda(a,a)
   
2. Moda(a,b)  Moda(b,a)  a = b
   
3. Moda(a,b)  Moda(b,c)  Moda(a,c)
   

Эта теорема описывает свойства предиката «быть модой» как свойства нестрогого порядка. Это отношение является таковым для модусов (мод), поскольку верна следующая теорема:

Теорема модусного порядка*.

1. Modus(a)  Moda(a,a)
   
2. Modus(a) Modus(b)  (Moda(a,b)  Moda(b,a)  a = b)
   
3. Modus(a)Modus(b)Modus(c)  (Moda(a,b)  Moda(b,c)  Moda(a,c))
   

Теорема модельной единицы. Modus(a)  b(Model(b,a)  Mod(a,a,b)), т.e., если a есть модус, то для некоторого b верно, что b есть модель a и a есть мода самого себя в этой модели b.

Такую модель, как я уже говорил выше, можно называть «модельной единицей» для модуса а. Модельная единица представляет из себя такие ограничивающие условия, которые оставляют модус неизменным, т.е. по сути не ограничивают его. Теорема модельной единицы утверждает, что любой модус обладает такой моделью.

Теорема антитранзитивности. Moda(b,a)  Moda(b,c)  Moda(a,c), т.e., если b есть мода a и b не есть мода c, то a не есть мода c.

Это свойство следует из свойства транзитивности, выражая его антипод, т.е. такую систему условий, когда свойство транзитивности не верно.

Теорема положительной эквивалентности. Отношение “” есть отношение положительной эквивалентности в следующем смысле:

(i) PModa(a)  a  a

(ii) a  b  b  a

(iii) a  b  b  c  a  c

Или:

Теорема положительной эквивалентности *.

(i) PModa(a)  a  a

(ii) PModa(a)  PModa(b)  (a  b  b  a)

(iii) PModa(a)  PModa(b)  PModa(c)  (a  b  b  c  a  c)

Таким образом, отношение «» есть отношение эквивалентности для положительных мод.

Теорема эквивалентности положительных модуса и тождественной моды. PModus(a)  PModa(a,a), т.e., a есть положительный модус е.т.е. a есть положительная мода самого себя.

Теорема эквивалентности положительных моды и модуса. PModus(a)  PModa(a), т.e., a есть положительный модус е.т.е. a есть положительная мода.

Следовательно, и для положительных мод-модусов их различие лишь относительно.

Первая теорема нулевой моды. Model(a)  NModus(b)  cMod(c,b,a), т.e., если a есть модель и b есть нулевой модус, то для некоторого c верно, что c есть мода b в a.

Нулевой модус имеет свои моды во всех моделях, причем, все эти моды нулевые:

Вторая теорема нулевой моды. NModus(a)  Moda(c,a)  NModa(c), т.e., если a есть нулевой модус и c есть мода a, то с есть нулевая мода.

Теорема модальности нулевого модуса. NModus(a)  NModa(a), т.e., нулевой модус есть одновременно нулевая мода.

А вот обратное доказать нельзя, т.к. в определении нулевой моды в общем случае ничего не говорится о ее моделях.

Вторая теорема нулевой моды*. NModa(a)  Moda(c,a)  NModa(c), т.e., если a есть нулевая мода и c есть мода a, то с есть нулевая мода. Иными словами, мода нулевой моды сама есть нулевая мода.

Теорема минимальности нулевого модуса. Modus(a)  NModus(b)  Moda(b,a), т.e., нулевой модус является модой любого модуса.

Теорема универсальности нулевой моды. Moda(a)  NModa(b)  Moda(b,a) – нулевая мода есть мода любой моды. Или:

Теорема универсальности нулевой моды*. Modus(a)  NModa(b)  Moda(b,a) - нулевая мода есть мода любого модуса.

Следовательно, у всякого модуса, как минимум, всегда есть две моды (не обязательно разные) – это тождественная мода и нулевая мода.

Теорема модальной несовместимости. PModa(a)  NModa(a)  Moda(a) – любая мода является либо положительной модой, либо нулевой, третьего не дано.

Теорема положительной транзитивности. PModa(a,b)  PModa(b,c)  PModa(a,c), т.e., если a есть положительная мода b и b есть положительная мода c, то a есть положительная мода c.

Теорема переноса положительной моды. PModa(a)  Moda(a,b)  PModa(b) – модус, обладающий положительной модой, сам есть положительная мода.

Теорема слабого равенства. (i) a  a

(ii) a  b  b  a

(iii) a  b  b  c  a  c

Эта теорема утверждает, что отношение «» есть отношение эквивалентности для любых объектов.

Первая теорема переноса моды. Moda(a)  a  b  Moda(b) – если а и b слабо равны, и а есть мода, то b также есть мода.

Следующие теоремы показывают тесную связь двух отношений эквивалентности «=» и «».

Первая теорема критерия модальности. Moda(a,b)  [c(Moda(c,a)  Moda(c,b))  Moda(a)] – а есть мода b е.т.е. а есть мода и любая мода а есть мода b.

Эта теорема дает критерий определения того, что а есть мода b. Для этого достаточно и необходимо доказать, что а есть мода и любая мода а есть мода b.

Теорема отношения равенств. a = b  a  b  Moda(a)  Moda(b) – а и b равны е.т.е. а и b слабо равны и а и b есть моды.

Следовательно, а и b равны, если они: 1) есть моды, и 2) равны по модам, т.е. любая мода а есть мода b, и наоборот.

Теорема отношения равенств*. a = b  a  b  Modus(a)  Modus(b) – а и b равны е.т.е. а и b слабо равны и а и b есть модусы.

Этот случай есть переформулировка предшествующего в силу эквивалентности понятий «мода» и «модус».

Теорема модальности равенства. a = b  Moda(a) – если a и b равны, то а есть мода. Утверждение прямо следует из Теоремы отношения равенств.

Теорема модальности равенства*. a = b  Modus(a) – если a и b равны, то а есть модус. Это следствие предыдущей теоремы и эквивалентности понятий «мода» и «модус».

Вторая теорема критерия модальности. Moda(a,b)  [c(Moda(b,c)  Moda(a,c))  Modus(b)] - а есть мода b е.т.е. b есть модус и любой модус а есть модус b.

Эта теорема интересна тем, что она дает как бы второй («верхний») критерий того, что а есть мода b. Для этого необходимо и достаточно показать, что b есть модус и всякий модус b есть модус а. Равносильность двух критериев («нижнего», модального, и «верхнего», модусного) выражается в следующей теореме:

Теорема верхней и нижней эквивалентности. [c(Moda(c,a)  Moda(c,b))]  [c(Moda(a,c)  Moda(b,c)] - любая мода а есть мода b е.т.е. любой модус а есть модус b.

Следовательно, проверив, что а и b есть модусы (или моды), мы можем далее с одинаковым успехом использовать для доказательства их равенства либо первый критерий («нижний»), показывая, что любая мода а есть мода b, и наоборот; либо – второй критерий («верхний»), показывая, что любой модус b есть модус а, и наоборот.

Теорема слабого включения как порядка.

1. a  a
   
2. (a  b)  (b  a)  a  b
   
3. (a  b  b  c)  a  c
   

Эта теорема показывает, что отношение слабого включения есть отношение нестрогого порядка на любых объектах.


Теорема инъективности. Mod(x,b,c,f)  Mod(y,b,c,f)  x =¹₂₃₄ y – если проектор f определен на модусе b и модели c, то он всегда дает одно значение на b и c (с точностью до равенства =¹₂₃₄).

Теорема отношения равенств. a = b  a =²₁ b  a =¹₂ b – равенство (=) между модами-модусами равносильно ²₁- и ¹₂-равенству.


Хочу заметить, что все доказанные выше теоремы даны «в условной форме» - как импликации или конъюнкции импликаций. В общем случае, как и в L-Онтологии, в Онтологии нельзя доказать, что нечто существует, например, существует нулевая мода или бесконечный модус (как и Лесьневский, я интерпретирую квантор х в смысле «для некоторого х», а не как «существует х»). Онтология совместима с пустым универсумом, когда нет никаких объектов. Это, в частности, означает, что именные переменные и константы могут интерпретироваться как пустые имена, не имеющие десигнатов. Присоединение к Онтологии тех или иных достаточных условий существования некоторых объектов будет образовывать уже некоторые частные версии Онтологии.