Тема Методологічні засади статистики

• Програма навчального курсу «Політологія» розділ І. Теоретико-методологічні засади політології, 2712.63kb.
• Розділ теоретико-методологічні засади стратегічного планування, 832.28kb.
• 4 Розділ Теоретико-методологічні засади державної міграційної політики, 817.42kb.
• Олефір Леонід Олексійович, перший заступник начальника головного управління освіти, 145.45kb.
• Розділ Методологічні засади зовнішнього стратегічного аналізу банківських установ, 788.68kb.
• Розділ Методологічні засади формування та реалізації державної інформаційної політики, 644.37kb.
• Зміст, 521.48kb.
• Дипломна робота тема: «Облік І аудит довгострокових зобов’язань підприємства на прикладі, 347.88kb.
• Зміст вступ, 1122.5kb.
• І. В. Козлик Прикарпатський університет про методологічні засади, 90.46kb.

Коефіцієнт зростання (К)	Середній коефіцієнт динаміки
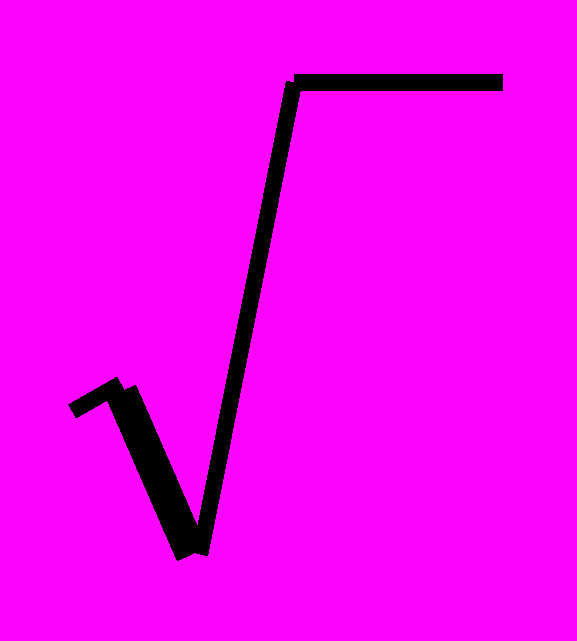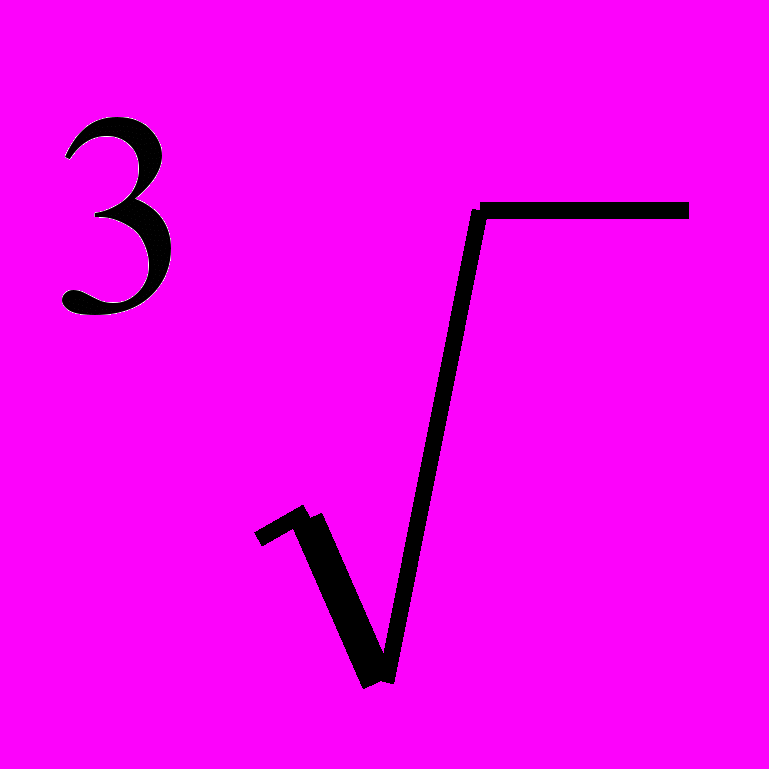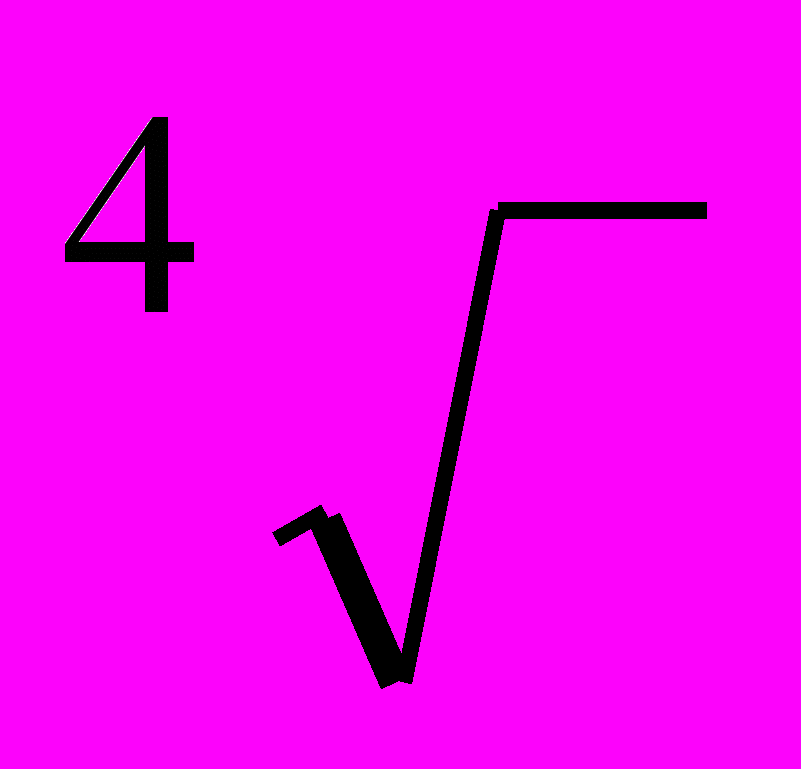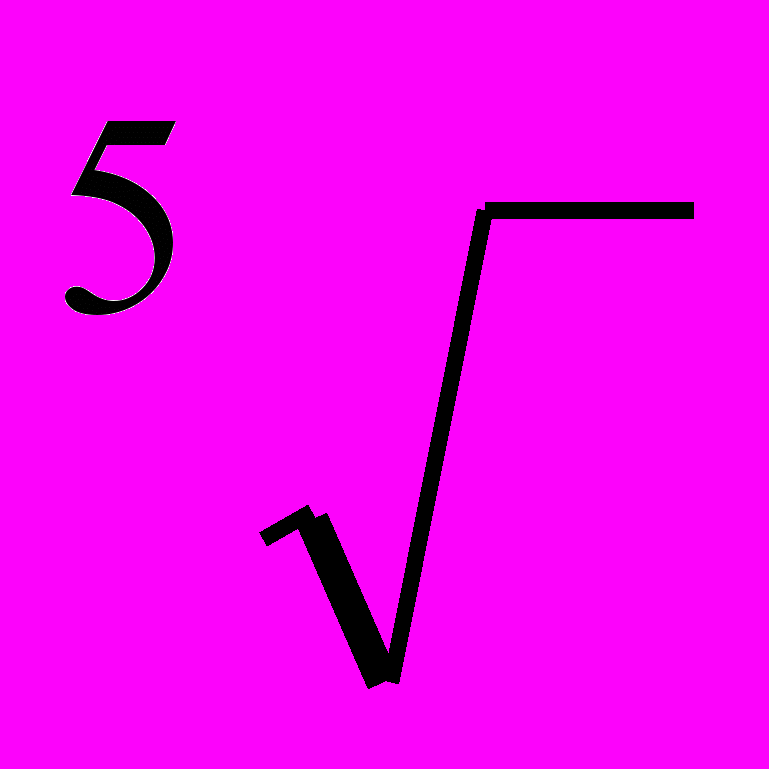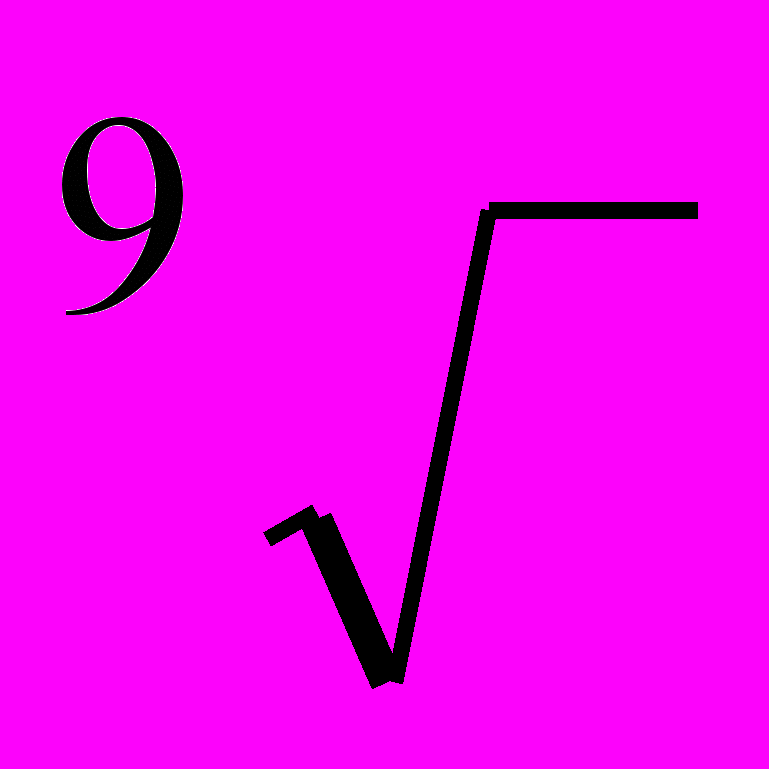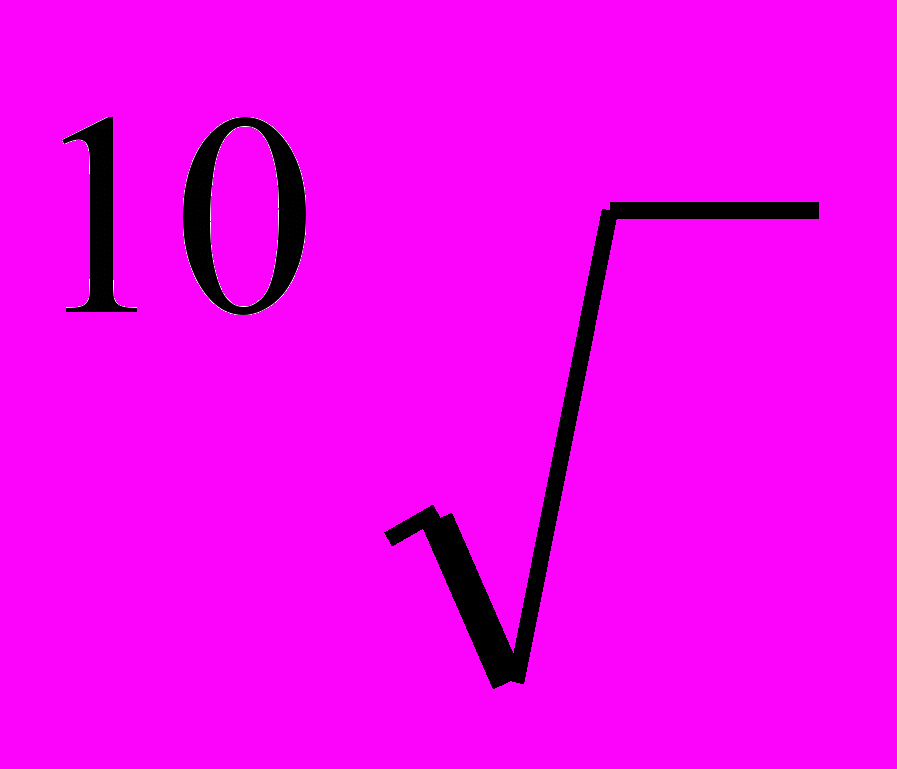0,860	0,9274	0,9510	0,9630	0,9703	0,9752	0,9787	0,9813	0,9834	0,9850
0,865	0,9301	0,9528	0,9644	0,9714	0,9761	0,9795	0,9820	0,9840	0,9856
0,870	0,9327	0,9546	0,9658	0,9725	0,9771	0,9803	0,9827	0,9846	0,9862
0,875	0,9354	0,9565	0,9672	0,9736	0,9780	0,9811	0,9834	0,9853	0,9867
0,880	0,9381	0,9583	0,9685	0,9748	0,9789	0,9819	0,9841	0,9859	0,9873
0,885	0,9407	0,9601	0,9699	0,9759	0,9798	0,9827	0,9848	0,9865	0,9879
0,890	0,9434	0,9619	0,9713	0,9770	0,9808	0,9835	0,9855	0,9871	0,9884
0,895	0,9460	0,9637	0,9726	0,9781	0,9817	0,9843	0,9862	0,9877	0,9890
0,900	0,9487	0,9655	0,9740	0,9791	0,9826	0,9851	0,9869	0,9884	0,9895
0,905	0,9513	0,9673	0,9754	0,9802	0,9835	0,9858	0,9876	0,9890	0,9901
0,910	0,9539	0,9691	0,9767	0,9813	0,9844	0,9866	0,9883	0,9896	0,9906
0,915	0,9566	0,9708	0,9780	0,9824	0,9853	0,9874	0,9890	0,9902	0,9912
0,920	0,9592	0,9726	0,9794	0,9835	0,9862	0,9882	0,9896	0,9908	0,9917
0,925	0,9618	0,9743	0,9807	0,9845	0,9871	0,9889	0,9903	0,9914	0,9922
0,930	0,9644	0,9761	0,9820	0,9856	0,9880	0,9897	0,9910	0,9920	0,9928
0,935	0,9670	0,9778	0,9833	0,9866	0,9889	0,9904	0,9916	0,9926	0,9933
0,940	0,9695	0,9796	0,9847	0,9877	0,9897	0,9912	0,9923	0,9931	0,9938
0,945	0,9721	0,9813	0,9860	0,9887	0,9906	0,9920	0,9930	0,9937	0,9944
0,950	0,9747	0,9830	0,9873	0,9898	0,9915	0,9927	0,9936	0,9943	0,9949
0,955	0,9772	0,9848	0,9886	0,9908	0,9924	0,9934	0,9943	0,9949	0,9954
0,960	0,9798	0,9865	0,9898	0,9919	0,9932	0,9942	0,9949	0,9955	0,9959
0,965	0,9823	0,9882	0,9911	0,9929	0,9941	0,9949	0,9956	0,9960	0,9964
0,970	0,9849	0,9899	0,9924	0,9939	0,9949	0,9957	0,9962	0,9966	0,9970
0,975	0,9874	0,9916	0,9937	0,9949	0,9958	0,9964	0,9968	0,9972	0,9975
0,980	0,9899	0,9933	0,9950	0,9960	0,9966	0,9971	0,9975	0,9978	0,9980
0,985	0,9925	0,9950	0,9962	0,9970	0,9975	0,9978	0,9981	0,9983	0,9985
0,990	0,9950	0,9967	0,9975	0,9980	0,9983	0,9986	0,9987	0,9989	0,9990
0,995	0,9975	0,9983	0,9987	0,9990	0,9992	0,9993	0,9994	0,9994	0,9995
1,000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000
1,005	1,0025	1,0017	1,0012	1,0010	1,0008	1,0007	1,0006	1,0006	1,0005
1,010	1,0050	1,0033	1,0025	1,0020	1,0017	1,0014	1,0012	1,0011	1,0010
1,015	1,0075	1,0050	1,0037	1,0030	1,0025	1,0021	1,0019	1,0017	1,0015
1,020	1,0100	1,0066	1,0050	1,0040	1,0033	1,0028	1,0025	1,0022	1,0020
1,025	1,0124	1,0083	1,0062	1,0050	1,0041	1,0035	1,0031	1,0027	1,0025
1,030	1,0149	1,0099	1,0074	1,0059	1,0049	1,0042	1,0037	1,0033	1,0030
1,035	1,0173	1,0115	1,0086	1,0069	1,0058	1,0049	1,0043	1,0038	1,0034
1,040	1,0198	1,0132	1,0099	1,0079	1,0066	1,0056	1,0049	1,0044	1,0039
1,045	1,0223	1,0148	1,0111	1,0088	1,0074	1,0063	1,0055	1,0049	1,0044
1,050	1,0247	1,0164	1,0123	1,0098	1,0082	1,0070	1,0061	1,0054	1,0049
1,055	1,0271	1,0180	1,0135	1,0108	1,0090	1,0077	1,0067	1,0060	1,0054
1,060	1,0296	1,0196	1,0147	1,0117	1,0098	1,0084	1,0073	1,0065	1,0058
1,065	1,0320	1,0212	1,0159	1,0127	1,0106	1,0090	1,0079	1,0070	1,0063
1,070	1,0344	1,0228	1,0171	1,0136	1,0113	1,0097	1,0085	1,0075	1,0068
1,075	1,0368	1,0244	1,0182	1,0146	1,0121	1,0104	1,0091	1,0081	1,0073
1,080	1,0392	1,0260	1,0194	1,0155	1,0129	1,0111	1,0097	1,0086	1,0077
1,085	1,0416	1,0276	1,0206	1,0164	1,0137	1,0117	1,0102	1,0091	1,0082