Geum.ru

Русаков Александр Александрович, д п. н., профессор, заведующий кафедрой высшей математики мггу им. М. А. Шолохова. Эта статья

Вид материалаСтатья
Подобный материал:

МАТЕМАТИКА И ИНФОРМАТИКА. ПРИМЕР СЛИЯНИЯ.




Николаев Юрий Павлович, ассистент кафедры математики СУНЦ МГУ им. М.В. Ломоносова.

Русаков Александр Александрович, д.п.н., профессор, заведующий
кафедрой высшей математики МГГУ им. М.А.Шолохова.



Эта статья – знакомство с элементами компьютерной алгебры. Здесь приведена блок-схема конструктивного определения алгебраического кольца с конечным носителем, которую можно довести до программы на языках программирования высокого уровня (например, Pascal или C++). Даны постановки задач для научно-исследовательских проектов по информатике в школе.


XXI Международная олимпиада по информатике (г. Пловдив, Болгария, 8-15 августа 2009 г.). Харитонов Михаил – учащийся 11 класса Специализированного учебно-научного центра Московского государственного университета им. М.В. Ломоносова – школы им. А.Н. Колмогорова получил серебро.[1]

Как в школе, так и в ВУЗе важной составляющей в подготовке профессионалов математиков-програмистов (будущих IT-специалистов) является фундаментальная составляющая. Мы считаем, что ядро этой фундаментальной составляющей есть фундаментальное знание математики.

Если ВУЗ часто работает с целевой аудиторией, отобранной на основе различных испытаний, то учителя в школе часто сталкивается с проблемой, что детей необходимо заинтересовать, мотивировать.

Здесь мы приводим тему, которую следует рассматривать как элемент факультатива или кружка по информатике, а на каком-то этапе и как фундамент для научно-исследовательского проекта школьников.

Быть может разбор представленной задачи в школе выглядит как внедрение в абстрактную алгебру, но мы постарались обратить внимание читателя на богатство этой темы для исследовательских проектов по информатике в школе.

Постановка задачи.

Следуя традициям преподавания алгебры в ФМШ №18, заложенными ещё такими преподавателями как А.Н. Колмогоров, А.А. Шершевский, А.Н. Земляков и др., под кольцом мы понимаем непустое множество 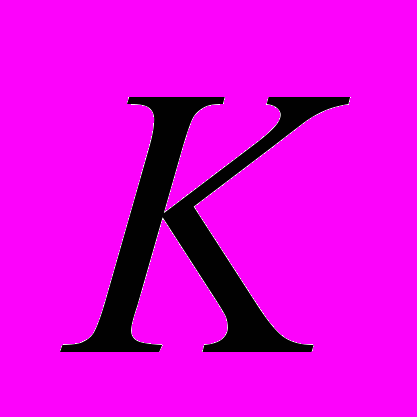, на котором заданы две абстрактные бинарные алгебраические операции  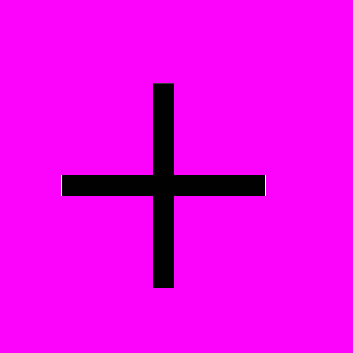(“сложение”) и  (“умножение”), удовлетворяющие следующим аксиомам.

А1. .

А2. .

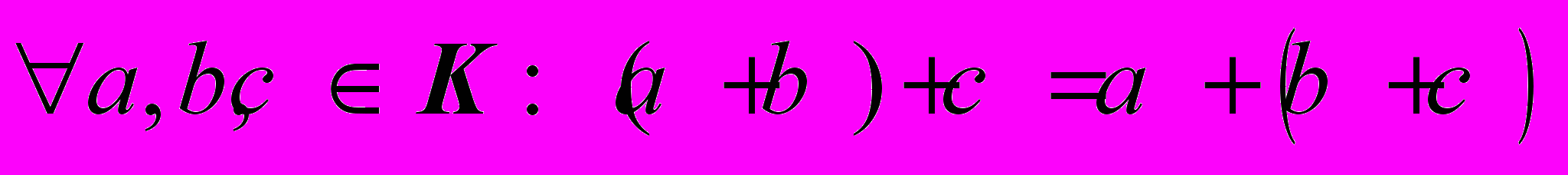А3. .

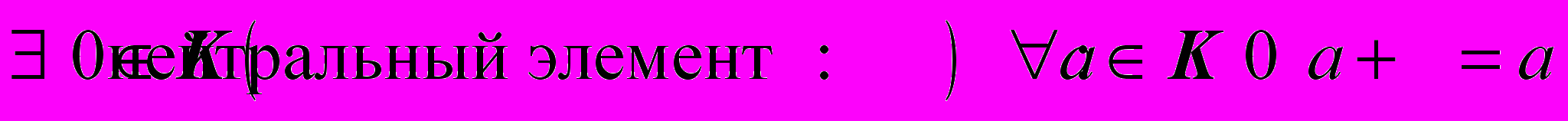А4. .

А5. .

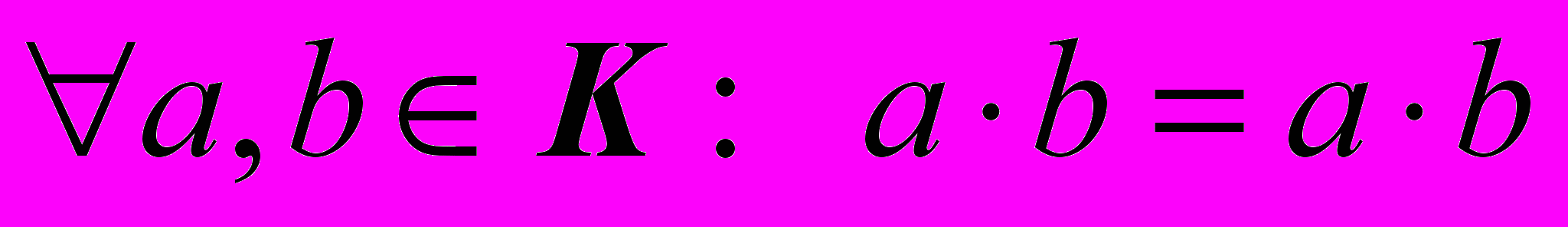А6. .

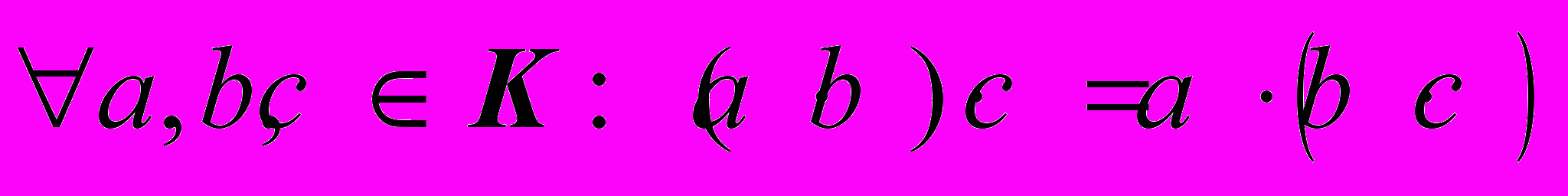А7. .

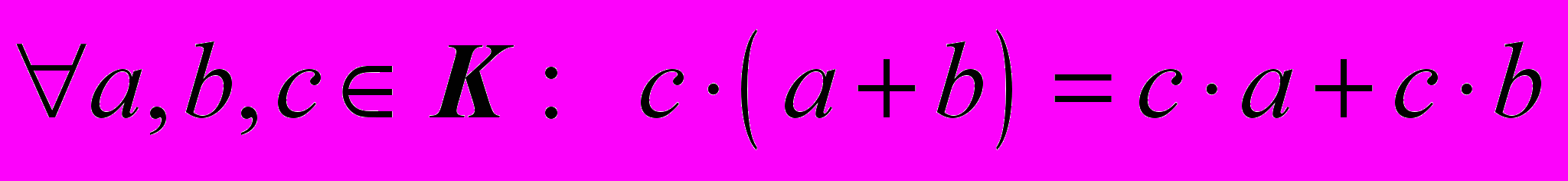Иначе говоря, 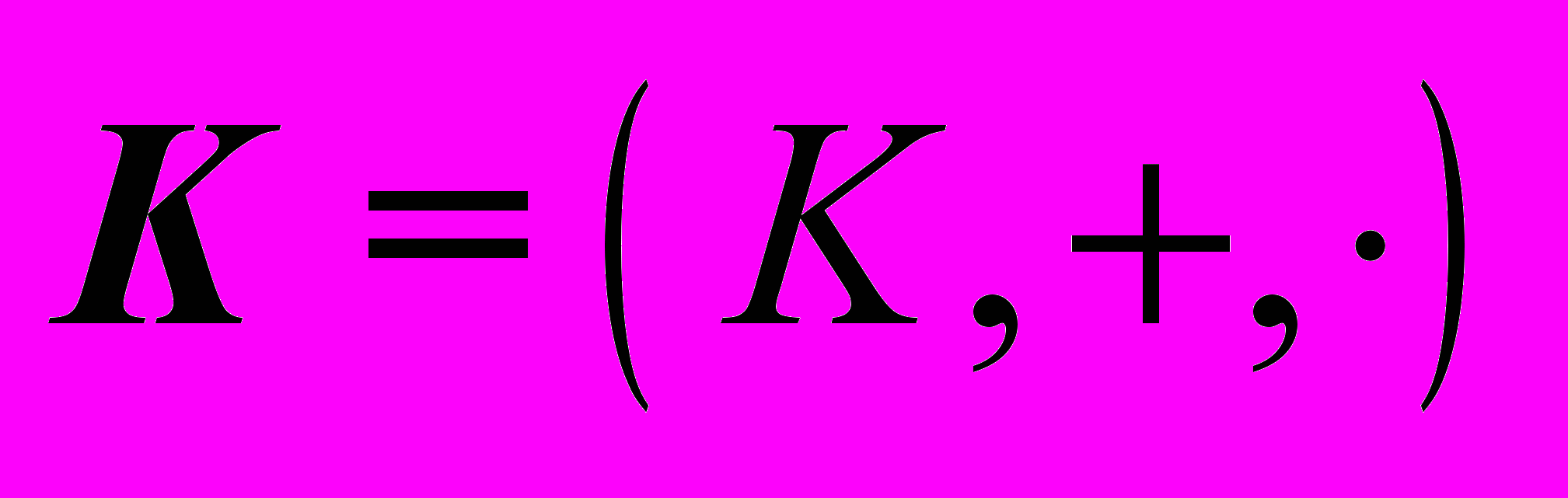– ассоциативное, коммутативное кольцо. Множество 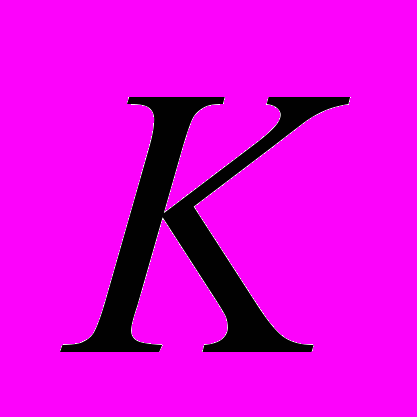называется носителем кольца 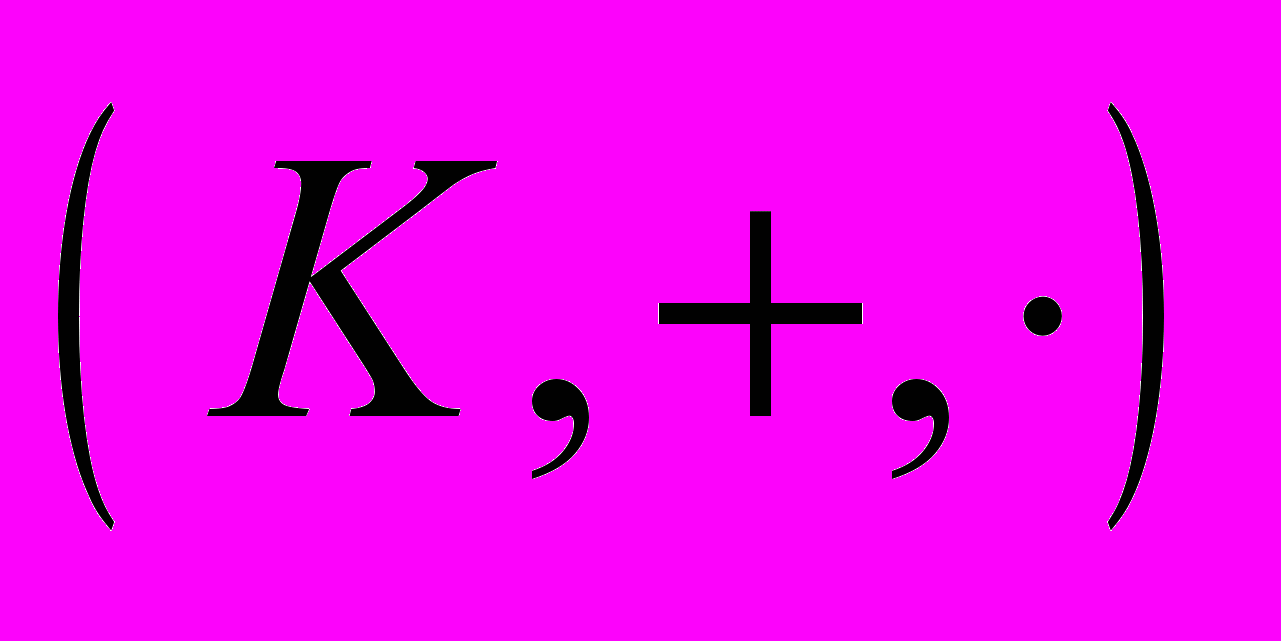[2].


Задача. Найти все кольца, носителем которых является двухэлементное множество 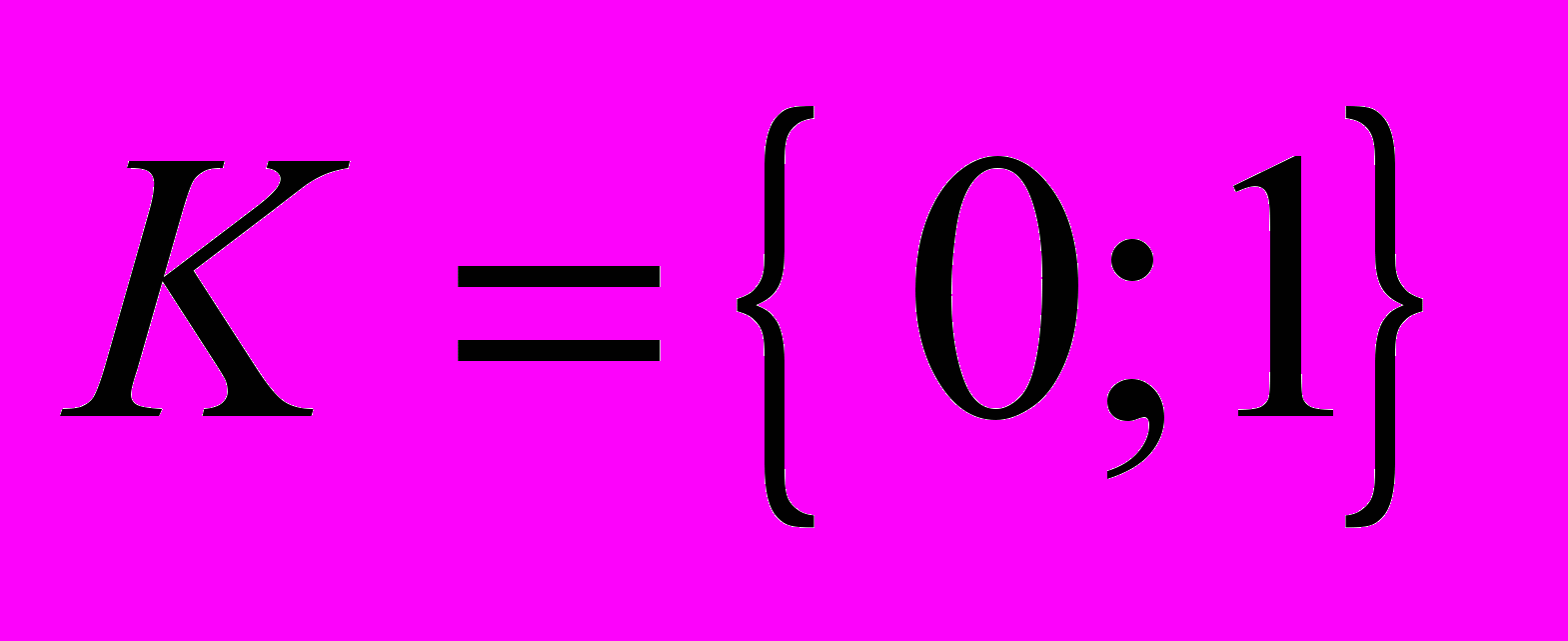(трёхэлементное множество ).

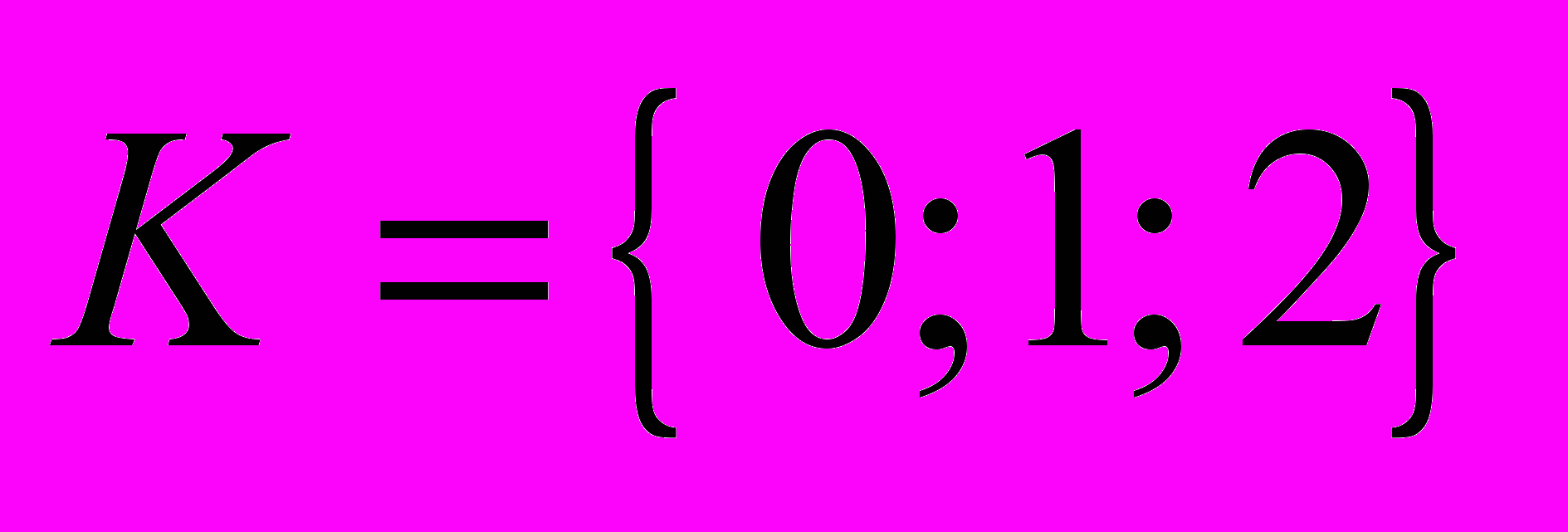Решение задачи.

Лемма. 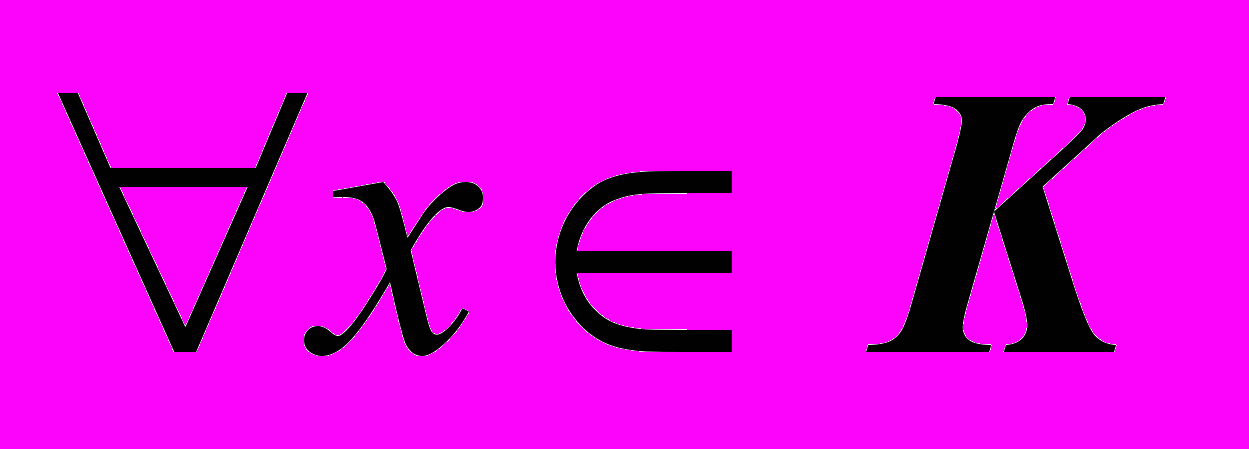выполнено: .

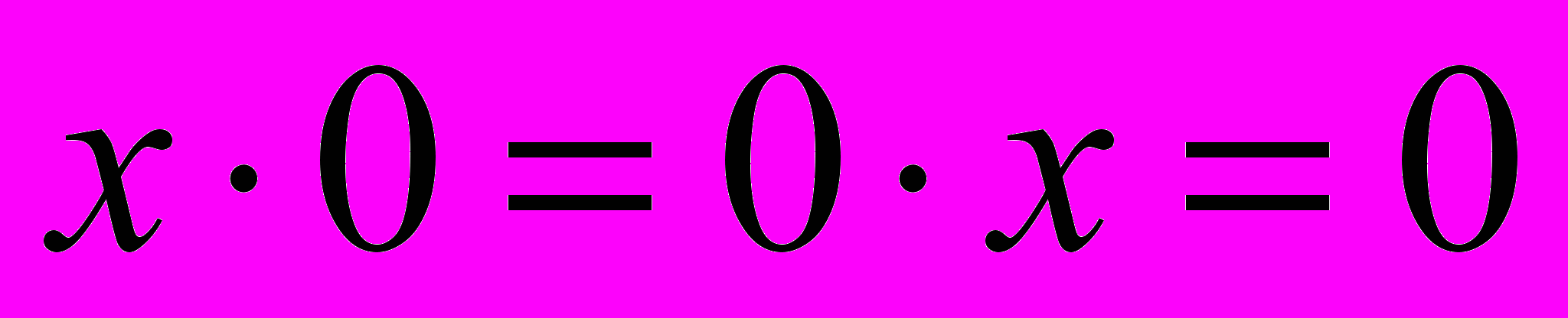Доказательство Леммы.

1. 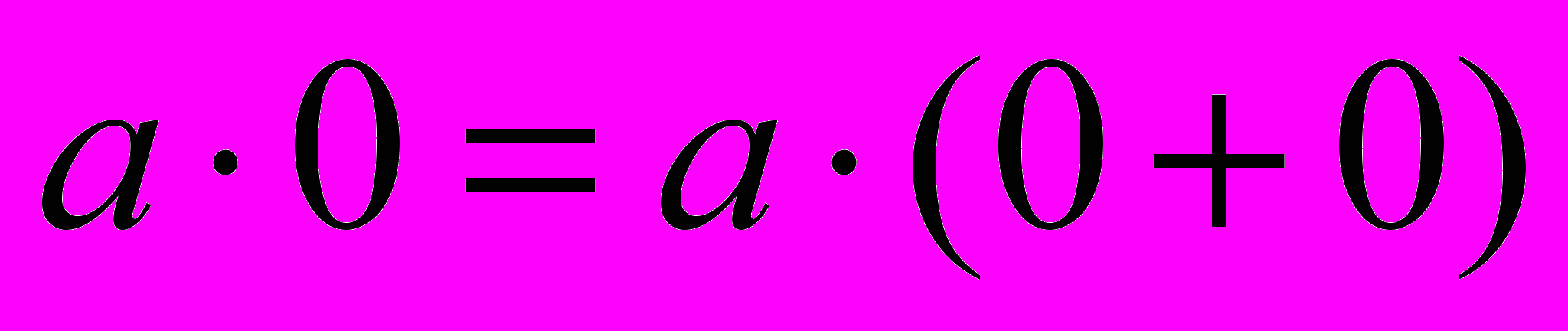– в силу определения нейтрального элемента в кольце.

2. 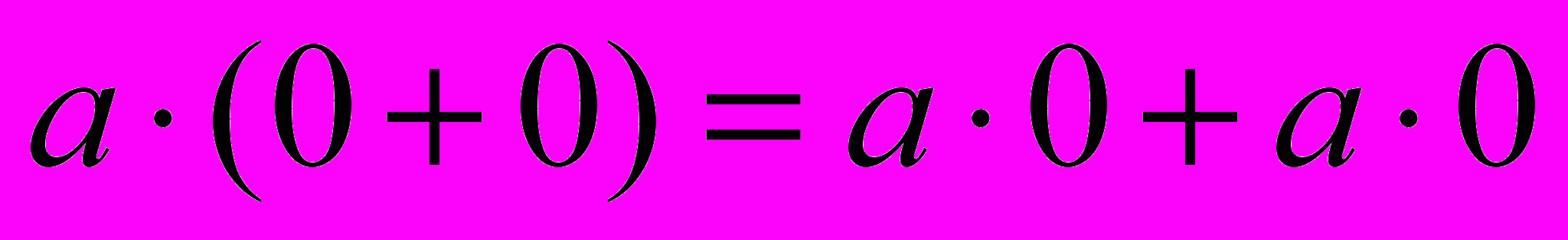– в силу дистрибутивности в кольце.

3. Получили, что 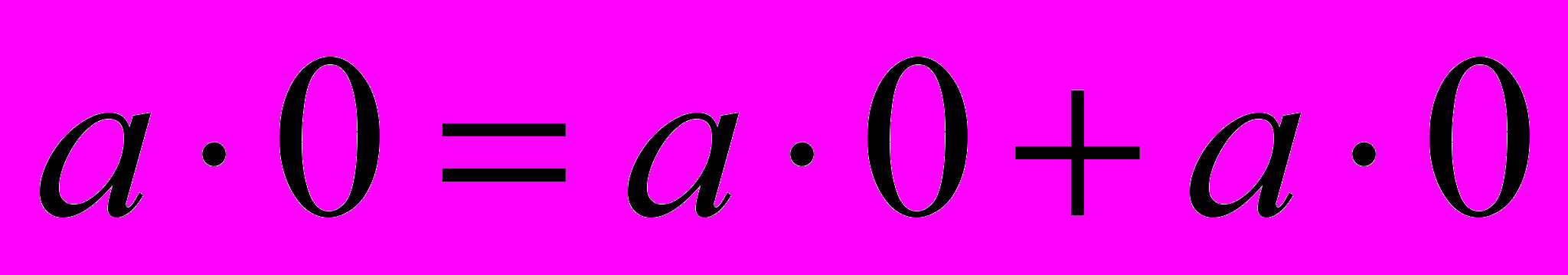. Добавим к обеим частям равенства элемент 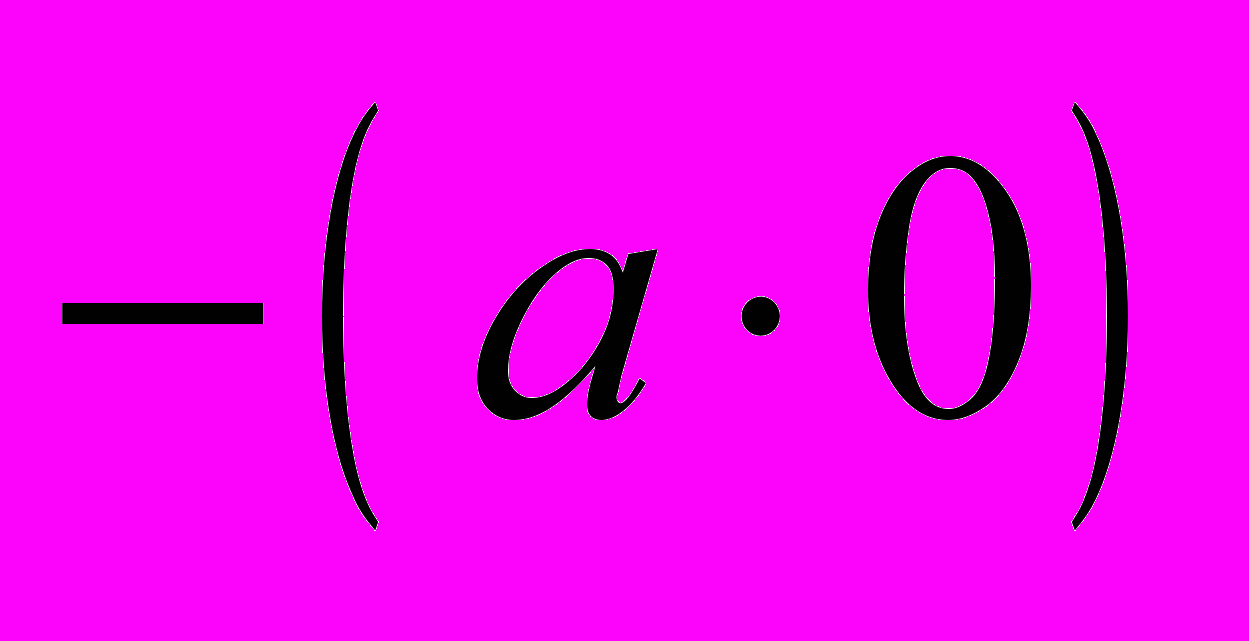противоположный к 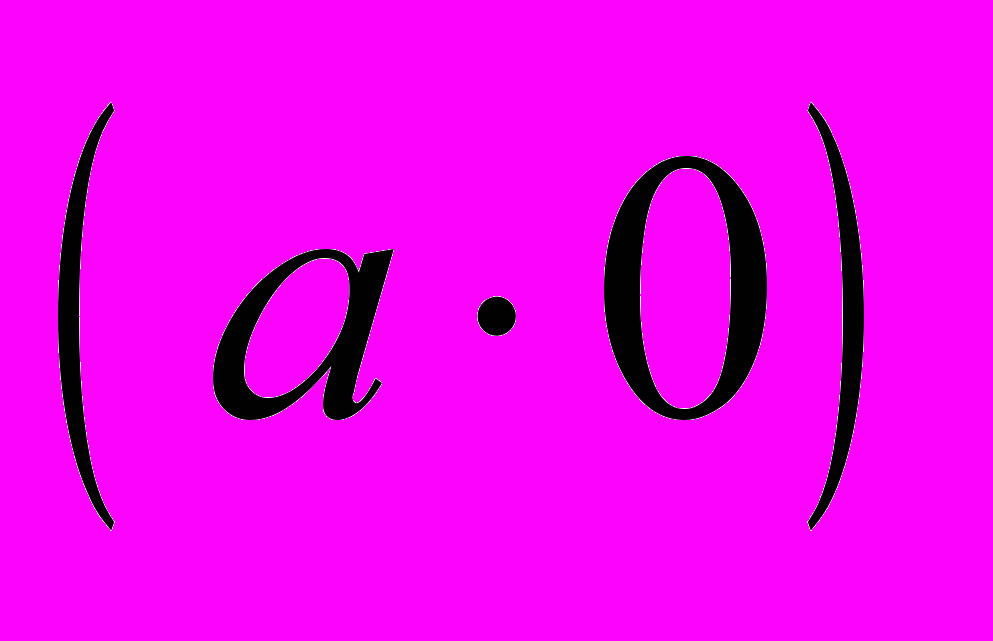, который существует в кольце по аксиоме А4.

4. Получим 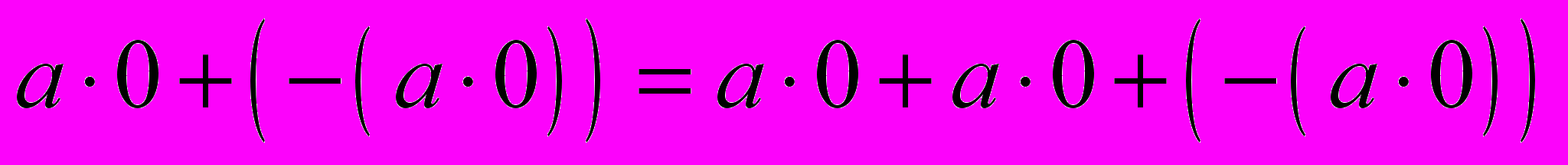. Откуда по определению противоположного элемента .

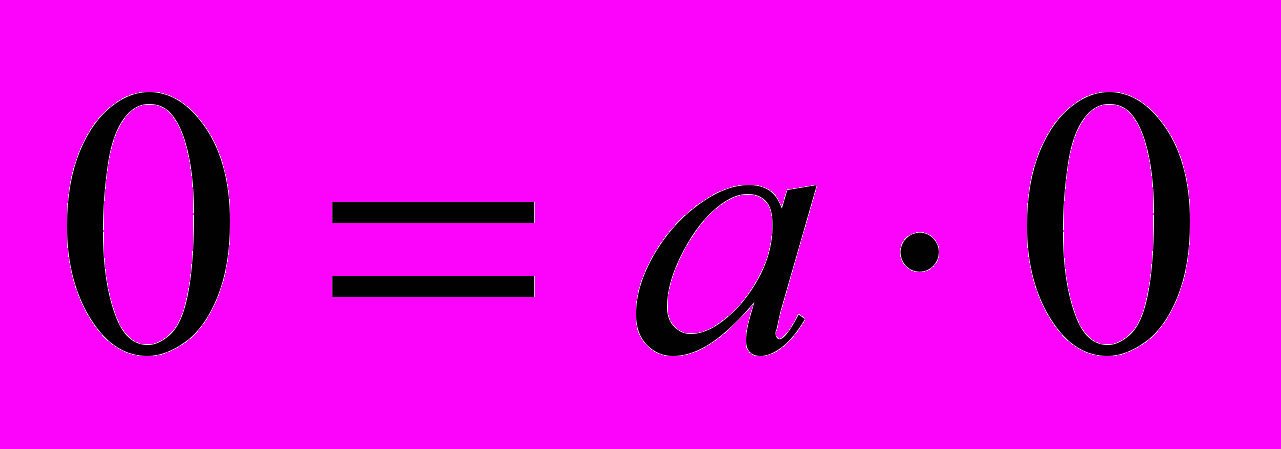Для умножения на нейтральный элемент справа в силу коммутативности операции умножения доказательство не требуется.

Лемма доказана.

Рассмотрим множество 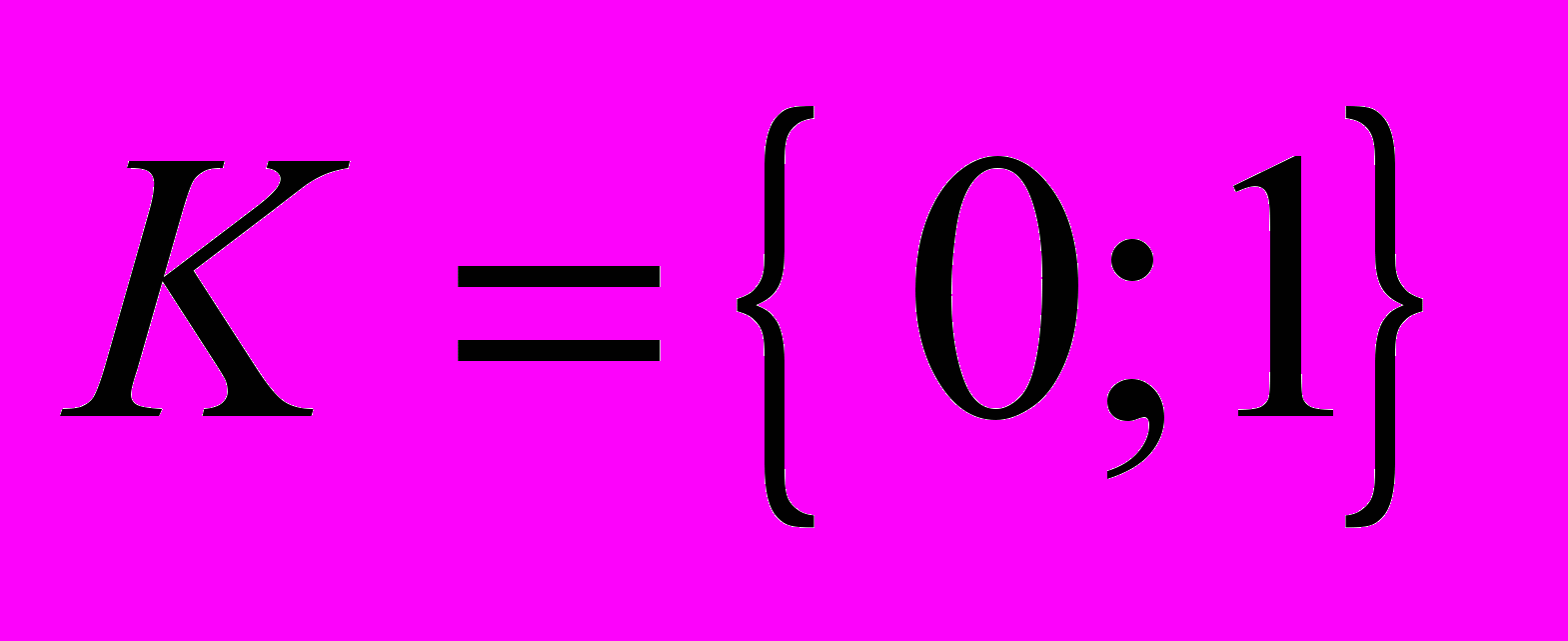. Выберем элемент, который будет нейтральным в кольце. Пусть это будет 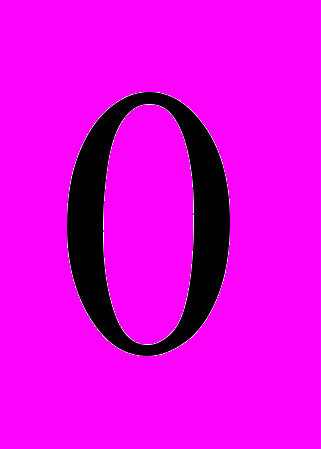. Тогда пользуясь Результатами леммы, начнем строить табличку для операции “умножение”: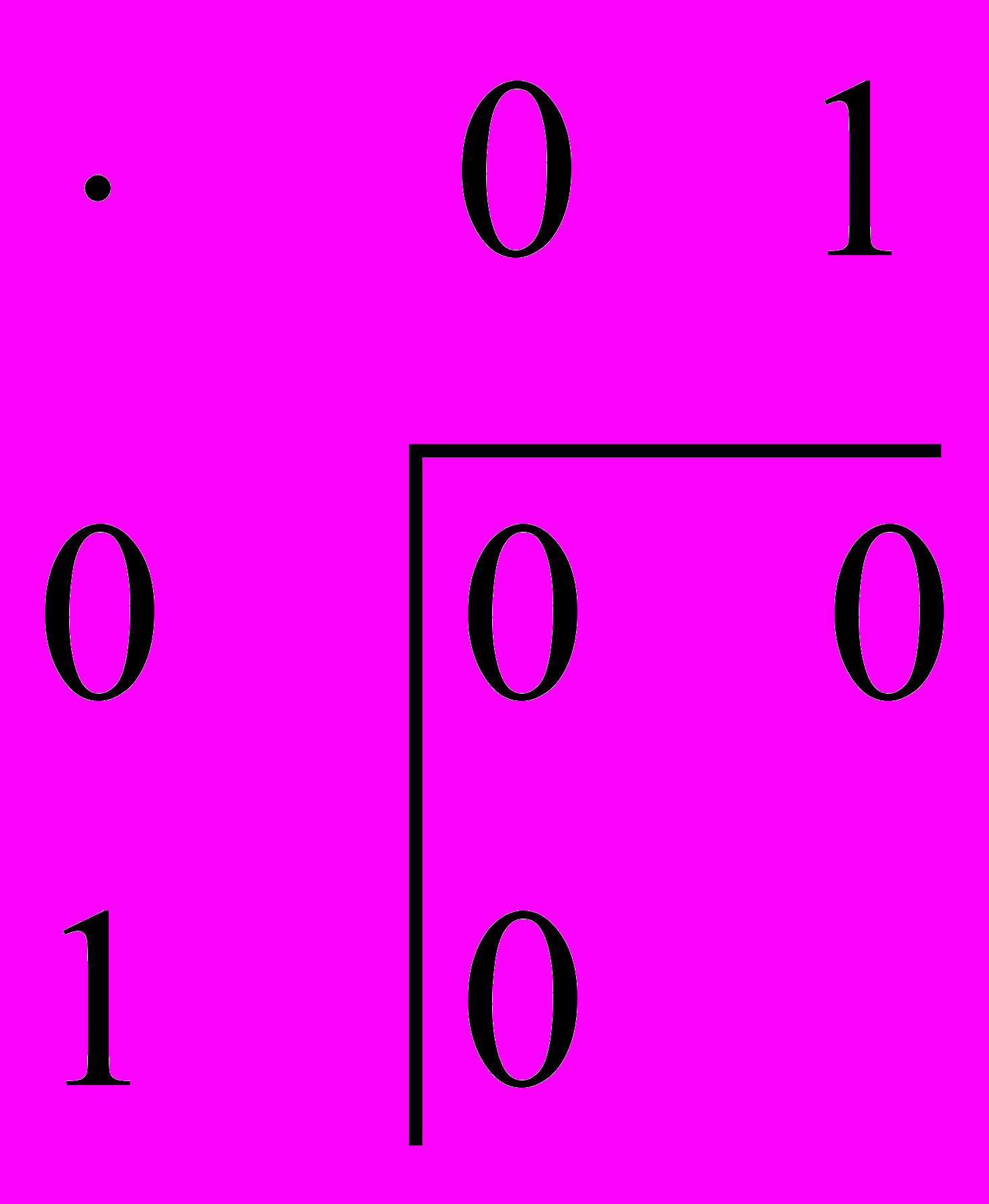



Осталась незаполненной всего одна клетка: результат операции “умножение” 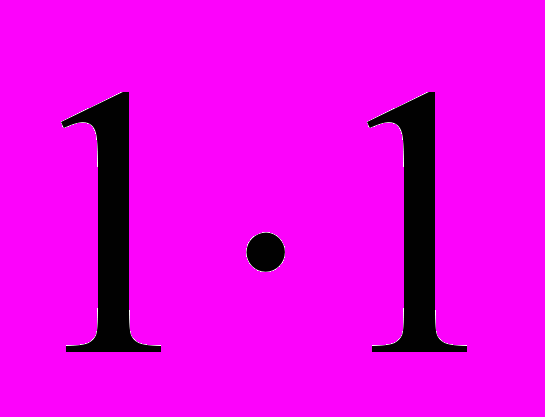, для которого есть две возможности 0 или 1.

Рассмотрим случай, когда результат операции 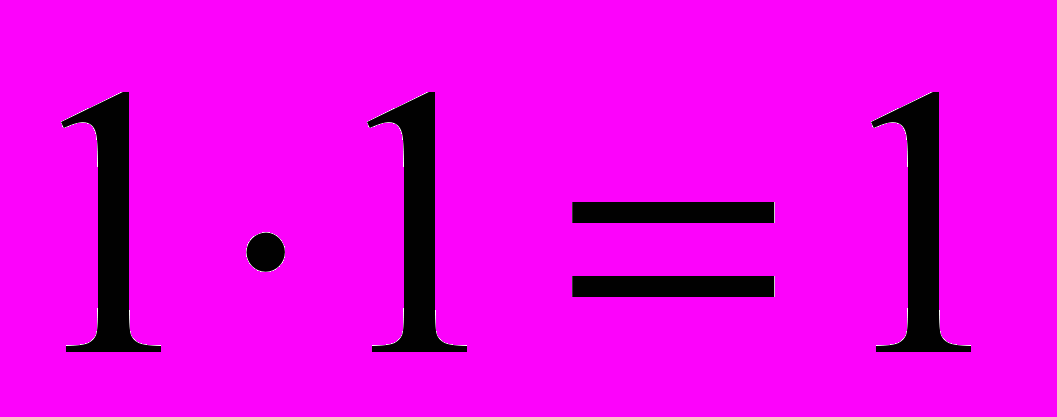. Тогда, учитывая, что нейтральным элементом является , получаем две таблички для операции “сложение”: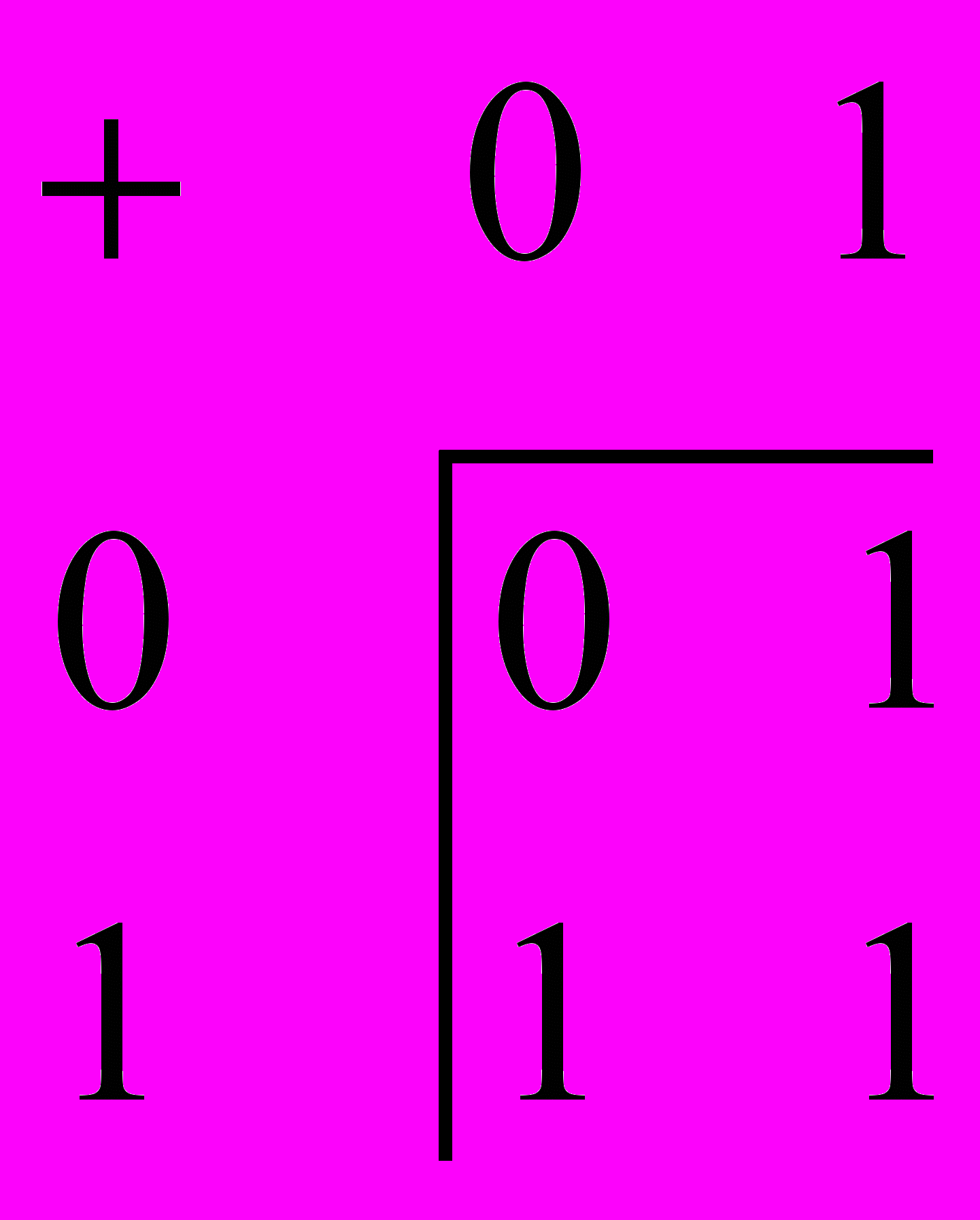

,

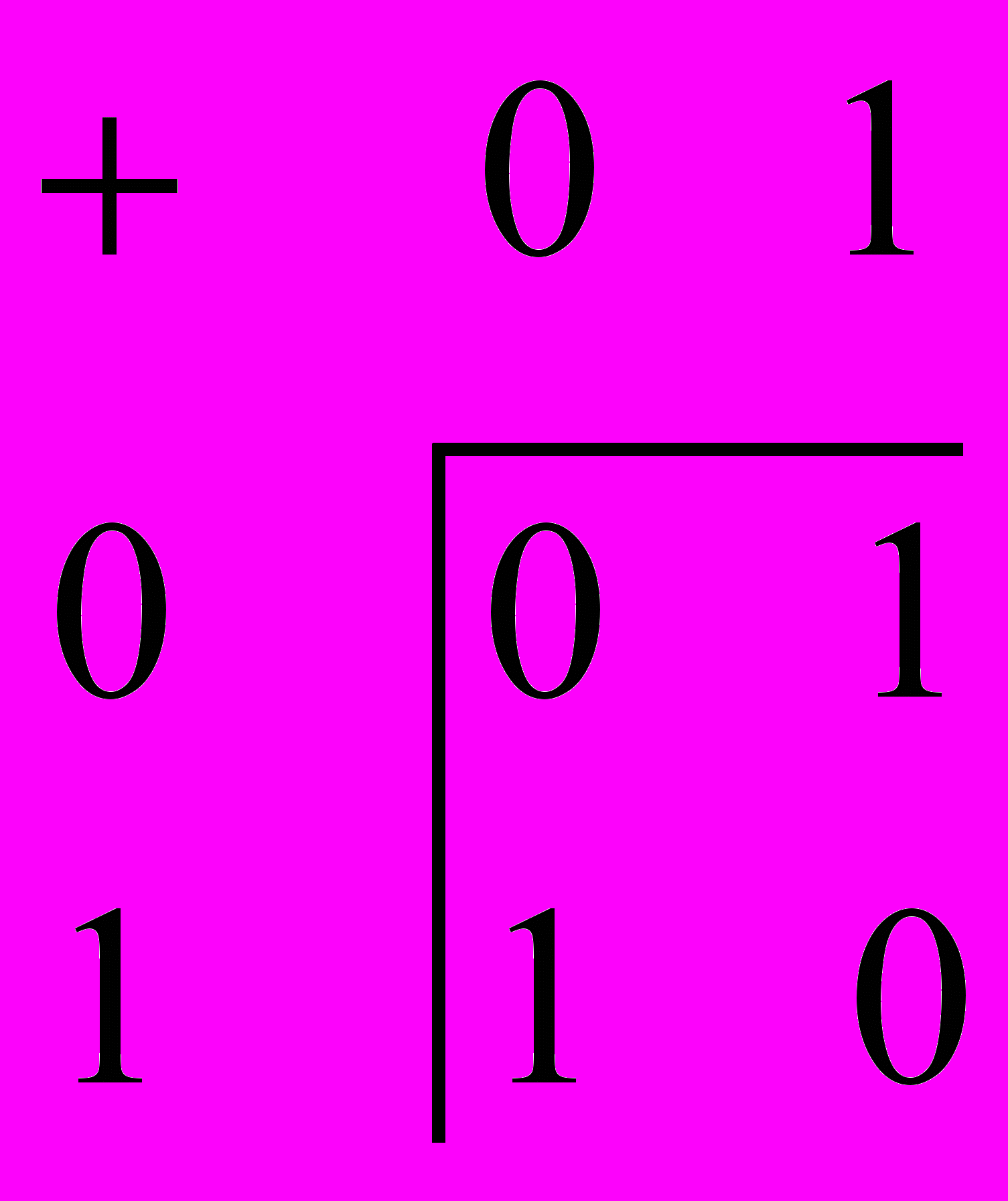которые также отличаются значением операции на элементах 1 и 1 (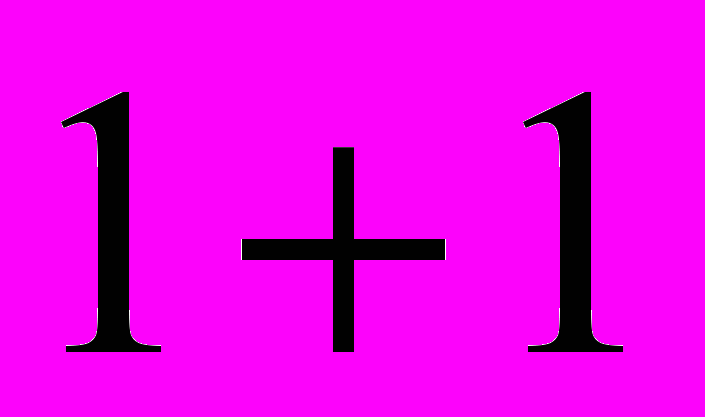). Однако первая «табличка-операция» не является кандидатом на операцию “сложение” в кольце (не удовлетворяет аксиоме А4), т.к. элемент 1 не имеет противоположного, при таком задании операции. Таким образом, получилось задать одну структуру кольца с операциями: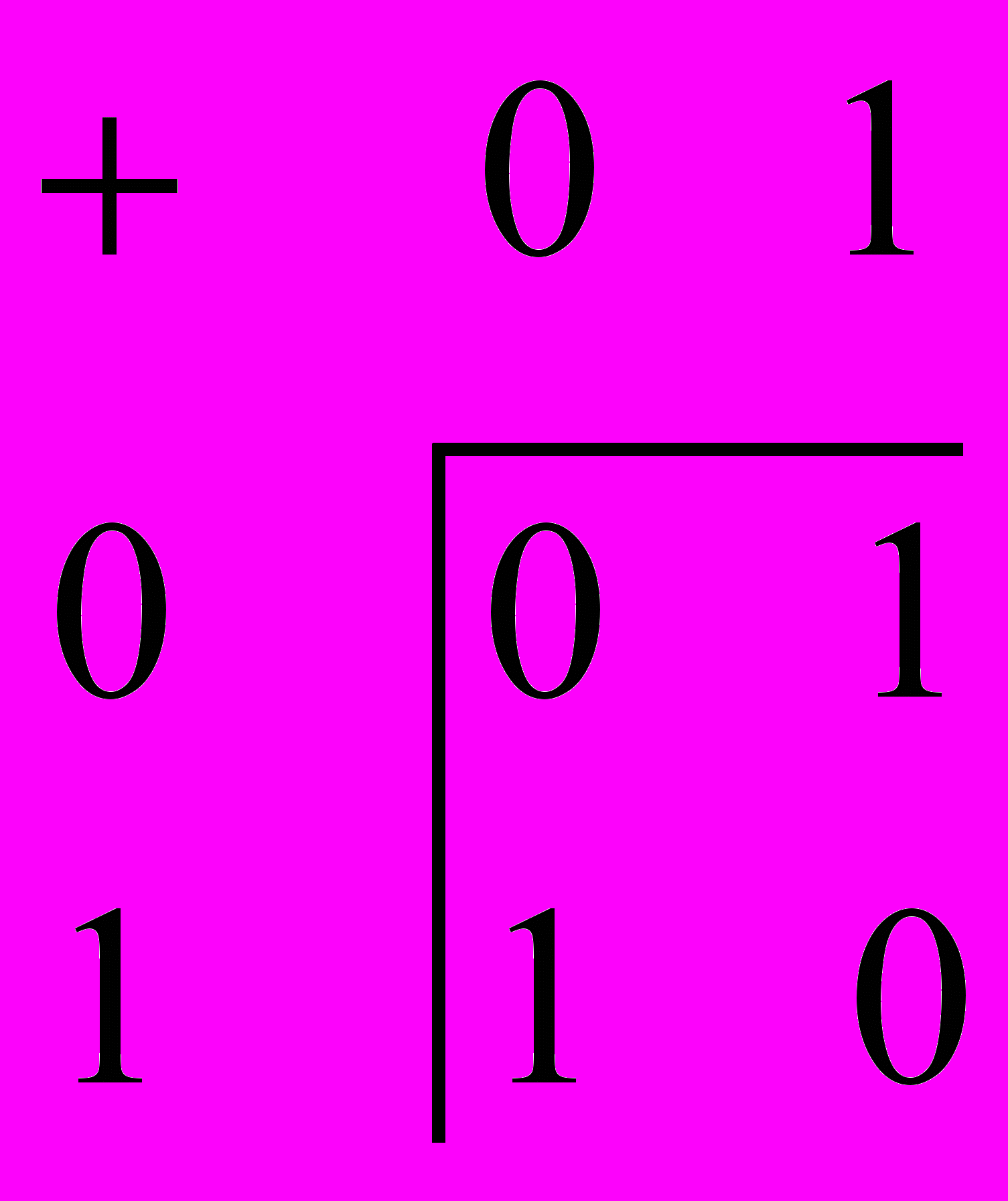

.

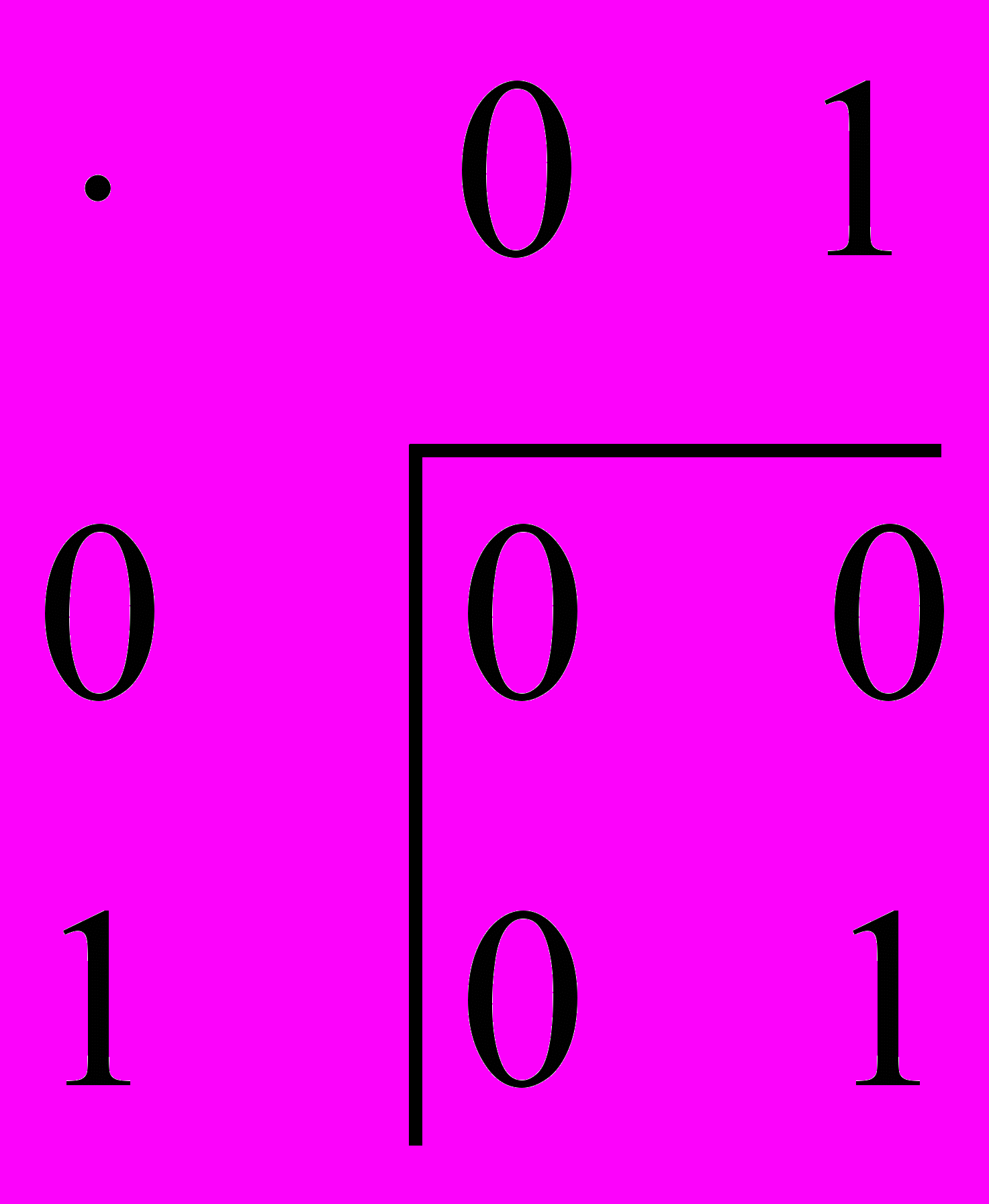Аналогично рассматривается второй случай, когда результат операции “умножение” 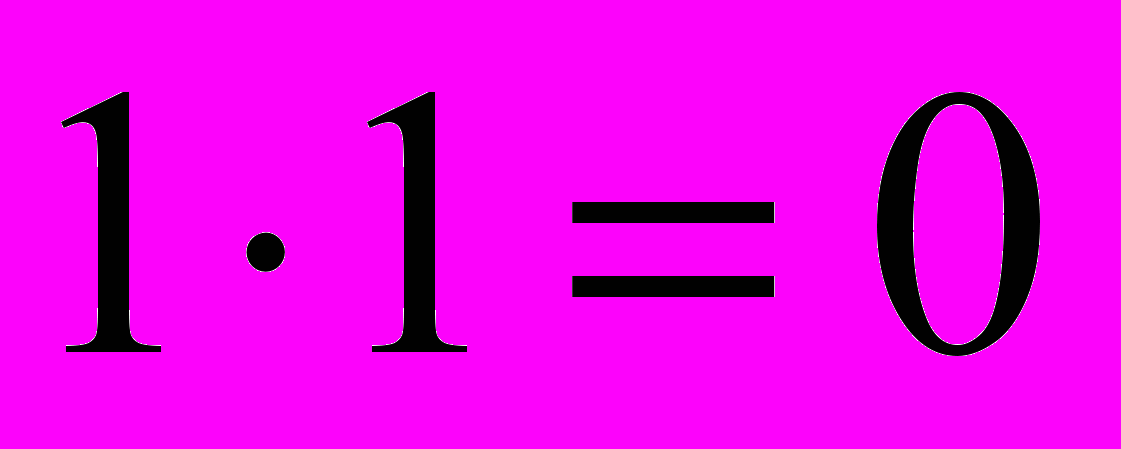. Пользуясь теми же соображениями, получаем ещё одну структуру кольца: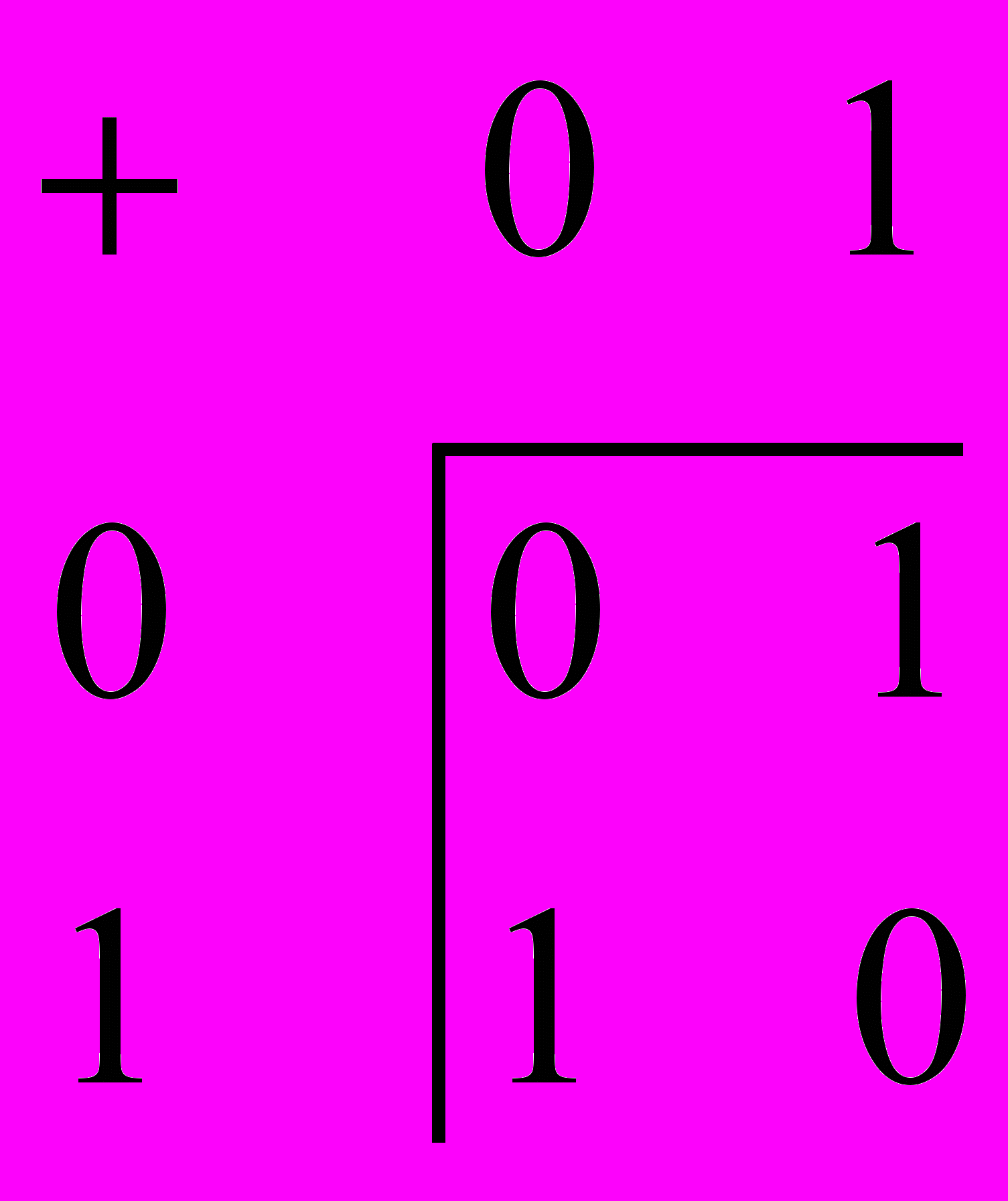

.

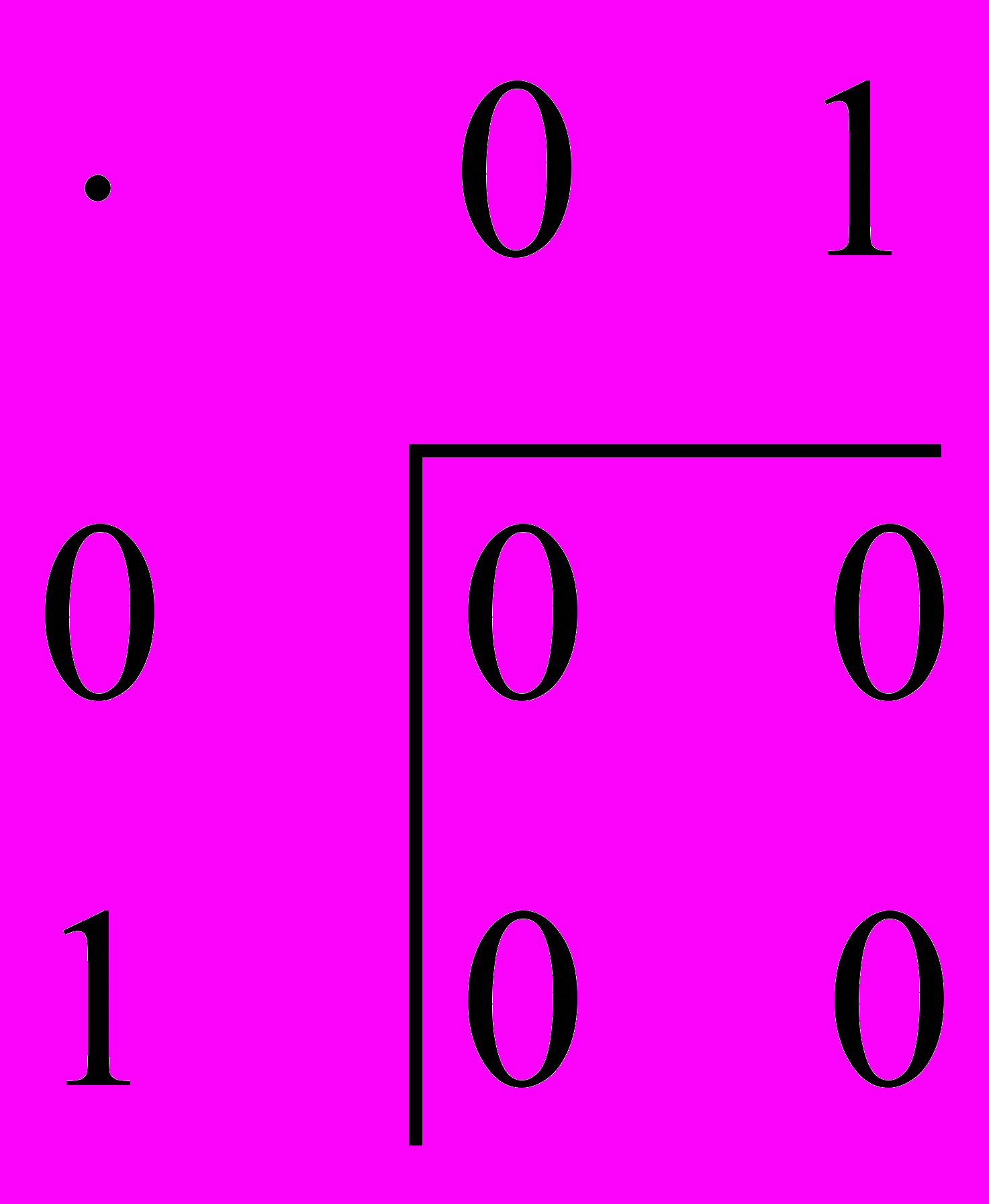Итак, в предположении, что нейтральным элементом является 0, мы получили два кольца на заданном множестве. Действуя аналогичным образом, мы сможем получить ещё два кольца, рассмотрев предположение, что нейтральный элемент 1. Последнее утверждение легко доказать, просто заменив в полученных структурах 0 на 1 и 1 на 0.

Ответом задачи является число 4. На заданном носителе можно построить 4 кольца. (Следует отметить, что с точностью до изоморфизма, колец с данным носителем 2, однако, понятие морфизма нужно специально определять и рассматривать, нам кажется, что в рамках факультатива или кружка это не обязательно.) [3]

Математика в информатике.

Приведенное решение задачи, хотя и использует теоретические утверждения и аксиомы, является конструктивным. Этот факт обладает привлекательностью с точки зрения информатики. По плану данного решения можно построить алгоритм или блок-схему, которые потом можно реализовать в виде программы на языке высокого уровня (Pascal или C++) и получить все кольца с носителями трех- и четырехэлементных множеств.

Конечно, уже достижение – написание такой программы. Улучшение, совершенствование алгоритма, например, сортировки, чтобы он работал быстрее и есть направление для дальнейшего развития. Эта задача из абстрактной алгебры предоставляет широкое поле для совершенствования своих профессиональных навыков программиста. Часто очередное усовершенствование программного продукта с небольшим теоретическим обоснованием – самостоятельный научно-исследовательский проект для школьника, который будет выигрышно смотреться на любом конкурсе таких проектов.

Решение задачи вводит учащегося в такую новую развивающуюся науку как компьютерная алгебра. Т.к. разобравшись с приведенной задачей, можно приступить к компьютерной реализации таких близких задач как построение (нахождение, полное описание) гомоморфизмов, изоморфизмов конечных алгебраических структур (колец, групп).

Важность и необходимость решения подобных задач мы видим, прежде всего, во взаимозависимости алгебраических структур и геометрических конфигураций: задача «укладки», упаковки, замощение паркетом, которые набирают вес в современных приложениях.

Литература.
  1. Сайт Всероссийской олимпиады школьников по информатике lymp.ru/.
  2. Земляков А.Н. Тезисы по алгебре, «Математическое образование» М.:№4(15) 2000г. с.2-40.
  3. Русаков А.А. Проектирование методической системы обучения математически, творчески одаренных детей на основе реализации идей А.Н. Колмогорова, докторская диссертация, Москва 2006 г.