Конспект книги талеб Нассин Николас. Черный лебедь. Под знаком непредсказуемости. М.: Издательство КоЛибри, 2009. 528с. Аннотация
| Вид материала | Конспект |
| Эти утешительные постулаты Первый главный постулат "Вездесущность гаусианы " Глава 16. Эстетика случайности Певец случайности Платонизм треугольников |
- Урок по стихотворению Н. А. Заболоцкого «Лебедь в зоопарке», 57.26kb.
- Механизм воздействия инфразвука на вариации магнитного поля земли, 48.07kb.
- Рекомендовано в качестве конспекта лекций Редакционно-издательским советом Томского, 1088.59kb.
- Статья «Под знаком качества»: «Под знаком «Качество Кубань», 1260.85kb.
- Дмитрия Зимина "Династия", 12036.48kb.
- Курс 1 семестр Реферат по заболеванию. План, 62.02kb.
- Е. Е. Черный замок: Фантастический роман": армада: "Издательство Альфа-книга, 6811.04kb.
- Габович Евгений История под знаком вопроса. "Нева", спб-Москва, 2005, 6103.7kb.
- Споры не затихают. "Эту книгу обязан прочитать каждый", считает британский журнал The, 6638.89kb.
- Хабаровск Под общей редакцией доктора сельскохозяйственных наук Н. В. Выводцева Хабаровск, 3694.25kb.
ооо.
Продолжим процесс дробления. Будем бросать40о ооо раз, ставя на кон по i центу и подходя, таким образом, все ближе и ближе к гауссиане. Рисунок показывает распределение результатов между 40 и минус 40 долларами, то есть восьмьюдесятью смысловыми точками. При ставке в i цент мы доводим их до 8ооо смысловых точек.
Пойдем дальше. Мы можем бросить монету 4000 раз, ставя по i/io цента. Ну а как насчет 400 ооо раз по i/iooo цента? Совершенная кривая Гаусса (как платоническая форма) — это отображение бесконечного числа бросков с бесконечно малыми ставками. Не пробуйте их себе представить — не получится. Нам нет смысла говорить о "бесконечно малых" ставках (поскольку у нас их бесконечное множество, а значит, мы имеем дело с тем, что математики называют беско-
\396\
Рис. 10. Более абстрактная версия: платоническая кривая
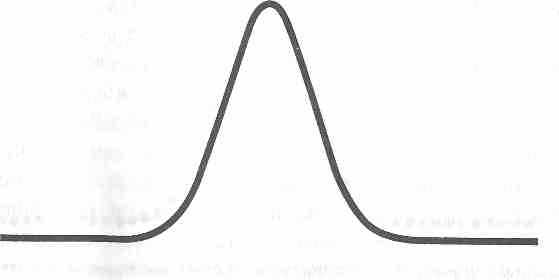
Бесконечное число бросков.
нечной структурой). Но хочу вас обрадовать: существует альтернатива.
Мы начали с простой ставки и пришли к чему-то абсолютно абстрактному. Начали с наблюдений и оказались в царстве математики. В математике вещи обретают абстрактную чистоту.
Но, поскольку чистых абстракций в природе не существует, пожалуйста, даже не пытайтесь постичь глубинный смысл фигуры нарисунке ю. Просто знайте, как ею пользоваться. Воспринимайте ее как градусник: не обязательно понимать, что означает температура, чтобы пользоваться показаниями градусника. Главное — знать соответствие между температурой и, скажем, комфортностью (или какими-то другими эмпирическими факторами). Шестьдесят градусов по Фаренгейту соответствуют приятной погоде; минус десять — не то, о чем следует мечтать. Не обязательно интересоваться действительной скоростью столкновений между частицами, которая помогла бы уяснить подоплеку понятия "температура". Градусы — это некое подсобное средство, с помощью которого ваше сознание
\397\
может перевести какие-то внешние явления на уровень чисел. Вот и гауссиана устроена так, что 68,2 процента наблюдений сосредоточиваются между минус одним и плюс одним стандартным отклонением от среднего. Я повторю: даже не пытайтесь понять, является ли стандартное отклонение средним отклонением — нет, не является, и многие (слишком) многие люди, использующие термин стандартное отклонение, этого не понимают. Стандартное отклонение — это вопрос простого соотношения, обычное число, с которым соизмеряются явления, если они действительно из разряда "гауссовых".
Стандартное отклонение часто называется сигмой. Также говорят о дисперсии (дисперсия — это сигма в квадрате).
Обратите внимание на симметричность "колокола". Одинаковый результат получается при отрицательной и при положительной сигме. Шансы спуститься ниже минус четырех сигм равны шансам перевалить через четыре сигмы, у нас они i к 32 ооо.
Как видите, основная идея "гауссовой кривой" (о чем я говорил выше) в том, что большинство наблюдений колеблется в рамках заурядного, среднего, в то время как шансы отклонения сокращаются быстрее и быстрее (экспоненциально), чем дальше вы уходите от центра. Если хотите ухватить главное, вот оно: резкое ускорение падения шансов при удалении от середины. Вероятность аномалий стремительно уменьшается. Ими можно спокойно пренебречь.
Из этого свойства вытекает высший закон Среднестана: поскольку большие отклонения чрезвычайно редки, их вклад в итог будет чрезвычайно мал.
В примере -: чамерами человеческого роста я брал за единицу отклонения десять сантиметров, показывая, как тает процент гигантов по мере увеличения роста. Это были отклонения на одну сигму; а еще ростовая таблица наглядно пока-
\398\
зывает, как происходит "соизмерение с сигмой", — ее использование в качестве единицы измерения.
ЭТИ УТЕШИТЕЛЬНЫЕ ПОСТУЛАТЫ
Выделим главные постулаты, определившиеся в ходе нашей игры в монетку, которая привела к протогауссовой, или рядовой, случайности.
Первый главный постулат: броски не зависят друг от друга. У монетки нет памяти, То, что вам выпали орел или решка, вовсе не означает, что в следующий раз вас ждет удача. Умение бросать монету не приходит со временем. Если ввести такой параметр, как память или мастерство бросания, вся эта гауссова конструкция зашатается.
Вспомним наши рассуждения из главы 14 о привязках и кумулятивном преимуществе. Обе теории утверждают, что сегодняшний выигрыш повышает шансы на выигрыш завтра. Поэтому вероятности зависят от истории и первый главный постулат, на котором строится гауссиана, в реальности не работает. В играх, конечно, прошлые выигрыши не должны увеличивать вероятность будущих, но в жизни это не так, и поэтому я такой противник обучения теории вероятности на примере игр. Если выигрыш влечет за собой дальнейший выигрыш, то у вас гораздо больше шансов стать свидетелем сорока выигрышей подряд, чем в пределах протогауссианы.
Второй главный постулат: "сумасшедших" прыжков не бывает. Размер шага, этого элементарного кирпичика классического случайного распределения, всегда известен: как раз один шаг. Он всегда определен. Мы не встречали ситуаций с "сумасшедшей" неравномерностью движений.
Помните, что, если один из этих двух главных постулатов отсутствует, ваши шаги (или подбросы монетки) не создадут
\399\
в итоге гауссиану. При определенных обстоятельствах вы можете столкнуться с из ряда вон выходящей масштабно-инвариантной случайностью мандельбротовского типа.
"ВЕЗДЕСУЩНОСТЬ ГАУСИАНЫ "
Всякий раз, когда я заявляю, что "гауссова кривая" вездесуща отнюдь не в реальной жизни, а только в умах статистиков, от меня требуют: "Докажи!" Как мы увидим в следующих двух главах, это сделать очень легко, а вот противоположное никому еще до сих пор доказать не удалось. Стоит мне высказать предположение, что существуют процессы, не описываемые гауссианой, меня просят это обосновать и, помимо фактов, "предъявить стоящую за ними теорию". В главе 14 мы рассматривали модель "деньги идут к деньгам", предлагавшуюся, чтобы оправдать неиспользование гауссианы. Разработчикам таких моделей приходится тратить уйму времени на подведение теоретической базы под возможные масштабируемые ситуации — как будто им надо за что-то извиняться. Теория-фигория! У меня с этим эпистемологическая проблема — с необходимостью оправдывать то, что миру не удается соответствовать идеализированной модели, которую сумел пропиарить какой-то слепец, отрешенный от реальности.
Я предпочитаю не моделировать возможные ситуации возникновения негауссовой случайности [впадая тем самым в грех слепого теоретизирования), а делать нечто противоположное: пристально изучать гауссиану и определять, где она действует, а где нет. Я знаю, где Среднестан. По-моему, именно приверженцы гауссианы часто (да что там — почти всегда) не вполне понимают, с чем они имеют дело, и должны обосновывать свои действия, а не наоборот.
\400\
Эта вездесущесть гауссианы — не свойство мира, а про-- блема, существующая в наших умах и вытекающая из нашего взгляда на мир.
В следующей главе мы обратимся к масштабируемости окружающего мира и к свойствам фрактала. А в той, что за ней, коснемся злоупотребления гауссианой в социоэкономике и "необходимости строить теории".
Я порой излишне горячусь, но только потому, что провел значительную часть своей жизни, размышляя над этой проблемой. С тех пор как я начал думать над ней и проводить разнообразные мысленные эксперименты вроде описанного выше, я тщетно искал вокруг себя, в мире бизнеса и статистики, кого-нибудь, кто был бы до конца интеллектуально последователен в смысле осознания угрозы Черного лебедя и отказа от гауссианы и ее инструментария. Многие, принявшие мою идею Черного лебедя, не смогли довести ее до логического завершения, а именно — не смогли признать, что нельзя использовать одну-единственную меру случайности, называемую стандартным отклонением [и называть ее "риском"); нельзя рассчитывать на простые ответы, когда речь идет о неопределенности. Отказ от гауссианы требует смелости, преданности истине и способности соединять разрозненные факты, требует желания глубже постичь случайность. И еще нужно не возводить чужую мудрость в абсолют.
Затем я начал знакомиться с физиками, которые отвергли гауссов подход, но стали жертвой другого заблуждения (иной формы платонизма), а именно — веры в точные предсказательные модели, эксплуатирующие в основном привязку из главы 14. Я не мог найти ни одного глубокого и технически подкованного ученого, который смотрел бы на мир случай-
\401\
ности и понимал его природу, видел бы в расчетах подспорье, а не самоцель. Мне потребовалось около полутора десятилетий, чтобы открыть для себя такого мыслителя. Человека, сделавшего многих лебедей Серыми: Мандельброта — великого Бенуа Мандельброта.
\402\
Глава 16. Эстетика случайности
Библиотека Манделъброта. — Был ли Галилей слеп? — Бисер перед свиньями. — Самоподобие. —Простая многосложность, или, может быть, многосложная простота, мира.
ПЕВЕЦ СЛУЧАЙНОСТИ
Одним грустным вечером я вдыхал запах старых книг в библиотеке Бенуа Мандельброта. Это было в августе 2оо5-го, и от жары старые французские книги сильнее пахли клеем, вызывая сильную обонятельную ностальгию. Обычно мне удается подавлять такие приступы ностальгии, но только не те, что накатывают на меня с волной музыки или запахов. Запах книг Мандельброта — это запах французской литературы, библиотеки моих родителей, многих часов, проведенных в книжных магазинах и библиотеках, когда я был подростком, когда меня окружали книги в основном (увы) на французском языке и когда я думал, что Литература превыше всего. (Мне не приходилось видеть столько французских книг
\403\
с той поры.) Как бы мне ни хотелось считать Литературу абстракцией, она имела материальное воплощение. У нее был запах, и я его ощущал.
Тот день был печальным еще и потому, что Мандельброт уезжал — как раз тогда, когда я удостоился права звонить ему в самое неурочное время только ради того, чтобы, например, спросить: почему до людей не доходит, что 8о/2о можно запросто трансформировать в 50/1? Мандельброт решил переехать в район Бостона — он не уходил на пенсию, а собирался работать в исследовательском центре, спонсируемом одной национальной лабораторией. Ему предстоял переезд в квартиру в Кембридже, и, покидая свой просторный дом под Нью-Йорком, он пригласил меня набрать у него книг.
Даже их названия звучали ностальгически. Я наполнил коробку французскими изданиями, такими как вышедшая в 1949 году "Материя и память" Анри Бергсона, — ее Мандельброт, похоже, купил, еще будучи студентом (ах, этот запах!).
После того как я множество раз упоминал Мандельброта, я наконец-то представлю его. Прежде всего — как первого человека с ученой степенью, с которым я когда-либо говорил о случайности, не чувствуя, что меня обманывают. Другие математики, специализирующиеся на вероятностях, швыряли в меня "винеровской мерой" и какими-то теоремами с русскими названиями типа теоремы Соболева или теоремы Колмогорова, без которых они как без рук. Им никак не удавалось ухватить суть предмета или хотя бы высунуться из своей маленькой скорлупки, чтобы увидеть со стороны ее эмпирические изъяны. С Мандельбротом все было не так: казалось, что мы были рождены в одной стране, встретились после многих горьких лет изгнания и наконец-то можем свободно поговорить на родном языке. Он — единственный учитель из
\404\
плоти и крови, который у меня был; главные мои учителя — это книги в моей библиотеке. Я слишком мало уважал математиков, занимающихся неопределенностью и статистикой, чтобы считать кого-то из них своим учителем. По моим представлениям, математики, натасканные на определенность, не должны совать нос в случайность. Мандельброт показал, что я не прав.
У него необычайно чистый и правильный французский язык, совсем как у поколения моих родителей в Леванте или у аристократов Старого Света. Поэтому, когда мне случалось слышать его не лишенный акцента, но совершенно стандартный американский английский, я каждый раз удивлялся. Он высок, у него лишний вес, отчего его лицо кажется младенческим (хотя я никогда не видел, чтобы он много ел), и его присутствие физически ощутимо.
Может показаться, что объединяющие нас с Мандельбро-том предметы — это из ряда вон выходящая неопределенность, Черные лебеди и скучные (иногда не слишком скучные) статистические понятия. Но, хотя мы и сотрудничаем в этих сферах, это не то, вокруг чего обычно крутятся наши разговоры: в основном мы обсуждаем литературные и эстетические материи или вспоминаем исторические байки о людях блестящего ума. Я имею в виду именно блестящий ум, а не ученость. Мандельброт может много чего порассказать о феноменальной когорте деятелей науки, с которыми ему доводилось работать на протяжении прошлого века, но так уж я устроен, что мне гораздо менее любопытны личности ученых, чем колоритных эрудитов. Подобно мне, Мандельброт интересуется просвещенными индивидуумами, в которых сочетается то, что считается несочетаемым. Среди его любимых персонажей — барон Пьер Жан де Менаш, с которым он познакомился в Принстоне в ipso-e годы, где тот делил ком-
\405\
нату с физиком Оппенгеймером. Де Менаш был в точности тем, что меня особенно занимает, — воплощением Черного лебедя. Он происходил из состоятельной купеческой семьи александрийских евреев, говорившей по-французски и по-итальянски, как все культурные левантинцы. Его предки переделали свою арабскую фамилию на венецианский манер (Menasce), добавили к ней походя венгерский аристократический титул и вращались среди особ королевской крови. Де Менаш не только обратился в христианство, но стал священником-доминиканцем и крупным исследователем семитских и персидского языков. Мандельброт все время расспрашивал меня об Александрии, поскольку неустанно искал таких уникумов.
Да и я, честно сказать, искал в жизни именно их — обладателей незаурядного интеллекта. Мой эрудированный и разносторонний отец (который, оставайся он в живых, был бы всего на две недели старше Бенуа М.) любил общество чрезвычайно культурных монахов-иезуитов. Я помню, как они, приходя, занимали мое место за обеденным столом. Один из них был "остепененным" медиком и физиком, но при этом преподавал арамейский язык местным студентам в Бейрутском институте восточных языков. Его прежним послушанием вполне могло быть преподавание физики в высшей школе, а еще раньше —- чтение лекций на медицинском факультете. Эрудиция такого рода производила на моего отца куда большее впечатление, чем конвейерная научная работа. Может, у меня врожденная неприязнь к bildung-sphilisters.
Хотя Мандельброт часто восхищался темпераментом эрудитов высокого полета и замечательных, но не очень известных ученых, вроде его старого друга Карлтона Гайдузека, человека, сумевшего докопаться до причин некоторых тропи-
\406\
ческих болезней, о своих связях с теми, кого принято считать великими, он не склонен был распространяться. Я далеко не сразу узнал, что он сотрудничал с огромным количеством ученых чуть ли не всех специальностей — о чем любой другой твердил бы с утра и до ночи. Хотя я уже несколько лет тесно знаком с ним, только на днях, беседуя с его женой, я выяснил, что он два года ассистировал как математик психологу Жану Пиаже. Еще одно потрясение я испытал, когда узнал, что он работал и с великим историком Фернаном Броделем. Но Мандельброт, казалось, был безразличен к Броделю. Его не тянуло поболтать о Джоне фон Неймане, под чьим началом он проходил стажировку. Его иерархия была перевернутой. Однажды я спросил Мандельброта о встреченном мною на вечеринке Чарльзе Трессере, безвестном физике, писавшем статьи по теории хаоса и пополнявшем свой заработок исследователя выручкой от продажи пирожных собственного изготовления. "Un homme extraordinaire!"* — вскричал Мандельброт и рассыпался в похвалах Трессеру. Но когда я спросил его об одном научном корифее, он ответил: "Типичный bon eleve, прилежный студент без глубины и без полета.". Корифей был нобелевским лауреатом.
ПЛАТОНИЗМ ТРЕУГОЛЬНИКОВ
Теперь о том, почему я называю это дело мандельбротовской, или фрактальной, случайностью. Каждый отдельный кусочек и деталь головоломки уже упоминались кем-нибудь раньше, скажем, Парето, Юлом и Ципфом, но именно Мандельброт а) соединил точки, б) связал случайность с геометрией (при-
Необыкновенный человек (фр.).
\407\
чем с её определенной областью) и в) придал предмету естественную завершенность. По правде говоря, многие математики знамениты сегодня отчасти потому, что он использовал их работы, чтобы подвести фундамент под собственные построения, — как делаю и я в этой книге. "Мне пришлось придумать себе предшественников, чтобы люди относились ко мне серьезно", — сказал он мне однажды, так что его ссылки на мнение авторитетов — всего лишь риторический прием. Почти всегда можно раскопать тех, кто уже высказывал данную мысль, и опереться на их вклад. Олицетворением большой идеи, носителем "брэндового имени" становится в науке тот, кто соединяет точки, а не тот, кто случайно сделал наблюдение. Даже Чарльз Дарвин, который, как утверждают невежды от науки, "придумал" выживание наиболее приспособленных, заговорил об этом не первым. Он написал во введении к "Происхождению видов", что излагаемые им факты не всегда новы; но его выводы, как ему кажется, "представляют интерес" (такова его по-викториански скромная формулировка). В конечном счете известность приобретают те, кто делает выводы и улавливает важность идей, видя их реальную ценность. Именно они способны развить тему.
Итак, вот что представляет собой мандельбротова геометрия.
геометрия природы
Треугольники, квадраты, крути и другие геометрические фигуры, которые заставляли многих из нас зевать в классе, — сами по себе прекрасные и чистые понятия, но, похоже, в сознании школьных учителей, а также современных архитекторов и дизайнеров, они встречаются чаще, чем в природе. Пусть бы так, да вот только большинство из нас об этом
\408\
не подозревает. Горы — не треугольники и не пирамиды; деревья — не окружности; прямых линий почти нигде не увидишь. Мать-природа не посещала уроков геометрии и не читала книг Евклида Александрийского. Ее геометрия полна зазубрин, но с собственной логикой, причем такой, которую легко понять.
Я уже говорил, что мы, похоже, от рождения склонны платонизировать и мыслить исключительно в рамках пройденного материала: любому, будь то хоть каменщик, хоть натурфилософ, не так легко вырваться из рабства рефлексов. Подумайте, что великий Галилей, разоблачитель лжи в других вопросах, написал следующее:
Великая книга Природы всегда лежит раскрытая перед нашими глазами, и истинная философия записана в ней. Но мы не можем прочитать ее, если не выучим сперва языка и символов, с помощью которых она написана. Она написана на языке математики, а буквы ее — треугольники, круги и другие геометрические фигуры.
Галилей что, был незрячим? Даже великий Галилей, со всей своей знаменитой независимостью ума, не сумел ясным взором взглянуть на мать-природу. Я уверен, что у него в доме были окна и что он иногда выходил на свет божий: ему следовало бы знать, что треугольники в природе найти нелегко. Гораздо легче промыть себе мозги.
Мы либо слепы, либо невежественны, либо и то и другое вместе. Ведь совершенно же очевидно, что геометрия природы — не евклидова, однако никто, почти никто, этого не видит.
Подобная (физическая) слепота равносильна игровой ошибке, заставляющей нас думать, что казино — это олицетворение случайности.
\409\
ФРАКТАЛЬНОСТЬ
Но сначала о том, что такое фракталы. Потом мы покажем, как они связаны с так называемыми степенными, или масштабируемыми, законами.
Слово фрактал введено Мандельбротом для описания геометрии неровного, ломаного (оно образовано от латинского fractus — дробный, фрагментарный]. Фрактальность — это повторение в разном масштабе геометрических узоров, плодящих все более и более мелкие версии самих себя. Каждая часть в некоторой степени напоминает целое. Я постараюсь показать в этой главе, как фракталы соотносятся с тем типом неопределенности, который должен носить имя Мандель-брота: мандедьбротовская случайность.
Прожилки в листьях выглядят как ветви; ветви выглядят как деревья; камни выглядят как маленькие горы. Когда предмет меняет размер, не происходит качественных изменений. Если взглянуть на побережье Британии с самолета, оно напоминает то, что ты видишь, глядя на его крохотный кусочек в увеличительное стекло. Такой род самоподобия подразумевает, что одно обманчиво короткое и простое правило повторения может использоваться либо компьютером, либо, более произвольно, матерью-природой, чтобы строить формы, кажущиеся очень сложными. Это правило может оказаться полезным для компьютерной графики, но, что важнее, именно так работает природа. Мандельброт выстроил математический объект, известный сейчас как множество Мандельброта, самый знаменитый объект в истории математики. Множество приобрело популярность у последователей теории хаоса, потому что оно плодит картины все возрастающей сложности, подчиняясь на вид пустяковому рекурсивному правилу (то есть такому, кото-
\410\
рое способно применять себя к себе же до бесконечности). Можно рассматривать этот объект во все более и более крупном масштабе, так и не достигая предела — формы будут по-прежнему узнаваемыми. Они никогда не повторяются, но обладают сходством друг с другом, общими семейными чертами.
Такие построения играют заметную роль в искусстве. Вот несколько примеров:
Визуальные искусства. Сейчас в основе большинства объектов компьютерной графики лежит та или иная разновидность мандельбротова фрактала. Фракталы также встречаются в архитектуре и живописи — разумеется, неосознанно включенные художниками в структуру произведения.
Музыка. Медленно напойте первые четыре ноты Пятой симфонии Бетховена: "Та-та-та-та!" Затем замените каждую отдельную ноту тем же самым наглом из четырех нот, так что получится такт из шестнадцати нот. Вы увидите [вернее, услышите), что каждая маленькая волна напоминает исходную большую. У Баха и Малера, например, музыкальная тема часто состоит из нескольких подтем, похожих на нее.
Поэзия. Поэзия Эмили Дикинсон, к примеру, фрактальна: крупное напоминает мелкое. Поэтесса, по мнению комментатора, "плетет продуманный узор из слов, размеров, рефренов, движений и звуков".
Сначала фракталы сделали Бенуа М. парией в математическом истеблишменте. Французские математики были в ужасе. Что? Картинки? Mon dieu! Это все равно что показать порнофильм собранию набожных православных бабушек в моем родном Амиуне. Поэтому Мандельброт некоторое время оставался интеллектуальным изгоем, работая в иссле-
\411\
довательском центре "Ай-би-эм" на севере штата Нью-Йорк. Это было типичное "в ж. деньги!", так как айбиэмовское жалованье позволяло ему заниматься чем хочется.
Но масса людей (прежде всего компьютерщиков) сразу схватила суть. Книга Мандельброта "Фрактальная геометрия природы", вышедшая в свет четверть века назад, произвела настоящий фурор. Ею зачитывались в художественных кругах, она дала толчок новым идеям в искусстве, в архитектурном дизайне, даже крупным индустриальным проектам. Ман-дельброту предложили место профессора медицины! Может статься, легкие самоподобны? На лекции Бенуа М. ломом ломились художники и артисты, за что его прозвали "рок-звездой математики". Компьютерный век помог ему стать одним из самых востребованных математиков в истории, причем гораздо раньше, чем он был признан обитателями башни из слоновой кости. Мы вскоре увидим, что его теория, вдобавок к универсальности, обладает одним необычным свойством: она на редкость проста для понимания.
Несколько слов о его биографии. Мандельброт приехал во Францию из Варшавы в 1936 году, в двенадцать лет. Из-за тягот нелегальной жизни в оккупированной нацистами Франции он, учась в основном самостоятельно, отчасти избежал традиционного галльского образования с его отупляющей зубрежкой алгебры. Позже на него сильно повлиял его дядя Шолем, видный представитель французского математического истеблишмента, возглавлявший кафедру в Коллеж де Франс. Поселившись в Соединенных Штатах, Бенуа М. работал в основном как ученый-прикладник, лишь спорадически занимая академические должности.
Компьютер играл две роли в новой науке, становлению которой помог Мандельброт. Во-первых, фрактальные объекты, как мы видели, могут генерироваться путем примене-
\412\
ния простого правила к самому себе, что идеально подходит для автоматической деятельности компьютера (или матери-природы). Во-вторых, в процессе генерирования интуитивных образов происходит постоянная притирка между математиком и создаваемыми объектами.
Посмотрим теперь, какое отношение все это имеет к случайности. Если быть точным, карьера Мандельброта началась именно с вероятности.
визуальный подход к крайнестану / среднестану
Я смотрю на ковер в своем кабинете. Если я буду изучать его через микроскоп, то увижу пересеченную местность. Если я стану разглядывать его через увеличительное стекло, то местность покажется мне более ровной, но все же весьма ухабистой. Но когда я смотрю на него с высоты своего роста, он выглядит почти таким же гладким, как лист бумаги. Ковер, обозреваемый невооруженным глазом, соответствует Сред-нестану и закону больших чисел: я вижу сумму волнистостей, которые сглаживаются. Это как гауссова случайность: моя чашка с кофе не подпрыгивает на столе, потому что суммарное движение всех ее частиц оборачивается стабильностью. Таким же образом, суммируя маленькие гауссовы неопределенности, получаешь определенность: это закон больших чисел-
Гауссиана не самоподобна, и поэтому моя кофейная чашка не прыгает.
Рассмотрим теперь прогулку в горы. Как высоко ни поднимешься над поверхностью земли, она будет оставаться неровной. Даже при взгляде с высоты зо ооо футов. Когда летишь над Альпами, вместо маленьких камешков видишь зазубрен-
\413\
ные вершины. Значит, некоторые поверхности — не из области Среднестана и изменение масштаба не приводит к их сглаживанию. (Заметим, что эффект выравнивания достигается, только если подняться на еще большую высоту. Наша планета представляется гладким шаром тем, кто наблюдает за ней из космоса, но это потому, что она слишком маленькая. Будь Земля крупнее, на ней нашлись бы горы, превосходящие по высоте Гималаи, и потребовалась бы еще большая удаленность от нее, чтобы их очертания стерлись. Точно так же, живи на Земле больше людей, пусть даже с тем же средним достатком, наверняка нашелся бы кто-то, чей капитал перекрыл бы состояние Билла Гейтса.)
Рисунки и и 12 иллюстрируют эту идею: глядя на первый рисунок, можно подумать, что на землю упала крышка от объектива.

Рис. 11. По-видимому, на землю уронили крышку от объектива. А теперь переверните страницу.
\414\
часть III. серые лебеди крайнестана
