В наноструктурах
| Вид материала | Документы |
- Электронные явления в наноструктурах, 128.7kb.
- А. В. Чаплик Экранирование и фриделевские осцилляции в наноструктурах, 267.43kb.
- Задачи изучения дисциплины: дать общие представления о наноструктурах и областях, 135.27kb.
- Наукові школи 2011, 16.29kb.
- Xxiii симпозиум «Современная химическая физика» Программа, 916.52kb.
- Доклад на научном семинаре физического факультета 20. 10. 2009, 48.81kb.
- Отчет о научно-исследовательской работе за 2008 год Тема нир: Исследование новых механизмов, 65.37kb.
- Программу составил профессор, д ф. м н. В. Д. Кулаковский Аннотация, 94.53kb.
Электронные явления
в наноструктурах
ПРИМЕНЕНИЕ ПОТЕНЦИАЛОВ НУЛЕВОГО РАДИУСА
К ИССЛЕДОВАНИЮ ЭЛЕКТРОННОГО ТРАНСПОРТА
В НАНОСТРУКТУРАХ
М.А. Пятаев
Мордовский государственный университет им. Н.П. Огарева, Саранск
Настоящая лекция посвящена применению модели потенциалов нулевого радиуса (точечных потенциалов) в некоторых задачах физики наноструктур. В лекции дается краткое ознакомительное введение в теорию потенциалов нулевого радиуса, и приводятся некоторые результаты, полученные с применением этой модели в задачах по исследованию проводимости наноструктур с короткодействующими примесями и точечными контактами.
Введение
Модель потенциала нулевого радиуса относится к там называемым явно решаемым моделям, при использовании которых стационарное уравнение Шредингера допускает точное аналитическое решение. Число явно решаемых моделей в квантовой механике весьма невелико, однако они играют важную роль в теории, поскольку точное решение может служить основой для понимания и описания физической природы явления, а в некоторых случаях дает и количественные результаты, обладающие достаточно широкой областью применимости. Модель точечных потенциалов может использоваться для описания примесей, дефектов и других короткодействующих потенциалов в любых системах. Впервые точечный потенциал был использован Э. Ферми в 1934 году. С тех пор модель приобрела значительную популярность, особенно в атомной и ядерной физике [1]. В последние годы метод начал широко применяться в физике наноструктур для моделирования одиночных короткодействующих возмущений. Еще одно применение потенциалов нулевого радиуса для моделирования контактов между структурами различной размерности, разработанное в последние несколько лет, будет описано ниже.
М

одель точечных потенциалов применима в том случае, когда радиус действия сил много меньше других характерных размеров системы, и в частности, много меньше дебройлевской длины волны частицы.
Ч
Рис.1. Прямоугольная потенциальная яма.
то же такое потенциал нулевого радиуса? В одномерном случае этот потенциал описывается хорошо известной
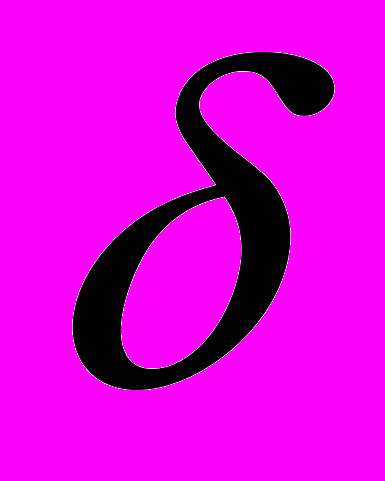 -функцией Дирака. Однако в двумерном и трехмерном случае корректное описание требует более сложной процедуры. Рассмотрим потенциальную яму, обладающую сферической (в трехмерном случае) или круговой (в двумерном случае) симметрией. Для определенности выберем яму с прямоугольным потенциальным профилем (Рис. 1), хотя конкретная форма профиля не столь существенна. Для получения точечного потенциала нам следует рассмотреть предел бесконечно узкой (
-функцией Дирака. Однако в двумерном и трехмерном случае корректное описание требует более сложной процедуры. Рассмотрим потенциальную яму, обладающую сферической (в трехмерном случае) или круговой (в двумерном случае) симметрией. Для определенности выберем яму с прямоугольным потенциальным профилем (Рис. 1), хотя конкретная форма профиля не столь существенна. Для получения точечного потенциала нам следует рассмотреть предел бесконечно узкой (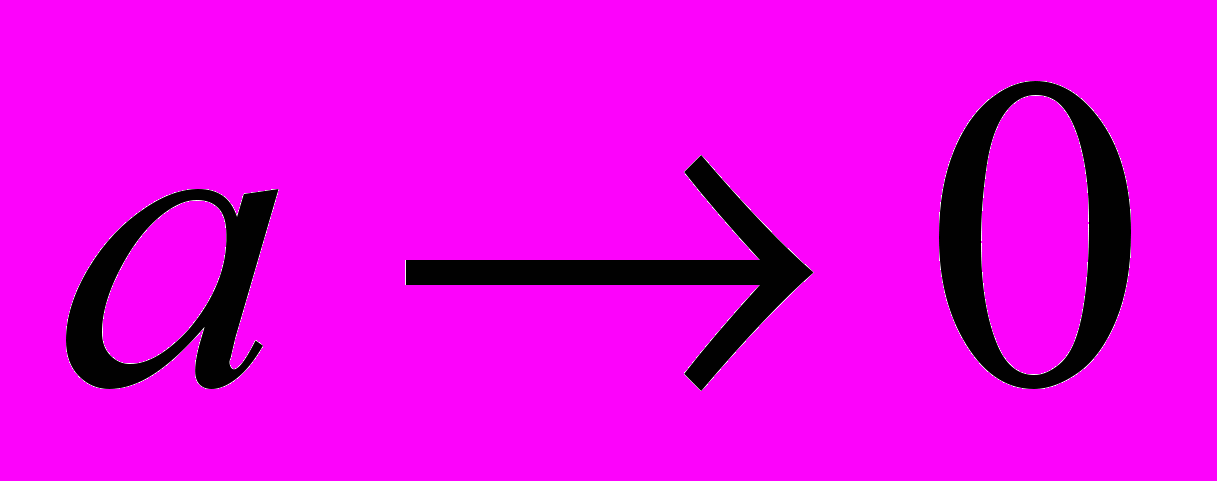 ) и бесконечно глубокой (
) и бесконечно глубокой (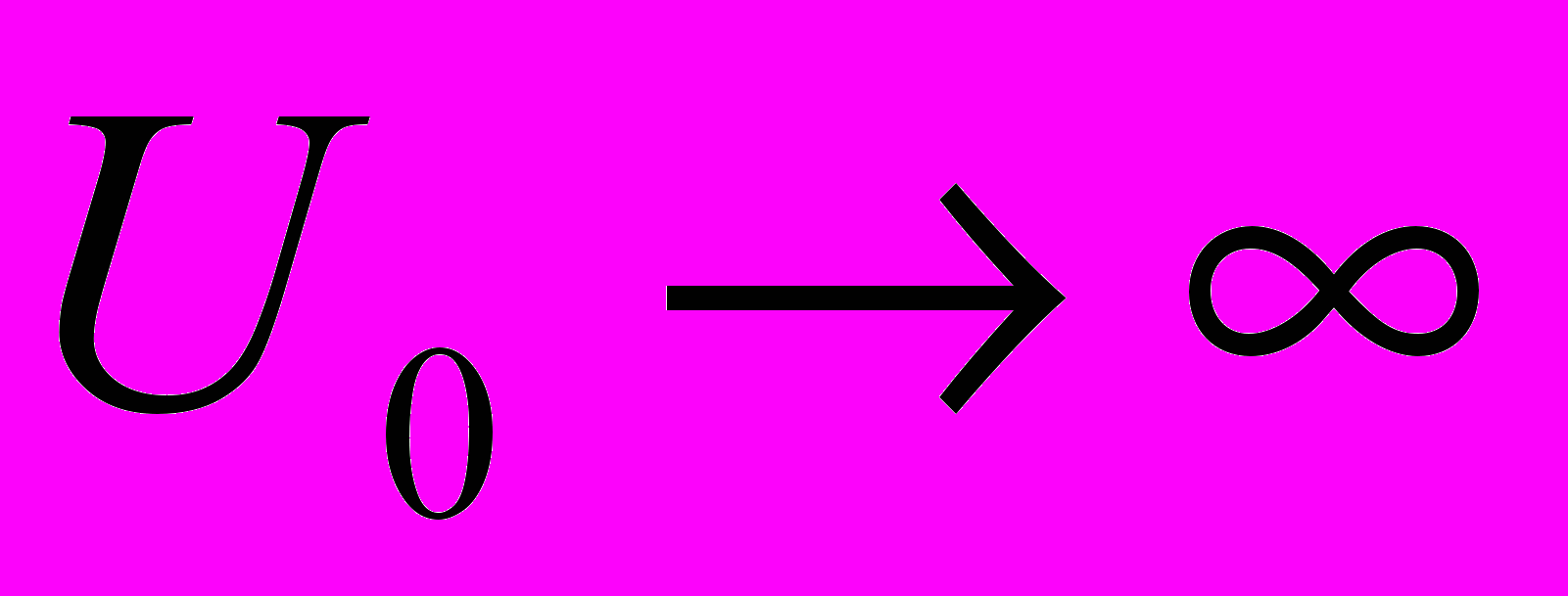 ) ямы. Выясним, по какому закону должна стремиться к бесконечности глубина ямы, чтобы в результате уровень
) ямы. Выясним, по какому закону должна стремиться к бесконечности глубина ямы, чтобы в результате уровень 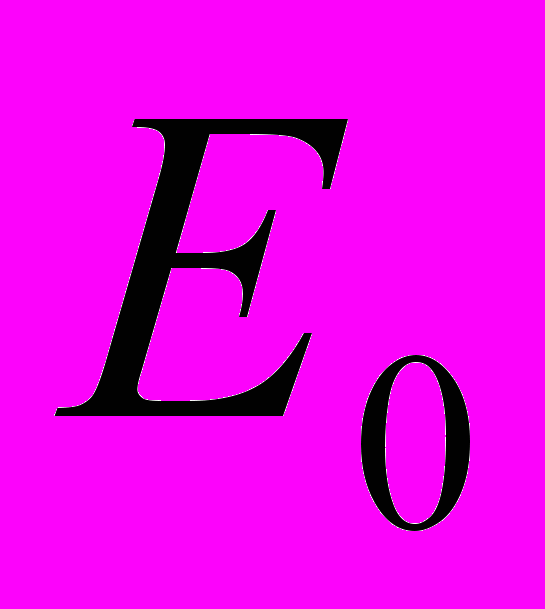 энергии связанного состояния частицы стабилизировался, то есть не стремился ни к нулю, ни к бесконечности. Отметим, что при стремлении ширины ямы к нулю, расстояние между уровнями возрастает, поэтому возможно добиться стабилизации лишь одного уровня. Таким образом, дискретный спектр одиночного точечного потенциала всегда имеет не более одного уровня. Как следует из решения соответствующего дифференциального уравнения, стабилизация уровня возможна только, если глубина ямы стремится к бесконечности по закону
энергии связанного состояния частицы стабилизировался, то есть не стремился ни к нулю, ни к бесконечности. Отметим, что при стремлении ширины ямы к нулю, расстояние между уровнями возрастает, поэтому возможно добиться стабилизации лишь одного уровня. Таким образом, дискретный спектр одиночного точечного потенциала всегда имеет не более одного уровня. Как следует из решения соответствующего дифференциального уравнения, стабилизация уровня возможна только, если глубина ямы стремится к бесконечности по закону 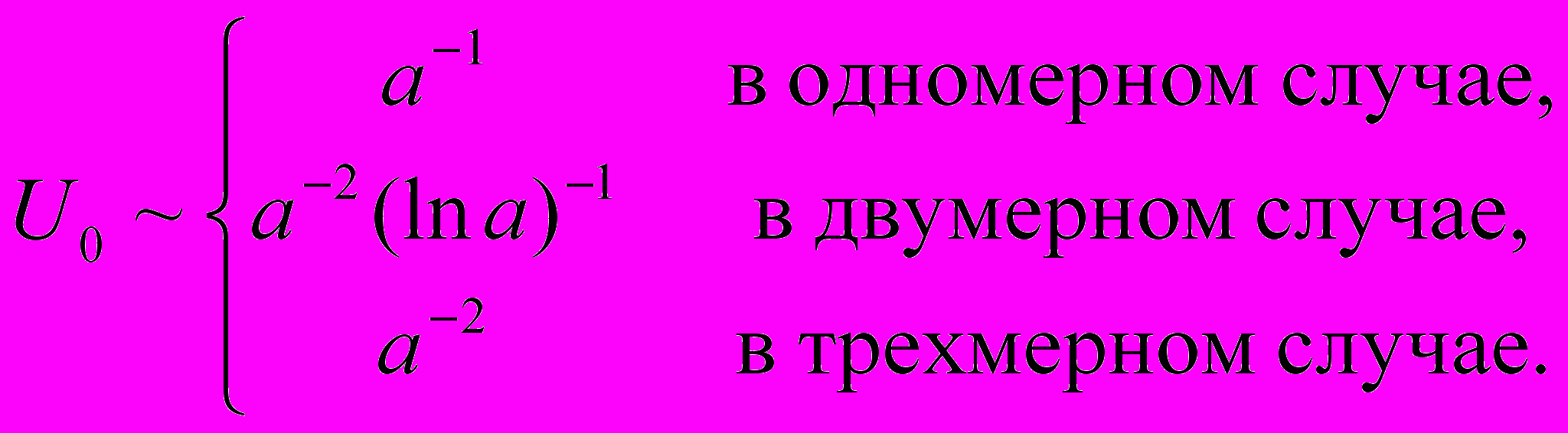 (1)
(1)Предел, получающийся в результате рассмотренного процесса, и называется точечным потенциалом. Отметим, что только в одномерном случае предел представляет из себя
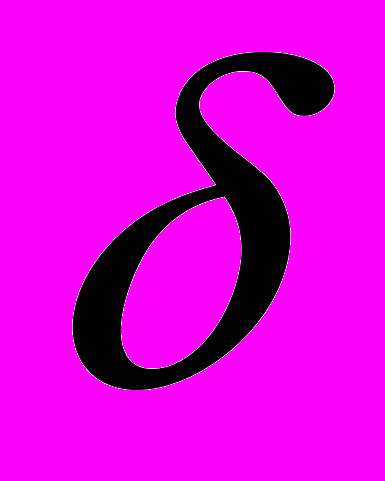 -функцию. В двумерном и трехмерном случае
-функцию. В двумерном и трехмерном случае 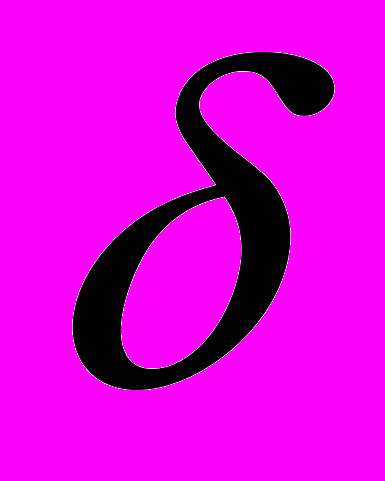 -функция была бы слишком сильным потенциалом, приводящим к падению частицы на центр.
-функция была бы слишком сильным потенциалом, приводящим к падению частицы на центр. Описание точечных потенциалов
Наиболее просто точечный потенциал может быть описан с помощью граничных условий, накладываемых на волновую функцию. В одномерном случае граничные условия связывают между собой скачок производной волновой функции и ее значение, в точке возмущения. В двумерном и трехмерном случае вид граничных условий оказывается несколько более сложным. Корректный вывод граничных условий можно получить с помощью теории расширений симметрических операторов [2,3]. Как следует из этой теории, волновая функция должна иметь сингулярность в окрестности точки
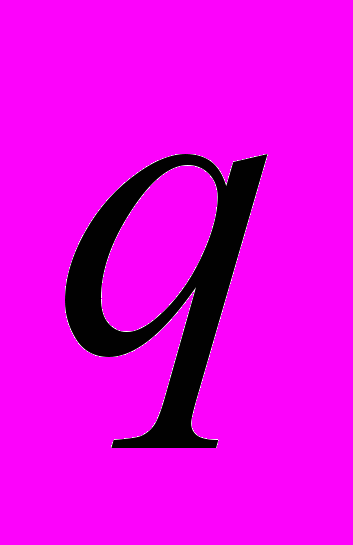 нахождения возмущения
нахождения возмущения  . (2)
. (2)Здесь
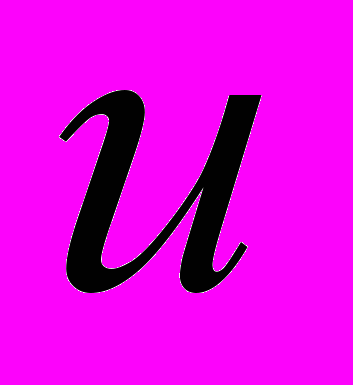 и
и 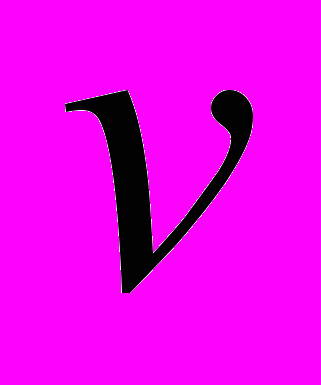 – комплексные коэффициенты, которые играют роль граничных параметров для волновой функции,
– комплексные коэффициенты, которые играют роль граничных параметров для волновой функции, 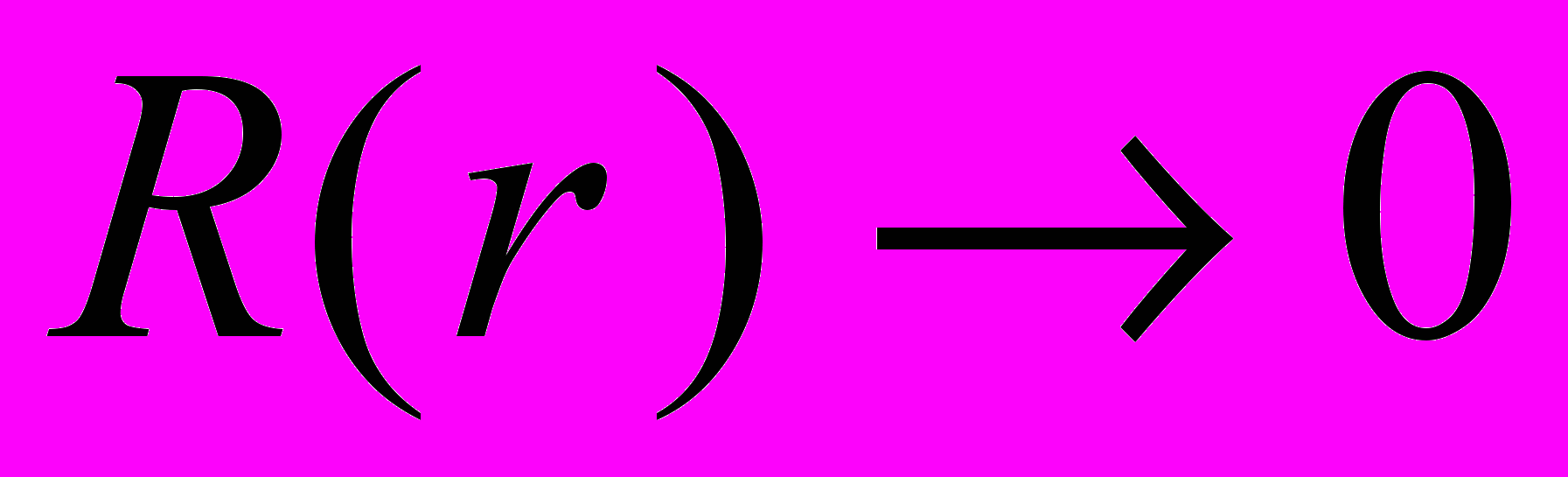 при
при  , а функция
, а функция  имеет вид
имеет вид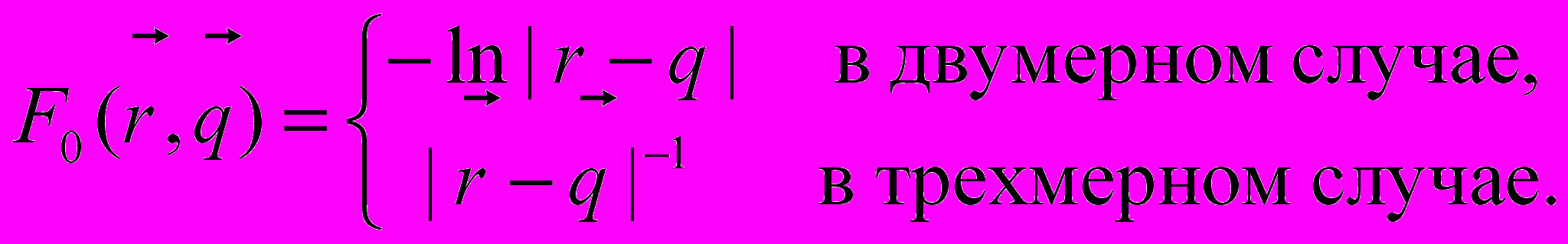 (3)
(3)Граничное условие представляет собой линейное отношение между коэффициентами в асимптотике волновой функции. В случае одиночного точечного потенциала это соотношение, имеет вид
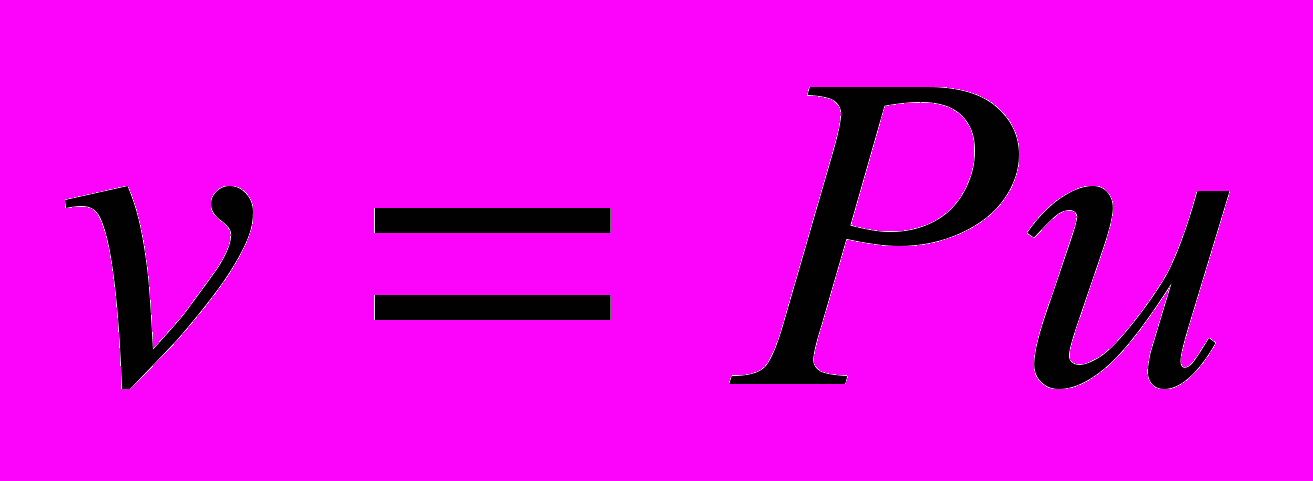 , (4)
, (4)где
 – действительное число, определяющее величину точечного потенциала. При этом предел
– действительное число, определяющее величину точечного потенциала. При этом предел 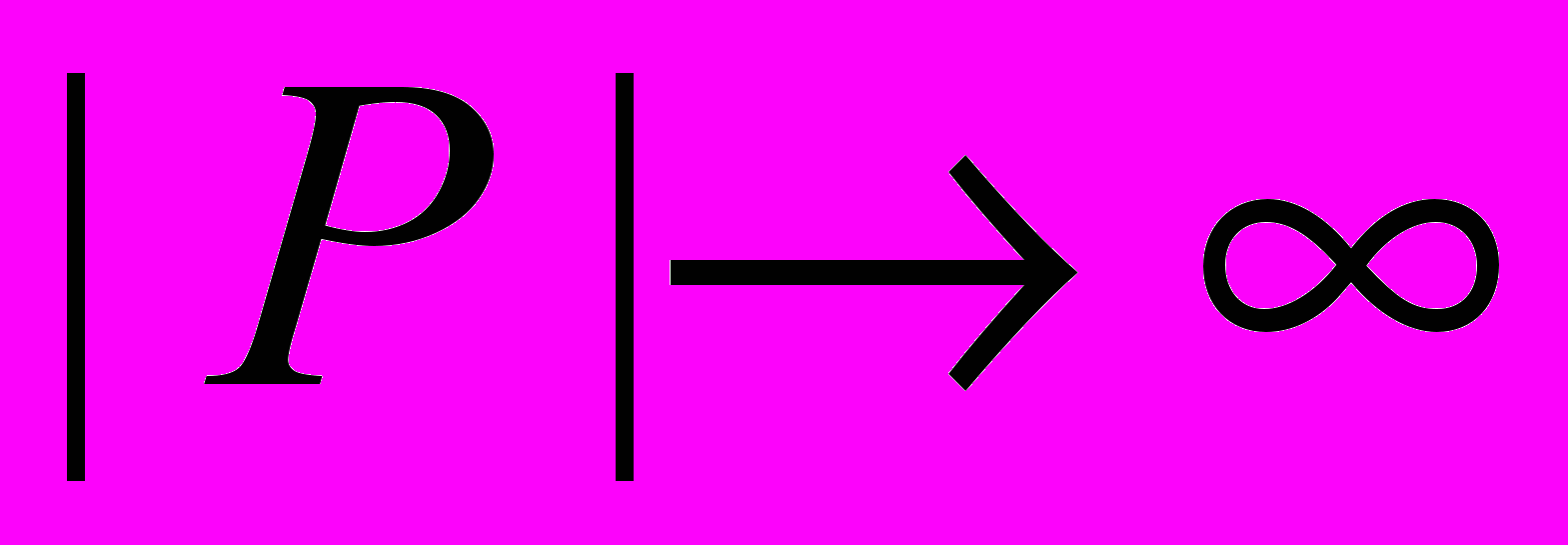 соответствует отсутствию точечного возмущения.
соответствует отсутствию точечного возмущения.Необходимость наличия сингулярности в волновой функции может быть понята с помощью менее строгого, но более простого рассуждения. Если рассматривать точечный потенциал как источник частиц, то становится ясно, что в двумерном и трехмерном случае плотность тока растекания вблизи точечного источника должна стремиться к бесконечности. Для этого волновая функция должна иметь сингулярность, описываемую формулой (3). Граничное условие означает в таком случае отсутствие тока через точечное возмущение, которое и должно иметь место, если потенциал описывает точечный дефект, а не источник частиц.
Одним из преимуществ рассматриваемой модели является возможность записать общий вид решения уравнения Шредингера практически сразу же после формулировки задачи. Оказывается, что решение уравнения Шредингера выражается через функцию Грина гамильтониана невозмущенной системы. Например, в случае непрерывного спектра волновая функция может быть записана в виде
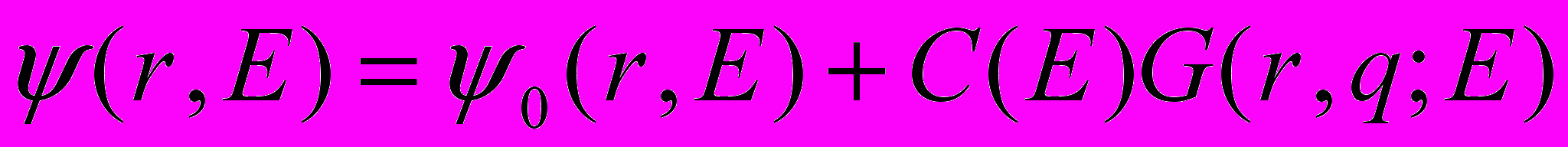 , (5)
, (5)где
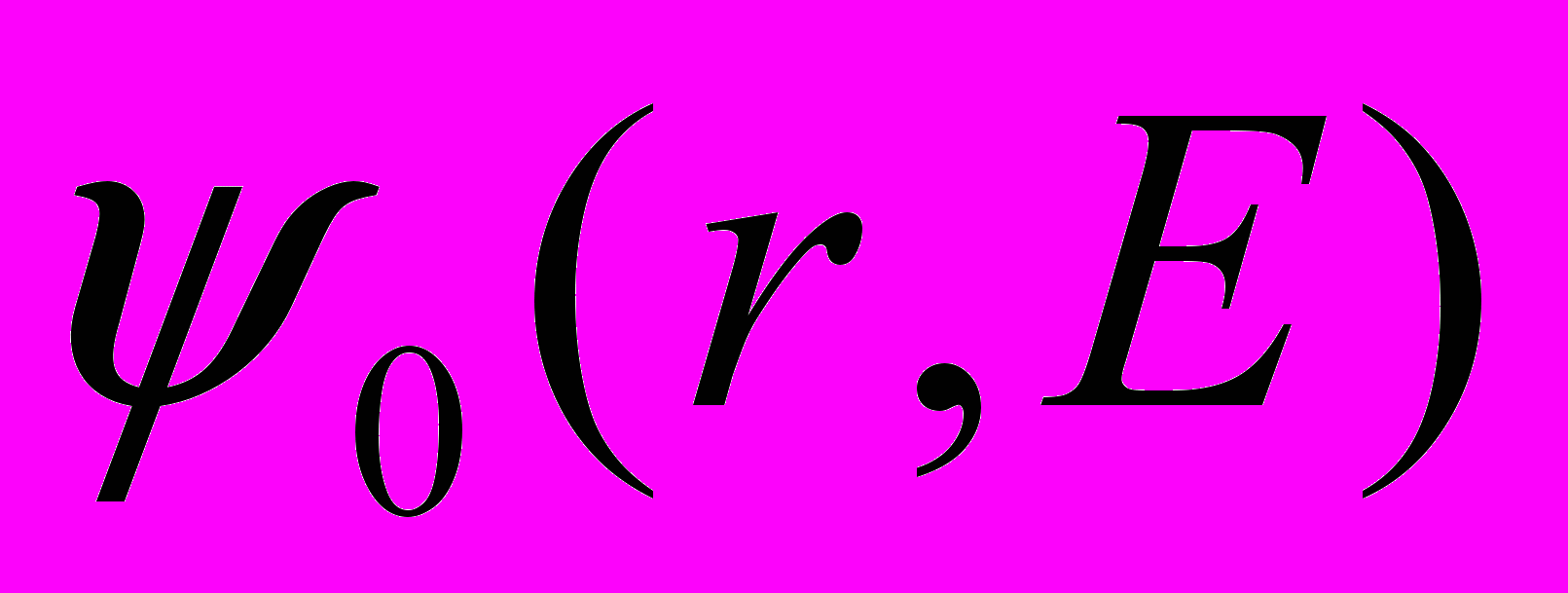 и
и 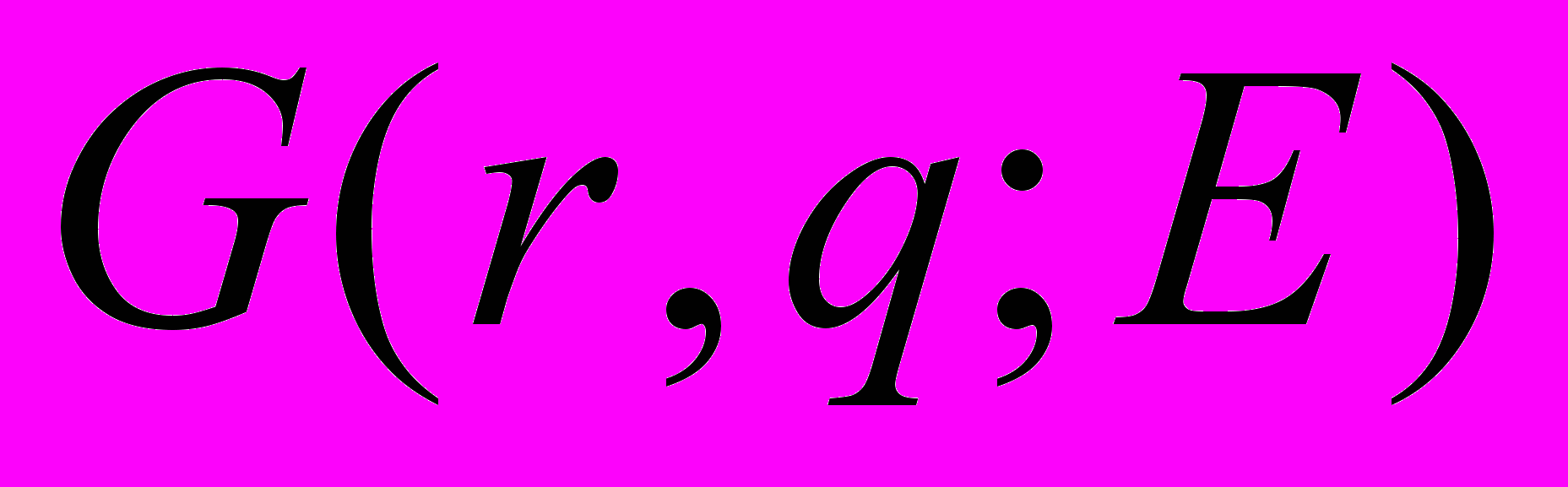 – собственная функция и функция Грина невозмущенного гамильтониана, а коэффициент
– собственная функция и функция Грина невозмущенного гамильтониана, а коэффициент  не зависит от координат и определяется из граничных условий. Решение уравнения Шредингера в этом случае сводится к определению коэффициента
не зависит от координат и определяется из граничных условий. Решение уравнения Шредингера в этом случае сводится к определению коэффициента  .
.Кондактанс нанострукутр с точечными примесями
Рассмотрим теперь некоторые результаты, полученные с помощью потенциалов нулевого радиуса при исследовании проводящих свойств наноструктур. Одной из особенностей электронного транспорта в наноструктурах является баллистический транспортный режим, в котором электрон пролетает через всю систему, не испытывая рассеяния. В таком случае описание транспортных свойств системы с помощью таких локальных характеристик, как, например, удельная проводимость становится невозможным, потому что, например, сопротивление двух последовательно соединенных проводников оказывается отличным от суммы их сопротивлений. Поэтому для характеристики проводящих свойств нанострукутр принято использовать величину, обратную полному сопротивлению системы, называемую кондактансом. Более подробную информацию читатель может найти в книге [4].
Большинство теоретических исследований электронного транспорта в наноструктурах посвящено нахождению зависимости кондактанса системы от химического потенциала. Отметим, что особенностью низкоразмерных систем является возможность управления концентрацией носителей заряда с помощью дополнительных электродов, прикладываемых к структуре и называемых затворами. Изменение концентрации приводит, в свою очередь, к изменению химического потенциала, поэтому для наноструктур оказывается актуальным теоретическое исследование зависимости различных физических величин от химического потенциала. На практике эти зависимости воспроизводятся путем изменения напряжения на затворе.
Как известно [4], зависимость кондактанса квазиодномерных наноструктур от химического потенциала при нулевой температуре носит ступенчатый характер. Каждая ступень соответствует включению новой подзоны размерного квантовая в процесс переноса заряда. Высота каждой ступени кратна величине
 , называемой квантом кондактанса. Увеличение температуры приводит к сглаживанию ступеней квантования.
, называемой квантом кондактанса. Увеличение температуры приводит к сглаживанию ступеней квантования. Как следует из теории Ландауэра-Бюттикера, при наличии рассеяния кондактанс системы при нулевой температуре выражается через коэффициенты прохождения электрона, поэтому основная задача состоит в нахождении коэффициентов прохождения из уравнения Шредингера.

Рис. 2. (a): кондактанс
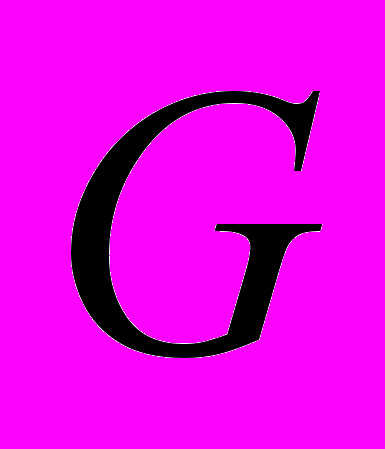 квантового цилиндра с одиночной примесью как функция химического потенциала
квантового цилиндра с одиночной примесью как функция химического потенциала  ; (b): кондактанс цилиндра при наличии двух примесей, расположенных на расстоянии
; (b): кондактанс цилиндра при наличии двух примесей, расположенных на расстоянии 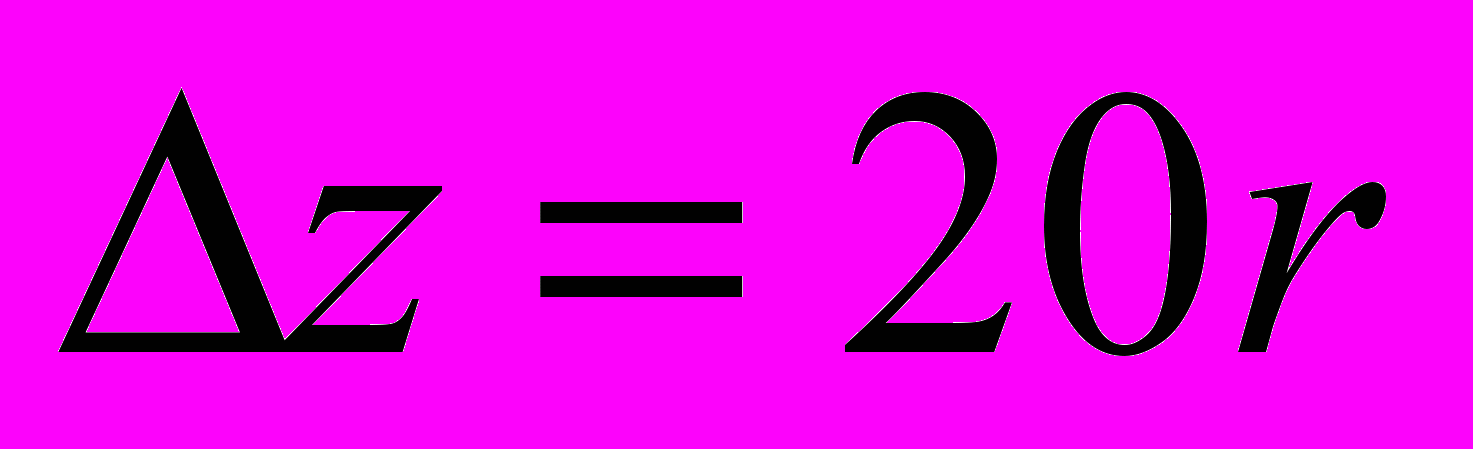 , где
, где 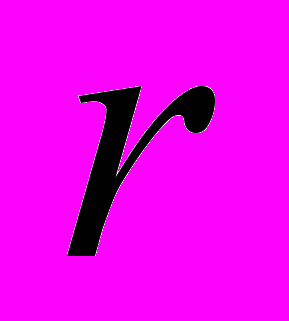 – радиус цилиндра,
– радиус цилиндра, 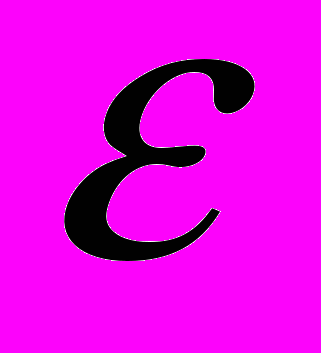 – характерная энергия системы. Пунктирной линией показан кондактанс невозмущенного цилиндра.
– характерная энергия системы. Пунктирной линией показан кондактанс невозмущенного цилиндра.Наличие одиночной точечной примеси приводит к появлению провалов на ступенях квантования (Рис. 2а). Провалы соответствуют резонансному отражению электронов от примеси. Увеличение силы точеного потенциала приводит к тому, что провалы смещаются в область меньших энергий, а их ширина увеличивается. Как показывает анализ, максимальная глубина каждого провала не превышает одного кванта кондактанса. При наличии нескольких примесей на графике появляются осцилляции, связанные с интерференцией электронных волн, многократно отраженных от примесей (Рис. 2b).
Следует отметить, что провалы появляются только на тех ступенях, для которых соответствующая волновая функция не обращается в ноль в точке нахождения примеси. Например, если удерживающий потенциал в квантовой проволоке обладает плоскостью симметрии, то поперечная составляющая волновой функции будет либо четной, либо нечетной функцией. При расположении примеси на оси такой проволоки рассеиваются только состояния с четными волновыми функциями, так как нечетные волновые функции имеют узел в точке нахождения примеси. Это, в частности, может приводить к возникновению фотогальванического эффекта при облучении структуры инфракрасным излучением [5].
Контакты между структурами различной размерности
Еще одним применением потенциалов нулевого радиуса является моделирование контактов между системами различной размерности. Теория потенциалов нулевого радиуса позволяет построить в этом случае явно решаемую модель с помощью граничных условий, накладываемых на волновую функцию в точке контакта. Роль граничных параметров на поверхности в этом случае играют коэффициенты асимптотики волновой функции, а в одномерных проводниках – волновая функция и ее производная. Граничные условия представляют собой линейные соотношения между граничными параметрами. Общий вид этих соотношений может быть определен из закона сохранения тока.

Рис. 3. Зависимость коэффициента прохождения
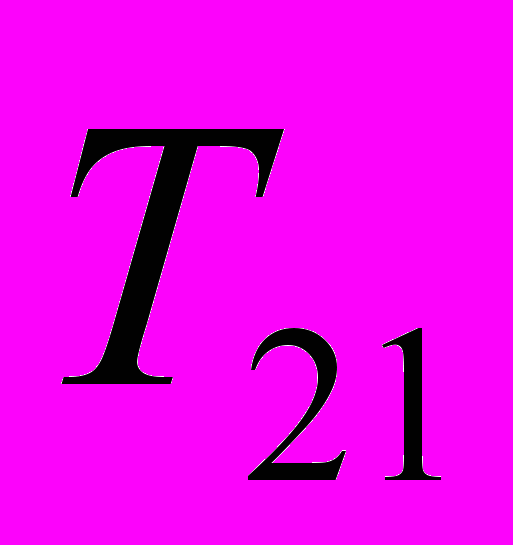 через квантовую сферу от безразмерного параметра
через квантовую сферу от безразмерного параметра  , где
, где 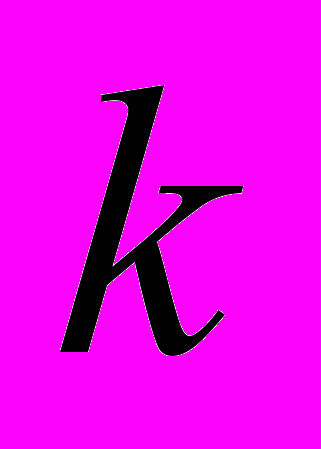 – волновое число электрона,
– волновое число электрона, 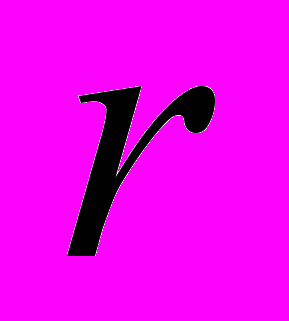 – радиус сферы. (а): угол между контактами
– радиус сферы. (а): угол между контактами  , (b): контакты присоединены диаметрально противоположно.
, (b): контакты присоединены диаметрально противоположно.Рассмотрим в качестве примера кондактанс квантовой сферы с двумя присоединенными одномерными проводниками [6,7]. Поскольку в одномерных проводниках имеется единственная электронная мода, кондактанс системы не превышает одного кванта кондактанса. В случае общего положения проводников коэффициент прохождения обращается в ноль точках дискретного спектра электронов на сфере, поэтому кондактанс осциллирует как функция химического потенциала (Рис. 3).
В окрестности каждого нуля кондактанса имеется пик, высота которого достигает единицы (Рис. 3а). Этот пик и расположенный рядом провал представляют собой асимметричный резонанс Фано [8]. Асимметричная кривая резонанса Фано является наиболее общей формой резонанса в квантовомеханической системе, в то время как симметричный резонанс Брейта-Вигнера оказывается частным случаем. Одной из особенностей резонансов Фано является возможность коллапса, при котором ширина пика и провала на графике уменьшается, сами пик и провал сближаются, а затем исчезают. Отметим, что амплитуда пика и провала при сближении остается неизменной. При коллапсе резонансов Фано возникают дискретные уровни, покруженные в непрерывной спектр, то есть состояния, в которых электрон локализован в ограниченной области пространства, несмотря на то, что его энергия лежит в непрерывном спектре.
В рассматриваемой системе коллапс резонансов Фано наблюдается при диаметрально противоположном присоединении проводников (Рис. 3b). При этом в транспорте на сфере участвуют только состояния с нулевым орбитальным моментом, а для всех остальных состояний волновые функции обращаются в ноль в обеих точках контактов, и такие состояния образуют дискретные уровни, погруженные в непрерывный спектр. Отметим, что коллапс резонансов Фано наблюдается также и в более простой системе – квантовом кольце с присоединенными проводниками [9]. Наличие резких резонансов в электронном транспорте делает подобные системы перспективными с точки зрения применения в приборах наноэлектроники, таких как резонансный туннельный диод или одноэлектронный транзистор. Модель точечных потенциалов позволяет аналитически исследовать свойства подобных систем, в частности, влияние положения контактов и примесей на параметры резонансов.
- Демков Ю.Н., Островский В.Н. Метод потенциалов нулевого радиуса в атомной физике. Л.: Изд-во Ленинградского ун-та. 1975 г.
- Павлов Б.С. ТМФ 59, 345 (1984).
- Bruning J., Geyler V.A. J. Math. Phys. 44, 371 (2003).
- Демиховский В.Я., Вугальтер Г.А. Физика квантовых низкоразмерных структур. М.: Логос. 2000 г.
- Pyataev M.A., Ulyanov S.N. Phys. Rev. B 79, 235428 (2009).
- Bruning J., Geyler V.A., Margulis V.A., Pyataev M.A. J. Phys. A: Math. Gen. 35, 4239 (2002).
- Гейлер В.А., Маргулис В.А., Пятаев М.А. ЖЭТФ 124, 851 (2003).
- Fano U. Phys. Rev. 124, 1866 (1961).
- Гейлер В.А., Демидов В.В., Маргулис В.А. ЖТФ, 73, 1 (2003).
СПЕКТР И БАЛЛИСТИЧЕСКИЙ ТРАНСПОРТ ЭЛЕКТРОНОВ
В ПОЛУПРОВОДНИКОВОЙ НАНОТРУБКЕ
И.А. Кокурин
Мордовский государственный университет им. Н.П. Огарева, Саранск
Цель настоящей работы – исследовать одноэлектронный спектр и баллистический транспорт двумерного электронного газа (ДЭГ) на цилиндрической поверхности с учетом спин-орбитального взаимодействия (СОВ), определяемого характерными для ДЭГ вкладами Рашбы [1] и Дрессельхауза [2]. Подобные нанотрубки могут быть получены сворачиванием напряженных гетероструктур на основе полупроводников A3B5 [3].
Для структур, выращенных в направлении [001], явно найден спектр одномерных подзон. Показано, что в зависимости от соотношения между расщеплением, вызванным СОВ Рашбы и Дрессельхауза, а также зеемановским расщеплением в магнитном поле, спектр одномерных подзон нанотрубки может иметь разнообразную структуру. Учет СОВ Дрессельхауза вносит асимметрию в спектр одномерных подзон по сравнению с системами, где преобладает СОВ Рашбы [4]. Поскольку гамильтониан Дрессельхауза зависит от направления кристаллографических осей, а ДЭГ формально можно свернуть в нанотрубку множеством способов, спектр существенно зависит от ориентации оси нанотрубки относительно кристаллографических осей. Изменяя константу Рашбы (возможность ее изменения была показана в [5,6] для планарных структур с ДЭГ) или магнитное поле можно управлять спектром, а следовательно, и транспортными режимами системы.
Обобщая транспортный формализм Ландауэра-Бюттикера на случай одномерных подзон с произвольным числом локальных экстремумов, получены выражения для баллистического кондактанса и дифференциального коэффициента термоэдс. Изучены зависимости кондактанса и термоэдс нанотрубки от химического потенциала электронного газа, магнитного поля, геометрических размеров системы, констант СОВ и температуры. Показана сильная зависимость транспортных характеристик от ориентации оси нанотрубки относительно кристаллографических осей.
Работа выполнена при поддержке АВЦП «Развитие научного потенциала высшей школы» (проект № 2.1.1/2656).
1. Ю.А. Бычков, Э.И. Рашба, Письма в ЖЭТФ 39, 66 (1984).
2. G. Dresselhaus, Phys. Rev. 100, 580 (1955).
3. V.Ya. Prinz, Physica E 23, 260 (2004); ibid. 24, 54 (2004).
4. Л.И. Магарилл, Д.А. Романов, А.В. Чаплик, ЖЭТФ 113, 1411 (1998).
5. J. Nitta, T. Akazaki, H. Takayanagi et al., Phys. Rev. Lett. 78, 1335 (1997).
6. D. Grundler, Phys. Rev. Lett. 84, 6074 (2000).
МАГНИТНЫЙ МОМЕНТ ДВУМЕРНОГО ЭЛЕКТРОННОГО ГАЗА С УЧЕТОМ СПИН-ОРБИТАЛЬНОГО ВЗАИМОДЕЙСТВИЯ
В.А. Миронов
Мордовский государственный университет им. Н.П. Огарева, Саранск
В работах посвященных исследованиям энергетического спектра двумерного электронного газа (ДЭГ) в присутствии спин-орбитального взаимодействия (СОВ) в модели Рашбы показано, что во внешнем магнитном поле появляются две системы уровней Ландау. Такое изменение в электронном спектре приводит к существенному изменению транспортных [1] и равновесных [2] характеристик электронного газа в низкоразмерных системах.
Для гетероструктур на основе GaAs в [2] найден электронный спектр в магнитном поле, нормального к плоскости двумерного электронного газа, и исследована его магнитная восприимчивость при слабом магнитном поле B и температуре газа T=0 при μ=const.
В настоящей работе в общем случае произвольного магнитного поля получено аналитическое выражение для магнитного момента M ДЭГ с учетом СОВ в модели Рашбы при постоянном числе электронов N в рассматриваемой системе.
Зависимость магнитного момента M от магнитного поля B имеет характер осцилляций с изменяющейся амплитудой. Появление осцилляций связано с переменным числом электронов на частично заполненном верхнем уровне лестницы. А изменение амплитуды обусловлено тем, что этот уровень может принадлежать различным "спиновым" лестницам уровней Ландау в зависимости от N, B и параметров энергетического спектра электронов. Кроме того, осцилляции являются периодичными по фактору заполнения, а значит и по обратному полю.
Случай магнитного момента при N=const реализуется на эксперименте, поэтому мы можем сравнить наши расчеты с экспериментальными результатами M.A. Wilde и соавторов [3]. Сравнение этих результатов показывает, что вычисленный нами магнитный момент хорошо воспроизводит основные характерные черты экспериментальных результатов, такие как зависимость амплитуды осцилляций от магнитного поля, наличие дополнительных скачков в намагниченности (на фоне основных, предсказанных Пайерлсом) при нечетных значениях фактора заполнения.
1. X.F. Wang, P. Vasilopoulos // Phys. Rev. B. – 2003. – V. 67. – P. 085313.
2. Yu.A. Bychkov, E.I. Rashba // J. Phys. C: Solid State Phys. – 1984. – P. 17. – P. 6039.
3. M.A. Wilde et al. // Phys. Rev. B. – 2006 – V. 73. – P. 125325.
ФОТОТОК В КВАНТОВОМ КОЛЬЦЕ С АСИММЕТРИЧНО ПРИСОЕДИНЕННЫМИ ПРОВОДНИКАМИ
А.А. Григорькин1, М.А. Пятаев2, С.Н. Ульянов2,
1Петербургский институт ядерной физики им. Б.П. Константинова, Санкт-Петербург
2Мордовский государственный университет им. Н.П. Огарева, Саранск
В работе исследуется электронный транспорт в квантовом кольце радиуса
 с присоединенными проводниками, находящемся в поле внешнего электромагнитного излучения. Кольцо и проводники считаются одномерными. Система находится во внешнем постоянном магнитном поле, направленном перпендикулярно плоскости кольца. Точки присоединения контактов расположены на кольце несимметрично, поэтому у системы отсутствует центр инверсии. При освещении кольца циркулярно поляризованным излучением в системе возникает постоянный ток, обусловленный взаимодействием электронов с бегущей электромагнитной волной на кольце.
с присоединенными проводниками, находящемся в поле внешнего электромагнитного излучения. Кольцо и проводники считаются одномерными. Система находится во внешнем постоянном магнитном поле, направленном перпендикулярно плоскости кольца. Точки присоединения контактов расположены на кольце несимметрично, поэтому у системы отсутствует центр инверсии. При освещении кольца циркулярно поляризованным излучением в системе возникает постоянный ток, обусловленный взаимодействием электронов с бегущей электромагнитной волной на кольце. Для моделирования контактов в работе использована теория потенциалов нулевого радиуса. Для нахождения тока используется неравновесная функция распределения, которая вычисляется с помощью формализма Кубо во втором порядке теории возмущений.
В результате в работе получено следующее выражение для фотоиндуцированного тока в кольце:
 , (1)
, (1)где
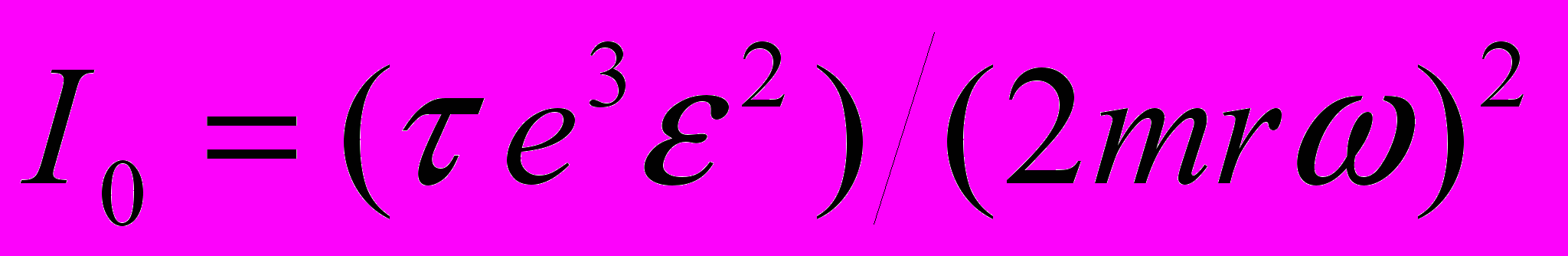 – характерный ток в системе,
– характерный ток в системе,  – частота падающего излучения,
– частота падающего излучения, 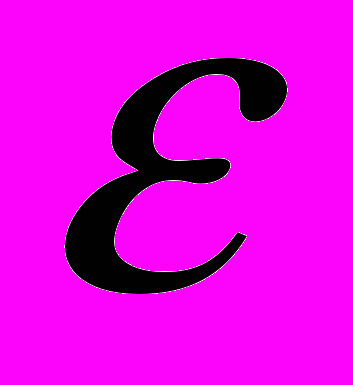 – амплитуда электрического поля в волне,
– амплитуда электрического поля в волне, 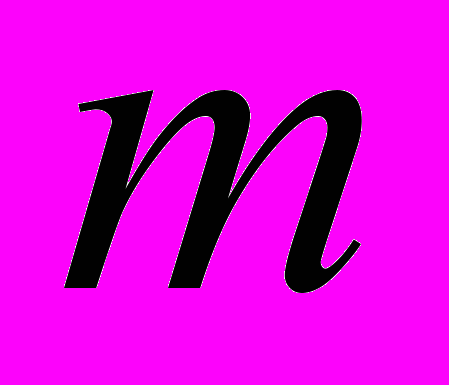 – эффективная масса электрона,
– эффективная масса электрона,  – время релаксации,
– время релаксации, 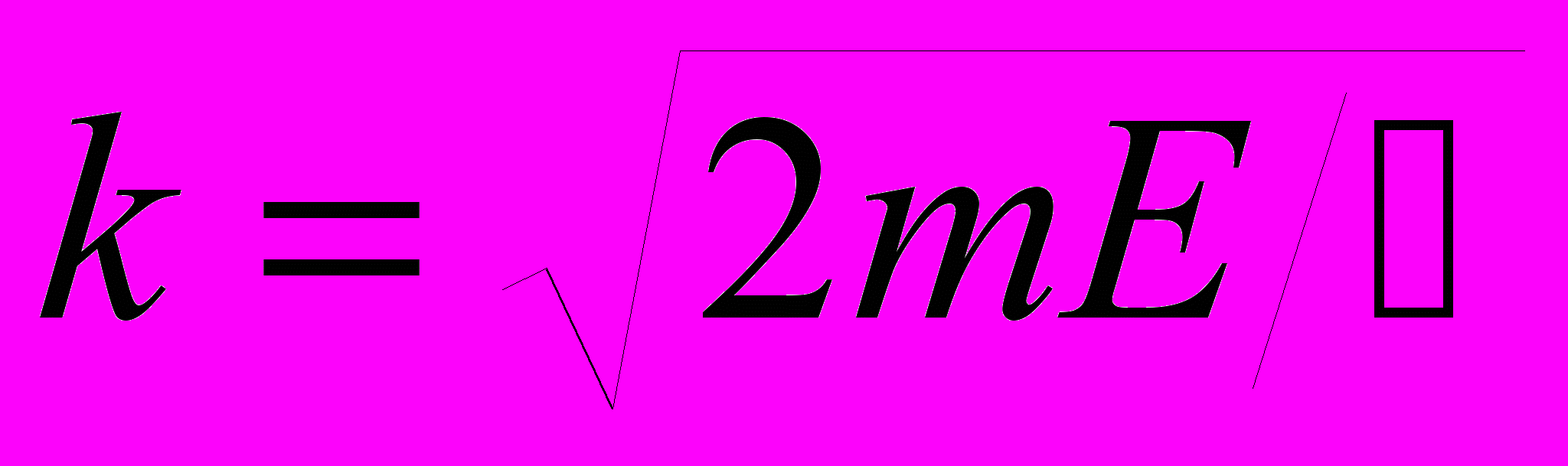 – волновое число электрона,
– волновое число электрона,  и
и 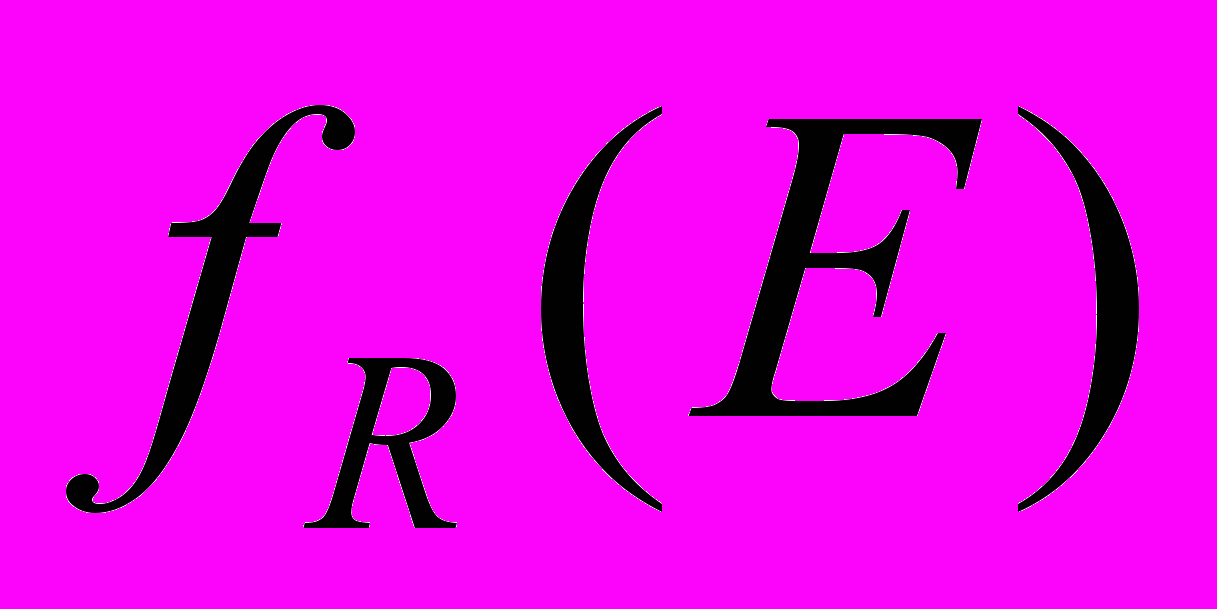 – поправки к функции распределения электронов, падающих на кольцо из левого и правого провода соответственно,
– поправки к функции распределения электронов, падающих на кольцо из левого и правого провода соответственно, 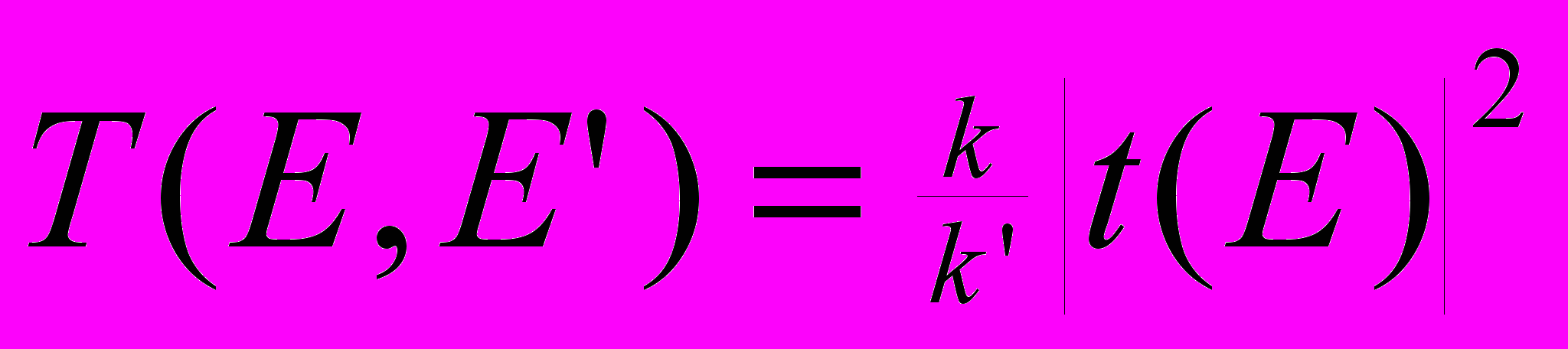 – коэффициент прохождения при неупругом рассеянии,
– коэффициент прохождения при неупругом рассеянии, 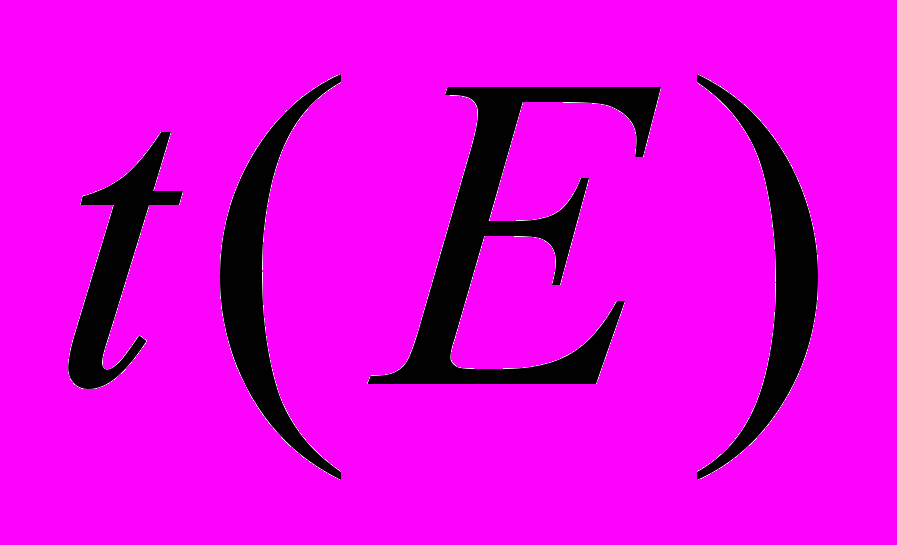 – амплитуда упругого рассеяния.
– амплитуда упругого рассеяния.В работе получены выражения для поправок к функции распределения и исследована зависимость тока от положения контактов, химического потенциала электронов, внешнего магнитного поля и частоты падающего излучения. Показано, что направление фототока может меняться при изменении параметров системы.
Работа выполнена при поддержке целевой программы «Развитие научного потенциала высшей школы (2009-2010гг.)» (грант № 2.1.1/2656).
ЭЛЕКТРОННЫЙ ТРАНСПОРТ В ЦЕПОЧКЕ КВАНТОВЫХ КОЛЕЦ
М.А. Кокорева, М.А.Пятаев
Мордовский государственный университет им. Н.П. Огарева, Саранск
В работе исследованы спектральные и транспортные свойства периодической квазиодномерной системы, состоящей из цепочки квантовых колец, имеющих точечные контакты друг с другом. Система помещена в магнитное поле, перпендикулярное плоскости колец.
С помощью теоремы Блоха и теории потенциалов нулевого радиуса получено следующее уравнение для определения электронного энергетического спектра системы:
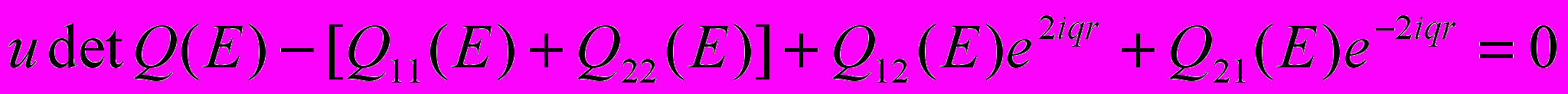 . (1)
. (1)Здесь
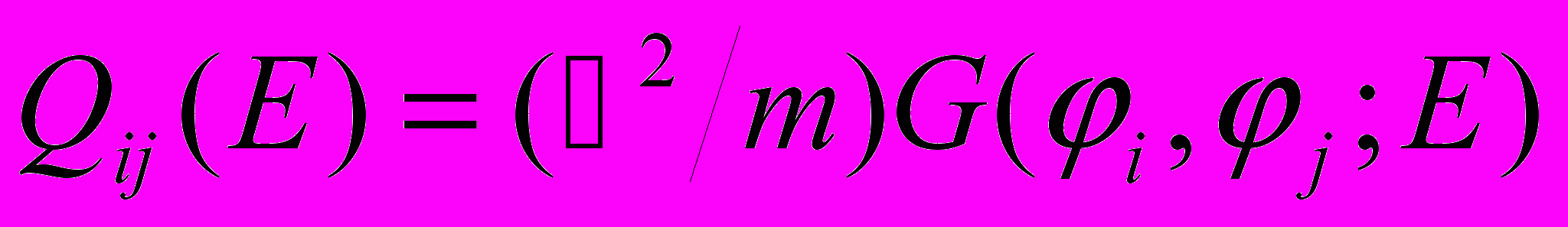 – матрица, получающаяся из функции Грина гамильтониана кольца,
– матрица, получающаяся из функции Грина гамильтониана кольца,  и
и  – углы, задающие положения контактов,
– углы, задающие положения контактов, 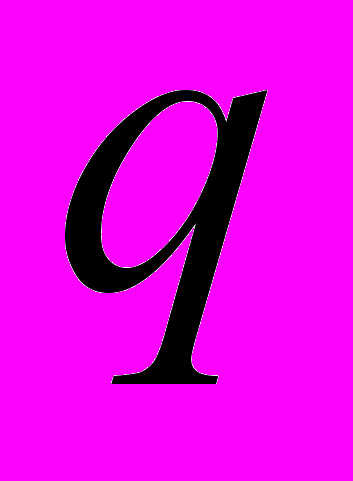 – квазиимпульс,
– квазиимпульс, 
 – радиус кольца,
– радиус кольца,  – энергия электрона,
– энергия электрона, 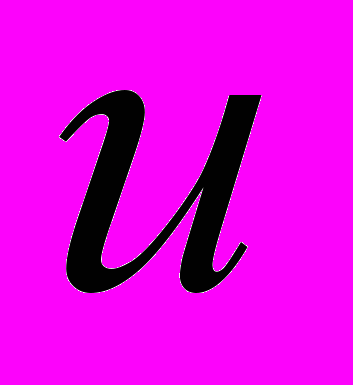 – параметр контакта,
– параметр контакта, 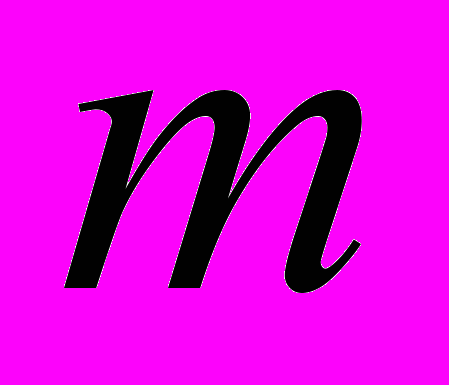 – эффективная масса электрона. Явный вид функции Грина приведен, например, в [1].
– эффективная масса электрона. Явный вид функции Грина приведен, например, в [1].С использованием найденного спектра определена зависимость кондактанса системы от энергии Ферми. Показано, что в общем случае спектр имеет зонную структуру, причем перекрытия зон не наблюдается, таким образом, уровень Ферми всегда пересекает не более одной зоны, и кондактанс системы не превышает одного кванта кондактанса. Кроме того, в спектре могут существовать дискретные уровни в запрещенной зоне. Этим уровням соответствуют электроны, локализованные на отдельных кольцах и не участвующие в переносе электрического заряда. Кратность вырождения уровней равна числу состояний в зоне Бриллюэна.
Ширина запрещенных зон в спектре меняется в зависимости от величины внешнего магнитного поля и от параметров контактов. В частности, при ослаблении связи между кольцами ширина запрещенных зон увеличивается, а разрешенных уменьшается. В пределе, соответствующем изолированным кольцам (
 ), разрешенные зоны вырождаются в дискретные уровни изолированного кольца.
), разрешенные зоны вырождаются в дискретные уровни изолированного кольца. Интересный эффект наблюдается при потоке магнитного поля, равном половине кванта магнитного потока. В этом случае все зоны спектра вырождаются в дискретные уровни, и кондактанс системы оказывается равным нулю, то есть наблюдается локализация электронов на кольцах в магнитном поле. Отметим, что при полуцелом потоке магнитного поля через кольцо, проводимость одиночного кольца с присоединенными проводниками также обращается в ноль [1].
Работа выполнена при поддержке целевой программы «Развитие научного потенциала высшей школы (2009-2010гг.)» (грант № 2.1.1/2656).
1. Гейлер В.А., Демидов В.В., Маргулис В.А. ЖТФ, 73, 1 (2003).
МАГНИТООПТИКА КВАНТОВЫХ ТОЧЕК
С ВОДОРОДОПОДОБНЫМИ ПРИМЕСНЫМИ ЦЕНТРАМИ
В.Д. Кревчик, А.В. Разумов, В.А. Гришанова, А.В. Калинина
Пензенский государственный университет, Пенза
Теоретически исследовано примесное магнитооптическое поглощение в квазинульмерной структуре с водородоподобными примесными центрами (ВПЦ). Теоретический подход основан на решении задачи о связанных состояниях электрона, локализаванного на ВПЦ в квантовой точке с параболическим потенциалом конфайнмента. В приближении эффективной массы для случая сильного магнитного поля, когда магнитная длина много меньше эффективного боровского радиуса соответствующая спектральная задача решена аналитически. В дипольном приближении рассчитаны коэффициенты примесного магнитооптического поглощения для случаев продольной и поперечной по отношению к направлению магнитного поля поляризации света. Показано, что для спектра примесного магнитооптического поглощения 0D-структур характерен квантоворазмерный эффект Зеемана. Найдено, что учет дисперсии радиуса квантовых точек в 0D-структуре приводит к размытию резонансных пиков в дублете. Установлено, что уширение полос в спектрах магнитооптического поглощения 0D-структур с ВПЦ связано с увеличением заряда остова ВПЦ. Выявлен дихроизм примесного магнитооптического поглощения, связанный с изменением правил отбора для магнитного квантового числа. Проведен анализ спектров примесного магнитооптического поглощения 0D-структур с D- - и ВПЦ, который позволил идентифицировать оптические переходы, связанные с фотоионизацией соответствующих примесных центров. Показано, что в случае 0D-структур с ВПЦ величина коэффициента поглощения в пиках дублета на два порядка больше соответствующей величины для 0D-структуры с D- -центрами.
АНОМАЛЬНЫЙ КВАНТОВОРАЗМЕРНЫЙ ЭФФЕКТ ЗЕЕМАНА
В СПЕКТРАХ МАГНИТООПТИЧЕСКОГО ПОГЛОЩЕНИЯ КВАЗИНУЛЬМЕРНЫХ СТРУКТУР С D−-ЦЕНТРАМИ
В.Д. Кревчик, А.В. Разумов, В.А. Гришанова, А.В. Калинина
Пензенский государственный университет, Пенза
В легированных полупроводниковых наноструктурах важным параметром, определяющим концентрацию носителей заряда, является энергия ионизации примесных центров. Возможность управлять этим параметром путем варьирования величины внешнего магнитного поля исследовалась как теоретически [1, 2], так и экспериментально [3] в случае D−-состояний в многоямной квантовой структуре GaAs/GaAlAs. Было показано [2, 3], что в магнитном поле вследствие гибридного квантования энергия связи D−-состояния в квантовой яме может в несколько раз превышать свое объемное значение (эффект магнитного вымораживания примеси). Следует ожидать, что в квантовых точках (КТ) из-за размерного ограничения по всем трем пространственным направлениям, эффект магнитного вымораживания D−-состояний будет более значительным. В КТ D−-состояния в условиях внешнего магнитного поля теоретически исследовались в работе [4], однако без учета спиновых состояний локализованного электрона. В данной работе в модели потенциала нулевого радиуса в приближении эффективной массы исследовано влияние внешнего магнитного поля на D−-состояния в КТ с параболическим потенциалом конфайнмента. Получено дисперсионное уравнение, определяющее зависимость энергии связи D−-состояния от величины магнитного поля и спиновых состояний локализованного электрона. Показано, что эффект вымораживания D−-состояний в КТ зависит от ориентации спина локализованного электрона и имеет место в случае антипараллельной ориентации спина относительно направления магнитного поля. Найдено, что спиновые состояния локализованного на D−-центре электрона проявляются в спектрах примесного поглощения 0D-структуры в виде аномального квантоворазмерного эффекта Зеемана, а также в зависимости порога примесного поглощения от гиромагнитного отношения.
- Кревчик В.Д., Грунин А.Б., Евстифеев Вас. В. // Известия высших учебных заведений. Физика. – 2005. - № 5. - с.25.
- Кревчик В.Д., Грунин А.Б., Евстифеев Вас. В. // ФТП. – 2006. – т. 40. - № 6. – с. 136.
- Huant S., Najda S.P., Etienne B. // Phys. Rev. Lett. – 1990. – v. 65. - № 12. – p.1486.
- Кревчик В.Д., Грунин А.Б., Зайцев Р.В. // ФТП. – 2002. – т. 36. - № 10. – с. 1225.
ВЛИЯНИЕ ДИЭЛЕКТРИЧЕСКОГО КОНФАЙНМЕНТА
НА МАГНИТООПТИЧЕСКИЕ СВОЙСТВА КВАНТОВЫХ ПРОВОЛОК
С ВОДОРОДОПОДОБНЫМИ ПРИМЕСНЫМИ ЦЕНТРАМИ
В.Д. Кревчик, А.В.Калинина
Пензенский государственный университет, Пенза
Теоретически исследовано влияние диэлектрического окружения на спектр примесного магнитооптического поглощения 1D – структур с учетом дисперсии радиуса квантовых проволок (КП), которая описывается функцией Гаусса. В дипольном приближении рассчитан коэффициент примесного магнитооптического поглощения 1D – структуры с учетом влияния диэлектрического окружения для случая, когда диэлектрическая проницаемость окружающей КП среды ε2 много меньше диэлектрической проницаемости КП ε1. Показано, что учет влияния диэлектрического окружения приводит к существенному изменению спектра примесного магнитооптического поглощения, связанному с кардинальной модификацией электронных состояний вдоль оси КП. Установлено, что в случае, когда ε2<<ε1, возможны оптические переходы двух типов: внутриподзонные и переходы электрона с примесных уровней в состояния квазинепрерывного спектра КП. Найдено, что для оптических переходов первого типа спектр примесного магнитооптического поглощения имеет ярко выраженный осциллирующий характер. Показано, что в случае оптических переходов второго типа происходит «подавление» примесного магнитопоглощения с уменьшением величины ε2.
ФОТОТОК В КВАНТОВОЙ ПРОВОЛОКЕ С ПРИМЕСЬЮ В МОДЕЛИ ПОТЕНЦИАЛА ЖEСТКОЙ СТЕНКИ
С.Н. Ульянов, М.А. Пятаев
Мордовский государственный университет им. Н.П. Огарeва, Саранск
В настоящей работе исследован электронный транспорт в квантовой проволоке, содержащей одиночную короткодействующую примесь при наличии внешнего электромагнитного излучения. Поперечное сечение проволоки описывается с помощью потенциала жесткой стенки, примесь моделируется с помощью потенциала нулевого радиуса. Для нахождения тока через систему используется подход, основанный на обобщении теории Ландауэра-Бюттикера [1-3]. Выражение для вероятности прохождения электрона при наличии излучения найдено путем решения нестационарного уравнения Шрёдингера, в котором волновая функция ищется в однофотонном приближении, в виде суперпозиции квазиэнергетических состояний [4].
В работе получены аналитические выражения для фототока и фотопроводимости квантовой проволоки при произвольном расположении примеси. Проведённые исследования зависимости фототока от химического потенциала электронов показали, что наиболее быстрое изменение фототока происходит вблизи пары дискретных составляющих электронного спектра, для которых выполняются резонансные соотношения при заданной частоте излучения. Аналогичная зависимость фотопроводимости представляет собой максимум и минимум, приходящиеся на указанную пару уровней.
Фототок и фотопроводимость линейно зависят от интенсивности падающего излучения. Выяснено также, что максимальные значения фототока пропорциональны полной длине проволоки и разности расстояний от примеси до торцов проволоки, а максимальные величины фотопроводимости пропорциональны квадрату полной длины проволоки.
Анализ показывает, что при смещении примеси относительно оси проволоки, может происходить изменение знака фототока и фотопроводимости, связанное с чередованием максимумов и минимумов электронной плотности в поперечном сечении проволоки. Амплитуда фотопроводимости быстро убывает с ростом температуры, при этом форма пиков сглаживается. Фототок более устойчив к изменению температуры.
Работа выполнена при поддержке РФФИ (грант 08-02-01035).
- Maaø F.A., Gorelik L.Y., Phys. Rev. B 53, 15885 (1996).
- Pershin Y.V., Piermarocchi C., Phys. Rev. B 72, 245331 (2005).
- Pershin Y.V., Piermarocchi C., Phys. Rev. B 75, 035326 (2007).
- Зельдович Я.Б. УФН 110, 139 (1973).
Прыжковая проводимость по примесям
в параболической квантовой яме в условиях внешнего поперечного электрического поля
В.Д. Кревчик, С. А. Губина
Пензенский государственный университет, Пенза
Теоретически исследована продольная прыжковая проводимость по примесям на переменном токе в квантовой яме (КЯ) с параболическим потенциалом конфайнмента. Полупроводниковая КЯ считается компенсированной и рассматривается случай низких температур, когда проводимость определяется переходами между состояниями с энергиями, близкими к уровню Ферми. Примесные центры описываются в рамках модели потенциала нулевого радиуса. В парном приближении проведён расчёт вещественной части продольной прыжковой проводимости по примесям Reσl(ω) в КЯ для случая, когда направление напряжённости электрического поля перпендикулярно оси размерного квантования. В приближении, кода характерная длина прыжка велика по сравнению с шириной КЯ, а величина kT много меньше ширины зоны примесных состояний, получена аналитическая формула для Reσl(ω). Исследована частотная зависимость прыжковой проводимости, а также её зависимость от параметров удерживающего потенциала и глубины залегания примесных уровней. Найдено, что основной вклад в прыжковую проводимость дают электронные переходы вблизи уровня Ферми в КЯ. Выявлена высокая чувствительность прыжковой проводимости к глубине залегания примесных уровней.
МОДЕЛЬ ДЕТЕКТИРУЮЩЕЙ СИСТЕМЫ СЦИНТИЛЛЯТОР−ФОТОДЕТЕКТОР НА ОСНОВЕ ПОЛУПРОВОДНИКОВОЙ КВАНТОВОЙ ЯМЫ
В.Д. Кревчик, Е.А. Тюрин
Пензенский государственный университет, Пенза
В последние годы все более широкое применение в экспериментальной ядерной физике находят твердотельные детектирующие системы (ТДС) — системы из сцинтиллятора и фотодетектора (ФТД). Наряду с известными преимуществами ТДС, по сравнению, например, с традиционными системами, сцинтиллятор-ФЭУ, им присущи и недостатки, связанные с нестабильностью характеристик, относительно низкими энергетическим разрешением и коэффициентом преобразования. Эти недостатки были предопределены выбором в качестве ФТД поверхностно-барьерных золото-кремниевых детекторов, спектральная чувствительность которых не совпадает со спектром высвечивания большинства существующих сцинтилляторов. Максимумы высвечивания последних лежат в коротковолновой области от 0,45 до 0,5 мкм, в то время как максимумы кривых спектральной чувствительности данного ФТД лежат в области длин волн порядка 0,7 мкм. В настоящей работе в качестве ФТД предлагается использовать фотоприёмник (ФП) на основе полностью обеднённой легированной сверхрешётки (ЛС) GaAs, функциональным элементом которой является параболическая квантовая яма [1,2]. В таком ФП фотовозбуждённые электроны и дырки разделяются полем ЛС, что приводит к высокой квантовой эффективности ФП. Из-за полного обеднения ЛС ведёт себя как очень высокоомный материал, позволяющий прикладывать вдоль слоёв сильные электрические поля с помощью селективных n+ - и p+ - электродов. Такой ФП может содержать более 20 тонких чередующихся n+ - и p+ - слоёв GaAs, варьируя толщину которых можно достичь спектрального согласования ФП и сцинтиллятора.
- Horikoshi Y., Ploog K. - Appl. Phys. A, 1985, v.37, p. 47.
- Херман М. - Полупроводниковые сверхрешётки: Пер. с англ. - М.: Мир, 1989. - 240 с.
ОСОБЕННОСТИ 2D-ТУННЕЛЬНЫХ БИФУРКАЦИЙ В УСЛОВИЯХ ВНЕШНЕГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ
В.Д. Кревчик, М.Б. Семёнов, В.А. Рудин, Н.Ю. Скибицкая, П.В. Кревчик
Пензенский государственный университет, Пенза
Исследована проблема управляемости двумерного диссипативного туннелирования в системе «игла кантилевера АСМ/ СТМ – квантовая точка», моделируемой 2D - осцилляторным потенциалом, взаимодействующим с термостатом, во внешнем электрическом поле. Методом инстантонов рассчитана вероятность 2D- туннельного переноса и исследована ее зависимость от величины внешнего электрического поля. Полученные зависимости качественно соответствуют отдельным экспериментальным ВАХ для системы «платинированная игла кантилевера АСМ/ СТМ – квантовая точка из золота», полученным в НИФТИ при ННГУ им. Н.И. Лобачевского. Экспериментально наблюдаемыми и устойчивыми оказываются предсказанные ранее 2D- туннельные бифуркации с диссипацией для случая параллельно туннелирующих взаимодействующих частиц. Помимо достаточно хорошего качественного соответствия теоретической и экспериментальной зависимости (за исключением небольших переходных областей), результат этой работы позволяет сделать вывод об экспериментальном обнаружении предсказанной ранее теоретически устойчивой 2D – бифуркации (смене режима туннелирования с синхронного на асинхронный). Вблизи этой точки (резкий излом на ВАХ) небольшой локальный минимум может быть следствием режима квантовых биений, также описанных в работах авторов, и которые учитывались в процессе численного анализа, представленного на рис.

Данная работа выполнена при частичной поддержке гранта Минобрнауки РФ по ФЦП «Развитие потенциала высшей школы» № 2.1.1/1647, а также в рамках тем. плана проведения фундаментальных научных исследований по заданию Рособразования, № 1.15.09.
НЕЛИНЕЙНОЕ ВЗАИМОДЕЙСТВИЕ МИКРОВОЛНОВОГО ИЗЛУЧЕНИЯ В ПОЛУПРОВОДНИКОВОЙ СВЕРХРЕШЕТКЕ
Н.Н. Хвастунов
Мордовский государственный университет им. Н. П. Огарева, Саранск
Полупроводниковые сверхрешетки (СР) привлекают внимание исследователей с точки зрения возможности использования их в качестве детекторов и усилителей терагерцевого (ТГц) излучения [1,2]. Классическая схема генерации [3], предложенная еще в начале 70-х годов прошлого века не позволила создать на практике работающее устройство из-за возникновения в режиме генерации электрических нестабильностей [4]. В начале текущего века возродился интерес к данной проблеме благодаря предложенным новым схемам генерации, теоретически позволяющим получить усиление в бездоменном режиме при определенных условиях, в частности, при использовании переменного поля накачки вместо постоянного [5]. Однако получить усиление удается далеко не на всех гармониках поля накачки и в ограниченной области параметров системы.
В данной работе мы демонстрируем, что введение в систему дополнительного постоянного магнитного поля существенно расширяет области усиления и снимает запрет на генерацию некоторых гармоник. Кроме того, мы показали, что магнитное поле может быть эффективным инструментом, позволяющим управлять коэффициентом усиления при заданном электрическом поле накачки.
Работа выполнена при поддержке АВЦП «Развитие научного потенциала высшей школы» (проект № 2.1.1/2656).
1. A. Wacker, Phys. Rep. 357, 1 (2002)
2. G. Platero, R. Aguado, Phys. Rep. 395, 1 (2004)
3. L. Esaki, R. Tsu, IBM J. Res. Dev. 14, 61 (1970)
4. А. А. Игнатов, В. И. Шашкин, ЖЭТФ 93, 935 (1987).
5.T. Hyart, A. V. Shorokhov, K. N. Alekseev, Phys. Rev. Lett. 98, 220404 (2007)
Влияние поверхности на электронный транспорт
через сверхпроводящую наноразмерную систему
О.Ю. Смолянкина, К.Н. Югай
Омский государственный университет им. Ф.М. Достоевского, Омск
Исследована модель свободной сверхпроводящей наночастицы, показано, что поверхностные состояния играют определяющую роль в формировании сверхпроводящих параметров данной системы. В спектре её возбуждений были выделены две щели, формируемые электронами в объёмных и поверхностных состояниях. Показано, что в макроскопическом пределе они стремятся к известному в теории БКШ коллективному параметру спаривания объёмного сверхпроводника, а в микроскопическом пределе определяющим становится тот из параметров, который обусловлен наличием поверхностных состояний в наночастице. Сделано предположение о влиянии поверхности на сверхпроводящие и транспортные свойства наночастицы, включённой в цепь электрического тока.
Далее рассмотрена модель сверхпроводящей наночастицы с током. Исследовано влияние поверхностных состояний наночастицы на её сверхпроводящие и транспортные свойства в случаях, когда она заключена между нормальными и между сверхпроводящими электродами. Показано, что в случае нормальных электродов одноэлектронный ток через сверхпроводящую наночастицу имеет только нормальную составляющую, а в случае сверхпроводящих электродов ток имеет как нормальную, так и сверхпроводящую составляющие. В каждом из рассмотренных случаев выделены две компоненты тока: объёмная и поверхностная – в соответствии с тем, через какие электронные состояния осуществляется транспорт носителей. Показано влияние поверхности на транспортные и сверхпроводящие свойства наноразмерной системы, включённой в цепь. Для количественной оценки и сравнения использованы экспериментальные данные группы Ralf, Black и Tinkham.
[1] Phys.Rev.Lett. 1996. Vol. 76. No. 4. P. 688-691.
[2] Phys.Rev.Lett. 1997. Vol. 78. No. 21. P. 4087-4090.
[3] Phys.Rev. B. 2002. Vol. 66. No. 14. P. 502-505.
[4] Phys.Rev. B. 2003. Vol. 68. No. 17. P. 2502-2505.
[5] Phys.Rev. B. 2005. Vol. 72. No. 15. P. 5408-5417.
[6] Phys.Rev. B. 2006. Vol. 73. No. 13. P. 2509-2512.
[7] Phys.Rev.Lett. 2008. Vol. 100. No. 14. P. 7202-7205.
МАГНИТНЫЙ МОМЕНТ КВАНТОВОЙ ЯМЫ И ТОЧКИ
В СКРЕЩЕННЫХ МАГНИТНОМ И ЭЛЕКТРИЧЕСКОМ ПОЛЯХ
В.А. Миронов
Мордовский государственный университет им. Н.П. Огарева, Саранск
Электрические поля обуславливают самые разнообразные явления в полупроводниках. Они вызывают качественные изменения квантовых состояний носителей тока и их энергетического спектра. Это приводит к зависимости макроскопических свойств полупроводников от приложенного поля E. Примерами таких явлений могут служить: эффект Франца-Келдыша - зависимость комплексной диэлектрической проницаемости от E, возникающая из-за возможности собственного поглощения фотонов с энергией, меньшей чем ширина запрещенной зоны; эффект Есаки - туннельный ток в вырожденном p-n-переходе; квантовый эффект Холла и другие.
В настоящей работе, с помощью метода работы [1], получены явные аналитические выражения для магнитного момента квантовой ямы и точки в скрещенных магнитном и электрическом полях. Исследованы осцилляции магнитного момента от электрического и магнитного полей. Найдены периоды осцилляций, как по магнитному, так и по электрическому полям, рассмотрены предельные случаи сильного магнитного и размерного квантования.
Вклад в магнитный момент M квантовой ямы и точки дают один линейный по магнитному полю и два осциллирующих слагаемых. Как показывает анализ, магнитный момент периодичен по квадрату величины электрического поля.
В случае сильного размерного квантования и сильного магнитного квантования период осцилляций момента квантовой ямы определяется только второй осциллирующей компонентой M. В области слабых полей осциллирующие слагаемые магнитного момента квантовой точки имеют одинаковый период по электрическому полю. А в случае сильного магнитного квантования, также как и для квантовой ямы, магнитный момент определяется вторым осциллирующим слагаемым.
Магнитный момент квантовой ямы в обоих предельных случаях испытывает периодические осцилляции по обратному магнитному полю типа Де Газа – Ван Альфена. А магнитные осцилляции квантовой точки периодически осциллируют по обратному полю только в случае сильного магнитного квантования.
1. L.I. Filina, V.A. Geyler, V.A. Margulis, O.B. Tomilin // Phys. Lett. A. – 1998. – V. 244. – P. 295.
