Относительность движения
| Вид материала | Документы |
- Повторительно-обобщающий курс, 864.61kb.
- Программа по физике механика, 42.61kb.
- Программа вступительных испытаний (с обеседования) по физике для лиц, поступающих, 55.5kb.
- Тема занятия, 28.84kb.
- Программа вступительного экзамена по физике в нки в 2011 году на базе среднего (полнего), 60.21kb.
- Тематическое планирование курса физики в 10 классе, 68.52kb.
- Урок решения задач по теме «Относительность механического движения», 28.22kb.
- Программа вступительного испытания по дисциплине Физика, 54.3kb.
- Примерные программы вступительных испытаний в высшие учебные заведения российской федерации, 47.51kb.
- ПрограммА для поступающих в Новочеркасское высшее военное командное училище связи (военный, 93.59kb.
Относительность движения
Движение одного и того же тела в разных системах отсчета будет различным. Например, движение точки на ободе колеса велосипеда относительно его корпуса происходит по дуге окружности, движение этой же точки относительно Земли - сложная кривая (циклоида).
Различными будут и параметры движения: скорость, перемещение. Величины, зависящие от выбора системы отсчета, в которой они измеряются, называются относительными. К ним относятся координаты, перемещение, скорость, путь, в некоторых случаях и ускорение. Относительна и траектория движения.
Выбор системы отсчета связан с соображениями удобства. Довольно часто с этих позиций принимают за тело отсчета Землю.
Если известны параметры движения тела в одной системе отсчета и скорость движения другой системы отсчета относительно первой, то можно определить параметры движения тела во второй системе отсчета (и наоборот).
Так, если в движущемся относительно Земли поезде пассажир пройдет по вагону, совершив перемещение s`, а за это время поезд переместится на величину s0, то в результате относительно Земли перемещение пассажира будет равно:
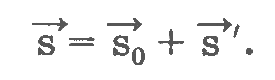
При равномерном движении одной системы отсчета относительно другой справедливо будет уравнение сложения скоростей:

где v - скорость движения тела относительно системы отсчета, принятой за неподвижную; v` - скорость тела в системе отсчета, движущейся относительно первой; v0 - скорость системы отсчета, движущейся относительно неподвижной системы отсчета.
Уравнение (1.1) называется классическим законом сложения скоростей. Этот закон впервые сформулировал Галилео Галилей (1564-1642).
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно, то нетрудно доказать, что ускорение тела остается при переходе от одной системы отсчета к другой постоянным (такие величины называются инвариантными, к ним относятся также промежутки времени движения).
В других случаях и ускорение является величиной относительной.
