Основы физики и электроники. Часть 2

Вид материала

Лекция

Подобный материал:

• Обучение учащихся средних общеобразовательных учреждений эмпирическим методам познания, 605.75kb.
• Новая интерпритация периодического закона д. И. Менделеева, 159.47kb.
• Программа дисциплины Электроника и микропроцессорная техника часть 2 "Основы цифровой, 133.66kb.
• В. И. Стражев 200 г. Регистрационный № физические основы электроники учебная программа, 116.78kb.
• Учебная программа по дисциплине электротехника и электроника лахтина, 44.8kb.
• Рабочая программа по дисциплине основы компьютерной электроники для студентов специальности, 487.92kb.
• Тольяттинский Государственный Университет Кафедра методики преподавания физики и физической, 381.94kb.
• Программа дисциплины радиофизические измерения Специальность: Радиофизика и электроника, 92.83kb.
• Рабочая программа утверждаю: по курсу общей физики (основы квантовой физики) для студентов, 85.65kb.
• Философские основы естествознания и кризис физики, 246.22kb.

Основы физики и электроники. Часть 2.

Лекция 2

Механические колебания системы с затуханием

§1. Свободные колебания пружинного маятника с трением

Добавим теперь в рассмотренную на прошлой лекции систему вязкое трение. Второй закон Ньютона запишется следующим образом: 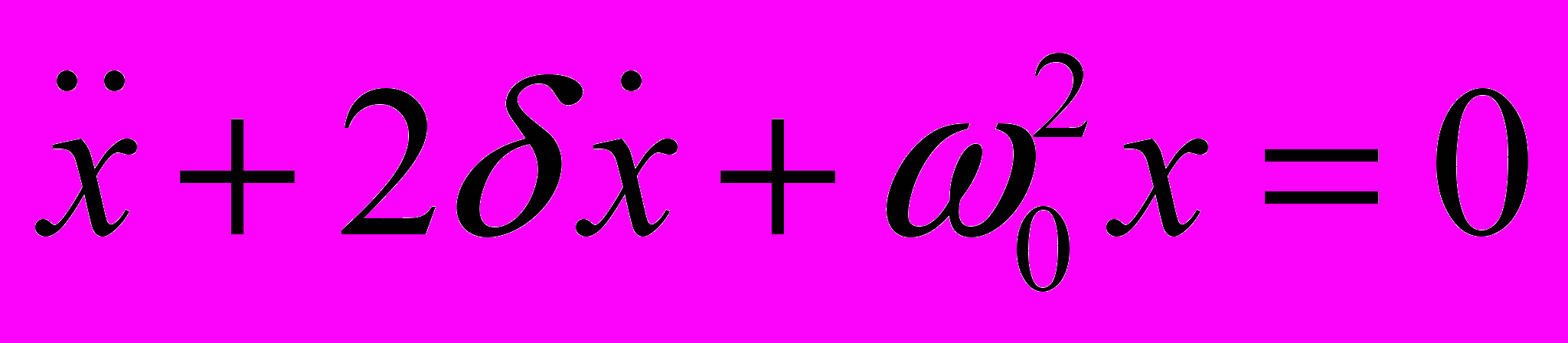, где 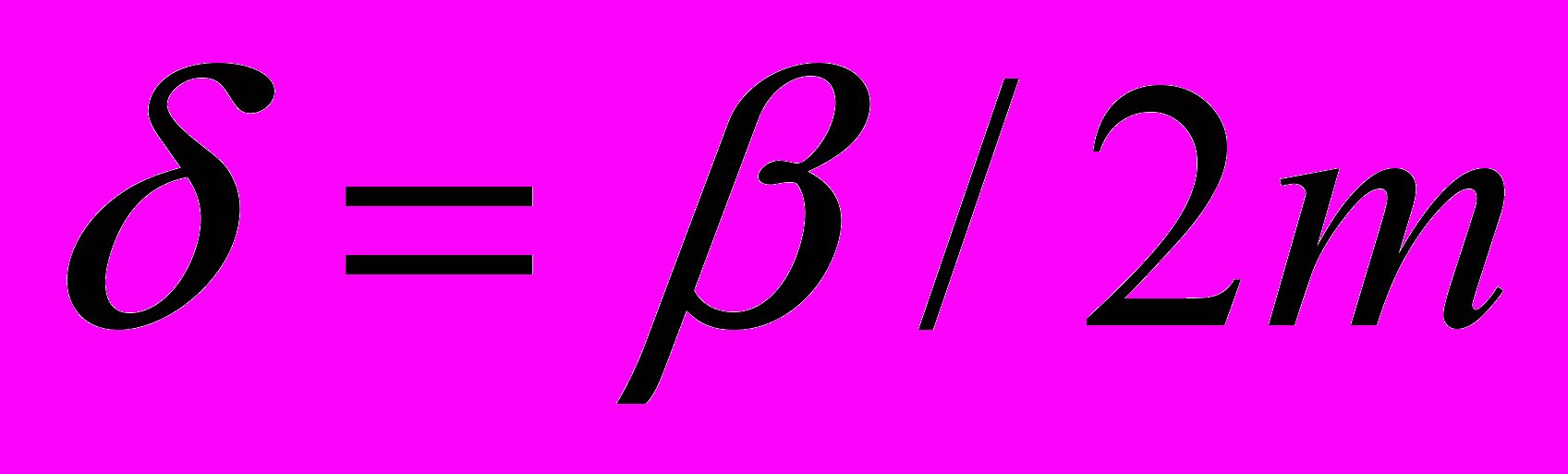. Будем искать решение в виде 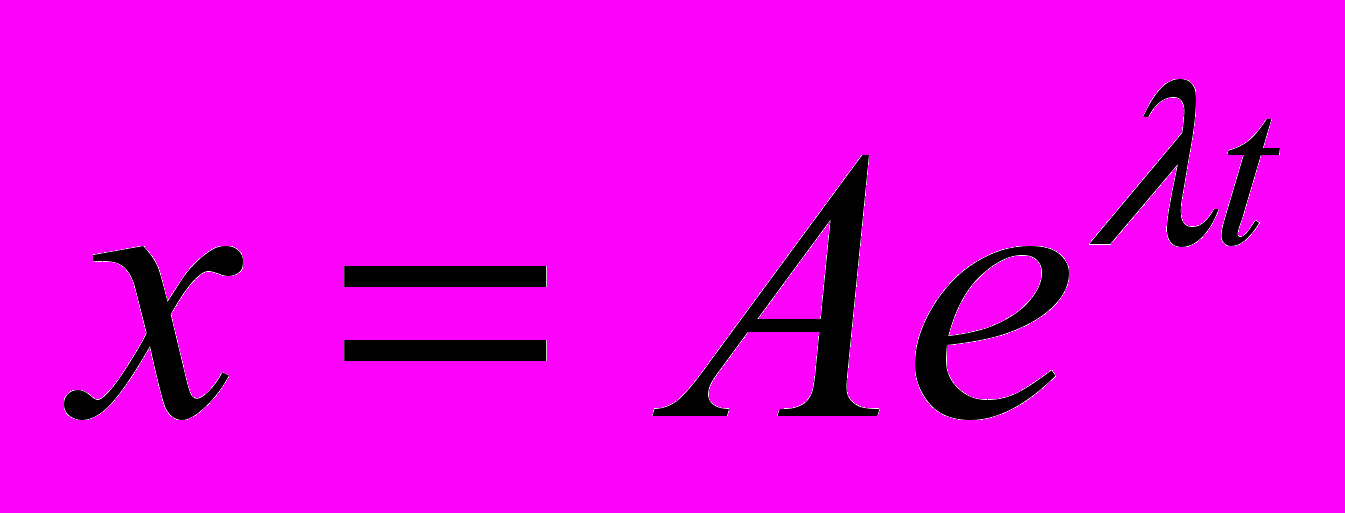. Подставляя этот вид решения в уравнение, получим: 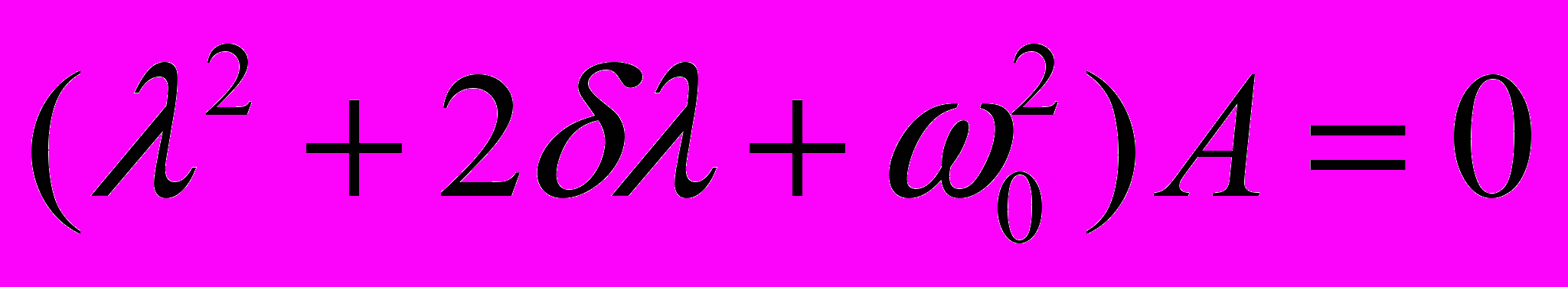. Отсюда имеем 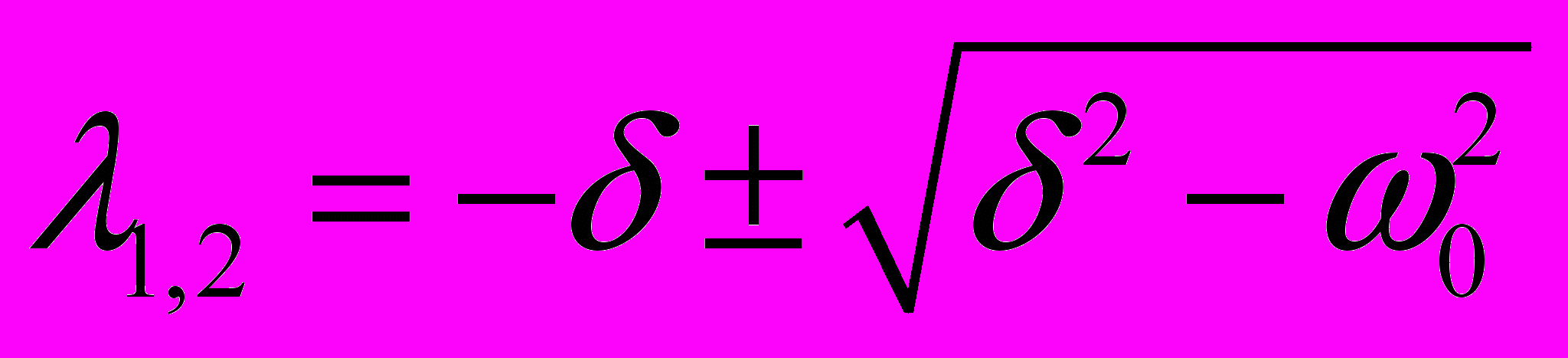. Таким образом, 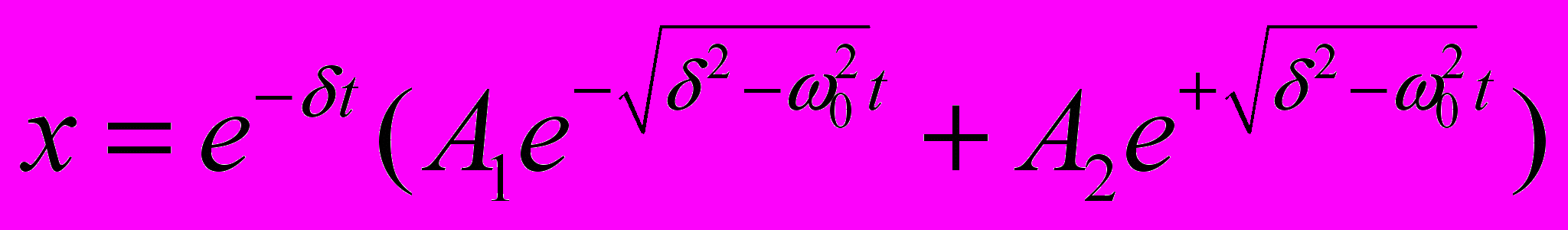. Рассмотрим два случая соотношения между 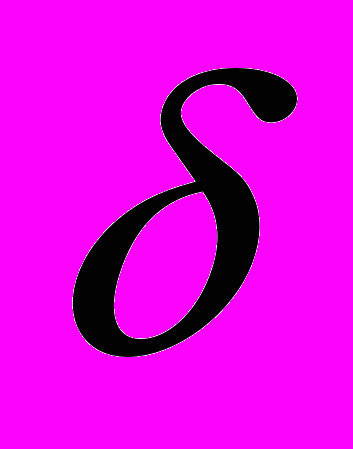и .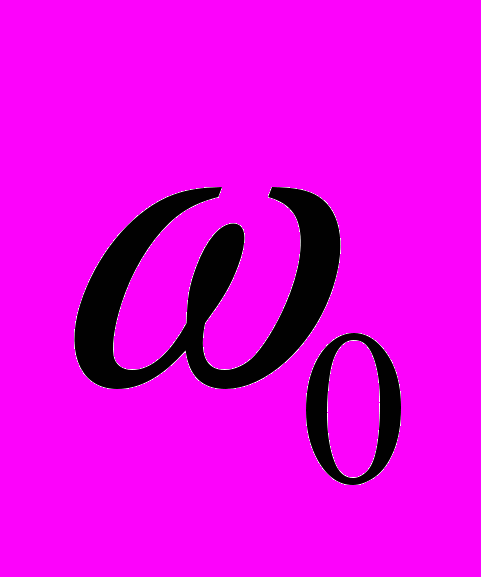

1) 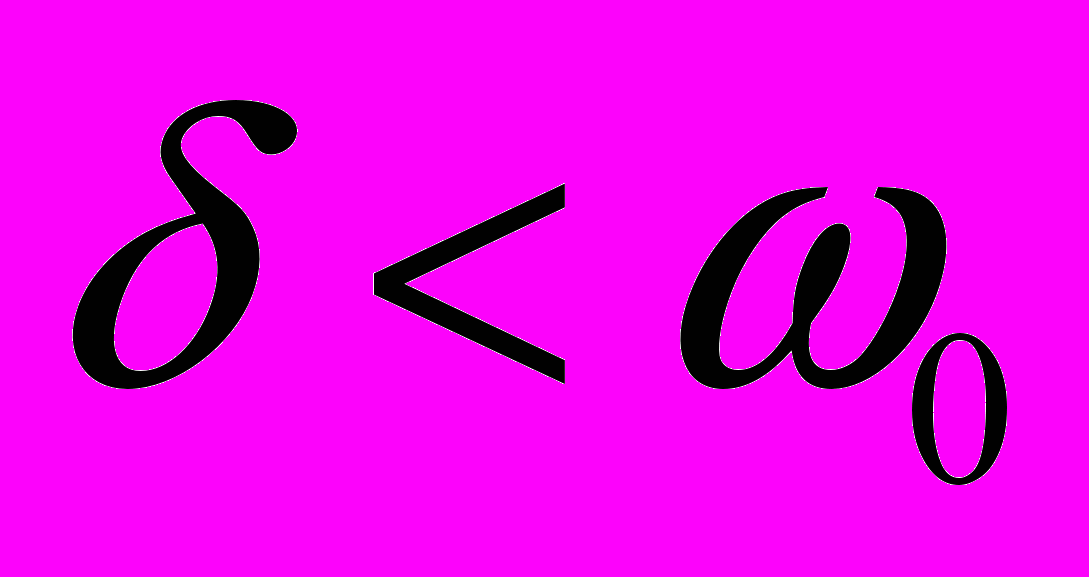(трение относительно мало).

В этом случае 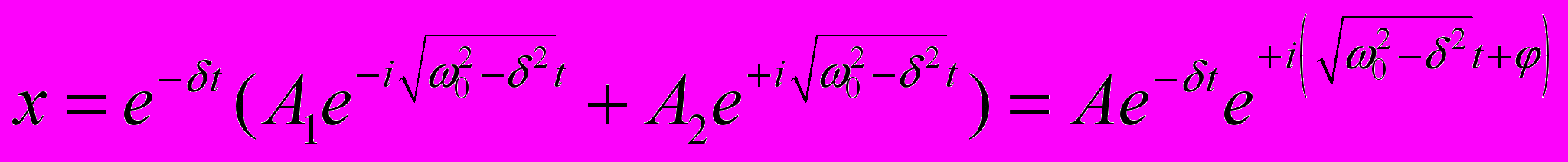. Таким образом грузик совершает гармонические колебания с частотой чуть меньшей собственной частоты системы, амплитуда которых убывает со временем тем быстрее, чем больше трение.

2) 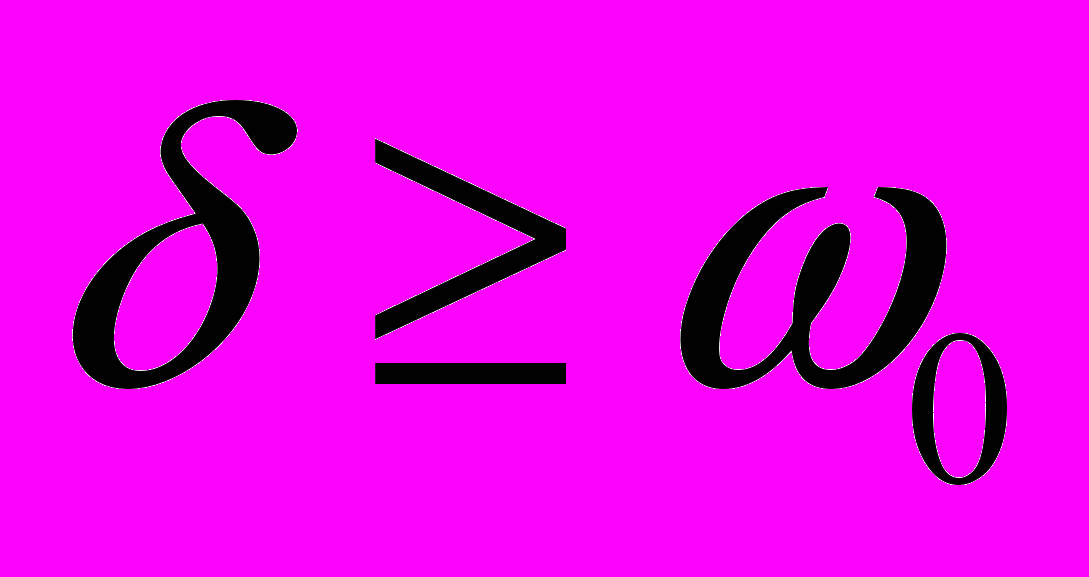(трение велико).

В этом случае в показателях экспонент стоят действительные числа, то есть никаких колебаний не происходит. Будучи выведенным из положения равновесия, грузик просто возвращается к нему.

§2. Вынужденные колебания пружинного маятника с трением

Пусть теперь на грузик действует гармоническая вынуждающая сила 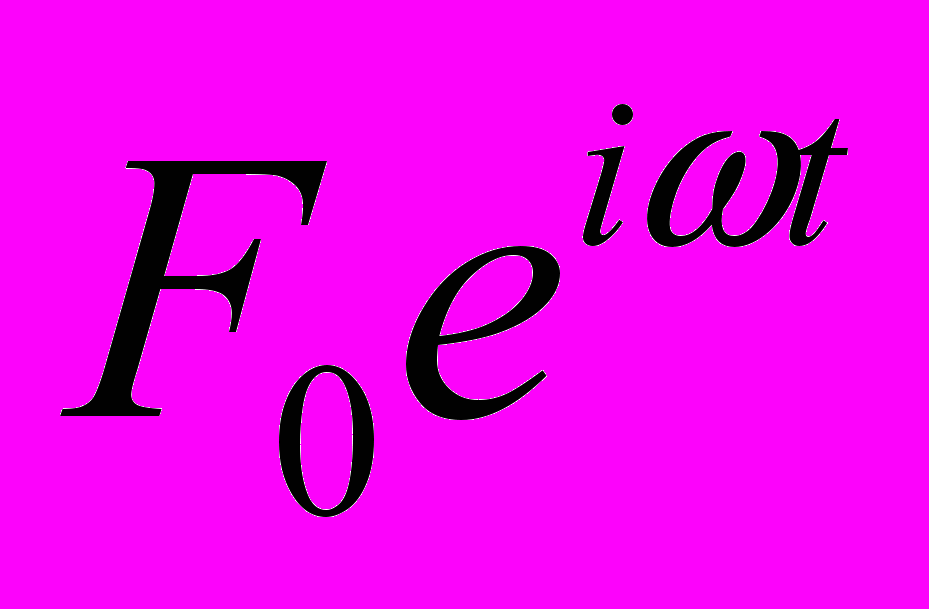. Уравнение, описывающее движение системы выглядит так: 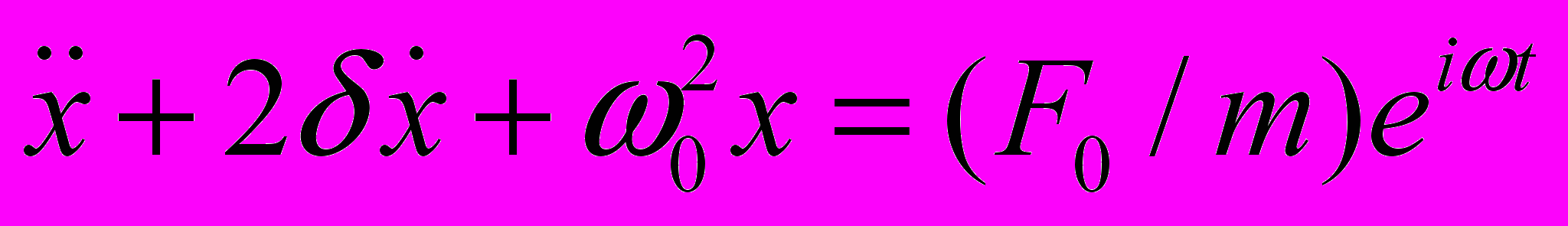. Будем искать установившееся решение в виде 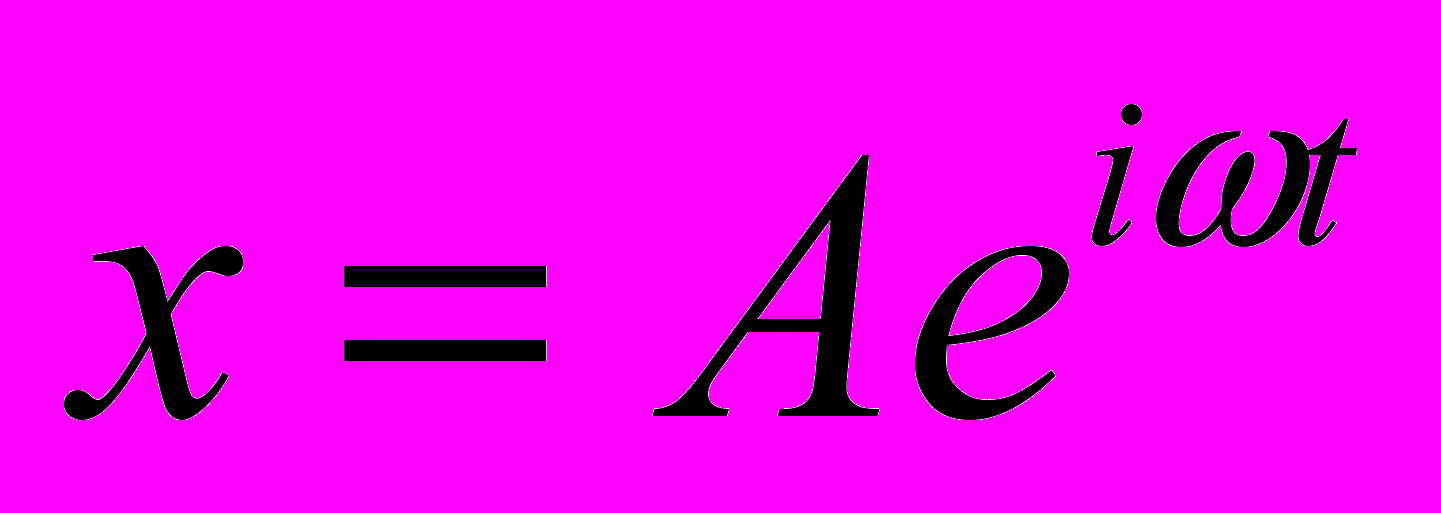. Подставляя этот вид решения в уравнение, имеем: 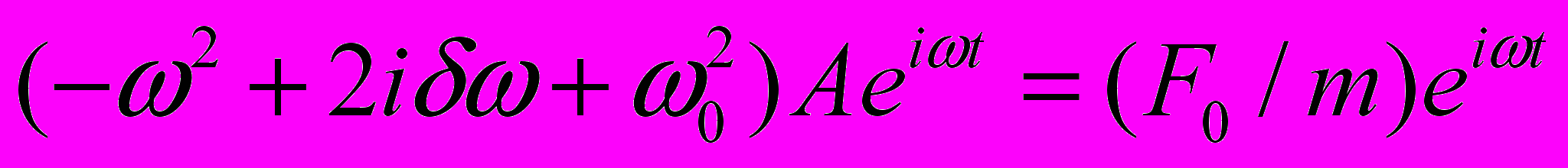. Отсюда 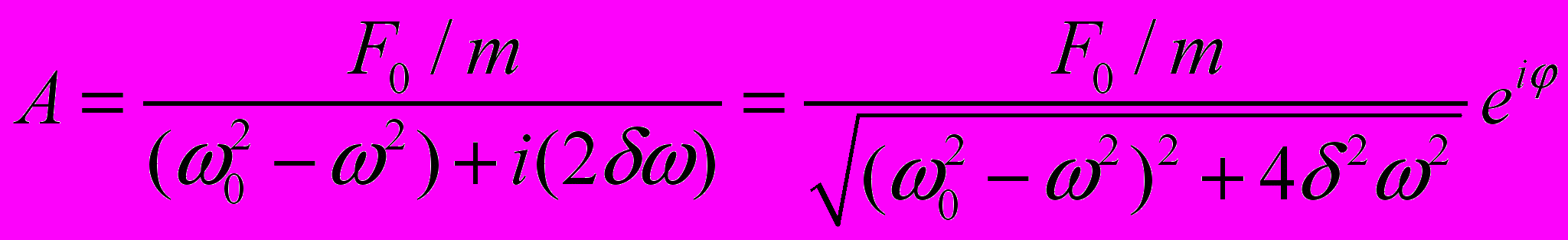, где .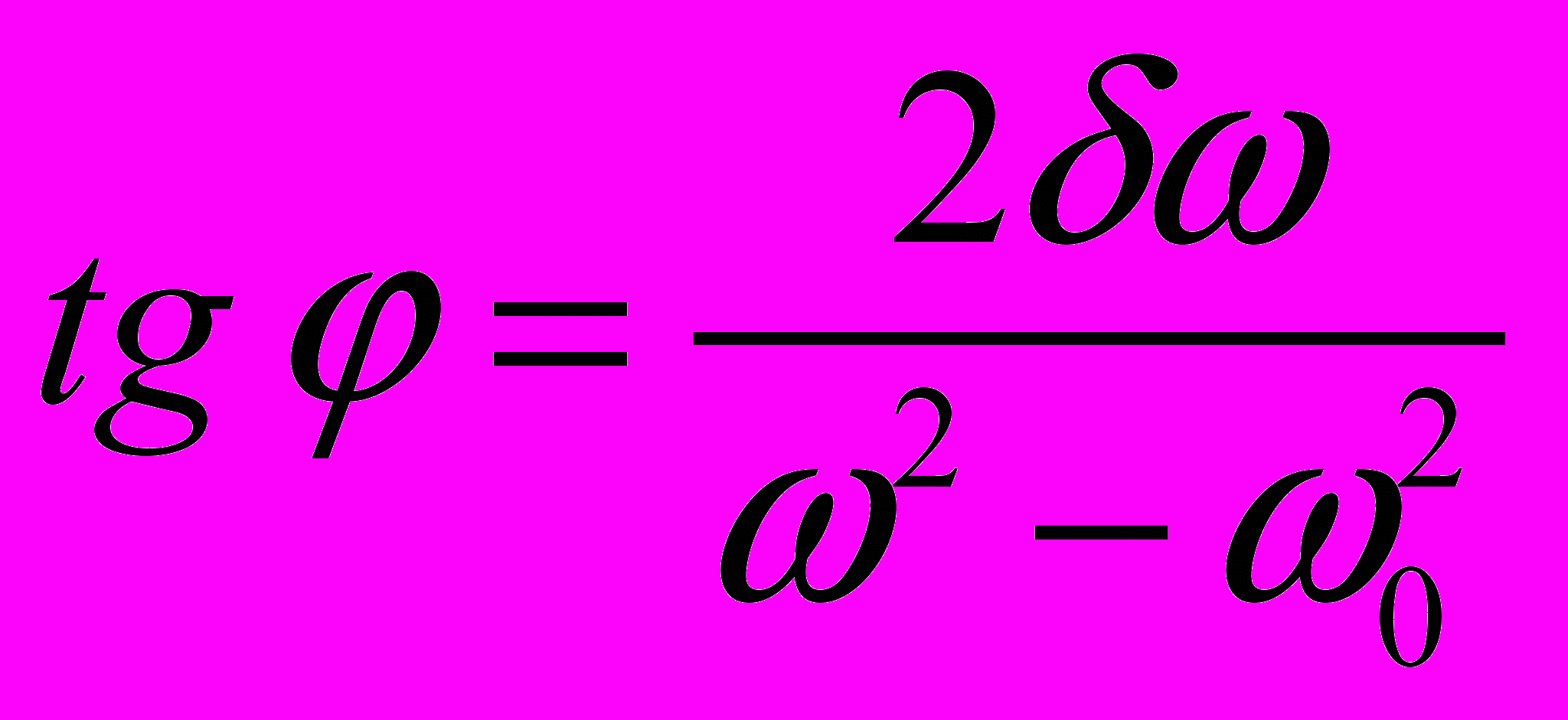

Таким образом, и амплитуда, и фаза вынужденных колебаний в такой системе зависят от частоты вынуждающей силы. Рассмотрим три случая.

1) 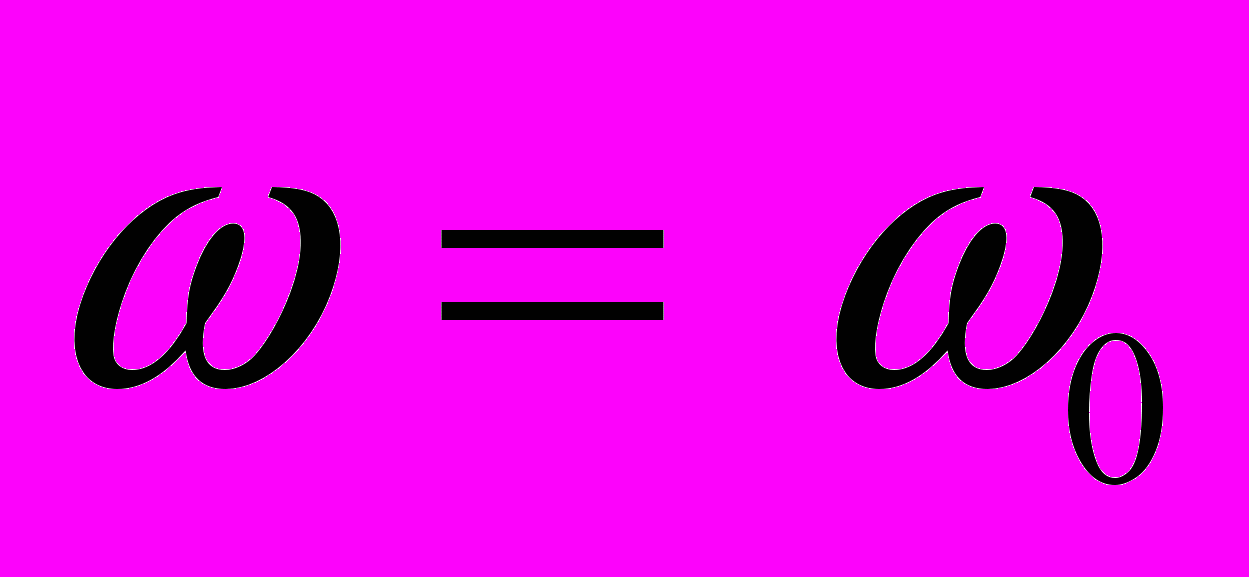. В этом случае , .

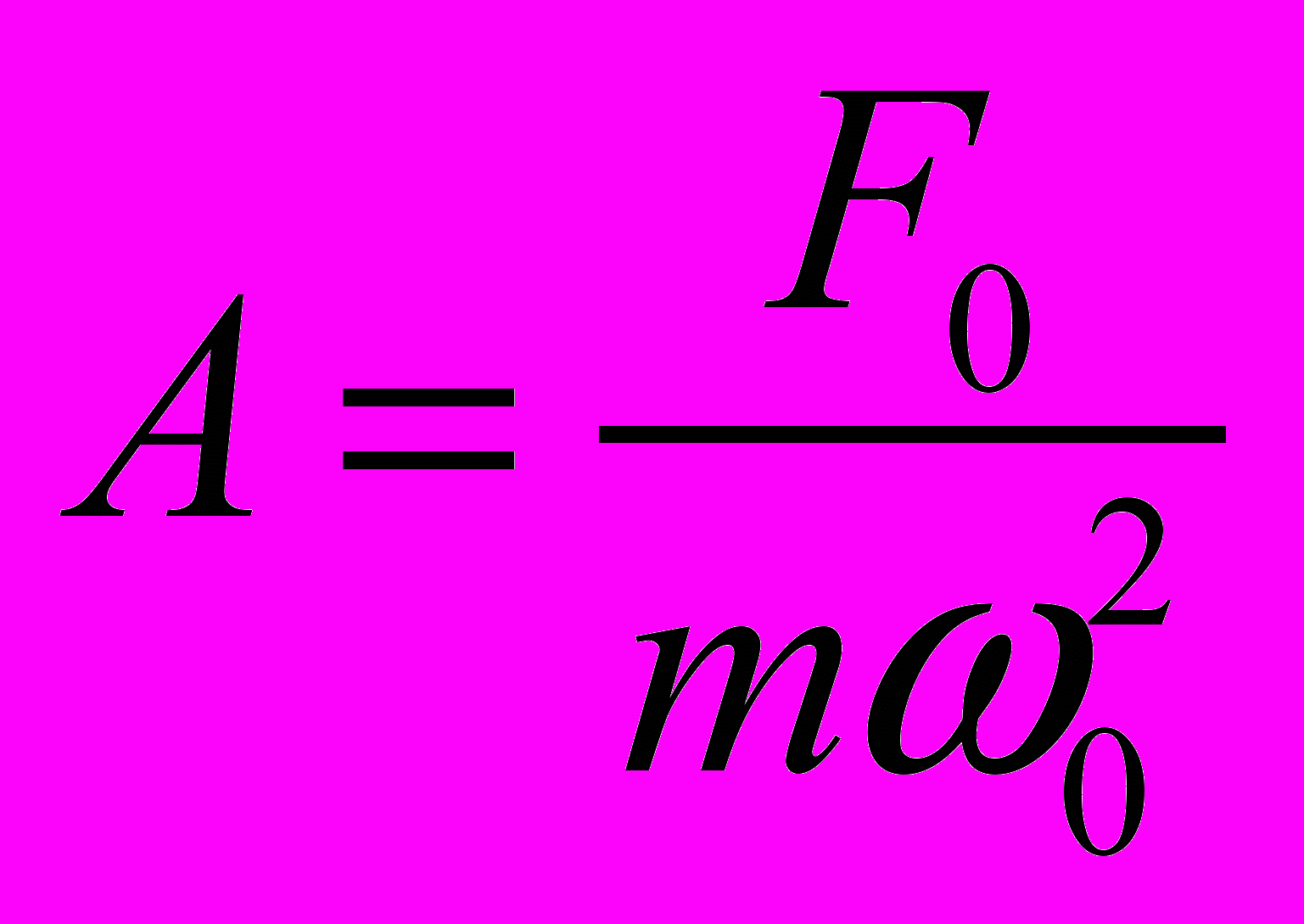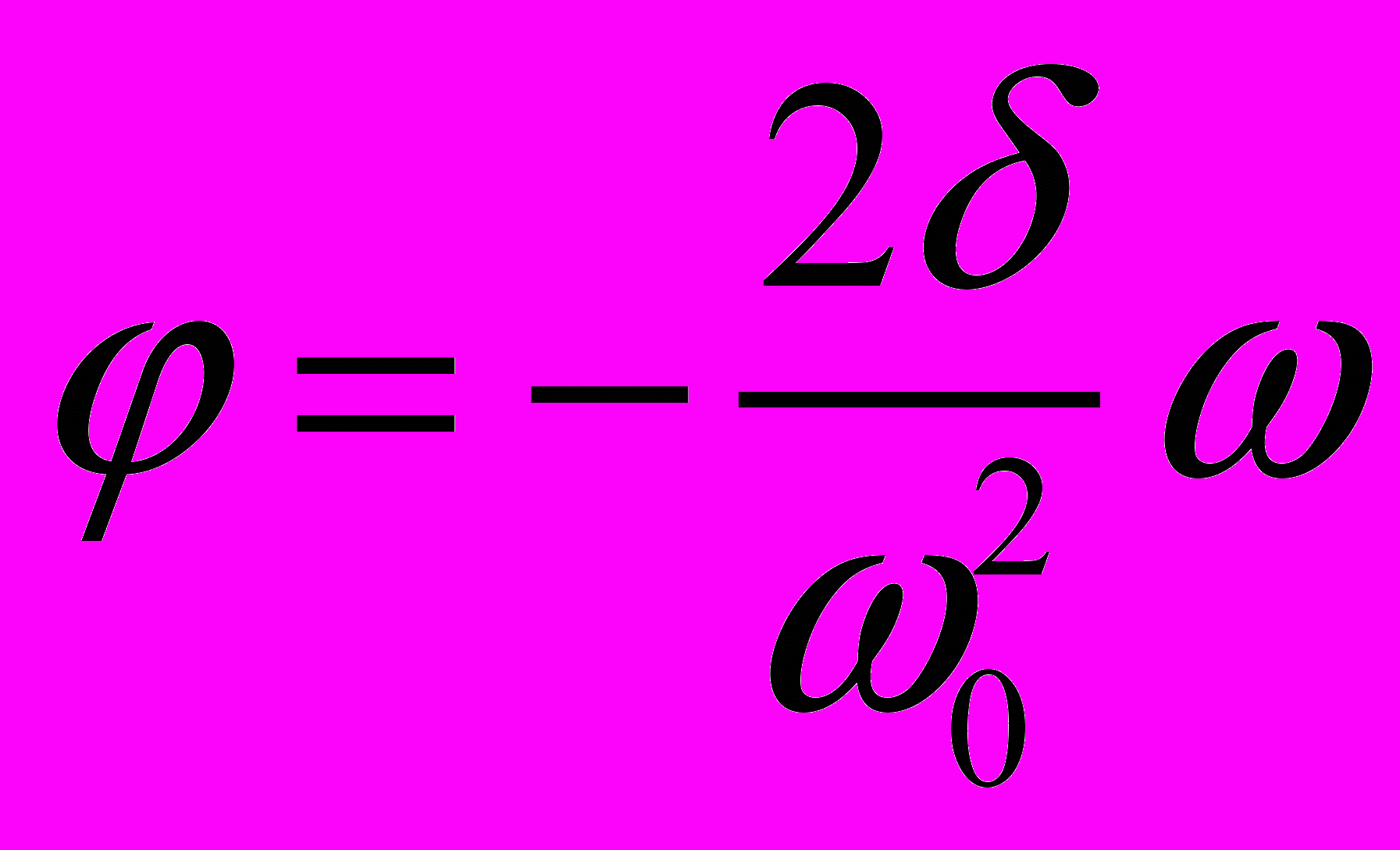2) 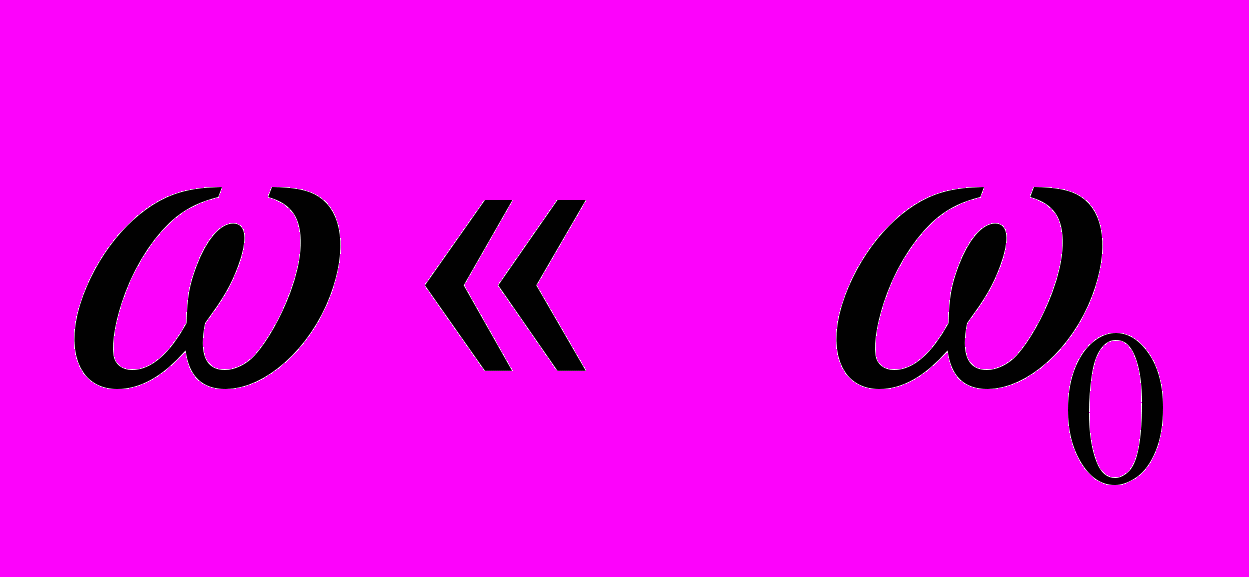. В этом случае , .

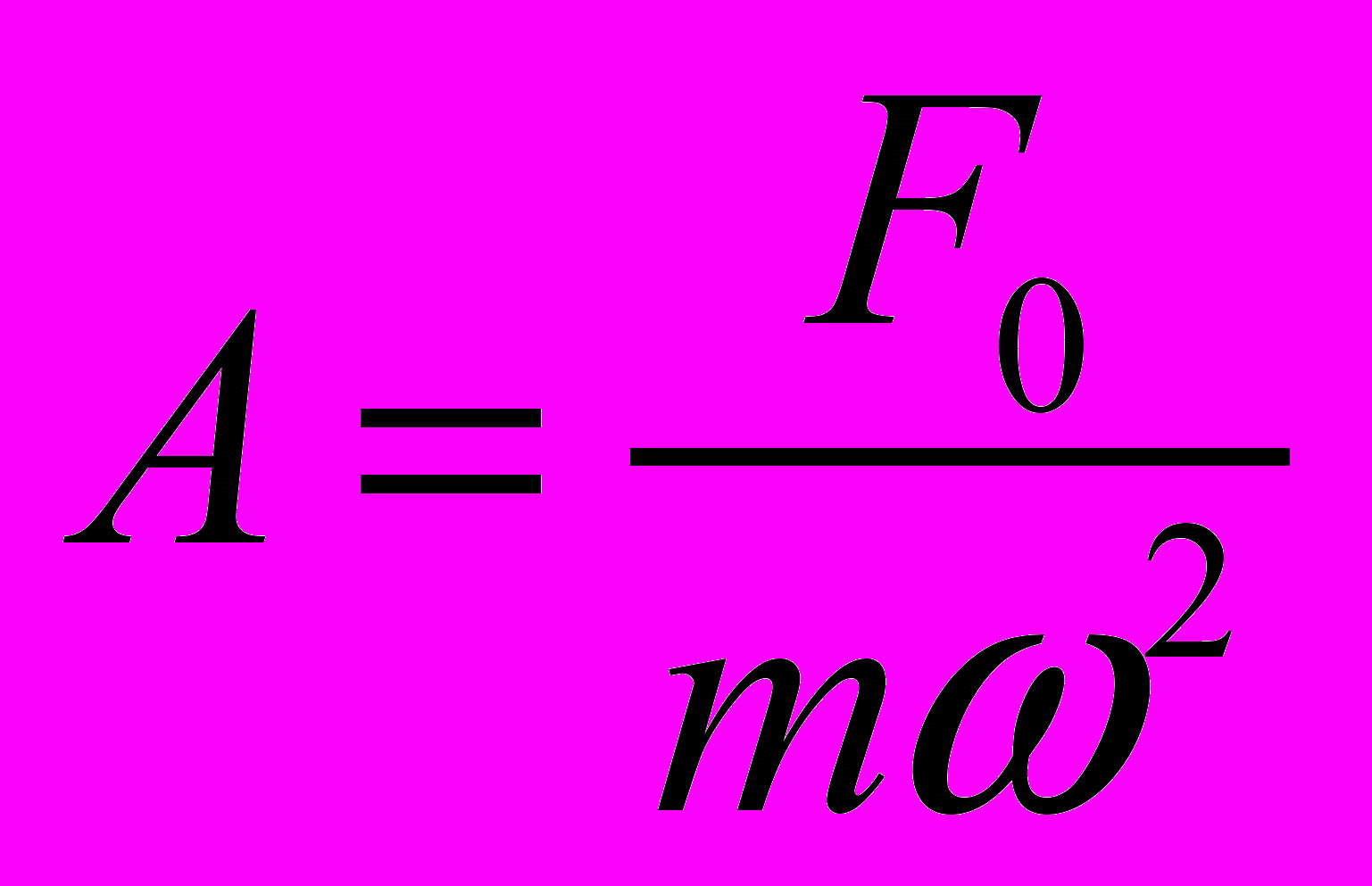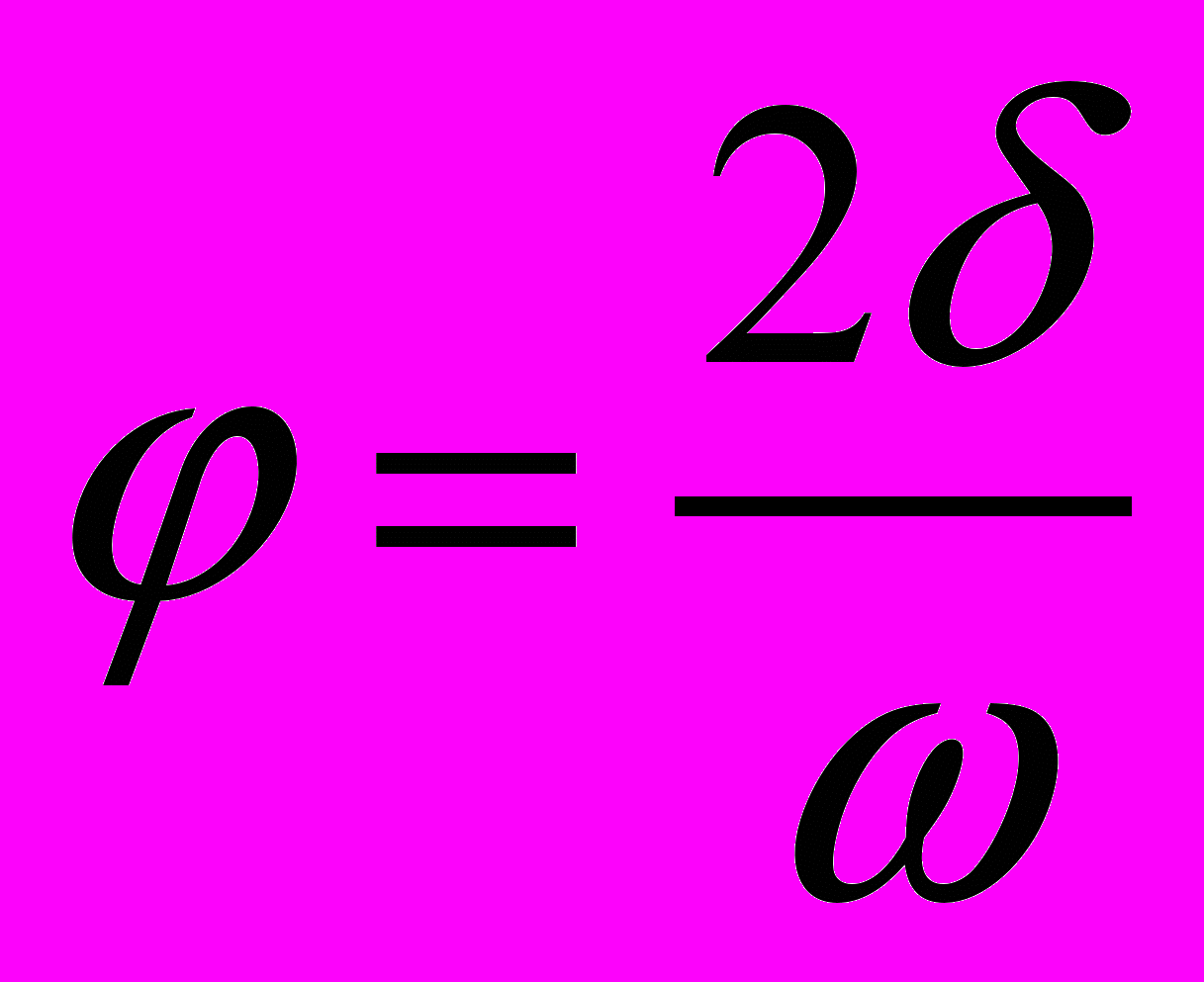3) 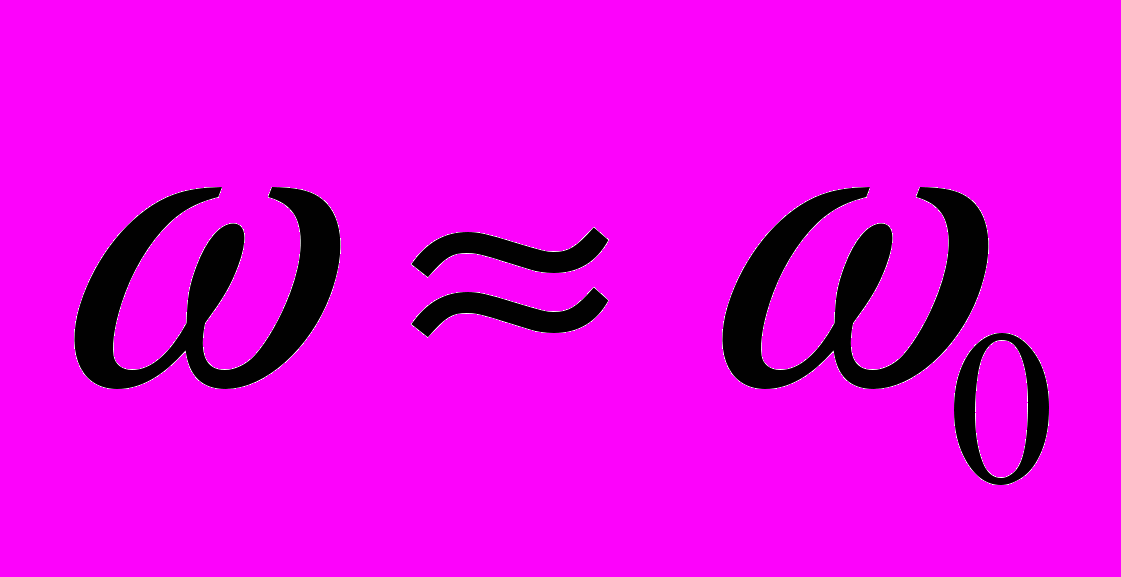. В этом случае , .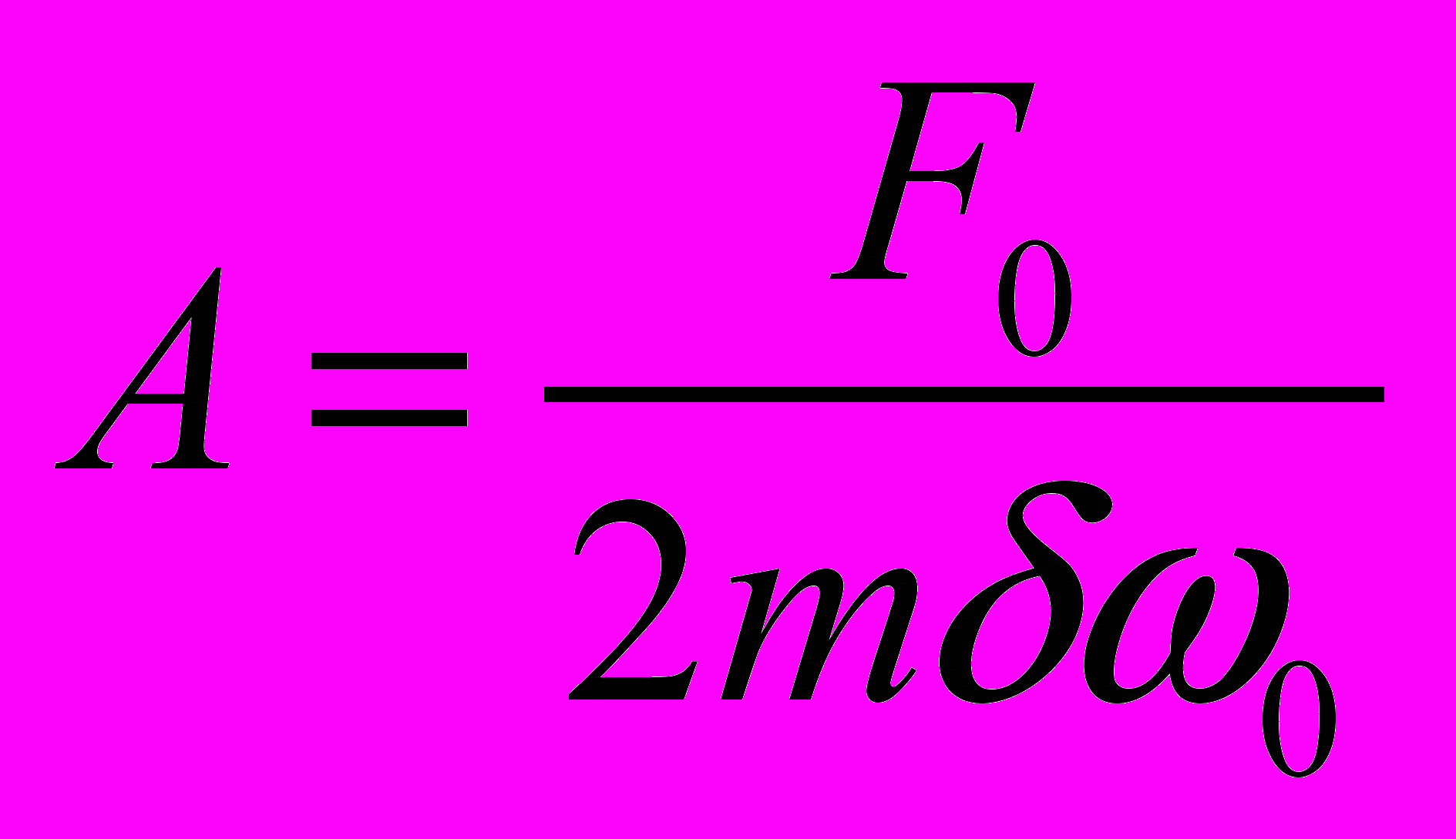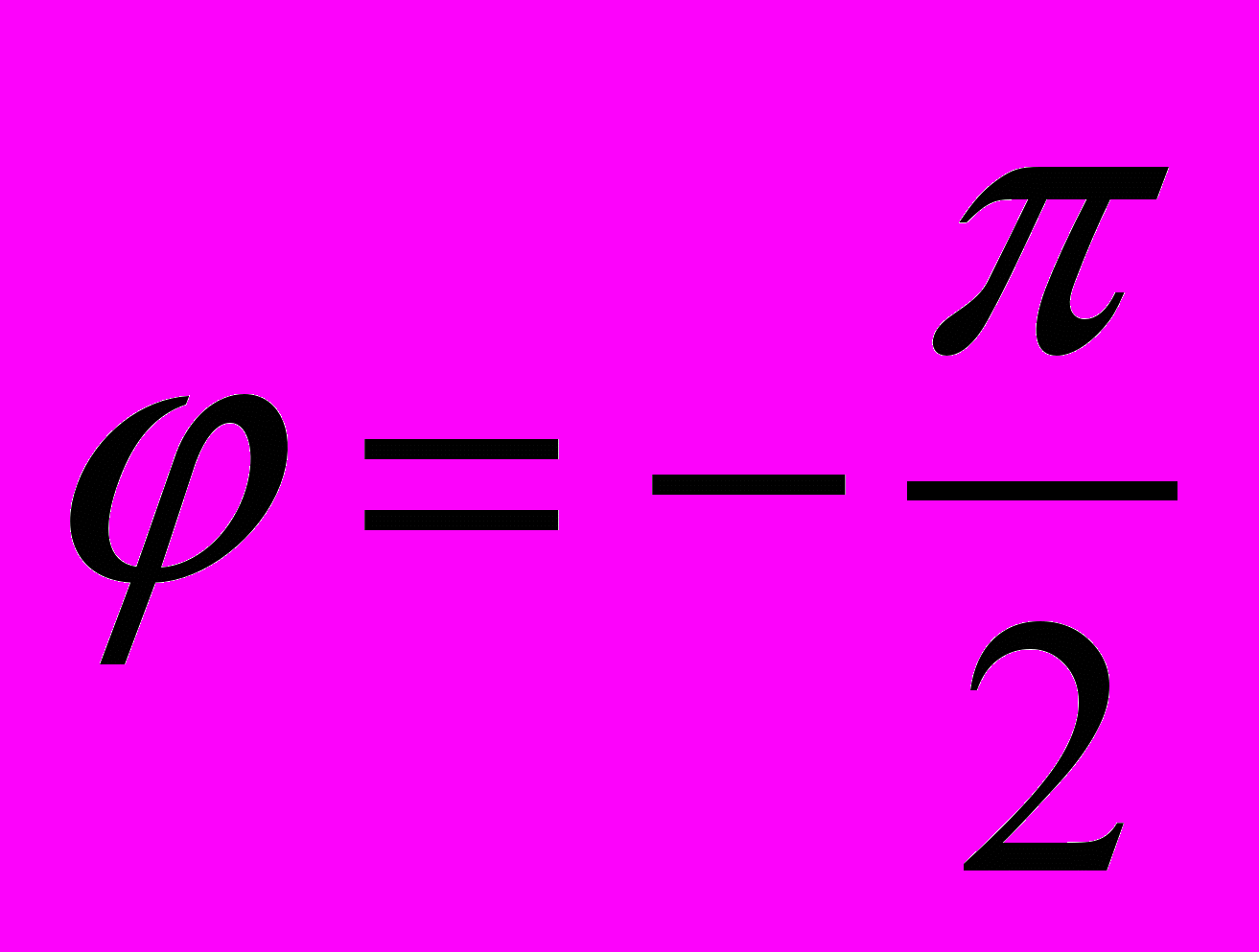