Geum.ru

Романов Сергей Викторович программа

Вид материалаПрограмма

Содержание


Всего часов
Молекулярная физика и термодинамика
Законы термодинамики.
Элементы статистической физики идеальных систем.
Элементы физической кинетики.
Список литературы
Задание по физике
Тема сминарских занятий
0 – задачи, которые студент должен решать в течение недели к следующему семинару и которые затем студенты должны разбирать в нач
II – задачи, которые студент должен решить обязательно для сдачи задания. Они должны быть оформлены студентами в своих тетрадях.
Задачи 0 группы
Текстовые задачи I, II и III групп
Подобный материал:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Московский физико-технический институт

(государственный университет)


УТВЕРЖДАЮ

Проректор по учебной работе

Ю.А. Самарский

___ декабря 2008 г.

ПРОГРАММА


по курсу: ФИЗИКА (МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА)

по направлению: 511600

факультет: ФНТИ

кафедра: физики и физического материаловедения

курс: I

семестр: 2

лекции: 32 часа

практические (семинарские) занятия: 32 часа

лабораторные занятия: 64 часа

самостоятельная работа: 2 часа в неделю

экзамен: 2 семестр

зачет: нет

ВСЕГО ЧАСОВ: 128


Программу и задание составил:

к.ф.-м.н. Романов Сергей Викторович


Программа утверждена на заседании кафедры физики и

физического материаловедения ___ декабря 2008 года


Заведующий кафедрой В.Г. Вакс

Согласовано:

Заведующий кафедрой общей физики А.Д. Гладун

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА


1.Основные понятия молекулярной физики.


Предмет исследования, его характерные особенности. Задачи молекулярной физики. Макроскопические параметры. Агрегатные состояния вещества. Уравнения состояния. Законы Авогадро, Бойля-Мариотта, Шарля и Гей-Люссака. Абсолютная температура. Уравнение состояния идеального газа


2. Законы термодинамики.


Равновесные и квазиравновесные процессы. Работа, теплота и внутренняя энергия. Первое начало термодинамики. Теплоёмкость. Закон равномерного распределения энергии теплового движения по степеням свободы. Классическая теория теплоемкостей. Элементы квантовой теории теплоемкостей. Адиабатический и политропический процессы (идеальный газ). Скорость звука в газах.

Второе начало термодинамики. Обратимые и необратимые процессы. Тепловые и холодильные машины. Теорема Карно. Равенство Клаузиуса. Термодинамическое определение энтропии. Энтропия идеального газа.

Неравенство Клаузиуса. Возрастание энтропии адиабатически изолированной системы.

Термодинамические функции и соотношения взаимности. Следствия соотношений взаимности: разность теплоёмкостей при постоянном давлении и объёме для произвольной гомогенной системы, изотермическое и адиабатическое сжатие жидкостей.

Термодинамические свойства твердых тел: тепловое расширение, термодинамика деформации стержней.

Уравнение Ван-дер-Ваальса. Описание отклонений от закона Бойля-Мариотта. Температура Бойля. Изотермы газа Ван-дер-Ваальса. Критическая точка. Приведённое уравнение. Закон соответственных состояний. Внутренняя энергия, теплоёмкости и энтропия газа Ван-дер-Ваальса. Адиабатический и политропический процессы для газа Ван-дер-Ваальса. Процесс Джоуля-Кельвина. Получение низких температур и сжижение газов. Адиабатическое расширение. Дросселирование.

Фазовые превращения. Фазовые переходы I и II рода. Условия равновесия фаз. Химический потенциал. Уравнение Клапейрона-Клаузиуса. Кривые фазового равновесия. Тройная точка. Эффекты перегрева и переохлаждения. Зависимость давления насыщенного пара от температуры. Теплоёмкость насыщенного пара.

Поверхностные явления. Краевые углы. Смачивание и несмачивание. Формула Лапласа. Термодинамика поверхности.

Зависимость давления пара от кривизны поверхности жидкости. Роль зародышей при образовании новой фазы. Кипение.


3. Элементы статистической физики идеальных систем.


Динамические и статистические закономерности. Макроскопические и микроскопические состояния. Случайные события и вероятность. Дискретные и непрерывные распределения. Плотность распределения. Средние величины и дисперсия.

Понятие функции распределения молекул по скоростям. Связь внутренней энергии одноатомного идеального газа с абсолютной температурой. Среднеквадратичная скорость теплового движения атомов.

Вывод явного выражения для функции распределения атомов по скоростям (распределение Максвелла). Распределение атомов по компонентам скорости и по абсолютным значениям скорости. Распределение атомов по скоростям в смеси нескольких газов. Функция распределения по скоростям относительного движения атомов.

Равновесное распределение плотности изотермического идеального газа во внешнем потенциальном поле. Распределение Больцмана. Барометрическая формула.

Распределение Гиббса и его свойства. Статистическое определение энтропии. Статистическая сумма. Вычисление теплоёмкостей. Третье начало термодинамики.

Флуктуации термодинамических величин. Влияние флуктуаций на чувствительность измерительных приборов.


4. Элементы физической кинетики.

Основные понятия физической кинетики. Время релаксации. Столкновения. Эффективное газокинетическое сечение. Прохождение пучка атомов через газ неподвижных рассеивателей, средняя длина свободного пробега (модель твердых шаров). Средняя длина свободного пробега атомов в “своём” газе и в смеси двух газов (модель твердых шаров). Модель Сёзерленда.

Явления переноса: вязкость, теплопроводность и диффузия. Коэффициенты вязкости, теплопроводности и диффузии в газах. Броуновское движение. Подвижность. Формула Эйнштейна. Явления переноса в разреженных газах. Эффузия. Вакуум: его получение и измерение.


СПИСОК ЛИТЕРАТУРЫ


Основная литература


1. Сивухин Д.В. Общий курс физики. Т.II. Термодинамика и молекулярная физика. – М.: Наука, 1975.

2. Белонучкин В.Е., Заикин Д.А., Ципенюк Ю.М. Основы физики. Курс общей физики. Т.2. Квантовая и статистическая физика. Под ред. Ю.М.Ципенюка. Часть V. Главы 1 – 4. М.: Физматлит, 2001.

3. Щеголев И.Ф. Элементы статистической механики, термодинамики и кинетики. – М.: Янус, 1996.

4. Лабораторный практикум по общей физике. Т. 1/ Под ред. А.Д.Гладуна. – М.: МФТИ, 2003.

5. Сборник задач по общему курсу физики. Ч. 1/ Под ред. В.А.Овчинкина. – М.: МФТИ, 2002.


Дополнительная литература


1. Рейф Ф. Статистическая физика (Берклеевский курс физики). Т.5. – М.: Наука, 1972.

2. ЛандауЛ.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. – М.: Наука, 1965.

3. Кириченко Н.А. Термодинамика, статистическая молекулярная физика. – М.: Физматкнига, 2005.

4. Коротков П.Ф. Молекулярная физика и термодинамика. – М.: МФТИ, 2001.

5. Фейнман Р., Лейтон Р., Сэндс Н. Фейнмановские лекции по физике. Вып.4. – М.: Мир, 1965.

6. Прут Э.В., Кленов С.Л., Овсянникова О.Б. Введение в теорию вероятностей в молекулярной физике. − М.: МФТИ, 2002.

7. Прут Э.В., Кленов С.Л., Овсянникова О.Б. Элементы теории флуктуаций и броуновского движения в молекулярной физике. − М.: МФТИ, 2002.

8. Заикин Д.А. Энтропия. – М.: МФТИ, 2003.

10. Булыгин В.С. Некоторые задачи теории теплопроводности. – М.: МФТИ., 2006.

11. Лоренц Г.А. Лекции по термодинамике. – М.: R&C Dynamics, 2001.

12. Зоммерфельд А. Термодинамика и статистическая физика. – М.: ИИЛ, 1955.

13. Ферми Э. Термодинамика. – Харьков, издательство ХГУ, 1969.

14. Майер Дж., Гепперт-Майер М. Статистическая механика. – М.: Мир, 1980.

11. Шредингер Э. Лекции по физике. – М.: R&C Dynamics, 2001.


ЗАДАНИЕ ПО ФИЗИКЕ

для студентов 1-го курса на весенний семестр

2008/2009 учебного года


Дата
№

сем
Тема

сминарских занятий
Задачи

0

гр.
I

гр.
II

гр.
III

гр.

9–14

февр.
1
Уравнение состояния. Первое начало термодинамики. Политропические процессы. Скорость звука в газах.
1, 2, 3,

4
1.1; 1.38; 2.24; (1.54)
Т-1; 1.58;2.6

1.8;

6

16–21 февр.
2
Истечение газа из отверстия. Второе начало термодинамики. Цикл Карно. Термодинамическое определение энтропии.

5, 6, 7, 8
2.13; 3.28; 4.19; (3.43)

2.10; 3.32; 4.21

T-2

23–28

февр.
3
Энтропия идеального газа. Необратимые процессы. Термодинамические функции и их свойства.

9, 10, 11, 12
4.40; 4.47; 5.39; (4.48)

4.58; 4.68; 4.75

4.44

2–7

март.
4
Термодинамика стержней: тепловое расширение, термодинамика деформации. Условия фазового равновесия.
13, 14, 15, 16
5.18; 5.32; 5.52; (11.2)
5.30; 5.42;

T-3
5.53

9–14

март.
5
Фазовые превращения.

Газ Ван-дер Ваальса.
17, 18, 19, 20
11.29; 11.73; 6.25; (6.73)
11.27; 11.34; 6.52
T-4

16–21 март.
6
Поверхностные явления.


21, 22, 23, 24
12.8; 12.17; 12.50; (12.61)
12.31; 12.38; 12.58
12.48

23–28

март.
7
Контрольная работа по 1-му заданию (по группам)

30 мар.–4 апр.
8
Сдача 1-го задания










6–11

апр.
9
Биномиальное распределение. Распределения Максвелла и Больцмана.
25, 26, 27, 28
7.19; 7.24; 8.6; (Т-5)
7.14; 7.16; 8.38
7.1

13–18

апр.
10
Статистическая сумма и внутренняя энергия. Статистическое определение энтропии. Температура.
29, 30, 31, 32
8.14; 8.55; 8.58; (T-6)
8.40; 8.48; 8.51
T-7

20–25

апр.
11
Теория теплоемкостей. Флуктуации.
33, 34, 35, 36
8.25; T-8; 9.6; (9.28)

8.7; 8.52; 9.23
9.7

27 апр.–2 мая
12
Длина свободного пробега. Процессы переноса.
37, 38, 39, 40
10.33; 10.82; 10.83; (10.35)
10.37; 10.68; 10.69
10.30

4–9 мая
13
Диффузия. Броуновское движение. Эффузия.
41, 42, 43, 44
10.98; 10.10610.134

(10.95)
10.77; 10.10710.118
10.97

11–16

мая
14
Контрольная работа по 2-му заданию (по группам)

18–23

мая
15
Сдача 2-го задания. Зачёт. Закрытие ведомостей.


Примечание


1. Номера задач указаны по “Сборнику задач по общему курсу физики. Ч.1. Механика, термодинамика и молекулярная физика” под ред. В.А. Овчинкина; Т – текстовые задачи.

2. При выполнении заданий предусмотрена следующая вариативность – в каждой теме семинара задачи разбиты на 4 группы:

0 – задачи, которые студент должен решать в течение недели к следующему семинару и которые затем студенты должны разбирать в начале семинара;

I – задачи, которые рекомендуется рассмотреть на семинарах. В скобках приведены номера дополнительных задач, которые могут быть разобраны на семинаре;

II – задачи, которые студент должен решить обязательно для сдачи задания. Они должны быть оформлены студентами в своих тетрадях.

III – задачи, которые не являются обязательными для решения при сдаче заданий студентами 1, 3 и 7 факультетов.

Преподаватель на семинарах может разбирать и другие задачи по своему выбору.


Задачи 0 группы

(в скобках указаны номера аналогичных задач из «Сборника»

под ред. В.А.Овчинкина)


1. Определить среднее расстояние между молекулами насыщенного водяного пара при температуре 100 оС.

Ответ: 3.7∙10–9 м.

2. (1.30). Рассматривая воздух как идеальный газ, показать, что при нагревании воздуха, находящегося в комнате, его внутренняя энергия не изменяется, если только внешнее давление остается постоянным.

3. (1.46). 1) Нагревается или охлаждается идеальный газ, если он расширяется по закону P2V = const? 2) Как температура газа зависит от объёма в этом процессе? 3) Какова его молярная теплоемкость в этом процессе?

Ответ: 1) Нагревается;

2) T ~ V1/2;

3) C = CP + R.

4. Скорость звука в воздухе при 0 оС составляет 332 м/с. Определить скорость звука в водороде при той же температуре. Молярную массу воздуха принять равной = 28.8 г/моль.

Ответ:  1260 м/с.

5. Найти КПД цикла, состоящего из двух изохор и двух изобар и проходящего последовательно через состояния: 1) Р, V; 2) 2P, V; 3) 2P, 2V; 4) P, 2V. Газ – идеальный одноатомный.

Ответ: 15.4 %.

6. (3.2). Тепловая машина Карно, имеющая КПД = 40%, начинает использоваться при тех же тепловых резервуарах как холодильная машина. Сколько тепла Q2 эта машина может перевести от холодильника к нагревателю за один цикл, если к ней за каждый цикл подводится работа А = 10 кДж?

Ответ: 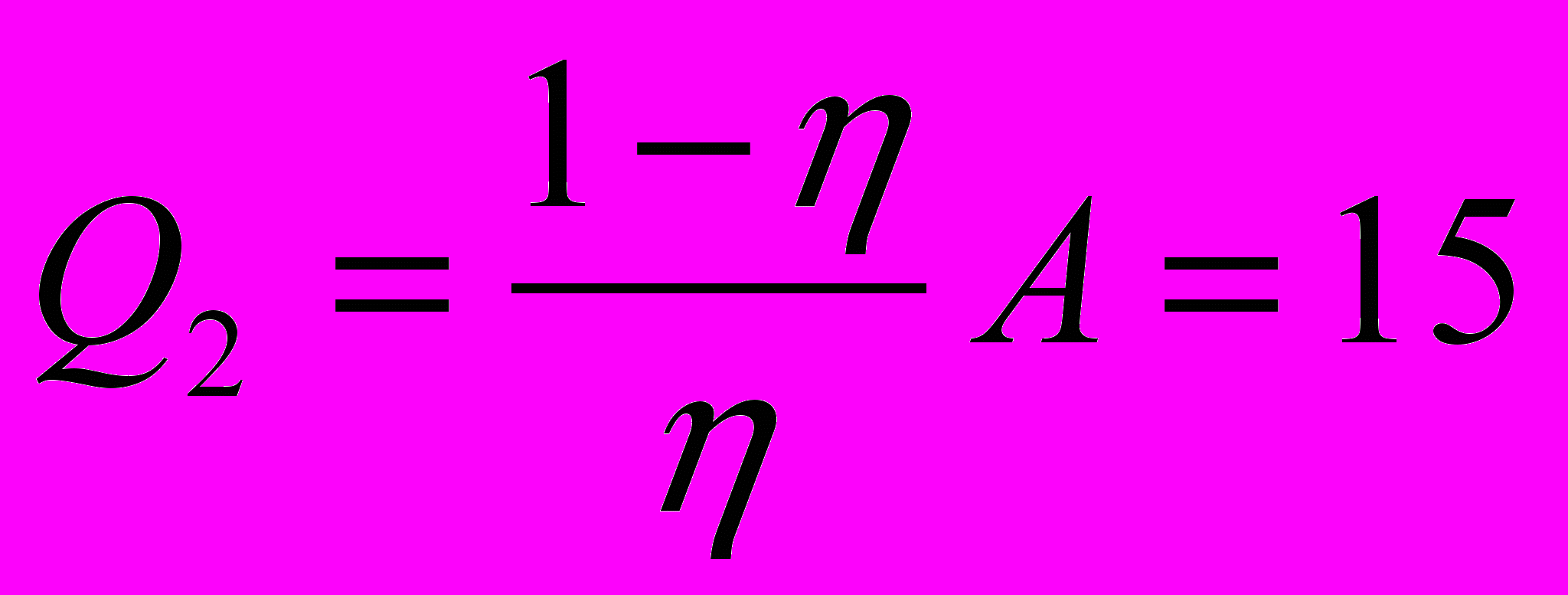кДж.

7. (4.8). Тепловые машины с произвольным веществом в качестве рабочего тела совершают обратимые термодинамические циклы, представленные на рисунках. Выразить КПД этих циклов через максимальную Т1 и минимальную Т2 температуры.




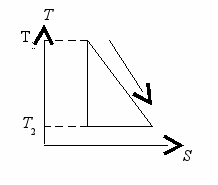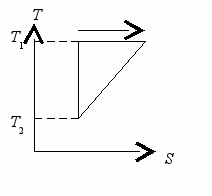Ответ: = (Т1 – Т2)/(Т1 + Т2); = (Т1 – Т2)/2Т1.


8. Тепловой насос используется для поддержания температуры 20 oС внутри дома, когда температура снаружи 3 oС. Найти минимальную работу, которую необходимо затратить, чтобы передать 100 Дж теплоты внутрь дома.

Ответ: 6 Дж.

9. Вычислить приращение энтропии одного моля азота при нагревании его от 100 оС до 200 оС

а) при постоянном объёме;

б) при постоянном давлении.

Ответ: а) 4.93 Дж/К; б) 6.9 Дж/К.

10. Теплоизолированный сосуд разделен на две равные части перегородкой, в которой имеется закрывающееся отверстие. В одной половине содержится 10 г водорода. Вторая половина откачана до высокого вакуума. Отверстие в перегородке открывают, и газ заполняет весь объем. Считая газ идеальным, найти изменение его энтропии.

Ответ: 28.8 Дж/К.

11. Вычислить, во сколько раз отличается изменение энтропии в процессе испарения 1 л воды от изменения энтропии в процессе таяния 1 кг льда, если теплота парообразования 2260 Дж/г при 373 К, удельная теплота плавления льда 335 Дж/г при 273 К.

Ответ:  4.9.

12. Для некоторого вещества зависимость внутренней энергии от температуры имеет вид U = aT4 + Uo при температуре 010 К. Найти зависимость теплоёмкости CV и энтропии S от температуры в этом диапазоне.

Ответ: CV(Т) = 4аТ3; S (T) = 4aT3/3.


13. Найти, во сколько раз изменение термодинамического потенциала 1 моля водяного пара превышает изменение термодинамического потенциала 1 моля воды при изотермическом увеличении давления от 1 до 2 атм. Считать пар идеальным газом, а воду – несжимаемой жидкостью.

Ответ: 1000.

14. В некотором диапазоне температур Т и объёмов V свободная энергия F изучаемой системы описывается соотношением 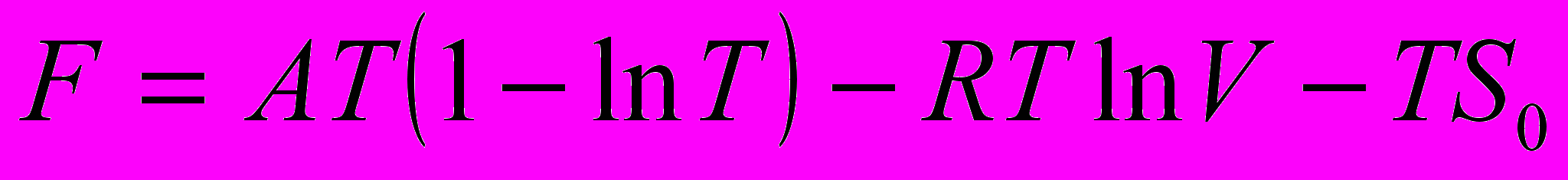, где А и S0 – константы. Доказать, что веществом системы является идеальный газ и выяснить физический смысл константы А.

Ответ: А = СV.

15. Уравнение состояния резиновой полосы имеет вид

,

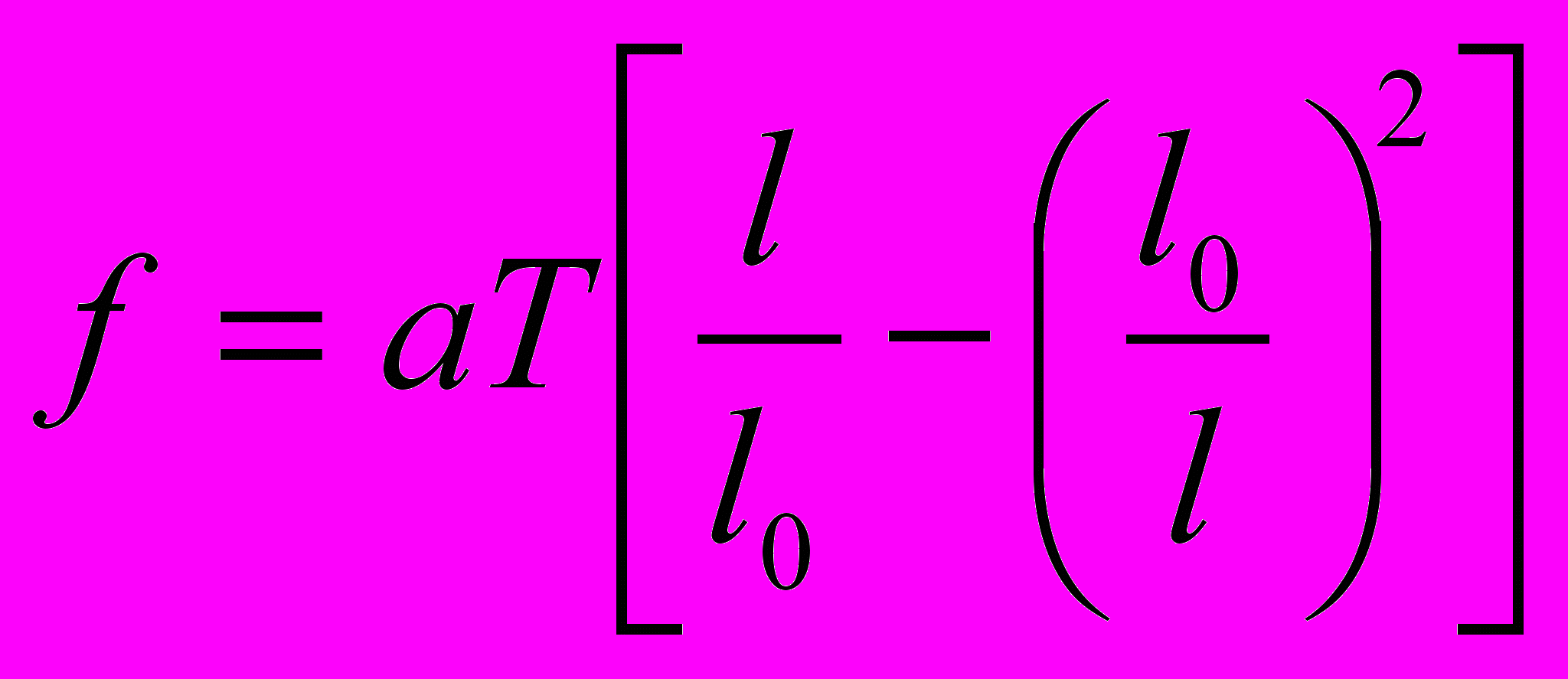где f – натяжение, а = 1.310-2 Н/К, l  длина, l0 = 1 м.

Найти изменение энтропии при изотермическом растяжении полосы от 1 м до 2 м. Внутренняя энергия при растяжении резиновой полосы зависит только от температуры.

Ответ:  0.013 Дж/К.


16. В замкнутый сосуд объема 22.4 дм3 поместили 1 моль кислорода и 1 моль водорода. Гремучую смесь подожгли. Какая максимальная масса воды может сконденсироваться в сосуде после охлаждения продуктов реакции до 100 oС?

Ответ: ~ 5 г


17. (11.6). Уксусная кислота при атмосферном давлении плавится при температуре 16.6 oС. Разность удельных объемов жидкой и твердой фаз кислоты равна 0.16 см3/г. При изменении давления на 40 атм температура плавления изменяется на 1 К. Найти удельную теплоту плавления уксусной кислоты.

Ответ: 185.6 Дж/г.


18. Давления насыщенного пара этилового спирта при температурах 313 К и 333 К равны 17.7 кПа и 47.9 кПа соответственно. Найти изменение энтропии при испарении массы 1 г этилового спирта, находящегося при температуре 323 К. Считать теплоту испарения постоянной в данном температурном диапазоне.

Ответ: 2.9 Дж/К.

19. (6.5). Найти критическую плотность воды, если критическое давление для воды равно Ркр = 218.3 атм, а критическая температура Ткр = 647.3 К, предполагая, что вода подчиняется уравнению Ван-дер-Ваальса.

Ответ: 0.189 г/см3.

20. (6.70). Критическая температура для гелия – 5.2 К. При какой температуре гелий в опыте Джоуля – Томсона должен охлаждаться?

Ответ: Т  35.1 К.

21. Жидкость плотности в хорошо смачиваемом ею капилляре поднимается на высоту h. Каково давление в жидкости на высоте h/3, если сосуд с капилляром находится в вакууме?

Ответ: P =  gh/3.

22. Определить работу, которую необходимо совершить, чтобы разделить сферическую каплю масла массой m = 1 г на капельки диаметром d = 21–4 см, если процесс дробления изотермический. Поверхностное натяжение и плотность масла равны соответственно = 26 дн/см и = 0.9 г/см3.

Ответ: ~ 8.7105 эрг.

23. При работе с отравляющими веществами опасно работать в комнате, когда они находятся в виде мелких капель, на примере разбитого ртутныого термометра. Оценить, во сколько раз давление пара над ртутью в виде капель с радиусом 10–6 см выше, чем над плоской поверхностью. При температуре 293 К коэффициент поверхностного натяжения ртути = 487 дин/см, молярная масса = 200.6, плотность = 13.55 г/см3.

Ответ: 1.81.

24. Оценить максимальный радиус капельки воды, которая будет испаряться при попадании в пересыщенный водяной пар, температура которого 369 К и давление 0.98105 Па. Давление насыщенного пара над плоской поверхностью при этой температуре 0.88105 Па, коэффициент поверхностного натяжения 0.06 Н/м.

Ответ: 6.510–9 м.

25. Скорости частиц с равной вероятностью принимают все значения от 0 до V0. Определить среднюю и среднеквадратичную скорости частиц, а также абсолютную и относительную среднеквадратичные флуктуации скорости.

Ответ: 0.5V0; V0/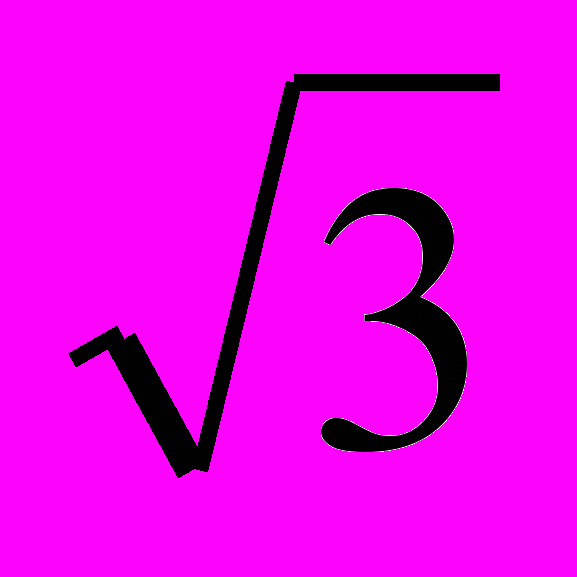; V0/2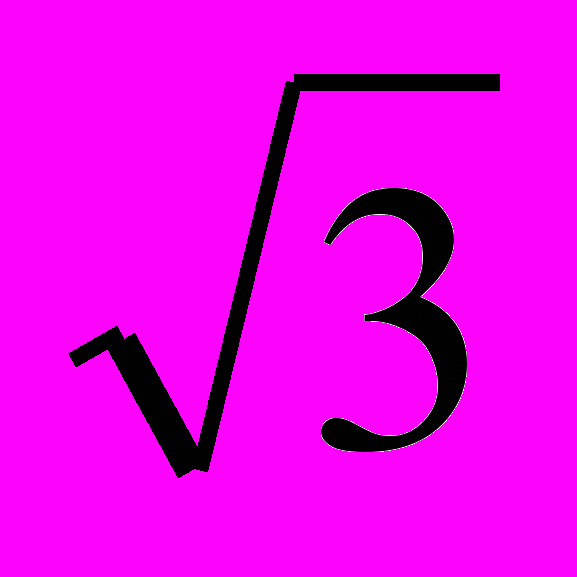; 1/.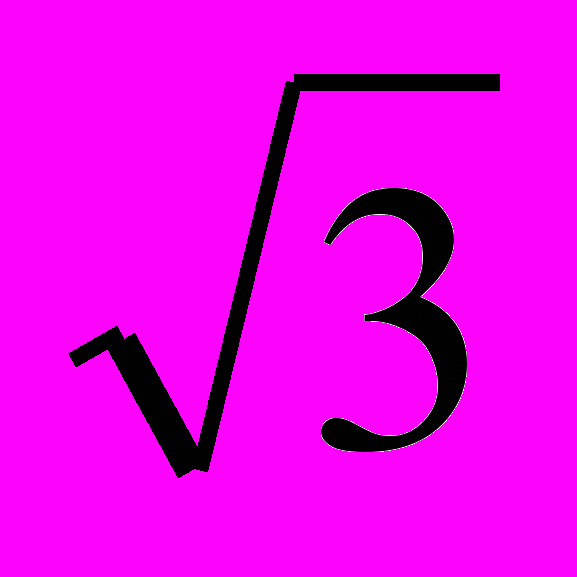

26. При какой температуре среднеквадратичная скорость молекул кислорода равна наиболее вероятной скорости молекул азота при температуре 27 оС?

Ответ:  44.4 оС.

27. Найти отношение средней квадратичной скорости молекул двухатомного газа к скорости звука в этом газе.

Ответ: 1.46.

28. Определить, на какой высоте в изотермической атмосфере плотность уменьшится в 5 раз, если известно, что на высоте 5.5 км она уменьшается в 2 раза.

Ответ: 12.8 км.

29. Молекула может находиться на двух уровнях: с энергиями 0 и 5.9710–21 Дж. Какова вероятность того, что при 250 оС молекула будет находиться на верхнем уровне?

Ответ: 0.304.


30. Потенциальная энергия частицы в магнитном поле может принимать два значения  . При какой температуре средняя энергия взаимодействия частиц с магнитным полем равна 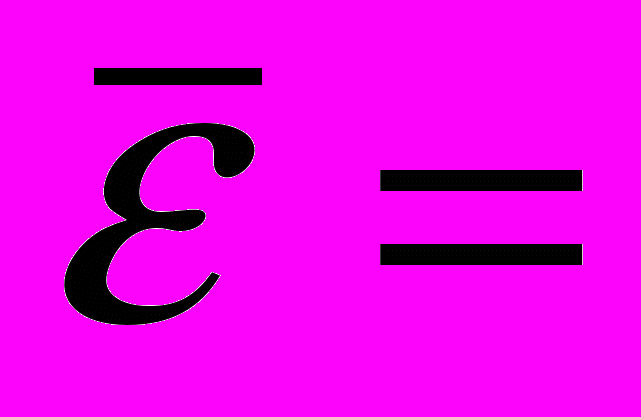/2?


Ответ: 2/(кln3).


31. Два тела с температурами 299 К и 300 К приведены в соприкосновение. От тела с большой температурой к телу с меньшей температурой перешло количество теплоты, равное 10–10 эрг. Во сколько раз вследствие этого перехода изменится вероятность состояния данных тел?

Ответ: ~ 3000.


32. Определить молярную энтропию кристалла, состоящего из двухатомных молекул типа АВ, при низкой температуре. Считать, что температура хоть и близка к абсолютному нулю, но все же достаточна, чтобы обеспечить разупорядоченность направлений.

Ответ: 5.76 Дж/(Кмоль).

33. (9.27). Известно, что тепловое движение механизма пружинных весов определяет при заданной температуре Т предел их чувствительности. Оценить предельно малую массу, которая может быть определена при однократном взвешивании на пружинных весах, если коэффициент жесткости пружины равен .

Ответ: .

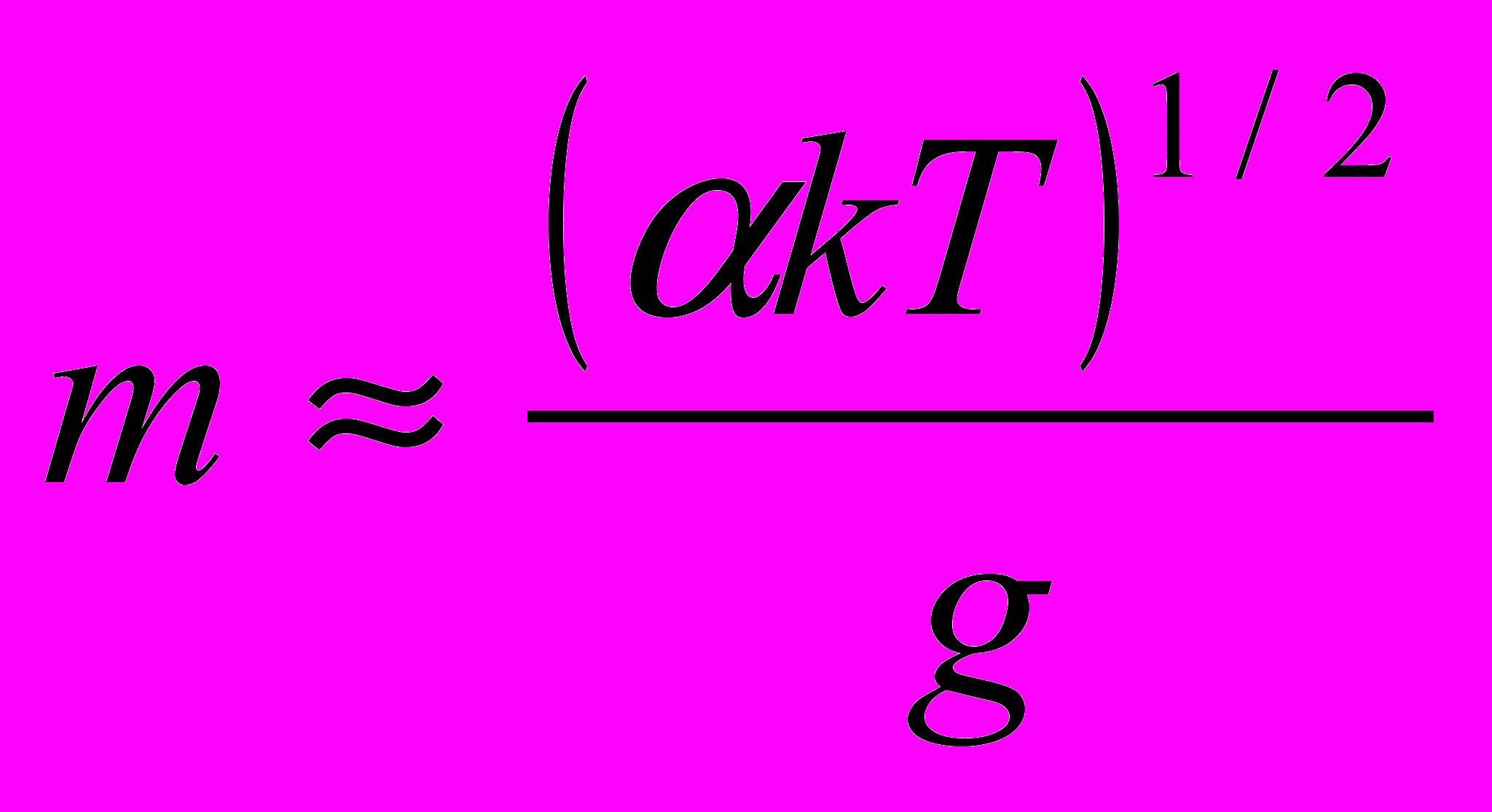34. Найти при 300 К среднеквадратичную относительную флуктуацию углового отклонения математического маятника, если длина маятника 10 см, масса 0.1 г.

Ответ: 6.510–9.

35. Оценить температуру, ниже которой можно не учитывать вращательные уровни для молекулы HD, если расстояние между атомами равно .

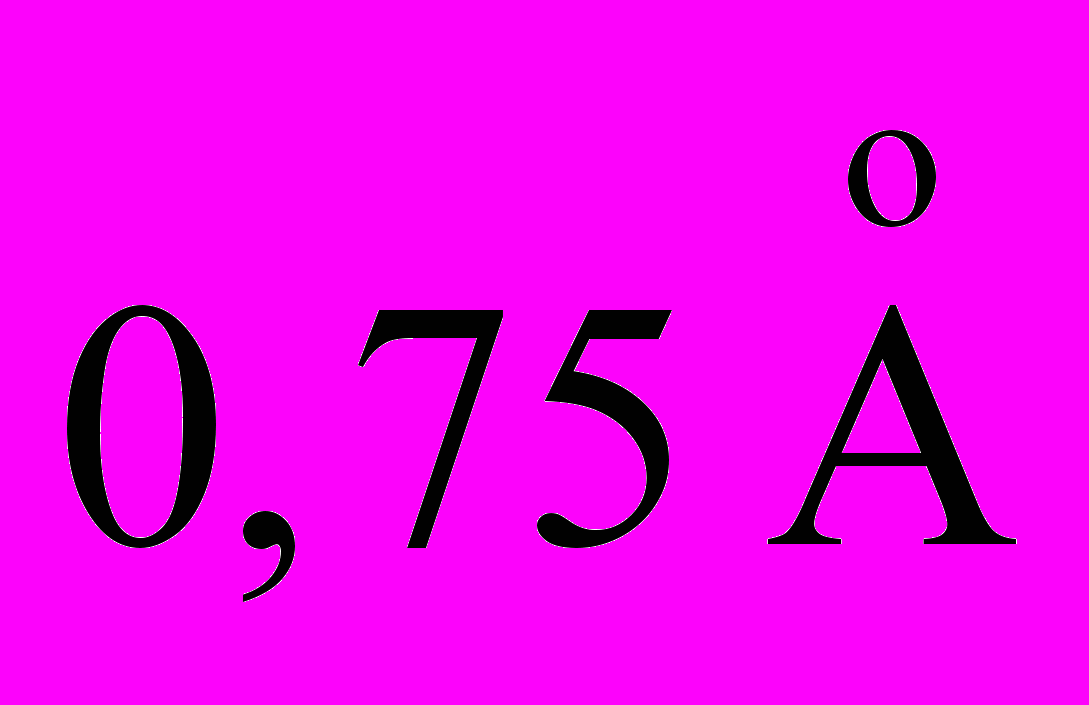Ответ: 64 К.

36. Собственная частота колебаний атомов = 1014 c–1 в молекуле Cl2. Оценить температуру, выше которой колебательную теплоёкость молекулы можно рассчитывать по классической теории. Какова будет при этом молярная теплоёмкость?

Ответ: 761 К; 7R/2.

37. (10.2). Сколько столкновений происходит ежесекундно в 1 см3 между молекулами кислорода, находящегося при нормальных условиях? Газокинетический диаметр молекулы кислорода d = 3.1∙10-8 см.

Ответ: 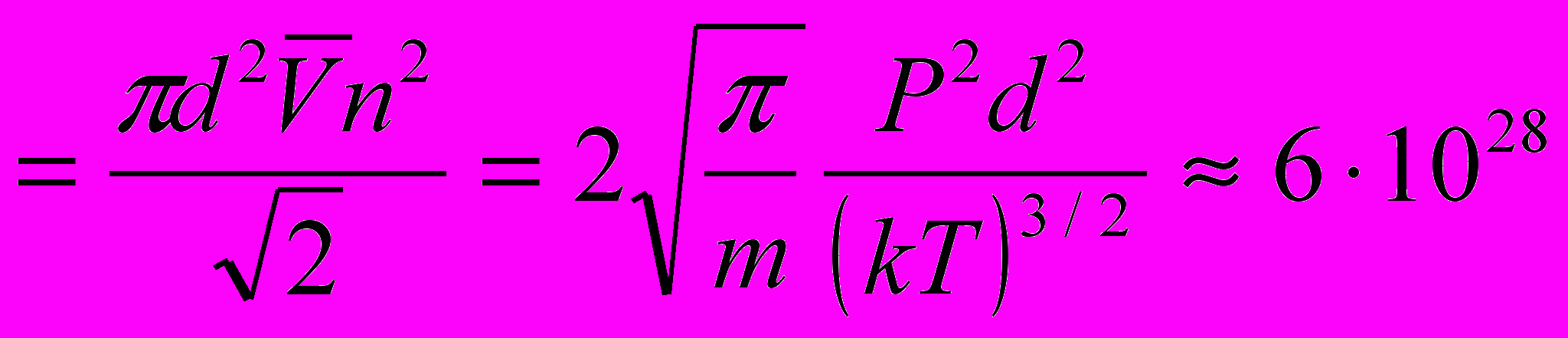см–3с–1.

38. (10.3). Идеальный газ нагревают при постоянном давлении. Как с изменением температуры изменяются длина свободного пробега и число столкновений его молекул в одну секунду z?

Ответ: ~ T; z ~ .

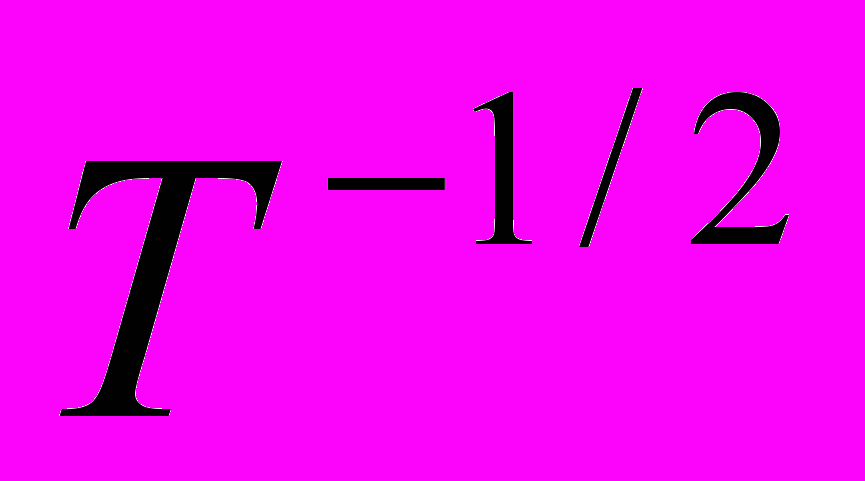39. Расстояние между стенками сосуда Дьюара равно l = 8 мм. Начиная с какого давления Р теплопроводность воздуха, находящегося между стенками сосуда, начнет уменьшаться при откачке? Температура воздуха Т = 290 К. Диаметр молекул воздуха d = 310-8 см.

Ответ: Р = 12.5 дн/см2 = 1.210–5 атм = 0.01 мм рт. ст.

40. Оценить значение средней длины свободного пробега и диаметр молекулы азота, если при 273 К и атмосферном давлении коэффициент вязкости равен 1.710–4 П.

Ответ: 0.910-5 см; 310–8 см.

41. (10.59). Оценить, на какое среднее расстояние l от своего исходного положения удалится за t = 10 c молекула воздуха при нормальных условиях, если средняя длина свободного пробега  = 610–5 см.

Ответ: ~ 2.5 см.

42. (10.99). Оценить размер алюминиевой частицы ( = 2.7 г/см3), взвешенной в жидкости с плотностью 0 = 1 г/см3 и вязкостью = 1 П, для которой скорость вязкого падения сравняется со скоростью теплового движения при комнатной температуре.

Ответ: 1.610–3 см.


43. Сосуд содержит равные массы гелия и азота. Как относятся массы газов, вытекающие из сосуда в вакуум через отверстие, размеры которого гораздо меньше длин свободного пробега обоих газов?

Ответ: гелия вытекает больше в 2.65 раз.


44. Два сосуда с идеальным газом соединены трубкой, диаметр которой заметно меньше длины свободного пробега в обоих сосудах. Температура в сосудах поддерживается постоянной и равной соответственно Т1 и Т2 = 2Т1. Найти отношение давлений Р2/Р1.

Ответ: .


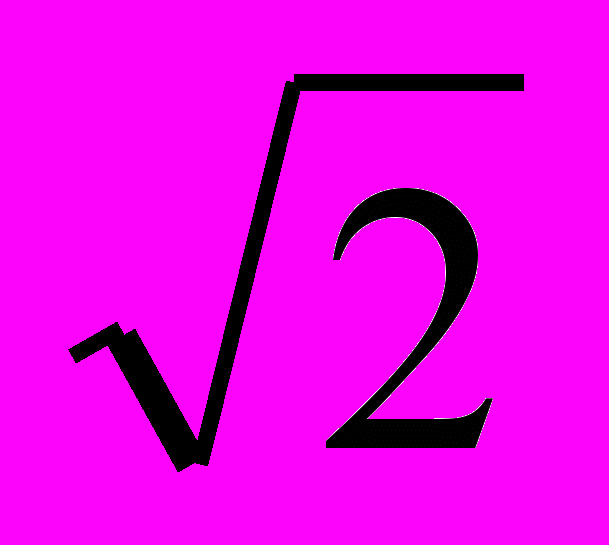Текстовые задачи I, II и III групп


Т-1. Длинный резиновый шнур изотермически растянули на 1 см, увеличив нагрузку на 0.1 Н. Не изменяя нагрузки, растянутый шнур нагрели, и его длина в результате нагрева уменьшилась на 4 см по сравнению с исхоной. Как надо после этого изменить нагрузку, чтобы при новой температуре длина шнура оказалась равной исходной?

Ответ: увеличить нагрузку на 0.4 Н.

T-2. В зимний день температура воздуха на улице, сначала равная 9ºС, понизилась ещё на 10ºС. Для обогрева комнаты используется тепловой насос, работающей между комнатой и улицей. Считая тепловой насос идеальной машиной, определить, во сколько раз при этом изменились затраты энергии для поддержания температуры в комнате, равной 21ºС.

Ответ: A2/A1 = 1.78.

Т-3. Тепловое расширение кристалла можно рассматривать на основе простой модели двух атомов, расположенных по соседству. Оценить величину коэффициента линейного теплового расширения, предполагая, что потенциальная энергия взаимодействия соседних атомов имеет вид: 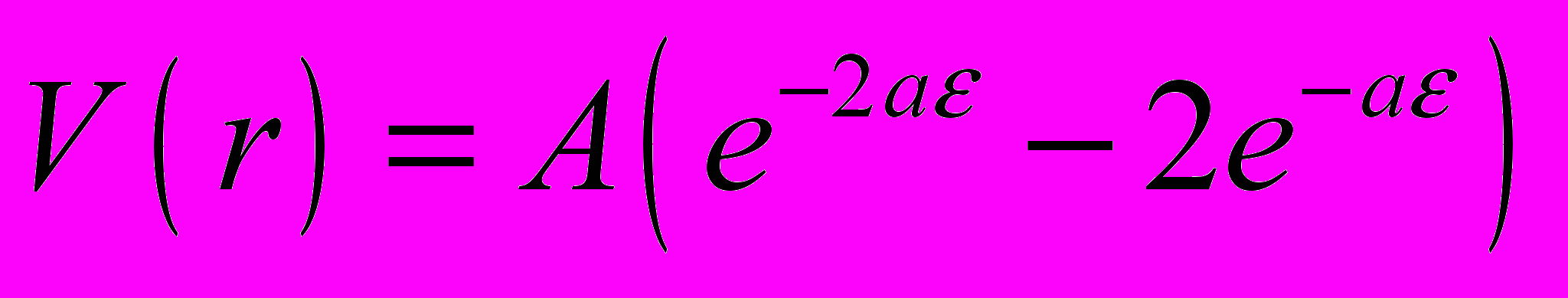, где А = 3 эВ; a = 1,5; 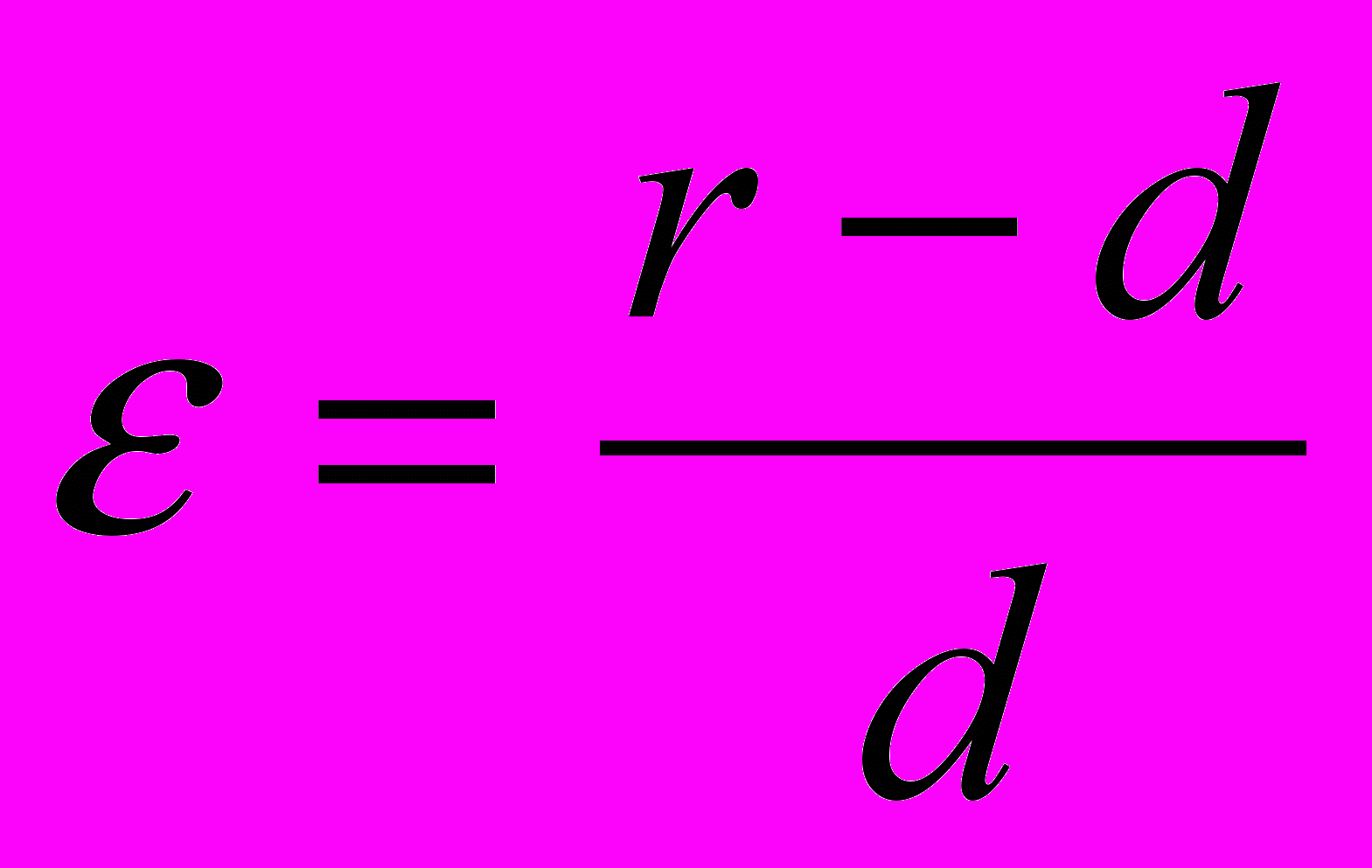, d – период кристаллической решётки.

Ответ: = 1.4∙10–5 град–1.

T-4. Расширение азота (N2) в процессе Джоуля-Томсона производится от описываемого уравнением Ван–дер–Ваальса начального состояния с температурой Т0 = 3Ткр (Ткр – критическая температура газа) до сильно разреженного, в котором газ можно считать идеальным. Найти начальный объём V0 и конечную температуру газа, соответствующие его максимально возможному охлаждению. Теплоёмкость СV не зависит от температуры. Критические параметры: Ткр= 126 К, Vкр = 114 см3/моль.

Ответ: 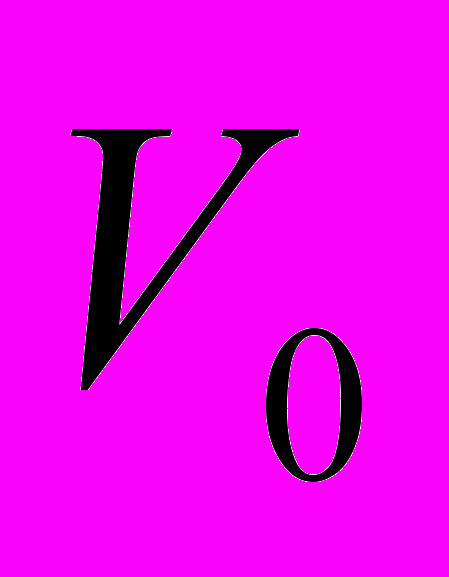= 114 см3/моль; = 351 К.

Т-5. В воздухе при нормальных условиях выделен объём V = 7.44∙10–20 см3. Какова доля времени, когда в этом объёме находится более двух молекул?

Ответ: 0.32.

Т-6. Сосуд разделен перегородкой на два различных объёма, так что в одном объёме содержится N1 атомов, в другом N2. Температура и давления газов одинаковы. Затем перегородку убирают, и газы перемешиваются. Вычислить изменение энтропии смешения, если а) газы различны и б) газы одинаковы. Газ – одноатомный, идеальный.

Ответ: а) ;

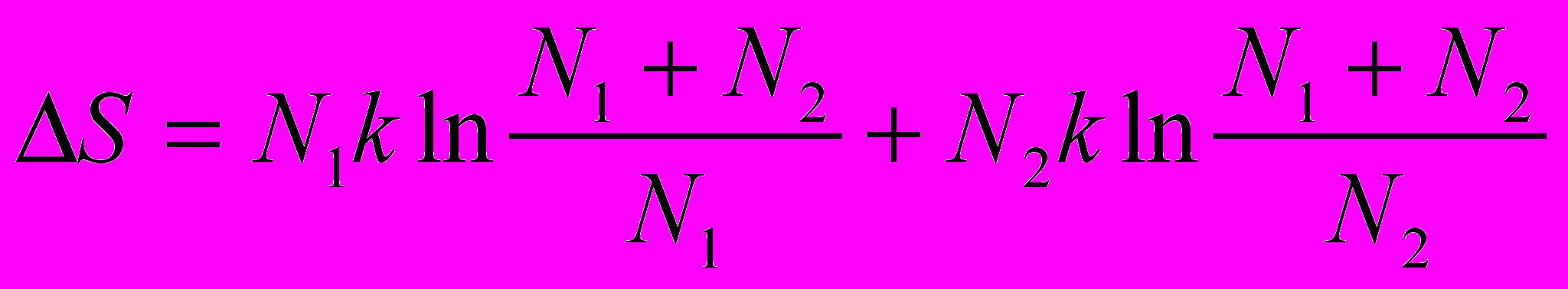б) .

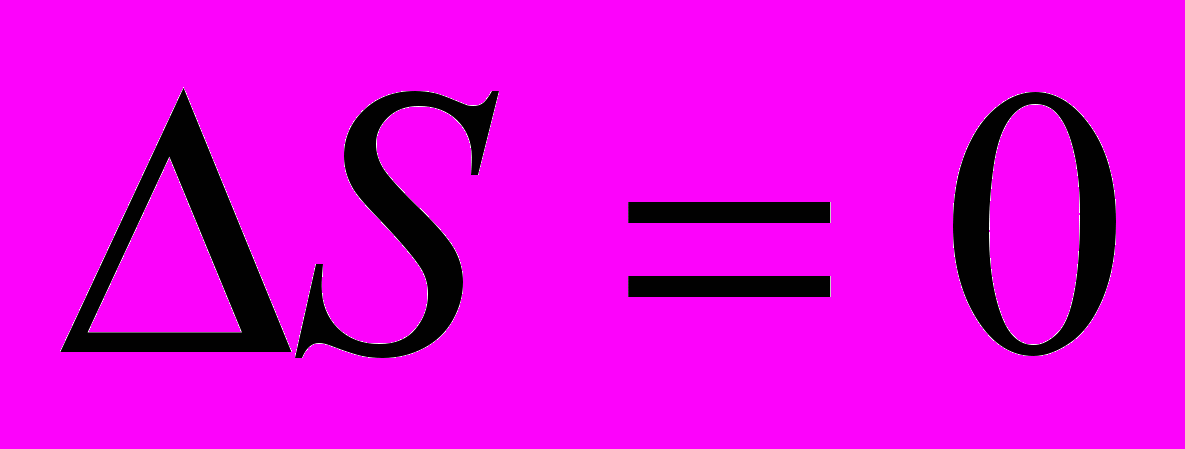T-7. Температура ансамбля квантовых гармонических осцилляторов, собственная частота которых равна 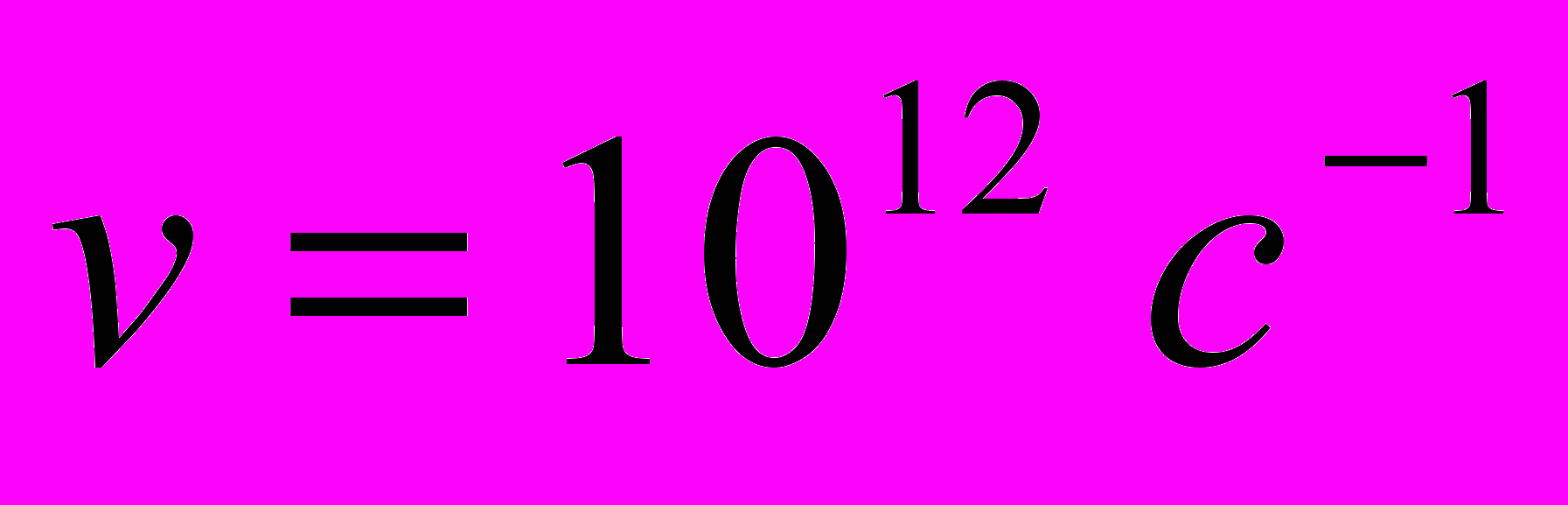, повысилась в 1.5 раза, при этом заселённость уровня с энергией 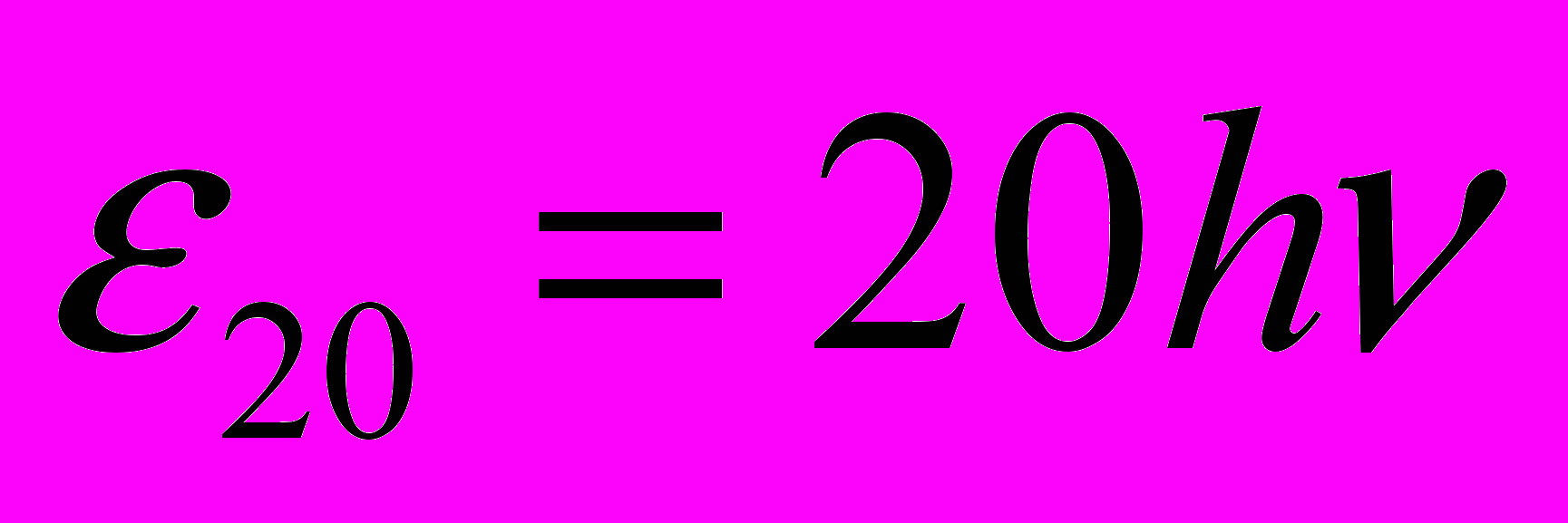(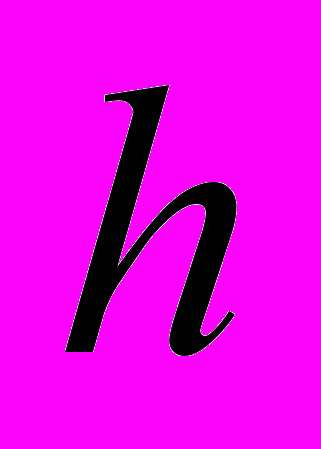— постоянная Планка) не изменилась. Определить начальную температуру ансамбля Т0, если можно принять, что .

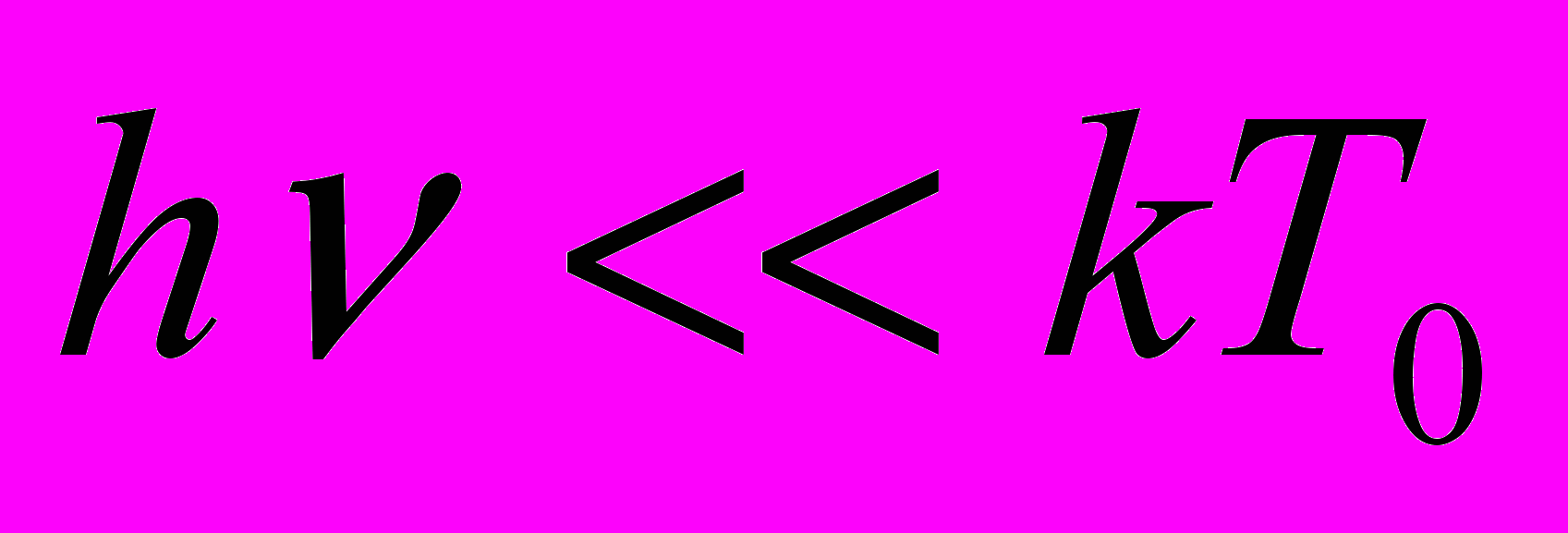Ответ: T0  781 K.

Т-8. Вычислить теплоёмкость моля одноатомного газа, состоящего из частиц, имеющих два дискретных уровня энерги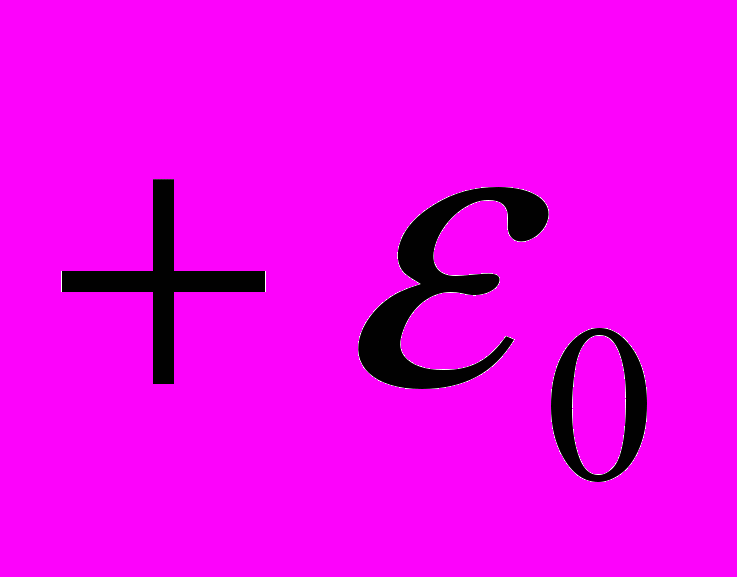и: и .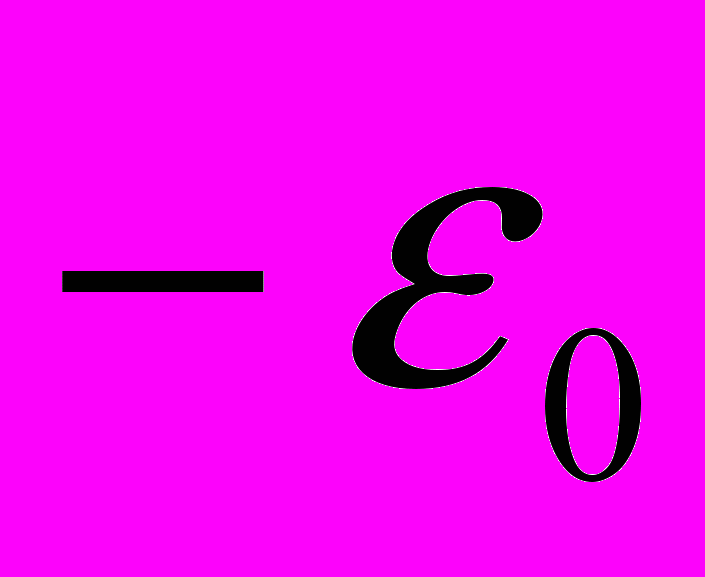

Ответ: 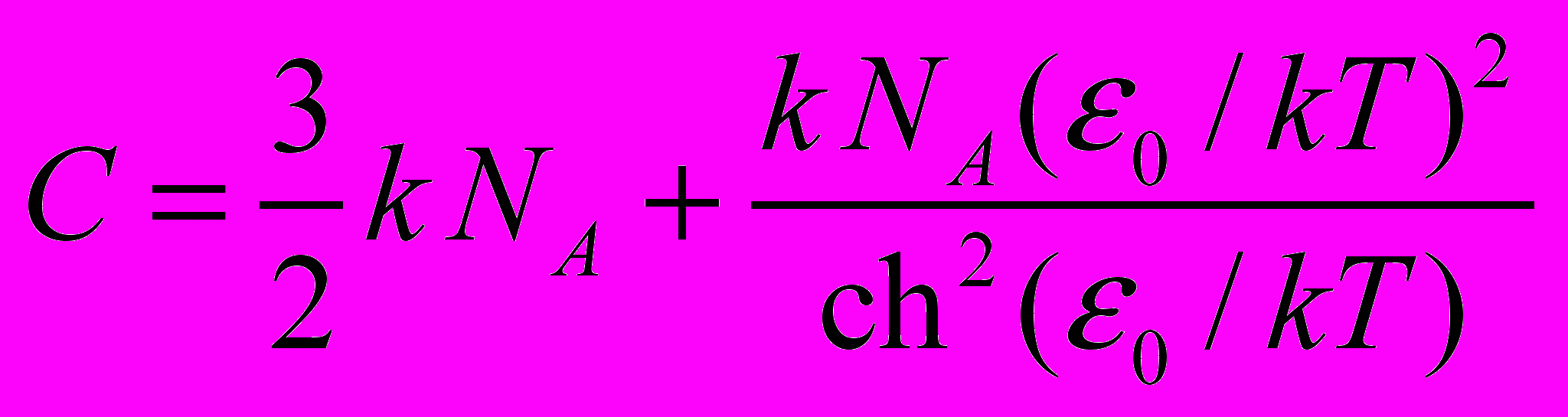,где 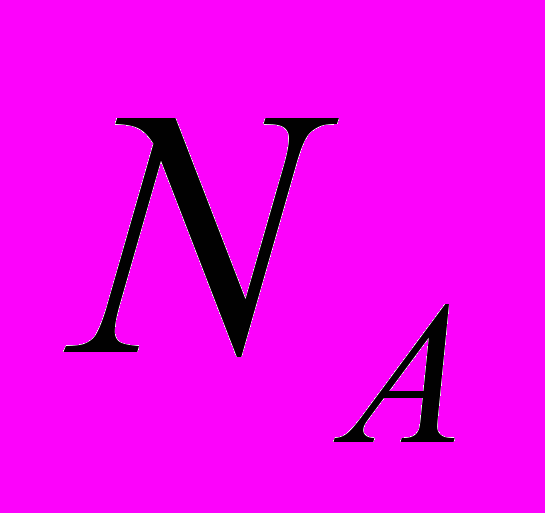– число Авогадро.


Усл. печ. л. 1,25 Тираж экз.