Старшинов Илья Донецкий национальный университет

Вид материала

Документы

Содержание Цель работы Экспериментальная процедура Выбор температуры Результаты и обсуждения

Подобный материал:

• Колонтай М. Я., Сунгатуллина, 46.25kb.
• В. А. Яковлева Донецкий национальный технический университет, 49.48kb.
• Общая гигиена и экология человека, 2520.44kb.
• Уважаемый коллега!, 100.29kb.
• Пособие рекомендовано к печати ученым советом Славянского государственного педагогического, 776.94kb.
• Донецкий национальный технический университет факультет экономики и менеджмента, 29.53kb.
• Информационное письмо международная научно-практическая конференция «актуальные проблемы, 37.7kb.
• Олимпиада для студентов старших курсов и выпускников вузов, поступающих в магистратуру, 32.2kb.
• Приглашени е гос вуз «Донецкий национальный технический университет» 17-20 апреля 2012, 67.89kb.
• Донецкий национальный университет учетно-финансовый факультет специальность: 0105 «Банковское, 201.14kb.

Старшинов Илья

Донецкий национальный университет

(Физика и астрономия)


Угловая зависимость коэффициента распыления при существенном вкладе термического механизма распыления


Ионное распыление материалов нашло множество применений в разных отраслях как фундаментальной, так и прикладной физики. Процесс ионного распыления является одним из базовых в современной микроэлектронике. Учет этого процессап играет важную роль в разработке ускорителей элементарных частиц и установок термоядерного синтеза. Распыление – один из прецизионных инструментов для нанотехнологии. Поэтому исследование механизмов распыления, сопровождающего взаимодействие ионов с поверхностью твердого тела, остается актуальным.

Процессы распыления обычно классифицируют по времени протекания [1]. Согласно классификации [1] они разделяются на быстрые (10^-15-10^-14 сек.) и медленные (10^-14-10^-12 сек.) столкновительные процессы, быстрые (10^-12-10^-10 сек.) и медленные (>10^-10 сек.) тепловые процессы. В диапазоне энергий падающих ионов от 1 до 100 кэВ основные закономерности распыления описываются каскадным механизмом, он считается доминирующим в таких условиях [2]. Однако до сих пор в ведущих исследовательских центрах делаются попытки выяснения вклада теплового механизма в общее распыление. В качестве критерия вклада используется идея Р.Келли [1], основанная на исследовании энергетического спектра распыленных частиц.

Столкновительные механизмы распыления связаны с выбиванием атомов либо падающим ионом, либо атомом каскада, который сформирован из атомов мишени, двигающихся за счет энергии, переданной им первичной частицей. Суть термического механизма заключается в том, что атомы, участвующие в каскаде столкновений, вызывают локальный перегрев поверхности (тепловой пик), который существует порядка 10^-12 - 10^-8 секунды. Этого перегрева иногда достаточно для того, чтобы вызвать испарение вещества с поверхности.

В настоящей работе рассматривается термический механизм распыления. Анализ основан на том факте [3], что угловая зависимость коэффициента распыления по термическому механизму может существенно отличаться от таковой при каскадном механизме. Особенностью настоящего рассмотрения является учет испарения образца вызванного макроскопическим разогревом ионным пучком.

В [3] был проведен расчет влияния угла падения ионов φ на выход распыления Y(φ) для термического механизма в модели Р. Келли [4]. Полученная угловая зависимость показана на рис. 1. Также на этом рисунке приведен ход зависимости Y(φ) для каскадного механизма, он может быть аппроксимирован Y(φ)~cos(φ)^-5/3[2,5]. Видно, что угловые зависимости принципиально отличаются для разных механизмов. Это отличие стимулировало попытку измерить угловую зависимость коэффициента распыления при существенном вкладе термического механизма. Для того, чтобы тепловые эффекты проявлялись ярко [4] можно увеличивать массу падающих частиц, либо увеличивать макроскопическую температуру мишени или выбирать материал с низкой энергией сублимации. В наших опытах был выбран цинк, как металл с одной из наименьших энергий сублимации и подбиралась температура мишени.

Первые эксперименты по измерению зависимости Y(φ), в условиях большого вклада термического механизма, в которых величина Y измерялась по глубинам кратеров в интервале 0^<φ<70^, показали [6] очень слабую зависимость Y(φ)~const. Такое поведение Y(φ) больше напоминает зависимость, рассчитанную для термического механизма, а не для каскадного. Однако при измерениях по глубинам кратера, существенным было влияние рельефа поверхности. Рельеф, развитый за время формирования кратера, нивелирует угловую зависимость т. к. становится трудно определить угол падения на мишень в каждой конкретной ее точке [7].

Цель работы

Была поставлена задача воспроизводимого измерения угловой зависимости коэффициента распыления при существенном вкладе термического механизма при малых дозах облучения (без развития рельефа). Поскольку выбор и стабилизация температуры были существенными условиями проведения эксперимента, особое внимание следовало уделить учету макроскопического нагрева образца распыляющим пучком, таким образом, чтобы измеренные значения коэффициента распыления не содержали вклада испарения вещества за счет разогрева мишени пучком.



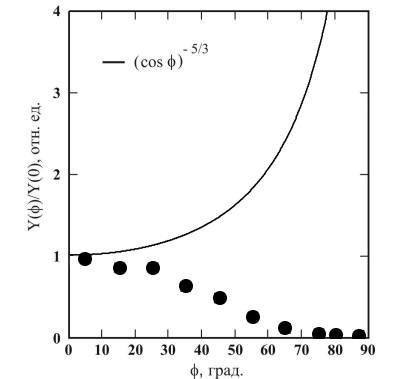
Рис1. Угловая зависимость коэффициента распыления.

Точки – расчет для термического механизма [3].

Экспериментальная процедура

Предварительно полированный образец Zn крепился в вакуумной камере на подогреваемом держателе и облучался пучком ионов Ar с энергией 20 кэВ. Плотность тока составляла от 10 до 40 мкА/см². Остаточное давление в камере составляло 1*10^-6 Тор.

Поскольку требовалось измерять изменения массы вещества обусловленного удалением с образца или осаждением на датчик ~ 10¹⁶ атомов, то для снятия угловой зависимости коэффициента распыления использовался метод кварцевого резонатора. Резонатор АТ среза работал на частоте f₀=4860 КГц в цепи автогенератора гармонических колебаний. В соответствии с [8] сдвиг частоты f(t) (f(t)=f₀-f(t), где f(t) - зависимость частоты генератора от времени), обусловленный изменением массы резонатора пропорционален скорости распыления образца. Тогда производная от изменения частоты связана с коэффициентом распыления:

d(f(t))/dt = k ∙ Y, где k- постоянная.

Кварцевая пластинка крепилась жестко под углом порядка 45^ на расстоянии 5 см от образца. Для исключения влияния осаждения на кварц паров цинка кристалл накрывался металлическим корпусом, в котором размещалась диафрагма диаметром 7 мм. Температура мишени регистрировалась с помощью хромель-алюмелевой термопары и универсального вольтметра В7-21, она поддерживалась постоянной с помощью компьютера. Угол падения ионов φ изменялся от 0^  до 75^   с помощью вращения держателя вокруг оси.

Время экспозиции составляло порядка 5-7 минут для каждого значения температуры или угла падения φ. Частота регистрировалась частотомером Ч3–41 с точностью ±1 Гц. Ее изменение составляло от 40 Гц/мин до 200 Гц/мин при облучении при разных температурах. Для учета влияния φ на геометрию сбора распыленного материала, дополнительно была измерена угловая зависимость распыления меди и определены корректирующие коэффициенты на основе сравнения измеренной кривой с Y(φ) для Cu, представленной в [9].


Выбор температуры

Для выбора оптимальной температуры мишени была измерена температурная зависимость коэффициента распыления Zn. Критерием выбора этой температуры являлось условие резкого возрастания зависимости Y(Т). Зависимость Y(Т) приведена на рис 2. Она находится в хорошем согласии с результатами работы [10]. При температурах больше 200^ C было заметно испарение образца без облучения. Показанная на рис. 2 кривая построена с учетом этого испарения, и отражает только распыление. Как видно из рис. 2. резкий рост коэффициента распыления наблюдается при температуре около 230^  С. При температуре 250^  С коэффициент распыления возрастает на порядок. Угловая зависимость коэффициента распыления измерялась при температуре 235^ С, что позволяло чувствовать локальный перегрев мишени.




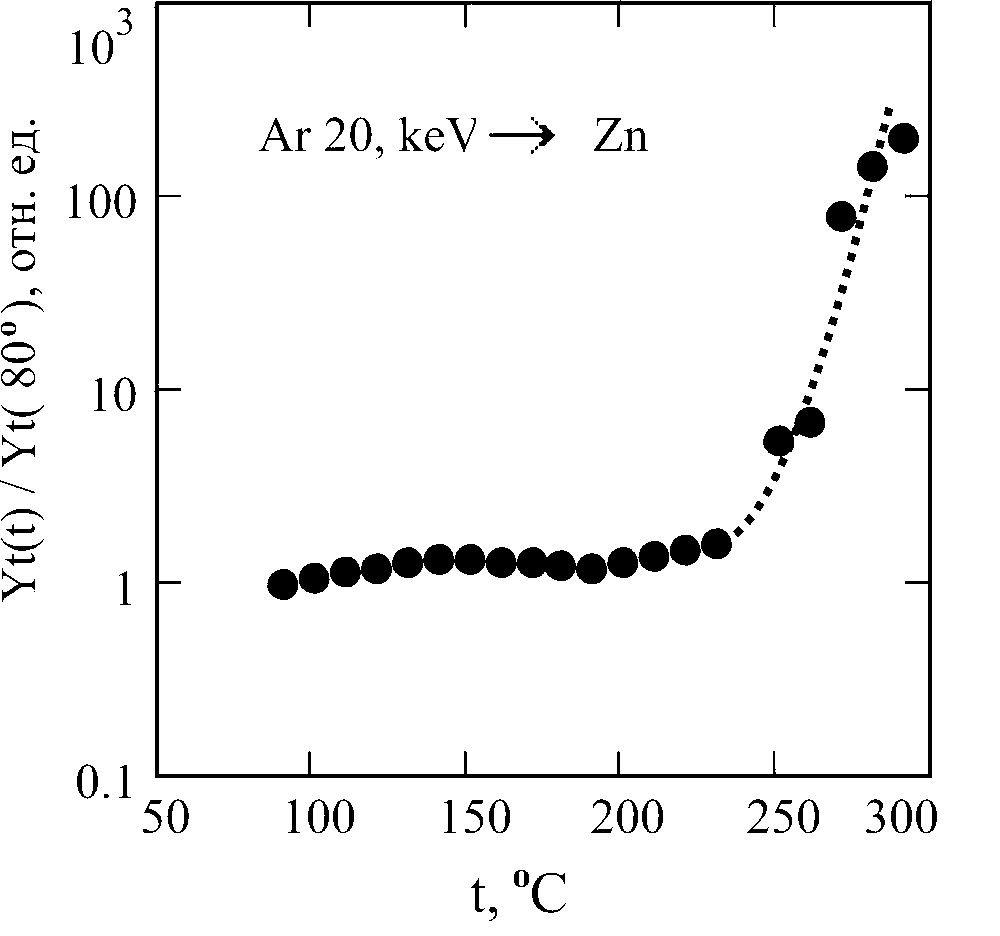
рис. 2. Температурная зависимость коэффициента распыления цинка.


Влияние температуры держателя образца на частоту генерации датчика представлено на рисунке 3. Рис. 3(а) показывает временную зависимость температуры держателя образца после включения нагревателя и ее временную стабильность. Рис. 3(б) показывает изменение частоты генератора при нагреве. Немонотонная зависимость изменения частоты от температуры соответствует классической кривой из [8]. Насыщение, достигаемое к 50 минуте разогрева показывает отсутствие дрейфа частоты при условии достаточно длительного предварительного разогрева. Программа – терморегулятор реализовывала пропорционально – интегральный закон поддержания температуры, точность поддержания температуры составляла ±1^ при всех изменениях параметров эксперимента.



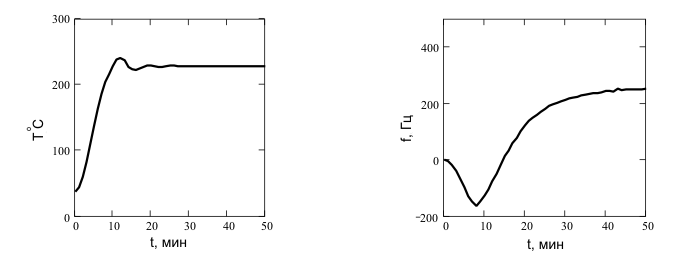
а б


Рис.3. Временные зависимости температуры держателя образца (а) и изменения частоты кварцевого генератора (б).


Результаты и обсуждения


1. Угловая зависимость с учетом разогрева распыляющим пучком. Временная зависимость изменения частоты (кривая 1) и производная по времени (кривая 2) для облучения при температуре 235^ показаны на рис. 4 а.




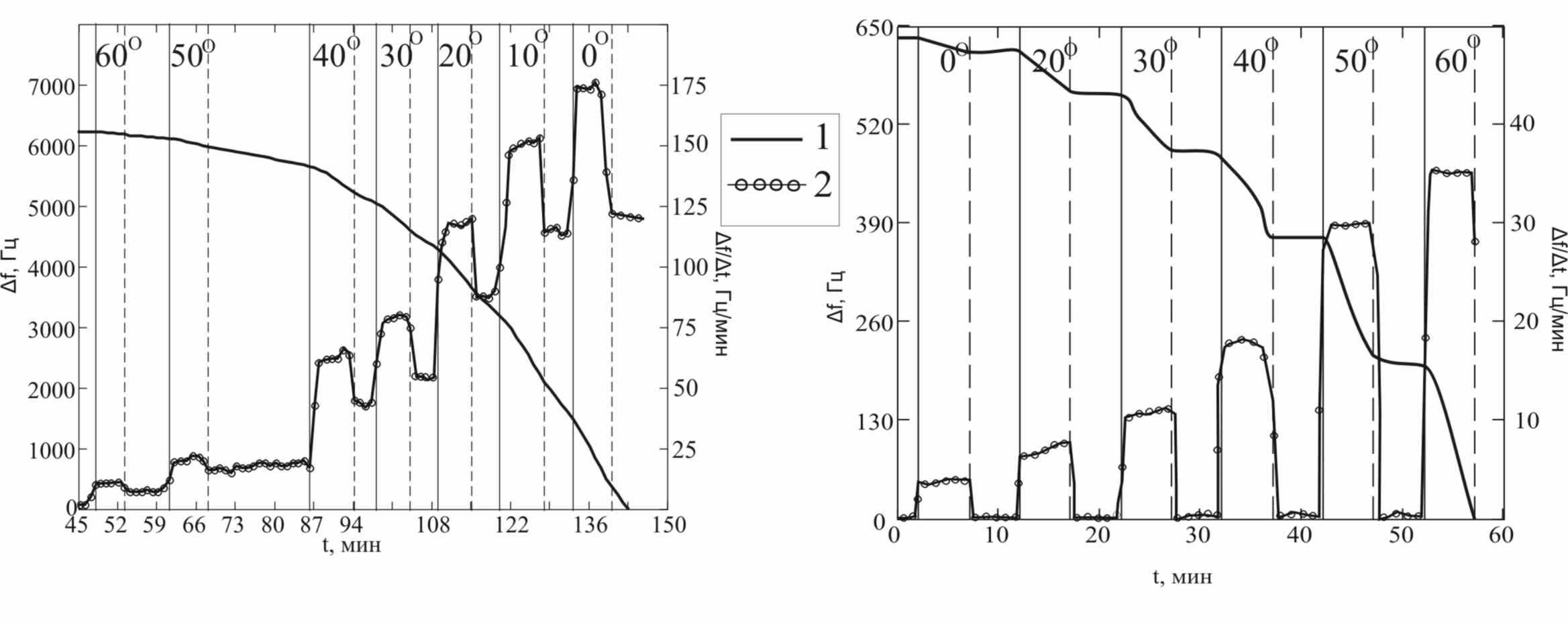
а б

Рис. 4. Зависимости изменения частоты f от времени – кривые 1 и зависимости производной изменения частоты (df/dt) от времени – кривые 2 для различных температур образца: а) 235^ С; б) 35^ С.


Вертикальные сплошные линии показывают момент открытия пучка, пунктирные линии – отмечают момент прекращения облучения образца. На графике, для каждого интервала в котором производилось облучение, указан угол, при котором оно происходило. Значение коэффициента распыления соответствующее определенному углу падения вычислялось как среднее значение производной за интервал времени облучения при этом угле падения. При вычислении величины, пропорциональной коэффициенту распыления производилась перенормировка, связанная с изменением плотности тока на поверхности при увеличении φ.

Из приведенных на рис. 4а зависимостей видно, что в паузах между облучением наблюдалось падение частоты не связанное с распылением материала. Это падение частоты было вызвано осаждением на кварцевую пластину материала, испаряющегося вследствие макроскопического разогрева образца. Для учета этого испарения вычислялась средняя скорость изменения частоты во время пауз между облучениями. Коэффициент распыления считался как разность значения среднего значения df/dt во время облучения и значения этой производной в последующей паузе без облучения. Угловая зависимость коэффициента распыления при T~230C;, найденная из соответствующих зависимостей на рис. 4а представлена на рис 5 (кривая 1).

На рис. 4б представлены аналогичные зависимости для процесса распыления при температуре близкой к комнатной. Эти зависимости показывают отсутствие испарения в паузах между облучением. Угловая зависимость коэффициента распыления, найденная из соответствующих зависимостей на рис. 4б представлена на рис 5 (кривая 2). Все зависимости на рис. 5 нормированы на соответствующие значения при φ=0^.

Сравнение кривых 1 и 2, представленных на рис. 5 с соответствующими зависимостями, приведенными на рис 1, показывает, что увеличение температуры образца приводит к изменению формы угловой зависимости до вида, который характерен для термического механизма распыления.

2. Влияние рельефа. Последовательность измерения кривых 1 и 2, показанных на рис. 5 позволяет утверждать, что доза облучения мала и вид зависимости 1 не связан с влиянием рельефа. Так, угловая зависимость при T=235C снималась до измерений при комнатной температуре, следовательно, доза облучения при ее измерении была меньше чем при низкотемпературном исследовании. Т.о. рельеф был более сильно развит при исследованиях при 35^ С.




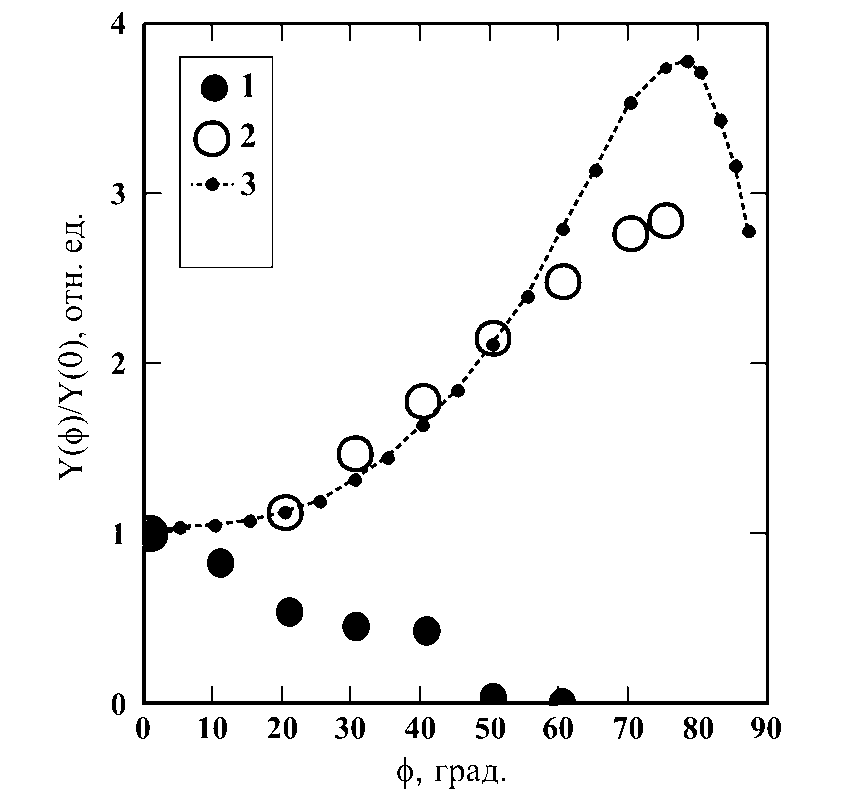
Рис. 5. Угловая зависимость выхода распыления Zn при облучении его Ar⁺, 20 кэВ:

1) T=235^ C; 2) Т = 35^ С; 3) расчет по SRIM-2003.


С использованием программы SRIM 2003 было произведено моделирование угловой зависимости коэффициента распыления Zn ионами Ar 20 кэВ. Программа SRIM моделирует выход распыления по столкновительному (каскадному) механизму. Расчетная зависимость приведена на рис. 5 (кривая 3). Видно, что угловая зависимость, снятая на холодном образце воспроизводит кривую для каскадного механизма, что позволяет сделать вывод о том, что рельеф не оказал существенного влияния на вид угловой зависимости при термическом механизме.

Различия в форме угловых зависимостей для каскадного и теплового механизмов распыления обусловлены влиянием ориентации пучка на условия выхода каскада на поверхность [2], влиянием ориентации на начальные и граничные условия развития теплового пика [4,3].

Заключение. Впервые экспериментально с учетом испарения вещества при повышенной температуре показано, что угловая зависимость выхода распыления в условиях, когда основной вклад в процесс дает термический механизм, соответствует модели Р.Келли [4]. Рельеф, который формируется на поверхности образца при малых дозах не вносит принципиальных изменений в вид угловой зависимости выхода распыления. Исследование угловой зависимости выхода распыления может быть более точным и дешевым методом выявления вклада термического механизма, чем изучение энергетического спектра распыленных частиц.

Литература

1. Р. Келли в сб. //Ионная имплантация в полупроводники и другие материалы: сб.статей.- 1980.- С.194-235.
   
2. Распыление твердых тел ионной бомбардировкой Ч-I//Под ред. Р·Бериша.-М. Мир, 1984- С.336.
   
3. И.А. Мельничук, В.Н. Варюхин, А.А. Богунец // Поверхность. №12, 2004, С.31-35.
   
4. R. Kelly // Radiation Effects. 1977. V. 32. P. 91.
   
5. P. Sigmund // Phys. Rev. 1969. V. 184. № 2. P. 383
   
6. И.А. Мельничук, А.А. Богунец, И.Н. Старшинов//Взаимодействие ионов с поверхностью, ВИП 2005. Мат XVII Межд. конф. М. 2005. т.1. стр. 140-142.
   
7. Жукова Ю.Н., Машкова Е.С., и др. // Изв. РАН. Сер. физ. 1994. Т. 58. №3. С. 92.
   
8. Альтшуллер Г. Б., Елфимов Н. Н., Шакулин В. Г. Кварцевые резонаторы: справочное пособие. М.: Радио и связь, 1984. – 243 стр.
   
9. E.S. Mashkova, V.A. Molchanov // Rad. Effects. 1987. V, 102, pp.125-141.
   
10. Пранявичус Л., Дудонис Ю. Модификация свойств твердых тел ионными пучками. – Вильнюс.: Мокслас, 1980.-242 с.