Сравнение типовых методов анализа и синтеза машинного агрегата …
| Вид материала | Документы |
СодержаниеS – номер гармоники ряда Фурье; – амплитуда гармоники; i Исходные данные для расчёта Список литературы |
- Программа курса «электрохимические методы анализа», 20.91kb.
- Распределенная информационная система анализа, синтеза и моделирования сау, 31.72kb.
- Формирование навыков фонематического анализа и синтеза у младших школьников, 190.12kb.
- Магистерской программы «Методы анализа и синтеза проектных решений», 31.38kb.
- Рекомендации по определению мер инженерно-технической защиты информации, 273.48kb.
- Математические модели и методы анализа и синтеза эвакуационных планов крупных городов, 254.84kb.
- Вопросы к экзамену по аналитической химии для студентов химического отделения физико-химического, 46.33kb.
- 05. 13. 12 Системы автоматизации проектирования (машиностроение), 22.99kb.
- Международная научная конференция «Информация, сигналы, системы: вопросы методологии,, 63.03kb.
- Отчет о научно-исследовательской работе за 2008 год Тема нир: Разработка новых нанотехнологий, 100.77kb.
Сравнение типовых методов анализа и синтеза машинного агрегата …
УДК 621.01(075)
В. В. РОМАНОВ, В. А. ЛЯСИЧ, Д. Е. ЛОПАТИН
СРАВНЕНИЕ ТИПОВЫХ МЕТОДОВ АНАЛИЗА И СИНТЕЗА МАШИННОГО АГРЕГАТА С МЕТОДОМ М. З. КОЛОВСКОГО
Созданный проф. М. З. Коловским метод динамического анализа и синтеза машинного агрегата (МА) постепенно завоёвывает все большую популярность. Как известно, этот метод предложен в качестве альтернативы методам анализа и синтеза, разработанным Виттенбауэром и Мерцаловым в начале XX века применительно к маховикам паровых машин. Если в качестве источника движения используется электродвигатель, то эти методы оказываются существенно некорректными. Как показывает опыт использования метода М. З. Коловского в учебном процессе КГТУ, точность расчёта постоянной составляющей приведённого момента инерции, как привода, так и МА в целом, существенно повышается.
Для расчёта постоянной составляющей
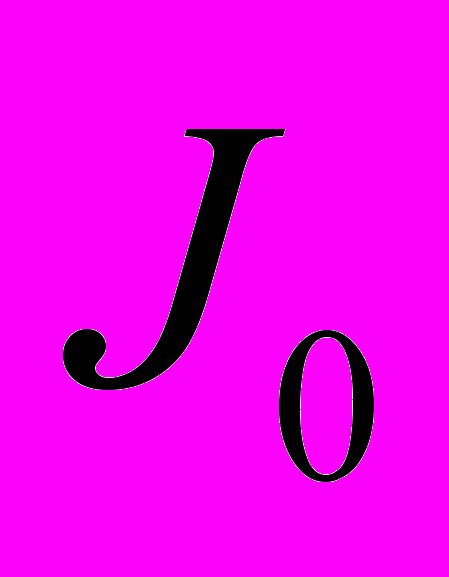приведённого момента инерции МА по заданному коэффициенту неравномерности движения [] звена приведения воспользуемся соответствующими формулами из работ [1, 2, 3] с некоторыми изменениями. Тогда  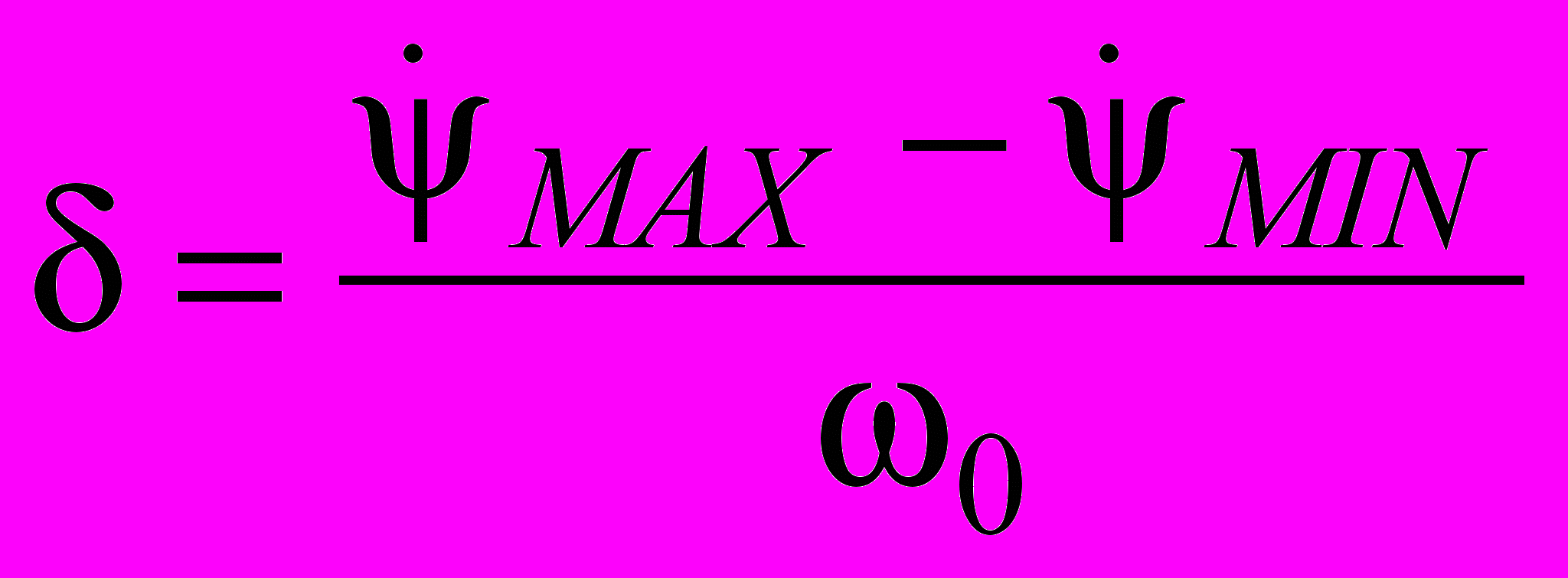, | (1) |
где 0 – средняя угловая скорость звена приведения;
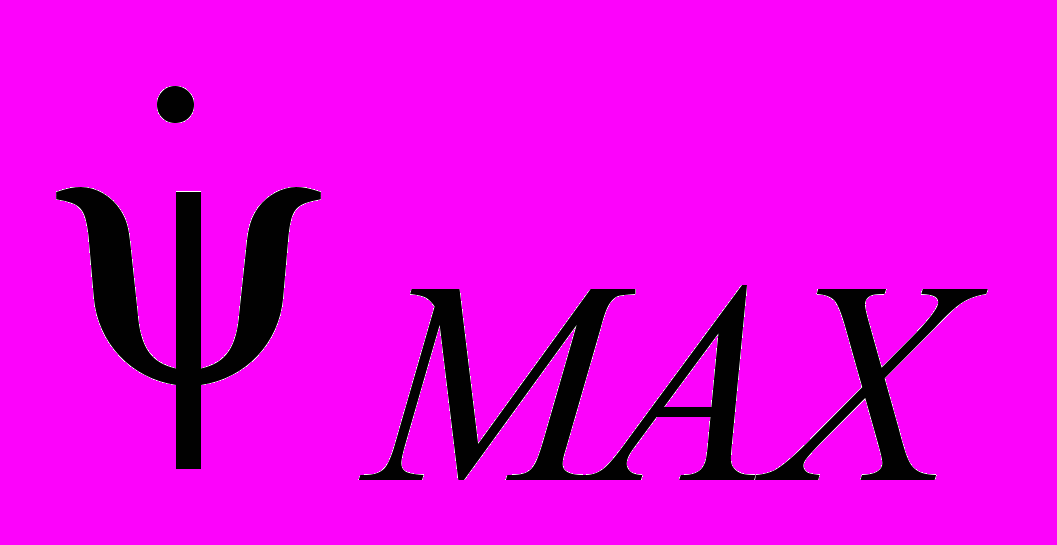и 
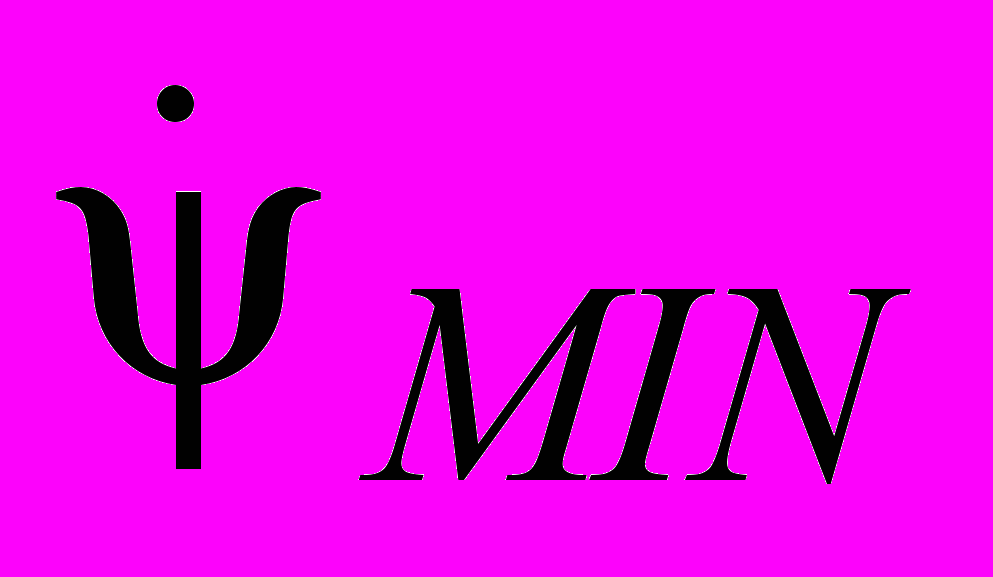– наибольшее и наименьшее отклонение скорости от 0. В этих работах наибольшая динамическая ошибка по скорости
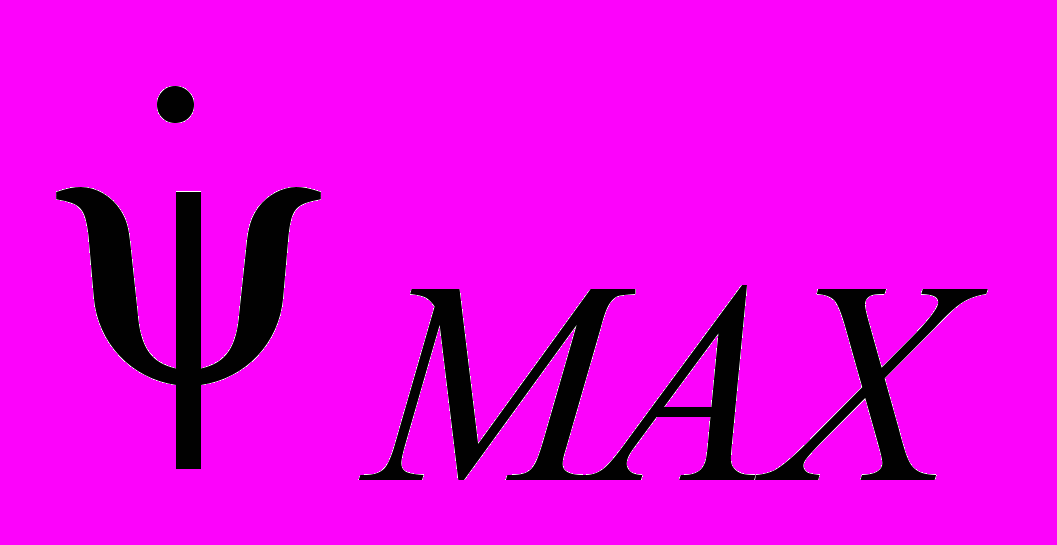определяется по амплитуде первой или, что точнее, доминирующей гармоники ряда Фурье, пренебрегая ролью других гармоник. Допустим, что для всех гармоник ряда выполняется условие:  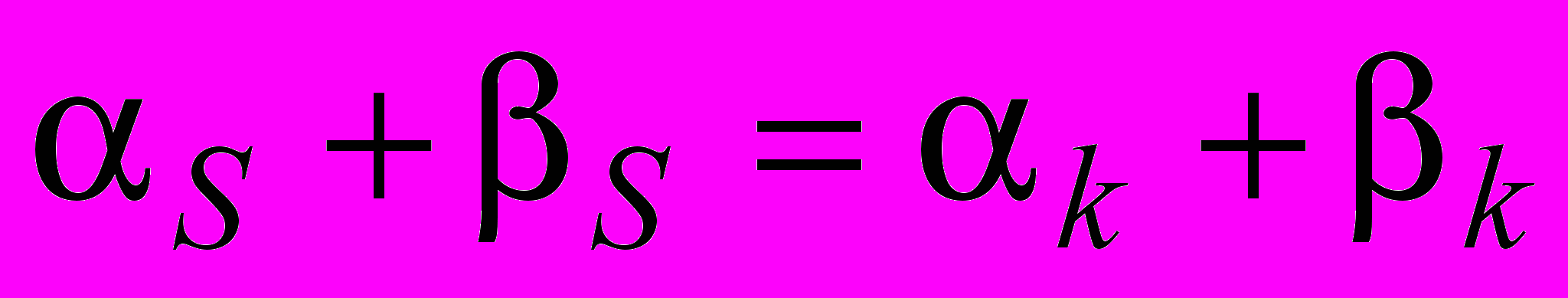, | (2) |
т. е. начальная фаза одинакова у всех гармоник. Тогда
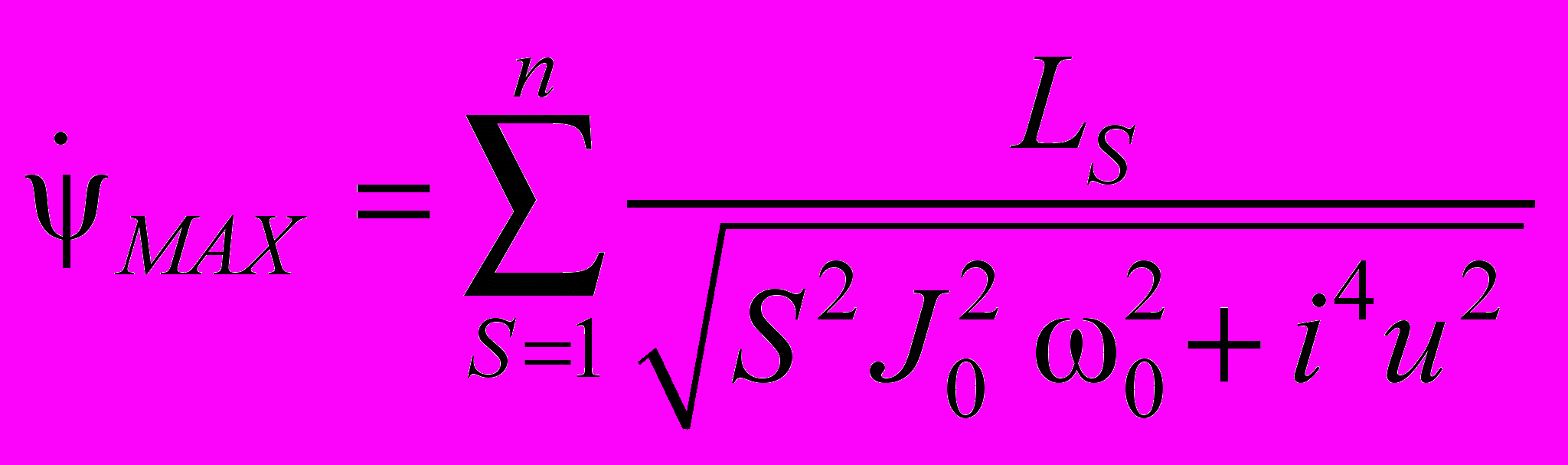 , | (3) |
где S – номер гармоники ряда Фурье;
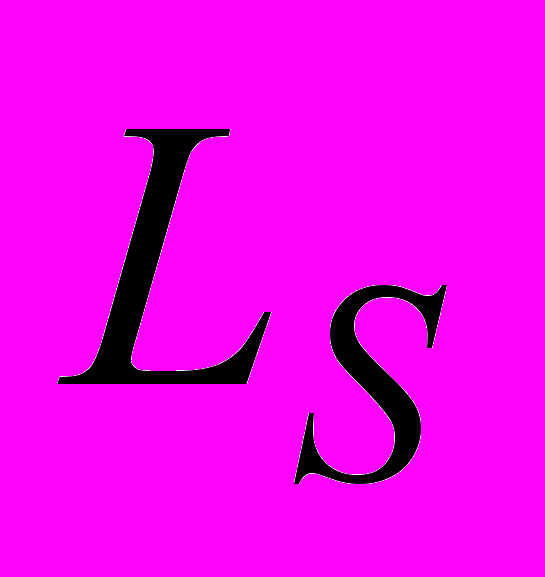– амплитуда гармоники; i – передаточное отношение от двигателя до звена приведения; u – крутизна механической характеристики двигателя. Точность формулы (3) при допущении (2) тем выше, чем сильнее одна из гармоник динамической ошибки доминирует над остальными.
Полагая, что
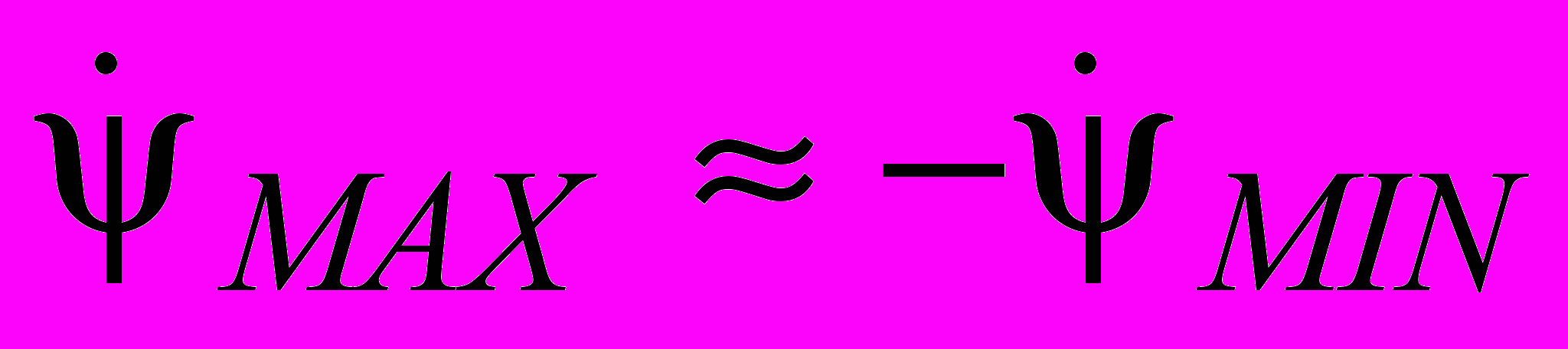, перепишем формулу (1) в виде:  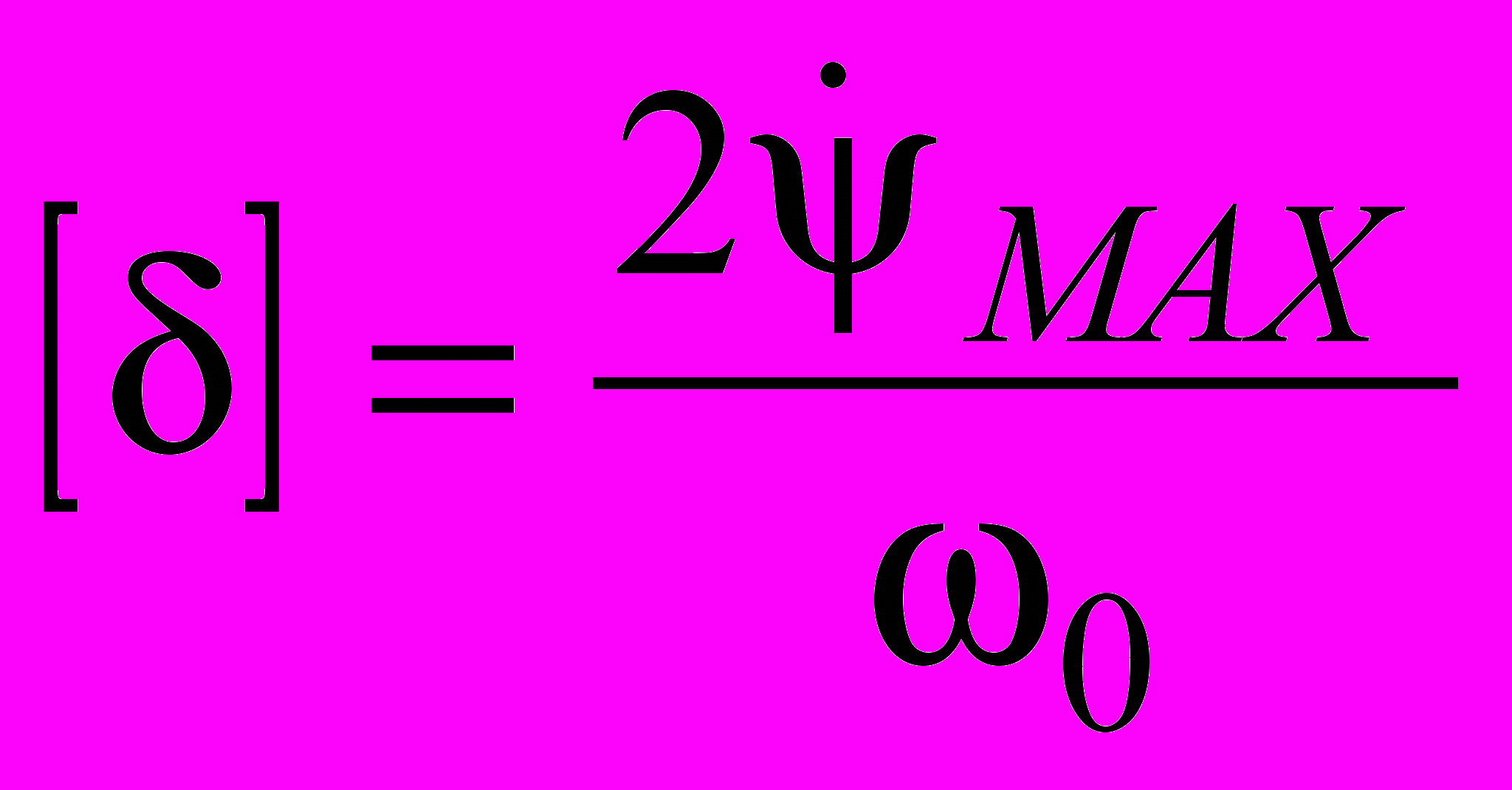. | (4) |
После подстановки (3) в (4) получим
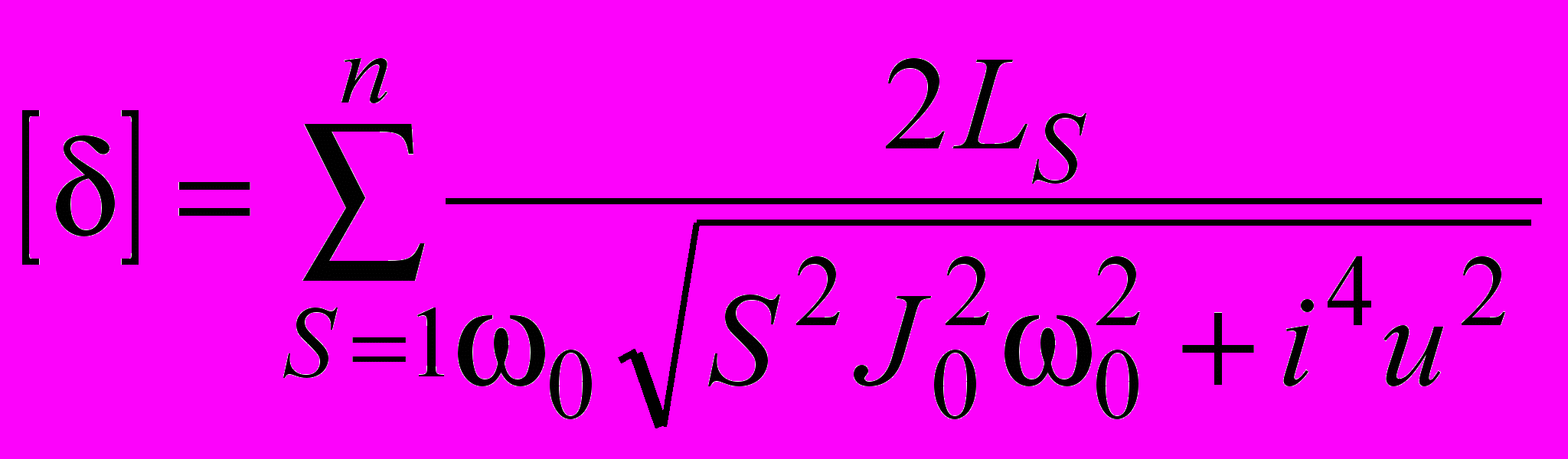 . | (5) |
Отсюда получаем уравнение
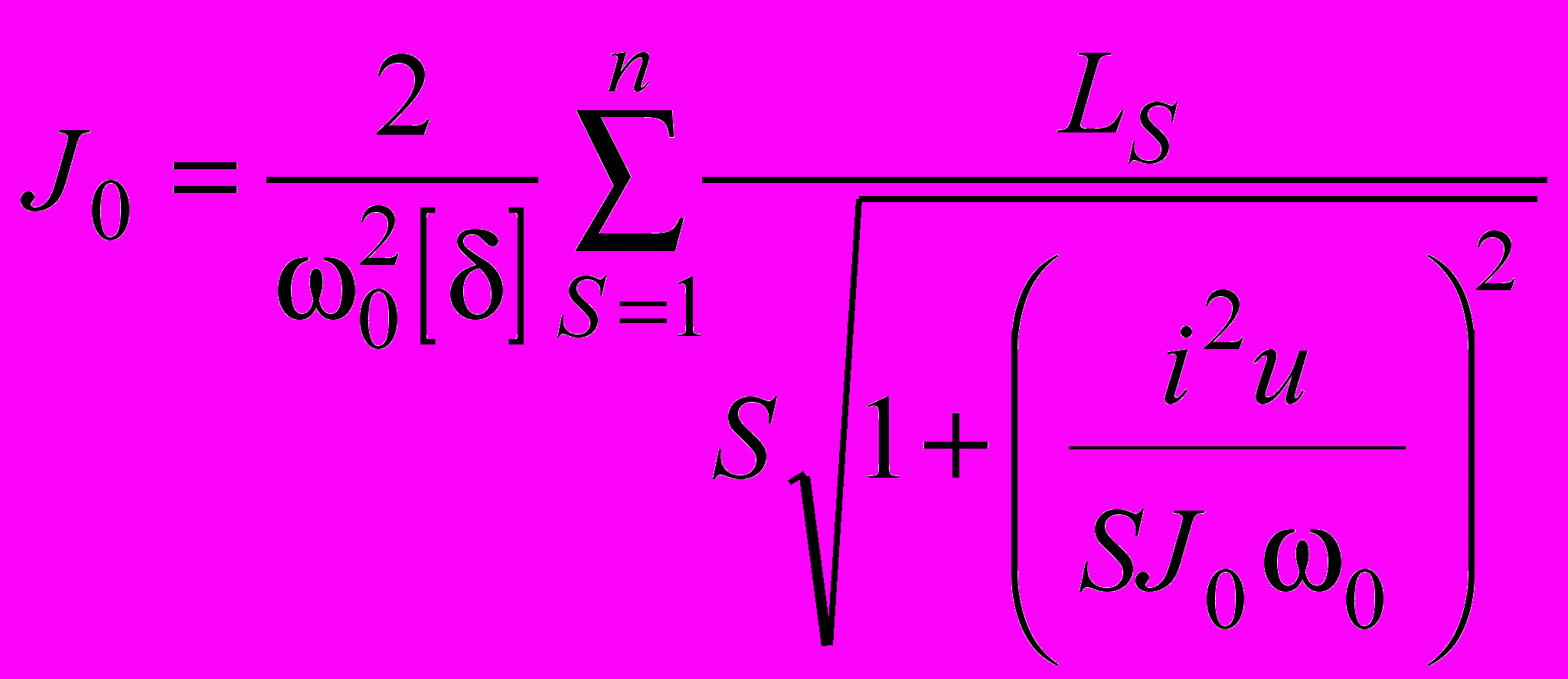 . | (6) |
Уравнение (6) решается методом последовательных приближений. Согласно [4] предлагается под знак корня подставить
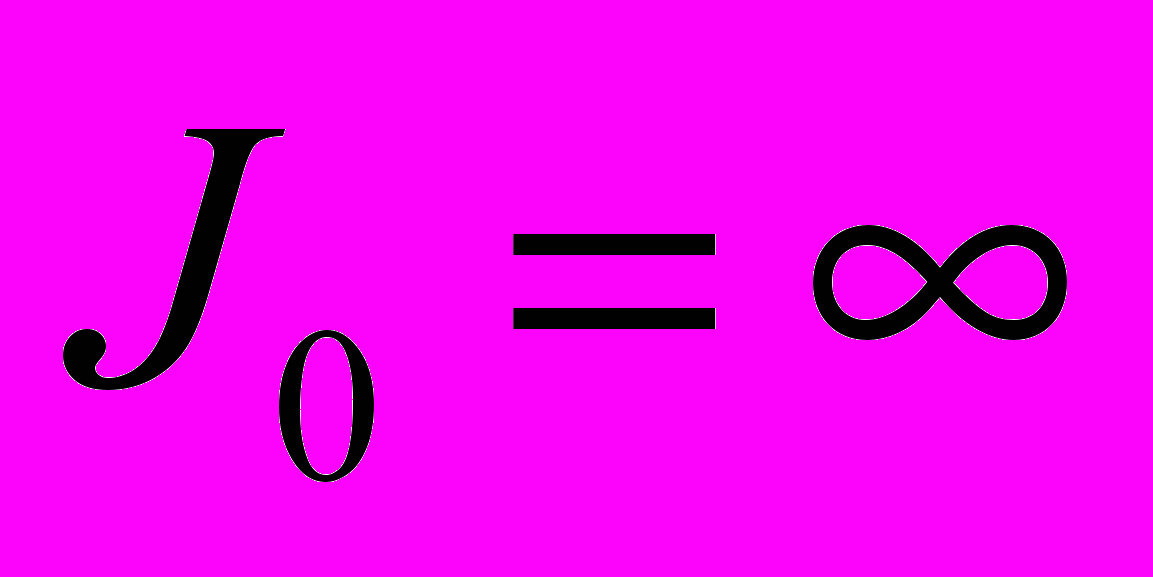. Тогда в нулевом приближении  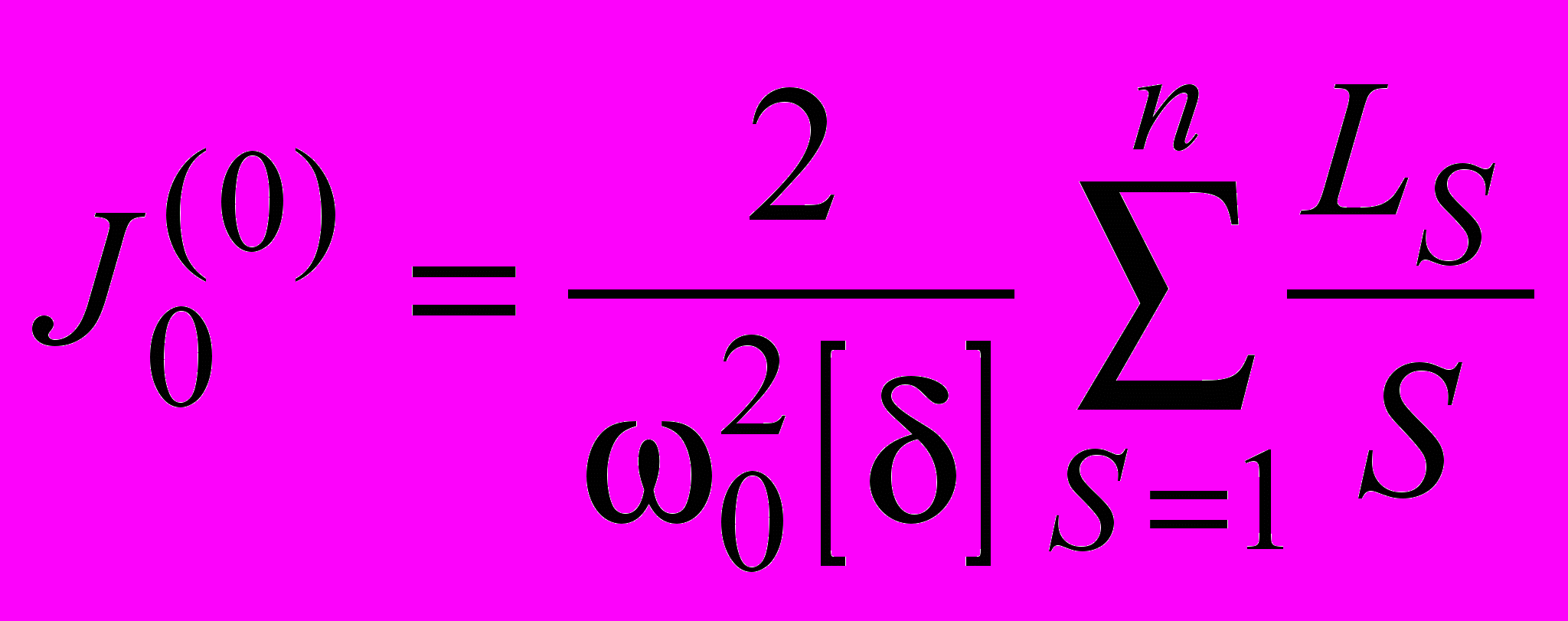, | (7) |
в первом приближении
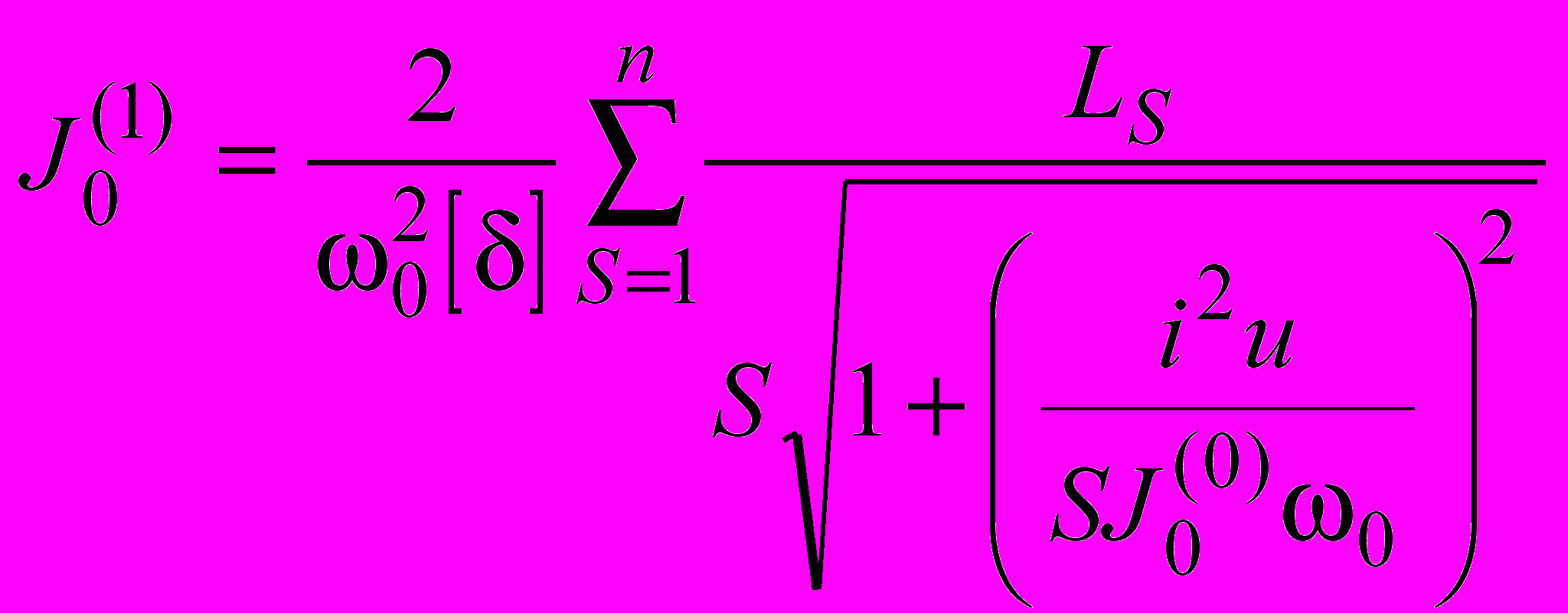 | (8) |
и т. д. Решение ведётся до такого приближения, когда последующий результат будет отличаться от предыдущего на 1 – 2 %.
Высокую корректность метода Коловского можно продемонстрировать на примере и сравнить результаты с решением, которое приведено в учебном пособии под редакцией А. С. Кореняко [5] для поперечно-строгального станка, кинематическая схема которого представлена на рис. 1.
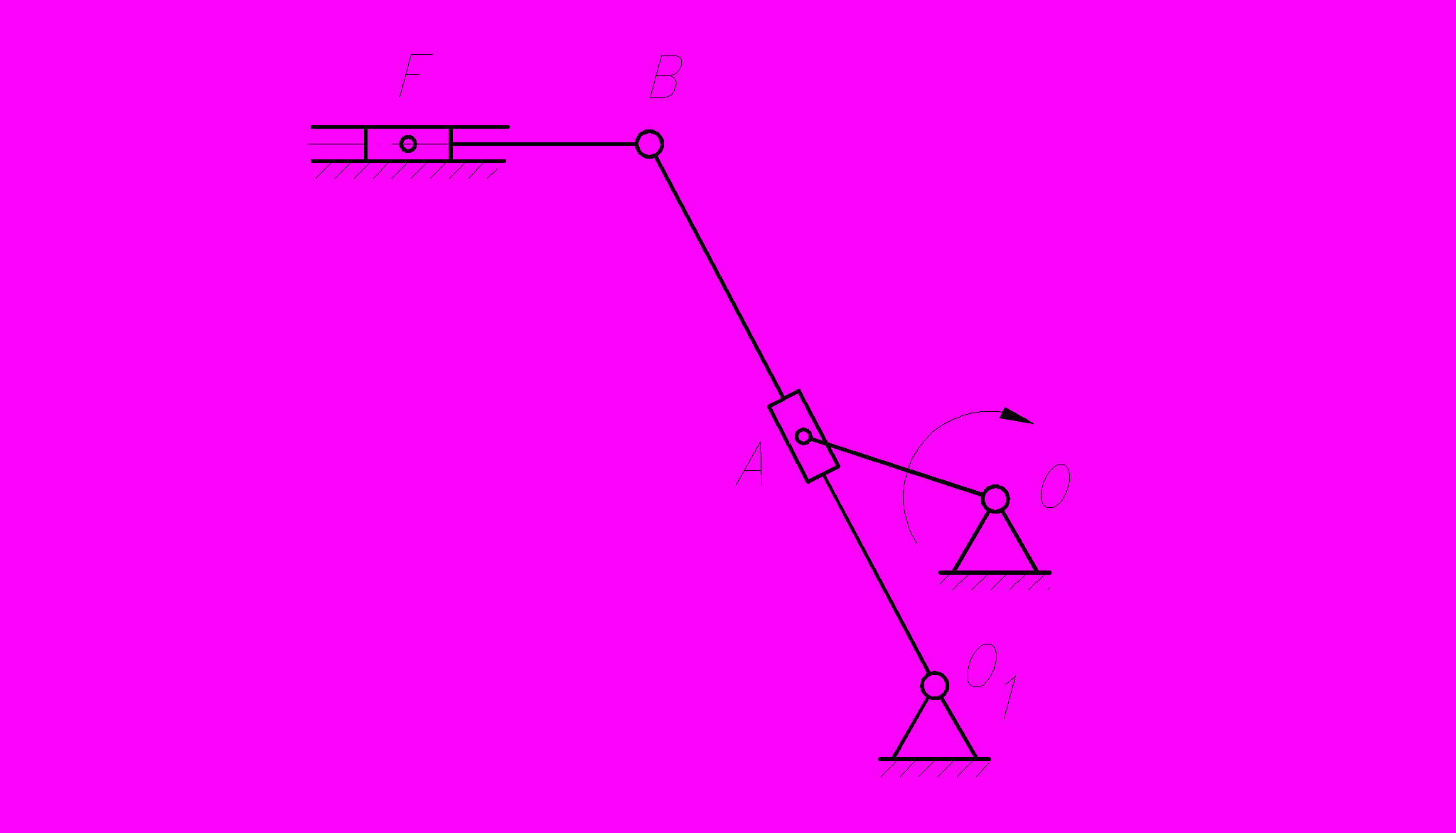
Рис. 1. Схема шестизвенного кулисного механизма поперечно-строгального станка
Звено приведения – кривошип ОА. Приведенные моменты сил МПР и моменты инерции JПР взяты из [5] и сведены в табл. 1. Коэффициент неравномерности движения звена ОА [] = 1/30. Передаточное отношение от двигателя до звена приведения i = 20. Момент инерции маховика на валу звена, рассчитанный по методу Мерцалова, JMX = 159 кгм2 [5]. Расчёт постоянной составляющей приведённого момента инерции по методу Коловского осуществлялся по тем же данным. Дополнительно учитывались: реальная мощность двигателя, равная 4 кВт [6], номинальная частота вращения двигателя 1430 об/мин, момент инерции ротора двигателя JP = 0,01125 кгм2 и [] = 1/30. Постоянная составляющая приведённого момента инерции привода
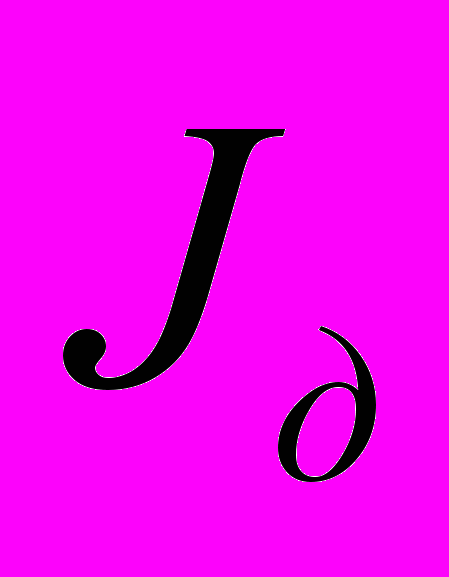получилась равной 49,1 кгм2. Учитывая, что 
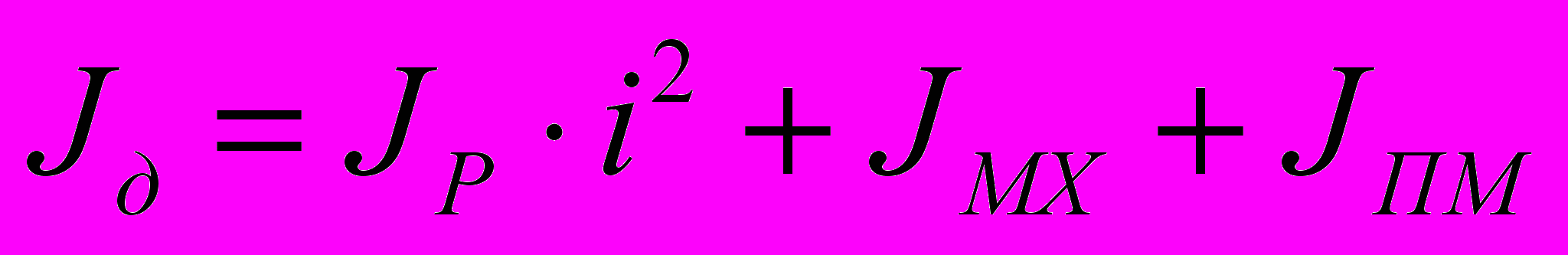(здесь 
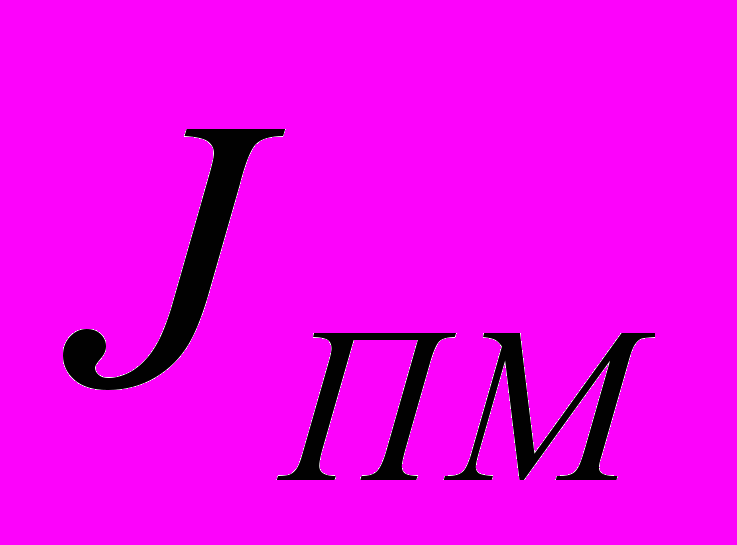– приведённый момент инерции передаточного механизма), момент инерции маховика примерно на половину меньше 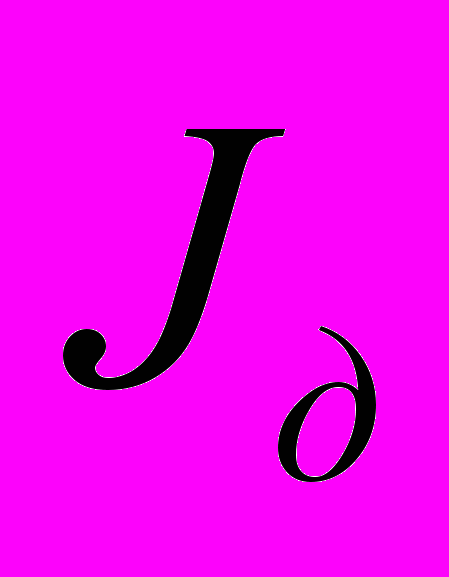. Из полученного результата видно, какую ошибку дает расчёт 
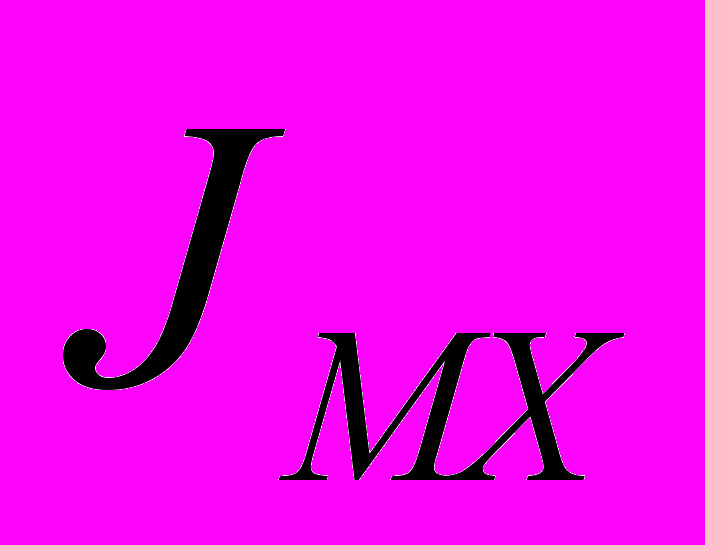по методу Мерцалова. Такая же ошибка получается и по методу Виттенбауэра.Таблица 1
Исходные данные для расчёта
| № | Моменты сил | Моменты инерции |
| положения | сопротивления, Нм | масс, кгм2 |
| 0 | 0 | 0 |
| 1 | -120 | 0,35 |
| 2 | -192 | 0,88 |
| 3 | -225 | 1,33 |
| 4 | -231 | 1,28 |
| 5 | -199 | 0,95 |
| 6 | -142 | 0,49 |
| 7 | 0 | 0,01 |
| 8 | 0 | 0,6 |
| 9 | 0 | 3,35 |
| 10 | 0 | 3,95 |
| 11 | 0 | 0,94 |
Расчёты по Коловскому ведутся с привлечением гармонического анализа с применением ряда Фурье. Точность аппроксимированных значений приведённых моментов сил МПР и моментов инерции масс JПР зависит от количества положений звена приведения.
На рис. 2, а приведён график заданных моментов сил сопротивления. На рис. 2, б представлен результат аппроксимации по 12 положениям и 6 гармоникам с отчётливо видимой погрешностью. Расчёт большого количества положений – задача трудоёмкая. В Костромском государственном технологическом университете этот недостаток был устранён созданием компьютерной программы, с помощью которой графики
и 
, построенные по 12-ти положениям, можно разбить на большее число положений от 24 до 360 с использованием сплайна Акимы. Таким образом, ошибка расчётов от аппроксимации этих графиков практически устраняется (рис. 2, в).Это позволяет применять без ограничений метод Коловского в научных и учебных целях.
Метод динамического анализа и синтеза МА по М. З. Коловскому следует отнести к большим достижениям отечественной науки по механике машин. Однако, к сожалению, некоторые авторы учебных пособий по ТММ, в том числе выпущенных недавно, игнорируют его, с чем нельзя согласиться [7, 8].
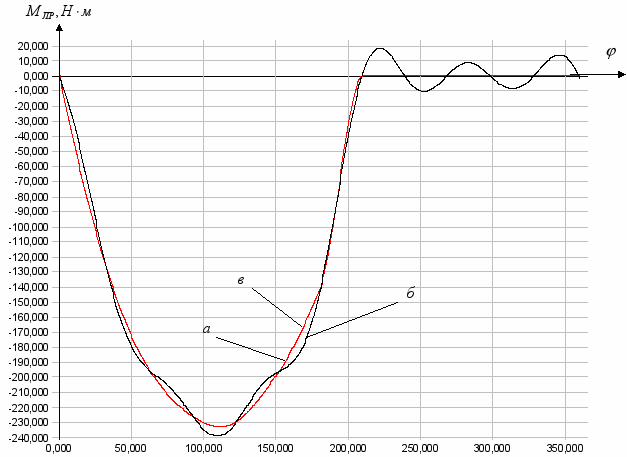
Рис. 2. Графики
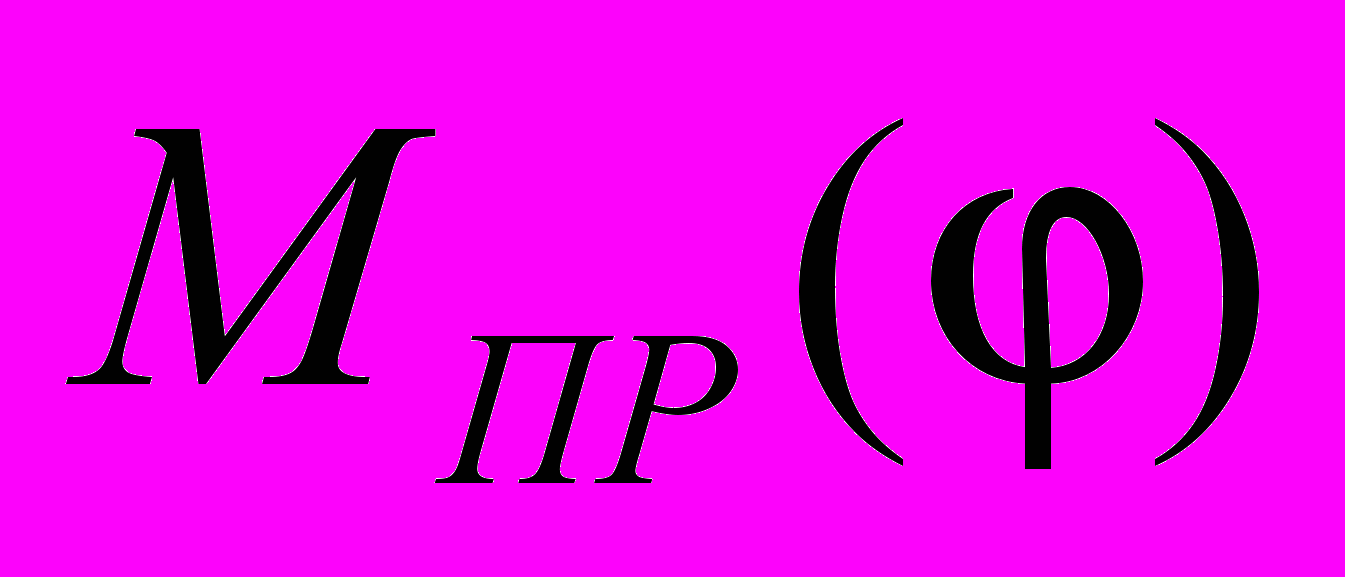: а – заданный момент сил сопротивления; б – аппроксимированный момент для 12 положений; в – аппроксимированный момент для 360 положенийСПИСОК ЛИТЕРАТУРЫ
- Коловский М. З. Динамика машин. – Л.: ЛПИ, 1980. – 80 с.
- Динамическое исследование машинного агрегата / М. З. Коловский, В. И. Лебедев, Ю. А. Семенов, А. В. Слоущ. – Л.: ЛПИ, 1982. – 23 с.
- Механика машин: учебное пособие для втузов / И. И. Вульфсон, М. Л. Ерихов, М. З. Коловский и др.; Под редакцией Г. А. Смирнова. – М.: Высш. шк., 1996. – 511 с.
- Программирование и вычислительная математика / Р. С. Гутер, П. Т. Резниковский. – Вып. 2. – М.: Наука, 1971. – 262 с.
- Курсовое проектирование по теории механизмов и машин / А. С. Кореняко, Л. И. Кременштейн и др.; Под ред. А. С. Кореняко. – М.: Машиностроение, 1964. – 324 с.
- Федотенок А. А. Кинематическая структура металлорежущих станков. – М.: Машиностроение, 1970. – 407 с.
- Теория механизмов и машин: уч. пособие / Ю. А. Матвеев, Л. В. Матвеева М.: Альфа–М.: Инфра–М.: 2009. – 320 с.
- Смелягин А. И. Теория механизмов и машин. Курсовое проектирование. Уч. пособие. – Новосибирск: Инфра–М.: изд-во НГТУ, 2008. – 263 с.
Поступила 12.02.2009
После доработки 10.10.2009
Теория Механизмов и Машин. 2009. №2. Том 7.