Расчет зубчатых и червячных передач в курсовом проектировании

Вид материала

Документы

Содержание 4.3. Определение допускаемых напряжений при расчете зубьев на изгиб 4.4. Определение предельно допускаемых напряжений 4.6. Выбор модуля зацепления 4.7. Определение суммарного числа зубьев 4.8. Определение чисел зубьев шестерни и колеса 4.9. Проверка межосевого расстояния

Подобный материал:

• Программные средства компьютерного проектирования зубчатых передач в обобщающих параметрах, 26.58kb.
• Проектный расчет зубчатых передач на персональных компьютерах методические указания, 656.92kb.
• О. В. Соболева формирование творческого мышления будущего инженера в курсовом и диплом, 107.37kb.
• Ижевский Государственный Технический Университет Министерство промышленности и транспорта, 233.33kb.
• 1. Предварительный расчет поверхности теплообмена, 39.68kb.
• Компьютерные технологии в курсовом и дипломном проектировании, 87.88kb.
• В. И. Молчанов Проектирование червячных передач с колёсами из неметаллических материалов, 538.53kb.
• Механическая обработка, 11.65kb.
• Название программы информационные технологии в эскизном проектировании и оптимизации, 135.84kb.
• 2. геометрический расчет прямозубой цилиндрической передачи, 92.65kb.

4.3. Определение допускаемых напряжений при расчете зубьев на

изгиб

Допускаемые напряжения изгиба [σ]_F определяются по формуле:

[σ]_F= σ_F0K_FL/S_F, (6)

где σ_F0- предел выносливости на изгиб при базовом числе циклов нагружения (табл.3); S_F- коэффициент безопасности (табл.3); K_FL – коэффициент долговечности

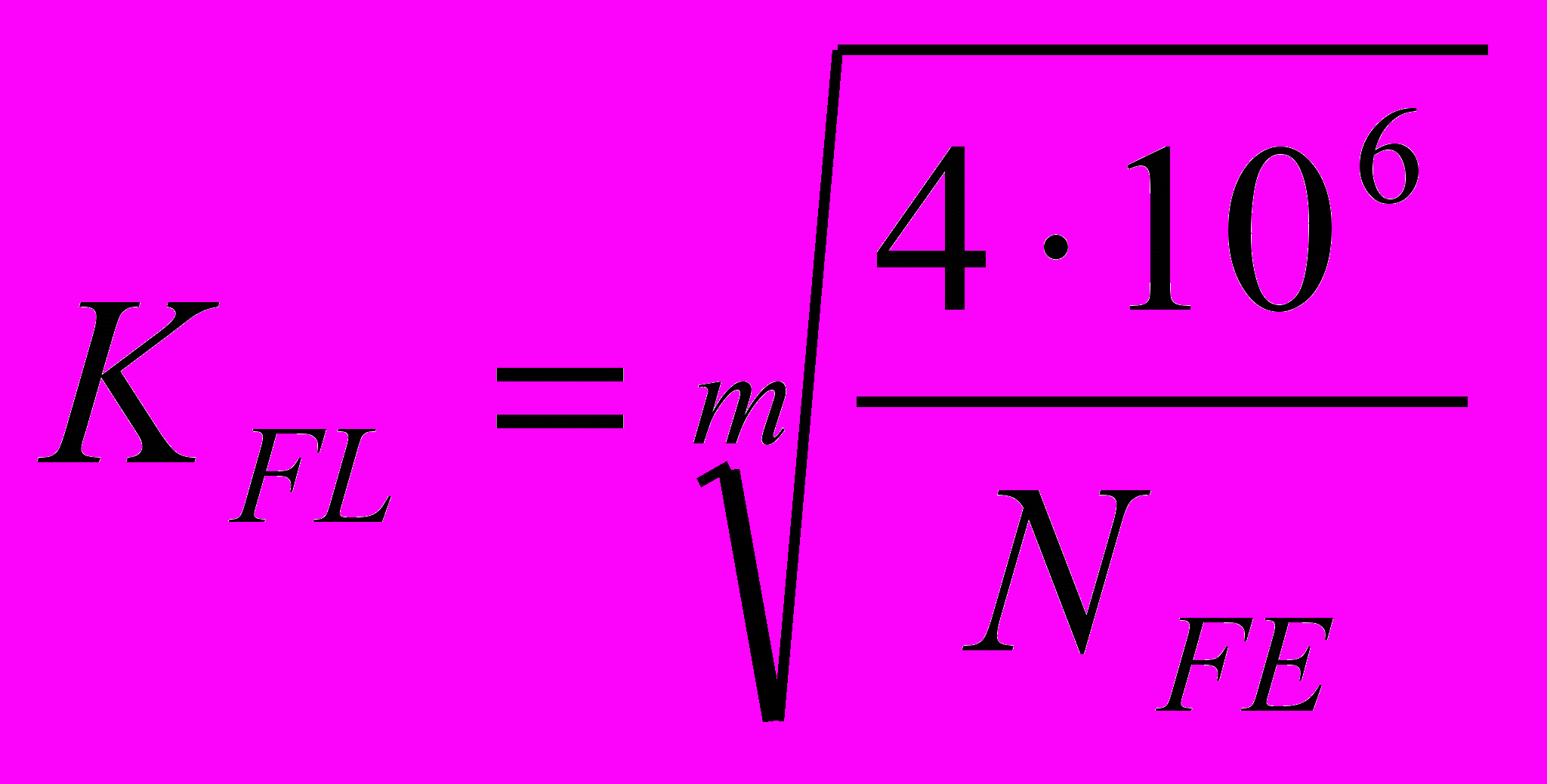, (7)

здесь m – показатель степени, зависящий от твердости: m=6 при твердости <350НВ; m=9 при твердости >350НВ; N_FЕ – эквивалентное число циклов нагружения зубьев за весь срок службы передачи, определяемое по формулам (3) или (4), но при этом в формуле (4) m=6 при твердости <350НВ; m=9 при твердости >350НВ.

Значения K_FL, принимаемые к расчету, могут быть в пределах

1< K_FL<2,08 при твердости <350НВ и 1<К_FL <1,63 при твердости >350HB.

Для реверсивных передач значения [σ]_F уменьшают на 20%.

4.4. Определение предельно допускаемых напряжений

При кратковременных перегрузках (расчет на пиковые нагрузки) предельно допускаемыеуле:

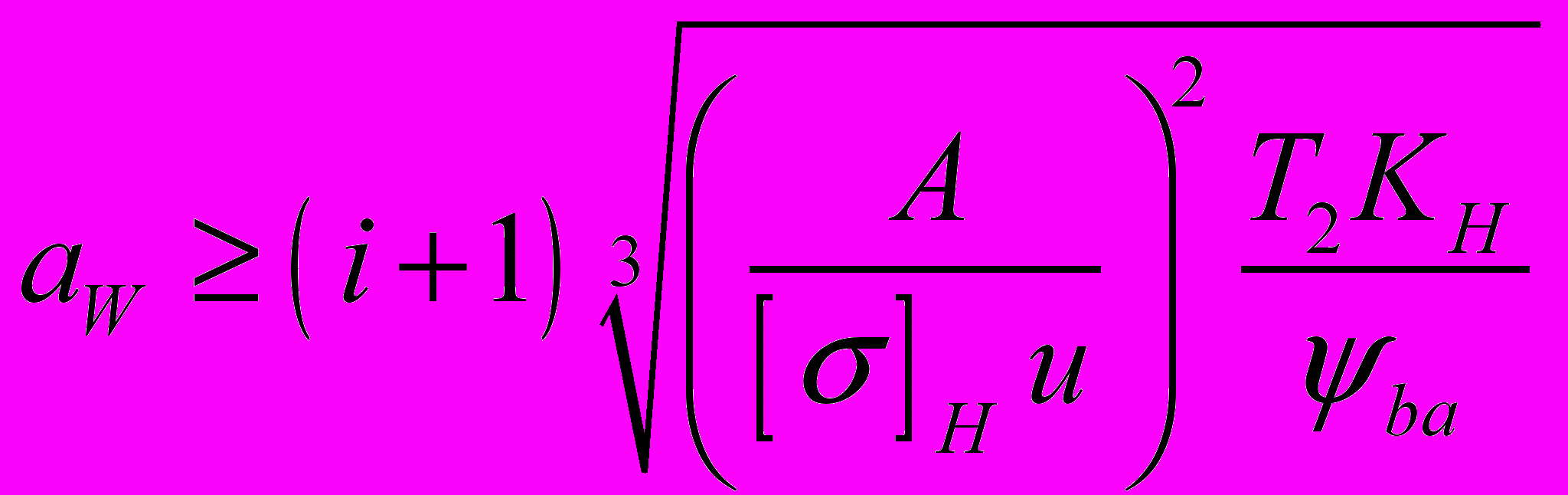, (8)

где i – передаточное отношение ступени редуктора; А – численный коэффициент, А=310 для прямозубых передач; А=270 для косозубых и шевронных передач; Т₂ – вращающий момент на валу колеса, Н·мм; ψ_ba=b₂/a_w – коэффициент ширины зубчатого венца. По ГОСТ 2185-66* ψ_ba может принимать значения: 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0; 1,25. Для прямозубых передач ψ_ba=0,125…0,25; для косозубых ψ_ba=0,25…0,4; для шевронных ψ_ba=0,5…1,0; К_Н – коэффициент нагрузки

К_Н = К_Нα· К_Нβ· К_Нυ,

где К_Нα- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. Для прямозубых передач К_Нα=1, для непрямозубых К_Нα=1,0…1,15; К_Нβ коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (табл. 4). К_Нυ- коэффициент динамичности нагрузки, К_Нυ= 1…1,1.

Таблица 4

Ориентировочные значения К_Нβ

Расположение колес относительно опор	Твердость
	<350НВ	>350НВ
Симметричное Несимметричное Консольное	1,0…1,15 1,1…1,25 1,2…1,35	1,05…1,25 1,15…1,35 1,25…1,45

По полученному значению а_w принимается ближайшее стандартное по ГОСТ 2185-66 (мм): 40; 50; 63; (71); 80; (90); 100; (112); 125; (140); 160; (180); 200; (224); 250; (280); 315; (355); 400 (значения в скобках менее предпочтительны).

4.6. Выбор модуля зацепления

При твердости зубьев шестерни и колеса <350НВ m=(0,01…0,02)а_w; при твердости зубьев шестерни >45 HRC и колеса <350НВ m=(0,0125…0,025)а_w; при твердости зубьев шестерни и колеса > 350 НВ m=(0,016…0,0315)а_w.

По ГОСТ 9563-80* принимается ближайшее стандартное значение модуля, (мм): 1,5; (1,75); 2,0; (2,25); 2,5; (2,75); 3,0; (3,5); 4,0; (4,5); 5,0; (5,5); 6,0; (7,0); 8,0; (9,0); 10… (значения в скобках менее предпочтительны).

Для косозубых и шевронных колес стандартным считают нормальный модуль m_n.

4.7. Определение суммарного числа зубьев

Для прямозубых передач z_Σ= z₁+z₂=2а_w/m; для косозубых и шевронных z_Σ= z₁+ z₂=2а_wсоsβ / m_n, где β – угол наклона зубьев. Для косозубых передач β=8…18º, для шевронных β=25…40º.

4.8. Определение чисел зубьев шестерни и колеса

z₁= z_Σ/(i +1); z₂=z_Σ - z₁,

при этом z₁>z_min=17cos³β.

По округленным до целых значениям чисел зубьев уточняется передаточное отношение i= z₂/z₁. Расхождение с принятым ранее номинальным передаточным отношением не должно превышать +2,5%.

4.9. Проверка межосевого расстояния

Для прямозубых колес а_w=0,5(z₁+z₂)m, для косозубых и шевронных а_w=0,5(z₁+z₂)m_n/cosβ. Если полученное значение а_w не соответствует ранее принятому стандартному, расхождение устраняется изменением угла наклона зубьев

сosβ=0,5(z₁+ z₂)m_n/ а_w,

где а_w – стандартное значение.

Вычисление сosβ производится с точностью до пяти значащих цифр. Действительный угол наклона зубьев β при этом определяется с точностью до 1секунды. Рекомендуется проверить расчеты, определив

d₁=z₁m_n/cos β; d₂=z₂m_n/cos β

c точностью до сотых долей миллиметра и убедиться, что расчетное межосевое расстояние 0,5(d₁+ d₂)= а_w соответствует принятому ранее.