Теория и методология управления запасами в цепях поставок
| Вид материала | Автореферат |
- Теория, методология и практика управления многопродуктовыми материальными потоками, 608.29kb.
- Кафедра экономики и управления курсовая работа по курсу: «Информационные технологии, 872.46kb.
- Рабочая программа дисциплины «теория логистики и управления цепями поставок» Рекомендуется, 302.36kb.
- Программа дисциплины Транспортировка в цепях поставок для направления 080500. 62 Менеджмент,, 343.96kb.
- Задачи дипломной работы: рассмотреть понятие, сущность и виды запасов на предприятии;, 167.6kb.
- Теория и методология управления рисками в туристско-рекреационном комплексе, 758.54kb.
- Теория и методология формирования системы управления инфраструктурными комплексами, 495.22kb.
- Экзаменационные вопросы бак (2010 2011) по курсу «Управление цепями поставок», 51.99kb.
- Катаргин Дисциплина "Сетевое моделирование и задачи управления запасами", 9.32kb.
- Бизнес-планирование Международный маркетинг Экономика организации Транспортировка, 17.95kb.
Разработан подход к формированию теории управления запасами, который предусматривает выявление и структуризацию элементов в виде нескольких разделов, важнейшими из которых являются: методы расчета показателей запасов; модели (стратегии) управления запасами в цепях поставок; методы управления (регулирования) запасов в многоуровневых логистических системах.
Одним из условий ускоренного развития управления запасами является формирование новой структуры прикладной теории управления запасами в цепях поставок. Решение данной задачи может быть достигнуто на основе принципов системного подхода: целостности, научной обоснованности и оптимальности, иерархичности, целевой направленности.
Суть предложенного в работе методического подхода состоит в следующем:
все многообразие моделей и методов управления запасами рассматривается как единое целое с учетом их взаимосвязи и взаимовлияния;
каждая модель (метод) формируется на базе научных подходов, предусматривающих постоянное изучение новых закономерностей и их практическую апробацию;
модели и методы управления запасами группируются в виде самостоятельных разделов;
каждый из разделов предполагает наличие собственных классификаций признаков и моделей (методов, алгоритмов, способов и т.п.) и позволяет решать задачи соответствующего уровня;
между моделями различных разделов соблюдается принцип иерархии, например, при формировании модели регулирования запасов в цепи поставок (высший уровень) учитываются параметры моделей (стратегий) управления запасами в звеньях логистической цепи (средний уровень), которые в свою очередь, базируются на методах расчета показателей запасов в элементах цепи (низший уровень).
На основании изложенного подхода структура прикладной теории управления запасами в цепях поставок (УЗЦП) может быть представлена в виде шести разделов.
I. Термины и определения теории запасов, классификация запасов;
II. Методы расчета показателей текущего, страхового и других видов запасов;
III. Модели (стратегии) управления запасами в цепях поставок;
IV. Методы управления (регулирования) запасов в многоуровневых (эшелонированных) логистических системах;
V. Проектирование систем управления запасов в цепях поставок;
VI. Специальные вопросы теории управления запасами.
Рассмотрим подробнее содержание некоторых разделов.
Второй раздел. Модели и методы расчета текущего, страхового и других видов запасов получили развитие в работах многих отечественных и зарубежных авторов. Обобщение многочисленных источников позволило нам выполнить их классификацию в виде трех групп (табл. 3).
Таблица 3
Классификация методов и моделей расчета показателей запасов
| Методы, модели (источники информации) | Типы решаемых задач | |
| Статистические (данные складского, бухгалтерского учета, специальные наблюдения) | Определение параметров и законы распределения | Расчет показателей текущего и страхового запасов, оценка дефицита |
| Аналитические (экономические показатели, экспертные оценки, теоретические предпосылки и др.) | Экономико-вероятностные (статические) | Одноцикловые задачи («газетчика», «булочника» и т.п.); расчет количества запасных частей с учетом надежности; оценка страхового запаса и дефицита |
| Экономико-математические | Расчет текущего запаса – оптимальная партия заказа (EOQ); расчет страхового запаса. | |
| Вероятностно-статистические | Расчет страхового запаса (формула Феттера); определение взаимосвязи между текущим и страховым запасом | |
| Исследование операций (все виды информации) | Имитационное моделирование | Для оценки и расчета различных видов запасов |
| Прогнозирование | Для оценки показателей текущего, страхового и сезонного запасов | |
| Теория массового обслуживания | Для расчета запасных частей (автомобили, спец. техника) | |
| Принятие решений | Комбинированные методы оценки показателей запасов | |
Третий раздел. Принципиальное отличие моделей третьего раздела от второго состоит в том, что при формировании стратегии управления рассматриваются два процесса. Первый процесс в общем случае отражает случайный расход текущего и страхового запасов, методы расчета показателей которых рассмотрены во втором разделе. Второй процесс включает операции управления, выполняемые менеджерами (прогноз расхода и планирование размера запасов, контроль, принятие решений, оформление заказов, организация поставок и др.). С точки зрения теории управления процессы первого вида – управляемые, операции процессов второго вида – управляющие, так как зависят от действия лица, принимающего решение.
Выполненные исследования показали, что моделям управления запасами посвящено большое количество работ, в которых проведены как классификации признаков, так и стратегий управления. В тоже время, анализ показал, что существующие классификации должны быть дополнены, по крайней мере, тремя признаками:
- по виду управляющих или регулирующих воздействий (пассивные, активные, комбинированные);
- по учету взаимосвязи между текущим, страховым запасом и дефицитом;
- по виду спроса (зависимый, независимый).
Обобщение различных подходов позволило нам усовершенствовать классификацию моделей (стратегий) управления запасами, табл. 4.
Таблица 4
Классификация моделей (стратегий) управления запасами
| Признак классификации | Характеристика модели (стратегии) |
| По виду процессов | Управляемые (поступление и расход запасов); управляющие (параметры стратегий, контроль уровней) |
| По виду спроса | Зависимые (заданы сроки и величины поставок, например, производственная логистика); независимые (например распределительная логистика) |
| По виду управляющих воздействий | Пассивные; полуактивные (прогнозирование); активные (концепции JIT, QR и другие) |
| По номенклатуре | Однономенклатурные; многономенклатурные |
| По виду контрольных уровней (параметров) | Критический уровень (точка заказа ROP); двухуровневая система; фиксированная периодичность заказа; комбинированные способы |
| По величине заказа (поставки) | Постоянные; Переменные |
Четвертый раздел. Тематика и структура четвертого раздела, включающего методы управления (регулирования) запасов в многоуровневых логистических системах, на наш взгляд, находится в стадии становления, несмотря на наличие отдельных разработок. Выполненный анализ ряда работ показал, что существует несколько вариантов для решения задач данного раздела, которые могут быть систематизированы в виде двух групп методов, первая из которых базируется на фактических данных или плановых показателях; вторая – на модели EOQ и ее модификациях, табл. 5.
Таблица 5
Методы управления (регулирования) запасов в многоуровневых системах
| Классификационные признаки | Характеристика метода |
| Методы, основанные на фактических данных или прогнозах | Реактивные, основанные на логической концепции «вытягивания) (pull); сетевое планирование; динамическое программирование |
| Методы, основанные на плановых показателях | Планирование потребности в запасах (на основе логистической концепции DRP); пропорционального регулирования и другие методы управления организационными системами (механизм обратных приоритетов, конкурсный механизм и т.п.) |
| Методы, основанные на модели EOQ | Многоуровневые системы снабжения (децентрализованная, линейная, эшелонированная); метод, основанный на декомпозиции распределительной сети в виде простых логистических цепей (ПЛЦ) |
Шестой раздел. В данном разделе следует отразить вопросы управления запасами, связанные со специфическими видами продукции (скоропортящиеся товары, опасные грузы и т.п.), финансовыми потоками (неравномерность платежей, инфляция и т.п.), информатизацией процессов управления запасами и др.
Таким образом, разработанная структура прикладной теории управления запасами в цепях поставок отражает современный уровень знаний в данной области и обобщает многообразие ситуаций и значительное количество вариантов реальных задач.
Предложен усовершенствованный вариант модели общих логистических затрат (TLC), основанный на системном подходе и принципах логистического менеджмента и учитывающий взаимосвязь и взаимовлияние между отдельными составляющими затрат, ограничения и нелинейность параметров, модификации вариантов классической модели оптимальной партии заказа.
Наиболее распространенной моделью прикладной теории логистики является модель оптимального или экономичного размера заказа EOQ. Расчет EOQ производится на основе аддитивной модели путем минимизации следующей функции затрат
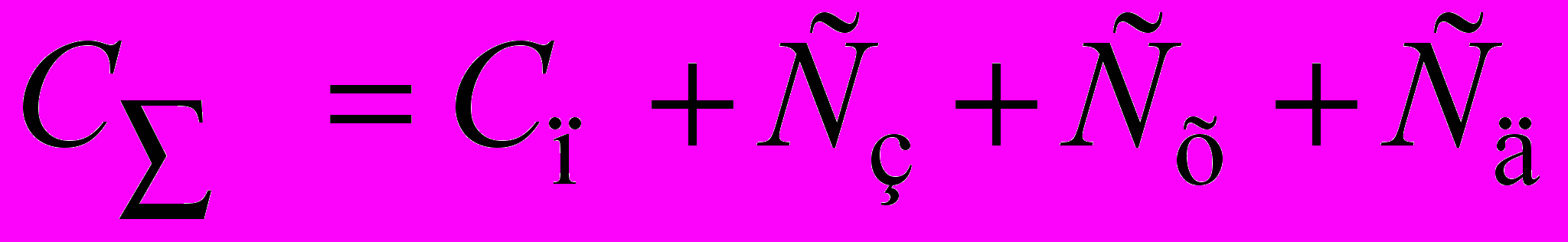, (1)где Сп, Сз, Сх – затраты, соответственно на приобретение продукции, оформление и выполнение заказа, хранение;
Сд – издержки, связанные с дефицитом продукции.
Проведенные исследования показали, что аддитивная модель требует усовершенствования и доработки в следующих направлениях.
Во-первых, включение в модель (1) еще одного вида затрат, названных нами «скрытыми» или «латентными». Это те виды затрат, который реально существует, но не учитывается в расчетной модели, например, затраты на хранение продукции в контейнерах, кузовах автомобилей или вагонах при разгрузке транспортных средств, прибывающих на склад, или затраты на содержание склада, когда наблюдается ситуация дефицита продукции и т.п.
Во-вторых, в модели (1) не отражена взаимосвязь и взаимовлияние между элементами затрат. О необходимости установления такой взаимосвязи говорится во многих работах, в частности, R.H Ballou. («треугольник логистического планирования»), Дж. Р Стока. и Д.М.Ламберта (шестиугольник, отражающий «влияния различных видов логистичсекой деятельности на общие логистические издержки»).
К основным компонентам, которые отражают связь и взаимовлияние между элементами модели, следует отнести:
- связь между текущим и страховым запасами при выборе стратегии управления запасами;
- связь между страховым запасом и дефицитом;
- особенности учета модифицированных вариантов модели EOQ;
- влияние конфигурации (расположения) различного вида складов в многоуровневых системах, расположение зон хранения и переработки внутри складов и т.д.
В-третьих, в аддитивной модели не представлены различные ограничения и нелинейности, которые имеют место при управлении запасами в цепях поставок. В первую очередь необходимо учесть оптовые или дифференциальные скидки при осуществлении закупок, а также ограничения, связанные с весовыми, габаритными, стоимостными и другими параметрами.
В-четвертых, помимо суммирования в общую зависимость должны быть включены:
модель, основанная на преобразовании случайных величин, для учета взаимосвязи между текущим и страховым запасом при различных стратегиях управления запасами;
вероятностная или аналитическая модель, отражающая связь между страховым запасом и дефицитом (состоянием дефицита); например, при выборе вероятности отсутствия дефицита соответственно изменяется величина страхового запаса, а с учетом стратегии управления запасами и величина текущего запаса, что, несомненно, отражается на общих затратах;
неоднозначность учета модификаций модели EOQ при хранении;
корректирующие зависимости, вытекающие из общего алгоритма выбора и построения транспортно-складской логистической сети, представленного в диссертации.
На основании вышеизложенного модель (1) может быть представлена в виде
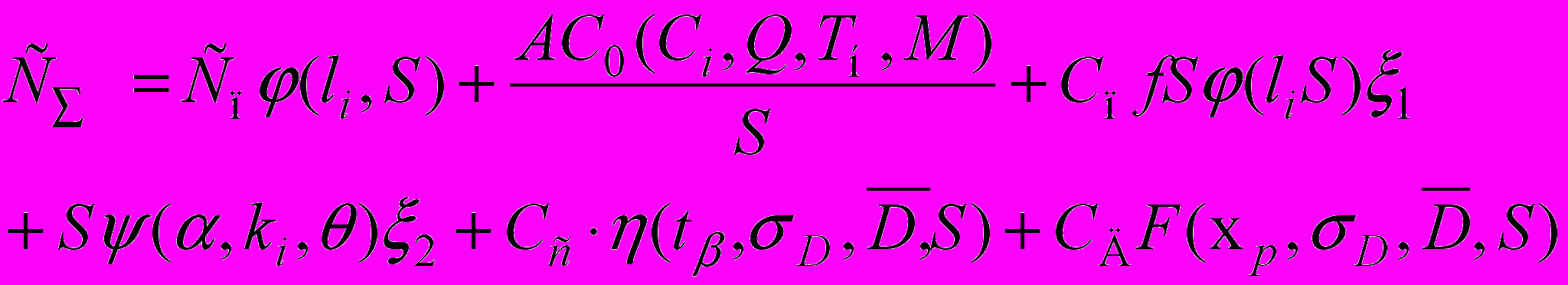, (2)при N ограничениях вида
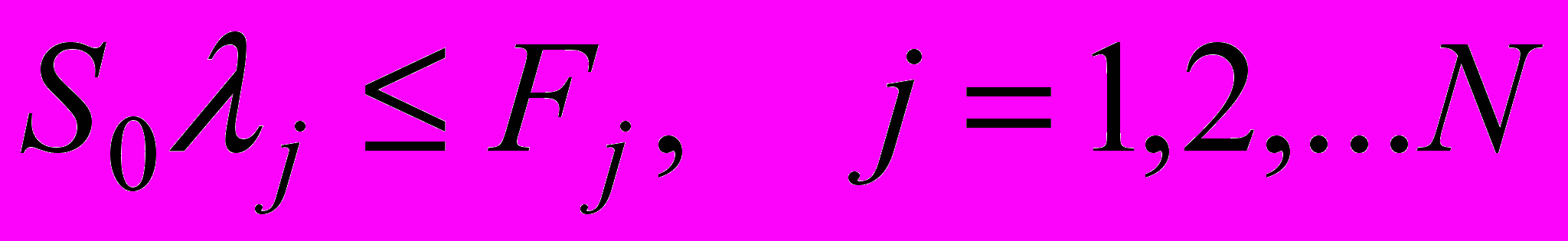, (3)где Сп – цена единицы продукции (без скидок);
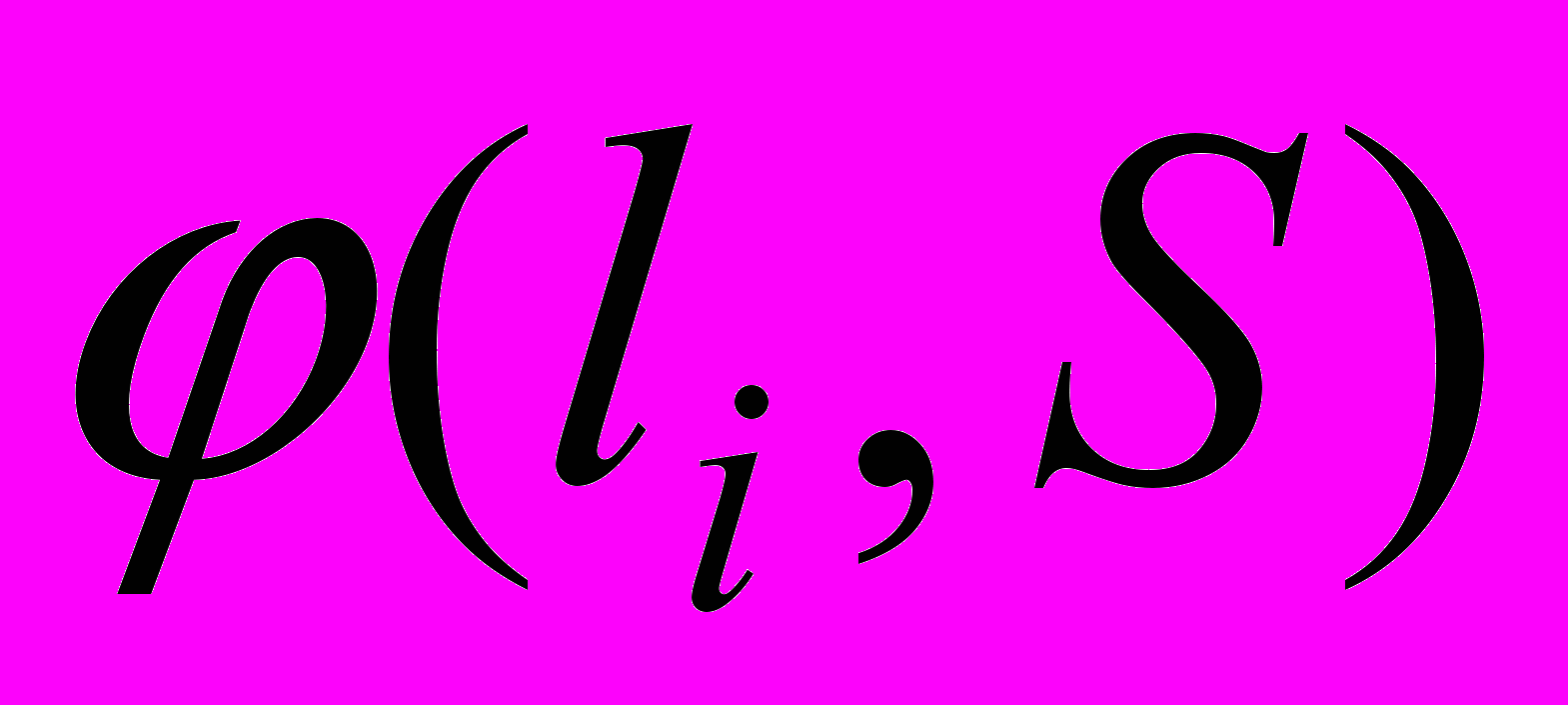- функция, отражающая изменение цены Сп в зависимости от размера партии заказа.С0(Сi, Q, Tн, M) – общие затраты на организацию и выполнение заказа (транспортировку), отражающие переработку на складе (Сi), грузоподъемность (грузовместимость) Q транспортного средства и его режимы работы Тн, а также, в некоторых случаях, конфигурацию транспортной сети, включающую М пунктов погрузки-разгрузки;
ξ1– коэффициент, отражающий учет модификации EOQ, например, среднюю величину заказа S0;
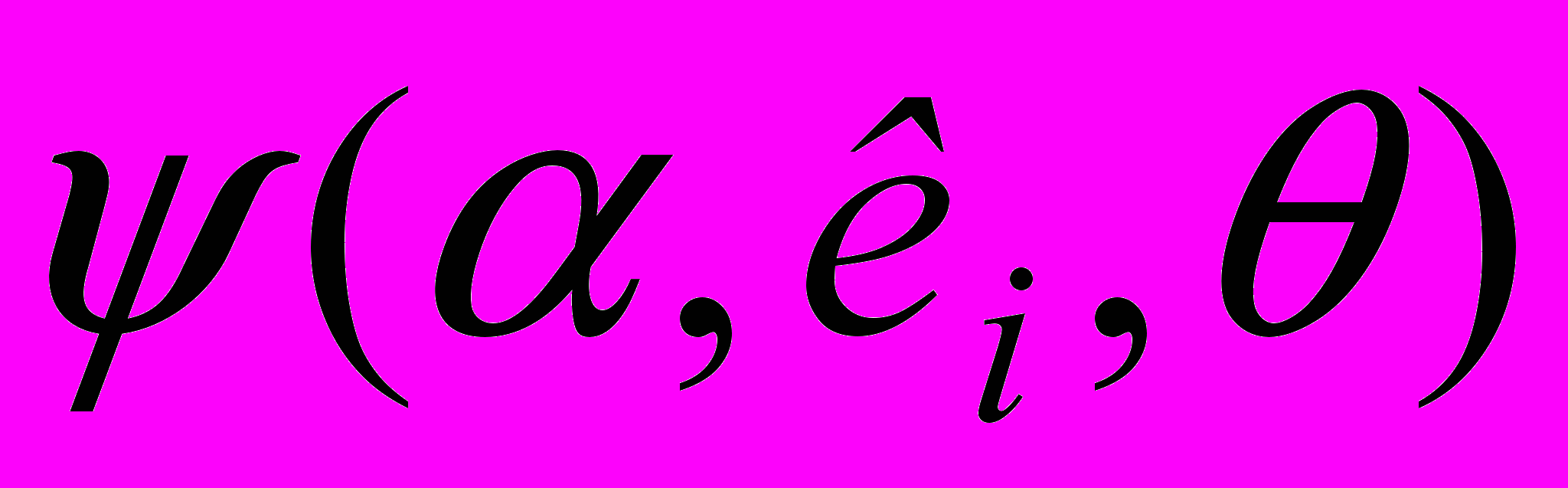– зависимость, отражающая затраты на хранение (при аренде склада);ξ2 – коэффициент, отражающий максимальную величину заказа для модификаций EOQ;
Сс – затраты на хранение единицы продукции страхового запаса (возможно
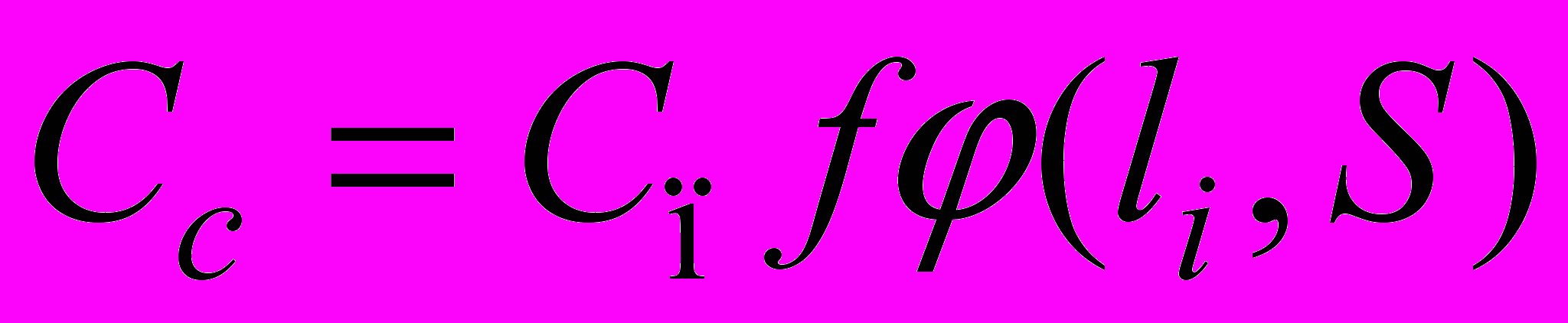);η(tβ,σD,
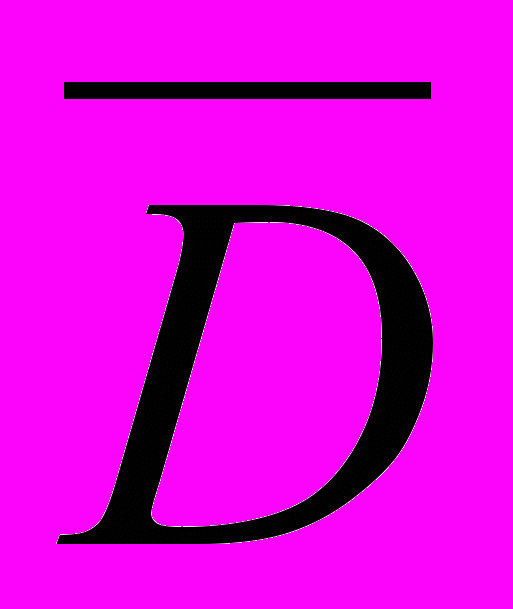, S) – функция, отражающая вероятностные характеристики наличия страхового запаса на складе;СД – издержки, связанные с дефицитом единицы продукции;
F(xp, σD,
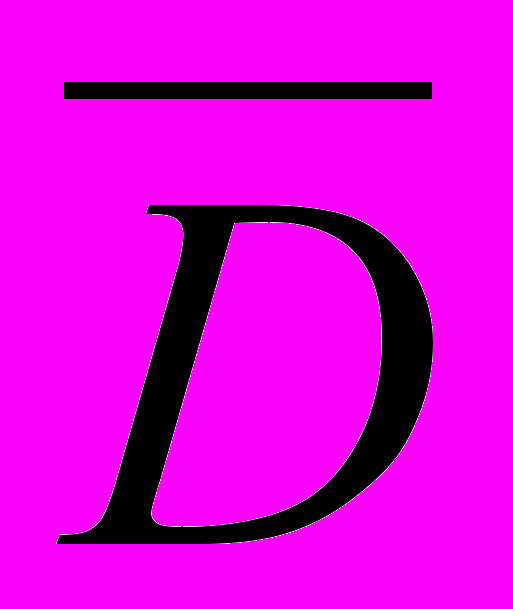, S) – функция, отражающая вероятностные характеристики наличия дефицита;Soj – оптимальная величина заказа (поставки);
λj – показатель, характеризующий j-е свойство продукции (масса, объем, цена и т.п.);
Fj – ограничение, связанное с j-м свойством продукции.
Таким образом, разработанная модель для расчета оптимальных партий заказа (поставок), во-первых, базируется на концепции общих (тотальных) затрат, во-вторых, учитывает максимальное количество связей между различными видами логистической деятельности (известных и исследованных в настоящее время), в-третьих, включает основные ограничения и модификации модели EOQ, в-четвертых, наиболее полно, на наш взгляд, отражает реальные процессы управления запасами в цепях поставок (в рамках модели EOQ).
Усовершенствована формула Харриса-Уилсона для расчета оптимальной партии заказа, учитывающая разные варианты затрат на хранение, неодновременность поступления различных видов продукции на склад, особенности учета скидок и немгновенность разгрузки поступающих партий поставок.
Известно, что при формировании модели расчета EOQ в качестве критерия оптимизации принимается минимум суммарных затрат С∑, включающих затраты на выполнение заказов СЗ и затраты на хранение запаса на складе СХ в течении определенного периода времени
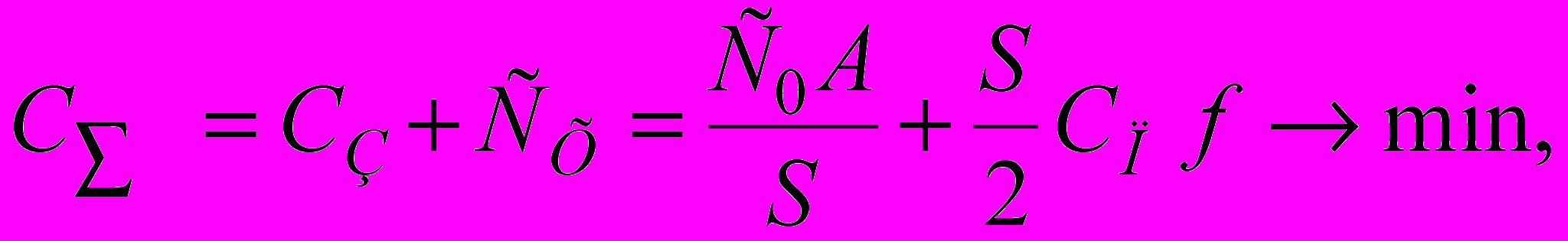(4)где С0 – затраты на выполнение одного заказа, руб.;
А – потребность в заказываемом продукте в течение рассматриваемого периода, ед.;
СП – цена единицы продукции, руб./ед.;
f – доля от цены СП, приходящаяся на затраты по хранению;
S – искомая величина заказа, ед.
Соответственно оптимальная величина заказа Sо, количество заказов N, периодичность заказов Т и минимальные суммарные затраты С∑min определяются по известным формулам, например, формула Харриса-Уилсона для оптимальной партии заказа (EOQ)
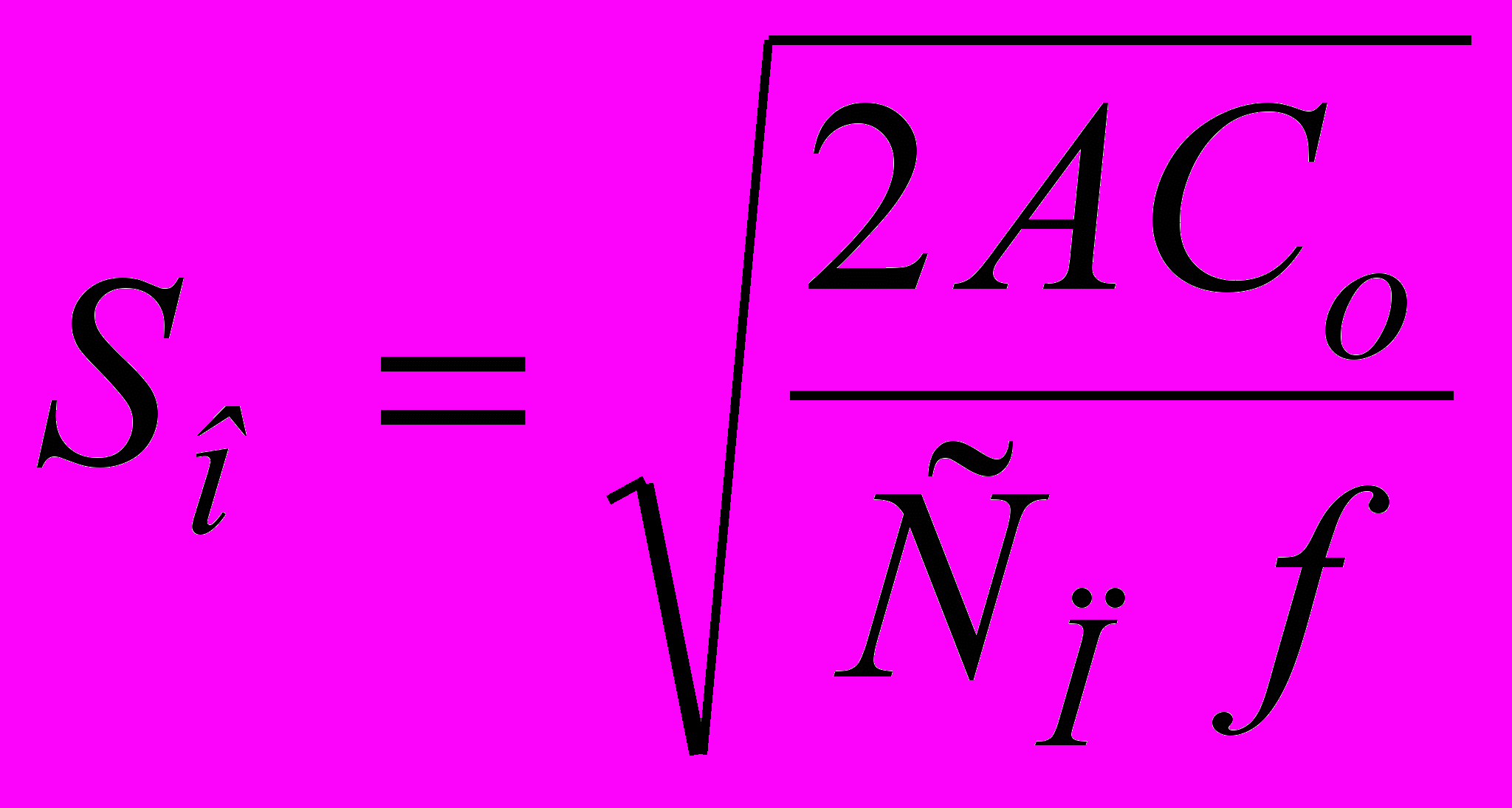, (5)минимальные суммарные затраты
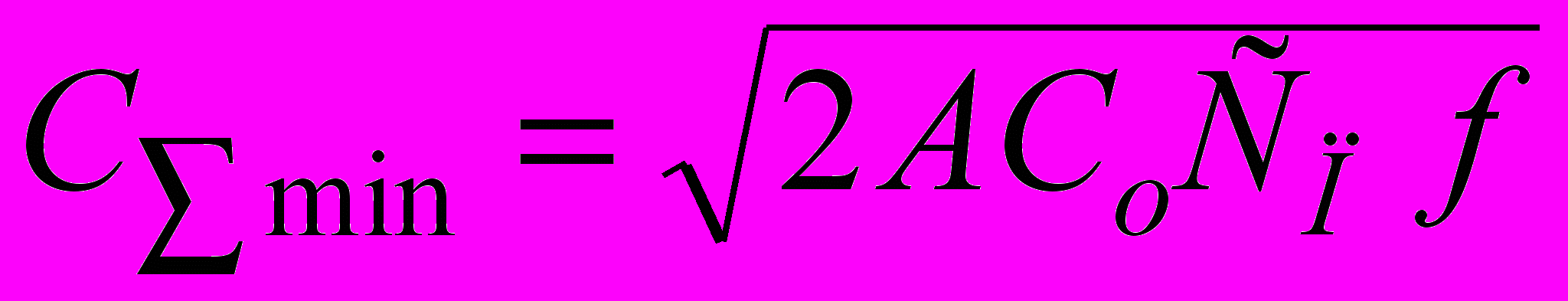(6)Проведенные исследования показали, что допущения, принятые при выводе формулы EOQ, требуют уточнения, в первую очередь, затраты на хранение. Так, практика аренды складских помещений говорит о том, что учитывается не средний размер партии S/2, а площадь (или объем) склада, которая требуется для всей поступившей партии
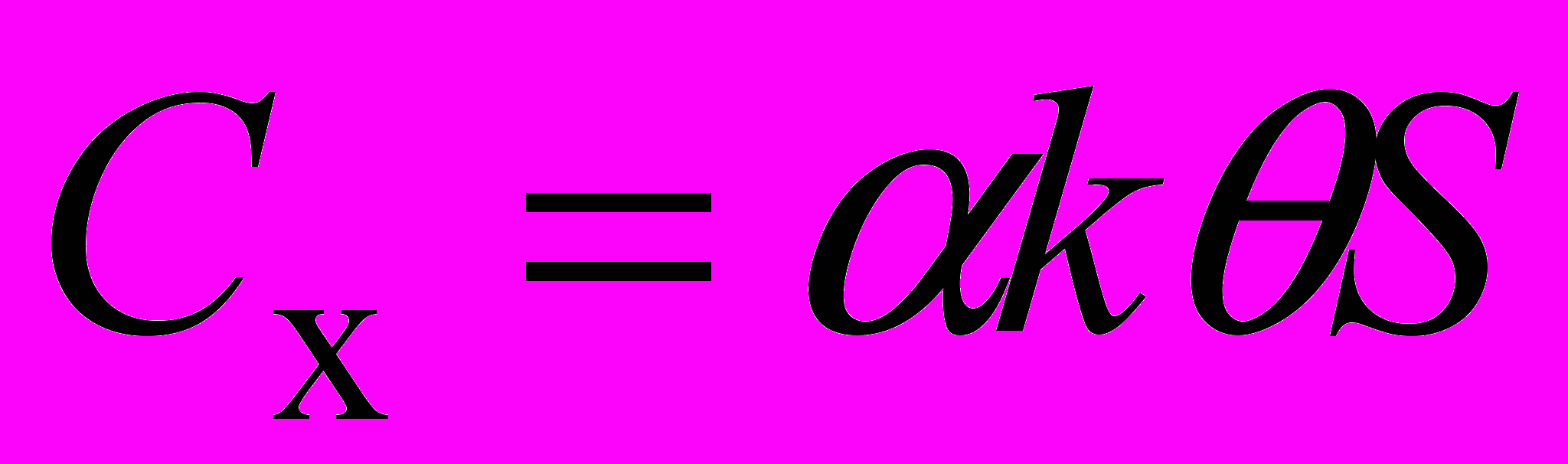, (7)где - затраты на хранение продукции в единицу времени с учетом занимаемой площади (объема) склада, руб.\м2 .ед. времени (руб.\м3 . ед. времени);
k - коэффициент, учитывающий пространственные габариты единицы продукции, м2\шт. (м3\шт.).
θ – коэффициент, учитывающий неодновременность поступления различных видов продукции на склад,
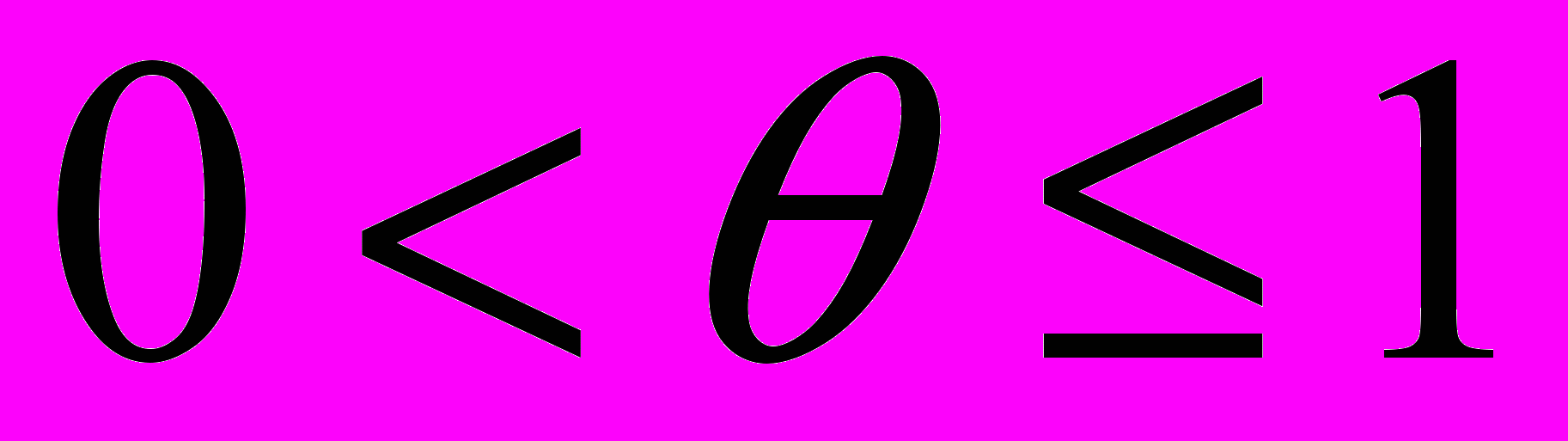.Коэффициент θ отражает преимущества современных технологий грузопереработки продукции на складах: по мере освобождения стеллажей (или ячеек) на них размещаются вновь поступающие партии продукции, не дожидаясь момента окончания расхода предыдущей партии. В результате повышается наполняемость склада, что приводит к снижению затрат на хранение.
При подстановке (7) в уравнение суммарных затрат и выполнении стандартных процедур оптимизации, находим величину EOQ
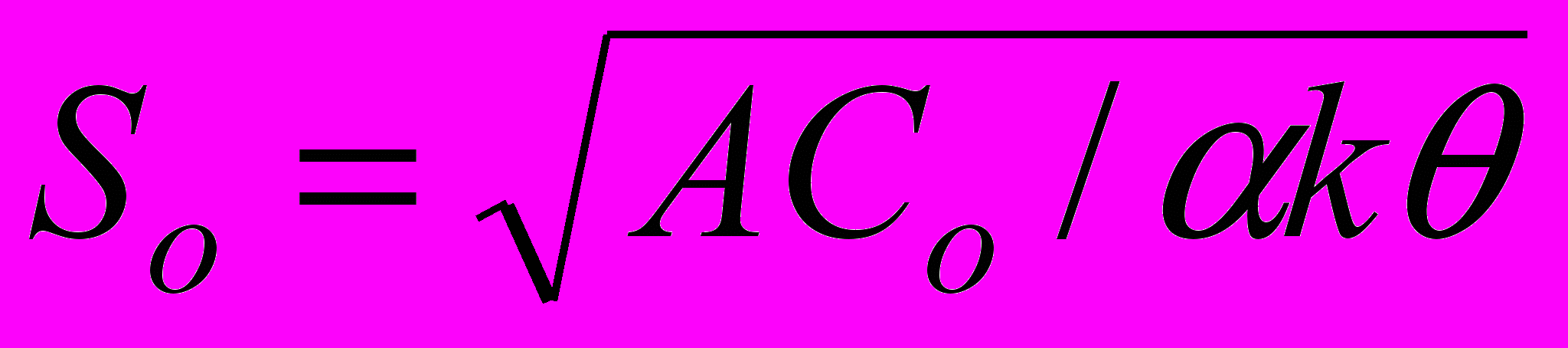(8)Анализ полученных зависимостей показал, что в общем случае целесообразно представить затраты на хранение в виде двух составляющих
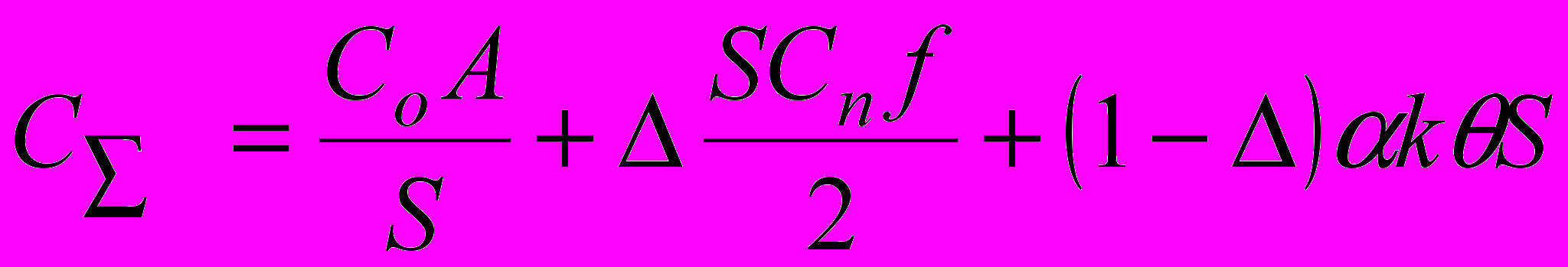(9)Дифференцированный учет затрат на хранение позволяет:
во-первых, формула (9) включает оба ранее рассмотренных подхода: при Δ=1 приходим к формуле Харриса-Уилсона (5); при Δ=0 – к формуле (8).
во-вторых, скидки на цену товара в зависимости от размера партии учитывается в первой составляющей затрат на хранение Cх1, т.е. Cп=φ(liS).
в-третьих, при учете не мгновенной разгрузки, т.е. постепенном пополнении (производственного) запаса, когда одновременно происходит перемещение продукции на склад и ее отпуск, фактически требуемая площадь (объем) склада меньше, чем поставляемая партия. Это означает, что в формуле (9) при расчете второй составляющей затрат на хранение CX2 учитывается величина S*, меньшая оптимального размера партии поставки So (соответствующей мгновенной разгрузке).
Формула (9) для удобства расчетов может быть представлена в виде
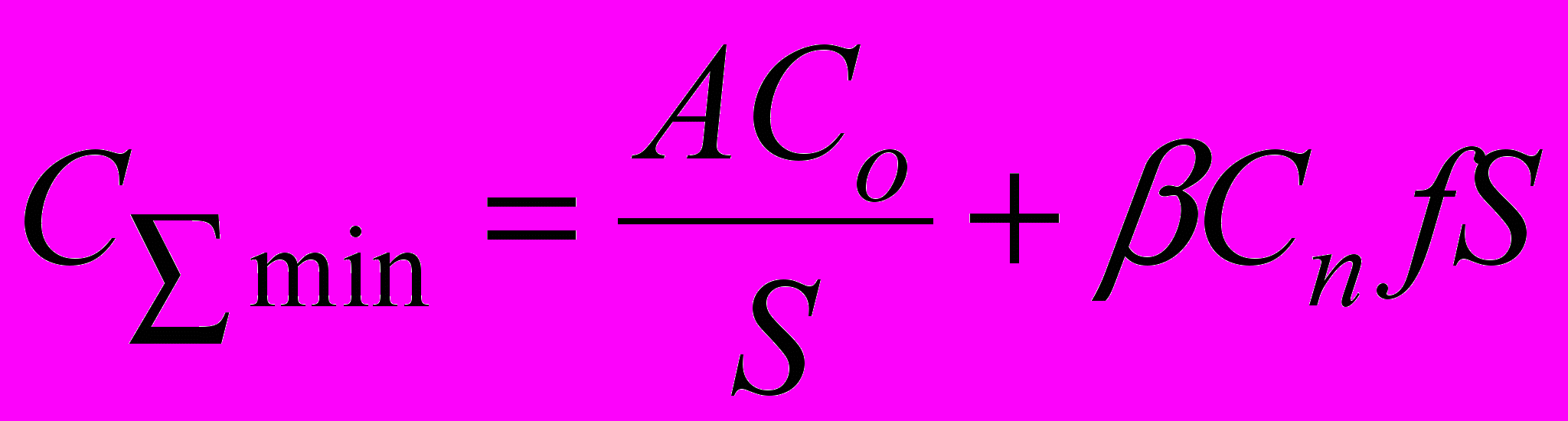, (10)где
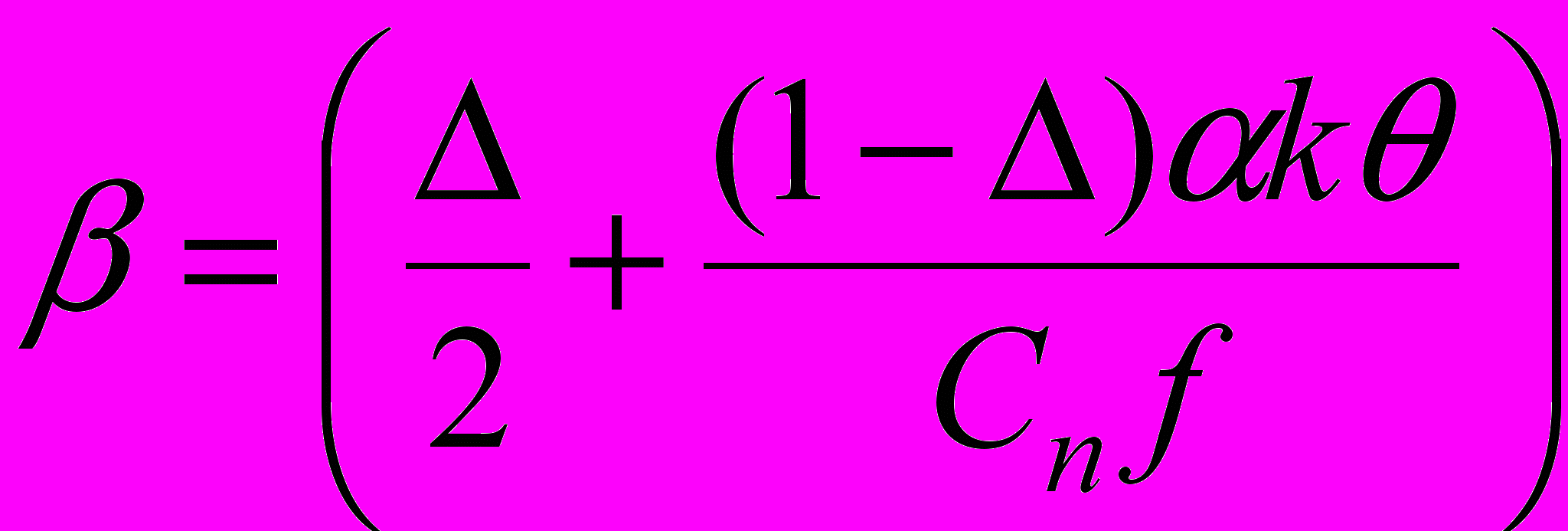
В этом случае расчет основных показателей So и С∑min производится по формулам аналогичным (5) и (6).
В диссертации приведены формулы для оценки точности расчета величины S0 и C∑min, основанные на линеаризации функции нескольких случайных величин.
Разработан принципиально новый подход к аналитическому описанию логистических сетей в виде простых логистических цепей (ПЛЦ); для каждого варианта ПЛЦ выведены формулы для расчета количественных и стоимостных показателей; отличие разработанного подхода состоит в том, что декомпозиция реальной сети в виде ПЛЦ персонифицирует роль каждого участника цепи поставок и учитывает добавленную стоимость от выполненных логистических операций.
Для формирования нового подхода к оптимизации логистических сетей необходимо ввести основные термины и определения, характеризующие простую логистическую цепь (ПЛЦ).
1. Под простой логистической цепью будем понимать часть логистической сети (канала), включающей не менее двух основных звеньев логистической системы (ЗЛС) – «поставщика» и «потребителя», связанных между собой несколькими логистическими операциями (функциями) по управлению и организации материального потока: оформление заказа, транспортировка, хранение продукции и др.
2. Расширение ПЛЦ возможно за счет основных посредников – «третья сторона» в логистике – перевозчиков, складов общего пользования (грузовые терминалы) и вспомогательных посредников, оказывающие услуги, связанные с финансовыми и информационными потоками.
3. Любая логистическая сеть (канал) в результате декомпозиции может быть представлена в виде отдельных ПЛЦ.
4. На «выходе» ПЛЦ цена единицы продукции возрастает по сравнению с ценой на «входе» в ПЛЦ за счет добавленной стоимости, образующейся при выполнении логистических операций (функций).
Известно, что основной зависимостью, отражающей интересы «трех сторон» в логистике (поставщика, потребителя, перевозчика и др.) является формула Харриса – Уилсона. Однако анализ данной зависимости показал, что она допускает различные интерпретации, поскольку основные элементы могут быть учтены различными способами в зависимости от:
- во-первых, кто осуществляет перевозку (поставщик, потребитель или посредник (перевозчик), кто хранит продукцию – потребитель (на собственном складе) или используется склад посредника (например, аренда), кто оформляет заказ – потребитель или посредник. Очевидно, что здесь возможны различные комбинации участников ПЛЦ;
- во-вторых, как рассчитываются затраты при хранении (пропорционально половине поступившей партии поставки или в зависимости от ее максимальной величины;
- в-третьих, как учитывается добавленная стоимость за транспортировку и организацию заказа в цене единицы продукции, поступившей на склад потребителя или посредника.
На рис.1 приведены несколько вариантов простых логистических звеньев.
Рассмотрим «классический вариант» суммарных затрат модели EOQ, формула (4), при условии, что затраты на выполнение заказа СЗ=Со+Ст , где Со, Ст – затраты, связанные соответственно с организацией заказа и его транспортировкой от поставщика до потребителя (рис.1А).
Очевидно, что классический вариант, во-первых, не конкретизирует роли участников, т.е. отражает обезличенное распределение затрат между поставщиком, потребителем (и перевозчиком); во-вторых, не учитывает добавленной стоимости в цене продукции, появившейся в результате выполнения заказа, при расчете затрат на хранение. Следовательно, на выходе простой логистической цепи цена единицы продукции СП1, отпускаемой со склада потребителя, который становится поставщиком в простой логистической цепи следующего (нижнего) уровня, должна учитываться с учетом добавленной стоимости ΔС, включающей затраты, связанных с выполнением логистических операций – оформление заказа, транспортировка и хранение на складе. Расчетная формула для СП1 может быть представлена в виде
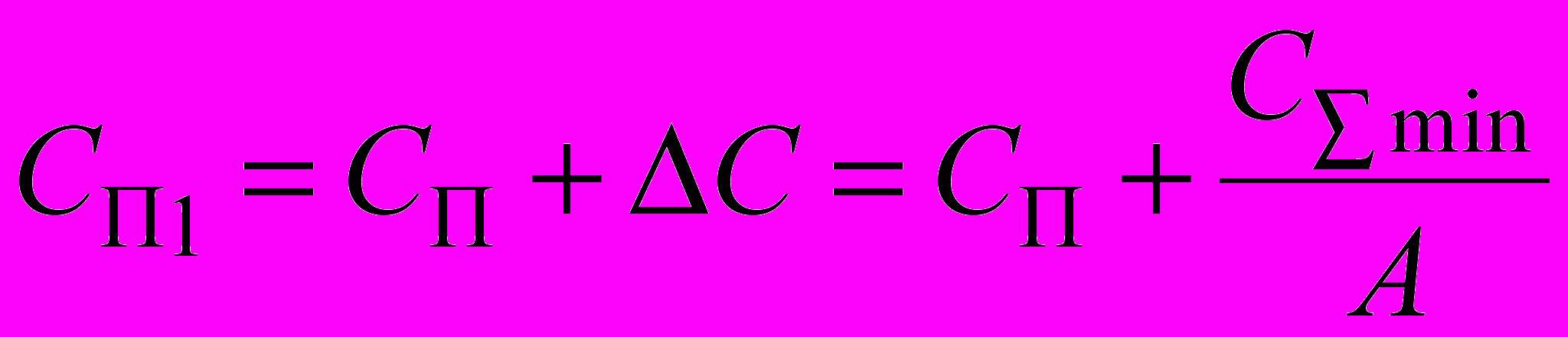(11)Возможная интерпретация классического варианта данной ПЛЦ соответствует, на наш взгляд, известной логистической концепции VMI (Vendor Managed Inventory), согласно которой поставщик или посредник берет на себя обязательство пополнять запасы потребителя и поддерживать их на необходимом уровне.
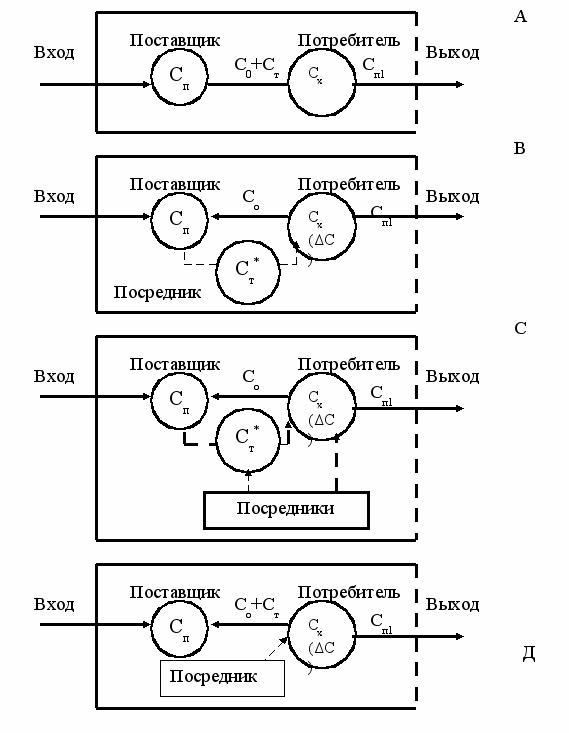
Сп, Сп1 – цена единицы продукции; С0 – затраты на оформление заказа; Ст, Ст* - различные варианты затрат на транспортировку партии; Сх, Сх (ΔС) – различные варианты затрат на хранение продукции; ΔС – добавленная стоимость
Рис.1. Варианты представления затрат основных участников простой логистической цепи.
В качестве одного из альтернативных вариантов рассмотрим случай, когда посредник (или поставщик) выполняет транспортировку, а оценка затрат на хранение продукции на складе потребителя включает добавленную стоимость за перевозку каждой единицы продукции, рис.1В. В общем случае данный вариант может быть представлен в виде системы
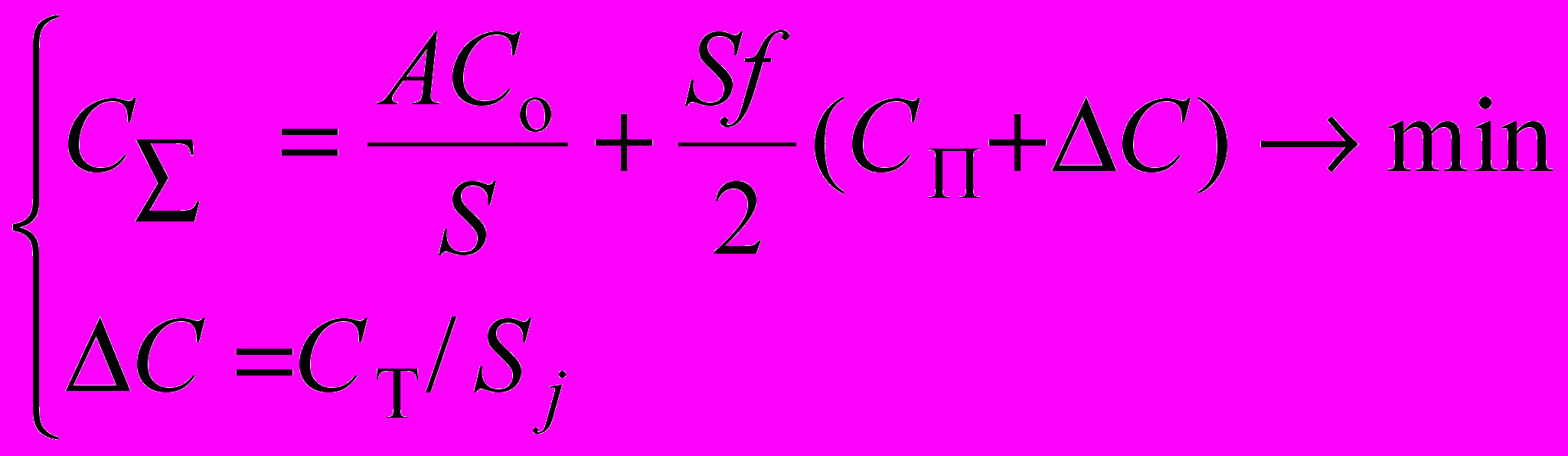, (12)Особенность системы (12) состоит в том, что при записи в виде двух уравнений удается отразить динамику (разновременность) протекания процессов, их последовательное выполнение, а именно: заказ – транспортировка - хранение. Решение системы (12) предполагает, что для нахождения оптимальной величины заказа So (из первого уравнения) необходимо знать ΔС. В свою очередь, входящее во второе уравнение ΔС зависит от Sj= So, т.е. оптимальной партии поставки определяемой из первого уравнения.
С учетом указанных особенностей выражение для суммарных затрат запишем в виде
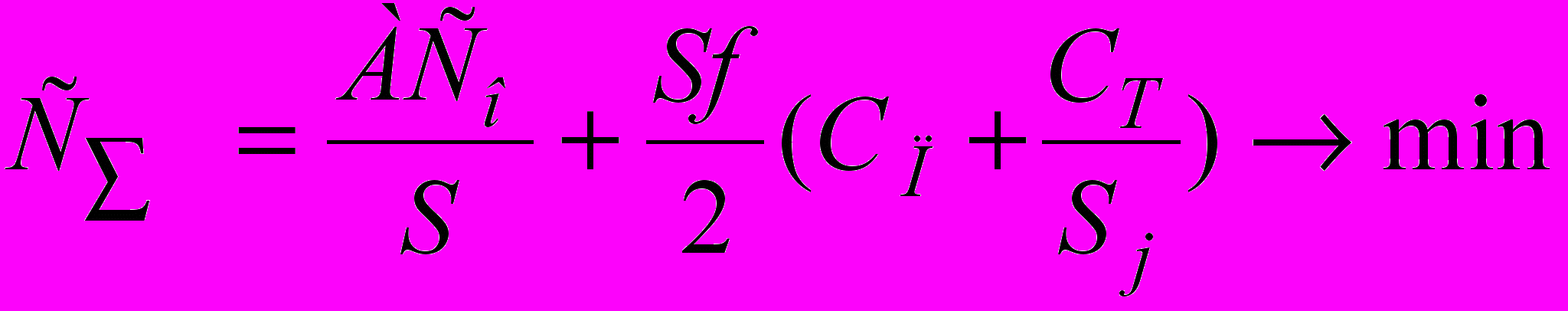(13)Для определения S можно воспользоваться двумя способами: численным и итерационным.
Следует подчеркнуть, что попытка упростить выражение (13), допустив, что Sj – это обычная переменная S , приводит к выражению
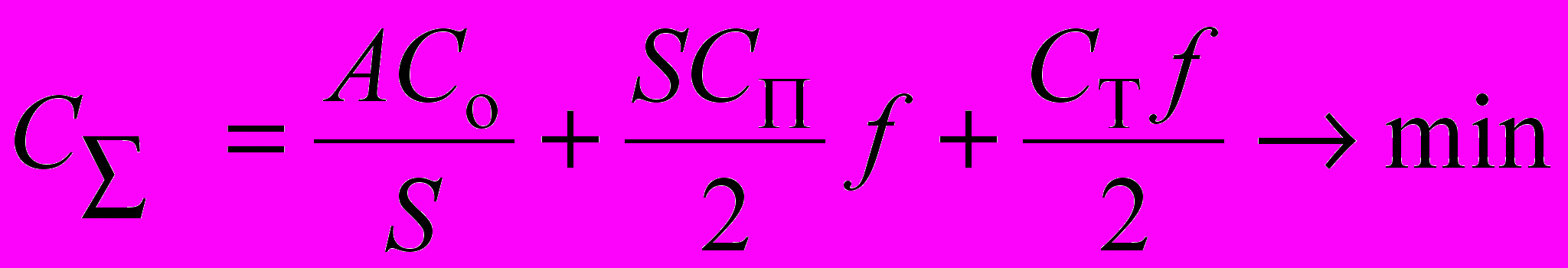(14)Тогда оптимальная партия поставки в результате применения стандартной процедуры оптимизации, должна рассчитываться по формуле
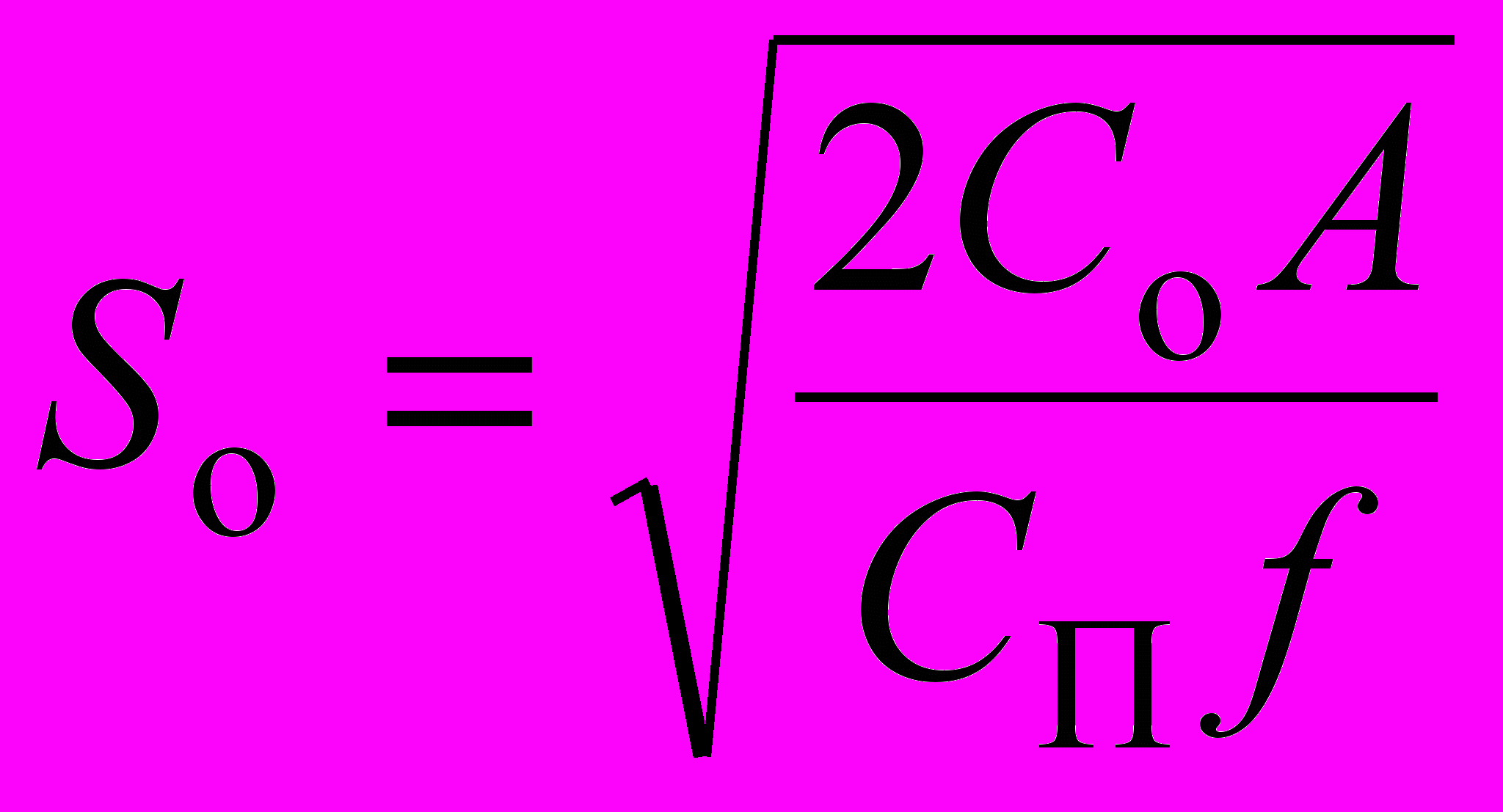(15)В табл. 6 приведены уравнения затрат для основных вариантов ПЛЦ.
Очевидно, что выражение для So соответствует восьмому варианту ПЛЦ, при котором расчет затрат на хранение не учитывает в цене товара добавленную стоимость за транспортировку.
Пример расчета ПЛЦ приведен в табл.7, из которой видно, что оптимальные затраты наблюдаются для четвертого варианта.
В диссертации приведены формулы для определения So и С∑min для всех вариантов табл. 6, а также примеры расчетов для логистических сетей, включающих несколько ПЛЦ.
Таблица 6
Варианты учета элементов простой логистической цепи и
добавленной стоимости в цене продукции
| Вариант (тип ПЛЦ) | Уравнения суммарных затрат С∑ и затрат на транспортировку | Комментарии |
| 1 (рис. А) |  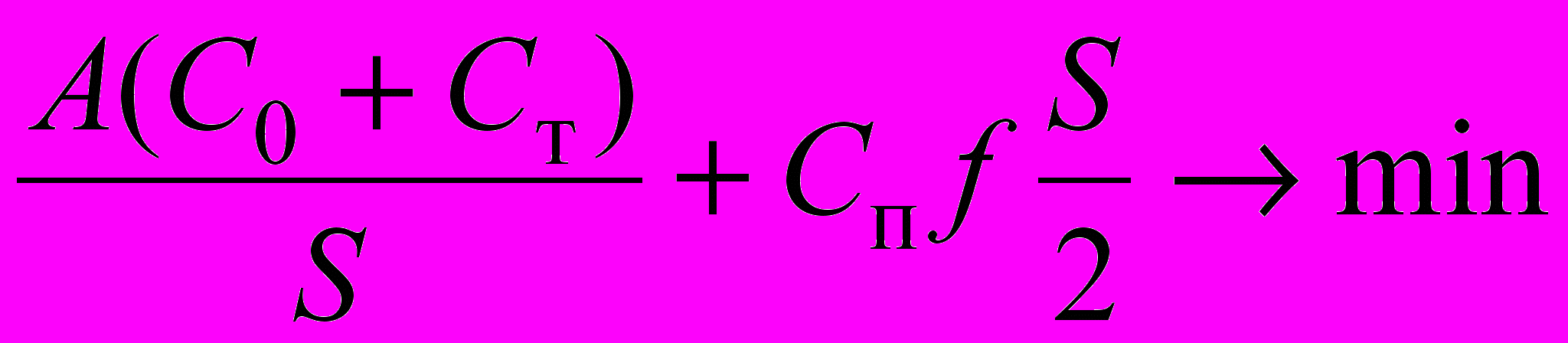 | Классическая модель EOQ (без конкретизации участников и учета добавленной стоимости). Возможно, что заказ, транспортировку и хранение совершает потребитель либо посредник. |
| 2 (рис. В) | 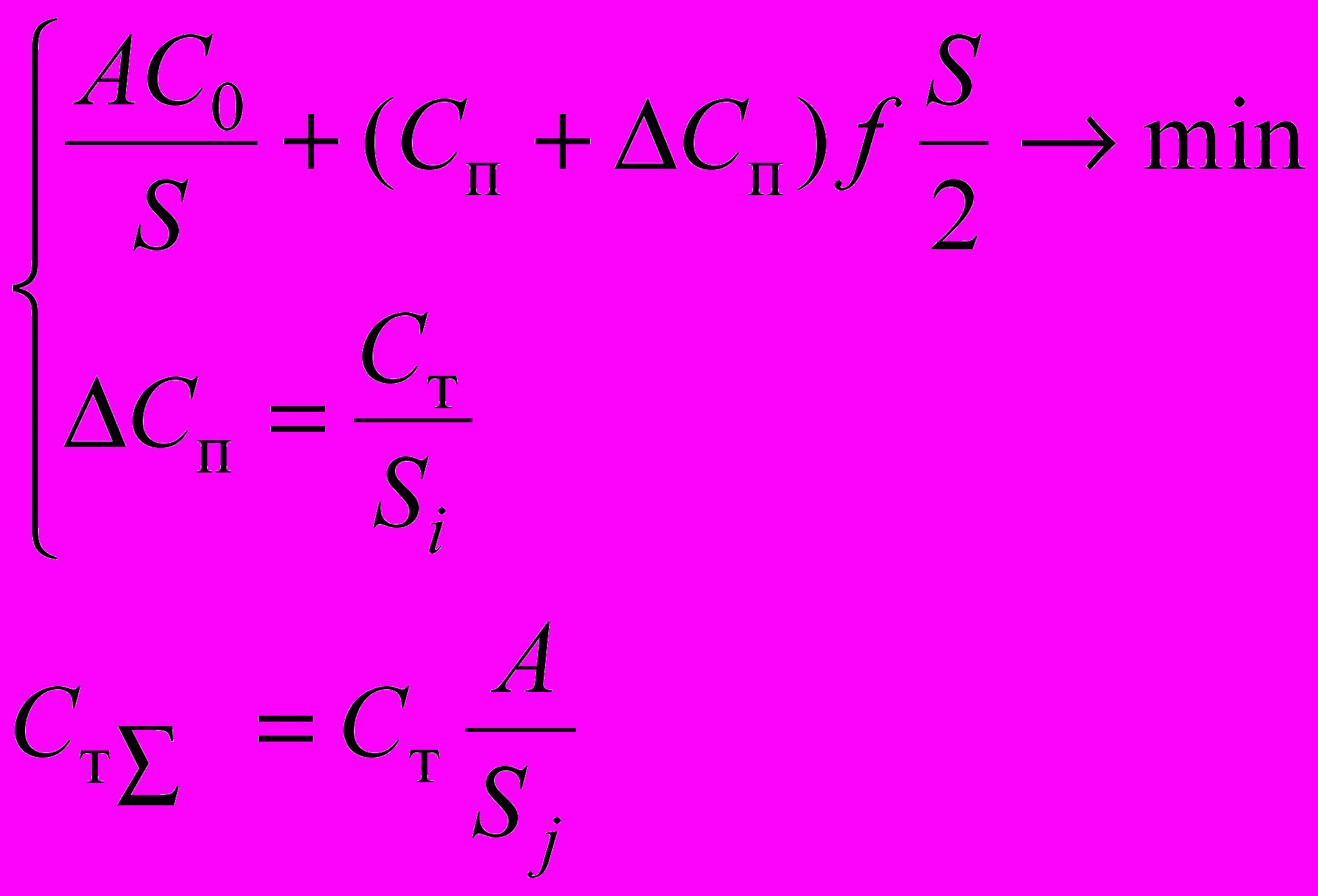 | Оформление заказа - потребитель; перевозка – посредник; при хранении (потребитель) в цене продукции учтена добавленная стоимость за транспортировку. |
| 3 | 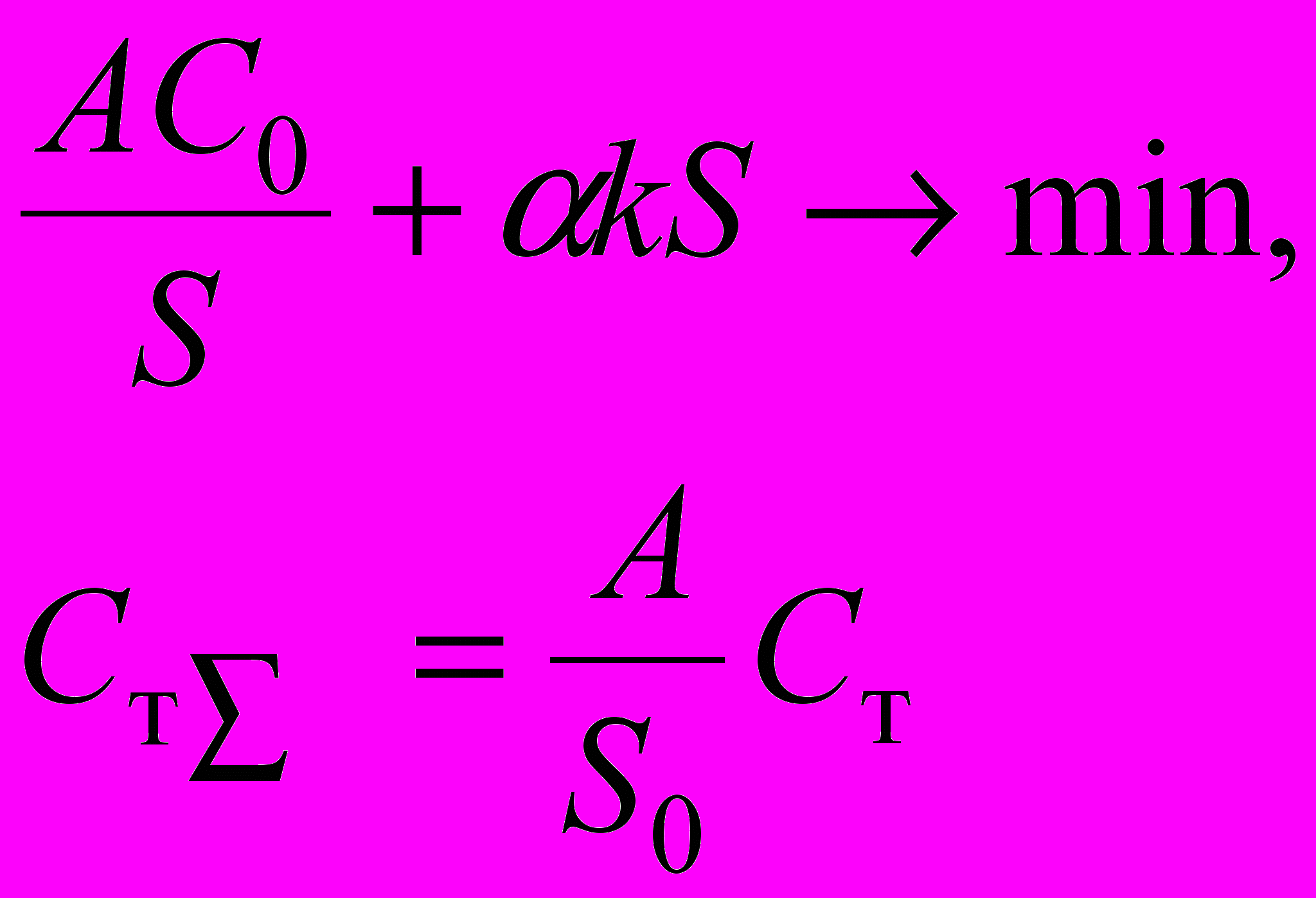 | Оформление заказа - потребитель; перевозка - посредник; при хранении добавленная стоимость не учитывается |
| 4 (рис. Д) | 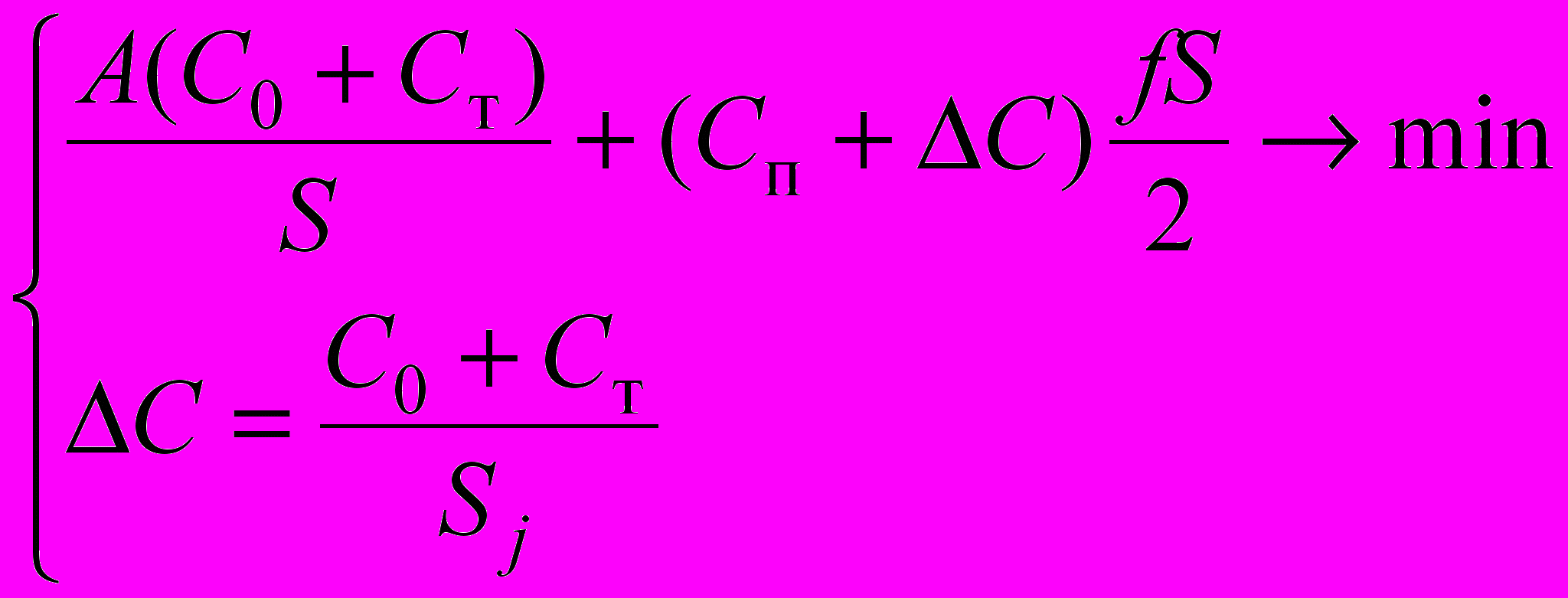 | Оформление заказа и транспортировка - потребитель; хранение – посредник; при хранении учитывается добавленная стоимость (оформление и транспортировка) |
| 5 | 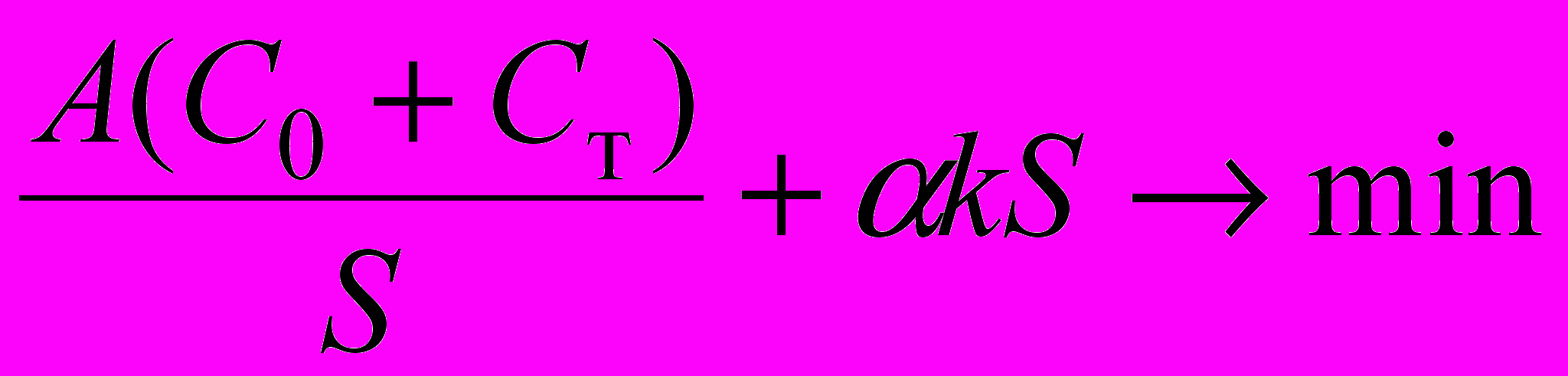 | Оформление заказа, транспортировка и хранение – потребитель (или VMI); добавленная стоимость не учитывается |
| 6* (рис. С) | 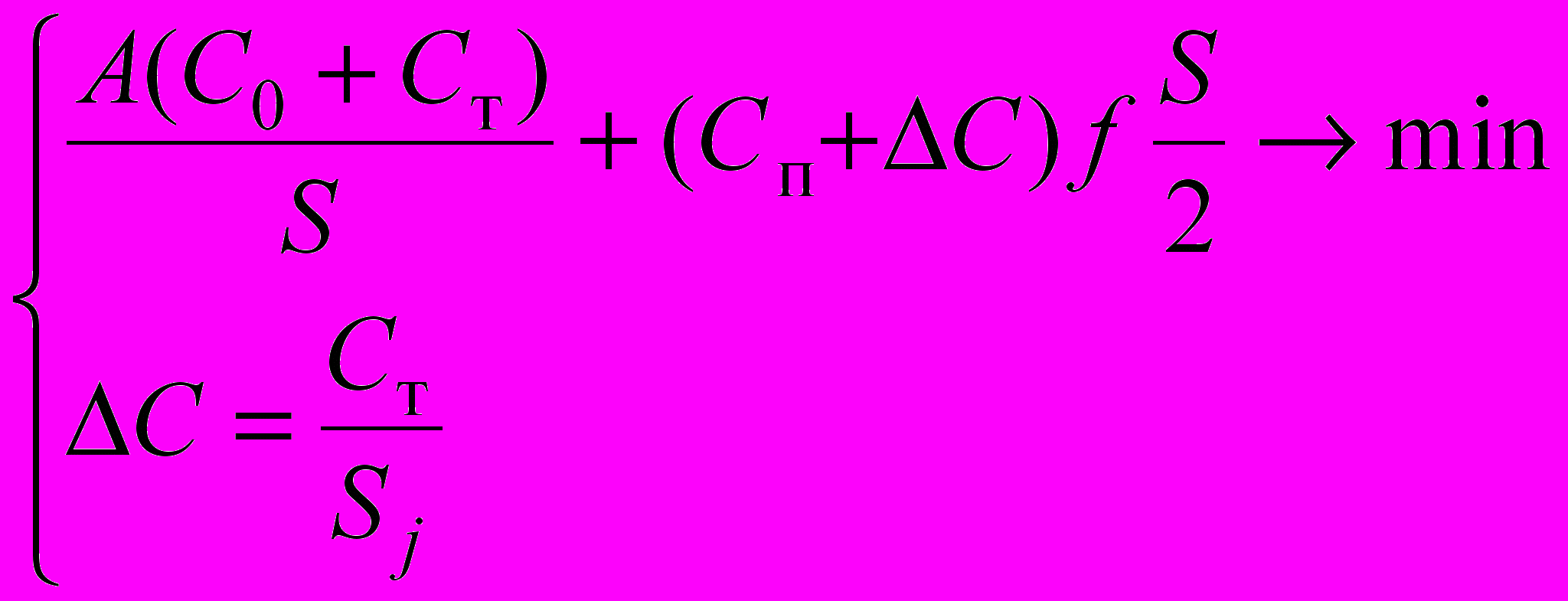 | Оформление заказа и транспортировка - получатель; хранение с учетом добавленной стоимости в цене продукта (только транспортировка) |
| 7 | 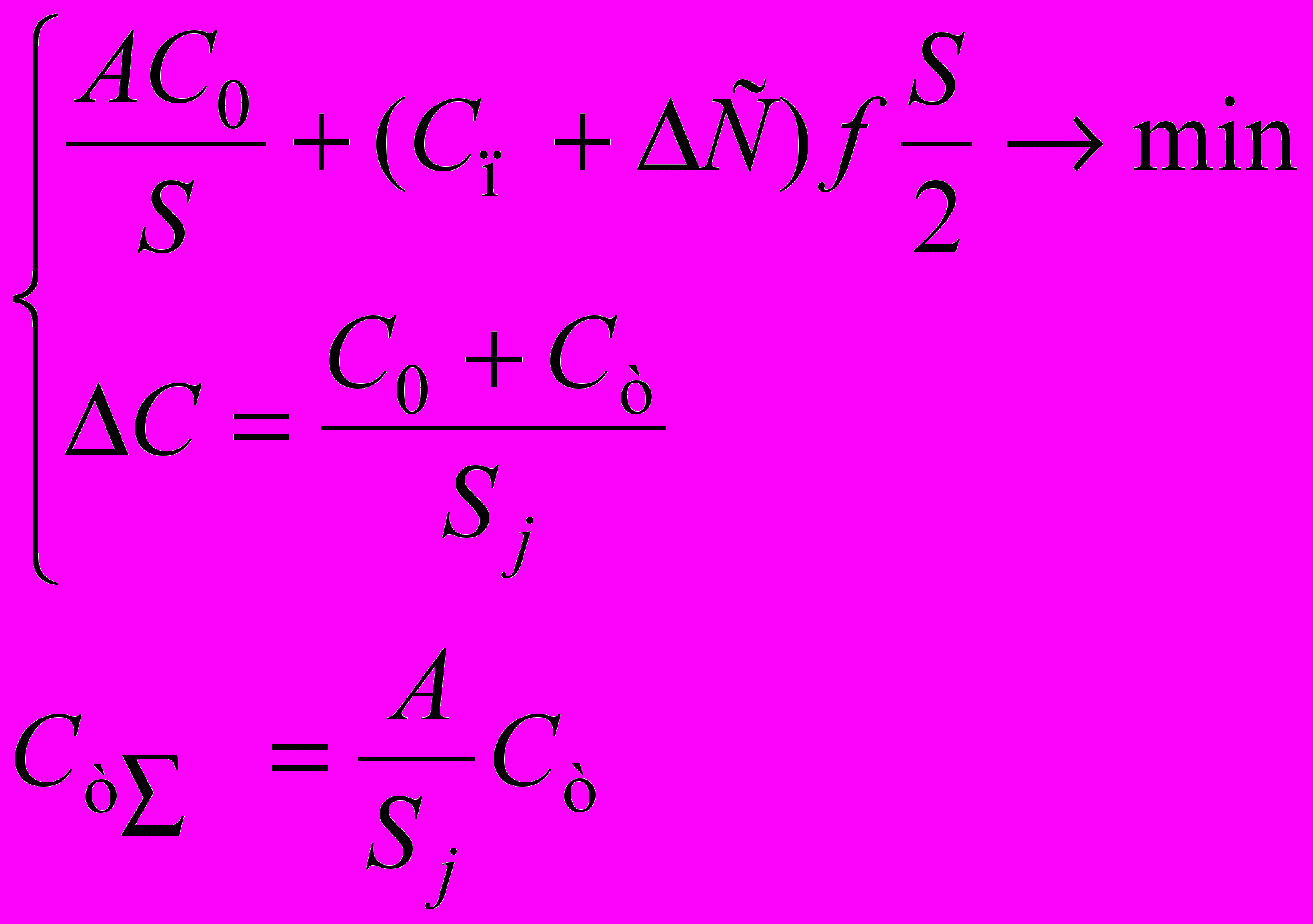 | Оформление заказа – получатель; транспортировка – посредник; посредник – хранение с учетом добавленной стоимости за оформление и транспортировку. |
| 8 | 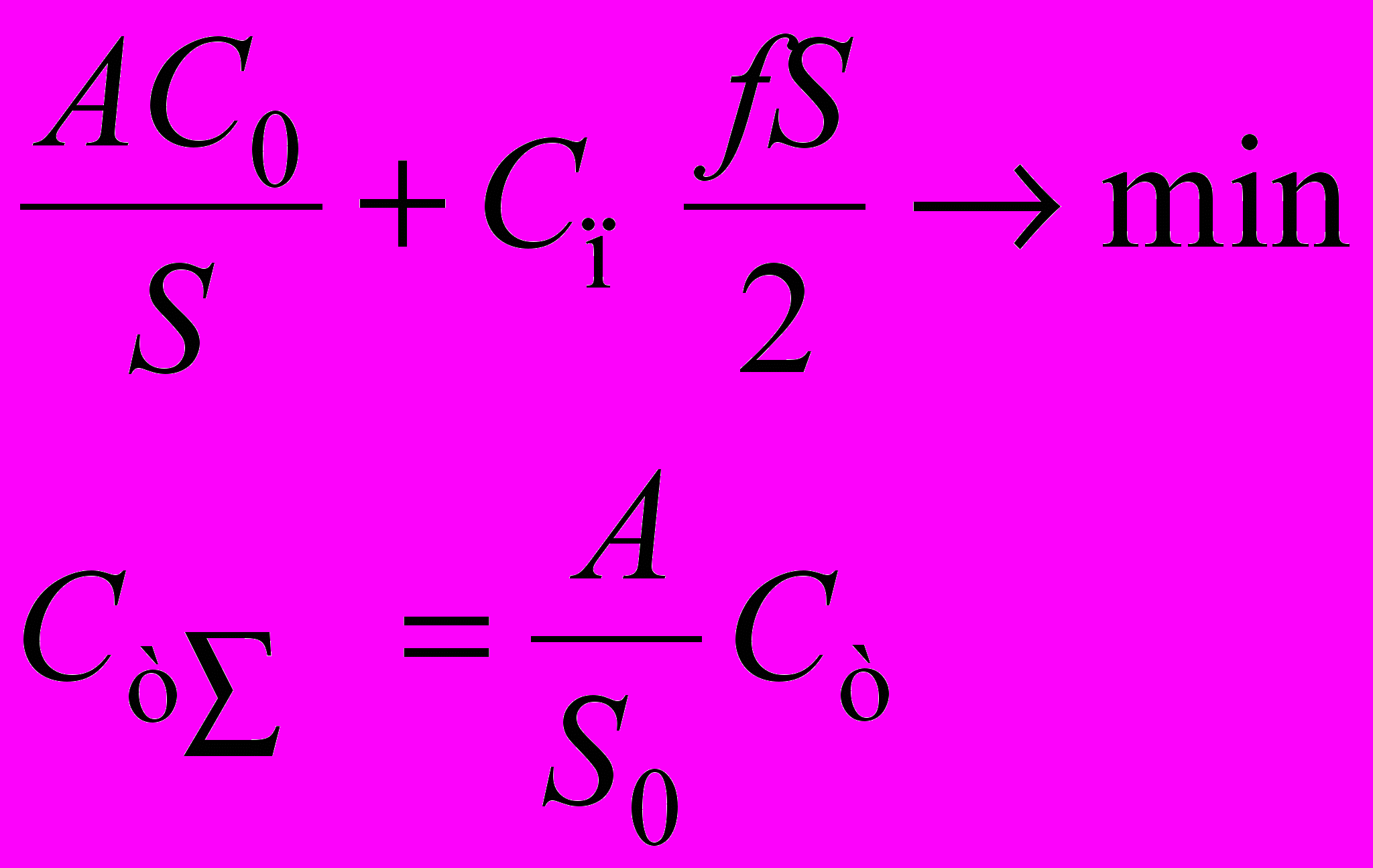 | Оформление заказа – получатель; транспортировка – посредник; хранение – получатель (или посредник) без учета добавленной стоимости при транспортировке. |
| * дискуссионный тип ПЛЦ, предусматривающий наличие хозрасчетных отношений внутри ЗЛС, например, со складом. | ||
Таблица 7
Результаты расчетов показателей для ПЛЦ-11
| Вариант (тип ПЛЦ) | Показатели | |||||||
| S0 | N | C∑min | C0∑ | Cх (Сх*) | Ст∑ (Ст∑*) | С∑об | Сп11 | |
| 1 | 285 | 2,08 | 623,6 | 103,8 | 311,8 | 208 | 623,6 | 11,84 |
| 2 | 163 | 3,68 | 368,0 | 184,0 | 184,0 | (294,3) | 662,4 | 11,903 |
| 3 | 110 | 5,47 | 548 | 274 | 274 | (438) | 985 | 12,44 |
| 4 | 326 | 1,84 | 551 | 92,3 | (276) | 183,4 | 551 | 11,72 |
| 5 | 190 | 3,15 | 948,6 | 158 | 474,3 | 316,3 | 948,6 | 12,38 |
| 6 | 284 | 2,11 | 633,6 | 105,8 | 211,2 | 316,8 | 633,6 | 11,86 |
| 7 | 187 | 3,22 | 312,6 | 160,8 | (160,8) | (257,2) | 570 | 11,75 |
| 8 | 167 | 3,59 | 360 | 180 | 180 | 287,4 | 647,4 | 11,87 |
| Примечание: Исходные данные для расчета: А=600 ед., Со=50 руб./зак., Ст=100 руб./зак., СП1=10,8 руб., f=0,15 | ||||||||
Уточнен критерий минимума общих затрат логистической сети, согласно предложенному критерию для каждой ПЛЦ, сформированной на основе модели оптимальной партии заказа EOQ, выбирается вариант с минимальными затратами, затем для всех ПЛЦ, входящих в анализируемую (проектируемую) логистическую сеть, указанные варианты суммируются.
Несмотря на то, что большое количество работ посвящено различным аспектам проектирования и реинжиниринга логистических систем (каналов, сетей), некоторые принципиальные вопросы их анализа и синтеза остаются малоисследованными.
Один из таких дискуссионных вопросов в логистике и управлении цепями поставок сводится к тому, как трактовать принцип минимума общих затрат в логистических сетях (системах). Ряд отечественных и зарубежных специалистов считают, что поскольку логистика позволяет охватить все этапы сферы обращения: «закупки (СЗ) – производство (СП) – хранение (СХ) – транспорт (СТ) – потребление», то данный критерий базируется на оптимальном значении каждого слагаемого,
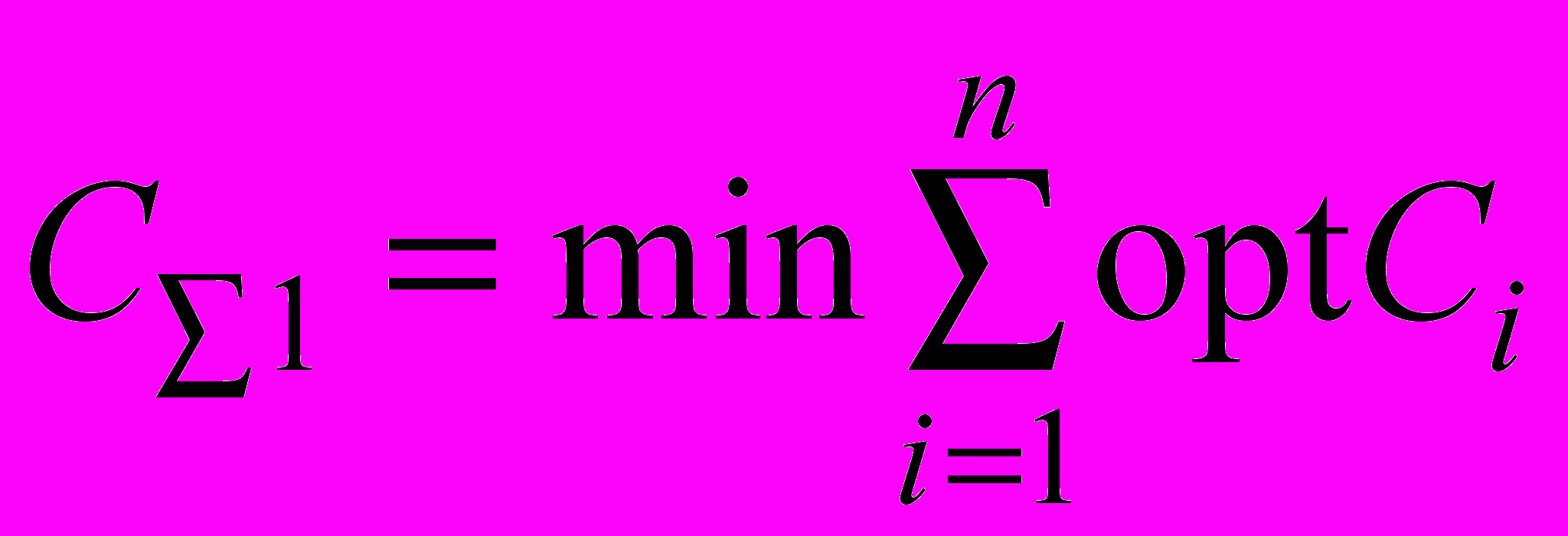, (16)где Сi – затраты, соответственно на закупочную деятельность (СЗ), производство (СП) и т.д.
К сожалению, помимо теоретического обоснования необходимости применения «принципа Парето» при оптимизации логистических систем во всех доступных автору работах отсутствуют прикладные разработки, позволяющие применить критерий (16) при проектировании и оптимизации цепей поставок.
Проведенный анализ и результаты расчетов позволяют сформировать критерий, отвечающий принципу минимума общих затрат логистической сети, основанный на ПЛЦ в виде
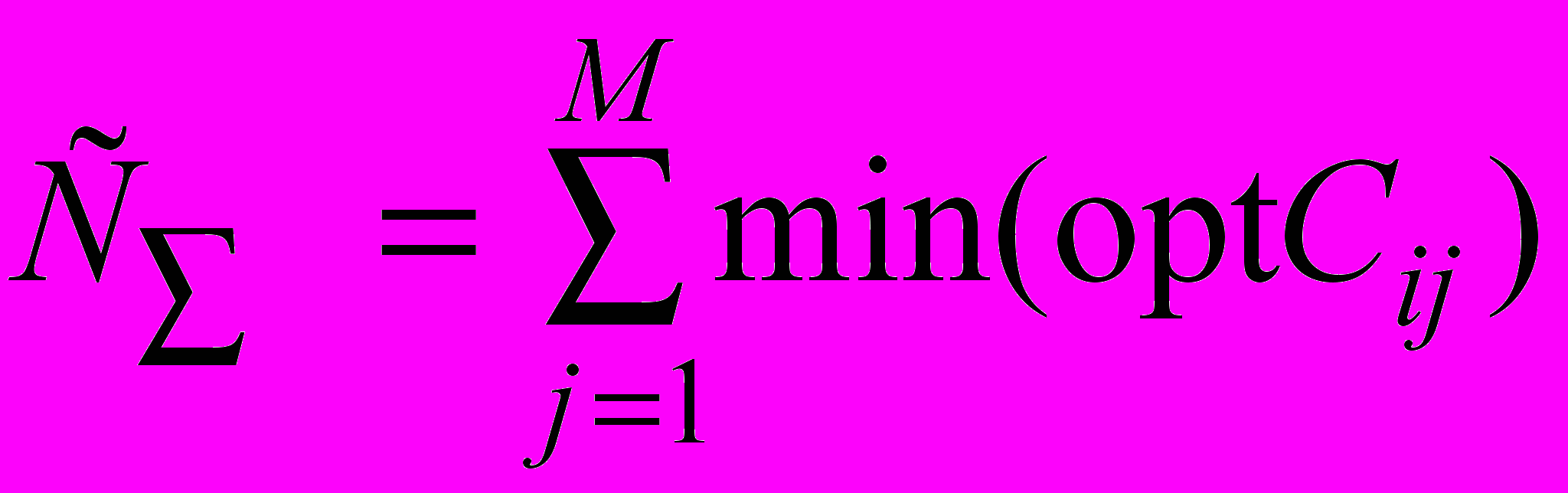, (17)где М – число ПЛЦ, входящих в логистическую сеть;
opt
- суммарные затраты i-го варианта j-й ПЛЦ, рассчитанные на основе модели EOQ (i=1,2,…,8);
- минимальная величина затрат в j-м ПЛЦ, j=1,…, М.На рис. 2 приведен пример логистической сети, включающей три ПЛЦ. Для принятых исходных данных в результате расчетов оказалось:
для ПЛЦ-01 (центральный склад – региональный центр) минимальные затраты соответствуют первому варианту, С∑01=1581 руб.
для ПЛЦ-11 (региональный центр – магазин 1) – четвертый вариант, С∑11=551 руб.;
для ПЛЦ-12 (региональный центр – магазин) – пятый вариант, С∑12=1400 руб.;
минимальные суммарные затраты для рассматриваемой логистической сети, согласно критерию (17) С∑=3532 руб.
Если расчет для каждой ПЛЦ данной сети производить на основе модели EOQ, то минимальные суммарные затраты составят 3652 руб.
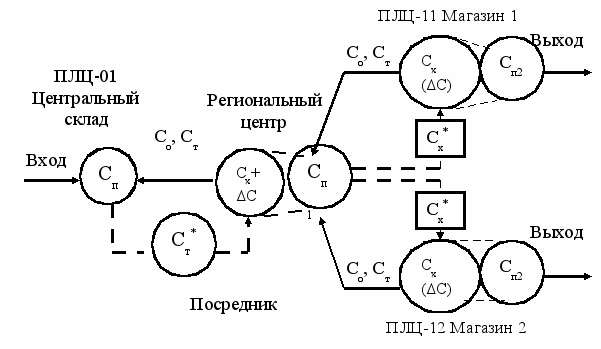
Рис. 2. Логистическая сеть, включающая три ПЛЦ: «центральный склад – региональный центр – магазины»
Очевидно, что полученные результаты отражают одно из перспективных направлений исследований, связанных с анализом и синтезом проектируемых логистических систем. Таким образом, выполнение требования минимизации затрат логистической сети будет соблюдаться, если каждая ПЛЦ, входящих в логистическую сеть поставок, будет спроектирована таким образом, чтобы затраты на организацию и выполнение логистических функций (операций) для нее были оптимальными.
Разработана классификация модифицированных моделей EOQ, включающая основные и синтезированные варианты, получены откорректированные и уточненные формулы для расчета параметров ряда модификаций: «экономического размера партии EBQ», «производственного заказа EPQ», дефицита с отложенным спросом и другие.
При решении задач производственной и распределительной логистики при зависимом спросе все чаще находят применение модели управления запасами типа LFL («партия за партией»), PPB («балансирование по отдельным периодам») и другие, основанные на так называемых модифицированных моделях EOQ.
Рассмотренные ранее формулы расчета EOQ не учитывают двух существенных составляющих:
- постепенную разгрузку прибывающей партии, которая занимает определенное время t1 и в ряде случаев соизмеримо с продолжительностью цикла Т;
- возможность возникновения дефицита, когда поступающие требования накапливаются и затем удовлетворяются при поступлении партии (отложенный спрос) либо оставляются без внимания и не учитываются (неудовлетворенный спрос).
Выполненный анализ показал, что различные подходы при описании модифицированных формул расчета EOQ целесообразно разбить на две группы. Первая – включает четыре базовые модели:
1) производственного заказа EPQ ( поступление и одновременное потребление за время t1, последующее потребление до конца цикла T);
2) экономичного размера партии EBQ (поступление без потребления за время t1, только потребления до конца цикла Т);
3) текущего запаса с дефицитом («отложенный спрос»);
4) текущего запаса с потерей требований при дефиците.
Вторая группа, названная нами синтезированной, также включает четыре модели, представляющие собой различные комбинации моделей первой группы, например, моделей 1 и 3 и др.
Следует подчеркнуть, что предложенная классификация должна быть дополнена вариантами, учитывающие частичное удовлетворение спроса при дефиците, т.е. часть требований накапливается и удовлетворяется при поставке партии, а часть теряется. Таких моделей три, например комбинация третьей и четвертой моделей и т.д.
Для большинства модифицированных моделей получены формулы для расчета основных показателей, однако некоторые из них требуют, корректировки и уточнения, связанных с более полным учетом затрат. Так, для моделей EPQ и EBQ вводятся затраты Сх, связанные с хранением продукции после изготовления на производственных участках или пребывающей на склад в контейнерах, кузовах автомобилей, вагонах; для моделей с дефицитом учитываются затраты, связанные с оплатой пустого склада Cc.
В диссертации приведены выводы для ряда модифицированных моделей. Для примера в табл. 8 приведены зависимости для моделей EPQ и EBQ.