Geum.ru

Экзамен осуществляется устно на русском языке. Время на испытание 4 часа

Вид материалаДокументы

Содержание


Теоретические вопросы
Подобный материал:
Дисциплина «Теория вероятностей и математическая статистика»


Общие положения


Перечень вопросов для подготовки абитуриентов к вступительному экзамену по дисциплине «Теория вероятностей и математическая статистика» в магистратуру высшего профессионального образования по направлению 231300 «Прикладная математика» предназначен для оказания помощи при подготовке к сдаче экзамена.

В ходе подготовки к экзамену следует руководствоваться Программой экзамена.

Предложенные вопросы позволяют выяснить базовые знания по дисциплине «Теория вероятностей и математическая статистика» в соответствии с требованиями Государственного образовательного стандарта по направлению подготовки «Прикладная математика» (квалификация магистр).

Прием вступительного экзамена осуществляет экзаменационная комиссия из научно-педагогического состава Академии. На прием экзамена выделяется один день.

Экзамен осуществляется устно на русском языке.

Время на испытание – 4 часа.

На экзамен выносится 2 (два) теоретических вопроса и 1 (одна) задача.

Оценка за ответы по каждому вопросу, определяется по следующим критериям:

«Отлично» – при наличии у абитуриента фундаментальных знаний по заданному вопросу, аргументированном и логически стройном построении ответа по существу вопроса. В ответе должны быть представлены определения, соответствующие рассматриваемому вопросу. Правильно решённая задача.

«Хорошо» – при наличии твердых и достаточно полных знаний по заданным вопросам, логически стройном построении ответа, понимании сущности вопроса, но при этом допущенных неточностях, ошибки в определениях, незначительные ошибки в детализации теоретических основ рассматриваемого вопроса. Правильно решенная задача.

«Удовлетворительно» – при наличии твердых знаний по сущности заданного вопроса, изложении ответа с ошибками либо существенные ошибки в представлении их содержания. Правильно решенная задача.

«Неудовлетворительно» – выставляется оценка за вопрос в случаях:

слабого знания материала, непонимания сущности излагаемого вопроса,

наличия грубых ошибок в ответе, неточности ответов, требующих дополнительных вопросов,

представление ответа, не соответствующего рассматриваемому вопросу

неправильно или нерешенная задача.

По результатам экзамена оценка:

«отлично» выставляется, если за ответы на вопросы билета получены отличные оценки при правильно решенной задачи и не более одной хорошей на дополнительно заданные вопросы;

«хорошо» – за ответы на вопросы билета получены отличные и хорошие оценки при правильно решенной задачи и не более одной удовлетворительной на дополнительные вопросы причем;

«удовлетворительно» – за ответы на вопросы билета получены положительные оценки и не более одной неудовлетворительной при правильно решенной задачи и не более одной не удовлетворительной на дополнительные вопросы;

«неудовлетворительно» – не выполнены условия на оценку «удовлетворительно».


Теоретические вопросы

к вступительному экзамену по дисциплине

«Теория вероятностей и математическая статистика»

в магистратуру Академии Гражданской защиты МЧС России

по направлению 231300 «Прикладная математика»

(квалификация магистр)


  1. случайные события. Виды случайных событий. Классическое, статистическое и геометрическое определение вероятности.
  2. Сумма событий. Теорема сложения вероятностей несовместных событий. Полная группа событий. Противоположенные события.
  3. Независимые события. Теорема умножений вероятностей независимых событий. Вероятность появления хотя бы одного события.
  4. Зависимые события. Условная вероятность. Теорема умножения вероятностей зависимых событий.
  5. Вероятность суммы совместных событий. Формула полной вероятности. Формула Бейеса.
  6. Схема Бернулли. Формула Бернулли.
  7. Асимптотические преобразования формулы Бернулли. Формула Пуассона.
  8. Определение наиболее вероятного числа испытаний в схеме Бернулли.
  9. Формулировка локальной и интегральной теорем Лапласа. Свойства функций Гаусса и Лапласа.
  10. Виды случайных величин. Закон распределения дискретной случайной величины. Биномиальное распределение.
  11. Математическое ожидание дискретной случайной величины. Вероятностный смысл математического ожидания. Свойства математического ожидания.
  12. Дисперсия дискретной случайной величины. Свойства дисперсии. Выражение дисперсии через центральный и начальный момент второго порядка.
  13. Математическое ожидание и дисперсия случайной величины X, распределенной по биноминальному закону.
  14. Математическое ожидание и дисперсия случайной величины X, распределенной по закону Пуассона.
  15. Простейший поток событий и его свойства. Формула Пуассона как математическая модель простейшего потока событий.
  16. Интегральная функция распределения случайной величины. Свойства интегральной функции. График интегральной функции дискретной случайной величины.
  17. Непрерывные случайные величины. Дифференциальная функция распределения вероятностей (функция плотности вероятностей). Свойства этой функции плотности. Вероятность попадания случайной величины в заданный интервал.
  18. Формулы для вычисления математического ожидания и дисперсии непрерывной случайной величины. Равномерно распределенная случайная величина. Ее математическое ожидание и дисперсия.
  19. Простейшее нормальное распределение случайной величины. Кривая Гаусса. Общий вид нормального распределения. Вероятностный смысл параметров, определяющих нормальное распределение. Влияние параметров нормального распределения на форму кривой.
  20. Показательный закон распределения случайной величины, ее математическое ожидание и дисперсия.
  21. Вероятность попадания в заданный интервал нормально распределенной случайной величины. вычисление вероятности заданного отклонения. Правило трех сигм.
  22. Показательный закон надежности.
  23. Закон распределения дискретной двумерной случайной величины. Интегральная функция распределения и ее свойства.
  24. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами параллельными координатным осям.
  25. Закон распределения непрерывной двумерной случайной величины. Дифференциальная и интегральная функции распределения их вероятностный смысл и свойства.
  26. Нахождение по интегральной функции распределения двумерной случайной величины интегральной и дифференциальной функций безусловного распределения составляющих.
  27. Необходимые и достаточные условия независимости двух случайных величин.
  28. Условные законы распределения составляющих двумерной случайной величины.
  29. Условные математические ожидания составляющих двумерной случайной величины. Уравнение регрессии.
  30. Корреляционный момент и коэффициент корреляции.
  31. Свойства корреляционного момента.
  32. Прямая средняя квадратичная регрессия Y на х.
  33. Нормальный закон распределения на плоскости.
  34. Условные математические ожидания составляющих двумерной нормально – распределённой случайной величины.
  35. Теорема Чебышева.
  36. Теорема Бернулли.
  37. Теорема Ляпунова.
  38. Выборка из генеральной совокупности X. Вариационный ряд. Статистический ряд. Гистограмма.
  39. Эмпирическая средняя 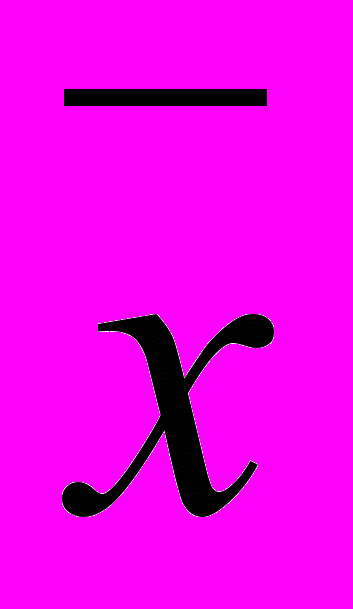- точечная оценка М(Х). Свойство состоятельности и несмещённости.
  40. Исправленная эмпирическая дисперсия S2 – точечная оценка D(Х). Свойство состоятельности и несмещённости.
  41. Определение доверительного интервала для М(Х), если нормально распределенная величина Х представлена выборкой и D(Х) = 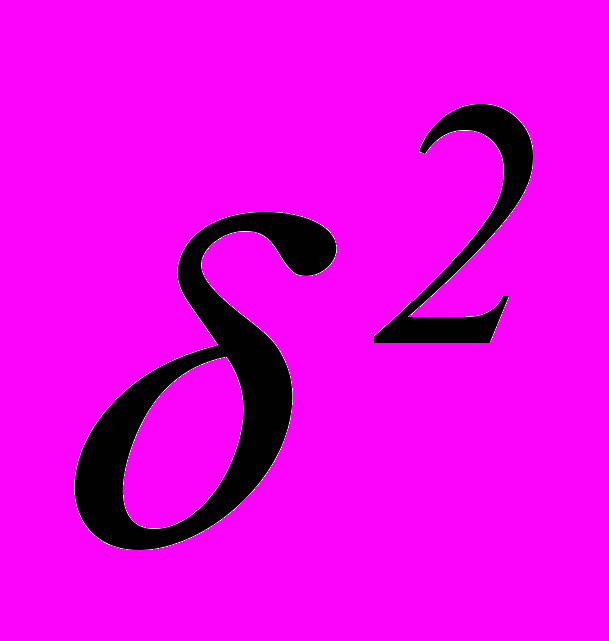известна.
  42. Определение доверительного интервала для М(Х), если нормально распределенная величина Х представлена выборкой и D(Х) неизвестна.
  43. Определение доверительного интервала для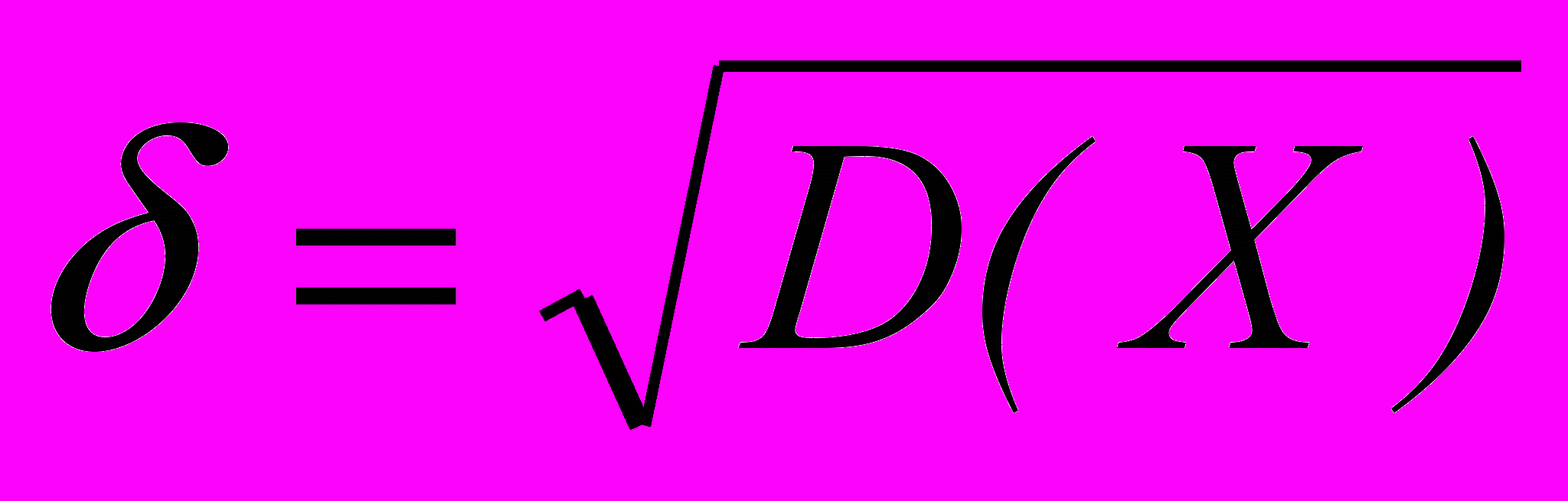, если нормально распределенная величина Х представлена выборкой.
  44. Критерий Пирсона в проверке гипотезы о нормальном законе распределения генеральной совокупности X, представленной выборкой.
  45. Метод максимума правдоподобия и метод наименьших квадратов.


Литература


  1. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения. –М.: Высшая школа, 2010.
  2. Кремер Н.Ш., Теория вероятностей и математическая статистика. –М.: Юнита-Дана, 2010.
  3. Гмурман В.Е. Теория вероятностей и математическая статистика. –М.: Высшая школа, 2001.
  4. Вентцель Е.С., Овчаров Л.А. Задачи по теории вероятностей и математическая статистика. –М.: КноРус, 2010.
  5. Гмурман В.Е. Руководство к решению зада по теории вероятностей и математическая статистика. –М.: Высшая школа, 2001.