Решение. Вспомогательная таблица имеет вид

Вид материала

Решение

Подобный материал:

• Тест по теме электронные таблицы ms excel Электронная таблица предназначена для, 30.47kb.
• Тест «Какие цели преследовали большевики, осуществляя нэп?»; Исторические документы, 155.12kb.
• 11. Электронные таблицы. Назначение и основные возможности. 8 класс, 24.13kb.
• Курс имеет вид лекций / обсуждений. Он содержит решение задач в малых группах, анализ, 1984.1kb.
• Тихонов Владимир Фёдорович Каждый вид спорта имеет свои корни. Одни только зарождаются,, 55.91kb.
• Центр международного сотрудничества и образовательных программ, 125.72kb.
• Лекция №6,7 Происхождение человека. Антропогенез, 221.09kb.
• «Таблица заведомо элементарных структур» тзэс (автор: Владимир Кишкинцев), 28.45kb.
• «Эритроциты. Переливание крови», 80.63kb.
• Сравнительная таблица сравнительная таблица действующей Конституции Кыргызской Республики, 2265.51kb.

Задание 3. Изучая зависимость между показателями X и Y, проведено обследование 9 объектов и получены следующие данные

X	10	14	21	24	33	41	44	47	49
Y	43	47	50	48	54	57	61	59	65

Полагая, что между X и Y имеет место линейная корреляционная связь, определите выборочное уравнение регресси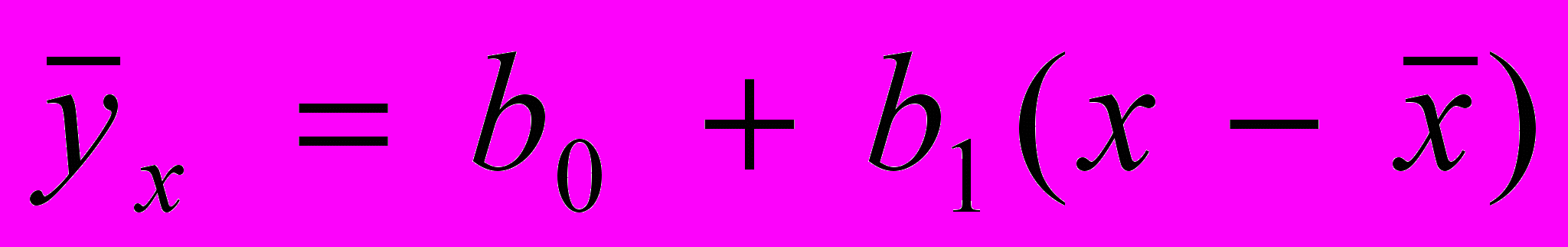и (или ) и выборочный коэффициент линейной регрессии 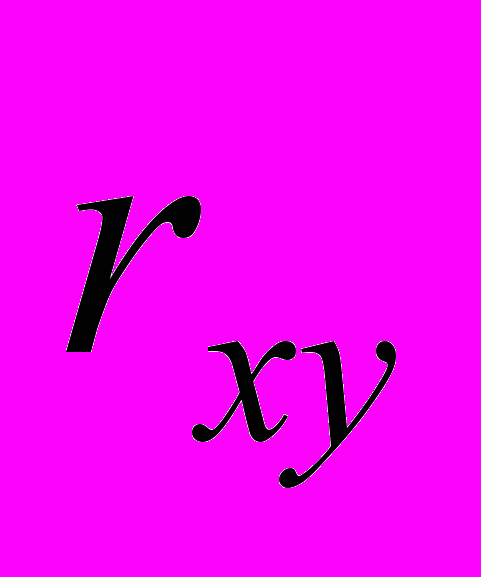. Постройте диаграмму рассеяния и линию регрессии. Сделайте вывод о направлении и тесноте связи между показателями X и Y.

Решение.

Вспомогательная таблица имеет вид:

№	x	y	x2	y2	xy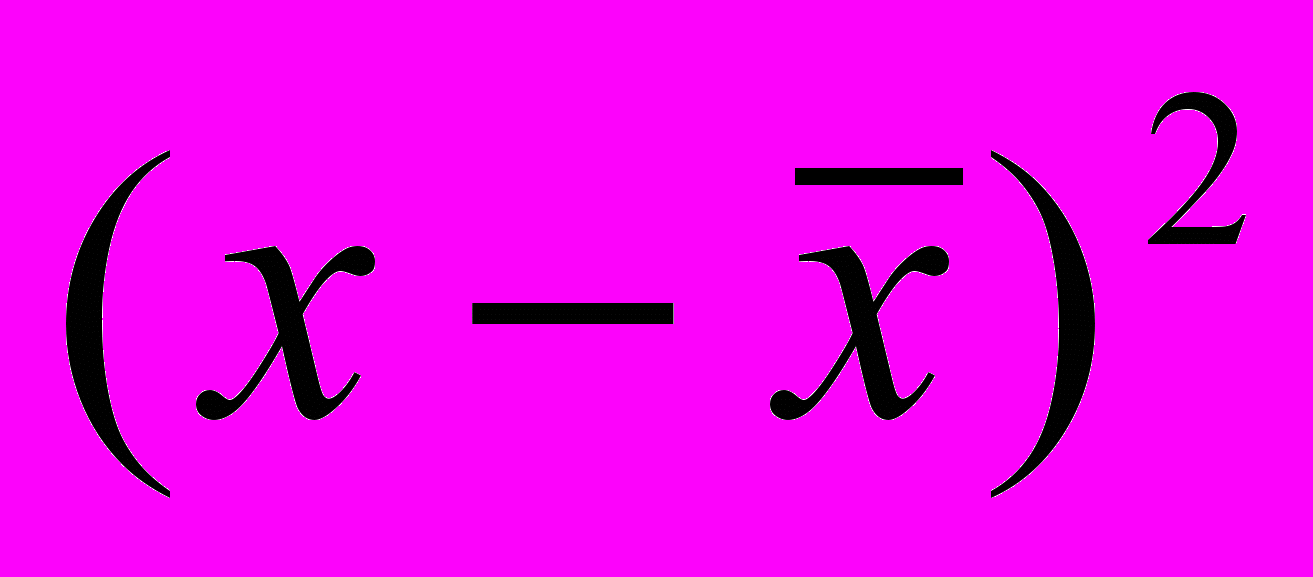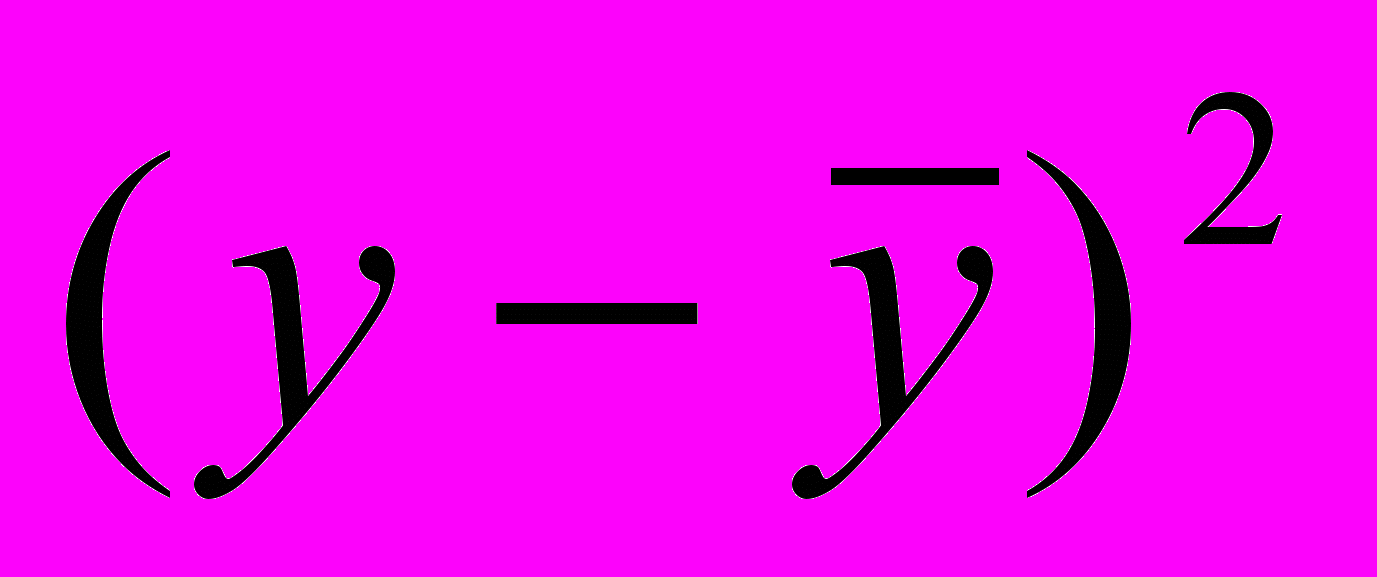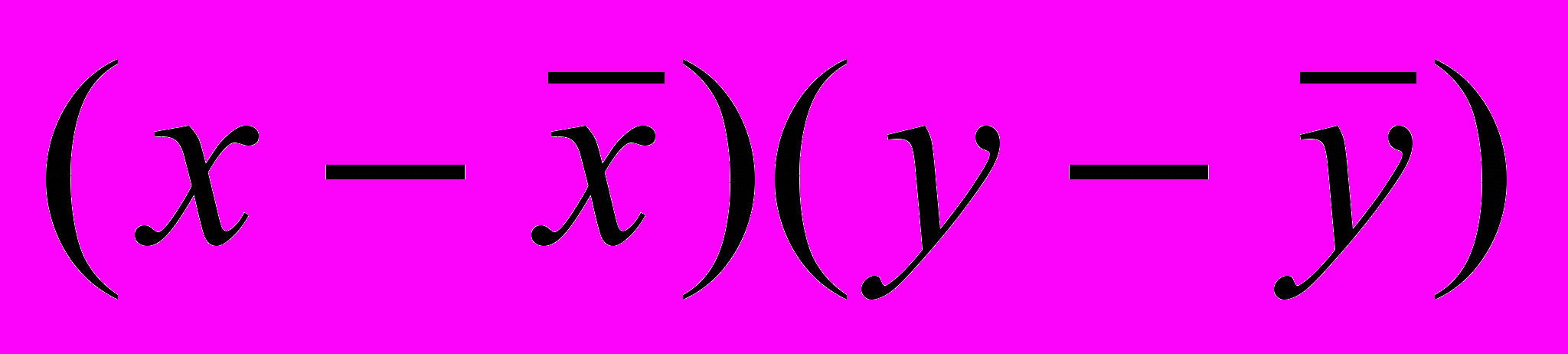
1	10	43	100	1849	430	(-21,4)2=457,96	(-10,8)2=116,64	231,12
2	14	47	196	2209	658	(-17,4)2=302,76	(-6,8)2=46,24	118,35
3	21	50	441	2500	1050	(-10,4)2=108,16	(-3,8)2=14,44	39,52
4	24	48	576	2304	1152	(-7,4)2=54,76	(-5,8)2=33,64	42,92
5	33	54	1089	2916	1782	1,62=2,56	0,22=0,04	0,32
6	41	57	1681	3249	2337	9,62=92,16	3,22=10,24	30,72
7	44	61	1936	3721	2684	12,62=158,76	7,22=51,84	90,72
8	47	59	2209	3481	2773	15,62=243,36	5,22=27,04	81,12
9	49	65	2401	4225	3185	17,62=309,76	11,22=125,44	197,12
Всего	283	484	10629	26454	16051	1730,24	415,32	831,91
Среднее	31,4	53,8	1181	2939,3	1783,4

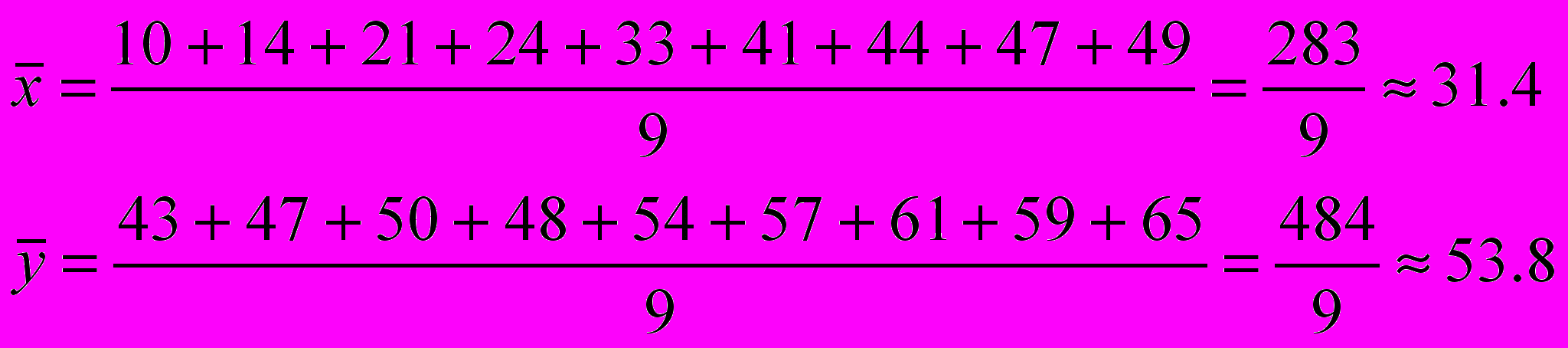
Построим уравнение регрессии y=a+bx,коэффициенты a и b находим методом наименьших квадратов, решая систему линейных уравнений

где п=9.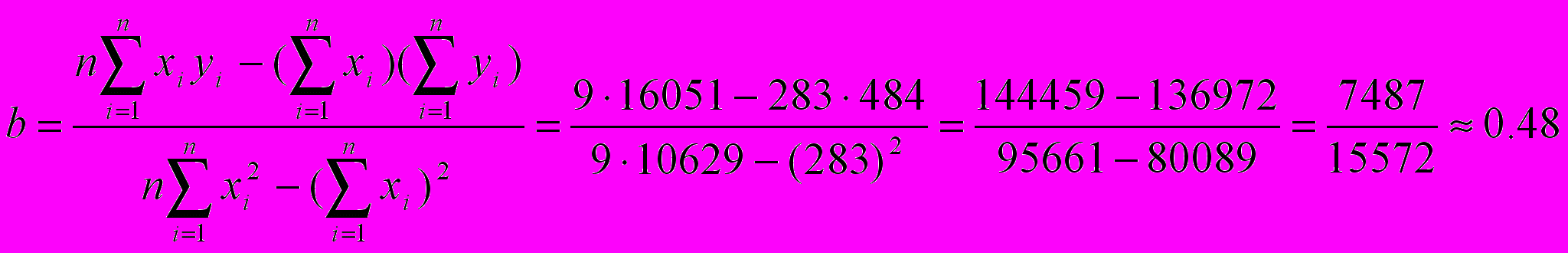





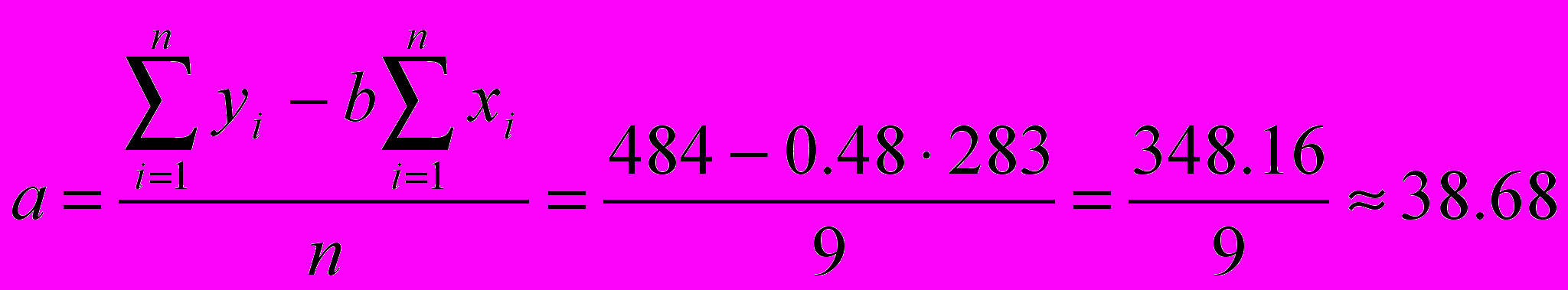
Уравнение регрессии имеет вид: y_х=38.68+0.48x

Второе уравнение регрессии

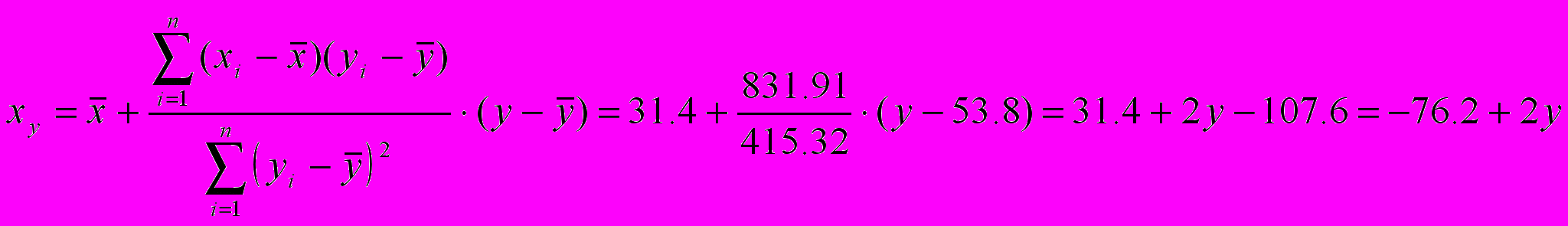x_y=-76.2+2y

Вычисляем выборочный коэффициент линейной регрессии







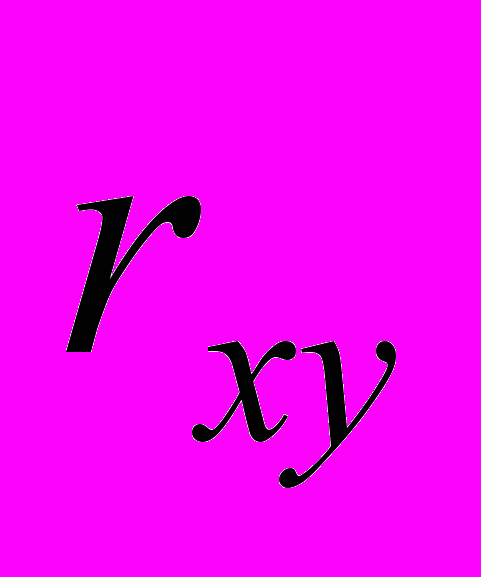
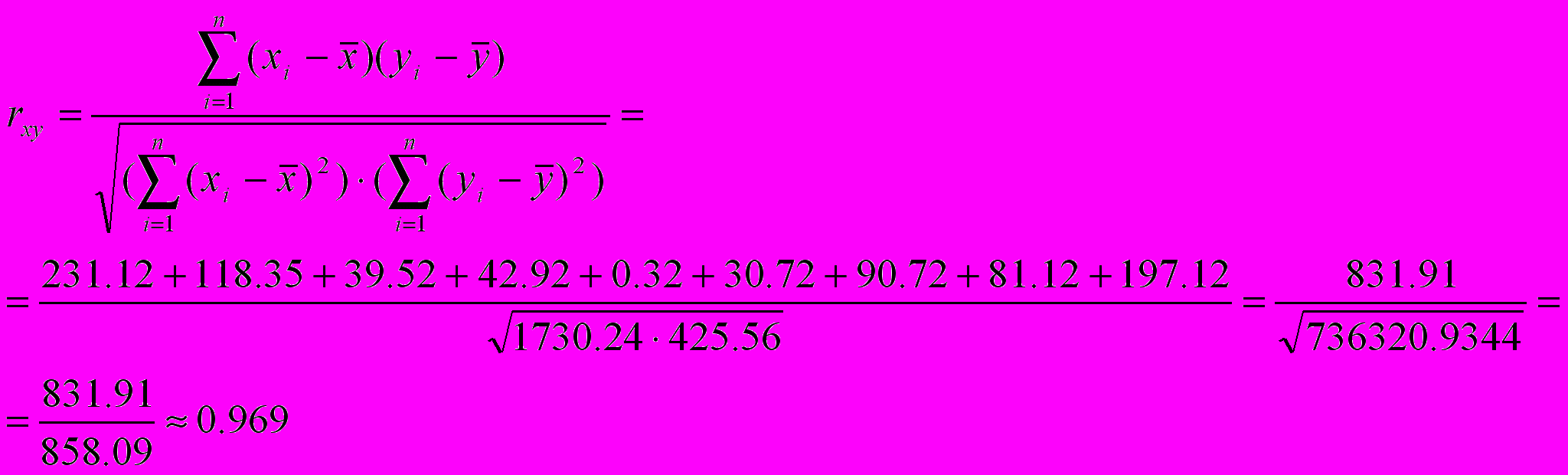
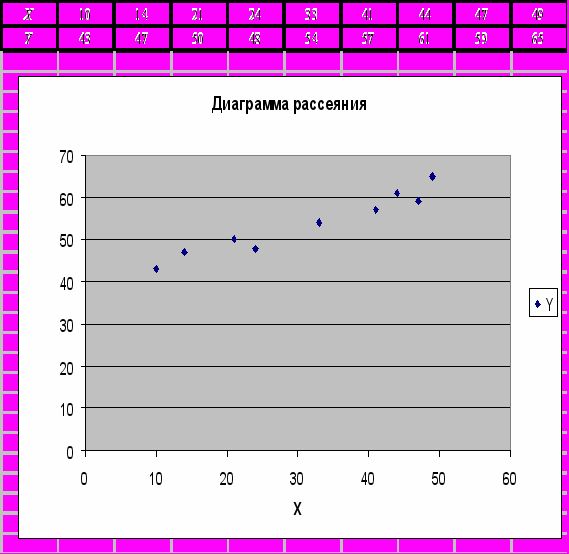
График линий регрессий



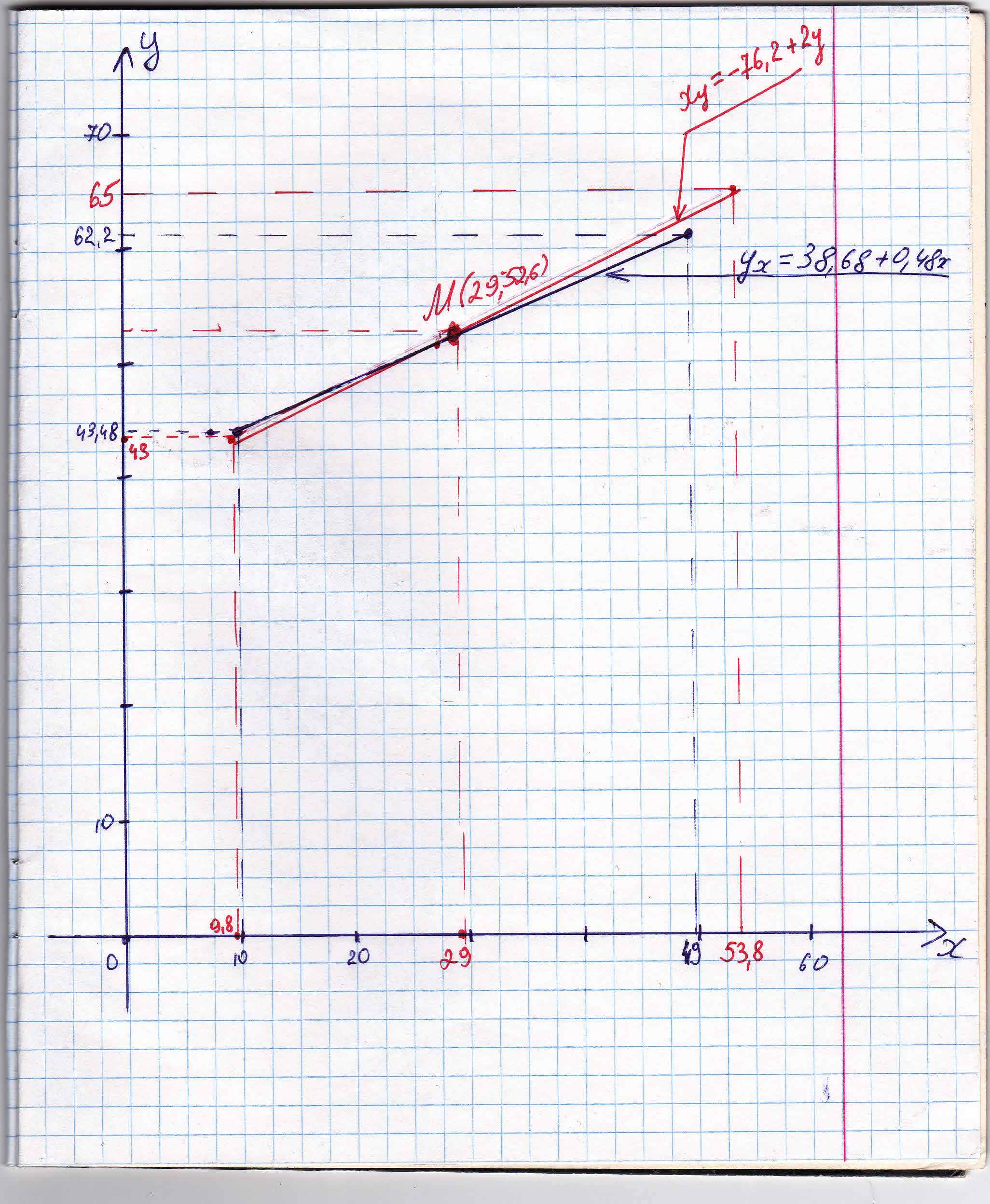
График линий регрессии отражает ряды теоретически ожидаемых значений функции по известным значениям аргумента. При этом, чем сильнее взаимосвязь между величинами x_i и y_i, тем меньше угол между линиями регрессии. В нашем случае r =0.969, линии уравнения регресии почти совпадают, так как корреляционная зависимость между признаками в этом случае переходит в функциональную.