Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной техники Кафедра вычислительной техники (специальность 220100). учебное пособие
| Вид материала | Учебное пособие |
- Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной, 1650.9kb.
- Рабочая программа для специальности: 220400 Программное обеспечение вычислительной, 133.96kb.
- Государственный Технический Университет. Факультет: Автоматики и Вычислительной Техники., 32.46kb.
- Образования Республики Молдова Колледж Микроэлектроники и Вычислительной Техники Кафедра, 113.64kb.
- Постоянное развитие и углубление профессиональных навыков в области информационных, 54.56kb.
- «Программное обеспечение вычислительной техники и автоматизированных систем», 1790.14kb.
- Задачи дисциплины: -изучение основ вычислительной техники; -изучение принципов построения, 37.44kb.
- Лекция №2 «История развития вычислительной техники», 78.1kb.
- Система контроля и анализа технических свойств интегральных элементов и устройств вычислительной, 582.84kb.
- Московский государственный инженерно-физический институт (технический университет), 947.05kb.
0.11.7 Излучательность
Сцену можно представить как набор поверхностей, обменивающихся лучистой энергией. Большинство реальных поверхностей является диффузными отражателями, когда падающий луч отражается или рассеивается во всех направлениях полусферы, находящейся над отражающей поверхностью. Особый здесь случай - отражение Ламберта (идеальная диффузия). Метод излучательности описывает баланс энергетического равновесия в замкнутой системе. Предполагается что поверхности идеально диффузны, т.е. после отражения падающий луч пропадает. Излучательность отдельной поверхности включает самоизлучение и отраженный или пропущенный свет.
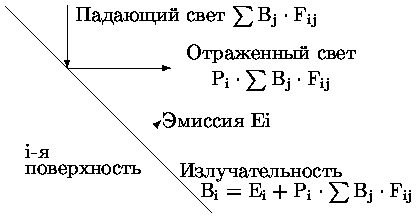
Рис. 0.4.22: Излучательность
Ei = [Энергия/ ед.площади ·ед.времени] - эмиссия,
Pi - безразмерный коэффициент отражения,
Bi - полный уровень света, исходящего от поверхности
Fij - форм-фактор - часть энергии, исходящая от одной поверхности и достигающая другой
Если поверхности сцены разделены на n элементов, имеющих постоянную излучательность, то взаимодействие потоков света в сцене описывается системой уравнений:
|
Так как форм-фактор определяет часть энергии, исходящей от одной поверхности и достигающей другой, то сумма всех форм-факторов элемента меньше 1.
Эта система уравнений решается итерационным методом с выбором в качестве начального приближения для излучательности эмиссии поверхности:
Bi0 = Ei,
и последующих приближений вида:
Bik+1 = Ei + Pi j = 1n Fij Bjk.
После определения излучательности каждого фрагмента производится вычисление излучательностей вершин таким образом, чтобы при билинейной интерполяции в пределах каждого фрагмента была обеспечена непрерывность закраски на границах.
Для этого в каждом многоугольнике значения излучательности для внутренних относительно многоугольника вершин фрагментов вычисляются как среднее значение излучательностей фрагментов, окружающих вершину (рис. 0.7.54). Определения излучательности внешних вершин выполняют экстраполяцией средних значений в смежных внутренних вершинах (см. рис. 0.7.54).
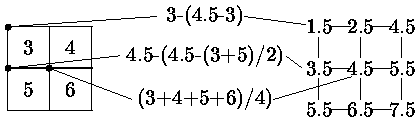
Рис. 0.4.23: Вычисление излучательности вершин
Формирование результирующего изображения выполняется после выбора требуемой точки наблюдения и проецирования сцены на картинную плоскость. Видно, что этот метод не зависит от точки наблюдения. При выводе определяется какой фрагмент отображается в каждом пикселе экрана. При этом используются z-буфер и кадровый буфер. Пересечение линии, соединяющей глаз и пиксел с плоскостью фрагмента, позволяет найди координату точки, отображаемую в текущий пиксел. Координата пересечения (x, y, z) преобразуется в координаты (u, v) на фрагменте. После этого значения излучательностей вершин используются при билинейной интерполяции трех значений излучательностей в пределах каждого фрагмента (рис. 0.7.55).
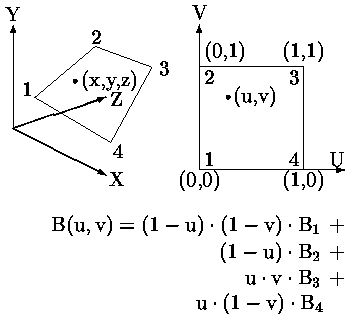
Рис. 0.4.24: Билинейная интерполяция излучательностей по значениям в вершинах
Наиболее трудоемкая часть метода излучательности - вычисление форм факторов.
Для двух неперекрытых элементарных площадок i и j форм-фактор определяет часть световой энергии, исходящей из одной площадки на другую, и имеет вид:
|
где r - расстояние между элементами dAi и dAj, i и j - углы между нормалями к элементам и соединяющим их отрезком (рис. 0.7.56).
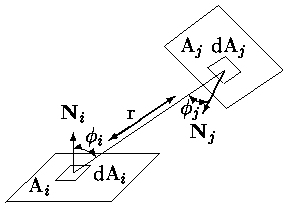
Рис. 0.4.25: Форм-фактор для двух элементарных площадок
Интегрируя по площади dAj получаем форм-фактор конечного элемента площади Aj относительно элементарной площадки dAi:
|
Выражение для форм-фактора между двух конечных неперекрытых площадок определяется как средняя площадь:
|
Взаимное перекрытие может быть учтено с помощью функции Hij, принимающей значение от 0 до 1 в зависимости от степени перекрытия площадки Aj площадкой Ai:
|
Вычисление этого интеграла, как правило, затруднено. Для его вычисления предложен т.н. алгоритм полукуба. Основная идея которого состоит в том, что если два любых фрагмента в пространстве после проецирования на полусферу заняли на ней одну и ту же площадь и место, то их формфакторы будут одинаковы. Это утверждение справедливо и при проецировании на любую другую окружающую поверхность, в том числе куб.
Куб строится таким образом, чтобы центр фрагмента, принимающего отраженные световые потоки, совпал с центром куба, а нормаль к фрагменту в этой точке примем за положительное направление оси Z. В этом случае полусфера заменяется верхней частью куба (полукубом). Разобьем плоскости полукуба на квадратные пикселы. Спроектируем все пространство на пять плоскостей полукуба при этом производится отсечение по пирамиде видимости с центром в центре куба. Если два фрагмента сцены проецируются на один и тот писел куба,
