Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной техники Кафедра вычислительной техники (специальность 220100). учебное пособие

Вид материала

Учебное пособие

Содержание 0.6.6  Трехмерное отсечение отрезка 0.6.7  Отсечение отрезка в однородных координатах 0.7  ОТСЕЧЕНИЕ МНОГОУГОЛЬНИКА 0.7.1  Алгоритм Сазерленда-Ходгмана 0.7.2  Простой алгоритм отсечения многоугольника

Подобный материал:

• Новосибирский Государственный Технический Университет. Факультет автоматики и вычислительной, 1650.9kb.
• Рабочая программа для специальности: 220400 Программное обеспечение вычислительной, 133.96kb.
• Государственный Технический Университет. Факультет: Автоматики и Вычислительной Техники., 32.46kb.
• Образования Республики Молдова Колледж Микроэлектроники и Вычислительной Техники Кафедра, 113.64kb.
• Постоянное развитие и углубление профессиональных навыков в области информационных, 54.56kb.
• «Программное обеспечение вычислительной техники и автоматизированных систем», 1790.14kb.
• Задачи дисциплины: -изучение основ вычислительной техники; -изучение принципов построения, 37.44kb.
• Лекция №2 «История развития вычислительной техники», 78.1kb.
• Система контроля и анализа технических свойств интегральных элементов и устройств вычислительной, 582.84kb.
• Московский государственный инженерно-физический институт (технический университет), 947.05kb.

0.6.6  Трехмерное отсечение отрезка

0.6.7  Отсечение отрезка в однородных координатах

0.7  ОТСЕЧЕНИЕ МНОГОУГОЛЬНИКА

Многоугольники особенно важны в растровой графике как средство задания поверхностей.

Будем называть многоугольник, используемый в качестве окна отсечения, отсекателем, а многоугольник, который отсекается, - отсекаемым.

Алгоритм отсечения многоугольника должен в результате отсечения давать один или несколько замкнутых многоугольников (рис. 0.3.20). При этом могут быть добавлены новые ребра, а имеющиеся или сохранены или разделены или даже отброшены. Существенно, чтобы границы окна, которые не ограничивают видимую часть отсекаемого многоугольника, не входили в состав результата отсечения. Если это не выполняется, то возможна излишняя закраска границ окна (см. рис. 0.3.20б).




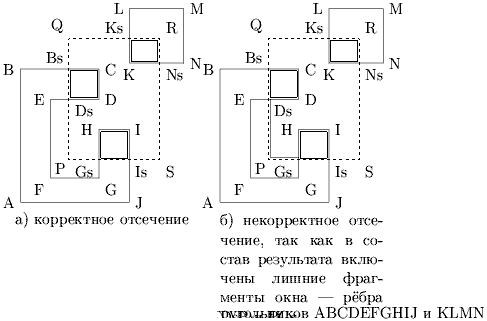
Рис. 0.3.18: Отсечение окном PQRS многоугольников ABCDEFGHIJ и KLMN

В принципе эту задачу можно решить с использованием рассмотренных выше алгоритмов отсечения линий, если рассматривать многоугольник просто как набор векторов, а не как сплошные закрашиваемые области. При этом вектора, составляющие многоугольник, просто последовательно отсекаются сторонами окна (рис. 0.3.21).




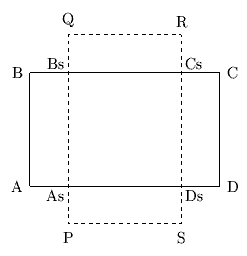
Рис. 0.3.19: Отсечение окном PQRS многоугольника ABCD, рассматриваемого как набор векторов. Генерируется вывод из двух векторов BsCs и DsAs.

Если же в результате отсечения должен быть получен замкнутый многоугольник, то формируется вектор, соединяющий последнюю видимую точку с точкой пересечения с окном (рис. 0.3.22а). Проблема возникает при окружении отсекаемым многоугольником угла окна (см. рис. 0.3.22б).




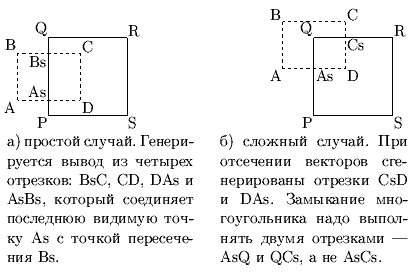
Рис. 0.3.20: Отсечение сплошного многоугольника окном.

Здесь мы рассмотрим три алгоритма корректно решающие задачу отсечения сплошного многоугольника. Первые два алгоритма быстро работают, но генерируют лишние ребра, как это продемонстрировано на рис. 0.3.20б. Последний алгоритм свободен от указанного недостатка.

В общем, при отсечении многоугольников возникают два типа задач - отображение части изображения попавшей в окно и наоборот, отображение изображения, находящегося вне окна. Все здесь рассматриваемые алгоритмы могут использоваться в обоих случаях.

0.7.1  Алгоритм Сазерленда-Ходгмана

Простой метод решения проблемы охвата отсекаемым многоугольником вершины окна предлагается в алгоритме Сазерленда-Хогдмана [40], когда весь многоугольник последовательно отсекается каждой границей окна, как это показано на рис. 0.3.23.




Рис. 0.3.21: Последовательное отсечение многоугольника сторонами окна.

При отсечении ребра, соединяющего очередную пару вершин K и L, возможны 4 случая взаимного расположения (рис. 0.3.24):

а) ребро на внутренней стороне границы,

б) ребро выходит из окна наружу,

в) ребро на внешней стороне границы,

г) ребро входит снаружи в окно.




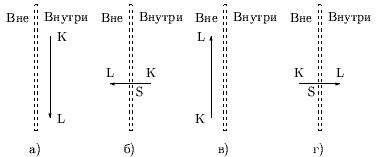
Рис. 0.3.22: Относительные расположения ребра и границы окна.

В случае а) в результат добавляется вершина L. В случае б) в результат заносится S - точка пересечения ребра с границей. В случае в) нет вывода. В случае г) выдаются точка пересечения S и конечная точка ребра L.

Для определения взаимного расположения и направленности используется векторное произведение вектора P₁P₂, проведенного из начальной в конечную точку текущего ребра окна, на вектор P₁S из начальной точки текущего ребра окна в очередную вершину S многоугольника (рис. 0.3.25).




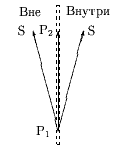
Если P₁P₂ ×P₁S < 0, то поворот от P₁P₂     к    P₁S по часовой стрелке, т.е. точка S внутри окна.
Если P₁P₂ ×P₁S > 0, то поворот от P₁P₂     к    P₁S против часовой стрелки, т.е. точка S вне окна.

Рис. 0.3.23: Определение взаимного расположения окна и вершины

Предложена аппаратная реализация этого алгоритма, состоящая из четырех идентичных ступеней отсечения без промежуточной памяти [28].

В алгоритме Сазерленда-Ходгмана в результат могут заноситься границы окна, даже если они и не ограничивают видимую часть отсеченного многоугольника. Это можно устранить дополнительным анализом, либо используя более сложный алгоритм отсечения.

0.7.2  Простой алгоритм отсечения многоугольника

В данном разделе рассматривается простой алгоритм отсечения, который подобно алгоритму Сазерленда-Ходгмана может генерировать лишние стороны для отсеченного многоугольника, проходящие вдоль ребра окна отсечения. Но этот алгоритм несколько более быстрый и использует те же подпрограммы обработки многоугольного окна отсечения, что и алгоритм Кируса-Бека.

Многоугольник отсекается одним ребром выпуклого окна отсечения. В результате такого отсечения формируется новый многоугольник, который затем отсекается следующим ребром и т.д., пока не будет выполнено отсечение последним ребром окна.

Основная здесь процедура - процедура отсечения отдельным ребром, определяющая взаимное расположение очередной стороны многоугольника и ребра отсекателя и генерирующая соответствующие выходные данные.

Возможны 9 различных случаев расположения ребра окна и отсекаемой стороны, показанных на рис. 0.3.26-0.3.28.




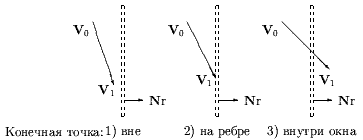
Рис. 0.3.24: Начальная точка вне ребра окна отсечения.

На них V₀ и V₁ - начальная и конечная точки отсекаемой стороны многоугольника, соответственно; Nr - нормаль к ребру окна отсечения, направленная внутрь окна.




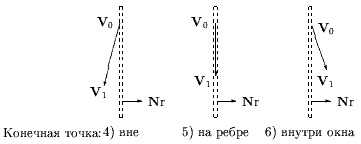
Рис. 0.3.25: Начальная точка на ребре окна отсечения.

Из этих рисунков очевидны правила генерации выходных данных, зависящие от варианта взаимного расположения:

1) Нет выходных данных.

2) В выходные данные заносится конечная точка.

3) Рассчитывается пересечение и в выходные данные заносятся точка пересечения и конечная точка.

4) Нет выходных данных.

5) В выходные данные заносится конечная точка.

6) В выходные данные заносится конечная точка.

7) Рассчитывается пересечение и в выходные данные заносится только точка пересечения.

8) В выходные данные заносится конечная точка.

9) В выходные данные заносится конечная точка.




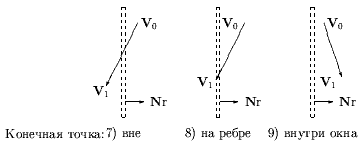
Рис. 0.3.26: Начальная точка внутри окна отсечения.

Для определения взаимного расположения, подобно алгоритму отсечения Кируса-Бека, используется скалярное произведение Q вектора нормали на вектор, проведенный из начала ребра в анализируемую точку. Пояснение см. на рис. 8.10.




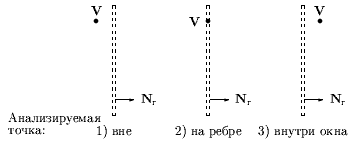
Рис. 8.10. Анализ расположения точки относительно ребра окна отсечения.

Таким образом, для определения взаимного расположения начальной V₀ и конечной V₁ точек отсекаемой стороны и ребра отсечения с вектором его начала R, надо вычислить:

Qn    =   (  V0   -  R  )  ·  Nr       и

Qk    =   (  V1   -  R  )  ·  Nr.

Расчет пересечения, если он требуется, производится аналогично алгоритму Кируса-Бека с использованием параметрического представления линии:

V(t)    =   V0   +  (  V1   -  V0  )  ·  t.

Вначале находится значение параметра t для точки пересечения по формуле (см. описание алгоритма Кируса-Бека):

t    =   -Qn  /  Pn,

где Qn - скалярное произведение вектора нормали к ребру окна на вектор из начала ребра в начальную точку стороны, уже вычисленное при определении расположения начальной точки, а Pn    =   (V₁ - V₀)·  Nr - скалярное произведение вектора нормали к ребру окна на вектор из начальной в конечную точки отсекаемой стороны.

Легко выразить это произведение через уже вычисленные величины Qn и Qk:

Pn = (V1 - V0)·  Nr = (V1 - V0 - R + R)·  Nr = (V1 - R)·  Nr   -  (V0 - R)·  Nr = Qk - Qn.

Таким образом, точке пересечения соответствует значение параметра t, равное:

t    =   Qn  /  (  Qn   -  Qk  ).

Значения координат пересечения находятся из:

Xp    =   X0   +  (X1  -  X0)·  t;      Yp    =   Y0   +  (Y1  -  Y0)·  t.

Описанный алгоритм реализован в процедуре V_Plclip, приведенной в Приложении 8.