Некоторые вопросы механики адгезионного разрушения
| Вид материала | Документы |
- Доктор технических наук, заведующий лабораторией физики прочности и механики разрушения, 418.09kb.
- Конспект лекций Утверждено редакционно-издательским советом университета Омск 2002, 466.51kb.
- Перед вами новая Сатанинская Библия. Она заимствована у Антона Шандора ЛаВея, с добавлением, 921.57kb.
- Секция Математические вопросы механики, 66.91kb.
- Проанализированы некоторые вопросы информационной, 306.83kb.
- Неизвестная гомеопатия, акупунктура и электродиагностика: клинические приложения квантовой, 462.66kb.
- Б. Е. Победря 1 год Задача годового курса 40 лекций + 40 семинар, 27.75kb.
- Теоретическая физика. Механика, 16.15kb.
- Организация, 1541.13kb.
- Вероятностный фактор при численном моделировании динамического разрушения, 73.07kb.
НЕКОТОРЫЕ ВОПРОСЫ МЕХАНИКИ АДГЕЗИОННОГО
РАЗРУШЕНИЯ
Р.В. Гольдштейн
Институт проблем механики Российской академии наук, г. Москва
В технике все большее распространение получают материалы и конструкции, сопротивление разрушению которых наряду с их деформационными и прочностными свойствами в значительной мере определяются кусочной однородностью строения (в качестве примера можно указать слоистые и волокнистые системы, материалы, армированные включениями). Один из характерных типов разрушения кусочно-однородных материалов и элементов конструкций – разрушение по границе соединения однородных по составу и механическим свойствам частей (адгезионное разрушение).
В докладе обсуждаются модели и отчасти методы расчета зарождения и развития трещин–отслоений при механических нагрузках и температурном воздействии. Рассматривается вопрос об оценке эффективного сопротивления росту трещин кусочно-однородных тел на примере слоистой системы. Отмечается, что возможны, по крайней мере, два пути повышения указанной характеристики. Один из них, связан с изменением скорости высвобождения энергии деформации тела, при продвижении трещин, за счет специального подбора сочетания деформационных характеристик, соединяемых однородных частей. Другой – с повышением сопротивления разрушению собственной зоны соединения (адгезионной трещиностойкости). Первый путь иллюстрируется примером решения задачи о дискообразной трещине на границе соединения слоев в слоистой среде. Реализация второго пути демонстрируется моделью адгезионной трещины, в которой явно вводятся нелинейно деформируемые связи между поверхностями трещины. При этом не предполагается малость области действия связей в сравнении с длиной трещины, что позволяет с единых позиций рассматривать как процессы зарождения отслоений, так и их развития. Показано, что, в частности, в соединениях полимер-полимер, управляя длиной полимерных соединительных цепей, можно оптимизировать адгезионную трещиностойкость соединения.
Обсуждается влияние дефектов кристаллической решетки в соединенных поликристаллических материалах на сопротивление адгезионному разрушению.
Анализируется возможность возникновения в кусочно-однородном теле упорядоченной системы (эшелона) отслоений.
Рассматриваются примеры анализа условий разрушения элементов слоистых конструкций в рамках адгезионной механике разрушения.
Доклад содержит изложение результатов работ по механике адгезионного разрушения, выполненных в Лаборатории механики прочности и разрушения материалов и конструкций.
ЭВОЛЮЦИЯ НАПРЯЖЁННОГО СОСТОЯНИЯ БОЛТОВОГО
СОЕДИНЕНИЯ ОРТОТРОПНЫХ ВЯЗКОУПРУГИХ ПЛАСТИНОК
А.Ю. Горохов, Н.А. Труфанов
Пермский государственный технический университет
В настоящее время композиционные материалы находят широкое применение во всех отраслях промышленности. Крайне актуальным является вопрос прочности и надёжности соединения композиционных материалов. Особенно интересно решение этого вопроса при учёте вязкоупругих эффектов. Известно, что в вязкоупругих телах даже при постоянной внешней нагрузке может произойти перераспределение напряжений.
В данной работе исследуется соединение ортотропных вязкоупругих пластинок болтом, поставленным с зазором. Задача решается в трёхмерной постановке. Свободные концы пластин нагружены равномерно распределёнными растягивающими усилиями. Между гайкой и композиционным материалом расположена шайба. Болт затянут. Сила, возникающая в результате затяжки болта, назначается из условия неподвижности стыка за счёт возникновения в нём сил трения и задаётся в виде перемещений под шляпкой болта и гайкой. Условие неподвижности стыка имеет вид:
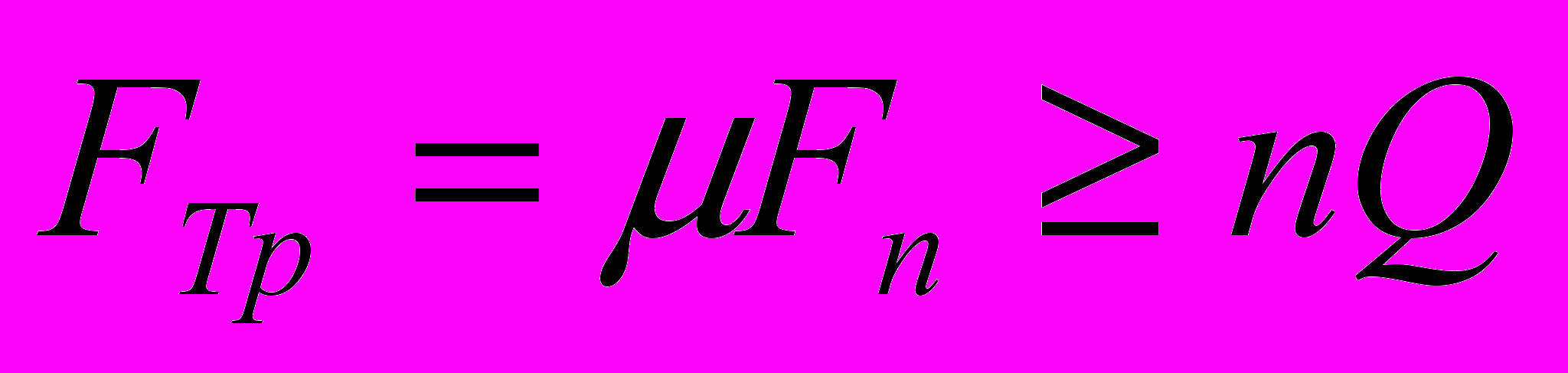 , где
, где  - сила трения в стыке между пластинами;
- сила трения в стыке между пластинами;  – нормальная реакция в стыке;
– нормальная реакция в стыке;  - коэффициент трения;
- коэффициент трения; 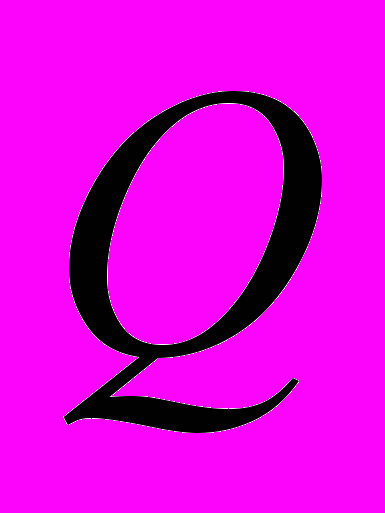 - растягивающее усилие;
- растягивающее усилие;  - коэффициент запаса. При такой постановке болт в соединении не работает на срез и смятие. Материал элементов крепления – сталь.
- коэффициент запаса. При такой постановке болт в соединении не работает на срез и смятие. Материал элементов крепления – сталь.Сначала производится постановка задачи в рамках линейной теории упругости, затем в рамках линейной теории вязкоупругости с несколькими независимыми интегральными операторами. Вязкоупругая задача решается методом квазиконстантных операторов. Для описания анизотропных компонент тензора функций релаксации ортотропного материала пластинок используется выражение в виде сумм экспонент:
 , где
, где 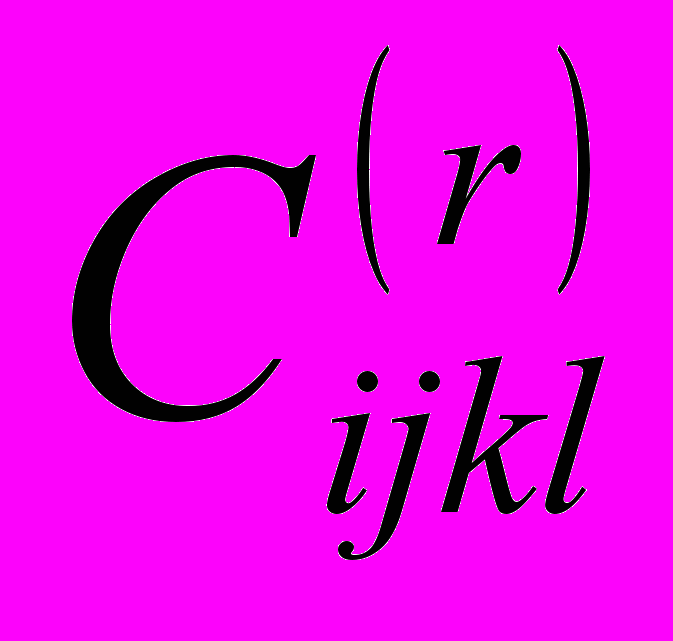 и
и  некоторые известные константы. Приводится расчёт показателей квазиконстантности для каждого рассмотренного оператора и производится оценка погрешности решения поставленной вязкоупругой задачи.
некоторые известные константы. Приводится расчёт показателей квазиконстантности для каждого рассмотренного оператора и производится оценка погрешности решения поставленной вязкоупругой задачи. Упругие задачи для каждого момента времени решаются методом конечных элементов с помощью пакета ANSYS. При этом используются трёхмерные 8-и узловые конечные элементы.
В результате работы:
1. Установлен и численно исследован эффект эволюции напряженного состояния при постоянном внешнем воздействии.
2. Дана постановка и получено конечно-элементное решение трехмерной краевой задачи анизотропной вязкоупругости применительно к анализу напряженно-деформированного состояния узла болтового соединения композиционных пластин. Показана возможность потери работоспособности соединения вследствие релаксации усилия затяжки болта.
3. Расчёт болтового соединения качественно и количественно подтверждает наличие эволюции напряжённого состояния в элементах конструкций из композиционных материалов и необходимость учета вязкоупругих свойств, при оценке их работоспособности.
ИССЛЕДОВАНИЕ ФРАГМЕНТАЦИИ СТЕКЛЯННЫХ ПЛАСТИН
В УСЛОВИЯХ КВАЗИСТАТИЧЕСКОГО НАГРУЖЕНИЯ
М.М. Давыдова, Д.М. Давыдов
Институт механики сплошных сред УрО РАН, Пермь
Проблемы фрагментации привлекают к себе внимание исследователей уже более столетия. В настоящей работе статистика фрагментации исследовалась в экспериментах на тонких стеклянных пластинах, нагруженных распределенной квазистатической нагрузкой. С этой целью была проведена конструкторская разработка и создана оригинальная пневматическая установка, обеспечивающая нагружающее усилие в диапазоне от 104 до 107 Н/м2 (Рис.1). Установка рассчитана для работы с образцами размером 60-60 мм и толщиной 1.3-1.5 мм. Стеклянная пластинка помещается в “пенал”, который позволяет сохранить картину фрагментации после снятия нагрузки. Пенал опирается по контуру на цилиндрическую поверхность и через резиновую мембрану подвергается повышенному давлению газовой среды. Затем в центре на стеклянный образец наносится надрез, который обеспечивает ”запуск” процессов трещинообразования и фрагментации. Картина фрагментации (содержимое пенала) снимается цифровой камерой. Компьютерная обработка данных эксперимента состоит из двух этапов. На первом - с помощью специально разработанного программного обеспечения цифровые фотографии преобразуются в схематическую картинку, которая соответствует системе трещин возникших в процессе фрагментации (Рис.1). На втором - схематическая картинка (Рис.1в) используется для расчета количества и величины фрагментов, а так же длины трещин. Фотографии картин фрагментации, приведенные на Рис.2, свидетельствуют о том, что увеличение давления приводит к возрастанию количества фрагментов (Рис 3). Причем при низких давлениях (Рис.2в) образуются только “радиальные” трещины, т.е. именно они первыми появляются при фрагментации. Чем выше нагрузка, тем больше возникает “тангенциальных” трещин, расположенных перпендикулярно или под углом к “радиальным”.
 a) |  б) |  в) |
Рис.1. Преобразование фотографии в схематическую картинку.
 а) |  б) |  в) |
Рис.2. Картины фрагментации при разных давлениях a)52,53*104 Н/м2; б) 31,36*104 Н/м2; в) 25,87*104 Н/м2.
Эксперименты, описываемые в настоящей работе, выполнены на тонких пластинах, и все фрагменты имеют толщину, равную толщине образца (2D фрагменты). Мелкие фрагменты, размеры которых в сотни раз меньше приведенных на фотографии (Рис.2), не учитывались. На рис.4а приведены интегральные функции распределения фрагментов по размерам для двух образцов, нагруженных давлением 7.76*105 Н/м2 (ромбы) и 4.00*105 Н/м2 (кружки). Для всех образцов экспериментальная функция распределения аппроксимируется экспоненциальной функцией вида
 , где
, где  - количество фрагментов,
- количество фрагментов,  - площадь фрагмента. Мы не обнаружили степенной зависимости для функции распределения. Причиной, видимо, является то, что учитывались только 2D фрагменты.
- площадь фрагмента. Мы не обнаружили степенной зависимости для функции распределения. Причиной, видимо, является то, что учитывались только 2D фрагменты.
Рис. 3. Зависимость количества фрагментов от давления.
Поскольку наша экспериментальная методика позволяет зафиксировать картину фрагментации с помощью цифровой фотокамеры, то кроме традиционных количества и размеров фрагментов можно подсчитать длину трещин во всем образце или его части. Фрактальная размерность
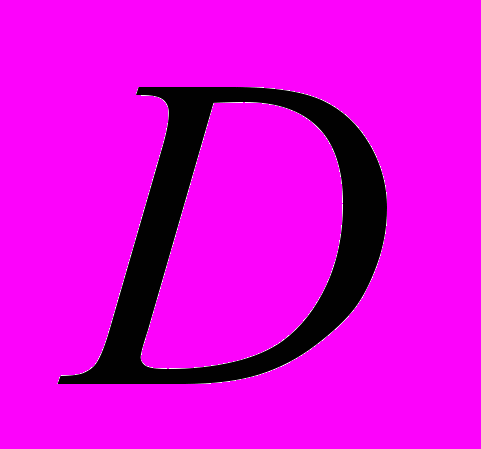 картины растрескивания определялась по формуле
картины растрескивания определялась по формуле  , где
, где  - длина всех трещин в квадрате размером
- длина всех трещин в квадрате размером  , центры которых совпадают с центром картины фрагментации. Минимальное количество квадратов, используемое для подсчета фрактальной размерности, равно 200. Пример определения фрактальной размерности приведен на Рис. 4б. Строгой закономерности изменения фрактальной размерности в зависимости от числа фрагментов или от давления не наблюдается. Мы можем констатировать только то, что
, центры которых совпадают с центром картины фрагментации. Минимальное количество квадратов, используемое для подсчета фрактальной размерности, равно 200. Пример определения фрактальной размерности приведен на Рис. 4б. Строгой закономерности изменения фрактальной размерности в зависимости от числа фрагментов или от давления не наблюдается. Мы можем констатировать только то, что 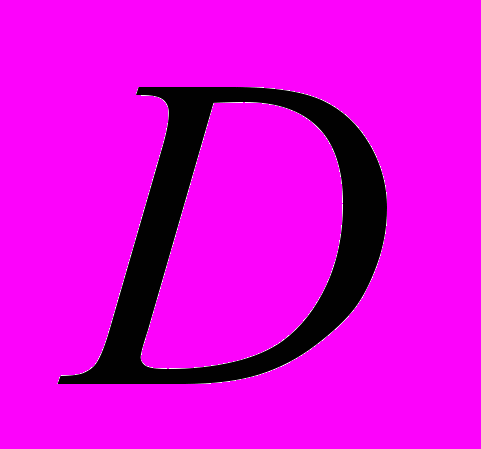 лежит в интервале от 1.59 до 1.83.
лежит в интервале от 1.59 до 1.83.  |  |
| а) | б) |
Рис.4. а) Интегральная функция распределения фрагментов по размерам; б) пример определения фрактальной размерности.
 .
.Выводы.
Результаты экспериментов показали:
- Количество фрагментов зависит от величины давления.
- Вид картины фрагментации, т.е. наличие только радиальных трещин (Рис.4с) или образование сложной системы ветвящихся трещин (Рис.4а) определяется величиной давления.
- Интегральная функция распределения фрагментов по размерам описывается экспоненциальной функцией. Последнее, скорее всего, определяется тем, что подсчет производился для фрагментов, толщина которых совпадает с толщиной пластины.
- Картины фрагментации самоподобны, причем суммарная длина трещин в квадрате со стороной
 подчиняется степенному закону
подчиняется степенному закону  . Где
. Где 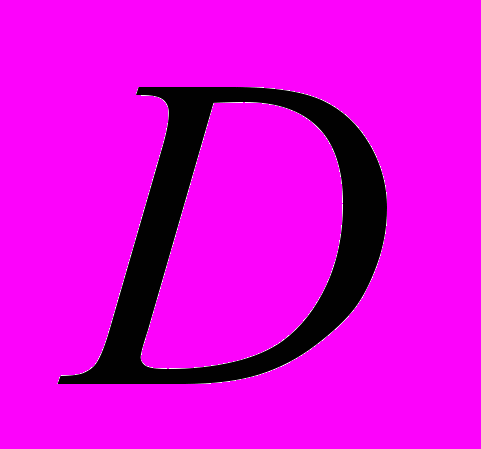 - фрактальная размерность, которая лежит в диапазоне
- фрактальная размерность, которая лежит в диапазоне  .
.
Работа проводится при поддержке Российского Фонда Фундаментальных Исследований (грант 05-01-00863, грант 04-01-97514р_офи, грант 04-01-96009 урал_а)
ПРОЦЕССЫ ПОГЛОЩЕНИЯ И ПЕРЕНОСА ЖИДКОСТЕЙ
В ВЫСОКОЭЛАСТИЧНЫХ НАБУХАЮЩИХ МАТЕРИАЛАХ
Е.Я. Денисюк
Институт механики сплошных сред УрО РАН, Пермь
Процессы деформирования и диффузии в твердых телах взаимосвязаны. Внедрение диффундирующего вещества в твердое тело порождает в нем внутренние напряжения, а неоднородное поле напряжений, вызванное внешними причинами, способно влиять на диффузионную кинетику переноса вещества. Такие явления называются механодиффузионными, а их теория основана на синтезе механики деформируемого твердого тела и теории диффузии.
Наиболее ярко механодиффузионные явления проявляют себя в высокоэластичных полимерных сетчатых материалах – химически сшитых эластомерах и полимерных гелях. Как известно, эти материалы могут испытывать большие упругие деформации. Другое их уникальное свойство состоит в том, что они способны поглощать низкомолекулярные растворители, многократно (в десятки и сотни раз) увеличиваясь в объеме. При этом они сохраняют свою форму и способность к обратимым упругим деформациям. Это явление называется ограниченным набуханием и объясняется молекулярной структурой данных материалов – они представляют собой пространственную полимерную сетку, состоящую из гибких макромолекулярных цепей, соединенных химическими связями.
Способность полимерных гелей поглощать, а затем высвобождать жидкость широко используется во многих современных технологиях, например, в биотехнологии (сепарация протеинов), в медицине и фармакологии (лекарственные гели), в сельском хозяйстве (увлажнители почвы), в биохимии (гелевые мембраны, служащие для разделения и анализа биорастворов) и т.д. Что касается эластомеров, то эти материалы часто эксплуатируются в физически агрессивных средах – органических растворителях и их парах. Поглощение и диффузия растворителя вызывает набухание материала, приводит к изменению его физико-механических свойств, порождает в нем внутренние напряжения и в конечном итоге может вызвать разрушение изделия. К этому следует добавить, что в физико-химии полимеров процессы набухания – это один из важнейших "инструментов" исследования физико-химических свойств и структуры полимерных сеток.
Данная работа посвящена исследованию фундаментальных закономерностей связанных процессов деформирования материала и диффузии растворителей в высокоэластичных, набухающих полимерных сетчатых материалах – эластомерах и полимерных гелях. Сформулирована общая система уравнений и физических соотношений, описывающая указанные процессы при конечных деформациях полимерной матрицы, которая получена в результате объединения нелинейной теории упругости, теории диффузии и термодинамики растворов. Она включает следующие уравнения [1,2]:
   | (1) |
– уравнение переноса растворителя;
   | (2) |
– уравнение баланса вещества упругой матрицы;
  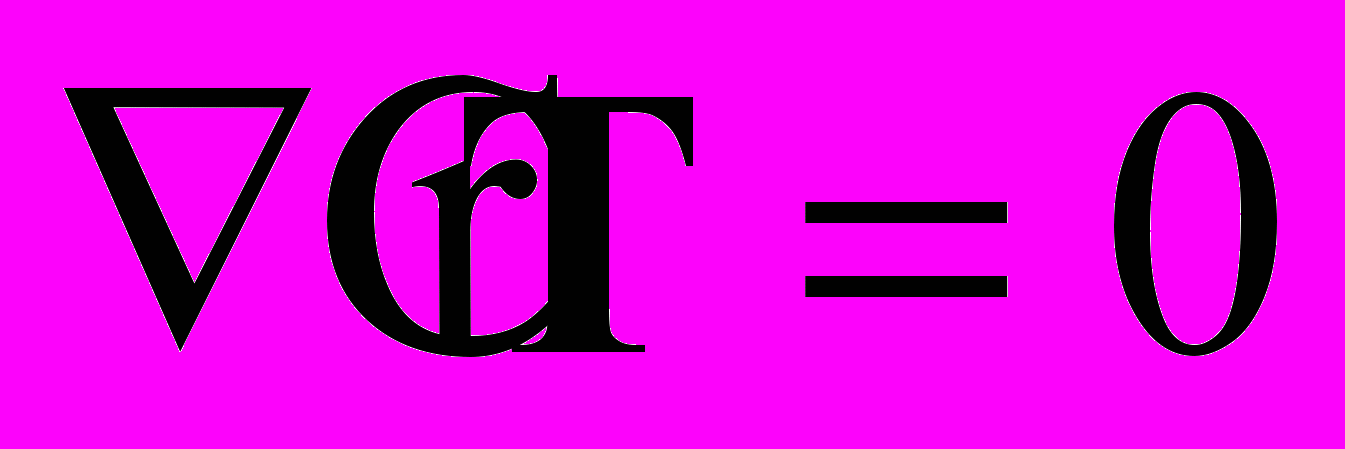 | (3) |
– уравнение механического равновесия;
  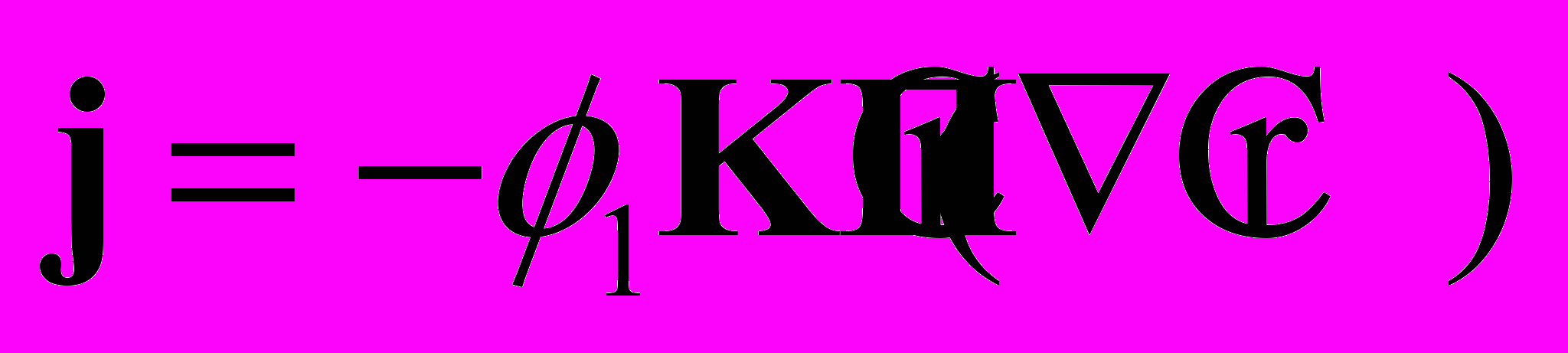 | (4) |
– физическое соотношение для плотности диффузионного потока растворителя.
Здесь n1 – концентрация растворителя; n2 – концентрация вещества упругой матрицы; v – поле скоростей движения упругой матрицы; j – плотность диффузионного потока растворителя; K – положительно определенный тензор второго ранга, характеризующий проницаемость материала и зависящий от концентрации растворителя и деформаций материала; T – тензор напряжений Коши; П – осмотический тензор напряжений; 1, 2 – объемная доля растворителя и вещества упругой матрицы соответственно. Упругий материал и жидкость считаются несжимаемыми. Осмотический тензор напряжений играет роль химического потенциала, а его дивергенция является движущей силой диффузии.
Вид тензора напряжений T и осмотического тензора напряжений П зависит от конкретной модели полимерных сеток. Предложены методы получения конкретных физических соотношений, характеризующих термодинамические и механические свойства системы «полимерная сетка – растворитель» из существующих теорий высокоэластичности.
Показано, что для описания процессов поглощения и диффузии растворителей в материалах, подвергнутых статическому нагружению, систему уравнений (1)–(4) удобно представить в базисе отсчетной конфигурации, в качестве которой можно использовать произвольное напряженно-деформированное состояние материала, например, начальное деформированное состояние или конечное термодинамически равновесное состояние. Полученная система уравнений позволяет эффективно формулировать конкретные задачи, описывающие неравновесные процессы поглощения и миграции растворителей в высокоэластичных, набухающих материалах, подвергнутых внешнему механическому нагружению.
Построена линеаризованная система уравнений, описывающая диффузионные процессы переноса растворителей в деформированных материалах. При этом, деформации материала, вызванные внешней механической нагрузкой, рассматриваются как конечные, а малыми считаются те деформации, которые возникают за счет поглощения и диффузии растворителя. Установлена связь констант линеаризованной теории с напряженно-деформированным состоянием материала и его упругими и транспортными свойствами в этом состоянии. Дана оценка области применимости линеаризованной теории.
Рассмотрены основные типы краевых задач нелинейной и линеаризованной теорий механодиффузии. Сформулированы и изучены частные математические модели, описывающие равновесные и неравновесные процессы деформирования и набухания полимерных сетчатых материалов в среде растворителя при различных видах механического нагружения: набухание ненагруженного материала (свободное набухание); набухание плоского слоя в условиях фиксированного одноосного и двуосного растяжения; процесс миграции растворителя, вызванный неоднородным полем напряжений, возникающим при разгибании цилиндрического сегмента в плоский слой. Изучено влияние внешней механической нагрузки на диффузионный режим поглощения растворителя. Показано, что вид механического нагружения материала оказывает существенное влияние на характер диффузионной кинетики поглощения растворителя. В частности, установлено существование качественно различных диффузионных режимов набухания полимерных сеток. Установлена их связь с условиями механического нагружения материала, а также с упругими, термодинамическими и транспортными свойствами системы «полимерная сетка – растворитель»; установлены причины и механизм так называемых аномалий кинетики сорбции, экспериментально наблюдаемых при набухании эластомеров и полимерных гелей в растворителях.
Полученные результаты могут быть использованы при проектировании изделий на основе эластомеров, предназначенных для работы в физически агрессивных средах, а также при создании и совершенствовании технологий, основанных на применении массообменных процессов в полимерных гелях.
Работа выполнена при финансовой поддержке РФФИ и Администрации Пермской области (проект РФФИ № 05-08-50033; проект РФФИ-Урал № 04-01-96039).
Литература
- Денисюк Е.Я., Терешатов В.В. Теория механодиффузионных процессов переноса многокомпонентных жидкостей в сшитых эластомерах // Прикл. механика и технич. физика.– 1997.– Т. 38, № 6.– С. 113–129.
- Денисюк Е.Я., Терешатов В.В. Нелинейная теория процессов набухания эластомеров в низкомолекулярных жидкостях // Высокомолек. соед. А.– 2000.– Т.42, № 1.– С. 71–83.
Специфические особенности упрочняющего
действия наночастиц в эластомерных матрицах
С.Е. Евлампиева, В.В. Мошев
Институт механики сплошных сред УрО РАН, г. Пермь
Хотя эффект упрочнения эластомеров наночастицами известен уже более ста лет и широко используется в промышленности, структурные механизмы, обуславливающие эту особенность до сих пор остаются предметом научных дискуссий. Непонятен очень высокий начальный модуль упругости, десятикратно превышающий величину, которую предсказывает механика сплошных сред. Значительный начальный гистерезис эластомерных композитов (при циклических испытаниях с постоянной амплитудой деформации) через небольшое число циклов почему-то исчезает, а поведение материала приближается упругому. Удивительным представляется, что свойства таких композитов нагревом около 100оС в течение суток возвращаются к первоначальному состоянию. Приходится допустить, что такое поведение материала является обратимым, а наблюдаемая изменчивость свойств при действии нагрузок обусловлена обратимой перестройкой его структуры.
Многие исследователи (Александров и Лазуркин (1944), Данненсберг (1966), Краус (1978), Эдвардс (1990) ) высказали гипотезу, что отмеченная специфика может быть объяснена, если допустить, что скрепление эластомерной матрицы с наполнителем не является абсолютно жестким и что под действием сдвиговой нагрузки матрица, в связи подвижностью адсорбционных связей, получает возможность двигаться по поверхности частиц. Новая структура фиксируется новой привязкой адсорбционных связей к частицам наполнителя. Самопроизвольный возврат к начальному состоянию затруднен недостаточной величиной энтропийной упругости макромолекул при нормальной температуре. Нагрев, увеличивая энтропийный возвращающий эффект, позволяет преодолеть сопротивление адсорбции и приводит к восстановлению первоначальной структуры и свойств системы (Соос, 1984).
В рамках рассматриваемой гипотезы нами была предпринята попытка построить соответствующую структурную модель. Одномерный вариант модели был рассмотрен ранее (Мошев, Евлампиева, 2003). Механические особенности элементов модели представлены упругой пружиной, моделирующей нелинейные свойства макромолекул, и эффективным трением, отображающим адгезионное сцепление. Две подложки, представляющие поверхность смежных частиц, объединены лежащей на них пружиной, представляющей макромолекулу, связанную с частицами силами адсорбции. Геометрия ячейки представлена длиной Lo, моделирующей длину молекулы, длиной Um, моделирующей размер частиц, длиной Lg, моделирующей промежуток между частицами. Предполагается, что наружные концы пружины скреплены с подложками. Приложение растягивающего усилия к подложкам, вызывает упругое удлинение перемычки Lg и соскальзывание некоторой части пружины, с поверхности подложек в промежуток между ними. С ростом растягивающего усилия в движение приходит все большая скользящая часть пружины, пока она не доходит до конца подложек, после чего в сопротивление включается и собственная упругость пружины. Дальнейшее растяжение приводит к разрыву пружины в зазоре между подложками, когда достигается ее предельное удлинение.
Механическое поведение одномерной модели может описывать структурную перестройку и гистерезисные потери при циклических нагружениях, а также открытую в середине шестидесятых годов пропорциональность работы разрушения и соответствующих гистерезисных потерь (Grosch, K., Harwood,J.A.C., Payne, A.R., 1966). Однако такая модель непригодна для описания различных концентрационных зависимостей.
Возникла необходимость в создании трехмерного структурного элемента. В качестве такого элемента была выбрана форма гексагональной изометричной призмы, содержащей в центре наночастицу. Это позволило сравнить концентрационные зависимости свойств с многочисленными опытными данными.
Для численных расчетов был выбран каучук со свободным сочленением сегментов длиной 2 нм, а в качестве наполнителя в нем - обычный технический углерод с максимальным, объемным наполнением
 и с приведенным диаметром частиц 40 нм.
и с приведенным диаметром частиц 40 нм. Н
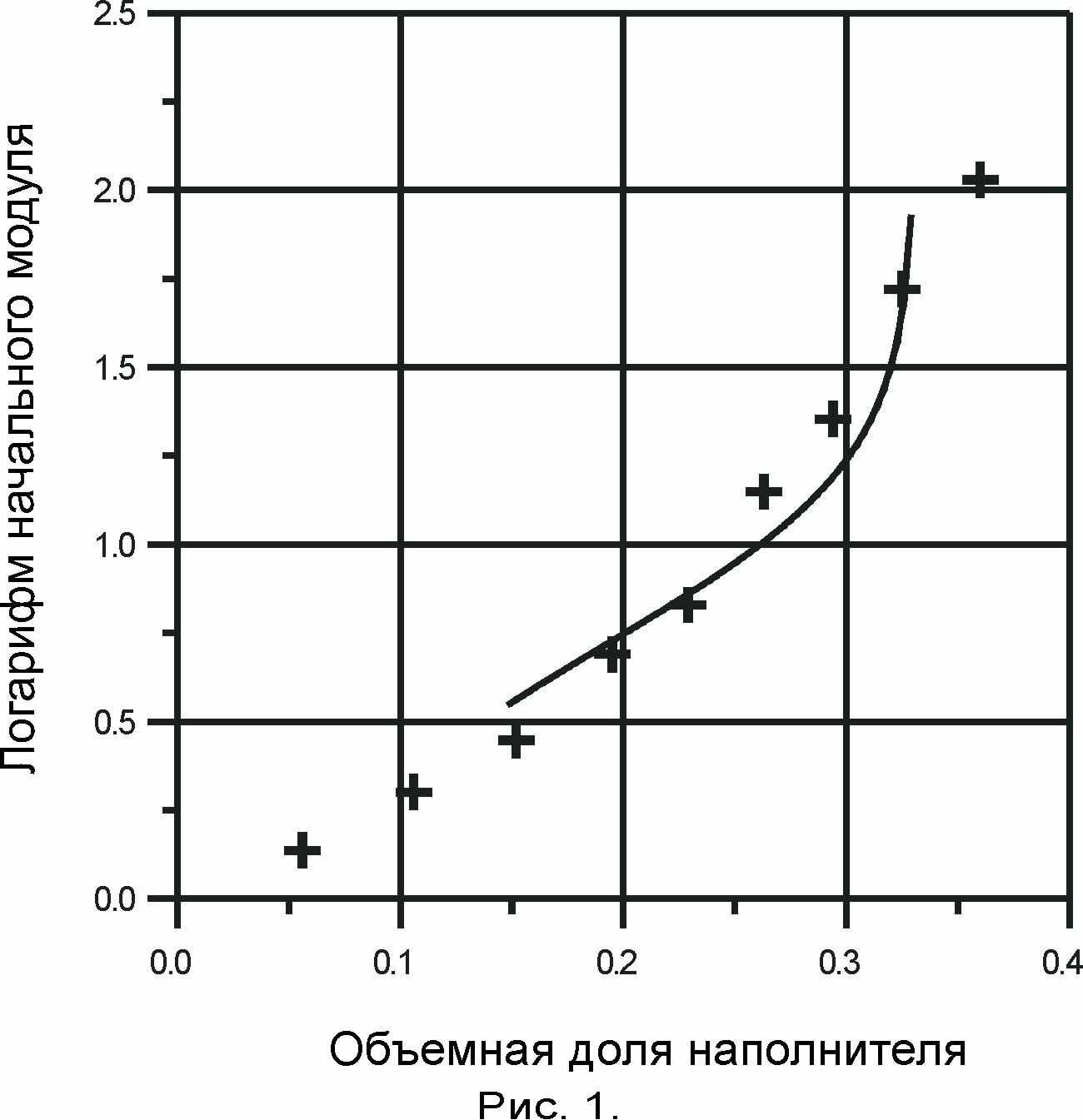
 а рис. 1. приведена зависимость начального модуля от объемной доли наполнителя (сплошная линия) и экспериментальные данные, полученные Федорсом в 1979 году (крестики). Из рисунка видно, что теоретические расчеты хорошо согласуются с экспериментальными результатами в области высоких объемных наполнениях. Можно предположить, что высокая начальная жесткость эластомерных композитов в таких условиях обусловлена тем, что промежутки между наночастицами оказываются меньше эластомерных молекул. Очень тонкие эластомерные прослойки между частицами обладают гораздо более высокой жесткостью, чем полноразмерные молекулы, так как включают в себя небольшое количество свободно сочлененных сегментов.
а рис. 1. приведена зависимость начального модуля от объемной доли наполнителя (сплошная линия) и экспериментальные данные, полученные Федорсом в 1979 году (крестики). Из рисунка видно, что теоретические расчеты хорошо согласуются с экспериментальными результатами в области высоких объемных наполнениях. Можно предположить, что высокая начальная жесткость эластомерных композитов в таких условиях обусловлена тем, что промежутки между наночастицами оказываются меньше эластомерных молекул. Очень тонкие эластомерные прослойки между частицами обладают гораздо более высокой жесткостью, чем полноразмерные молекулы, так как включают в себя небольшое количество свободно сочлененных сегментов.Ранее этот эффект был установлен Пейном и Виттакером (1972) при циклических испытаниях наполненных каучуков. Расчетные кривые хорошо воспроизводят опытные данные Пейна (рис.2.).
 Трехмерная модель позволила объяснить зависимость начального модуля (в произвольных единицах) от диаметра частиц наполнителя (рис. 3). В согласии с экспериментальными данными начальный модуль уменьшается с увеличением размера частиц. Однако эта зависимость исчезает, когда размер частиц превышает 50 нм при объемных концентрациях менее 15%.
Трехмерная модель позволила объяснить зависимость начального модуля (в произвольных единицах) от диаметра частиц наполнителя (рис. 3). В согласии с экспериментальными данными начальный модуль уменьшается с увеличением размера частиц. Однако эта зависимость исчезает, когда размер частиц превышает 50 нм при объемных концентрациях менее 15%.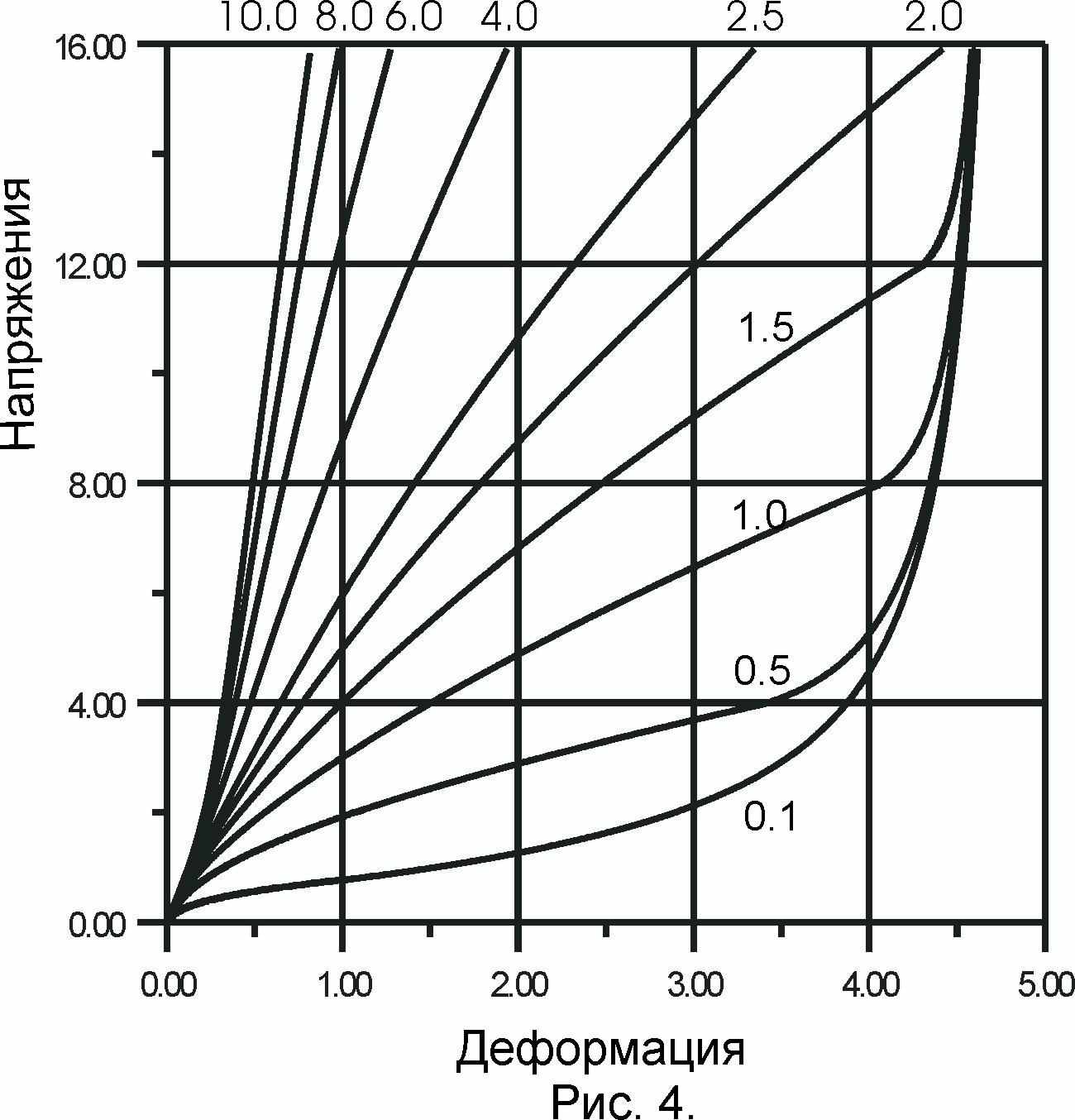 Рис. 4. демонстрирует влияние адгезионной прочности на кривые растяжения для обычно применяемого 25%-го объемного наполнения технически углеродом. Увеличение адгезионного сцепления от 0,1 до 2 сохраняет разрывные деформации, на высоком уровне, близкими к максимальной величине 4,5 при одновременном значительном повышении модуля упругости. При более высокой прочности сцепления разрывные деформации начинают быстро снижаться.
Рис. 4. демонстрирует влияние адгезионной прочности на кривые растяжения для обычно применяемого 25%-го объемного наполнения технически углеродом. Увеличение адгезионного сцепления от 0,1 до 2 сохраняет разрывные деформации, на высоком уровне, близкими к максимальной величине 4,5 при одновременном значительном повышении модуля упругости. При более высокой прочности сцепления разрывные деформации начинают быстро снижаться. Р
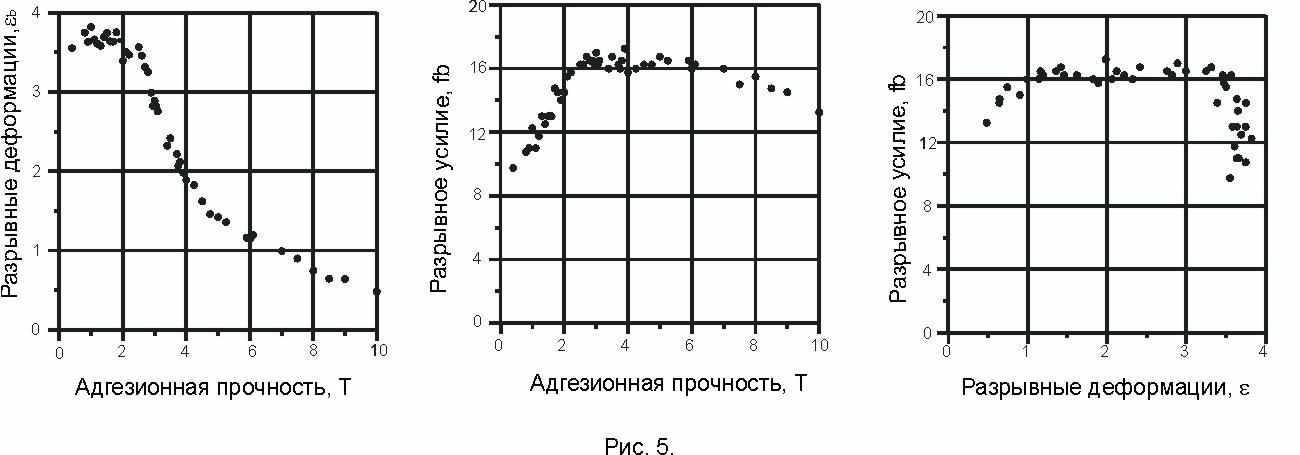 ис.5. показывает, как разрывные деформации и разрывные усилия зависят от адгезионного сцепления, а также как разрывные деформации связаны с разрывными усилиями. Последняя зависимость качественно согласуется с экспериментальными данными по разрушению, описанными Смитом в 1977 году. Увеличение адгезионной прочности в численных экспериментах позволяет моделировать уменьшение температуры или уменьшение скорости растяжения в реальных экспериментах.
ис.5. показывает, как разрывные деформации и разрывные усилия зависят от адгезионного сцепления, а также как разрывные деформации связаны с разрывными усилиями. Последняя зависимость качественно согласуется с экспериментальными данными по разрушению, описанными Смитом в 1977 году. Увеличение адгезионной прочности в численных экспериментах позволяет моделировать уменьшение температуры или уменьшение скорости растяжения в реальных экспериментах.Работа поддержана проектом РФФИ и Администрацией Пермской области “Урал-РФФИ” № 04-01-96038.
Выводы
Модель демонстрирует наличие двух механизмов усиления композита: первого на начальной стадии нагружения, наблюдаемого как эффект Пейна, и обусловленного очень высокой жесткостью слоев матрицы между близко расположенными соседними частицами, и второго, связанного с нелинейным упругим предразрывным упрочнением макромолекул эластомера.
Показано, как собственная жесткость матрицы в нанокомпозитах зависит от размера и концентрации частиц наполнителя.
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ДИНАМИКИ
КОНЦЕНТРАЦИОННО-КАПИЛЛЯРНОГО разрывА
ГОРИЗОНТАЛЬНОГО СЛОЯ ЖИДКОСТИ
А. Л. Зуев, К. Г. Костарев, А. В. Шмыров
Институт механики сплошных сред УрО РАН, 614013, Пермь,
Академика Королева, 1.
Известно, что локальное внесение растворимого поверхностно-активного вещества (ПАВ) на свободную поверхность слоя жидкости вызывает концентрационно-капиллярную конвекцию, которая приводит к деформации поверхности — в месте внесения ПАВ возникает углубление [1-2]. При определенном соотношении толщины слоя и объема ПАВ деформация развивается до разрыва слоя, частично осушая его подложку. Нами экспериментально изучена эволюция разрыва слоя в случаях, когда в качестве подложки использовались полностью смачиваемая твердая поверхность, несмачиваемая твердая поверхность и слой другой нерастворимой жидкости (двухслойная система жидкостей).
На середину поверхности достаточно тонкого (с толщиной от 0,10 до 8,00 мм) слоя дистиллированной воды, помещенного в чашку Петри диаметром 10 см, с помощью дозирующей пипетки наносилась капля изопропилового спирта объемом от 0.5 до 100 мкл. Спирт, коснувшись водной поверхности, быстро растекался по ней, локально понижая коэффициент поверхностного натяжения жидкого слоя. Это вызывало в приповерхностной области интенсивное осесимметричное течение Марангони, также направленное к краям кюветы, в результате чего в ее центре и происходило обнажение дна. Характерно, что радиус образовавшейся сухого участка при этом оказывался меньше, чем радиус пятна растекшегося ПАВ, а возникающий краевой угол жидкости, соприкасающейся дном, был отличен от нуля. Изменение радиуса осушенного дна от времени в зависимости от толщины слоя и объема капли ПАВ регистрировалось видеокамерой с частотой 25 Гц.
В случае полной смачиваемости водой подложки слоя (стеклянное дно кюветы) площадь сухого участка оказалась пропорциональна объему внесенной капли ПАВ. По мере растворения спирта концентрационно-капиллярное течение в жидкости затухало и разрыв исчезал. В случае несмачиваемой подложки (фторопласт), было обнаружено, что разрыв исчезал, только если диаметр возникающей сухой зоны оказывался меньше некоторого критического значения. При бóльших значениях диаметра разрыв слоя продолжал существовать и после полного растворения ПАВ.
В системе из двух горизонтальных жидких слоев также возможно существование стационарного разрыва верхнего жидкого слоя. Оказалось, что основным, но не обязательным, условием сохранения разрыва является преобладание поверхностного натяжения верхнего слоя над натяжением нижнего (например, вода поверх четыреххлористого углерода [3]). Получен ряд соотношений, определяющих устойчивость разрыва в зависимости диаметра разрыва от толщины верхнего слоя, времени, диаметра экспериментальной кюветы, вязкости и плотности жидкостей. Показано, что возникновение стационарного разрыва обусловлено наличием двух положений механического равновесия слоя, потенциальный барьер между которыми может быть преодолен путем внесения возмущений в систему жидкостей — локальным введением микродоз ПАВ или механическим способом. Определена величина потенциального барьера для различных пар жидкостей. Получены кривые устойчивости системы двух жидких слоев для возникновения и исчезновения стационарного разрыва. Экспериментальные данные хорошо совпадают с результатами аналитических расчетов. При этом толщина разрываемого слоя и диаметр области разрыва существенно увеличились по сравнению со слоем на твердой поверхности, а количество ПАВ, необходимого для разрыва слоя, уменьшилось. В то же время диаметр стационарного разрыва практически не зависел от объема вводимого ПАВ.
 a) | |  б)  в) Фотография стационарного разрыва жидкого слоя, расположенного на жидкой подложке (а) и схематическое изображение двухслойной системы (вид сбоку) до разрыва (б) и после (в). |
Работа выполнена при поддержке проекта РФФИ–Урал № 04-01-96057.
Литература
- Briskman V.A., Legros J.-C., Velarde M.G., Viviani A., Zuev A.L. Experimental studies of Marangoni convection in thin liquid layers caused by soluble surfactant // Proc. 1st Int. Symp. on Microgravity Research and Applications in Physical Sciences and Biotechnology, Sorento, Italy, 10-15 September 2000. ESA SP-454, 2001. P. 207-214.
- Зуев А.Л. Концентрационно-капиллярная деформация тонкого слоя // Термо- и концентрационно-капиллярные эффекты в сложных системах. Екатеринбург: УрО РАН, 2002. С. 56-67.
- Костарев К.Г., Шмыров А.В. Стационарные разрывы поверхности двухслойной системы несмешивающихся жидкостей // Конвективные течения. Вып. 2. Пермь: ПГПУ, 2005. С. 60-72.
НЕЛИНЕЙНЫЕ РЕЗОНАНСНЫЕ ВЗАИМОДЕЙСТВИЯ ВОЛН
В СТРУКТУРИРОВАННЫХ И ПОВРЕЖДЕННЫХ
МАТЕРИАЛАХ
В.И. Ерофеев
Нижегородский филиал Института машиноведения им. А.А. Благонравова РАН, Нижний Новгород
Основываясь на нескольких нелинейных математических моделях сред с микроструктурой (среда Коссера, двухкомпонентная твердая сдвиговая смесь; пористый материал; среда Био с полостями, содержащими жидкость), исследован эффект фазово-группового синхронизма (длинно-коротко-волновый резонанс) при распространении продольной упругой волны. Показано, что в результате взаимодействия низкочастотной волны (вибрационное поле) и высокочастотной волны (ультразвук), генерируется ультразвуковая волна суммарной частоты. Эта волна может находиться в фазово-групповом синхронизме с вибрационным полем. Расчеты качественно соответствуют данным о наблюдении генерации ультразвука сейсмическими воз ми напряжениями. Показано, что наличие квадратичной нелинейности приводит к резонансным взаимодействиям трех волн, одна из которых является плоско поляризованной продольной волной и две – циркулярно поляризованными (спиральными) сдвиговыми волнами. Частоты и волновые числа взаимодействующих волн связаны условиями фазового синхронизма и удовлетворяют дисперсионным уравнениям. Установлено, что в среде реализуется эффект распадной неустойчивости, когда продольная волна высокой частоты распадается на две сдвиговые волны более низких частот. Процесс взаимодействия проявляется в виде пространственных биений. Длина волны огибающей уменьшается с увеличением амплитуды продольной волны. Наличие кубической нелинейности приводит к возможности реализации четырехволновых резонансных взаимодействий спиральных сдвиговых волн.
Получены уравнения, описывающие динамические процессы в материалах, по-разному сопротивляющихся растяжению и сжатию. Показано, что наличие поврежденности приводит к тому, что при распространении в среде сдвиговой волны появляется квадратичная нелинейность (в случае распространения сдвиговой волны в идеально – упругой среде, самая младшая нелинейность по сдвиговым колебаниям была бы кубической). Для разномодульных материалов выявлены основные закономерности генерации второй гармоники. Найдены зависимости, связывающие амплитуды волн, распространяющихся на основной и удвоенной частотах, с параметрами поврежденности. Получена характерная длина, на которой следует ожидать значительной перекачки энергии основной волны в энергию второй гармоники, что дает возможность оценить интегральный параметр поврежденности материала. На основе построенной математической модели и экспериментов с образцами найдена зависимость между параметром поврежденности и пластической деформацией.
Предлагается теоретическая модель, позволяющая описывать распространение плоской продольной акустической волны в твердом теле с дислокациями. Анализируется влияние дислокаций на дисперсию фазовой скорости волны, величину и характер затухания. Показывается, что в зависимости величины затухания от частоты имеется пик, положение которого определяется характеристиками твердого тела и дислокационной структуры. Модель также позволяет теоретически описывать закономерности распространения продольной акустической волны в твердом теле с увеличивающейся плотностью дислокаций и изменяющейся дислокационной структурой. В отличие от классической модели Гранато-Люке, предлагаемый подход учитывает междислокационное взаимодействие, что позволяет описывать эксперименты, изучающие закономерности распространения упругих волн в циклически нагружаемых или деформируемых образцах. Анализируется влияние плотности дислокаций на величину затухания и скорость распространения упругой волны. Показано, что в зависимости величины затухания от плотности дислокаций в твердом теле имеется пик. Производится сравнение полученных результатов с экспериментальными данными по зависимости затухания и скорости распространения волны от количества циклов нагружения или величины деформации. Сформулированы критерии возникновения модуляционной неустойчивости акустической волны, распространяющейся в твердом теле с дислокациями. Описывается влияние дислокационной структуры на эволюцию нелинейных акустических волн. Теоретически получены соотношения, связывающие параметры дислокационной структуры с шириной и амплитудой волновых пакетов, формирующихся из квазигармонической волны в результате модуляционной неустойчивости. Производится сравнение с экспериментальными данными по самомодуляции акустических волн.
Вибрационное взаимодействие включений
в вязкой жидкости
А.А. Иванова1, В.Г. Козлов2
1 Пермский государственный педагогический университет,
614990, Пермь, Сибирская, 24
2 Институт механики сплошных сред УрО РАН,
614013, Пермь, Академика Королева, 1
Дается обзор и анализ результатов экспериментального исследования нового типа подъемных сил вибрационной природы, действующих на твердые включения в вязкой жидкости и проявляющихся на расстоянии вязкого взаимодействия. Рассматриваются подъемная сила, действующая на тело, совершающее колебания вблизи твердой границы, взаимодействие синфазно колеблющихся сферических тел, вибрационное взаимодействие взвешенных в жидкости тяжелых частиц [1–3]. Показано, что на расстоянии, сравнимом с толщиной слоя Стокса, характер вибрационного взаимодействия включений качественно отличается от высокочастотного случая – направление осредненной вибрационной силы оказывается противоположным. При этом на тела, колеблющиеся вблизи твердой границы, действует вибрационная сила отталкивания; взвешенные в вязкой жидкости твердые частицы испытывают силу взаимного притяжения в направлении оси вибраций, и силу отталкивания – в перпендикулярном. Сила такого взаимодействия велика, она может обеспечить вибрационное поднятие тяжелых тел в поле силы тяжести. Другим проявлением вязкого взаимодействия является вибрационное объединение (конденсация) взвешенной в жидкости сыпучей среды в блоки с устойчивой границей раздела с чистой жидкостью. В этом случае возможна вибрационная стабилизация фронта оседающей в жидкости сыпучей среды. Экспериментальным эффектам дается теоретическое описание.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант РФФИ-Урал № 04-01-96055).
Литература
- Иванова А.А., Козлов В.Г., Кузаев А.Ф. Вибрационная подъемная сила, действующая на тело в жидкости вблизи твердой поверхности // Докл. АН. 2005. Т. 402. № 4. С. 1–4.
- Иванова А.А., Кузаев А.Ф. Влияние вязкости жидкости на взаимодействие сферических тел // Конвективные течения… / Перм. гос. пед. ун-т. Пермь, 2005. Вып. 2. С. 100–110.
- Козлов В.Г. О вязком гидродинамическом взаимодействии частиц сыпучей среды в вибрационных полях // Конвективные течения… / Перм. гос. пед. ун-т. Пермь, 2005. Вып. 2. С. 111–122.
СЛОИСТЫЕ ПЬЕЗООБОЛОЧКИ С ВНЕШНИМИ
ЭЛЕКТРИЧЕСКИМИ ЦЕПЯМИ ПОД ДЕЙСТВИЕМ
ДИНАМИЧЕСКИХ НАГРУЗОК
Е.П. Клигман, В.П. Матвеенко, Н.А. Юрлова
Институт механики сплошных сред УрО РАН, г.Пермь, Россия
Использование в оболочечных конструкциях современных материалов, обладающих пьезоэлектрическими свойствами, позволяет оптимизировать динамическое поведение создаваемых систем. Наличие внешних электрических RLC-цепей, соединяющих электродированные поверхности пьезоматериалов, увеличивает число параметров, влияющих на резонансные частоты, формы собственных колебаний и показатели демпфирования конструкции. Динамические характеристики таких систем определяются из решения либо спектральной задачи электроупругости, которая формулируется в комплексной форме, либо задачи об установившихся вынужденных колебаниях. В спектральной задаче найденные комплексные собственные функции будут определять формы и фазы колебаний, а комплексные собственные значения – резонансные частоты и показатели демпфирования. Целенаправленное изменение параметров внешних RLC-цепей позволяет оптимизировать динамические характеристики конструкций.
Вариационное уравнение движения тела, состоящего из упругого и пьезоэлектрического элементов, может быть получено на основе соотношений линейной теории упругости и квазистатических уравнений Максвелла и уравнения закона Ома для цепей переменного тока с RLC-элементами.
Если механическая нагрузка, действующая на систему, отсутствует, то решение может быть представлено в виде
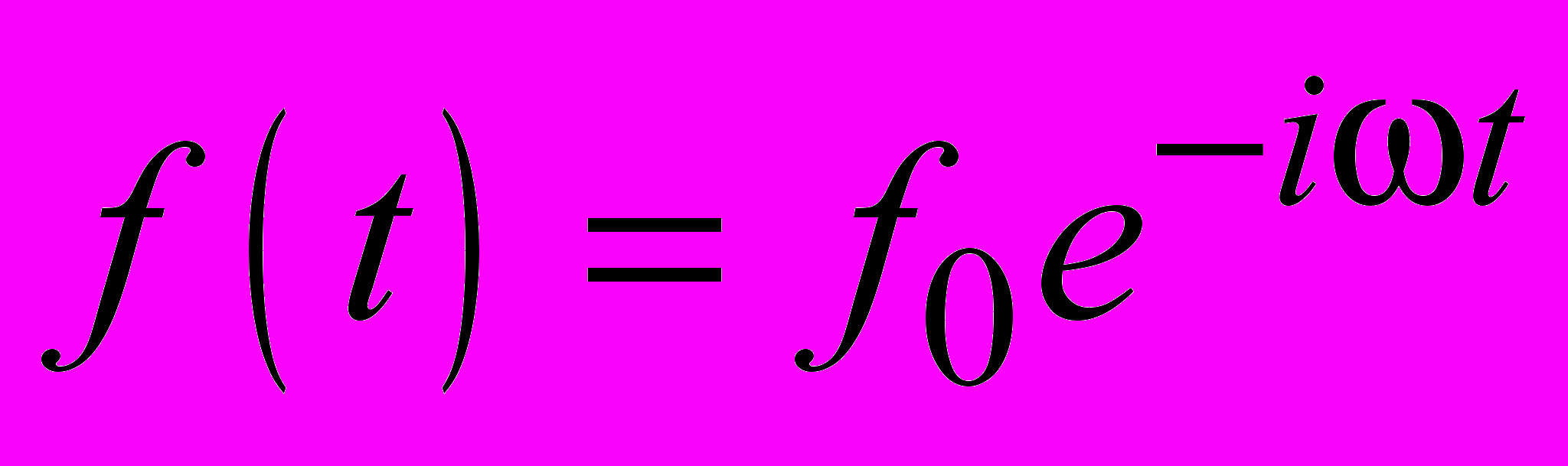 , что приводит к задаче на собственные значения.
, что приводит к задаче на собственные значения. (1)
(1)где
 ,
,  – тензоры напряжений и деформаций;
– тензоры напряжений и деформаций;  – вектор перемещений;
– вектор перемещений; 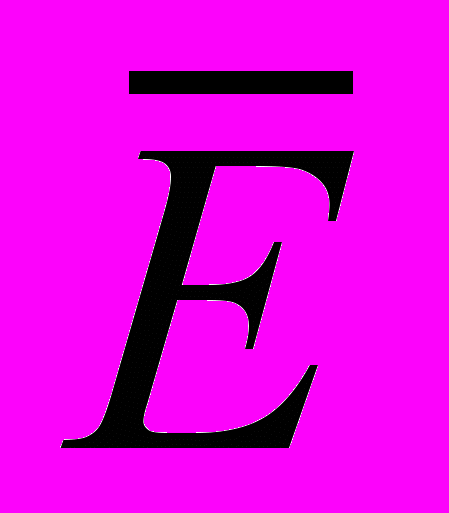 – вектор напряженности электрического поля;
– вектор напряженности электрического поля;  – плотность материала;
– плотность материала;  –электрический потенциал;
–электрический потенциал;  - тензор упругих констант;
- тензор упругих констант; 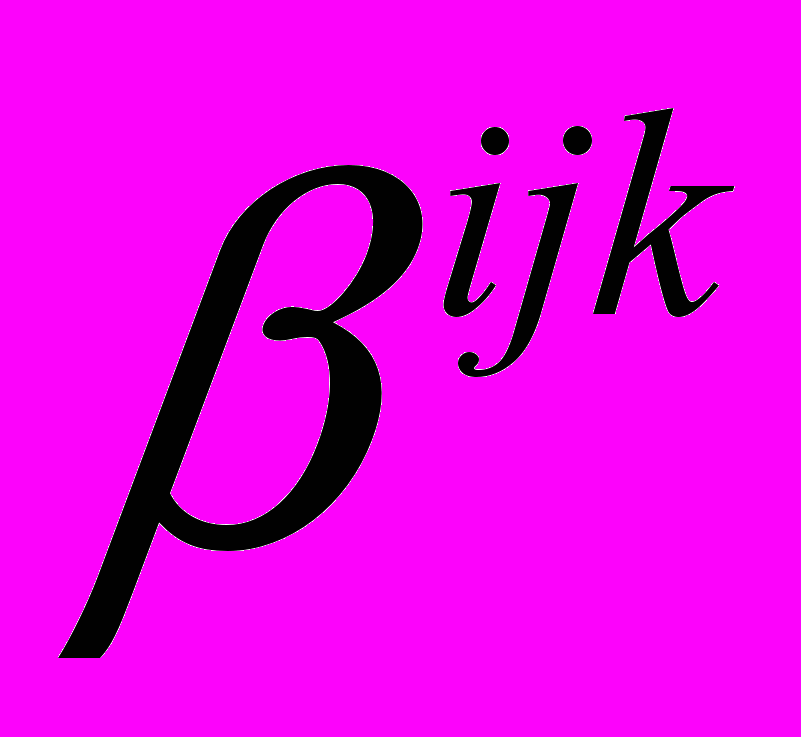 и
и 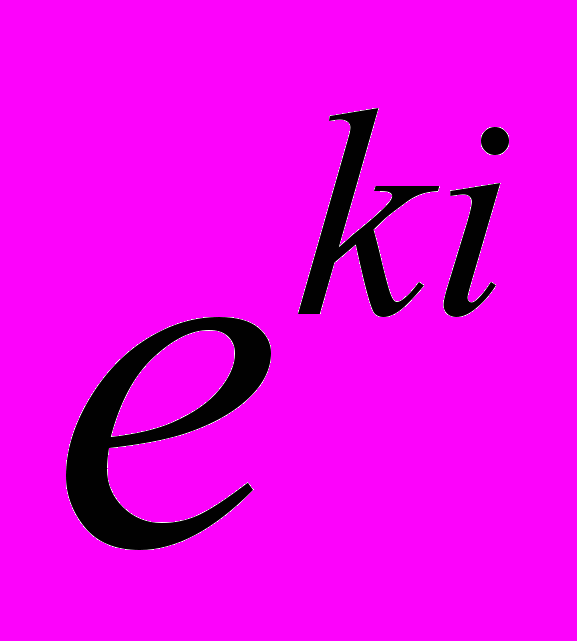 - тензоры пьезоэлектрических и диэлектрических коэффициентов; R – сопротивление, L – индуктивность и C – ёмкость внешней цепи;
- тензоры пьезоэлектрических и диэлектрических коэффициентов; R – сопротивление, L – индуктивность и C – ёмкость внешней цепи;  - часть рассматриваемого тела, выполненная из упругого или вязкоупругого материала;
- часть рассматриваемого тела, выполненная из упругого или вязкоупругого материала;  - часть рассматриваемого тела, выполненная из пьезоэлектрика.
- часть рассматриваемого тела, выполненная из пьезоэлектрика. Применение пьезоматериалов для создания оболочечных конструкций требует использования моделей оболочек, учитывающих все компоненты тензоров напряжений и деформаций. Это объясняется тем, что такие материалы, как правило, поляризованные в направлении толщины, проявляют свои свойства при трансверсальном деформировании. Учет всех компонент тензоров напряжений и деформаций может быть осуществлен в рамках шестимодальной теории оболочек Тимошенко.
Д
 ля расчета слоистых оболочек используется модифицированный вариант гипотезы ломаной нормали, позволяющий адекватно описывать слои с существенно различными электромеханическими характеристиками.
ля расчета слоистых оболочек используется модифицированный вариант гипотезы ломаной нормали, позволяющий адекватно описывать слои с существенно различными электромеханическими характеристиками.В
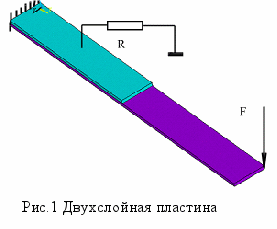
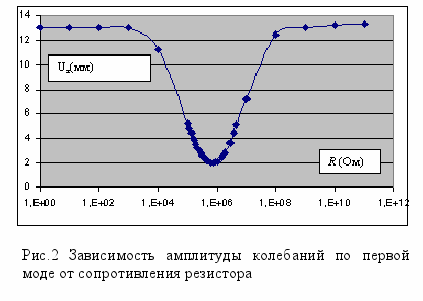 качестве примера рассматривается задача об установившихся вынужденных колебаниях защемленной по одной стороне двухслойной пластины, один слой которой обладает пьезоэлектрическими свойствами и в два раза короче другого (см рис 1). Размеры пластины: 2 x 20 см толщина каждого слоя 0,2. Материал 1- PZT-4, материал 2 - сталь. Для упрощения процедуры расчета предполагается, что сталь обладает слабо выраженными вязкоупругими свойствами, которые характеризуются коэффициентом демпфирования (тангенс потерь) равным 1×10-8. Целью исследования был выбор величины сопротивления R, обеспечивающий минимум амплитуды поперечных колебаний Uz в окрестности первого резонанса. Возбуждение колебаний осуществлялось гармонической силой F=1Н. Результаты расчета иллюстрируют рисунки 2 и 3. Как видно из рис.2, оптимальное значение сопротивления равно примерно 1Мом.
качестве примера рассматривается задача об установившихся вынужденных колебаниях защемленной по одной стороне двухслойной пластины, один слой которой обладает пьезоэлектрическими свойствами и в два раза короче другого (см рис 1). Размеры пластины: 2 x 20 см толщина каждого слоя 0,2. Материал 1- PZT-4, материал 2 - сталь. Для упрощения процедуры расчета предполагается, что сталь обладает слабо выраженными вязкоупругими свойствами, которые характеризуются коэффициентом демпфирования (тангенс потерь) равным 1×10-8. Целью исследования был выбор величины сопротивления R, обеспечивающий минимум амплитуды поперечных колебаний Uz в окрестности первого резонанса. Возбуждение колебаний осуществлялось гармонической силой F=1Н. Результаты расчета иллюстрируют рисунки 2 и 3. Как видно из рис.2, оптимальное значение сопротивления равно примерно 1Мом.Д
R (Ом)
 ля оценки скорости затухания динамических процессов при оптимальном значении сопротивления в программной среде ANSYS был выполнен расчет пластины подвергнутой воздействию импульсной силы F=1Н, длительностью 10-7 с. Процесс затухания колебаний показан на рис.4.
ля оценки скорости затухания динамических процессов при оптимальном значении сопротивления в программной среде ANSYS был выполнен расчет пластины подвергнутой воздействию импульсной силы F=1Н, длительностью 10-7 с. Процесс затухания колебаний показан на рис.4. Т
 аким образом, проведенные исследования подтверждают высокую эффективность разработанной методики гашения опасных колебательных процессов в механических системах.
аким образом, проведенные исследования подтверждают высокую эффективность разработанной методики гашения опасных колебательных процессов в механических системах.Работа выполнена при поддержке РФФИ (код проекта 03-01-00557).
Библиографический список
- Е.П. Клигман, В.П. Матвеенко, Н.А. Юрлова. Динамические характеристики тонкостенных электроупругих систем // Известия РАН, МТТ.- 2005.- №2. С. 179-187.
О НЕЛИНЕЙНЫХ МЕХАНИЗМАХ ПРИ ПЕРЕХОДЕ
К ТУРБУЛЕНТНОСТИ В ПОГРАНИЧННЫХ СЛОЯХ
В.В. Козлов
Институт теоретической и прикладной механики СО РАН,
Новосибирск, Россия
В докладе представлены результаты исследований синусоидальной (см. Рис.1) и варикозной (Рис.2) неустойчивости полосчатых структур на нелинейной стадии ламинарно-турбулентного процесса в сдвиговых течениях. Обсуждается поведение течения в процессе пространственной эволюции полосчатых структур с генерированным на них вторичным высокочастотным возмущением. Рассмотрены различные сценарии возникновения и развития когерентных вихревых структур, исследованных как в физическом, так и в численном экспериментах. Показаны особенности развития синусоидального и варикозного случаев разрушения продольной стационарной полосчатой структуры, такие как модуляция структуры в трансверсальном и продольном направлениях частотой вторичного возмущения, появление новых полосчатых структур вниз по потоку и возникновение и развитие локализованных по пространству нестационарных образований типа ламбда-структур([1]-[2]).


Литература
- Литвиненко Ю.А., Чернорай В.Г., Козлов В.В., Лёфдаль Л., Грек Г.Р., Чун Х. О нелинейной синусоидальной и варикозной неустойчивости в пограничном слое./ДАН, 2005, № 1, с. 51-53.
- Литвиненко Ю.А., Чернорай В.Г., Козлов В.В., Лёфдаль Л., Грек Г.Р., Чун Х. О нелинейной синусоидальной и варикозной неустойчивости в пограничном слое (обзор) / Теплофизика и аэромеханика, 2004, том 11, №3,стр.339-365.
