Обработка и передача изображений

Вид материала

Литература

Содержание Method of image compression using discrete chebyshov polynomials Применение преобразования фурье для измерения структурных параметров изображения наполненных полимерных материалов Application of fourier transformation to the measurement of structural parameters of the image of the filled polymeric materials Выделение признаков на последовательности изображений Г к последовательности значений функции  Х, но и особенностями изменения этих признаков на последовательности изображений, полученной последовательным многократным приме Allocation of attributes on sequence of images The literature Цифровая обработка изображений микроциркуляторного русла Алгоритм подсчета площади занимаемой сосудами. Алгоритм скелетизации изображения сосудистой сети бульбарной конъюнктивы. Алгоритмы измерения параметров сосудистой сети бульбарной конъюнктивы. Digital image processing of microcirculation images Описание алгоритма. Экспериментальные исследования. Семантическое сжатие видеопоследовательностей с движущимися транспортными средствами Semantical compression of videos containing moving vehicles Подсистема спектрального обнаружения межкадровых изменений в кодеке MGDCT 2 . Алгоритм спектрального обнаружения изменений в блоке 3. Описание подсистемы обнаружения изменений ... Полное содержание

Подобный материал:

• Обработка и передача изображений, 213.76kb.
• Анализ, обработка и передача динамических изображений в моделях виртуальной реальности, 80.25kb.
• Обработка и передача изображений, 243.48kb.
• Обработка и передача изображений, 289.83kb.
• Обработка и передача изображений, 149.44kb.
• Обработка и передача изображений, 241.81kb.
• 1. Информационные технологии. Структура информационного процесса. Сбор, обработка,, 1016.5kb.
• Обработка и передача изображений, 203.92kb.
• Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
• Обработка и передача измерительной информации, 201.84kb.

Полученные результаты

В результате исследований было получено, что изображения с плавными градациями яркости и цвета могут быть подвергнуты сильному сжатию при использовании чебышевских преобразований. Разработанные нами устойчивые вычислительные алгоритмы для осуществления ортогональных преобразований дискретных сигналов на основе классических ортогональных полиномов Чебышева дискретной переменной позволяют преодолеть трудности, связанные с неустойчивостью счета при осуществлении чебышевских преобразований, требующих вычисления полиномов высоких степеней относительно длины сигнала.

Выводы

На основе ортогональных полиномов Чебышева дискретной переменной могут быть сконструированы эффективные алгоритмы для осуществления дискретных ортогональных преобразований сигналов и их сжатия. При численной реализации этих алгоритмов непременно следует учитывать асимптотическое поведение самих ортогональных полиномов. Это позволяет добиться устойчивости в вычислениях при осуществлении как прямых, так и обратных дискретных ортогональных преобразований, основанных на применении указанных полиномов.

Литература

1. R. Mukundan and O. Hunt, “A comparison of discrete orthogonal basis functions for image compression,” in Proc. Conf. Image and Vision Computing New Zealand (IVCNZ’04), 2004, pp. 53–58.
   
2. Радченко Ю.С., Агибалов А.А., Булыгин А.В., Радченко Т.А. Экспериментальный кодек чебышевского сжатия/восстановления изображений (gdct) и программный комплекс для его исследования.// Труды 9ой международной конференции Международная конференция "Цифровая обработка сигналов и её применение" DSPA-2007. – 2007. – С. 286-289.
   
3. Федосеев В.А. Компрессия изображений с помощью дискретных ортогональных преобразований, определенных на развертках двумерных областей//сб. "Компьютерная оптика", вып. 28, 2005. С.132-135.
   
4. Sharapudinov T., Luguev T., Processing and Compression of Time Series by Orthogonal Polynomials // 8th International Conference “Pattern Recognition and Image Analysis: New Information Technologies” (PRIA-8-2007): Conference Proceedings. Vol.2. – Yoshkar-Ola, 2007. – p.44-47.
   
5. Шарапудинов И.И. Многочлены, ортогональные на дискретных сетках. – Махачкала: изд-во Даг. гос. пед. ун-та, 1997.
   

METHOD OF IMAGE COMPRESSION USING DISCRETE CHEBYSHOV POLYNOMIALS

Luguev T., Magomed-Kasumov M., Sultanov E., Sharapudinov T.

Math and computer science department Dagestan Scientific Center of RAS

Orthogonal transforms based on orthogonal systems of functions are frequently used in image compression. One of the most popular transforms in image processing is DCT that is used in JPEG image compression algorithm. Another transforms that are researched in recent times are polynomial transforms. Particularly, Discrete Chebyshev Transform has similar compression ratio as DCT and it works better for some classes of images [2]. But the numeric realization of algorithms producing discrete orthogonal transformations based on the discrete orthogonal polynomials causes significant difficulties concerning instability of the calculation. It impelled us to search possible ways of the organization of computational algorithms producing discrete multinomial transformations devoid of destructive effects of instability. The methods examined by us are based on the modification of recurrence relations of Chebyshev's polynomials, orthogonal on the nets.

Since images are two-dimensional signal, two-dimensional discrete transformations are usually applied to it. Herewith the image is dividing to blocks (8х8, 32х32) that are handling separately. This segmentation method doesn't take into account characteristics of the input graphic information. It is well-known that one-dimensional discrete orthogonal transformations have lesser computational complications in comparison with two-dimensional ones [3]. Application of one-dimensional discrete transformations to scanning of two-dimensional regions, taking into account two-dimensional signal correlation, may be more efficient.

Application of the Discrete Chebyshev Transform is the most reasonable for images with smooth brightness and color gradations [3]. Therefore we suggest the method that realizes scanning of matrixes of image brightness and color to one-dimensional discrete signals and implements segmentation of obtained signals to blocks of different length so that there will be no abrupt jumps of brightness and color. Consequently image parts with smooth brightness and color gradations will get in large blocks but segments that are rich of small details and sharp gradations will get in smaller blocks. At the cost of this suggested algorithm makes possible efficient compression images of any class.

References

1. R. Mukundan and O. Hunt, “A comparison of discrete orthogonal basis functions for image compression,” in Proc. Conf. Image and Vision Computing New Zealand (IVCNZ’04), 2004, pp. 53–58.
   
2. Fedoseev V.A. Compressia izobrazheniy s pomoshyu discretnyh orthogonalnih preobrazovaniy, opredelennih na razvertkah dvumernih oblastey //sb. "Komputernaya optika", vip.28, 2005. P.132-135.
   
3. Sharapudinov T., Luguev T., Processing and Compression of Time Series by Orthogonal Polynomials // 8th International Conference “Pattern Recognition and Image Analysis: New Information Technologies” (PRIA-8-2007): Conference Proceedings. Vol.2. – Yoshkar-Ola, 2007. – p.44-47.
   




ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ ДЛЯ ИЗМЕРЕНИЯ СТРУКТУРНЫХ ПАРАМЕТРОВ ИЗОБРАЖЕНИЯ НАПОЛНЕННЫХ ПОЛИМЕРНЫХ МАТЕРИАЛОВ

Абраменко Е.А.

Алтайский государственный университет

Установлено, что на свойства наполненных полимеров влияет множество факторов: химическая природа, размер, форма, удельная поверхность частиц наполнителя и т.д. Причем, их влияние на структуру неоднозначно. Поэтому разработка таких материалов требует методов исследования структуры, которые позволили бы подойти к осознанному регулированию свойств, приведению их в соответствие с требованиями конкретных условий эксплуатации. В настоящее время эффективные методы и подходы к исследованию макроструктуры дисперсно-наполненных материалов разработаны далеко не в полной мере.

Во многих странах идёт активный поиск оптимальных методов анализа компьютерных изображений. Предъявляемые требованиям к результатам работы этих методов очень высоки. Они должны обладать высокой точностью, быть достаточно универсальными, обладать не большими вычислительными требованиями. К сожалению пока не удалось обнаружить метод, с помощью которого можно было бы с одинаковым успехом анализировать разные типы изображений.

Так для анализа структуры материалов, содержащих частицы наполнителя, часто используют несколько методов анализа – фрактальный, текстурный и классический амплитудный метод.

При исследовании материалов с высоким содержанием частиц наполнителя, часто прибегают к фрактальным методам анализа, однако данные методы плохо работают при исследовании материалов с низким содержанием наполнителя. Это связано с тем, что основная характеристика фракталов – фрактальная размерность [1, 2], имеет прямую зависимость от сложности рисунка, который получается в результате взаимодействия частиц наполнителя и исходного материала.

Так же стоит помнить, что при подсчёте значения любой фрактальной размерности большое влияние оказывает выбранный шаг (размер окна), с помощью которого совершается обсчет изображения. Так, например, фрактальная размерность одного и того же изображение подсчитанная окном 5х5 точек будет меньше, чем при использовании окна размером 3х3.

Другими часто используемыми методами анализа изображений являются методы, основанные на работе с матрицей самого изображения, т.н. амплитудные методы [3]. Такие как подсчёт площадей фигур находящихся на изображении, перепадов яркости, максимумы и минимумы, средние значения и т.д. Однако, здесь существует ещё больший недостаток. В вопросах, которые касаются анализа изображений, полученных при помощи оптических методов, возникает ошибка, связанная с качеством снимка и условиями при которых он был получен. Так изменение яркости или резкости изображения приводит к существенному изменению результата. Перечисленные способы анализа могут быть применены к снимкам, которые являются результатом использования электронных, рентгеновских и прочих не оптических методов изучения структуры материала.



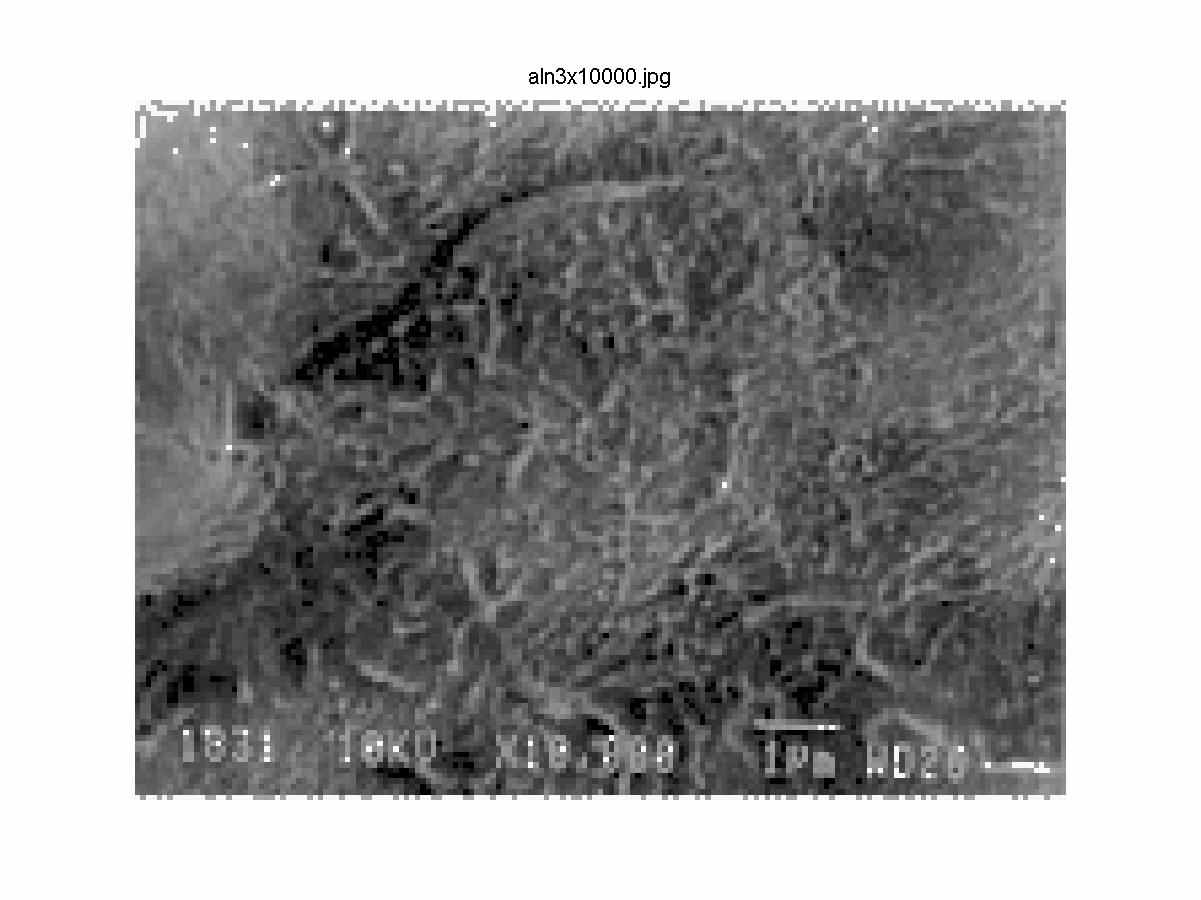
Рис.1 Электронный снимок и его карта текстурного распределения структуры полимера, наполненного ALN с концентрацией 3%.

Третьим звеном являются текстурные методы исследования. Классическими считаются такие параметры текстуры как, энтропия, энергия, матрица смежности и др. Однако, как и в случае с классическими методами анализа возникает вероятность ошибки, связанной с качеством и процессом получения изображения. Для того чтобы избежать данных погрешностей был разработан метод основанный на переходе от исходного изображения к его текстурной картине.

Используя аналитический механизм, были выделены области с различной текстурой, каждому виду текстуры был присвоен свой уникальный индекс. Данный индекс, при создании текстурного изображения, выступает в качестве метки для определённого цвета. Т.о. мы имеем возможность, как для визуального анализа текстурной картины, так и для математического анализа матрицы индексов. Переходя от исходного снимка к его текстурной карте, возникает возможность нивелировать вклад от внешних факторов, оказывающих влияние на получаемое изображение. На рис. 1 приведен снимок, полученный при помощи электронного микроскопа, а также его текстурная карта.

В дальнейшем на основе полученной текстурной карты подсчитывается преобразование Фурье (ПФ), позволяющее выделить основные пиковые значения, отличающие изображения с различными наполнителями и концентрациями. Смысл значения ПФ в том, что оно позволяет выделить из текстурной картины амплитуды и их периодичность, характеризующие распределение и величину изменчивости текстуры. С физической точки зрения – данное преобразование позволяет оценить, насколько сильно меняется структура объекта, и связать это изменение с теми физико-химическими параметрами, которые обуславливают данное изменение.

Результаты оценок по текстурным картам (количественно охарактеризованным значением преобразования Фурье) сравнивались с величинами степени кристалличности, полученными для выбранных объектов исследования (данные по степени кристалличности приведены в [4]). Оказалось, что характер зависимостей от концентрации значения преобразования Фурье схож с закономерностью изменения от концентрации степени кристалличности исследуемых объектов (рис. 3).

Так как степень кристалличности непосредственно влияет на структуру материала, можно полагать, что значение преобразования Фурье реагирует на структурные изменения.

Использование преобразования Фурье позволяет проводить как качественный анализ спектра, так и его количественную интерпретацию.



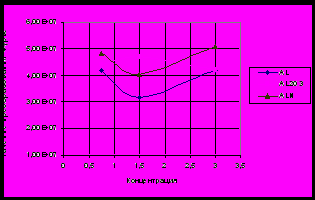
а)



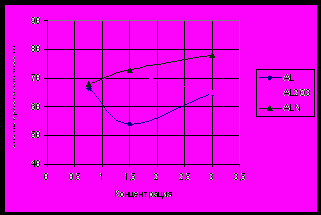
б)

Рис.2 а) Зависимости значения преобразования Фурье от концентрации и б) зависимость степени кристалличности от концентрации.

Приведенные данные показывают, что метод не только реагирует на степень кристалличности полимера, но и различает материалы по свойствам.

Таким образом, можно утверждать, что метод, предложенный в [5], работает как для оптических снимков, так и для электронных.

Выбранные объекты исследования различаются по степени активности наполнителя [4], которая, в свою очередь, оказывает существенное влияние на структуру полимера. С увеличением активности возрастает процент частиц наполнителя, образовавших кристаллическую связь с материалом. Так для AL, обладающим наименьшей степенью кристалличности, будет характерно спекание частиц наполнителя между собой, а для ALN наоборот, повышенное взаимодействие с полимером. Эта закономерность отражается на получаемой текстурной картине. А значит создание физико-математического метода, способного с одной стороны измерить периодичность текстуры, а с другой характеризующего связь с физическими свойствами объекта, позволит изучать соотношения «структура – свойства», в том числе и при различной активности наноразмерных металлических порошков.

Литература

1. Громов Ю.Ю. Земской Н.А. Фрактальный анализ и процессы в компьютерных сетях: Учеб. пособие. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 108с.
   
2. Боголюбов А.Н., Петухов А.А. Оптическая дифракция на фрактальных решетках. Вестник Московского Университета. Серия 3. Физика. Астрономия. 2008. №2, С. 7-10.
   
3. О.В. Синицын, Обработка и анализ данных зондовой микроскопии. Обзор программного обеспечения. Нано- и микросистемная техника, 2007, №2. С2-7.
   
4. Филиппов П.В., Крюкова И.М. Исследование свойств наполненного полиэтилена// Труды VI международной науч.-практ. конференции студентов, аспирантов и молодых ученых: Современные техника и технологии СТТ'2000 28 февраля - 3 марта 2000 г. - Томск: Изд-во ТПУ, 2000. С. 331-333.
   
5. Абраменко Е.А., Минакова Н.Н., Ушаков В.Я.Исследование свойств полиэтилена с наноразмерными наполнителями специальной обработкой изображений макроструктуры //Известия вузов. Физика. -2008. - № 7.- С. 41 – 45.
   

APPLICATION OF FOURIER TRANSFORMATION TO THE MEASUREMENT OF STRUCTURAL PARAMETERS OF THE IMAGE OF THE FILLED POLYMERIC MATERIALS

Abramenko E.

Altay State University

It is established that the properties of filled polymers are influenced by a set of factors: the chemical nature, the size, the form, a specific surface of particles of the filler, etc. Besides , their influence on the structure is in a way ambiguous. Therefore the development of such materials requires methods of structure analysis which would help to provide the mindful regulation of properties, and bring them in accordance with the definite service conditions. Nowadays effective methods and approaches to the research of a macrostructure of the disperse-filled materials are not fully developed.

As for the analysis of the structure of the materials containing particles of the filler, some new methods of analysis are used. They are fractal, textural and classical peak methods.

In the given article the method of measurement developed on the basis of the textural approach and the mathematical device is presented. This method allows us to describe the interconnection between the physical and chemical properties of the filled polymer and its structure.




ВЫДЕЛЕНИЕ ПРИЗНАКОВ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЗОБРАЖЕНИЙ

Жизняков А.Л., Зуев В.В.

Муромский институт (филиал) Владимирского государственного университета

Целью работы является построение подхода к описанию цифровых изображений, основанного на анализе поведения группы признаков на последовательности изображений.

Под изображением будем понимать функцию f(x,y), определенную на подмножестве Р плоскости R₂ и принимающую действительные значения.

Будем считать, что каждому изображению f можно поставить в соответствие конечный набор признаков X = X₁, X₂, …X_n, однозначно определяющий f среди множества других изображений заданных на Р.

Последовательностью изображений {f_n} назовем, каким-либо образом упорядоченное, некоторое множество изображений f, присвоив каждому его элементу индекс {f_n}={f₀, f₁,… f_n}. (1).

Ограничим все многообразие рассматриваемых последовательностей изображений случаем, когда формирование последовательности можно описать некоторым оператором. Таким образом, каждое последующее изображение последовательности, представляет собой результат воздействия оператора Т на предыдущее.

Так как каждое изображение из исходного множества f однозначно характеризуется набором признаков X, можно построить тождественную (1) последовательность {X_n} = {X₀, X₁, X_{2 …}}.

Будем считать, что если имеется некоторая последовательность изображений {f_n}, упорядоченная по какому-либо набору признаков X, то соседние изображения в этой последовательности могут иметь некоторую степень сходства (подобия). Т.е. если некоторый признак х присутствует, на изображении f_k {f_n}, то весьма вероятно, что он проявится и на соседних изображениях f_k-1 {f_n} и f_k+1 {f_n}, k = 1..N-2. Понятно, что чем сильнее связаны между собой изображения последовательности, тем длиннее (в среднем) оказывается подпоследовательность изображений {… f_k-2, f_k-1, f_k, f_k+1, f_k+2...}, k = 1..N-2, (2), содержащих один и тот же признак (особенность).

Это позволяет говорить о наличии фактора наследственности признаков в последовательности изображений.

В то же время, очевидно, что, так как связь между изображениями последовательности будет уменьшаться по мере их удаления друг от друга (увеличения разности индексов изображений последовательности), то некоторые признаки, отчетливо проявляющиеся на одном изображении, могут быть менее заметны на другом или совсем исчезнуть.

Это можно охарактеризовать как изменчивость признаков в последовательности изображений.

Рассмотрим возможность формального введения понятий наследственности и изменчивости наборов признаков.

Рассмотрим последовательность, составленную из элементов {X_n}, определяющих один и тот же признак (например, какой-нибудь i-ый признак) для всех изображений исходной последовательности {x⁽ⁱ⁾_n} = {x₀⁽ⁱ⁾, x₁⁽ⁱ⁾,… x_n⁽ⁱ⁾}.

Оператором принадлежности признака назовем оператор, определяющий уровень вхождения признака x⁽ⁱ⁾ в нечеткое множество Х⁽ⁱ⁾, то есть степень соответствия отдельной реализации признака на последовательности изображений его предельному (эталонному) значению _i : _i[x_j⁽ⁱ⁾][0,1].

Тогда каждому набору признаков Х_j изображения f_j{f_n} можно поставить в соответствие вектор Х_j = (₁х₁, ₂х₂, .. _kх_k )^Т, где к – число признаков.

Для каждого признака введем пороговый оператор Г: Г_i[x_j⁽ⁱ⁾]{0,1}. (3).

В результате применения (3) к исходному вектору Х_j характеризующему изображение f_j, получим некоторый вектор _j, состоящий из нулей и единиц:  = (₁, ₂,… _к)^Т, _i  {0,1}, i = 1, 2,…k.

Пусть имеются два соседних изображения f_m и f_m+1 последовательности {f_n}. Им соответствуют вектора _m и _m+1. Рассмотрим пары элементов (^m_i, ^m+1_i), i = 1, 2,..k. Совпадение элементов в такой паре означает, что на обоих изображениях f_m и f_m+1 либо присутствует один и тот-же признак, либо его нет на обоих изображениях.

Под изменчивостью последовательности изображений будем понимать процесс потери старых признаков или приобретения новых при переходе к каждому следующему изображению последовательности.

Для характеристики изменчивости можно, например, воспользоваться выражением:

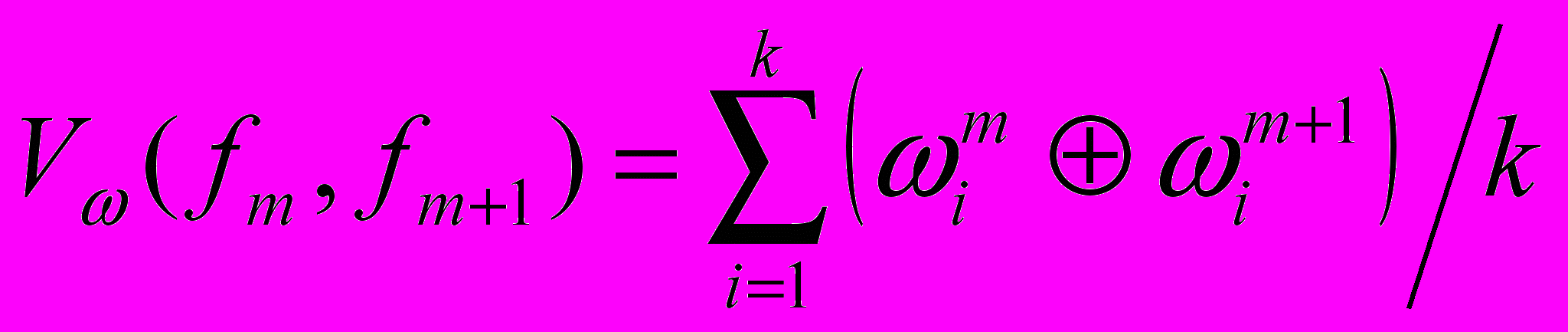, где  - операция неравнозначности (сумма по модулю 2).

Под наследственностью последовательности изображений будем понимать процесс сохранения признаков при переходе к каждому следующему изображению последовательности.

Учитывая связь понятий наследственности и изменчивости, характеристику наследственности признаков можно ввести в следующем виде: .

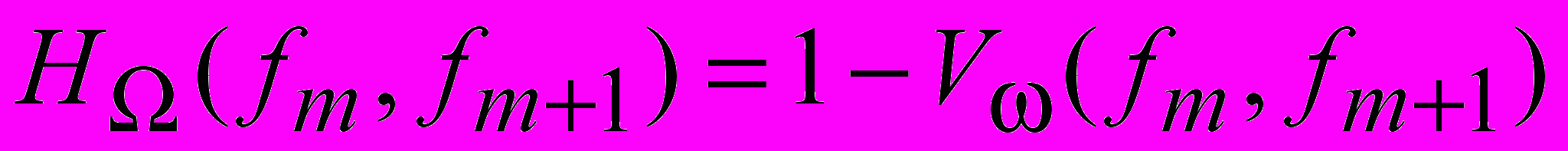Кривой распределения признака x(i) на последовательности изображений {f_n} назовем график функции _i(j)  _i[x_j(i)], принимающей дискретные значения в точках j{0,1,..n}.

Последовательности реализаций некоторого признака на последовательности изображений, также будет соответствовать последовательность, состоящая из нулей и единиц  = {₁, ₂,… _n}, _j  {0,1}, j = 1, 2,…n. (4)

Индекс i элемента последовательности , для которого выполняется (_i-1 = 0)  (_i = 1) назовем точкой появления признака.

Индекс j элемента последовательности , для которого выполняется (_j-1 = 1)  (_j = 0) назовем точкой исчезновения признака.

Результат применения оператора Г к последовательности значений функции _i(j), назовем нормированной кривой распределения признака x(i) на последовательности изображений {f_n}.

Длину участка нормированной кривой распределения признака x(i), на котором, функция Г_i(j) принимает значение равное единице, назовем глубиной вложения признака x(i) на последовательности изображений {f_n}.

Исходя из этого, будем считать, что изображение f, можно характеризовать не только множеством признаков Х, но и особенностями изменения этих признаков на последовательности изображений, полученной последовательным многократным применением оператора T, к анализируемому изображению. При этом, один признак, совпадающий для двух разных изображений, в силу разного характера наследственности и изменчивости, определяемого свойствами этих изображений, по разному будет вести себя на их последовательностях.

Литература

Zhiznjakov A.L., Sadykov S.S.,Gai V.E. Analysis of impact behavior of feature’s group at image sequence. 9^th International Conference “Pattern Recognition and Tmage Analysis: New Information Technologies” (PRIA-9-2008): Conference Proceedings. Vol.2.-Nizhni Novgorod, 2008.-404 p.(pp.365-366)


ALLOCATION OF ATTRIBUTES ON SEQUENCE OF IMAGES

Zhiznjakov A., Zuev V.

Murom institute (branch) of Vladimir State University

Building an approach to description of digital images, based on analysis of impact behavior of feature’s group at image sequence is the aim of this article.

An image is the function f(x,y), defined at subset Р of R2 plane, which can possess only real values.

Suppose, that each image f can be characterized by finite set of features, which unambiguously defines f at set of all images that belongs to Р.

Define a sequence of images {f_n} as ordered set of images f, {f_n}={f₀, f₁,… f_n}. (1)

Because each image of source set f unambiguously characterized by set of features X, sequence identity to (1) can be created {X_n} = {X₀, X₁, X_{2 …}}.

Consider an sequence, which consists of elements {X_n}, which defines the same feature (for example, i-th feature) for all images of source sequence {x⁽ⁱ⁾_n} = {x₀⁽ⁱ⁾, x₁⁽ⁱ⁾,… x_n⁽ⁱ⁾}.

Introduce an operator of feature membership, which defines a level of feature entering x⁽ⁱ⁾ into fuzzy set Х⁽ⁱ⁾, that is degree of conformity of some feature realization at image sequence to it limit (standard) value _i : _i[x_j⁽ⁱ⁾][0,1].

Then to each set of feature Х_j of image f_j{f_n} can be established vector Х_j = (₁х₁, ₂х₂, .. _kх_k )^Т, where к – amount of features.

The curve of feature x(i) distribution at image sequence {f_n} denote an graph of function _i(j)  _i[x_j(i)], which takes discrete values at points j{0,1,..n}.

Hence will be consider, that image f, can be characterized not only by the set of features Х, but features of mutability of this feature at image sequence, which is result of applying repeatedly many of T, to analyzed image. At the same time, the same feature, consilient for two different images, by virtue of different nature of heredity and mutability, will have different behavior at this sequences.

The literature

Zhiznjakov A.L., Sadykov S.S.,Gai V.E. Analysis of impact behavior of feature’s group at image sequence. 9^th International Conference “Pattern Recognition and Tmage Analysis: New Information Technologies” (PRIA-9-2008): Conference Proceedings. Vol.2.-Nizhni Novgorod, 2008.-404 p.(pp.365-366)




Цифровая обработка изображений микроциркуляторного русла

Кузнецов И.А., Грибов Е.Н.

Томский государственный университет систем управления и радиоэлектроники

В области медицины цифровая обработка изображений стала ядром цифровых медицинских диагностических систем, позволяющих повысить качество диагностики. Медицина сегодня является высокотехнологичной отраслью. Одна из важнейших задач современной медицины является разработка эффективных методик ранней диагностики различных патологий. Инновационные медицинские разработки в целом характеризуют важную тенденцию, заключающуюся в изменении парадигмы современной медицины. Из лечебной она превратится в профилактическую и далее - прогностическую. Намечен переход от модели «жалоба-диагноз-лечение» к модели «диагностика-прогноз-профилактика» [1].

В Томском государственном университете систем управлении и радиоэлектроники, на кафедре телевидения и управления ведется работа по созданию цифровой медицинской диагностической системы для конъюнктивальной биомикроскопии. Оценка состояния микроциркуляторного русла по изображению бульбарной конъюнктивы (БК) является сегодня перспективным направлением в связи с неинвазивностью и оперативностью обследования [2].

Данная статья посвящена результатам работы по созданию программного обеспечения для цифровой медицинской диагностической системы, использующейся в данный момент в клинической практике ГУ НИИ кардиологии ТНЦ СО РАМН. Работа ведется коллективом аспирантов под руководством доцента Дементьева А.Н. и разделена на задачи. Первая задача заключается в том, что для изучения микроциркуляторного русла и определения параметров сосудов необходимо подготовить изображение сосудистой сети с помощью адаптивных алгоритмов, которые в данном случае являются наиболее перспективными. Вторая задача заключается в измерении параметров сосудов БК по изображению, прошедшему предварительную обработку и реализации алгоритмов бинаризации и скелетизации.

Алгоритм предварительной обработки БК включают в себя следующие основные этапы:

• Регистрация изображения в формате *bmp.
  
• Преобразование цветного изображения в монохроматическое.
  
• Обработка сосудистой сети с помошью алгоритма с адаптивным порогом.
  
• Бинаризация изображения
  
• Обработка изображения БК адаптивным алгоритмом шумоподавления.
  

Для более детального изучения микроциркуляторного русла БК используется видеорегистрация с большим увеличением. Результатом видеорегистрации является изображение БК в *.BMP-формате.

Простейший из методов пороговой обработки состоит в автоматическом выборе порога по яркости (нахождении среднеарифметического значения яркости) изображения или в его определении его на основании визуального изучения гистограммы значений яркости изображения бульбарной конъюнктивы [3].

Анализ полученных результатов показал, что при выставлении глобального порога происходит достаточно большая потеря сосудов, остается фон - значения яркости, которые также удовлетворяют глобальному порогу. Оставшийся фон далее трудно обработать, т.к. он имеет схожие с сосудами значения яркости. При последующей бинаризации и скелетизации будет трудно получить правильный скелет сосудистой сети БК. Используя данный алгоритм невозможно эффективно обработать изображение с помощью единого глобального порога.

В такой ситуации необходимо применить подход, при котором исходное изображение разбивается на подобласти, в каждой из которых используется свое значение порога. Поскольку порог, применимый для пикселя, оказывается зависящим от характеристик подобласти изображения, содержащей данный пиксель, такое преобразование коэффициента фильтрации является адаптивным [3]. Разработанный алгоритм позволяет считать среднее значение яркости для каждой подобласти разбиения, которое далее задается как локальный порог. Данный алгоритм позволяет выделить все сосуды как те, которые имеют большое значение яркости и поэтому не могли быть выделены при обработке алгоритмом с глобальным порогом, так и те, которые имеют малое значение яркости (и были выделены при глобальном пороге) и выглядят черными на рисунке1 (а). Недостаток этого алгоритма заключается в том, что в подобластях, где обработка дала неверный результат, доля точек фона расположена группами пикселей с нулевым значением яркости. Для удаления больших групп пикселей используется адаптивный алгоритм шумоподавления, основанный на расширении маски фильтра, что позволяет работать с объектами разного размера. Результаты работы алгоритма с глобальным порогом по яркости и двух адаптивных алгоритмов представлены на рисунке 1.



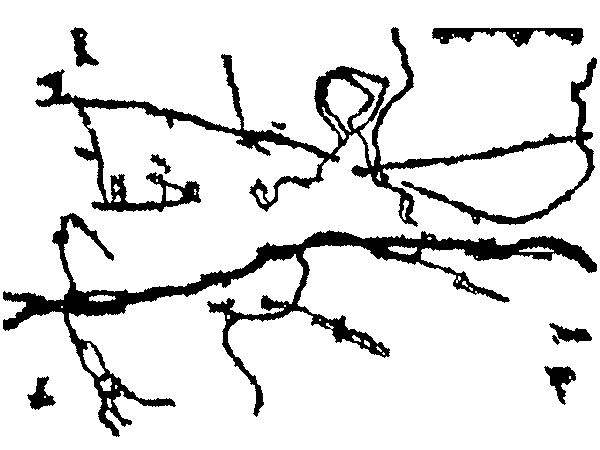
а) б)

Рис. 1 – Результат обработки чёрно-белого изображения бульбарной конъюнктивы с помощью алгоритма с глобальным порогом по яркости (а) и с помощью алгоритма с адаптивным локальным порогом по яркости и адаптивным алгоритмом шумоподавления (б)


Анализируя результаты работы двух адаптивных алгоритмов, видим, что сохранена целостность сосудов и сведена к минимуму потрея сосудов. Изображение бульбарной конъюнктивы подготовлено для скелетизации и измерения параметров сосудов. Адаптивный алгоритм позволил выделить сосуды, имеющие разные значения яркости за счет изменения параметров фильтра в зависимости от средних значений яркости областей.

На следующем этапе работы по проекту был разработан ряд алгоритмов, которые позволяют по подготовленному изображению (прошедшему процедуры адаптивной фильтрации) измерить параметры сосудов в пикселях цифрового изображения: длина, ширина, извитость, неравномерность и т.д. [4]. При известном масштабе фотоснимка есть возможность пересчитать значения параметров сосудов из пикселей в единицы системы СИ.


Алгоритм подсчета площади занимаемой сосудами.

Алгоритм подсчета площади занимаемой сосудами достаточно прост. После фильтрации на бинаризованном изображении все чёрные пиксели (пиксели с нулевой яркостью) принимаются за сосуды, а все белые (пиксели с максимальной яркостью) – за фон. Для того чтобы посчитать площадь всех сосудов в таком случае необходимо подсчитать количество пикселей с нулевой яркостью. Пример изображения, по которому измеряется площадь сосудов, представлен на рисунке 1 (б).

Алгоритм скелетизации изображения сосудистой сети бульбарной конъюнктивы.

Важным для практики является подход, в котором представление формы плоской области строится путем сведения ее к графу. Такое сокращенное представление можно получить, выделяя остов этой области с помощью алгоритма утончения (этот процесс иначе называют скелетизацией). Процедуры утончения занимают центральное место в широком классе прикладных задач обработки изображений, от автоматического контроля печатных плат до подсчета волокон асбеста в воздушных фильтрах [3].

На рисунке 2 (а) приведен результат работы алгоритма скелетизации сосудистой сети бульбарной конъюнктивы, полученный после обработки изображения, представленного на рисунке 1 (б).



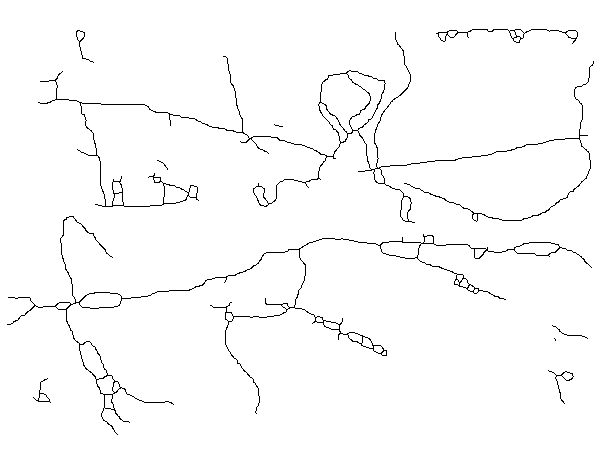
а) б)

Рис. 2 - Изображение сосудистой сети БК после обработки алгоритмом скелетизации (а) и участок картированного скелетизованного изображения (б)


На рис. 2 (б) представлена одна из областей элементов матрицы значений яркости. Значению «0» соответствует белый цвет (фон), а значению «1» - черный цвет (сосуды). Каждому сосуду с помощью алгоритма картирования скелетизованного изображения БК присваиваются индивидуальный номер, по которому его можно легко отследить, просматривая матрицу отсчетов яркости бинаризованного изображения. Все пиксели со значением «1» заменены на индивидуальные номера сосудов и представляют собой последовательности цифр на рис. 2 (б).

Алгоритмы измерения параметров сосудистой сети бульбарной конъюнктивы.

Измерение длины сосудов осуществляется по скелетизованному изображению БК (см. рис. 2(а)). Для того чтобы измерить общую длину сосудов, достаточно подсчитать количество ненулевых элементов на скелетизованном изображении БК.

Однако, для того, чтобы измерить длину отдельных сосудов, необходимо картировать скелет БК, т.е. присвоить каждому сосуду свой отличительный признак. Разработанный алгоритм измерения длины сосудов позволяет присвоить каждому сосуду свой номер и, фактически, сделать его уникальным (рис. 2(б)).

Алгоритм измерения ширины сосуда тесно связан с алгоритмом измерения длины сосудов, а точнее с алгоритмом предварительного картирования. Основная идея состоит в том, чтобы двигаясь по картированному скелетизованному изображению измерять ширину на нескелетизованном изображении.

Анализ полученных результатов обработки тестового изображения разработанными алгоритмами показал высокую точность измерения параметров сосудов. Погрешность измерения параметров сосудов зависит от исходного изображения (изображения после обработки алгоритмами фильтрации) и не превышает 3-5%.

В ходе проделанной работы были также разработаны алгоритмы, позволяющие измерить такие параметры изображения как общую площадь сосудов, количество сосудов, общую длину и среднюю для всего изображения ширину сосудов.

Для работы с алгоритмами и просмотра результатов создан пользовательский интерфейс в интегрированной программной среде Delphi 7.0 Studio, написанный на языке Object Pascal [5]. Программа внешне ничем не отличается от тех приложений, с которыми привык работать пользователь в Windows OS. Пользователь имеет возможность одновременно видеть исходное изображение бульбарной конъюнктивы и обработанное изображение, а также измеренные параметры сосудов и другие аналитические данные.

В качестве следующих шагов в рамках проводимой работы предполагается усовершенствование алгоритмов адаптивной фильтрации и картирования, обработка цветных изображений, увеличение скорости работы программы, переход к измерению параметров сосудов непосредственно в системе СИ, создание библиотеки с разработанными алгоритмами (для патентования), увеличение количества измеряемых параметров.

Литература

1. Точное измерение жизни ссылка скрыта
   
2. Дементьев А.Н.
   
3. Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М.: Техносфера, 2005 г. – 1072 с. ISBN 5-94836-028-8.
   
4. Е.Э. Константинова, Л.А. Иванова. Метод количественной и качественной оценки изображений бульбарной конъюнктивы в диагностике состояния микроциркуляции при сердечно-сосудистой патологии. Инструкция по применению. Республиканский научно-практический центр «Кардиология».
   
5. Архангельский А.Я. Программирование в Delphi 7. – М.: ООО «Бином-Пресс», 2003 г. – 1152 с.: ил.
   

Digital image processing of microcirculation images

Kuznetsov I., Gribov E.

Tomsk state university of control systems and radioelectronics

In modern theoretical and clinical medicine a problem of microcirculation analysis has a one of main places. At present possibilities of noninvasive analysis of conjunctiva microcirculation are expands. At the same time with digital and analog technique development broad possibilities of visualization and qualitative conjunctiva images acquisition has appear. These images allow realizing an automatic complex diagnostics of conjunctiva. An area of biomedical imaging technologies was recently added to the European Roadmap as one of prospective areas.

At the first step of working with conjunctiva digital images there was a problem with noise reduction in images, i.e. a digital filtering was required. In the framework of this task a sequence of algorithms was developed and tested. This sequence contains both standard single-point and multi-point noises reduction algorithms and unique adaptive filtering algorithms. An adaptability of complex filtering algorithms was provided by image segmentation operating and by vasculature images features.

Using of algorithm sequence result in images which contains vessels of conjunctiva with low portion of noises. Algorithms had been tested with bank of colored and black-and-white images. Results of testing were satisfied and acceptable for further image processing and conjunctiva vessels parameters measurement.

Next stage of project was conjunctiva vessels parameters measurement automation. Solving this problem a series of auxiliary algorithms was developed. Particularly, an algorithm which allows mapping of vasculature was developed. This algorithm assigns an individual number to each vessel. After that a possibility of vessels parameters measurement has appears. Then tables with information about parameters of every vessel can be received.

At the end, algorithms of vessels length and width measurement, total vessels area counting, middle length and middle width of all vessels calculation were developed.




вейвлет сжатие и нелинейная обработка неподвижных цифровых изображений с использованием оптимального базиса класса добеши на каждой ступени разложения

Кириллов С.Н., Косткин И.В.

Рязанский государственный радиотехнический университет

390005 г. Рязань, Гагарина 59/1

Введение. В настоящее время значительно возрос интерес к различным алгоритмам сжатия изображений. Это связано с развитием таких отраслей науки и техники как исследование дальнего и ближнего космоса, компьютерная графика, правоохранительная деятельность и др., где информация имеет характер монохромного изображения. При этом различные снимки приходиться хранить и передавать по каналам связи[1]. Однако в ряде практических задач изображения содержат шумы, связанные как с внутренними физическими явлениями внутри аппаратуры регистрации, так и с внешним неблагоприятном воздействием. Очевидным решением в этом случае является предварительная фильтрация зашумленного изображения, но это в свою очередь ведет к дополнительным вычислительным затратам и потери части информации изображения в результате фильтрации. Поэтому необходимо применять различные эффективные алгоритмы совместной нелинейной обработки и сжатия данных, с целью снижения вычислительных затрат, а также экономии места на физических носителях информации и снижения требований к используемым каналам связи.

Обобщенно сжатие изображений можно представить в виде трех основных этапов: – декоррелирующего преобразования, процедуры квантования и энтропийного кодирования [1].

Одним из первых стандартов сжатия изображений с потерями является стандарт JPEG[1,2], использующий в качестве декоррелирующего преобразования дискретное косинусное преобразование. В 2000 году предложен новый стандарт сжатия цифровых неподвижных изображений JPEG 2000[2], где в качестве декоррелирующего преобразования используется вейвлет разложение. Данный стандарт позволяет сжимать изображения от 2 до 200 раз без заметной потери в качестве. Однако указанные алгоритмы не предусматривают возможности одновременной нелинейной обработки и сжатия цифровых изображений. В связи с этим возможна модификация алгоритма стандарта JPEG 2000, когда ведется адаптивная обработка коэффициентов ВПР в зависимости от зашумленности снимка. Ранее в целях увеличения коэффициента сжатия в [2] был получен вектор оптимальных базисов класса Добеши на каждой ступени разложения. Дополнительно для уменьшения влияния шума необходимо определить оптимальную функцию трешелдинга коэффициентов ВПР, обеспечивающих наибольший коэффициент сжатия при максимально возможной степени подавления шума.

Описание алгоритма. Исследования предлагаемого метода сжатия проводилось на изображениях в градации серого 0…255. В результате исследований был предложен алгоритм поиска оптимальной функции трешелдинга при использовании вейвлет-сжатия на основе оптимального базиса на каждом уровне ВПР [2]. В целом предлагаемый алгоритм состоит из следующих этапов:

1. В соответствии с рекомендациями [2] выполняется пятиуровневое вейвлет преобразование сигнала с использованием своего базиса Добеши 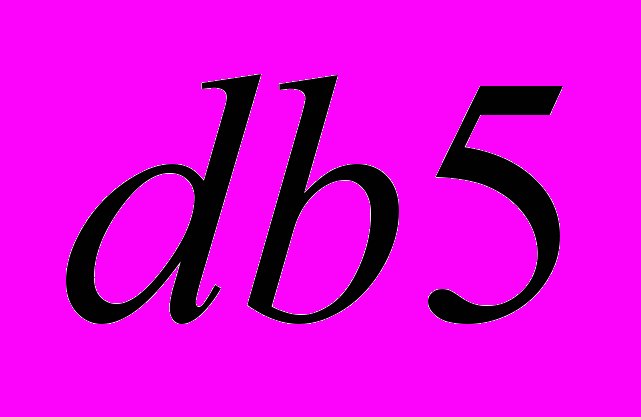, , 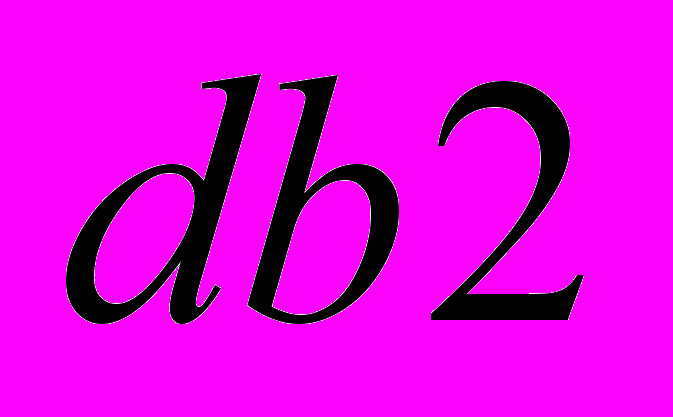, , 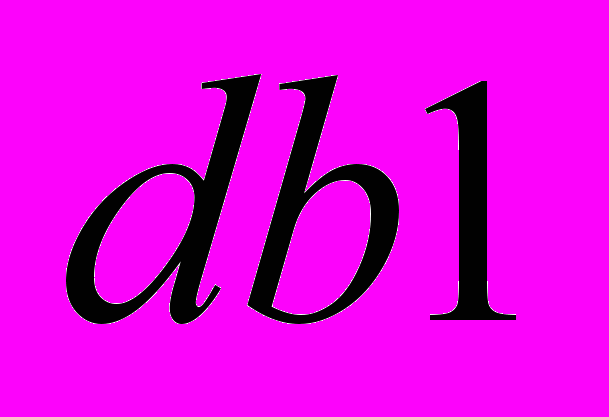, 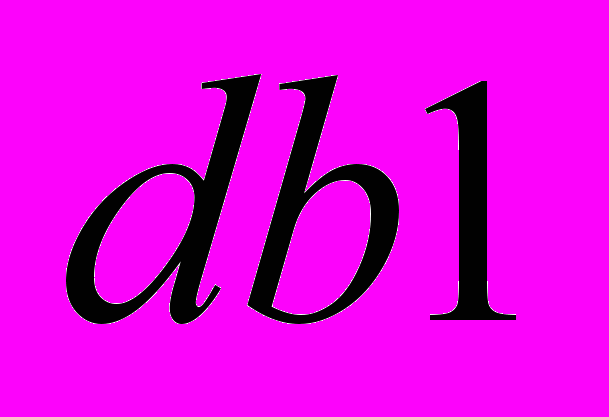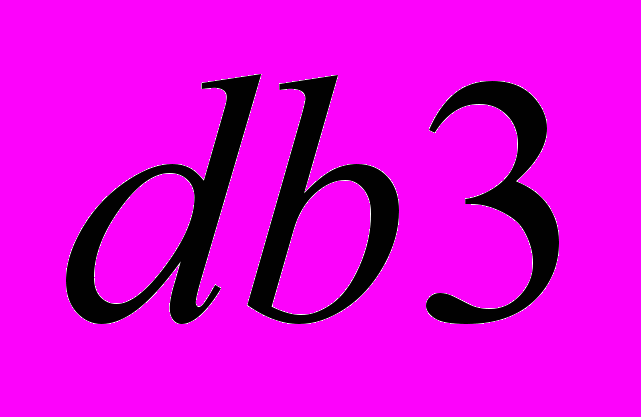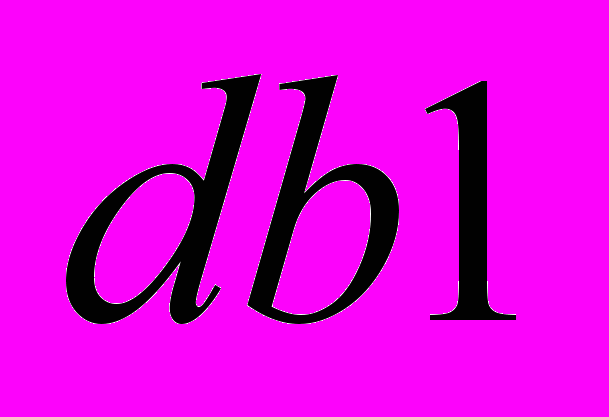на каждом уровне разложения соответственно: , (1), где 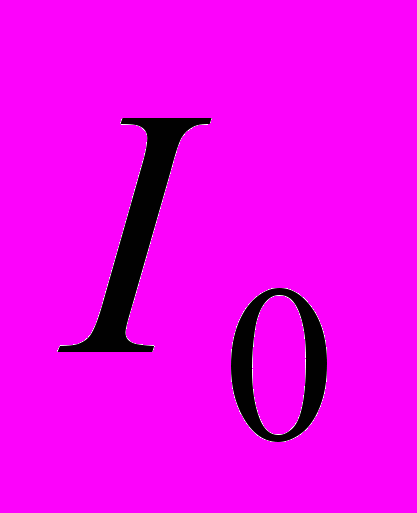- исходное изображение, - результат пятиуровнего вейвлет разложения, - базис, применяемый на i-ой ступени вейвлет разложения.
   
2. Оценивается величина дисперсии коэффициентов ВПР в каждой из ветвей.
   
3. Задается уровень визуального качества восстановления отфильтрованного цифрового снимка .
   
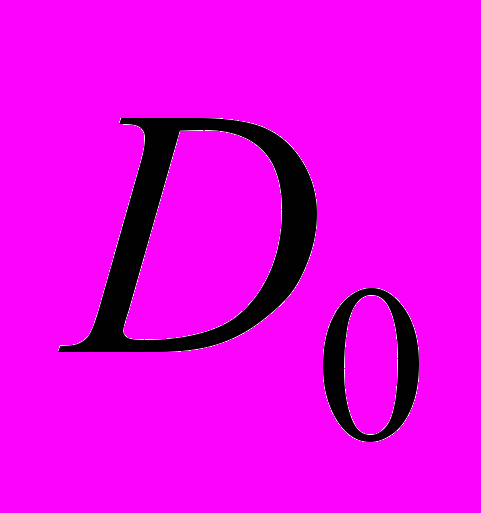4. Выбирается соответствующая 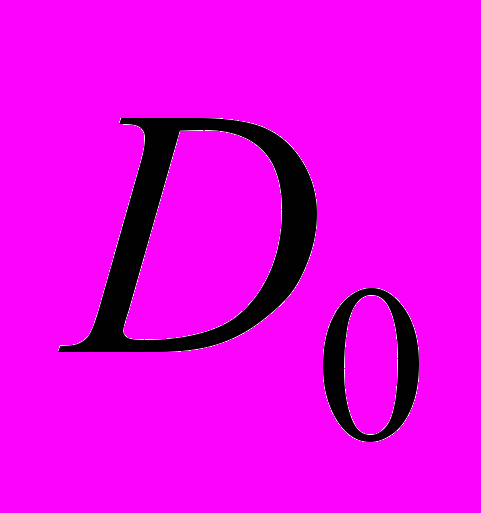зона нечувствительности в районе нуля в полученной функции трешелдинга.
   
5. На основе статистических данных о дисперсии распределения коэффициентов ВПР в соответствующих ветвях для каждой ветви строятся функции трешелдинга, которые представляют собой функции градационного преобразования для приведения коэффициентов ВПР к заданному виду распределения. Причем указанная обработка ведется на первых двух уровнях ВПР, для того чтобы не затронуть более значимые коэффициенты, которые не поддаются жесткому статистическому описанию. Функция трешелдинга строиться на основе алгоритмов преобразования данных к заданному закону распределения. В начале исходное распределение преобразуется в равномерное, после чего из равномерного получается требуемый закон распределения. Две указанные операции функционального преобразования можно объединить в одно, что позволяет получать разнообразные функции преобразования вейвлет-коэффициентов.
   
6. Преобразуется полученная на шаге 3 матрица коэффициентов 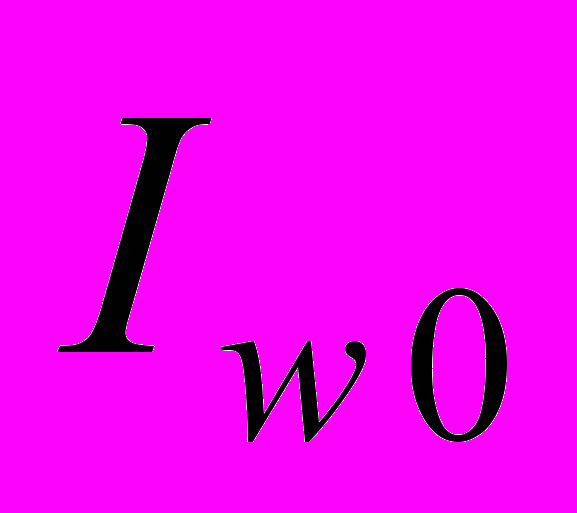в матрицу строку путем построчного считывания.
   
7. Применяется к полученной строке алгоритм кодирования длин серий. В рассматриваемом случае, аналогично стандарту JPEG, самым часто встречающимся символом признается 0, поскольку происходит обнуление коэффициентов вейвлет преобразования (2). Элемент кодируемой последовательности представляется в виде пары чисел, где первое число указывает на количество нулей, которые необходимо вставить за значащим элементом, а второе число является значащим элементом.
   
8. Применяется к полученной на шаге 5 строке алгоритм кодирования Хаффмана, причем анализируются не полученные пары чисел, а каждое число в отдельности. Алгоритм Хаффмана был выбран потому, что он гарантирует получение коэффициента сжатия больше или равного 1, в то время как остальные методы сжатия данных без потерь такой гарантии не дают[1]. Принцип его функционирования состоит в следующем: анализируются вероятности появления каждого символа сжимаемой последовательности и символам с наибольшей вероятностью присваивается код наименьшей длины, при этом создается таблица кодов для всех символов кодируемой последовательности.
   

Экспериментальные исследования. Результат работы указанного алгоритма представлен на рис. 1, который представляет собой зависимости пикового отношения сигнал-шум (PSNR) восстановленного после компрессии изображения от коэффициента сжатия исходного зашумленного изображения, где зависимость 1 – результат работы предложенного алгоритма, а зависимость 2 – результат работы известного алгоритма сжатия.

Из анализа приведенной зависимости следует, что использование алгоритма одновременной фильтрации и сжатия позволяет получить более высокое значение PSNR, по сравнению с известным вейвлет-сжатием, однако при значениях коэффициента сжатия более 16 раз, алгоритмы дают приблизительно одинаковый результат, что объясняется более сильными искажениями вносимыми в результате сжатия цифрового изображения.

Таким образом, показано преимущество предложеного алгоритм совместной нелинейной обработки и сжатия неподвижных цифровых изображений с применением вейвлет преобразования на основе вектора оптимальных базисов класса Добеши на каждом уровне разложения, обеспечивающих максимальный коэффициент сжатия при наибольшем подавлении шума по сравнению с известными алгоритмами компрессии цифровых снимков.



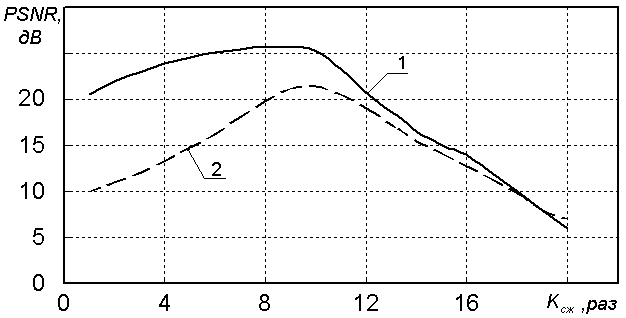
Рис. 1

Литература

1. Р. Гонсалес, Р. Вудс. Цифровая обработка изображений. М.: Техносфера, 2006г. 1072 с.
   
2. Кириллов С.Н. Косткин И.В. Алгоритм сжатия цифровых изображений с использованием синтезированного базиса на каждой ступени вейвлет-пакетного разложения // Доклады 10-й Международной конференции «Цифровая обработка сигналов и ее применение» Москва, 2008. Т.2. С. 480-483.ЦОС.
   
3. Блаттер К. Вейвлет анализ. Основы теории. М.: Техносфера. 2004.280с
   

SIMULTANEOUS VEYVLET-FILTERING And COMPRESSION of the STILL DIGITAL IMAGES With USE the OPTIMUM BASIS FOR EACH STEP of the DECOMPOSITION

Kirillov S. Kostkin I.

Ryazan state radioengineering university

In row of the practical problems images haves noise connected with internal physical phenomenas inside registration equipments Preliminary filtering noise images is evident decision in this case, but it provide to additional calculating expenses and loss of the part of image information in filtering result. So, you necessary to use different efficient algorithms to joint filtering and compressions data.

This standard allows compressing the images from 2 before 200 once without observable loss qualitative. However, these algorithms do not provide simultaneous filtering and compressions digital images. In this connection possible modification of the algorithm of the standard JPEG 2000, when it is doing adaptive processing a WPT factors depending on extent of the noise in the picture. This allows defining optimum threshold function for WPT factors, which providing maximum of the compression factor with best extent of the noise suppression.

This method of the compression was studied in grey gradations 0…255. As a whole proposed algorithm consists of the following stage:

1. Five level wavelet transformation of the signal is executed with use of its base Dobeshi 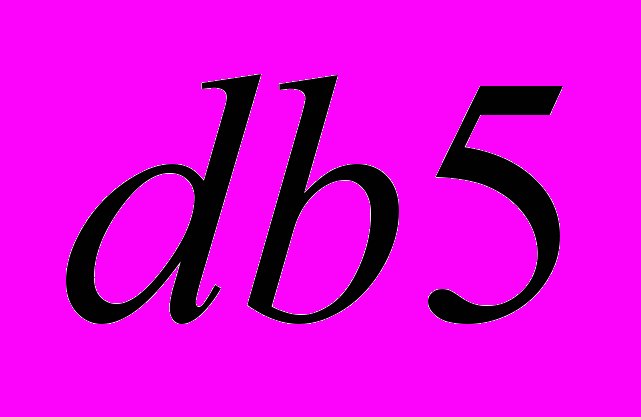, , 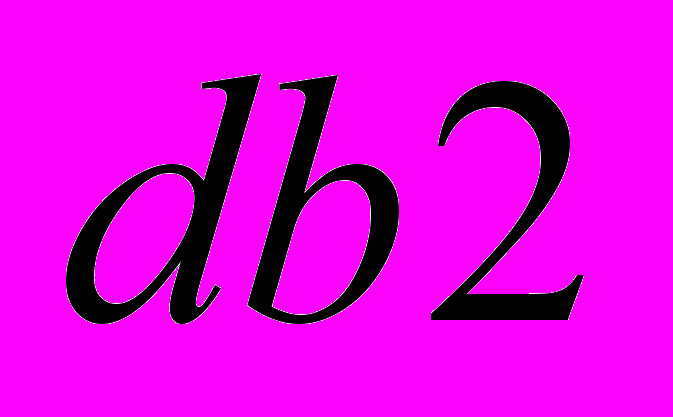, , 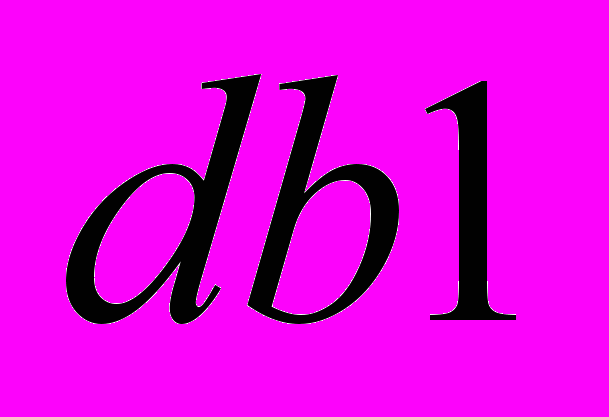, 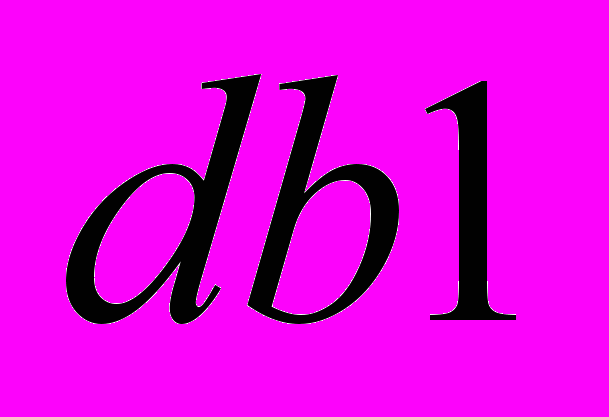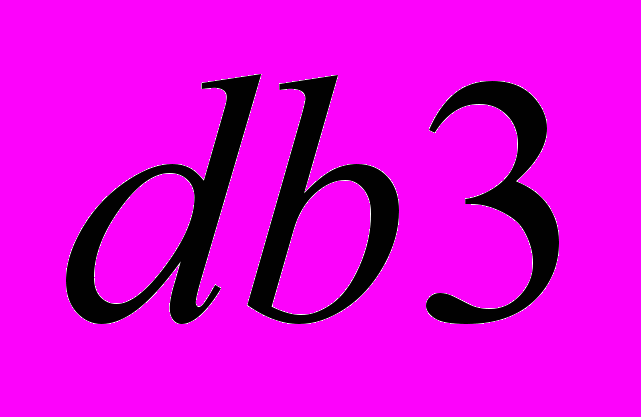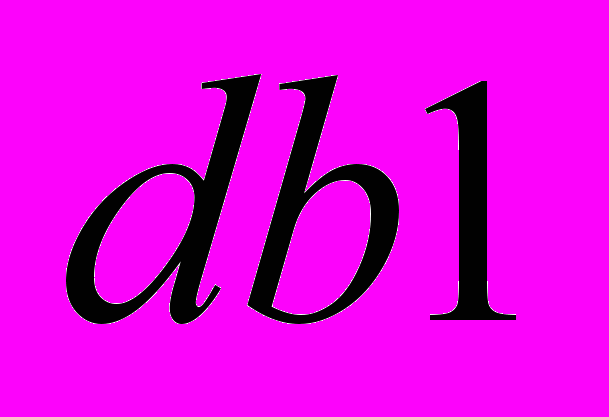on each level respectively.

2. It Is estimated value to dispersions factor WPR in each of branches.

3. Threshold function are built for each branch.

4. It is assigned level visual quality, which images will be restored after decompression, by change value threshold level.

5. It is zeroized all factors wavelet transformations, if their module is less or given value threshold level.

6. It is got on the step 3 matrixes factor are converted to matrix line by the way of the row wise sensing.

7. To get line it is use algorithm of the lengths series coding.

8. To get on step 5 data it is use algorithm of the Huffman coding.

Thereby, it is designed new algorithm of the compression still digital image with using joint wavelet filtering and compressions data with use the optimum base on each level wavelet transform, which providing maximum of the compression factor with best extent of the noise suppression.




СЕМАНТИЧЕСКОЕ СЖАТИЕ ВИДЕОПОСЛЕДОВАТЕЛЬНОСТЕЙ С ДВИЖУЩИМИСЯ ТРАНСПОРТНЫМИ СРЕДСТВАМИ

Кузьмин С.А.

Санкт-Петербургский Государственный Университет Аэрокосмического Приборостроения

Системы видеонаблюдения получают все более широкое распространение в связи с удешевлением и повышением производительности аппаратных средств. При этом объемы видеоинформации, которые необходимо оцифровать и передать потребителю, резко возрастают с увеличением количества используемых камер, разрешением кадра, частотой съемки. Например, для передачи несжатой видеопоследовательности кадров размером 720х576 пикселей с частотой 25 кадров в секунду, при условии, что используются 3 канала изображения, квантованные на 256 градаций яркости, требуется канал с пропускной способностью 29,6 МБ/сек. Конечно, оптико-волоконные линии способны пропускать большие объемы информации, но ведь их использование не всегда целесообразно. Поэтому актуальной является задача сжатия видеоинформации, передаваемой от камер наблюдения к конечному потребителю. При этом сжатие не должно сильно ухудшать качество видеоинформации, чтобы потребитель мог принимать верные решения.

Рассмотрим случай наблюдения потока транспортных средств, движущихся по шоссе в поле зрения камеры. Цели наблюдения могут быть разные (коммерческий осмотр и подсчет, классификация и подсчет транспортных средств для различных городских служб, распознавание номерных знаков для силовых структур), но суть одна и та же: передать исходную информацию от видеокамер наблюдения и извлеченную из видеопотоков семантику (результат анализа видеоинформации некими алгоритмами).



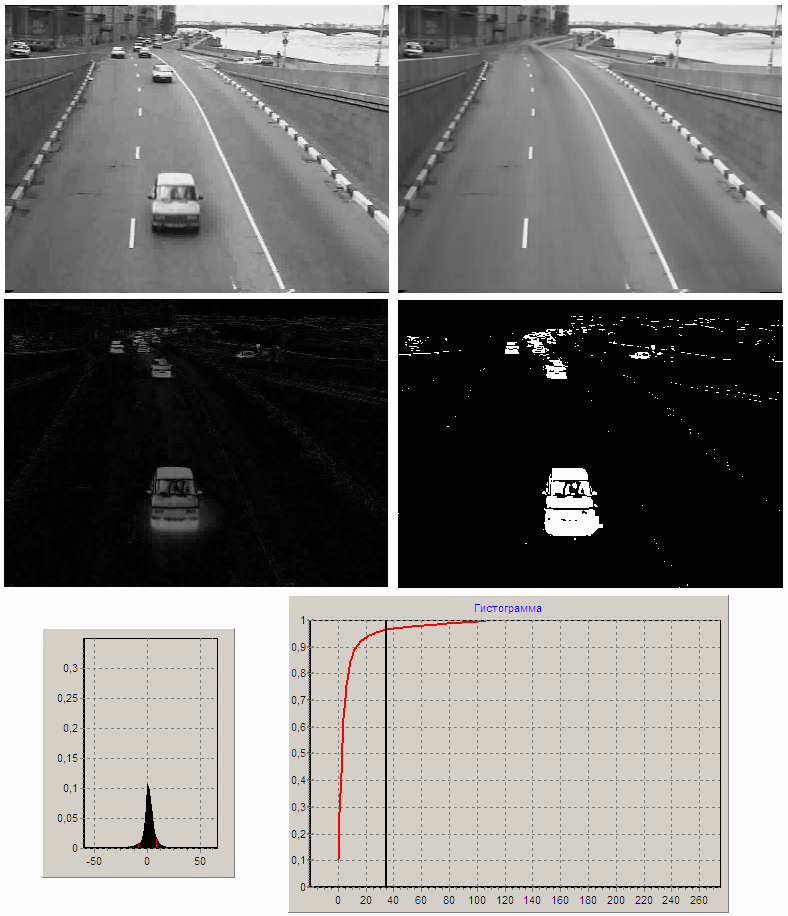
Рис. 1. Установка порога бинаризации разностного изображения на основе определения момента перехода на горизонтальный участок функции распределения яркости в изображении


В данной задаче камера является неподвижной относительно трассы, что позволяет применить для анализа видеоинформации метод вычитания оценки фона из кадра. Отделить объекты от фона можно, если известны модели объектов или модель фона, но разнообразие транспортных средств не позволяет задавать некие яркостные эталонные описания, в то время как фоновая составляющая сцены может быть оценена. Таким образом, на основании кадров видеосъемки наблюдаемого участка магистрали строится попиксельная модель фона. Способов построения оценки фона много: от простого усреднения во времени до представления модели фона как совокупности нескольких распределений яркости (смеси гауссианов). По результатам исследований в качестве метода оценки фона был выбран вариант адаптивного взвешенного суммирования, известный как фильтр Калмана. Его преимущество надо остальными алгоритмами заключается в малых требованиях к объему памяти при высоком качестве формируемой модели фона. Суть работы фильтра Калмана сводится к взвешенному суммированию имеющейся оценки фона в пикселе и значения яркости пикселя в текущем кадре. Сумма весовых коэффициентов равна единице. Если яркость пикселя в текущем кадре сильно отличается от имеющейся оценки фона, то вес имеющейся оценки при взвешенном суммировании будет значительно больше веса яркости пикселя в текущем кадре. Таким образом формируется значение новой оценки фона.

Движущиеся транспортные средства имеют высокий контраст относительно фона, что и позволяет при сформированной оценке фона производить сегментацию видеокадров. Под сегментацией в данном случае подразумевается принятие для каждого пикселя решения об его принадлежности к одному из классов: не фон (объект, тень), фон. Результатом работы алгоритма вычитания оценки фона из кадра является бинарное изображение, называемое изображением «движущихся областей». На основании изображений оценки фона и текущего кадра также формируется бинарное изображение «движущихся контуров»[1]. При переводе разностных изображений (изображений разности кадра и оценки фона, изображений разности контурных препаратов кадра и оценки фона) в бинарный вид используется оригинальный алгоритм, заключающийся в обнаружение момента перехода на горизонтальный участок функции распределения яркости в изображении (рис.1). Изображения движущихся областей и движущихся контуров после шумоподавления объединяются с помощью операции «ИЛИ». Полученное изображение обрабатывается набором ранговых фильтров (медианными фильтрами, операторами «псевдонаращивания» и «псевдоэрозии» [2]).

Возможность для сжатия как раз связана с характером видеопоследовательности: есть быстро меняющие положение автомобили и есть практически неизменная на коротком временном отрезке фоновая составляющая сцены, представляемая оценкой фона. Таким образом, информация об движущихся объектах (динамической составляющей) должна передаваться очень часто, в то время как оценку фона можно обновлять время от времени (например, раз в 10-15 минут). Итак, есть движущиеся области на передающей стороне и оценка фона на передающей стороне. На приемную сторону передается изображение оценки фона, на которое в дальнейшем производится вкрапление движущихся объектов с помощью операции матирования. Под матированием понимается способ объединения информации из нескольких изображений с использованием альфа-канала. При этом битовая плоскость, представляющая альфа-канал, является своеобразным триггером, пропускающим яркость пикселей одного из объединяемых изображений в итоговое изображение в случае определенного значения показателя прозрачности альфы, и непропускающим яркость второго изображения в этом же случае.

Рассмотрим пример операции матирования (рис. 2): ,

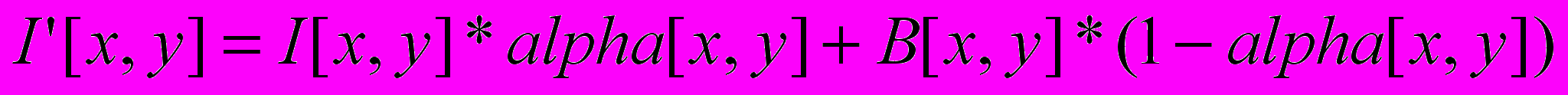где 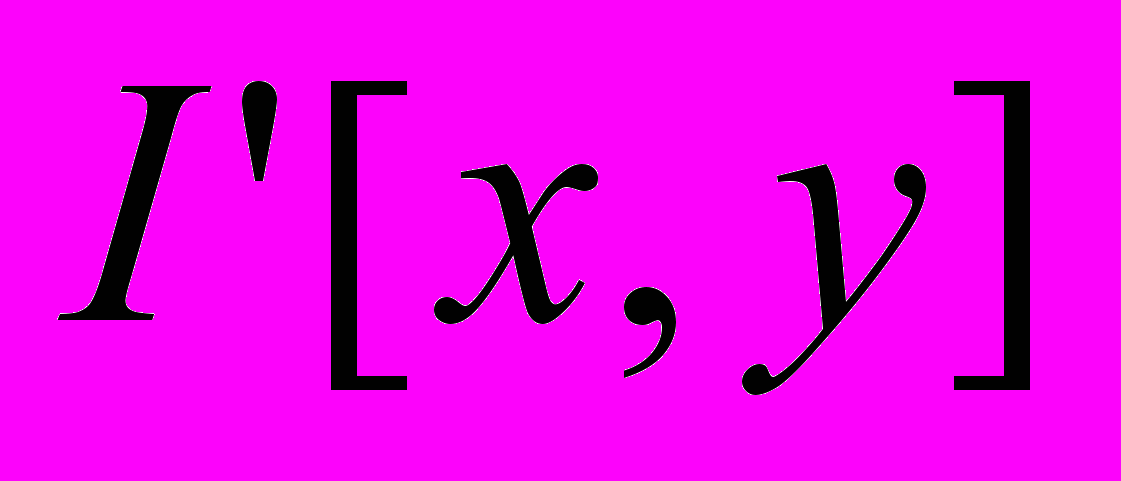– яркость пикселя с координатами [x,y] цветного изображения, синтезированного на основе двух кадров и альфа-канала; 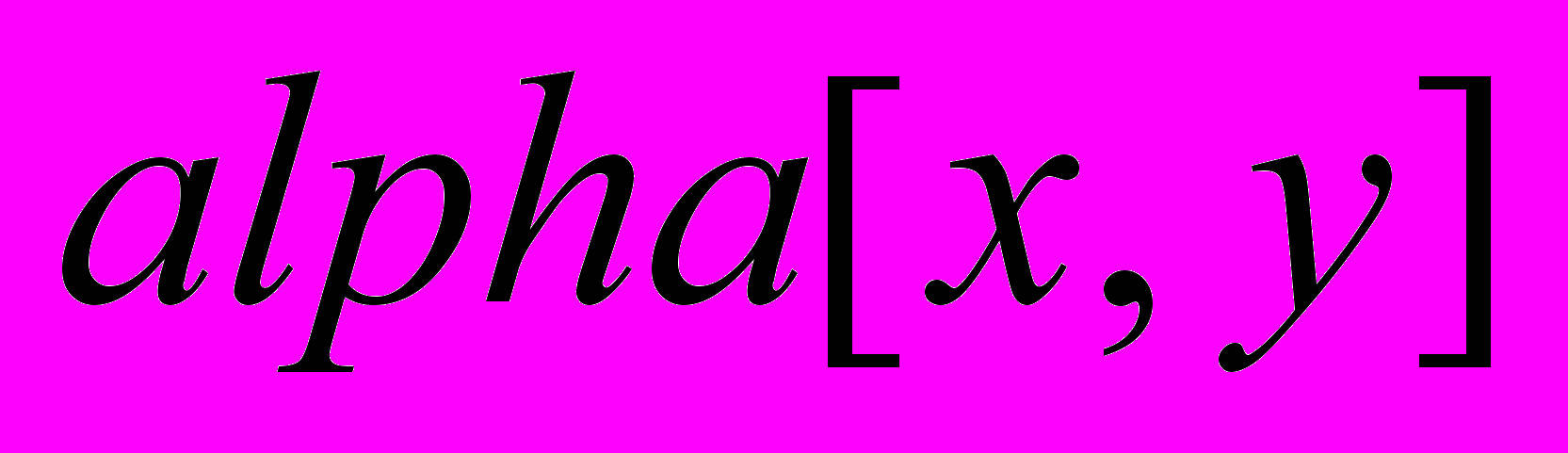– яркость пикселя с координатами [x,y] однобитного (бинарного) изображения альфа-канала; 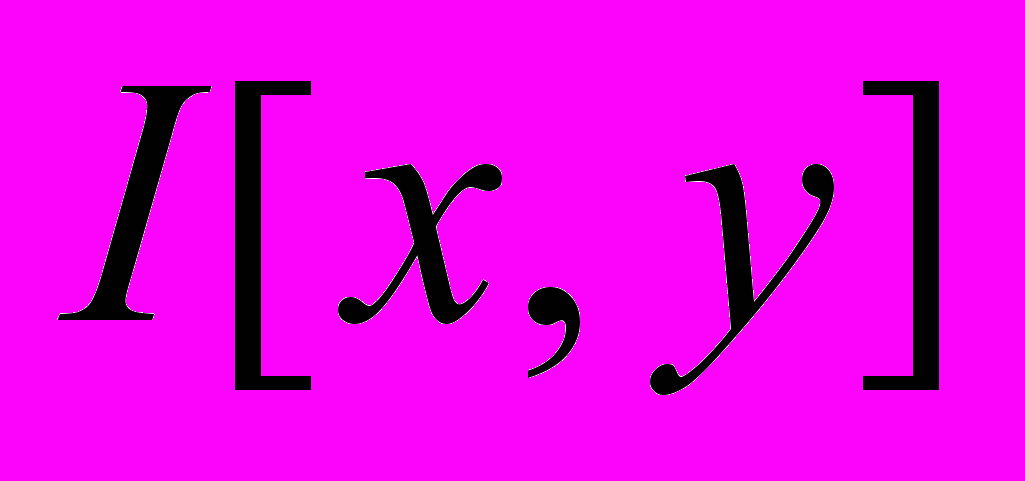– яркость пикселя с координатами [x,y] цветного изображения, поступающего от камеры; 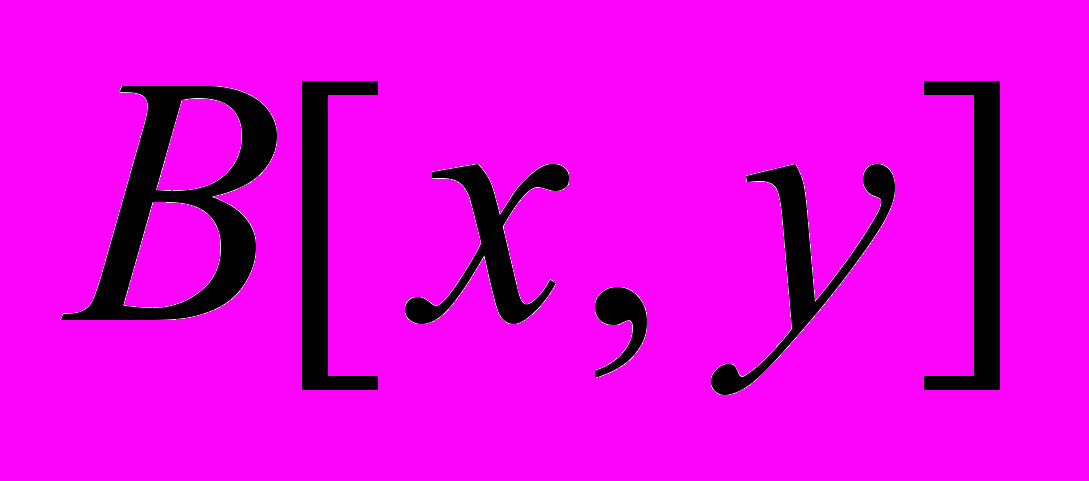– яркость пикселя с координатами [x,y] цветного изображения оценки фона.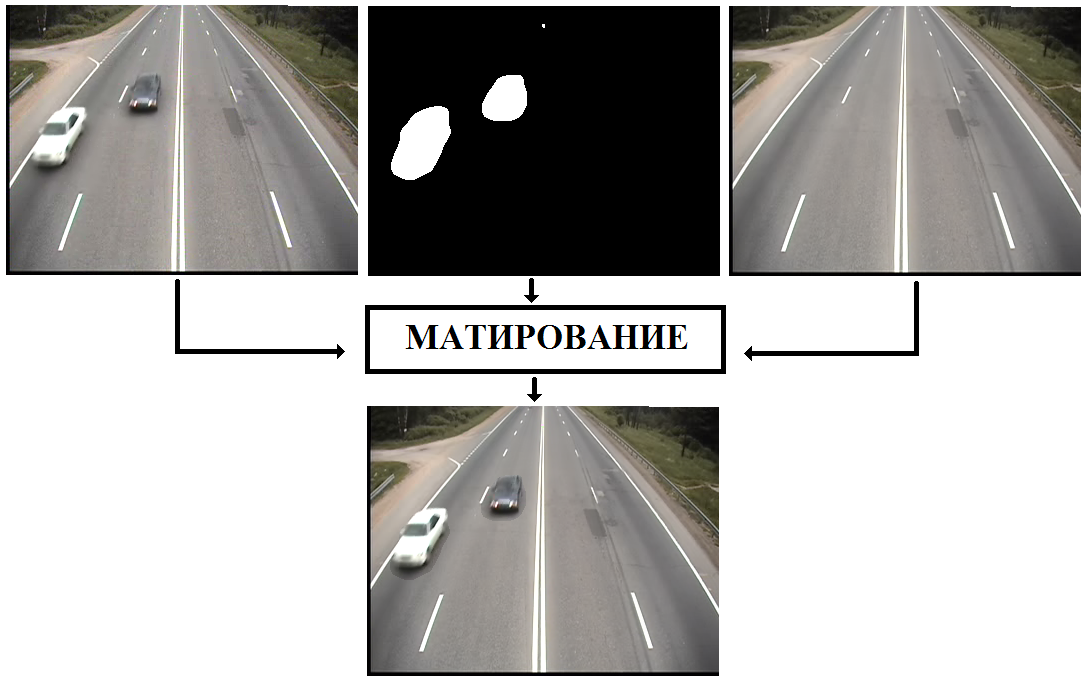



Рис. 2. Пример операции матирования. В качестве альфа-канала выступает изображение с движущимися объектами. Изображение оценки фона получено с помощью попиксельного применения Калмановской фильтрации видеопотока в направлении оси времени


На бинарном изображении альфа-канала доля белых пикселей от площади изображения составляет всего пять процентов, т.е. яркости большинства пикселей кадра незначительно отличается от яркостей пикселей изображения оценки фона и не представляют для нас никакого интереса. Представляется возможным передавать изображение только тех участков текущего кадра, которые в результате операции матирования, были бы включены в синтезированное изображение (рис. 3). Таким образом, передачей только динамической составляющей сцены можно получить сжатие объема видеопотока в 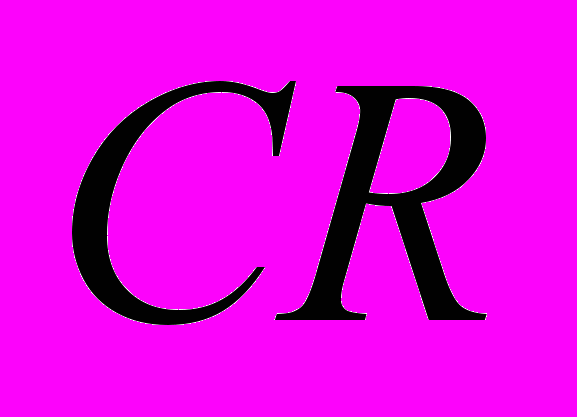=20 раз. Если разметить бинарное изображение с выделенными областями, провести его разметку, т.е. пронумеровать области, то по каналу связи можно передавать только содержимое стробов, охватывающих области. При этом простейший формат потока данных может иметь следующий вид:

Начало кадра101; строб1: координаты левого верхнего края строба1, содержимое строба1; ….. строб3: координаты левого верхнего края строба3, содержимое строба3; Начало кадра102; …



Рис. 3. Динамическая составляющая сцены – движущиеся объекты


Содержимое стробов может быть закодировано алгоритмами кодирования длин строк (RLE), с помощью кодовой книги (LZW), с помощью вейвлет-преобразования и т.п. К уменьшению объема данных также приводит простое масштабирование (уменьшение площади изображения) и изменение битности изображения.

На качество синтезированного изображения влияют: яркостные искажения во входном кадре (тени, помехи), яркостные искажения в изображении оценки фона (в силу инерционности процесса оценивания), яркостные искажения в изображении альфа-канала (выделение недвигавшихся областей и пропуск двигавшихся областей), используемые алгоритмы сжатия содержимого стробов.

Литература

1. Кузьмин С.А. Обработка видеоинформации в системе мониторинга транспортных потоков//Доклады 9-й Международной конференции и выставки «Цифровая обработка сигналов и её применение». – М., 2007. Т. 2. С. 361-365.
   
2. Кузьмин С.А. Исследование помехоустойчивости ранговых операторов//Доклады 10-й Международной конференции и выставки «Цифровая обработка сигналов и её применение». – М., 2008. Т. 2. С. 501-504.
   

SEMANTICAL COMPRESSION OF VIDEOS CONTAINING MOVING VEHICLES

Kuzmin S.

Saint-Petersburg State University of Aerospace Instrumentation

Video monitoring systems are widely used, because of two reasons: their cost is decreasing and their abilities are increasing during last years. In the same time, the sizes of video clips, which needs to be digitized and transmitted to consumer, rapidly became huge with the increase of quantity of used cameras, frame resolution and temporal sampling frequency. This means, what the task of compression is very important in the case of transmitting video to consumer. The compression shouldn’t severely decrease image quality, since consumer want to make right decisions.

Let us study the case of traffic flow monitoring, the cars are moving on the road in the field of view of the camera. In this task camera is immobilized about the road, what give us an opportunity to use the algorithm of background subtraction for video analysis. The Kalman filter was chosen as a method for background estimation.

Moving vehicles has high contrast about background, what give an opportunity to make segmentation of video frames, if background estimation is already calculated. Segmentation in this case is decision making process for each pixel about it class: “not a background”, background. The result of background subtraction is a binary image, called image of “moving regions”. The binary image of “moving contours” is calculated from current frame and background estimation. The threshold value for making binary images from difference images in chosen by original algorithm, which seek for the moment of transition to the horizontal part of probability function of pixel intensities. The filtered “moving regions” and “moving contours” images are combined by logical operation OR. The ranking operators are applied to the resulting image.

The possibility of compression is linked to the content of video: fast moving cars and almost static at the short time frame background, which represented by the background estimation image. This means, what information about moving objects should be transmitted very frequently, but background estimation can be updated with much longer period. Thus, we have moving regions and background estimation at transmitting side. We have to transmit background estimation image to the receiver side. This image will be modified for each frame by means of mating. The regions with moving objects would be inserted in then background estimation image. The mating is a method for combination of several images with the use of alpha channel. We can reduce the amount of transmitted information if we would send only regions of current frame, which would be inserted in background image at receiver side. We segment binary image (enumerate all the regions) and send to the consumer only content of boxes around moving regions. The content of regions can be encoded by any modern algorithm: RLE, LZW, wavelet and so on. The downscaling of image and reduction of intensity resolution (quantity of bits per color channel) also give reduction of amount of transmitted data.

