Рич Р. К. Политология. Методы исследования: Пер с англ. / Предисл. А. К. Соколова
| Вид материала | Анализ |
- Рич Р. К. Политология. Методы исследования: Пер с англ. / Предисл. А. К. Соколова, 6313.29kb.
- Н. Ю. Алексеенко под редакцией д-ра биол наук, 1890.25kb.
- Сорокин П. А. С 65 Человек. Цивилизация. Общество / Общ ред., сост и предисл., 11452.51kb.
- Дэвид Дайчес, 1633.42kb.
- Mathematics and the search for knowledge morris kline, 498.28kb.
- Указатель литературы по методам и методикам исследования общие вопросы психологического, 348.83kb.
- edo ru/site/index php?act=lib&id=186 Густав Эдмунд фон Грюнебаум Классический, 2844.73kb.
- «хм «Триада», 9393.37kb.
- Анастази А. А 64 Дифференциальная психология. Индивидуальные и групповые разли- чия, 11288.93kb.
- Шелтон Г. М. – Ортотрофия. Основы правильного питания, 3135.34kb.
14. СТАТИСТИКА I: АНАЛИЗ ОДНОМЕРНЫХ РАСПРЕДЕЛЕНИЙ
Зачастую в политологических исследованиях одни таблицы и графики не дают достаточных сведений о данных для успешного решения исследовательских задач. Иногда это проблема сложности (или слишком много градаций переменных, или слишком большой массив, или задействовано слишком много переменных, для того чтобы данные годились для непосредственного анализа), иногда – вопрос точности (степень различий небольших колебаний переменных может оказаться важной, а при оценке таблицы или схемы “на глазок” их бывает трудно уловить). В случаях, подобных нашему, когда нужен более глубокий анализ, ученые прибегают к статистическому анализу.
Статистика с этой точки зрения – это количественные значения, которые оценивают распределения градаций или взаимосвязи между переменными. Статистика является своего рода математической стенографией, дающей возможность визуально и с большой точностью оценить, что показывают (а иногда – что не показывают) данные. “Каковы политико-философские взгляды типичного студента колледжа? Всегда ли белые избиратели отличаются в своих партийных пристрастиях от негров? Какие действия или ситуации в мировом сообществе вероятнее всего могут привести к возникновению вооруженного конфликта? “Если мы располагаем верными данными для анализа, статистика в состоянии ответить как на эти, так и на многие другие вопросы.
Статистика чрезвычайно сложна. Однако так же верно и то, что многие из основных принципов и приемов статистического анализа необычайно просты, очень быстро запоминаются и могут увести вас в изучении вашего предмета гораздо дальше, чем вы думаете. Фактически если вы изучали алгебру в средней школе, то вы знаете о математике все, что вам понадобится; вы будете удивлены, насколько интуитивно очевидны многие математические выкладки. [c.392]
Следует уточнить, что эта глава и две последующие не научат вас ни всему тому, что можно узнать о статистике, ни даже всему тому, что можно узнать о конкретных статистических методах, которые мы будем обсуждать. Тем не менее к тому моменту, когда вы прочитаете эти главы, вы будете иметь достаточно полное представление о том, что такое статистическая процедура и как ее можно применять (или почему ее нужно применять); у вас также появится некоторое понимание того, что лежит за цифрами и подсчетами; вы сможете относительно легко применять некоторые специальные статистические методы. Все вместе эти навыки позволят вам использовать статистический анализ в своем исследовании и глубже и критичнее воспринимать то, что вы читаете в научных журналах и других политологических исследованиях.
Эту главу мы посвятим изучению статистических методов, которые позволят нам ответить на следующие вопросы о массиве данных: “Как выглядят одномерные распределения? Как выглядит типичная единица массива? Насколько она типична?”
В каждом случае мы рассмотрим различные статистические методы для различных типов измерения – номинального, порядкового и интервального. Из ссылка скрыта вы помните, что эти типы (уровни) отличаются один от другого тем, что первый просто дифференцирует категории, второй ранжирует их, в третьем устанавливается постоянный интервал различий между ними. Иными словами, цифры эминальной, порядковой и интервальной шкал есть различные виды цифр с разными свойствами. Если точнее, цифры номинального измерения мало содержательны, данные не очень много могут сказать нам. Поскольку они лишь разделяют объекты на группы и служат не более чем ярлыками для этих групп, их нельзя складывать или вычитать. Соответственно применить сложные методы статистического анализа к номинальным данным нельзя. (цифры же интервальных шкал гораздо более содержательны и точны, они несут гораздо больше информации о тех данных, которые они представляют. Их можно складывать, вычитать, возводить в квадрат и изменять по-всякому. В результате они дают возможность более гибкого подхода и применения более сложных методов анализа. Именно по этим причинам к разным уровням измерения [c.393] применяются разные методики. И именно по этим причинам, конечно, необходимо применять эти методики правильно. [c.394]
ИЗМЕРЕНИЕ СРЕДНЕЙ ТЕНДЕНЦИИ И ДИСПЕРСИИ
Для описания распределения признаков по значениям одной переменной используют два типа статистических процедур. Первый – измерение средней арифметической величины признака – помогает нам выявить наиболее типичные значения, одно или несколько, которые наилучшим способом представляют весь комплекс признаков по этой переменной. Вообразите, что нам сказали, будто так называемый средний американец – это “синий воротничок”, получивший среднее образование и вместе со своей женой имеющий в среднем 1,7 ребенка. Понятно, что не каждый американец отвечает этим требованиям, но если бросить на американцев этакий общий взгляд, то приведенный набор характеристик может оказаться весьма близким к тому общему впечатлению, которое у нас сложится. Вот именно такое представление об усредненном или типичном случае мы получаем при измерении средней арифметической величины. И именно это измерение было использовано при выявлении наиболее типичных свойств американцев.
Однако, как уже отмечалось, не все американцы обладают такими характеристиками. Многие являются “белыми воротничками”, либо специалистами, либо даже безработными, некоторые закончили только начальную школу, у других – более высокое образование, иные имеют 10 или 20 детей, другие же не женаты и детей не имеют. Иными словами, “типичный” американец представляет лишь среднюю тенденцию внутри совокупности, но не отражает точно каждый отдельный признак. Ну, а поскольку такой типичный признак найден, мы вправе задать вопросы:
“Насколько это типично? Насколько правильно эти усредненные признаки отражают распределение свойств всех единиц массива по данной переменной?” Мы ответим на них, если используем другой тип статистических расчетов – дисперсию. Измеряя дисперсию, мы узнаем, как колеблется (варьирует) отклонение от того среднего значения, которое мы нашли, в каких случаях можно быть уверенным, что наше среднее значимо, и не является ли отклонение [c.394] настолько большим, что наиболее типичный признак на самом деле не является репрезентативным для всей совокупности.
В связи с этим возникает важная проблема, которую дует обсудить, прежде чем двигаться куда-либо дальше. Статистика – это могучее средство анализа; она можно сказать о наших данных гораздо больше, чем можно выявить любым другим путем. Но сама по себе статистика бездумна. Можно произвести любые статистические счеты на любом массиве данных и, казалось бы, выжать из данных все до последней капли. Однако многие из этих “результатов” по двум причинам могут оказаться бессмысленными. Первую причину мы уже обсуждали, логика ее станет яснее по мере дальнейшего продвижения. Говоря проще, уровень сложности анализа может превосходить уровень сложности, заложенный в данных. Если выбранный нами метод требует сложить две цифры, а данные основаны на номинальной шкале, для которой неприемлема сама концепция сложения, то вообще-то механически можно сложить значения двух кодов, однако результат этого окажется бесполезным. Так, если код 1 представляет рабочих – “синих воротничков”, код 2 – “белых воротничков”, а 3 – специалистов, то мы, конечно, можем к ому прибавить два и получить три, но неужели мы действительно будем утверждать, что один рабочий – “синий воротничок” плюс один рабочий – “белый воротничок” равны одному специалисту? Конечно, нет.
Другая причина, по которой результаты статистические расчетов могут оказаться незначимыми, –это то, что одна статистика сама по себе часто не может представить всю картину целиком. Если единственный наиболее типичный уровень образования американцев – это средняя школа, но только 25% всего населения достигли этого уровня и остановились на нем, то насколько много в действительности может сказать нам это среднее значение? Не так уж много. И много ли вы знаете людей, которые действительно имеют 1,7 ребенка? Таким образом, хотя мы можем точно подсчитать и представить эти цифры, нельзя останавливаться только на них. Каждое измерение средней арифметической должно быть взвешено или оценено сопутствующим измерением дисперсии. И еще (мы обсудим это позже): всегда, когда мы имеем дело с [c.395] расчетами, каждое измерение взаимосвязей между двумя переменными следует сопровождать измерением статистической значимости, т.е. следует обозначить, насколько точно найденные величины представляют существенные связи между данными переменными. Таким образом, статистические расчеты должны не только соответствовать уровню измерений данных, но и быть существенно значимыми, если мы хотим получить от них максимум пользы.
Любое измерение средней тенденции и дисперсии основано на общей оценке градаций переменных и единиц массива, которая называется частотным распределением. Частотное распределение – это упорядоченный подсчет количества признаков по каждому значению какой-либо переменной. Представьте, например, что мы задали 100 респондентам вопрос об их занятии в настоящее время и затем распределили их ответы по типам. Тогда частотное распределение для переменной “тип занятий” может выглядеть так, как это показано в табл. 14.1.
Таблица 14.1.
Частотное распределение: типы занятий респондентов
| Код | Значение | Число случаев |
| 1 2 3 4 5 | “Синие воротнички” “Белые воротнички” Специалисты Фермеры Безработные | 25 23 22 20 10 |
В частотном распределении исследователь просто перечисляет все значения переменной и показывает, сколько имеется случаев каждого значения. Та же самая информация может быть представлена в виде гистограммы, как показано на рис. 14.1. Используя эту информацию, можно выделить наиболее типичный случай и определить его репрезентативность. [c.396]
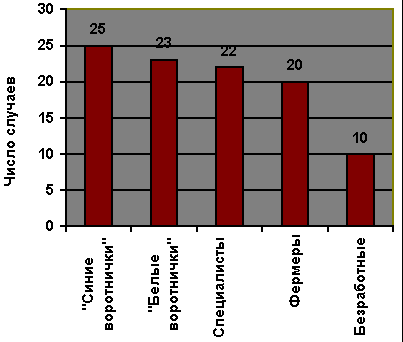
Рис. 14.1. Гистограмма: тип занятий респондентов
ИЗМЕРЕНИЯ ДЛЯ НОМИНАЛЬНЫХ ПЕРЕМЕННЫХ
Как мы уже отмечали, для различных уровней измерений подходят различные способы исчислений средней тенденции и дисперсии. Поскольку “тип занятий” – номинальная переменная, давайте начнем изучение этих [c.396] исчислений с рассмотрения статистических процедур, подходящих для номинального уровня измерения. На этом уровне, где цифры просто обозначают категории безотносительно к порядку их расположения, единственно возможный способ измерения средней тенденции – это исчисление моды. Мода – это просто наиболее часто встречающееся значение признака, т.е. то значение, которое наиболее часто может встречаться в серии зарегистрированных наблюдений. В нашем случае это первая категория, или градация “синие воротнички”. Можно назвать их как модой, так и модальной категорией. (Распределенное, в котором две категории имеются с наибольшим количеством случаев, называется распределением с двумя модами, или бимодальным, возможно также распределение с большим количеством таких категорий.) Таким образом, занятие уровня “синих воротничков” являются наиболее типичными в нашем примере из 100 человек.
Однако ясно, что большинство людей в этом примере (фактически ровно75%) не являются рабочими – “синими воротничками”, т.е., даже если мы выделим наиболее типичное значение в данном распределении, информация эта не обязательно полностью верно отражает картину. [c.397] Более точно об этом можно судить, если подсчитать точное значение дисперсии для номинального уровня измерений, или коэффициент вариации, формула которого выглядит следующим образом:
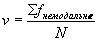
или
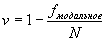 ,
,где Σfнемодальное – сумма всех случаев, не входящих в модальную категорию;
fмодальное – количество случаев в модальной категории;
N – общее число случаев.
По сути дела, этот коэффициент дает нам процентную долю всех признаков, которые не входят в модальную категорию. В нашем примере
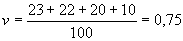 ,
,или, по упрощенной формуле
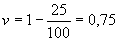
Значение коэффициента вариации колеблется между 0 (когда все случаи принимают одно и то же значение) и 1–1/N (когда каждый случай имеет свое значение). В общем, чем меньше коэффициент вариации, тем типичнее, или значимее (верно отражает картину), мода. В случае бимодального или многомодального распределения произвольно выбирается одно модальное значение в зависимости от целей подсчетов, и v определяется так, как указано выше. [c.398]
ИЗМЕРЕНИЯ ДЛЯ ПОРЯДКОВЫХ ПЕРЕМЕННЫХ
Когда мы имеем дело с данными порядкового уровня, у нас несколько больше информации, поскольку коды представляют не только категоризацию, но и относительные позиции, или ранжирование. Выбор способа измерения средней тенденции и дисперсии должен как отражать этот факт, так и использовать его возможности. Наиболее подходящий способ измерения средней тенденции для порядковых данных – медиана. Медиана – это просто [c.398] значение среднего признака в упорядоченном ряду, признака, до и после которого находится равное количество признаков. Вычисление медианы, таким образом, требует лишь того, чтобы отсчитать с обоих концов частотного распределения равное количество признаков, до тех пор пока не доберемся до срединного, и определить затем его значение. Там, где имеется нечетное количество признаков, можно определить единственный срединный признак (например, для 99 признаков 50-я от любого конца частотного распределения единица будет иметь 49 единиц как до, так и после себя). Значение этого признака и будет медианой. Если же N (количество единиц) – четное число, появятся две срединных единицы (например, для 100 единиц 50-я и 51-я вместе составят середину распределения). Если обе эти единицы имеют одно и то же значение, оно и будет медианой. Если у них разные значения, медианой будет среднее арифметическое между ними. Поясним на примере. Давайте рассмотрим распределение уровней образования по трем массивам данных (см. табл. 14.2).
Таблица 14.2.
Уровни образования по трем массивам
| Код | Значение | Массив 1 (N) | Массив 2 (N) | Массив 3 (N) |
| 1 2 3 4 5 Общее количество | Начальная школа Незаконченное среднее Законченное среднее Высшее Наличие ученой степени | 25 23 22 20 9 99 | 25 23 22 20 10 100 | 10 40 35 10 5 100 |
В первом массиве выделяется один срединный случай (50-й с обоих концов), определяется его значение и выясняется, таким образом, что медианный уровень образования – 3, или “законченное среднее”. Во втором массиве выделяется два срединных случая (50-й и 51-й с обоих концов), определяется, что каждый принимает одно и то же значение и выясняется, что медиана – опять 3. В третьем [c.399] же массиве срединные случаи включают две категории – “незаконченное среднее” и “законченное среднее”. Здесь медианой является среднее арифметическое между этими величинами, т.е. (2+3)/2=2,5. Поскольку дробные значения не имеют смысла в порядковом измерении, эта цифра просто говорит нам, что середина распределения лежит примерно между 2 и 3.
Любой из нескольких способов измерения дисперсии для порядковых переменных, называемый квантильным рангом, показывает, насколько плотно различные значения группируются вокруг медианы, или опять насколько типична или репрезентативна медиана для распределения в целом. Квантиль – это мера положения внутри распределения. Например, персентиль делит совокупность на 100 равных частей так, что первый персентиль – это такая точка или значение в этой совокупности (считая от меньшего значения вверх), ниже которой находится 1% всех случаев, второй персентиль – такая точка или значение, ниже которой находятся 2% всех признаков, и т. д. Или, используя более знакомый пример, будущий студент колледжа, достигший 85-го персентиля в тесте на эрудицию, дошел до уровня более высокого, чем уровни 85% всех, кто проходил тест. Точно так же дециль делит совокупность на десятки (например, третий дециль – это точка, ниже которой находятся 30% случаев), квантиль – на пятые доли, квартиль – на четвертые. Любой из них может быть использован для определения дисперсии вокруг медианы, хотя децильные и квантильные ранги наиболее часто встречаются в литературе.
Давайте проиллюстрируем эту процедуру на примере квантильных рангов. Квантильный ранг (q) определяется следующим образом:
q = q4 – q1,
где q4 – четвертый квантиль (значение, ниже которого находится 4/5, или 80% всех признаков);
q1 – первый квантиль (значение, ниже которого находится 1/5 или 20% всех признаков).
Чем меньше степень разброса величин между этими двумя точками совокупности, тем плотнее сгруппированы случаи вокруг медианы и тем точнее представляет медиана всю совокупность. В массиве 2 табл. 14.2, например, [c.400] где N=100, можно подсчитать q, определив 81 признак (ниже которого расположено 80% признаков) и 21 признак (ниже которого расположены 20% признаков), начиная наш счет внутри частотного распределения с наименьших значений. Затем мы вычитаем значение 21-го признака из значения 81-го (q=q4–q1=4–1=3) и получаем квантильный ранг. В массиве 3 подобные вычисления выделяют квантильный ранг, равный единице (q=3–2=1), показывающий при сравнении, что это распределение лучше представлено своей медианой, равной 2,5, чем второй массив – своей медианой, равной 3. Внимательное изучение этих двух частотных распределений подтвердит обоснованность нашего вывода.
Одна из трудностей интерпретации квантильных рангов состоит в том, что они чрезвычайно чувствительны к изменениям в количестве градаций самой переменной. Чем больше градаций, тем вероятнее большой разброс. Поэтому квантильные ранги не всегда поддаются интерпретации в случаях сравнений переменных с разным количеством градаций. Для переменных же с примерно равным количеством градаций для построчного или постолбцового сравнения значений одной переменной или для какого-либо абсолютного измерения разброса вокруг медианы они вполне подходят. [c.401]
ИЗМЕРЕНИЯ ДЛЯ ИНТЕРВАЛЬНЫХ ПЕРЕМЕННЫХ
Интервальные данные, безусловно, предоставляют нам наиболее полную информацию, включая категоризацию, ранжирование и установление интервалов. Интервальные значения могут быть подвержены любым арифметическим манипуляциям. Следовательно, приступая к исчислению средней тенденции и дисперсии для интервальных данных, мы можем и должны принять эту информацию о дополнительных возможностях во внимание.
Главной единицей для интервальных данных является среднее геометрическое, определяющее место средней точки в распределении с позиций как количества признаков от каждого конца распределения до этой точки, так и расстояние между ней и каждым признаком. Среднее геометрическое распределения – это то, что многие люди обычно связывают с термином “среднее арифметическое”. [c.401]
Давайте проиллюстрируем нахождение среднего геометрического на примере рис. 14.2. Если все признаки распределения имеют равные веса, и если они расположены на оси на равных интервалах так, что признаки с предельными значениями наиболее удалены от средней точки в том или ином направлении, а случаи с равными значениями расположены на равноудаленных точках оси, то точка среднего геометрического будет расположена в центре оси, где сумма значений и интервалов одной стороны уравновешивается суммой значений и интервалов другой. Как ясно из рисунка, и веса (количество признаков) и интервалы (крайние значения) важны для определения среднего геометрического.
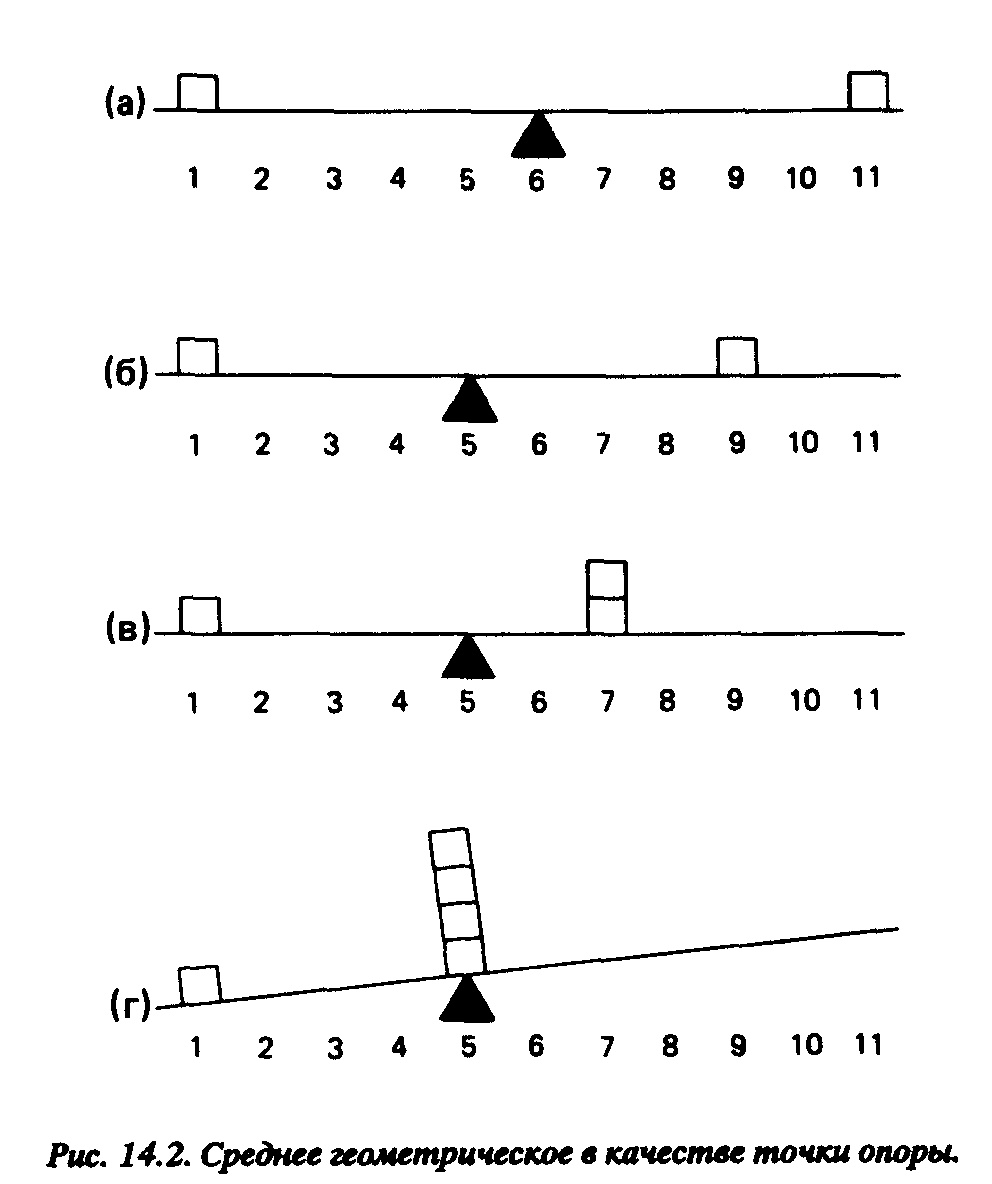
Среднее геометрическое распределения, обозначаемое
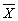 , вычисляется по следующей формуле:
, вычисляется по следующей формуле: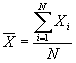 ,
,где Xi – значение каждого отдельного случая;
N – количество случаев;
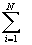 – знак суммы всех отдельных случаев от 1 до N.
– знак суммы всех отдельных случаев от 1 до N.Обратите внимание, что в подсчете используются сложение и деление, два арифметических действия, произведенные с самими значениями (что принципиально отлично от просто количества случаев с данным значением) с подсчетом как всех значений, так и интервалов. Это и есть те манипуляционные возможности, которые отличают интервальные данные от данных более низких уровней измерения.
Заметьте, однако, еще, что, как видно из рис. 14.2г, именно потому, что среднее геометрическое чувствительно к величине интервалов, оно зависит от кренов в распределении, которые вызываются наличием одного или нескольких предельных признаков. Иными словами, небольшое количество случаев с предельными значениями может сделать значение среднего геометрического меньше или больше, чем реально репрезентативное. Давайте посмотрим, как это может получиться.
