Geum.ru

Лабораторная работа 5 Вариант 11 Цель работы

Вид материалаЛабораторная работа
Подобный материал:
Лабораторная работа 5

Вариант 11


Цель работы: изучение методов численного интегрирования обыкновенных дифференциальных уравнений, практическое решение уравнений на ЭВМ, сравнительный анализ рассмотренных методов.

Данная работа выполнена с помощью метода Рунге-Кутта четвертого порядка точности, а так же были определены максимальная и интегральная оценки.

Метод Рунге–Кутта часто применяется для решения дифференциальных уравнений и систем уравнений из-за его высокой точности. Отличительная особенность метода – уточнение наклона интегральной кривой за счет вычисления производной не только в начале текущего отрезка интегрирования, но и, например, в середине отрезка или четырехкратное вычисление производных в методе четвертого порядка.

Рассмотрим задачу Коши

.

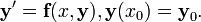Тогда значение в следующей точке вычисляется по формуле:



где h — величина шага сетки по x и вычисление нового значение проходит в четыре этапа:









Исходя из вышеизложенного, для решения систем дифференциальных уравнений выбирается наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений.

-     этот  метод является одноступенчатым и одношаговым

-     требует  информацию только  об одной  точке

-     имеет небольшую погрешность

-     значение функции  рассчитывается  при каждом шаге.

Необходимо определить близость полученного заданным методом решения к точному значению с помощью оценок:

Максимальной оценки

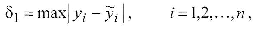
Интегральной оценки

Здесь- точное решение,- полученное приближенное решение.


Блок-схема