Рабочая программа и контрольные задания для студентов заочного обучения по специальности 260704 «Технология текстильных изделий» специализации «Прядение натуральных и химических волокон»
| Вид материала | Рабочая программа |
- Методические указания и контрольные задания по дисциплине «Прядение натуральных и химических, 192.91kb.
- Рабочая программа и контрольные задания для студентов заочного обучения специальности, 137.08kb.
- «Технология текстильных изделий», 2132.56kb.
- Программа и контрольные задания для учащихся-заочников по специальности 2-36, 764.27kb.
- Программа, методические указания и контрольные задания для студентов 5 курса заочного, 2134.85kb.
- Программа, методические указания и контрольные задания для студентов 5 курса заочного, 439.54kb.
- Программа и контрольные задания по учебной дисциплине по выбору «экономика переходного, 280.62kb.
- Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
- Методические указания Биохимия, 792.43kb.
- Рабочая программа, письменные консультации и контрольные задания для студентов специальностей, 715.54kb.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИИ И ДИЗАЙНА»
Кафедра технологии прядения и нетканых материалов
ОПТИМИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ПРЯДЕНИЯ НАТУРАЛЬНЫХ И ХИМИЧЕСКИХ ВОЛОКОН
Рабочая программа и контрольные задания для студентов заочного обучения по специальности 260704 «Технология текстильных изделий»
специализации «Прядение натуральных и химических волокон»
Составители:
О. М. Иванов
Б. С. Михайлов
Санкт-Петербург
2008
Утверждено
на заседании кафедры
04.09.2008 г.,
протокол № 1
Рецензент
А. А. Мороков
Оригинал подготовлен составителями.
Подписано в печать 10.11.2008 г. Формат 60 × 84 1/16.
Печать трафаретная. Усл. печ. л. 1,0. Тираж 50 экз. Заказ
Отпечатано в типографии СПГУТД
1
91028, С.-Петербург, ул. Моховая, 26.
ВВЕДЕНИЕ
Курс «Оптимизация технологических процессов прядения натуральных и химических волокон» имеет целью дать инженерам-технологам знания и навыки в области оптимизации процессов прядения, что позволит будущим специалистам квалифицированно выбирать наиболее эффективные технологические режимы выпуска продукции, обеспечивая ее конкурентоспособность на рынке.
Для эффективного проведения технологических процессов прядильного производства в целях повышения производительности, снижения затрат энергии, труда и сырья необходимо уметь определять оптимальные режимы работы объектов.
Для изучения методов оптимизации технологических процессов прядильного производства в учебные планы включена дисциплина "Оптимизация технологических процессов". На эту дисциплину отводится 90 ч в 9-м семестре (по дневной форме обучения).
В результате изучения данной дисциплины студенты должны знать основные методы оптимизации технологических процессов прядильного производства, уметь определять оптимальные параметры заправки оборудования и планов прядения.
Изучение данной дисциплины опирается на знание студентами высшей математики, вычислительной техники, теории и технологии процессов прядильного производства.
Учебным планом предусмотрено изучение дисциплины на VI курсе в следующем объеме:
| Обучение заочное | Всего по дисциплине |
| Всего часов в том числе: | 90 |
| Лекции, ч | 8 |
| Лабораторные занятия, ч | 8 |
| Курс | 6 |
| Зачет (семестр) | - |
| Экзамен (семестр) | 11 |
| Самостоятельная работа, ч | 74 |
Объем курса охватывает материал, который сообщается студентам на лекциях, лабораторных занятиях и консультациях, изучается самостоятельно в процессе работы с учебной литературой, в том числе и специальной по технологии нетканых материалов.
РАБОЧАЯ ПРОГРАММА
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ. НАИМЕНОВАНИЕ ТЕМ
И ИХ СОДЕРЖАНИЕ
Тема 1. Общие вопросы методов оптимизации
Основные понятия, используемые в задачах оптимизации технологических процессов. Виды оптимизационных задач. Примеры некоторых типов задач. Основные классы оптимизационных задач.
Тема 2. Методы безусловной одномерной оптимизации целевой функции
Аналитический и численные методы определения оптимума в задачах одномерной оптимизации.
Тема 3. Методы безусловной оптимизации многомерной целевой функции
Аналитический метод определения оптимума в задачах безусловной многомерной оптимизации (с использованием измерения Сильвестра).
Об алгоритмах численных методов многомерной безусловной оптимизации.
Тема 4. Решение оптимизационных задач на основе диссоциативно-шагового метода
Тема 5. Линейное программирование
Оптимизационные задачи, решаемые в прядильном производстве методами линейного программирования. Геометрический метод и симплекс метод решения задач линейного программирования.
Тема 6. Нелинейное программирование
Геометрический смысл и особенности задач нелинейного программирования. примеры задач, решаемых данным методом.
Тема 7. Использование метода неопределенных множителей Лагранжа в задачах условной многомерной оптимизации
Сущность метода. Примеры задач, решаемых в прядильном производстве данным методом.
Тема 8. Метод динамического программирования
Сущность метода. Примеры применения данного метода в прядильном производстве.
Тема 9. Оптимизация технологических процессов прядильного
производства на основе динамических моделей
Оптимизация процессов преобразования развеса питающего продукта на шляпочных и валичных чесальных машинах.
Оптимизация процесса вытягивания первого рода (при перематывании нитей, при растяжении жгута на штапелирующих машинах).
Оптимизация процесса ложного кручения на самокруточных прядильных машинах, на машинах для текстурирования химических нитей и др.
Тема 10. Использование метода статистического имитационного моделирования при оптимизации процесса штапелирования жгутов на ленточно-разрывных машинах
Распределение времени по дисциплине.
| Форма обучения | Номер семестра | Всего часов | Из них | ||
| лекции | лабораторные занятия | самостоятельная работа | |||
| Заочная | 11 | 90 | 8 | 8 | 74 |
СОДЕРЖАНИЕ ЛАБОРАТОРНЫХ ЗАНЯТИЙ
| 1. | Поиск экстремума функции одной переменной на заданном интервале для произвольной функции. |
| 2. | Многомерная безусловная оптимизация. |
| 3. | Выбор оптимального состава смеси по стоимости методом линейного программирования. |
| 4. | Применение диссоциативно-шагового метода. |
| 5. | Выбор оптимального плана производства материалов разных артикулов. |
| 6. | Использование методов нелинейного программирования. |
| 7. | Метод неопределенных множителей Лагранжа. |
| 8. 9. 10. 11. 12. | Динамическое программирование. Оптимизация ложного кручения. Оптимизация процесса вытягивания первого ряда. Преобразование развеса продукта на чесальной машине. Оптимизация процесса штапелирования. |
САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ
Самостоятельная работа включает изучение учебной и научно-технической литературы, посвященной тематике дисциплины, но выходящей за рамки лекционного курса; выполнение расчетных заданий по определению влияния различных параметров на технологические процессы производства нетканых материалов; решение задач оптимизации различных технологических процессов производства нетканых материалов.
ПРАВИЛА ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
В соответствии с учебным планом по курсу «Оптимизация технологических процессов» студенты заочного отделения выполняют контрольное задание. Необходимые данные для выполнения контрольного задания студенты выбирают самостоятельно по номеру варианта, который соответствует последней цифре номера зачетной книжки. Контрольное задание по курсу «Оптимизация технологических процессов» должно быть выполнено студентом до его прибытия на лабораторно-экзаменационную сессию. Выполнение контрольной работы и получение зачета по ней является необходимым предварительным условием допуска студента к очным занятиям по данному курсу.
Для выполнения контрольного задания прежде всего надо уяснить, что требует каждый вопрос задания, подобрать соответствующий материал и, изучив его, дать обоснованные ответы.
Каждый вариант состоит из 4 заданий.
Первый вопрос требует описания основных положений, областей использования методов оптимизации.
Для ответа на эти вопросы следует использовать материалы из учебника –Севастьянов А. Г., Севастьянов П. А. «Оптимизация механико-технологических процессов текстильной промышленности» (М., 1991), изложенные на с. 6 33 (общие вопросы оптимизации); 39 – 45, 58 68 (аналитические методы определения оптимума); 93 102 (примеры задач, решаемых методами линейного программирования); 131 142 (особенности задач нелинейного программирования); 150 160 (использование метода неопределенных множителей Лагранжа), 181 189 (диссоциативно-шаговый метод), 218 226 (решение многокритериальных задач).
Второй вопрос требует проведения расчетов по заданной математической модели для построения зависимостей критерия оптимизации y от факторов x1 и x2.
В третьем вопросе следует использовать аналитический метод оптимизации. Он изложен на с. 39 41, 58 62 (использование критерия Сильвестра) указанного выше учебника. Можно использовать также учебник по высшей математике «Дифференциальное и интегральное исчисления» (см. параграф « Максимум и минимум функции нескольких переменных» в главе «Функции нескольких переменных»).
Четвертый вопрос требует ознакомления с ДШМ методом оптимизации, изложенным на с. 181 189 учебника Севостьянова А. Г.и Севостьянова П. А.
Содержание отчета должно показать, что студент ясно представляет себе существо вопроса. Качество выполненной работы оценивается по полноте и правильности ответов на вопросы, правильности решения задач и по форме изложения.
Не зачтенное контрольное задание возвращается студенту для исправления ошибок и выполнения указаний проверяющего. Исправленное задание вторично представляется на проверку.
ВАРИАНТЫ ЗАДАНИЙ
Вариант 1
1. Сущность методов безусловной оптимизации, линейного и нелинейного программирования, диссоциативно-шагового метода, методов решения многокритериальных задач.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
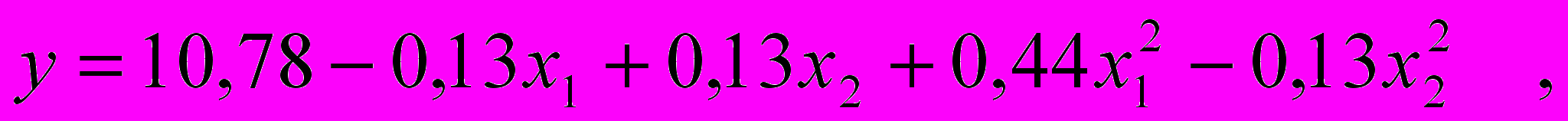
где y – относительная разрывная нагрузка одиночной нити, сН/текс;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1 и x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно - шаговый метод поиска оптимума.
Вариант 2
1. Основные понятия, используемые в задачах оптимизации. Виды оптимизационных задач. Привести примеры использования методов безусловной оптимизации, линейного и нелинейного программирования, диссоциативно-шагового метода, методов решения многокритериальных задач..
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
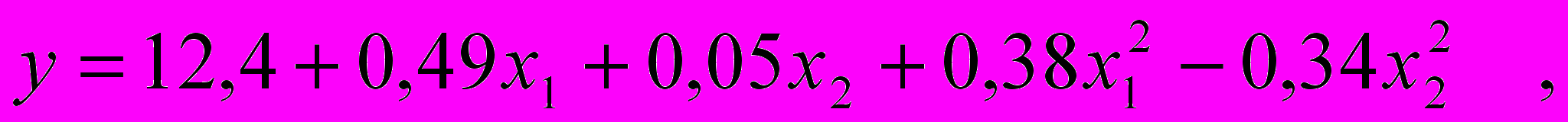
где y – коэффициент вариации по разрывной нагрузке, %;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 3
1. Области применения методов оптимизации. Привести примеры.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
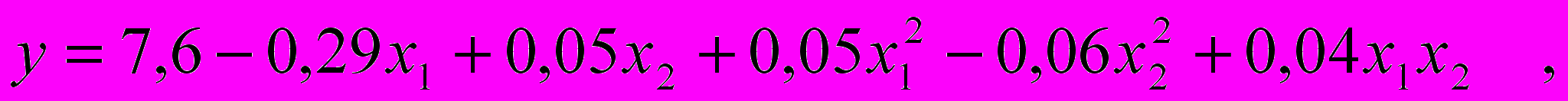
где y – относительная разрывная нагрузка нити по пасме, сН/текс;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 4
1. Сущность методов безусловной оптимизации, линейного и нелинейного программирования, диссоциативно-шагового метода, методов решения многокритериальных задач.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
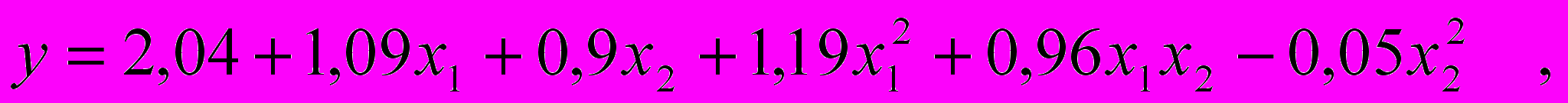
где y – коэффициент вариации по линейной плотности (по пасме), %;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 5
1. Области применения методов оптимизации. Привести примеры.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
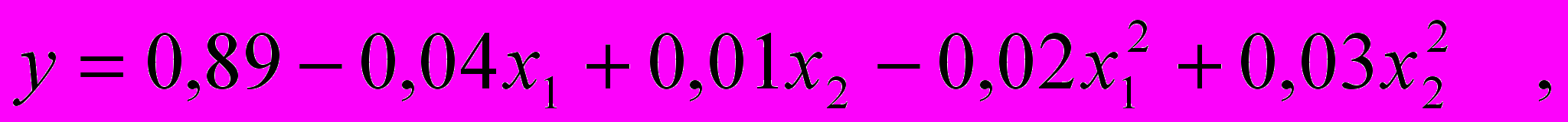
где y – показатель качества по одиночной нити;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 6
1. Основные понятия, используемые в задачах оптимизации. Виды оптимизационных задач. Привести примеры использования методов безусловной оптимизации, линейного и нелинейного программирования, диссоциативно-шагового метода, методов решения многокритериальных задач.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
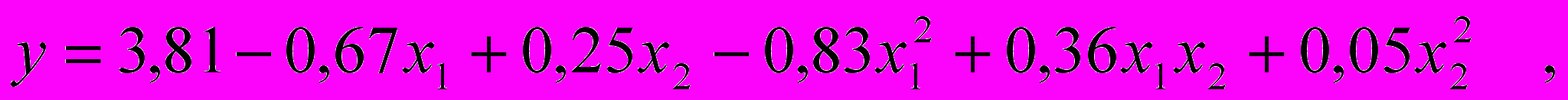
где y – показатель качества по пасме;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 7
1. Основные понятия, используемые в задачах оптимизации. Виды оптимизационных задач. Привести примеры использования методов безусловной оптимизации, линейного и нелинейного программирования, диссоциативно - шагового метода, методов решения многокритериальных задач.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
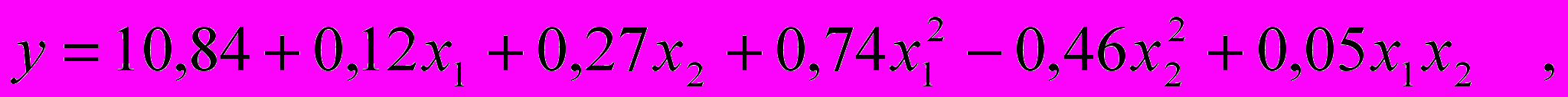
где y – коэффициент вариации пряжи по «устеру», %;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 8
1. Основные области применения методов оптимизации. Привести примеры.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
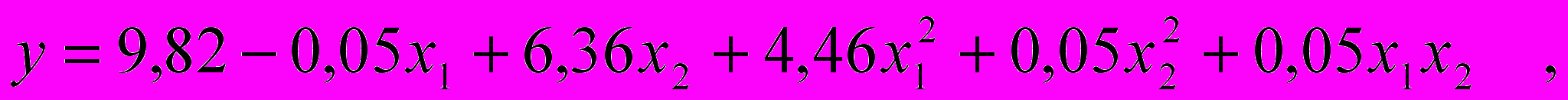
где y – число толстых мест на 1000 м пряжи;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 9
1. Сущность методов безусловной оптимизации, линейного и нелинейного программирования, диссоциативно-шагового метода, методов решения многокритериальных задач.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
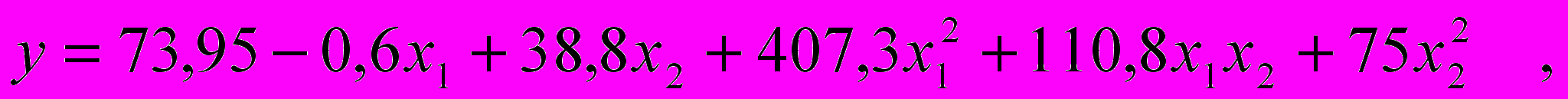
где y – число непсов на 1000 м пряжи;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодированном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Вариант 10
1. Области применения методов оптимизации в технологии прядения. Привести примеры.
2. В результате проведения эксперимента получено следующее регрессионное уравнение:
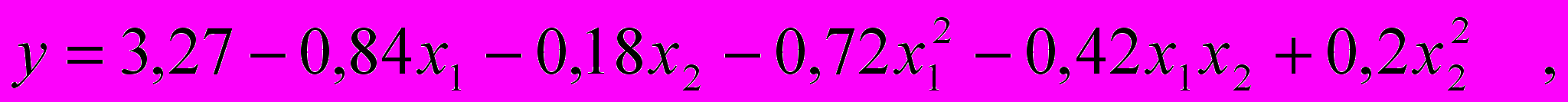
где y – обобщенный показатель качества пряжи (ОПК), который определяется:
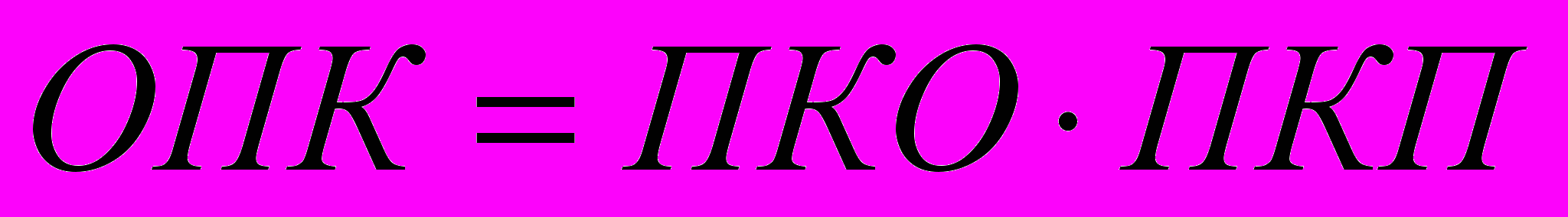 ,
, где ПКО – показатель качества по одиночной нити;
ПКП – показатель качества по пасме;
x1 – скорость шляпочного полотна;
x2 – частота вращения съемного барабана.
Уровни варьирования факторов x1, x2 приведены в таблице.
| Факторы | Условное обозначение (в кодирован- ном виде) | Уровни варьирования | ||
| -1 | 0 | +1 | ||
| Скорость шляпочного полотна, мм/мин | x1 | 90 | 120 | 150 |
| Частота вращения съемного барабана, мин-1 | x2 | 15,2 | 16,4 | 17,6 |
Используя приведенное уравнение, построить графики зависимости y от x1, x2. Дать анализ полученных зависимостей.
3. Найти оптимальный режим работы чесальной машины, используя аналитический метод определения оптимума.
4. Найти оптимальный режим работы чесальной машины, используя диссоциативно-шаговый метод поиска оптимума.
Библиографический список
- Иванов, О. М. Моделирование и оптимизация технологических процессов производства нетканых материалов: метод. указания к лаб. работам/ О. М. Иванов. – СПб.: СПГУТД, 2000.
- Бакустина, Р. С. Расчет характеристик свойств волокон в смеси/
Р. С. Бакустина. – СПб.: СПГУТД, 2001.
- Михайлов, Б. С. Модели оптимизации смеси волокон/ Б. С. Михайлов. – СПб.: СПГУТД, 2004.
- Смирнов, Г. П. Формирование волокнистых холстов в производстве нетканых материалов/ Г. П. Смирнов, А. В. Просвирницын. – СПб.: СПГУТД, 2004.
- Иванов, О. М. Нетканые материалы. Методы оптимизации технологических процессов/ О. М. Иванов. – СПб.: СПГУТД, 2007.
О
ПТИМИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ПРЯДЕНИЯ НАТУРАЛЬНЫХ И ХИМИЧЕСКИХ ВОЛОКОН
Составители:
О. М. Иванов
 Б. С. Михайлов
Б. С. Михайлов