Geum.ru

Методические указания и контрольные задания для студентов-заочников Салаватского индустриального колледжа специальности №140613

Вид материалаМетодические указания
Модель внешней среды организации
К такого рода задачам относятся, например, следующие
Рисунок 5 - Набор точек аппроксимирован с помощью многочленов первого и второго порядка
Вопросы для самоконтроля
Номер и наименование занятия
Подобный материал:
1   2   3   4   5   6

Модель внешней среды организации


При создании модели организации как управляемой системы нельзя не учитывать процессы взаимодействия предприятия и окру­жающей его внешней среды. При этом следует выделить и обосновать параметры, достоверно отображающие взаимосвязи между элемента­
ми внешней среды и составляющими внутренней среды организации. Таких взаимосвязей существует большое множество, но для построе­ния моделей берутся только те, которые обладают наибольшей устой­чивостью и имеют решающее значение для функционирования организации. Обычно во внешней среде, с которой взаимодействует предприя­тие, выделяют два уровня:
  1. микросреда — среда прямого воздействия;
  2. макросреда — среда косвенного воздействия.

К микросреде относятся:
    • поставщики;
    • партнеры;
    • акционеры;
    • потребители продукции;
    • конкуренты;
    • органы власти и государственного управления;
    • общественные организации;
    • законы и законодательные акты.
    • Макросреда учитывает следующие факторы:
    • политические;
    • экономические;
    • демографические;
    • социально-культурные;
    • научно-технические;
    • природные и географические.

Характеристиками внешней среды являются следующие парамет­ры:
      1. взаимосвязанность всех факторов — определяет степень влия­ния одного фактора на другие;
      2. сложность — определяет число и разнообразие факторов, ока­зывающих значительное влияние;
      3. динамичность — определяет относительную скорость измене­ния внешней среды;
      4. неопределенность — характеризует относительное количествоинформации о внешней среде и уверенность в ее достоверности.

К внешней среде организации также относятся инфраструктура (транспорт, связь и пр.), средства массовой информации и т. п.

Рассмотрение взаимодействия предприятия с внешней средой его функционирования является одним из ключевых моментов при пост­роении модели и организации системы управления. Ни одна органи­зация не может существовать в изоляции от множества других пред­приятий, фирм, учреждений. Каждое из них оказывает определенное воздействие на процесс функционирования данной организации. Например, несвоевременные поставки сырья (из-за задержек со сто­роны поставщиков или транспортных проблем) могут нарушить сро­ки поставок готовой продукции на рынки сбыта. Все подобные мо­менты должны быть учтены, для этого в системе управления должны иметься необходимые механизмы для корректировки таких ситуаций и сведения к минимуму их негативных последствий.

Анализ внешней среды предприятия служит инструментом, с по­мощью которого можно контролировать внешние факторы, для про­гнозирования потенциальных угроз развитию организации, а также открывающихся новых возможностей.

При анализе экономических факторов прежде всего необходимо рассматривать темпы инфляции, изменение налоговых ставок, меж­дународный платежный баланс, уровень занятости населения в це­лом и в данной отрасли, платежеспособность организаций. Кроме того, следует учитывать жизненные циклы различных товаров и услуг, уро­вень конкуренции в отрасли, изменение доли рынка, занимаемой организацией, емкость рынка.

При анализе политических факторов рекомендуется отслеживать состояние соглашений по торговле между странами, таможенной по­литики, нормативных актов местных и центральных органов власти, правового регулирования экономики. Также надо обращать внима­ние на состояние и изменения в антимонопольном законодательстве, кредитную политику местных властей и т. п.

В области научно-технического развития необходимо следить за появлением новых технологий, материалов, изменениях в способах сбора и обработки информации, совершенствованием средств связи и вычислительной техники. Подобные изменения могут оказывать как положительное, так и негативное воздействие. Последний случай свя­зан с появлением новых перспективных технологий у конкурентов, что может нарушить конкурентоспособность вашей организации.

Анализ факторов конкуренции означает постоянный контроль со стороны организации за действиями конкурентов. Здесь можно вы­делить четыре диагностические зоны: анализ будущих целей конку­рентов, оценка их текущей стратегии, оценка перспектив развития конкурентов и отрасли в целом, изучение сильных и слабых сторон конкурентов. Слежение за деятельностью конкурентов позволяет организации быть готовой к потенциальным угрозам ее развитию и функ­ционированию.

Анализ социальных факторов включает в себя отслеживание из­менений общественных ценностей, социальных установок, отноше­ний в обществе и т. п. В условиях нестабильной экономики социальная сфера порождает множество проблем, с которыми приходится стал­киваться организации. Для того чтобы эффективно решать подобные проблемы, организация как социальная система должна изменяться, приспосабливаться к внешней среде.

Анализ внешней среды обычно завершается составлением переч­ня как внешних опасностей, так и возможностей, открывающихся перед организацией. Форма представления данного перечня может быть различной. Как правило, он включает в себя взвешенные факто­ры в упорядоченной последовательности по степени их воздействия на предприятие и оценку данного воздействия. Для наглядности вне­шние факторы в этом перечне можно расположить в два столбца: в одном — факторы, создающие благоприятные возможности для орга­низации, в другом — угрожающие факторы, расположенные по сте­пени убывания воздействия.


Вопросы для самоконтроля:
  1. Понятие процесса моделирования.
  2. Классификация моделей.
  3. Этапы построения.


Тема 2.4 Специализированное прикладное обеспечение: математический пакет MathCad, EWB


Студент должен:


знать:

• назначение и принцип действия математического пакета MathCad.


уметь:.

• работать с математическим пакетом MathCad.


Назначение математического пакета MalhCad, основные возможности.


Методические указания


Вычислительная мощь компьютера позволяет использовать его как средство авто­матизации научной работы. Для решения сложных расчетных задач используют программы, написанные специально. В то же время, в научной работе встречается широкий спектр задач ограниченной сложности, для решения которых можно ис­пользовать универсальные средства.

К такого рода задачам относятся, например, следующие:
  • подготовка научно-технических документов, содержащих текст и формулы,
    записанные в Привычной для специалистов форме;
  • вычисление результатов математических операций, в которых участвуют числовые константы, переменные и размерные физические величины;
  • операции с векторами и матрицами;
  • решение уравнений и систем уравнений (неравенств);
  • статистические расчеты и анализ данных;
  • построение двумерных и трехмерных графиков;
  • тождественные преобразования выражений (в том числе упрощение), аналитическое решение уравнений и систем;
  • дифференцирование и интегрирование, аналитическое и численное;
  • решение дифференциальных уравнений;
  • проведение серий расчетов с разными значениями начальных условий и дру­гих параметров.

К универсальным программам, пригодным для решения таких задач, относится, например, программа Mathcad. Это автоматизированная система, позволяющая динамически обрабатывать данные в числовом и аналитическом (формульном) виде. Программа Mathcad сочетает в себе возможности проведения расчетов и подготовки форматированных научных и технических документов.

Научно-технические документы обычно содержат формулы, результаты расчетов в виде таблиц данных или графиков, текстовые комментарии или описания, другие иллюстрации. В программе Mathcad им соответствуют два вида объектов: формулы и текстовые блоки. Формулы вычисляются с использованием числовых констант, переменных, функций (стандартных и определенных пользователем), а также обще­принятых обозначений математических операций. Введенные в документ Mathcad формулы автоматически приводятся к стандартной научно-технической форме записи. Графики, которые автоматически строятся на основе результатов расчетов, также рассматриваются как формулы. Комментарии, описания и иллюстрации размещаются в текстовых блоках, которые игнорируются при проведении расчетов.

Чтобы буквенные обозначения можно было использовать при расчетах по форму­лам, этим обозначениям должны быть сопоставлены числовые значения. В про­грамме Mathcad буквенные обозначения рассматриваются как переменные, и их значения задаются при помощи оператора присваивания (вводится символом «:»). Таким же образом можно задать числовые последовательности, аналитически опре­деленные функции, матрицы и векторы.

Если все значения переменных известны, то для вычисления числового значения выражения (скалярного, векторного или матричного) надо подставить все число­вые значения и произвести все заданные действия. В программе Mathcad для этого применяют оператор вычисления (вводится символом «=»). В ходе вычисления автоматически используются значения переменных и определения функций, задан­ные в документе ранее. Удобно задать значения известных параметров, провести вычисления с использованием аналитических формул, результат присвоить некото­рой переменной, а затем использовать оператор вычисления для вывода значения этой переменной.

Изменение значения любой переменной, коррекция любой формулы означает, что все расчеты, зависящие от этой величины, необходимо проделать заново. Такая необходимость возникает при выборе подходящих значений параметров или условий, поиске оптимального варианта, исследовании зависимости результата от начальных условий. Электронный документ, подготовленный в программе MathCad, готов к подобной ситуации. При изменении какой-либо формулы программа автоматически производит необходимые вычисления, обновляя изменившиеся значения и графики. Например, если документ содержит формулы х := 4; 4х = 2, то, изменив значение переменной х, мы сразу же увидим, что изменился и результат расчета: х := 9; 4х = 3.

При проведении расчетов с использованием реальных физических величин учи­тывают их размерность. Чтобы расчет был корректен, все данные должны быть приведены в одну систему единиц — в этом случае результат расчетов получится в этой же системе. Здесь скрывается характерный источник ошибок при расчетах вручную. В программе Mathcad единицы измерения (в любой системе) присоединяют к значению величины с помощью знака умножения. Данные автоматически преобразуются в одну и ту же систему единиц (по умолчанию СИ) и обрабатыва­ются в этом виде. Размерный результат выдается вместе с полученной единицей измерения. Например:

v := 100-kph t :<= 0.5-yr (kph — километры в час, уr — годы) s := v-t s = 4.383-108 m (результат получен в метрах)

При работе с матрицами приходится применять такие операции, как сложение матриц, умножение, транспонирование. Часто возникает необходимость в обраще­нии матриц и в декомпозиции (разложении в произведение матриц специального вида). Для квадратных матриц представляет интерес поиск собственных значений и собственных векторов. Программа Mathcad позволяет выполнить все эти опера­ции с помощью стандартных обозначений математических операторов (сложение, умножение) или встроенных функций.

Уравнения и системы уравнений, возникающие в практических задачах, обычно можно решить только численно. Методы численного решения реализованы и в программе Mathcad. Блок уравнений и неравенств, требующих решения, записы­вается после ключевого слова given (дано). При записи уравнений используется знак логического равенства (комбинация клавиш CTRL+=). Значения переменных, удовлетворяющие системе уравнений и неравенств, находятся с помощью стан­дартной функции find.

При обработке результатов экспериментов часто встречаются задачи статистического анализа серий данных. Для такого рода задач программа Mathcad предоставляет средства интерполяции данных, пред­сказания дальнейшего поведения функции, а также построения функций заданного вида, наилучшим образом соответствую­щих имеющемуся набору данных.




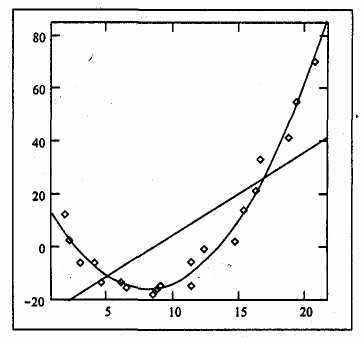
Рисунок 5 - Набор точек аппроксимирован с помощью многочленов первого и второго порядка


При статистическом анализе можно также использовать стандартные функции рас­пределения вероятности и генераторы слу­чайных величин с заданным распределе­нием.

При аналитических вычислениях результат получают в нечисловой форме в результате тождественных преобразований выражений. Простейшие преобразования — это раскрытие скобок, приведение подобных членов, применение тригонометрических тождеств.

Более сложные преобразования позволяют находить аналитические решения неко­торых уравнений и систем. Для такого рода вычислений в программе Mathcad используют оператор аналитического вычисления (клавиатурная комбинация CTRL+.), а также команды меню Symbolics (Аналитические вычисления). Перемен­ные при аналитических вычислениях рассматриваются как неопределенные пара­метры. Результат можно использовать для анализа решения при различных значе­ниях этих переменных. При аналитическом решении уравнений и систем за одну операцию можно найти все существующие решения.

Дифференцирование и интегрирование заданных функций вручную — обычно несложная, но трудоемкая операция. В программе Mathcad для вычисления про­изводной, а также неопределенных и определенных интегралов могут использо­ваться символические вычисления с помощью меню Symbolics ► Variable (Аналити­ческие вычисления ► Переменная). Если функция не задана аналитически или не позволяет получить первообразную в виде формулы, имеется возможность числен­ного дифференцирования и численного расчета определенных интегралов. Напри­мер, при вычислении интеграла

Численные методы используют и для решения дифференциальных уравнений. С помощью программы Mathcad можно решать уравнения и системы уравнений первого порядка с заданными начальными условиями. Уравнение более высокого порядка надо сначала преобразовать в систему уравнений первого порядка.


Вопросы для самоконтроля:
  1. Назначение математического пакета
  2. MalhCad, основные возможности.



4 ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ


№ темы

Номер и наименование занятия

2.1
Практическая работа 1. Знакомство с программой MathCad

2.2
Практическая работа 2. Построение и анализ простейших математических операций в MathCad

2.3
Практическая работа 3. Функции. Интервальная переменная

2.4
Практическая работа 4. Графики. Вычисление сумм и произведений