Задача использования ресурсов

Вид материала

Задача

Подобный материал:

• Информационные услуги сети Интернет Ресурс, 111.01kb.
• Методика анализа трудовых ресурсов 6 Анализ использования трудовых ресурсов ООО «Викинг», 35.11kb.
• Отчетный год, 372.6kb.
• За курс 9 класса билет, 42.57kb.
• И операций по проверке финансовых и связанных с ними вопросов деятельности хозяйствующих, 30.04kb.
• Технико-экономическое обоснование использования котельных на альтернативных видах топлива, 61.96kb.
• О возможности использования природных ресурсов в целях ускорения социально-экономического, 46.91kb.
• Анализ использования трудовых ресурсов, 136.48kb.
• Брановский Ю. С. Использование цифровых образовательных ресурсов на лекциях, 61kb.
• Планирование и прогнозирование использования природных ресурсов. Природные ресурсы, 30.51kb.

Задача использования ресурсов


Постановка задачи


Для изготовления нескольких видов продукции P₁, Р₂, ..., Р_n используют m видов ресурсов S₁, S₂, ..., S_т. Это могут быть различ­ные материалы, электроэнергия, полуфабрикаты и т.п. Объем каждого вида ресурсов ограничен и известен (b₁,. b₂, …, b_m).

Известно также a_ij ( i = 1, 2, …, m, j = 1, 2, ..., n) - количество каждого i-го вида ресурса, расходуемого на производство единицы j-го вида продукции. Кроме того, известна прибыль, получаемая от реализации единицы каждого вида продукции (с₁, с₂, ..., с_n),

Условия задачи можно представить в виде табл. 1.1.

Таблица 1.1

		aij
Питательное	Объём	aij
вещество	ресурсов	P1	P2	…	Pn
S1	b1	a11	a12	…	a1n
S2	b2	a12 aij	a22	…	a2n
...	…	…	…	…	…
Sт	bm	am1	am2	…	amn
Прибыль		c1	С c2	…	cn

Пусть х_j ( j = 1, 2, …, n.) - количество каждого вида продукции, которое необходимо произвести.

Для первого ресурса имеет место неравенство-ограничение


a₁₁ х_{1 +} a₁₂ х _{2 + … +} a_1n х_{n >=} b₁


Аналогичные неравенства будут и для остальных видов ресурсов. Сле­дует учитывать также, что все значения х. > 0, j = 1,2, ..., n.

Общая прибыль, получаемая от реализации всей продукции, может быть представлена как функция


Z(Х) = c₁ х₁ + с₂х₂ + ... + с_nх_n


Необходимо эту функцию максимизировать.


Таким образом, математическая модель задачи использования ресурсов запишется в виде


Z(Х) = c₁ х₁ + с₂х₂ + ... + с_nх_n max,




a₁₁ х_{1 +} a₁₂ х _{2 + … +} a_1n х_{n <=} b₁

a₂₁ х_{1 +} a₂₂ х _{2 + … +} a_2n х_{n <=} b₂

………………………………………

a_m1 х_{1 +} a_m2 х _{2 + … +} a_mn х_{n <=} b_m


х_j >= 0, j = 1, 2, …, n.


В более компактной форме целевую функцию и систему ограниче­ний можно записать, используя знак суммирования,


Z(Х) =


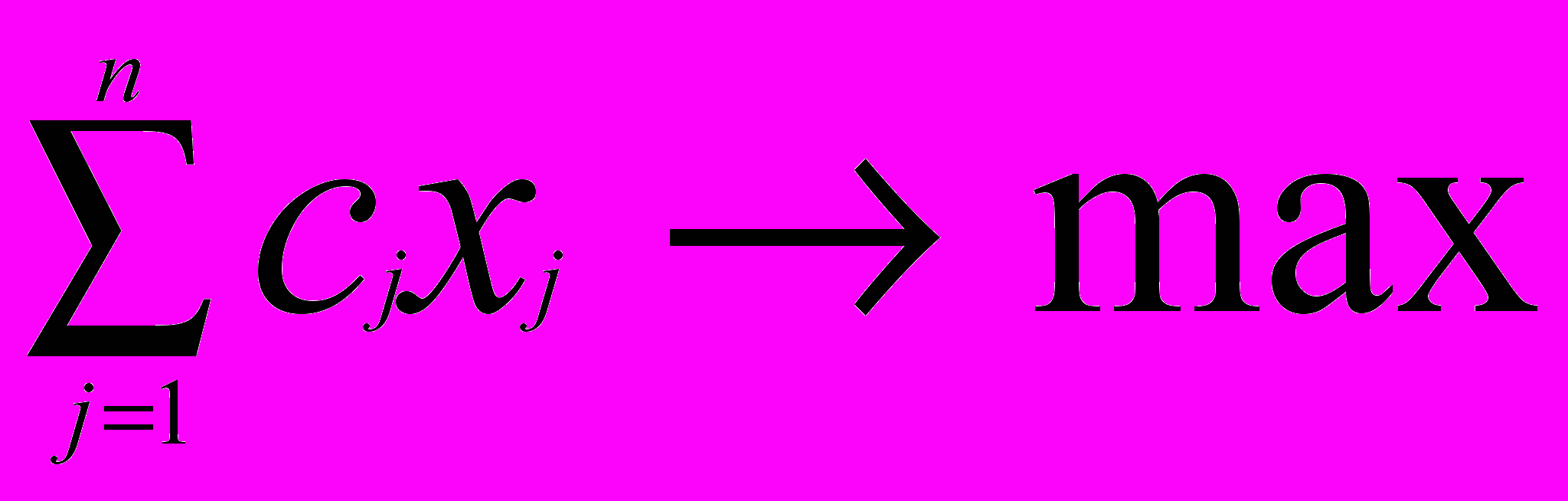
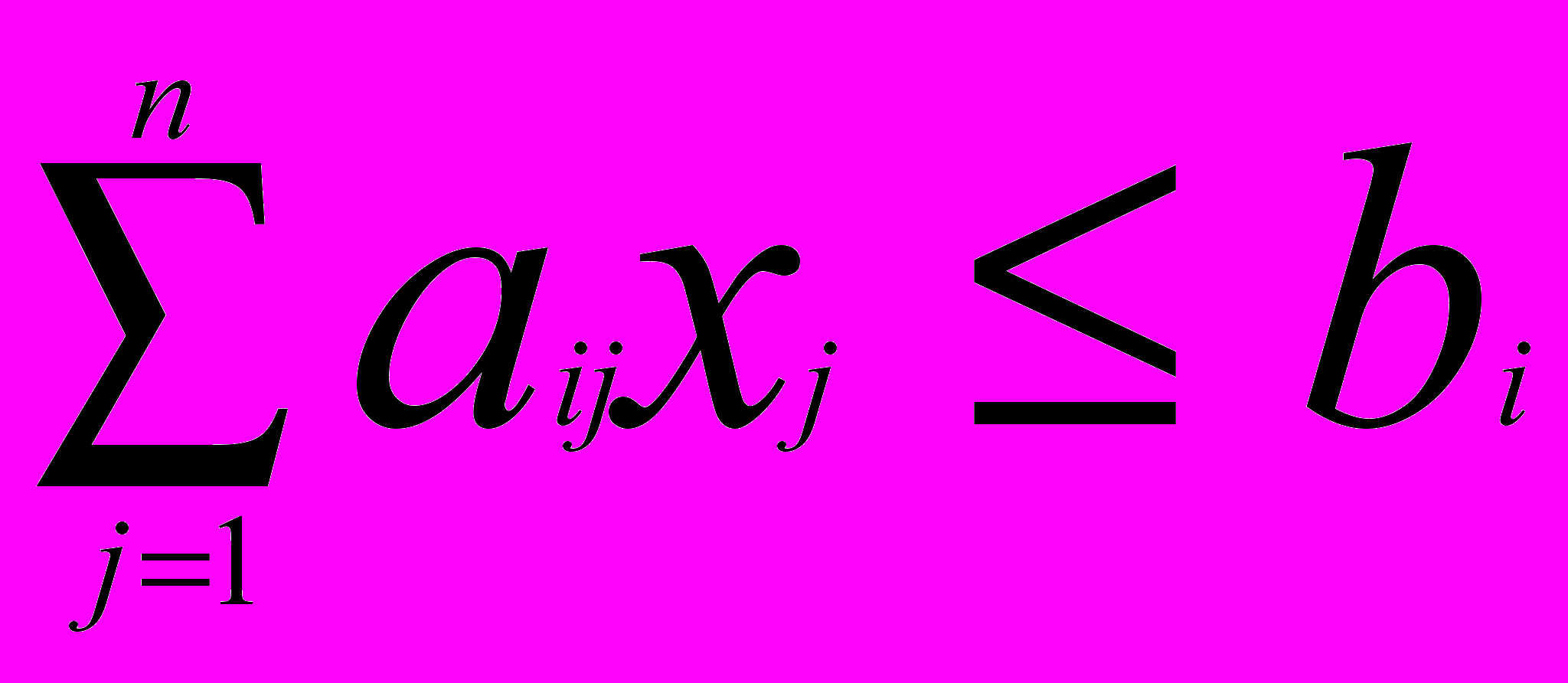, i = 1, 2, …, m,


х_j >= 0, j = 1, 2, …, n.


Задача о составлении рациона питания


Постановка задачи


Требуется составить ежедневный рацион питания животного на осно­ве имеющихся видов кормов так, чтобы общая стоимость использован­ных кормов была минимальной. При этом животное не должно полу­чать менее определенного количества питательных веществ, например, таких, как жиры, углеводы, белки, витамины и т.п.

Каждый вид корма содержит разную комбинацию этих веществ. Из­вестна цена единицы веса каждого корма.

Пусть имеются n различных кормов (продуктов) P₁, Р₂, ..., Р_n и пере­чень из т необходимых питательных веществ S₁, S₂, ..., S_т. Обозначим через a_ij содержание (в весовых единицах) i-го питательного вещества в единице j-го корма, а через b_i минимальную суточную потребность жи­вотного в i-м питательном веществе. Через х_j обозначим количество каж­дого вида корма в ежедневном рационе. Очевидно, что х_j >= 0.

Условия задачи можно представить в виде табл. 1.2.

Таблица 1.2

	aij
Питательное					Суточная
вещество	P1	P2	…	Pn	потребность
S1	a11	a12	…	a1n	b1
S2	a12 aij	a22	…	a2n	b2
...	…	…	…	…	…
Sт	am1	am2	…	amn	bm
Стоимость 1 кг	c1	С c2	…	cn	-
1 кг корма

Для первого вида питательного вещества неравенство-ограничение примет вид

a₁₁ х_{1 +} a₁₂ х _{2 + … +} a_1n х_{n >=} b₁


Аналогично запишутся неравенства и для остальных питательных веществ.

Общие затраты на весь рацион питания животного можно найти на основе линейной функции


Z(Х) = c₁ х₁ + с₂х₂ + ... + с_nх_n


Эту функцию нужно минимизировать.

Итак, математическая модель задачи составления рациона питания имеет вид


Z(Х) = c₁ х₁ + с₂х₂ + ... + с_nх_n min,




a₁₁ х_{1 +} a₁₂ х _{2 + … +} a_1n х_{n >=} b₁

a₂₁ х_{1 +} a₂₂ х _{2 + … +} a_2n х_{n >=} b₂

………………………………………

a_m1 х_{1 +} a_m2 х _{2 + … +} a_mn х_{n >=} b_m


х_j >= 0, j = 1, 2, …, n.